New types of complex motion of a simple camphor boat

Abstract

We discuss the motion of a rectangular camphor boat, considering the position of a camphor pill in relation to the boat's stern as the control parameter. The boat moves because the pill releases surface active molecules that decrease the surface tension and support the motion. We introduce a new experimental system in which the boat rotates on a long arm around the axis located at the centre of a Petri dish; thus, the motion is restricted to a circle and can be studied under stationary conditions for a long time. The experiments confirmed two previously reported modes of motion: continuous motion when the pill was located at the boat edge and pulsating (intermittent) motion if it was close to the boat centre (Suematsu et al., J. Phys. Chem. C, 2010, 114(21), 9876–9882). For intermediate pill locations, we observed a new, unreported type of motion characterised by oscillating speed (i.e. oscillating motion). Different modes of motion can be observed for the same pill location. The experimental results are qualitatively confirmed using a simple reaction-diffusion model of the boat evolution used in the above-mentioned paper.

---

1 Introduction

Nonequilibrium systems where self-propelled objects exhibit collective motion are classified as examples of active matter, and they have been intensively investigated for a few decades.^1–3 Studies on active matter extend beyond physical and chemical systems as they cover the evolution of cell population, a flock of birds, a school of fish, and even crowds of people.^4,5 The self-propelled motion of a single object has also attracted wide attention because it can be essential to understand collective behaviour. To extract physical aspects of self-propelled motion, a non-biological self-propelled object is suitable for investigation, because it is more controllable compared with complex biological systems. Many types of non-biological self-propelled objects have been reported so far, e.g. Janus particles,^6–9 swimming droplets,^10–15 Quincke rollers,^16,17 and so on.

A camphor boat made of a boat-shaped piece of floating material with a piece of camphor at its stern is a spectacular example of a system that transforms the chemical energy of surface-active molecules into the kinetic energy of a floating object.^18–25 It is difficult to tell when and where the first camphor boats were studied,^26,27 but definitely there were toys in the Edo period in Japan.²⁸ The boat motion can be explained considering the flux of camphor molecules from the source to the air through a surface layer. Camphor is amphiphilic, and the water surface tension is a decreasing function of the camphor surface concentration.^21,29,30 The location of the camphor piece below the boat is asymmetric. Consequently, the camphor surface concentration is high in the stern region close to the camphor piece and low around the bow because most camphor molecules get dissipated before reaching the bow area. Therefore, the surface tension is high near the bow and low at the stern. The difference between the surface tensions at the bow and the stern defines the force acting on the boat. The location of the camphor piece determines this difference. One can consider the distance between the edge of the camphor piece and the stern as the control parameter and study what type of motion occurs depending on it.

If a camphor piece is located at the boat's stern, then the boat motion is continuous, and it is characterised by a constant speed. Only 12 years ago, Nakata and collaborators reported another type of possible boat motion.³¹ When the camphor piece was located at a distance from the stern, they observed the pulsating (intermittent) motion characterised by narrow peaks of high speed separated by long time intervals when the boat did not move. However, the experiments were performed with boats freely moving inside a Petri dish (15.5 cm). The typical speeds of the considered boats were a few cm s⁻¹, which meant that, in the reported experiments, the boat collided with dish walls a few seconds after it was placed on the water surface. Having in mind strong perturbations of boat velocity in collisions, we anticipate that the used experimental setup does not allow for verification if the observed type of motion is stable or not.

In this paper, we report results obtained using a new experimental setup with a boat that can rotate on a long arm around the axis located at the centre of the Petri dish (cf.Fig. 1). Therefore, the boat trajectory is one-dimensional and it can be studied under stationary conditions for more than 1 hour. Our experiments confirmed two types of previously reported motion: continuous motion when the camphor source is located at the boat edge and pulsating motion if the pill is close to the centre. At the intermediate distances between the pill and the boat edge, we observed a new, unreported type of motion characterised by an oscillating speed that is always larger than zero. This type of motion is qualitatively different from pulsations because in the oscillating mode the boat never stops. Moreover, the period of oscillations weakly depends on the distance between the pill and the bow. We observed that modes of boat motion (continuous, oscillating and pulsating) are metastable and they can appear for the same source location. The experimental results are compared with simulations performed using a simple one-dimensional, reaction-diffusion model of boat motion with dimensionless parameters. For parameter values almost identical to those used in ref. 31, the transition between continuous motion and pulsations occurs in a narrow range of distances between the pill position and the boat edge. We found another set of dimensionless model parameters for which simulations confirm the existence of all three modes of motion observed in experiments.

Fig. 1 Illustration of the experimental setup for long-time continuous observation of unperturbed camphor boat motion. The diameter of the Petri dish is 20 cm. Panel (b) shows details of the axis, arm, and boat. A black dot on the arm above the boat is used for location tracing. Panel (c) illustrates the boat from below, shows the location of the camphor pill, and defines the control parameter d of experiments representing the distance between the pill and the right edge for the boat located as illustrated. Panel (d) is a schematic illustration of the boat with its dimensions.

The manuscript is organised as follows. Section 2 reports experimental results and describes the types of motion observed for different locations of the camphor source. Section 3 presents the results of simulations and compares them with those of experiments. The final Section includes discussion of results and suggests perspectives for future studies.

2 Experiments

2.1 Experimental setup and data analysis

The experimental setup and the construction of a boat are illustrated in Fig. 1. The boat motion was observed in a Petri dish with a 20 cm diameter. The Petri dish was filled with MilliQ water to obtain a 4 mm water layer. An l = 15 mm long boat was folded from a 0.05 mm thin aluminum sheet into the shape shown in Fig. 1(c and d). The boat width was 4 mm, and the bends on each boat side were 2 mm high. These bends were supposed to reduce the spread of the camphor in the direction perpendicular to the long side of the boat. Thus, the boat construction was identical to that described in ref. 31 A disk-shaped camphor pill with a radius of r = 1.5 mm and a height of 1 mm pressed in a pill maker from commercially available (1R)-Camphor (98% purity, Sigma-Aldrich). It was glued below the boat using LOCTITE 454 glue (Henkel). The distance d between the boat edge and the camphor disk indicated in Fig. 1(d) was the control parameter in our experiments. For d = 0 mm, the pill touches the boat edge. If d = 6 mm, then the pill is centrally located below the boat. If d > 6 mm, then the camphor disk is on the other side of the boat centre and the boat rotation in the inverse direction can be anticipated. The boat was fixed at the end of a 70 mm long arm attached to the vertical axis (a 0.8 mm steel needle was used) glued at the dish centre. The arm was lifted above the water level (cf.Fig. 1(b)), and thus the boat could rotate around the axis with low friction. The perimeter of the circle that represented the boat trajectory was circa 44 cm. The boat motion was recorded using a SONY NEX VG20EH digital camera at a rate of f = 25 fps.

The recorded movie was divided into frames and digitised using the ffmpeg³² and ImageJ³³ software to extract the position of the black dot centre (cf.Fig. 1(b)) as a function of the frame number. This was the basic quantity for the analysis of experimental results. The coordinates of the dot centre undergo fluctuations because, in the process of digitisation, the number of pixels associated with the dot can be different at various frames. Another source of noise affecting the dot trajectory comes from the difference between the diameters of the axis and the arm hole. To ensure low friction rotation, the hole in the arm is by 0.2 mm larger than the axis diameter. This can produce uncontrollable shifts in the dot position. The final data processing was performed using the Mathematica software.³⁴ Knowing the axis location, we can express the boat location in the radial coordinates (R,ϕ). The plot of radius R(n) as a function of the frame number n brings important information on the quality of data analysis. In a typical case, R(n) had a noisy character and the amplitude of radii was below 0.05 mm. The angular velocity ω(n) corresponding to the frame #n was obtained from the angular change of dot locations on frames #(n + 1) and #(n − 1):

The boat speed at the frame n, corresponding to time t [s] = n/f, was calculated as v(n) = ω(n)R(n). The clockwise and counter clockwise motions are distinguished by speed sign (negative and positive, respectively). Finally, all quantities describing the motion are transformed to functions of real time.

2.2 Experimental results

Let us start the presentation of the experimental results with an example of continuous motion illustrated in Fig. 2. It covers over half an hour-long observation of the boat motion for d = 2.5 mm. Fig. 2(a) presents the values of speed calculated for all frames as a function of time. It can be seen that the speed is systematically decreasing with time. The decrease was fast at the initial stage of the experiment (t < 200 s) and next slowed down. In our opinion, it is related to the continuous dissolution of camphor in water and the fact that the contribution of the dissolved camphor molecules to the surface layer decreases the overall surface tension which in turn would decrease the magnitude of surface tension gradients induced by the pill. The function v(t) has a large dispersion of the order of 10 mm s⁻¹ resulting from large fluctuations in the instant speed value. Three colour fragments of the v(t) curve represent 10 s long time intervals, as illustrated in Fig. 2(b). They start at times t₁ = 100 s (green), t₂ = 1000 s (blue) and t₃ = 2000 s (purple). In each of these intervals, the boat speed showed a qualitatively similar, random behaviour. As expected, the speed averaged over the whole 10 s interval was decreasing with time, and it was equal to 24.8 mm s⁻¹, 21.0 mm s⁻¹ and 18.9 mm s⁻¹ in the above-mentioned intervals, respectively. On the other hand, the standard deviations of speed in these intervals were the same and equal to 1.73 mm s⁻¹, 1.75 mm s⁻¹ and 1.71 mm s⁻¹, respectively.

Fig. 2 (a)The boat speed as a function of time in the continuous motion observed for d = 2.5 mm. The coloured parts of plotted v(t) are expanded in (b) showing 10 s long fragments of results starting at times t₁ = 100 s (green), t₂ = 1000 s (blue) and t₃ = 2000 s (purple). A short part of the movie showing this experiment is included in the ESI† as the “SI-continuous-L2-2p5mm.mp4” file.

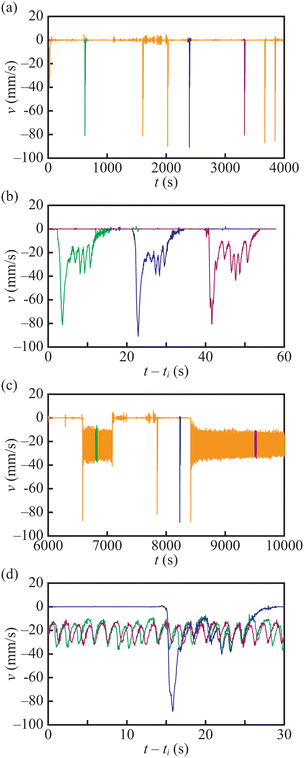
Fig. 3 illustrates the case when the continuous mode of motion co-exists with the oscillating one. The analysed experiment was almost 2 hours long. As shown in Fig. 2(a), we see that speed decreases with time. Three colour fragments of the v(t) plot represent 10 s long time intervals expanded in Fig. 3(b). They start at times t₁ = 500 s (green), t₂ = 2500 s (blue) and t₃ = 5500 s (purple). The boat speed averaged over the 10 s interval was equal to 29.0 mm s⁻¹, 24.8 mm s⁻¹ and 25.7 mm s⁻¹, respectively. The results shown in Fig. 3(a) differ qualitatively from those shown in Fig. 2(a) because the standard deviation of speed was not constant but significantly increased to around t = 1000 s and decreased to the initial values of t > 4000 s. The values of standard deviation in the marked intervals were equal to 2.19 mm s⁻¹, 4.44 mm s⁻¹, and 1.94 mm s⁻¹. Fig. 3(b) relates this change with the character of motion. At the beginning and at the end of the experiment, the motion is continuous, and it is characterised by a similar speed and dispersion as found for d = 2.5 mm. Around t = 2500 s, regular oscillations of speed with the amplitude of 10 mm s⁻¹ and the period of 1 s are observed. It is worthwhile to emphasize that the oscillating mode of motion is different from the pulsating (intermittent) mode of motion as described in ref. 31 because the boat speed is always significantly greater than zero.

Fig. 3 (a) The boat speed as a function of time observed for d = 3.0 mm. Three coloured parts of the v(t) plot are expanded in (b) showing 10 s long fragments of results starting at times t₁ = 500 s (green), t₂ = 2500 s (blue) and t₃ = 5500 s (purple). (c) The boat speed as a function of time in the subinterval [1500 s, 4000 s] when oscillating motion was observed. The coloured parts of v(t) shown in (c) are expanded in (d) illustrating 10 s long fragments of v(t) starting at times t₁ = 1904.0 s (green), t₂ = 2903.3 s (blue) and t₃ = 5504.5 s (purple). A short part of the movie from this experiment is included in the ESI† as the “SI-oscillating-small-amplitude-L5-3mm.mp4” file.

Fig. 3(c and d) present a more detailed analysis of the oscillating mode observed for d = 3 mm. Locations of time intervals for the detailed plots are shown in Fig. 3(d). As before, they are 10 s long and start at times t₁ = 1904.0 s (green), t₂ = 2903.3 s (blue) and t₃ = 5504.5 s (purple). The precise selection of the initial times synchronises locations of speed maxima within the short time interval. Fig. 3(d) shows that both the amplitude (∼ 15 mm s⁻¹) and period of oscillations (∼ 1.1 s) remain the same during the whole 1 h long time interval when the boat motion is oscillating. We did not observe a decrease in the average speed in the oscillating mode. The average speeds in 10 s long intervals starting at times given in brackets were 25.0 mm s⁻¹ (1900 s), 24.8 mm s⁻¹ (2500 s), 23.8 mm s⁻¹ (2903.3 s), and 24.5 mm s⁻¹ (3903.5 s). The values of standard deviation were equal to 4.71 mm s⁻¹ (1900 s), 4.44 mm s⁻¹ (2500 s), 4.50 mm s⁻¹ (2903.3 s) and 3.73 mm s⁻¹ (3903.5 s). On the basis of the results shown in Fig. 3, we can then conclude that the observed oscillating mode of motion is metastable and can co-exist with the continuous motion for some values of the control parameter d.

For yet larger distances between the pill and the boat edge, a pulsating motion in which sharp pulses of speed were separated by time intervals when the boat was still (intermittent motion in ref. 31 terminology) appeared. The results of a long experiment in which such a type of motion is observed are shown in Fig. 4. In this case, d = 8 mm, which means that the pill is located 4 mm away from the left edge of the boat (cf.Fig. 1(d)) and the boat rotates clockwise. Fig. 4(a) illustrates the motion observed during the first hour of the experiment. The burst of motion lasts for circa 20 s, and the following period of standstill is a few hundred seconds long. As seen in Fig. 4(a), the dispersion of lengths of time intervals when the boat does not move is huge, from ∼ 100 s to over 1000 s. On the other hand, the bursts of speed are quite similar. Three coloured peaks of speed marked in Fig. 4(a) are magnified in Fig. 4(b) with t₁ = 620 s, t₂ = 2370 s and t₃ = 3285 s. The character of v(t) at different peaks is very similar. A large initial peak of ∼ 90 mm s⁻¹ is followed by a few small amplitude oscillations of speed before the boat stops. The small amplitude oscillations are similar to those illustrated in Fig. 3d. Fig. 4(c) illustrates the interesting phenomenon that the maximum peak velocity does not change in time, and after 2 hours of motion, it is the same as at the beginning of the experiment. At this stage of motion, the small amplitude oscillations appear to be more stable. After the first peak of speed observed at around 6600 s in Fig. 4(c) small oscillations continued for ∼ 8 minutes. Similar oscillations continued for over half an hour after the peak that appeared at around 8400 s. Fig. 4(d) compares v(t) in the oscillating motion observed within the intervals marked in Fig. 4(c) with the relaxation of a speed pulse. It confirms that small amplitude oscillations following a peak of speed are of the same type as metastable oscillations discussed above because they have the same amplitude and period. The average speeds in 30 s long intervals starting at times 6800 s and 9500 s were 20.5 mm s⁻¹ and 21.0 mm s⁻¹ with standard deviations of 7.3 mm s⁻¹ and 5.9 mm s⁻¹, respectively, and thus they are similar to those measured for d = 3 mm (cf.Fig. 4(d)). The results of Fig. 4(c) illustrate that oscillating motion and pulsating motion can co-exist for the boats characterised by the same value of d.

Fig. 4 The boat speed as a function of time observed for d = 8.0 mm. (a) The initial 4000 s long stage of the experiment when the pulsating motion is observed. Three coloured parts of v(t) plot are expanded in (b) showing 10 s long fragments of results starting at times t₁ = 620 s (green), t₂ = 2370 s (blue) and t₃ = 3285 s (purple). (c) The boat speed as a function of time for the late evolution t∈ [6000 s,10000 s] when pulsating motion and oscillating motion co-exist. The coloured parts of v(t) shown in (c) are expanded in (d) illustrating 30 s long fragments of v(t) starting at times t₁ = 6800 s (green), t₂ = 8215 s (blue) and t₃ = 9500 s (purple). A short part of the movie from this experiment is included in the SI as the “SI-pulsating-L5-8mm-x5.mp4” file.

Fig. 5 illustrates an interesting type of pulsating motion combined with the inversion of angular velocity. This type of motion is observed for the camphor pill located close to the boat centre. Fig. 5 plots the boat speed observed in a 260 s fragment of trajectory recorded 950 s after the experiment was initiated. At the initial stage, the pulsating motion was observed. Three coloured pulses of speed appearing at ∼ 10 s, ∼ 75 s and ∼ 240 s are expanded in Fig. 5(b). The time evolution of speed seems independent on the direction of motion. We believe that the inverse in the rotation direction results from interactions between the surface distribution of camphor and the residual flow of water below the boat. Let us assume that within a given pulse of speed, the boat moves to the left. It means that the concentration of camphor on the right end of the boat is larger than that on its left end. When the boat stops, a small, nonrelaxed flow from right to left may still exist because the boat is additionally held by arm friction. This flow can modify the distribution of camphor around the boat and reduce its concentration at the right end of the boat. As a result of such imbalance, the next pulse is inverted to the previous one. A similar mechanism of rotation inversion after a forced stop was observed for camphor-propelled rotors.^35,36

Fig. 5 The inversion of boat rotation observed for d = 7.0 mm. (a) The boat speed in the 260 s long time interval starting 950 s after the boat motion was initiated. Three coloured fragments of the v(t) plot expanded in (b) start at times t₁ = 958 s (green), t₂ = 1018 s (blue) and t₃ = 1164 s (purple). A movie illustrating this type of motion is included in the ESI† as the “SI-inversion-L3-7mm.mp4” file.

The experimental results show that, for small values of d, the continuous motion dominates. For larger d, it co-exists with an oscillating one, and for a pill located yet closer to the boat centre, the pulsating mode is observed. For example, for d = 3 mm, continuous motion co-exists with the oscillating one. For d = 8 mm (equivalent to the effective distance d_eff = min (d,(l − d − 2r)) = 4 mm), oscillating motion co-exists with the pulsating one. Table 1 summarises the results of many experiments where continuous and oscillatory motions were observed. We present values of the average speed v_av, the standard deviation of instantaneous speed, as well as the values of v_min and v_max. The values of v_min and v_max were selected such that over 90% of the instantaneous speed values belong to the interval [v_min, v_max]. Moreover, we included the statistics of speed values measured in a single experiment for different intervals of time to illustrate how the listed quantities change with time. We found that the probability distribution of instantaneous speed values nicely differentiates continuous motion from oscillatory motion. In the first case, the distribution is unimodal with a single, pronounced maximum, whereas, for the oscillatory motion, it is bimodal or flat in [v_min, v_max]. In Fig. 6(a), we plot the range of boat speeds observed for different types of motion at different d_eff. For all types of motion, the range of speeds strongly depends on the motion type but does not seem to depend on the value of d_eff. Fig. 6(b) illustrates the period of oscillating motion and the mean time between speed bursts in the pulsating mode. The period of oscillating motion slowly increases with d_eff whereas the average time between pulsed is a fast-increasing function of d_eff. Fig. 7(c and d) repeat information shown in Fig. 6(a and b) but present it with dimensionless variables d′ = d_eff/r, v′ = v/v₀ and T′ = T/ (r/v₀), where . The introduction of such dimensionless units allows us to compare experimental results with simulations based on arbitrarily selected parameters.

Table 1 The parameters characterising the boat speed obtained for different values of d_eff in continuous and oscillating modes of motion

d eff (mm)	Experiment ID	Time interval	v av mm s^−1	v min mm s^−1	v max mm s^−1	Standard deviation mm s^−1
Continuous
1	2-1	[0, 1450 s]	19.0	17.	21	1.2
2.5	2-2.5	[100 s, 1100 s]	22.4	18.	27	2.1
2.5	2-2.5	[1100 s, 2100 s]	20.2	17.	23	1.9
3	4-3	[0 s, 2000 s]	20.8	17.	25	2.4
3	5-3	[100 s, 900 s]	29.0	25.	33	2.5
3	5-3	[5100 s, 7100 s]	24.8	22.	29	1.9
4	5-4	[100 s, 1600 s]	22.2	19.	26	2.2
4	5-4	[1600 s, 3200 s]	20.9	17.	25	2.1
Oscillating
3	5-3	[1100 s, 4100 s]	24.6	16.	34	4.6
4	5-8	[6600 s, 7000 s]	20.7	10.	34	7.1
4	5-8	[8600 s, 11000 s]	21.2	12.	31	5.5
5	5-5	[0 s, 1000 s]	20.3	11.	30	5.5
5	5-5	[2000 s, 4000 s]	20.7	16.	26	3.3
5	5-7	[5240 s, 5640 s]	17.7	8.	32	7.2
5.5	5-6.5	[2805 s, 2815 s]	14.6	6.	25	6.4

---

Fig. 6 (a) The range of boat speeds observed for different modes of motion as a function of the distance d_eff. Red disks, blue squares, and green circles correspond to continuous, oscillating, and pulsating motion. (b) The period of oscillating motion and the mean time between speed bursts in the pulsating mode as a function of d_eff.

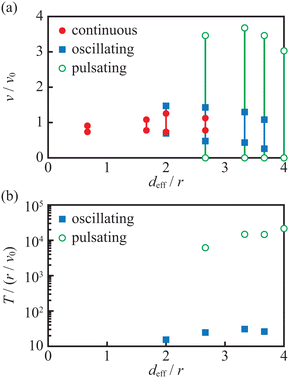Fig. 7 (a) The range of boat speeds observed for different modes of motion as a function of the distance d_eff/r. (b) The period of oscillating motion and the mean time between speed bursts in the pulsating mode as a function of d_eff/r. This plot shows the same results as in Fig. 6 but with dimensionless units. The notation of symbols used is the same as in Fig. 6.

3 Numerical simulations of camphor boat motion

In this section, we discuss if the types of motion observed in experiments can be confirmed in numerical simulations. The authors of ref. 31 demonstrated that the transition between the continuous motion and the pulsating one can be explained qualitatively using a model that combines the Newton equation of boat motion with one-dimensional reaction-diffusion for the time evolution of the camphor surface concentration. We show that with some modification of parameters, also oscillating motion is predicted by this model.

The basic equations in our theoretical approach describing the time evolution of the boat velocity v(τ) and the distribution of the camphor c(τ,y) in the interval Ω = [0,Λ] where the boat is located are

v′(τ) = Γ(c(τ, y_f)) − Γ(c(τ, y_b)) − μv(τ)(1 + η|v(τ)|) (2)

∂_τc(τ, y) = ∂_y(D(y)∂_yc(τ, y)) − v(τ)∂_yc(τ, y) − K(y)c(τ, y) +S(y) (3)

The model introduced in ref. 31 as well as the model used in our paper do not take into account the convection flow resulting from the concentration distribution of camphor (i.e., Marangoni flow). In such an approach, all hydrodynamic effects are roughly approximated by the effective diffusion constant. The reference system in the model used for our simulation is linked to the boat, not the dish as in ref. 31, and the convection term in eqn (3): −v(τ)∂_yc(τ, y) appears just as the result of coordinate transformation. Such a transformation is convenient computationally because the position of the boat is fixed and consequently the positions of the nodes in the corresponding mesh for Ω used to solve eqn (3) numerically are fixed with respect to the boat. Moreover, because of the choice of coordinates for eqn (3), it is more natural to consider the Newton eqn (2), governing the motion of the camphor boat, for the velocity v instead of for the position of the boat.

We consider the dimensionless version of this model, with the same scaling of variables as in ref. 31 which for example means that all distances in the model are given in the r unit and the time unit is scaled by r²/D₀, where D₀ is the diffusion coefficient of camphor at the free water surface. The concentration is scaled by its highest possible value.

Eqn (3) was solved under the non-flux conditions at the ends of the interval Ω:

∂_yc(τ, 0) = ∂_yc(τ, Λ) = 0, τ ∈ T (4)

In our calculations, Λ = 500 and the boat length l = 10.0. The mesh dimension used in our simulations Δy = 0.1 was half of that in ref. 31. Also, there was a big difference in the time steps: Δτ = 0.01 against Δτ = 0.5 in this paper. Such an increase in the time step was possible because we applied a fully implicit scheme to solve the diffusion-reaction-convection equation eqn (3), which is of course unconditionally stable. We also performed simulations for finer time steps receiving similar results. The system of both eqn (2) and (3) was solved using the variables v and c from the previous step to calculate them at the current time. We applied the same approximation method (the finite volume method) to the diffusion eqn (3). This was necessary to deal with the discontinuity of the diffusion coefficient across the boat edges.

The initial conditions for eqn (2) and (3) described the boat that was standing and there was no camphor at the water surface:

v(0) = 0 (5)

c(0, y) = 0, y ∈ Ω (6)

The function Γ is defined as follows:

The definition of Γ is crucial for quantitative simulations of the boat motion because it converts the camphor concentration into the surface tension. The function Γ should be decreasing, which reflects the reduction of the surface tension with the increasing camphor concentration. The parameters c₁ = 0.001, c₂ = 0.2005, c₃ = 0.4 define its shape. Here, as well as in the following part of the Section, we copy the values of parameters from ref. 31. The only two parameters that differ are Γ₁ and η and in the following we discuss our choice. There was a mistake in the value of parameter of Γ₁ in the definition given in ref. 31 as it implies that the surface tension increases with concentration. Our set of parameters includes just a single change that solves the problem: we used Γ₁ = 0.01 instead of Γ₁ = 1 for water sufficiently saturated with camphor, whereas Γ₀ = 0.1 holds its value. Using these values we obtained simulation results that were quantitatively comparable with previously published results. It is also worth mentioning an incorrect form of the coefficient A in ref. 31 (see formula (A9) therein).

The first two terms on the right-hand side of eqn (2) represent the force acting on the boat, which is generated by the difference in surface tensions at the bow y_f = y_p − l/2 and at the stern y_b = y_p + l/2. It should be noted that the position of the boat centre y_p (y_p = Λ/2) is constant in our simulations. The third term describes the motion friction with the linear friction coefficient μ and the coefficient contributing to the nonlinear friction increase η.

We assumed that the diffusion coefficient D of camphor molecules below the boat is significantly smaller than that corresponding to the free water surface. In our simulations, we describe D(y) by the piecewise constant function:

where Δ = 0.0001. In our dimensionless variables, the diffusion coefficient on the free water surface is equal to 1.

The term K(y)c(τ,y) describes the dissipation of camphor from the surface. We assume that the main process is evaporation; thus, it does not occur below the boat. We use K(y) in the form

where k = 0.01 is the evaporation rate.

In simulations, we used the following expression for the supply rate of camphor molecules S(y):

where y_c = y_p + l/2 − d − r is the position of the pill centre, s is the constant supply rate of camphor molecules from the pill and the term (1 −c(τ,y)) takes into account the influence of surface saturation on the supply rate (in the dimensionless formulation, the maximum of the concentration c is equal to 1). In our case, s = 0.0002.

At the beginning, we verified if oscillations can be observed for the values of parameters given above, μ = 0.02 and η = 50.0 used in ref. 31 and for the corrected values of Γ₀ = 0.1 and Γ₁ = 0.01. For these parameters, the value of speed at d/r = 0 was v₀ = 0.016. The results are shown in Fig. 8. They are quantitatively similar to those in ref. 31 (Fig. 7 and 8 therein). For example, if we compare the maximum speeds observed in pulsating motion, then the values are close. In our simulations, the maximum velocity in the pulsating mode becomes almost constant for d/r > 1.4 (cf.Fig. 8(a)). For these parameter values, the transition from continuous motion to the pulsating one occurs in a very narrow range 1.0 < d/r < 1.1 and we did not observe oscillating motion.

Fig. 8 (a) Minimum and maximum velocities v versus the distance d/r between the boat's stern and the camphor pill. The inset illustrates velocity as a function of time for pulsating motion observed for d/r = 1.4. (b) The period T of pulsating motion as a function of distance d/r. The results were obtained for parameters from ref. 31 except for Γ₀ = 0.1 and Γ₁ = 0.01. Red disks and green circles indicate the continuous and pulsating motions, respectively.

Next, we searched for a change in model parameters to predict the oscillating motion. We found the important role of the value of η and stable oscillations appeared if the nonlinear contribution to the boat friction was neglected (η = 0.0 in eqn (2)). For such parameters, the value of speed at d/r = 0 was v₀ = 0.02. The results are presented in Fig. 9. Fig. 9(c–h) illustrate the boat speed as a function of time for different values of d/r. The stable mode of boat motion changes from continuous to oscillating motion for d/r in the interval [0.8,0.9], and the transition between oscillating motion and pulsating motion occurs when 1.2 < d/r < 1.4. The minimum and maximum velocities v observed in the stable mode of boat motion as a function of distance d/r presented in Fig. 9(a) are qualitatively comparable to the experimental results (cf.Fig. 7).

Fig. 9 Results of simulations with parameters from ref. 31 except of Γ₀ = 0.1, Γ₁ = 0.01 and η = 0.0. (a) Minimum and maximum velocities v observed in stable boat motion as a function of the distance d between the boat's stern and the camphor pill.(b) Period T of oscillating or pulsating motion as a function of d/r. Red disks, blue squares, and green circles show continuous, oscillating, and pulsating motions, respectively. (c–h) Speed as a function of time for different values of d/r: (c) 0.9, (d) 1.0, (e) 1.1, (f) 1.2, (g) 1.4, and (h) 1.6.

By selecting η = 0.0, we reduced the drag to the boat motion. The values of speed for d/r = 0 were almost identical: v₀ = 0.016 and v₀ = 0.02 for η = 50.0 and η = 0.0, respectively. However, for η = 0.0, the increase in the maximum peak velocity for pulsating mode was substantial compared to the case of η = 50.0. This can be seen in Fig. 8(a) and 9(a). Moreover, for η = 0.0, we did not obtain a plateau in the maximum speeds observed in pulsating motion for large d/r which was observed in experiments. On the other hand, the dependence of the periods on d/r for the case η = 0.0 (Fig. 9(b)) seems to match better the experimental data than the results for η = 50.0 (Fig. 8(b)).

Although the set of parameters discussed above predicts oscillations, we were not able to find the mode multistability that appeared in our experiments. In simulations, the multistability corresponds to different numerical solutions. We expected to find them starting from other initial conditions. A number of tests were performed for a few selected values of d/r, but all of them converged to the same type of motion.

Simulations explain the origin of different motion types. As the camphor source is closer to the stern than the bow, the concentration of camphor near the stern is always higher. Therefore, if the pill is not centrally located, we can assume that the concentration at the bow is practically zero. Another important factor is a significant difference between the diffusion coefficient of camphor molecules at the free surface and below the boat. It slows the camphor concentration relaxation when the source is away from the stern. If the camphor pill is close to the stern, the camphor supply to the water surface is little affected by the boat speed and the camphor surface concentration around remains constant. As a result, the boat speed does not change. Now let us consider a boat with the pill located at some distance from the stern. Due to slow diffusion below the boat, the difference in camphor concentration between the stern and the bow needs some time to develop. When it becomes large enough, the boat moves and shifts to a region where the water surface is fresh and the camphor surface concentration at the stern is smaller. As a result, the boat slows down. Now the balance between speed and camphor supply from the source to the stern area becomes important. If the pill is not so far away from the stern, the diffusion may be large enough to increase the camphor concentration at the stern, and the boat moves faster. The process repeats, and speed oscillations are observed. For larger distances between the pill and boat's stern, the motion supporting the camphor concentration close to the stern needs more time to develop; thus, the boat stops. After the concentration gradient develops, the boat makes a jump to a new location, and the process repeats.

4 Discussion and conclusions

We reported the results of our study on the motion of a camphor boat in a new experimental setup allowing for a long boat observation under stationary conditions. Many parameters can influence the boat motion, such as the water level,³⁷ the size and shape of the water tank, the boat length, the size of the camphor pill,²⁰ the arm length³⁸ and the distance between the boat trajectory and the dish wall. We focused on the distance d between the pill edge and the stern as the control parameter. Making such a choice, we were inspired by the results of Suematsu et al.,³¹ who reported a qualitative change in the character of motion (from continuous to pulsating) at a specific value of d. Our experimental setup allowed us to observe unperturbed boat motion for a long time; thus, we were able to identify metastable modes. Our experiments confirmed two types of previously reported motion types. When the camphor source was located at the boat's stern or when d was small, the continuous motion with a constant velocity dominated. The speed of continuous motion hardly depends on d. If the distance d was large, the pulsating type of motion characterised by bursts of speed separated by long intervals of time with negligible motion was observed. The lengths of these intervals are random, but their average increases with d.

We discovered a new, unreported type of boat motion characterised by a periodic boat speed. This type of motion is qualitatively different from pulsations because, in the oscillating mode, the boat never stops. The oscillations of speed are characterised by a minimum of > 6 mm s⁻¹ and an amplitude of > 20 mm s⁻¹. The period of such oscillations is short in the range between 1 and 2 s. Moreover, the period of oscillations weakly depends on the distance between the pill and the stern. Oscillations of speed were observed for distances d between those corresponding to continuous motion and pulsations. Therefore, our results indicate that with the increase in d the boat motion changes from continuous, through oscillating to pulsating. We observed that modes of boat motion (continuous, oscillating, and pulsating) are metastable, and they can co-exist for the exact camphor source location.

To simulate the boat motion, we used a simple one-dimensional model in which a reaction-diffusion equation described the spread of camphor molecules on the water surface. For the set of parameters similar to those used in ref. 31, the model predicted a sharp transition between continuous motion with a constant speed and the pulsating motion in a narrow range of d, but the oscillation mode did not appear. Our goal was to show that the previously introduced model can give oscillatory motion with minimal changes in its parameters. We achieved it by changing the value of a single parameter η, contributing to a nonlinear resistance from 50.0 to 0.0. It means that we removed nonlinearity in the Newton equation. Our selection of dimensionless parameters was focused only on the qualitative agreement between simulations and experiments and not on the quantitative one (compare Fig. 7, 8, and 9). It can be noticed that the selected values of dimensionless parameters do not quantitatively match the experimental observations. For example, the actual ratio in surface tension between pure water and water fully covered with camphor is 2 instead of 10, as in our set of dimensionless parameters. We are currently working on simulations based on accurate dimensional parameters.

We think that our report opens up many interesting questions for further experimental and theoretical investigation. In our opinion, the boat vibrations co-exist characterised by an amplitude of a few cm s⁻¹. They can be seen in Fig. 4(a) in the time intervals [1800 s, 2000 s] and Fig. 4(c) in the time intervals [7300 s, 7400 s]. A long time of vibrations indicates that this mode of boat motion can also be metastable. Whether vibrations can appear only for a large d, where the pulsating motion is dominant, is still an open question and requires further experimental investigation. Vibrations were most often observed in between bursts of motion but could also prevail for longer times, up to several hours. One can speculate that the vibrations should be dominant for the camphor pill centrally located below the boat. For the central source position, camphor diffusing under the boat does not produce a sufficient surface tension difference to overcome the forces counteracting motion.

The open theoretical questions include the explanation of the character of bifurcations between the modes and verification if mode multistability at a single value of d can be obtained within the formulated one-dimensional model. Concerning numerical simulations, it will be interesting to investigate if the simple, 1-dimensional model can predict pulsations with the inverse of rotation direction and the boat vibrations. In our opinion, the explanation of pulse inversion goes beyond this model and requires the inclusion of the water flows, as it was performed in our previous work.³⁶ The explanation of boat vibrations may require a substantial noise contribution to the evolution equations. Another interesting problem is the qualitative description of the relaxation of the boat speed. The experimental results show that when d is large the pulse of speed has a single maximum and after it, the boat uniformly slows down (cf. the green pulse shown in Fig. 5(b)). Such a type of speed relaxation was observed for both sets of model parameters considered in our simulations. However, pulses of speed observed for smaller d have a more complex structure composed of a few maxima as illustrated in Fig. 4(b). This indicates that the pulse of speed relaxes first to the oscillating mode and next the speed decreases to zero. Such behaviour was not seen for the sets of parameters considered in our calculations. We plan to continue working on these problems in our future studies.

Author contributions

RL did the experiments with the rotating boat. TR performed the numerical simulations. HK wrote a procedure for dot tracing. HK, YK, and JG performed the analysis of experimental results. All authors were involved in the writing of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Two authors (JG and TR) are grateful for funding from the European Union Horizon 2020 research and innovation program under the Marie Skłodowska-Curie grant agreement no. 734276 (CONIN). Additional funding was received from the Polish Ministry of Science and Higher Education for the implementation of the project No. 734276 in the years 2017–2021. Another author (RL) received funding from the European Union’s Horizon 2020 research and innovation program under the Marie Skłodowska-Curie Grant Agreement No. 711859 and support for science awarded by the Polish Ministry of Science and Higher Education for the implementation of an international co-financed project in the years 2017–2022.

References

1. A. Mikhailov and V. Calenbuhr, From Cells to Societies: Models of Complex Coherent Action, Springer, 2002.
2. S. Ramaswamy, Annu. Rev. Condens. Matter Phys., 2010, 1, 323–345.
3. C. Bechinger, R. Di Leonardo, H. Löwen, C. Reichhardt, G. Volpe and G. Volpe, Rev. Mod. Phys., 2016, 88, 045006.
4. T. Vicsek and A. Zafeiris, Phys. Rep., 2012, 517, 71–140.
5. N. J. Suematsu, A. Awazu, S. Izumi, S. Noda, S. Nakata and H. Nishimori, J. Phys. Soc. Jpn., 2011, 80, 064003.
6. J. R. Howse, R. A. L. Jones, A. J. Ryan, T. Gough, R. Vafabakhsh and R. Golestanian, Phys. Rev. Lett., 2007, 99, 048102.
7. W. F. Paxton, A. Sen and T. E. Mallouk, Chem. – Eur. J., 2005, 11, 6462–6470.
8. H.-R. Jiang, N. Yoshinaga and M. Sano, Phys. Rev. Lett., 2010, 105, 268302.
9. H. Ke, S. Ye, R. Carroll and K. Showalter, J. Phys. Chem. A, 2010, 114, 5462–5467.
10. T. Toyota, N. Maru, M. Hanczyc, T. Ikegami and T. Sugawara, J. Am. Chem. Soc., 2009, 131, 5012–5013.
11. S. Thutupalli, R. Seemann and S. Herminghaus, New J. Phys., 2011, 13, 073021.
12. Z. Izri, M. N. van der Linden, S. Michelin and O. Dauchot, Phys. Rev. Lett., 2014, 113, 248302.
13. S. Yabunaka and N. Yoshinaga, J. Fluid Mech., 2016, 806, 205–233.
14. C. C. Maass, C. Krüger, S. Herminghaus and C. Bahr, Annu. Rev. Condens. Matter Phys., 2016, 7, 171–193.
15. S. Michelin, Annu. Rev. Fluid Mech., 2023, 55, 77–101.
16. A. Bricard, J.-B. Caussin, N. Desreumaux, O. Dauchot and D. Bartolo, Nature, 2013, 503, 95–98.
17. A. N. Kato, K. A. Takeuchi and M. Sano, Soft Matter, 2022, 18, 5435–5445.
18. S. Nakata, Y. Iguchi, S. Ose, M. Kuboyama, T. Ishii and K. Yoshikawa, Langmuir, 1997, 13, 4454–4458.
19. Y. Hayashima, M. Nagayama and S. Nakata, J. Phys. Chem. B, 2001, 105, 5353–5357.
20. M. Nagayama, S. Nakata, Y. Doi and Y. Hayashima, Phys. D, 2004, 194, 151–165.
21. N. J. Suematsu, T. Sasaki, S. Nakata and H. Kitahata, Langmuir, 2014, 30, 8101–8108.
22. Self-organized Motion, ed. S. Nakata, V. Pimienta, I. Lagzi, H. Kitahata and N. J. Suematsu, The Royal Society of Chemistry, 2019.
23. R. Tenno, Y. Gunjima, M. Yoshii, H. Kitahata, J. Gorecki, N. Suematsu and S. Nakata, J. Phys. Chem. B, 2018, 122, 2610–2615.
24. S. Nakata, M. Nagayama, H. Kitahata, N. J. Suematsu and T. Hasegawa, Phys. Chem. Chem. Phys., 2015, 17, 10326–10338.
25. M. Shimokawa, M. Oho, K. Tokuda and H. Kitahata, Phys. Rev. E, 2018, 98, 022606.
26. C. Tomlinson and W. A. Miller, Proc. R. Soc. London, 1862, 11, 575–577.
27. R. J. Strutt, Proc. R. Soc. London, 1890, 47, 364–367.
28. S. Nakata, private information.
29. Y. Karasawa, S. Oshima, T. Nomoto, T. Toyota and M. Fujinami, Chem. Lett., 2014, 43, 1002–1004.
30. Y. Ikura, R. Tenno, H. Kitahata, N. Suematsu and S. Nakata, J. Phys. Chem. B, 2012, 116, 992–996.
31. N. J. Suematsu, Y. Ikura, M. Nagayama, H. Kitahata, N. Kawagishi, M. Murakami and S. Nakata, J. Phys. Chem. C, 2010, 114, 9876–9882.
32. FFmpeg, https://ffmpeg.org/.
33. W. Rasband, ImageJ, U. S. National Institutes of Health, Bethesda, Maryland, USA, https://imagej.nih.gov/ij/, 1997–2018.
34. Mathematica, Version 12.3, W. R. Inc., Champaign, IL, 2021.
35. S. Nakata, K. Kayahara, H. Yamamoto, P. Skrobanska, J. Gorecki, A. Awazu, H. Nishimori and H. Kitahata, J. Phys. Chem. C, 2018, 122, 3482–3487.
36. Y. Koyano, H. Kitahata, S. Nakata and J. Gorecki, Chaos, 2020, 30, 023105.
37. Y. Matsuda, N. J. Suematsu, H. Kitahata, Y. S. Ikura and S. Nakata, Chem. Phys. Lett., 2016, 654, 92–96.
38. Y. Koyano, M. Gryciuk, P. Skrobanska, M. Malecki, Y. Sumino, H. Kitahata and J. Gorecki, Phys. Rev. E, 2017, 96, 012609.

---

Footnote

† Electronic supplementary information (ESI) available: SI-continuous-L2-2p5mm.mp4 - a fragment of movie from experiment for d = 2.5 mm showing the continuous motion (cf. Fig. 2), SI-oscillating-small-amp-L5-3 mm.mp4 - a fragment of movie from experiment for d = 3 mm showing the oscillating motion with a small amplitude (cf. Fig. 3), SI-oscillating-large-amp-L5-5 mm.mp4 - a fragment of movie from experiment for d = 5 mm showing the oscillating motion with a large amplitude, SI-pulsating-L5-8 mm-x5.mp4 - a fragment of movie from experiment for d = 8 mm showing pulsating motion (accelerated 5 times, cf. Fig. 4), and SI-inversion-L3-7 mm.mp4 - a fragment of movie from experiment for d = 7 mm showing inversions of rotations (accelerated 4 times, cf. Fig. 5). See DOI: https://doi.org/10.1039/d2cp05707g

---