Open Access Article
Open Access ArticleEffects of layer-by-layer coating on activated carbon electrodes for capacitive deionization
Sergio
Orozco-Barrera
 ,
Guillermo R.
Iglesias
,
Guillermo R.
Iglesias
 ,
Ángel V.
Delgado
,
Ángel V.
Delgado
 ,
Sergio
García-Larios
,
Sergio
García-Larios
 and
Silvia
Ahualli
and
Silvia
Ahualli
 *
*
Department of Applied Physics, Faculty of Science, University of Granada, 18071 Granada, Spain. E-mail: sahualli@ugr.es
First published on 25th February 2023
Abstract
Recently, the need for obtaining, reusing, or purifying water has become a crucial issue. The capacitive deionization (CDI) method, which is based on the electric double layer (EDL) concept, can be applied to ion adsorption from an aqueous solution. This process is carried out by applying a potential difference to highly porous electrodes while pumping salty solution between them, partially removing the ions present in the solution and keeping them in the surface of the electrodes. The use of coated carbon electrodes with one polyelectrolyte layer, turning them into “soft electrodes” (SEs), has been proved to improve the efficiency of the system with respect to its original configuration. In this work, we investigate the effect on the ion adsorption and the efficiency of the process when implementing the coating technique known as layer-by-layer (LbL) on the electrode. This consists in successively coating the electrode surfaces with polyelectrolyte layers, alternating their charge polarity in each step. We tested the effect of the number of layers deposited, as well as the impact of this technique by using different carbons. We found that the second polyelectrolyte layer adheres more than the first layer, serving as a support or seed when it is not dense and uniformly distributed. In contrast, if the first layer is well adhered, a third layer is needed to observe improvements in adsorption and process efficiency. The adsorption of the polymer layers depends in any instance on the porosity of the carbon.
1. Introduction
Methods for non-consumable-water treatment have been studied for years now. Following this line, and based on the “electrochemical demineralization of water” proposed by Blair, Murphy et al.1 capacitive deionization (CDI) emerges as a renewable alternative to traditional methods2 at a functional level with low energetic costs. This technique is based on electric double layer (EDL) properties3,4 to partially remove ions from a saline solution being pumped between a couple of highly porous electrodes facing each other when applying a potential difference between them. With the application of this potential difference, ions migrate to their oppositely charged electrode, contributing to the EDL formation on the interface until the electrode surface charge is completely screened. The EDL has the typical storage properties of a capacitor, and its capacitance will be higher the larger the usable interfacial area between the solution and the electrode. It is then necessary to use materials such as activated carbon for the electrode surface, due to its high conductivity and specific surface area (high porosity): its large number of pores act as microscopic channels for ion storage. This desalination process has been found to be optimum when desalinating solutions up to 10 g L−1.In the search for an improvement of this method, promising results in desalination have been found by coating the carbon electrodes with polyelectrolyte (PE) layers, turning them into so-called “soft electrodes” (SE). These PE layers are chosen to have a positive (negative) charge density when adhered to the positively (negatively) charged electrode surface, favoring the counterion transport and blocking the coion one from entering or exiting the EDL.5,6 This method is similar to “membrane assisted-CDI” (MCDI)7–9 although with a lower overall performance, but with the advantage of a lower economic cost and ease of preparation. Furthermore, considering that the PE coating does not add to the system a higher internal resistance, setting up this technique is a more than plausible approach.
One of the reasons why SE has a lower performance than MCDI is that the polymer charge density is small compared to that of an ion exchange membrane. Besides, the coating is not uniform in the sense that not all the surface of the macropores is lined with the polymer. For that reason, in the present work, the use of SEs has been approached with the application of PE multilayers and the consideration of its impact on ion transport and adsorption. This multiple coating technique is known as Layer-by-Layer (LbL),10 widely used due to its simple application:11,12 PE layers are successively deposited onto the desired surface while alternating their charge polarity. This work has been experimentally addressed to prepare these LbL-coated carbon electrodes for CDI use (a scheme of the LbL-electrodes is shown in Fig. 1). On the other hand, a theoretical model has been proposed to bring light to the ion transport behavior while using these electrode configurations with multiple PE layers. The coating is strongly dependent on the size and porosity of the macropores, which is where the PE chains are deposited. Two different activated carbons have been used as a base of the electrodes, in order to study possible differences in coating and adherence of the PE layers depending on the characteristics of the carbon used, such as its specific surface area, electrical resistance, and porosity.
2. Experimental
2.1. Materials
For the experimental work, 10 mM NaCl (Sigma-Aldrich, Darmstadt, Germany) solutions were prepared. The water used was previously deionized and filtered with a Milli-Q Academic System (Millipore, Molsheim, France).The carbon particles employed for the preparation of the electrodes were SR23 (MAST Carbon International Ltd, UK) and YP-80F (Kuraray Co. Ltd, Japan), which are ideal for this work due to their huge available surface area (SSR23 = 959 m2 g−1; SYP-80F = 2271 m2 g−1) for ion adsorption and storage. The pore size distribution is 7 nm for the SR23 carbon,13 and 1 nm for the YP-80F as specified by the manufacturer. Black carbon (Alfa Aesar, Termo Fisher, Germany) has also been used in small quantities to boost the electrical conductivity of the electrodes.14
In order to prepare the polyelectrolyte coatings, aqueous solutions of poly(diallyldimethyl-ammonium chloride) (PDADMAC, with a molecular weight of 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1, cationic) and poly(sodium 4-styrenesulfonate) (PSS, molecular weight of 100
000 g mol−1, cationic) and poly(sodium 4-styrenesulfonate) (PSS, molecular weight of 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1, anionic) were prepared. Both polymers were purchased from Sigma-Aldrich.
000 g mol−1, anionic) were prepared. Both polymers were purchased from Sigma-Aldrich.
2.2. Setup
The experimental setup was based on two planar electrodes, facing each other at a distance of 500 μm by a nylon spacer. Each of these electrodes was formed by a 10 cm long and 5 cm wide graphite plate used as a current collector, onto which the activated carbon was deposited (see Fig. 2). The carbon on the electrode was previously prepared as a mixture of the given activated carbon powder and black carbon (5% black carbon; 95% activated carbon), and a 33 g L−1 solution of poly(vinylidene-fluoride) (PVDF, manufactured by Arkema, Colombes, France, as Kynar HSV 900, with a molecular weight of approximately 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) in 1-methyl 2-pyrrolidone (Sigma Aldrich). For the SR23 activated carbon, 3 g of the SR23 + black carbon were mixed with 10 g of PVDF. In the case of YP-80F activated carbon, 3 g of the YP-80F + black carbon and 12 g of PVDF were mixed. The final carbon suspension was deposited onto the graphite collector as a 500 μm layer using the doctor blade technique, and dried at 60 °C for 24 h.
000) in 1-methyl 2-pyrrolidone (Sigma Aldrich). For the SR23 activated carbon, 3 g of the SR23 + black carbon were mixed with 10 g of PVDF. In the case of YP-80F activated carbon, 3 g of the YP-80F + black carbon and 12 g of PVDF were mixed. The final carbon suspension was deposited onto the graphite collector as a 500 μm layer using the doctor blade technique, and dried at 60 °C for 24 h.
The polymeric coating of the electrodes was carried out by immersing them in a 200 mM aqueous solution of the corresponding polyelectrolyte (PDADMAC for the positive electrode, PSS for the negative electrode) for 6 h under constant magnetic stirring. In order to carry out the Layer-by-Layer process, both electrodes were immersed alternately into the polyelectrolyte solution with opposite charge density, favoring its adherence via electrostatic interactions. Electrophoretic mobilities were measured in each step in order to check whether the coating was done correctly. In addition, diameters of 400 ± 120 nm for the YP-80F bare carbon particles compared to diameters of 640 ± 130 nm and 460 ± 100 nm for the PDADMAC-coated and PSS-coated ones, respectively, show a slight increase due to the coatings. Note that the uncertainty in the measurements comes from the polydispersity of the carbon particles.
Once the electrodes were prepared, the measurement cell was set up as described above. The desalination process took place by pumping the saline solution through the cell from a 5 L container. The cell is connected to an Iviumstat.h (Ivium, The Netherlands) potentiostat working at constant voltage. Changes in conductivity and temperature were measured at the exit of the cell with a 529670 probe (Leybold, Dresden, Germany) and continuously read by a Leybold 524D10 Cassy Lab interface. The exit solution was returned to the original container, which was large enough to keep the inlet conductivity appreciably constant during successive working cycles (Fig. 2).
Each CDI cycle involves two steps: in the adsorption one, the electrodes are powered by applying a constant voltage (1.2 V) from the source, which drives ions from the solution flow to the macropores of the electrode with opposite charge, decreasing the measured conductivity. During the desorption step, the stored ions are released to the main solution flow, allowing the carbon pores to become empty for the following adsorption step. Desorption was carried out by externally short-circuiting the electrodes (Zero-Voltage, ZV, condition), draining the pores, and returning the ions to the solution, which was detected as an increase in the on-line conductivity sensor.
From the conductivity values, the concentration difference is calculated via the relationship:
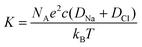 | (1) |
3. Results and discussion
3.1. SR23 carbon electrodes
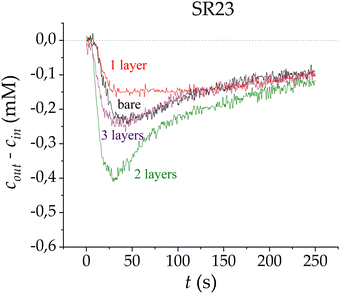
The CDI process using SEs has been studied previously,6,9,15 with promising results over both those obtained with the standard CDI technique and with membrane-assisted CDI. The coating of SR23 with the first layer of polymer (Fig. 3) provokes a slightly lower saline concentration difference compared with that obtained using the bare carbon. The similarities between these curves can be explained by considering that the effectiveness of the coating depends on the polyelectrolyte layer charge density and thickness.
For this reason, the surface composition of the coated carbons has been analyzed by using EDX (Energy Dispersive X-rays) spectroscopy. The sample was prepared via lyophilization and transversally cut in order to be able to observe how much the polymer has penetrated into the carbon pores. Fig. 4 shows the carbon sample, as well as the presence of sulfur and sodium ions as indicators for the PSS layer.
As shown in Fig. 4, the first polyelectrolyte coating is not uniform along the entire carbon sample, reducing the performance of the layer in salt adsorption. However, it indeed improves the efficiency of the process as we will see in Section 3.3. It can be appreciated that not all the carbon is coated and that some of the carbon surface is covered as a whole without penetration of the polyelectrolyte in the inner region of the macropores. This image confirms our assumptions and supports the decision to add another layer with opposite polarity whose adhesion will be favored by the presence of the first layer.
A third layer was also deposited using the LbL technique, and measurements were made by connecting the electrodes with the same polarity as the charge sign of the last deposited layer. Fig. 3 shows the adsorption stages for the multilayer-electrode configurations, and the electrode polarities are kept equal in sign as their last layers for each measurement. As observed, the addition of the third layer does not produce any improvement over the bare electrodes; this adsorption loss might be due to the similarities this configuration has with respect to the electrodes with only one layer (SE). In contrast, the major improvement in adsorption can be appreciated when coating the electrodes with two layers, with a peak that is almost twice that obtained with bare electrodes.
These results suggest that the first polyelectrolyte layer partially penetrates the macropores, which does not seem to be improving the performance of the system. Nonetheless, although this first polymeric layer was not evenly adhered or dense on the macropores, it acts as a support for the second layer to strongly adhere to the previous one. Therefore, the first coating of the electrodes was not completely efficient but serves as a seed so that the second layer does adhere optimally.
3.2 YP-80F carbon electrodes
This positive impact of the first PE layer might be explained because of a better adherence of this first polymeric layer onto the electrode surface, unlike the observations for the previously studied carbon. Intrinsic carbon properties could be the reason for this main difference when coating the electrodes, as the larger specific surface area of this carbon will favour a better adherence being expected for the layer. This matches the data available for both carbons used: the first PE layer seems to be more evenly deposited for the YP-80F carbon, whose specific area, 2271 m2 g−1, is more than twice that of SR23. The macropore/micropore size distribution also plays an important role, as smaller micropores (1 nm in the case of YP-80F, and 6–7 nm for SR23) are less accessible for the PE layer to penetrate them, whereas wider macropores are easily lined by the polymer. Our results indicate that the YP-80F carbon surface would seem even and continuous to the polymer coating, favoring its adherence.
The application of a third layer gives way to an adsorption peak that is similar to that corresponding to the one-layer configuration, with a notable increase in the area under the adsorption curve, improving the performance of adsorption.
3.3. Efficiency, salt adsorption and consumed energy
To quantify the performance of each electrode configuration in CDI processes, three main parameters were calculated: the specific adsorption coefficient (SAC), the charge efficiency and the energy per ion consumed in the process.16The specific adsorption coefficient, SAC, expresses the ratio of grams of ions adsorbed per gram of electrode:
 | (2) |
 | (3) |
The charge efficiency of the system, Δ, was calculated as the ratio between the total number of adsorbed salt moles and the charge transferred between the electrodes in the same amount of time. Therefore, when an ion is retired per charge unit deposited on the electrodes, the efficiency will take its maximum value (Δ = 1).7,17 Then:
 | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 487 (C mol−1) is the Faraday constant.
487 (C mol−1) is the Faraday constant.
The energy consumed per ion removed from the solution in the adsorption stage, E, was calculated as:
 | (5) |
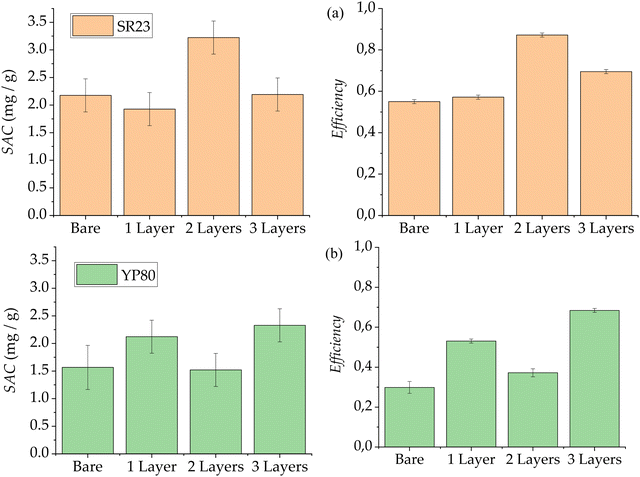
These calculated parameters are shown in Table 1 and graphically displayed in Fig. 7a for SR23 electrodes, and in Table 2 and Fig. 7b for YP-80F electrodes. By comparing to a capacitor, the capacitance C is obtained from exponentially fitting the adsorption-stage current curve, with a characteristic time τ equal to RC, where R is the system resistance. Note that the PE layers (in pairs) barely affect the system resistance, as the differences observed amount to less than 1 Ω, comparable with those of the ion exchange membranes.18,19
| SR23 | |||
|---|---|---|---|
| Electrode configuration | Charge efficiency (±0.01) | SAC (mg g−1) (±0.3) | Energy per ion (kT) |
| Bare | 0.55 | 2.2 | 42 ± 4 |
| 1 Layer | 0.57 | 2.0 | 41 ± 4 |
| 2 Layers | 0.87 | 3.2 | 27 ± 3 |
| 3 Layers | 0.70 | 2.2 | 34 ± 4 |
| YP-80F | |||
|---|---|---|---|
| Electrode configuration | Charge efficiency | SAC (mg g−1) | Energy per ion (kT) |
| Bare | 0.30 ± 0.03 | 1.6 ± 0.4 | 78 ± 7 |
| 1 Layer | 0.53 ± 0.01 | 2.1 ± 0.3 | 44 ± 4 |
| 2 Layers | 0.37 ± 0.02 | 1.5 ± 0.3 | 63 ± 5 |
| 3 Layers | 0.68 ± 0.01 | 2.3 ± 0.3 | 34 ± 4 |
For SR23 carbon (Fig. 7a), we observe similar behavior between the obtained SAC for bare electrodes and SEs (one layer). However, the calculated charge efficiency is slightly higher in the coated electrode case. This could be explained for a first weak or partial layer attached to the surface of carbon as can be seen in Fig. 4. The use of a second layer gives way to a notable improvement in the amount of adsorbed ions, reaching the maximum value of almost 3.5 mg of NaCl removed from the feed solution for each gram of carbon. This result shows that the second coating is denser than the first one (and probably promoted by the presence of the first layer), in the case of SR23 carbon, increasing the capacity of the cell. The efficiency of the two layer-electrode configuration reaches a remarkable value of almost 0.9. Finally, application of a third polymer layer brings about similar results in capacity to the bare carbon electrodes, but still involves an efficiency improvement over both bare and soft electrodes.
For YP-80F (Fig. 7b) carbon electrodes, and as expected from the adsorption curves, the calculated SAC improves in the cases of one-layer and three-layer configurations, reaching the maximum value with the latter, of around 2.3 mg g−1. The adsorption capacity decline observed in the curve corresponding to two-layer configuration is also exhibited in the SAC, reaching the minimum value: 1.5 mg g−1.
Charge efficiency has a similar behaviour and is inverse to SAC, as the efficiency is higher in the case of YP-80F electrodes with three polymeric layers, with a value of almost 70%. Despite the SAC being minimum for the two-layers configuration, its efficiency value turns out to be slightly higher than the one obtained with bare carbon electrodes. The minimum efficiency value is around 30% for bare carbon showing that, despite having stored a lot of charge, it is not able to remove ions from the solution main stream as will be seen from the theoretical predictions.
As mentioned above and displayed in Fig. 7, although the charge efficiency of the polyelectrolyte-coated electrodes is increased in all the cases shown over that of bare electrodes, SAC is improved or reduced depending on whether the use of multiple layers favours ion transport or if it blocks it, respectively. Therefore, improvements in the adsorption capacity of the system have been quantified and such improvements are found with an even number of polyelectrolyte layers for SR23 carbon electrodes, and an odd number of them for YP-80F ones.
Finally, the consumed energy (see Tables 1 and 2) yields opposite trends than the efficiency, as expected: the larger the energy spent, the lower the efficiency of the system. This relationship holds as the minimum energy spent takes a value of around 27 kBT per ion in the two layers-electrode configurations for the SR23 carbon, and a value of around 34 kBT for the three layers-electrodes in the case of YP-80F.
4. Theoretical predictions
The interface between a coated porous electrode and ionic solution can be modeled assuming that the polymeric layer covers the macropore walls, affecting only the ion transport between these and the micropores (Fig. 8). We consider that the polymer layer is a region with a certain charge distributed in a volumetric region that extends from the macropore surface and it is permeable to the ions. | ||
| Fig. 8 Scheme of the positioning of the PE layer on the electrode surface. The layer coats the macropore walls, regulating the ion flux to the micropores. | ||
Two regions have to be considered to determine the electric potential profile and the ion distribution by solving Poisson's equation, namely, the external region, where charge is given by the ion concentration; and the polymer shell, where the polymer charge density, ρpol, also has to be taken into account. This is shown in the following equation:
 | (6) |
 | (7) |
The model proposed for a single PE layer can be extended to several layers by modifying the set of equations (eqn (6)) and their corresponding boundary conditions (the electric field satisfies the Gauss law on the solid surface and vanishes far from this; the electric potential is continuous between successive polyelectrolyte layers) in order to predict the ion distribution around the solid surface, and thus deduce the impact of the multiple coating.
The time response of the ion concentration at the cell outlet can be predicted. For this, a 1-D model is used (as described by Tang et al.20 and Biesheuvel et al.21 and modified in ref. 6 and 9) which only considers one spatial variable along the cell for a coated electrode with one polymer layer. In this model, the cell is divided into i subcells (i = 1, …, M; being M the total number of subcells) perpendicular to the solution flow so that, for each ionic species j present in the solution, each subcell has an ion concentration cj,i. This subcell concentration suffers changes due to the ion transport from the previous cell (i − 1), as well as the ion flux from the macropores to the micropores, and vice versa, Jj,i,mA→mi:
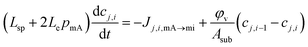 | (8) |
At the same time, the charge density of the micropores, ρmi,i, in contact with the macropores in the i-th subcell varies according to each ion species flux contribution:
 | (9) |
| Jj,i,mA→mi = zjDjcSEj,iLeff−1Δϕtr,i | (10) |
The electric potential difference is calculated as the difference between the external voltage applied to the cell, Vext, and the potential drop observed along the EDL (including Stern and diffuse layers). Then:
| Δϕtr,i = Vext/VT − 2|ΔψStern + Δψd| | (11) |
 | (12) |
This model must be modified for the multilayer case. The ion transport and the EDL screening can be modeled as the charge stage of an RC circuit. Then, the addition of multiple layers is equivalent to the arrangement of resistors in series, as the current intensity will take the same value through the different layers. For the single-layer case, if we compare eqn (10) to Ohm's law:
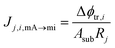 | (13) |
 | (14) |
 | (15) |
 | (16) |
| ΔΨk,i = Jj,i,mA→miRj,k | (17) |
Fig. 9a and b show the ionic concentration profile near a positively charged surface, coated with two polymeric layers of alternate charge polarities, obtained by solving the set of eqn (6). In Fig. 9 we can observe the formation of the EDL next to the surface. In cases (a) and (b) there is a coating of two polymer layers, in such a way that the ionic concentration increases or decreases with respect to that of the medium, 10 mM, depending on the ion polarity with respect to the polymer layer charge. Alternatively, Fig. 9c, without polymer coatings, shows that the EDL is formed with an excess of counterions and defect of coions from the medium (10 mM). The effect of the PE layer is to produce an excess (defect) of ionic concentration that brings about an increase (reduction) in the flow of that type of ions, favoring (blocking) their adsorption (desorption). This enhances the efficiency of the process because the entry of counterions is promoted to compensate the surface electric charge, while the exit of coions is prevented.
To simulate the case of the SR23 carbon electrode, based on EDX images (Fig. 9a and 10a) and the behaviour of the experimental results, the fitted value of the first layer's charge density was lower than that of the second layer. Since the charge density of the second layer is higher in this case, the counterion (Na+) transport is highly favoured while the coion (Cl−) transport is strongly blocked.
Using these ionic concentration distributions, eqn (8)–(17) can be solved to obtain the theoretical predictions of the dynamic response of the SR23 carbon electrode for one and two polymeric layers in the adsorption step. In the latter case, the electrode charge polarity is identical to that of the external polymer coating (Fig. 5). The predicted relative conductivity (Fig. 10a) has the same behaviour as the experimental results (Fig. 3), regarding the increase in salt adsorption with the addition of the second layer. The model predicts that adding a second PE layer on top of the first one of lower charge density and different polarity results in a higher adsorption and efficiency (Table 1) than the weakly deposited first layer.
To simulate the YP-80F carbon electrode case, the charge densities of both layers have been assumed to be similar but with opposite sign. Fig. 10b shows the ionic concentration profile, with their transport favoured in one of the layers (where it acts as a counterion) and strongly blocked in the other one (acting as a coion). As a result, the combination of the two layers with identical charge densities give way to an antagonistic effect, which leads to a lower adsorption predicted at the cell outlet. Note that the theoretical prediction using this assumption agrees very well with the experimental results (Fig. 6), showing even a desorptive-like “hump” behaviour (Fig. 10b).
5. Conclusions
Capacitive deionization (CDI) is based on the properties of the electrical double layer of porous electrodes. Properties such as their overall porosity and their micro/macro-porous distribution are fundamental in determining the storage capacity for ion adsorption when applying a potential difference between two electrodes in contact with a salt solution. The functionalization of the electrodes using polyelectrolyte coatings opens a new way to improve the performance of the method and its capability to implement, in the near future, ion selective adsorption.29 For both aims, the use of successive layers of alternating charge signs to reinforce the adsorption or to set one of the layers to be selective to one of the ionic species is found to be very interesting. In this work, we found that such layers improve the adsorption and efficiency, although the results depend on the internal structures of the porous structure of the activated carbon.Surface modification has been studied for two different activated carbon electrodes, denominated SR23 and YP-80F, coating them with up to three PE layers using the Layer-by-Layer (LbL) technique to analyze the impact of the coating and its dependence on carbon properties such as porosity and specific surface.
SR23 carbon electrodes present a weak adherence of the first PE layer, although this favours the coating of the following layer, with an opposite charge density polarity, acting as a support. This second layer provides the highest ion adsorption and efficiency values, reaching respectively 3.2 mg g−1 and 87% of efficiency, to be compared to 2.2 mg g−1 and 55% for bare SR23. It is highlighted that these results have been achieved when the polarity of the surface charge of the electrode coincides with that of the outer layer.
On the other hand, coating with an odd number of PE layers seems to be more consistent on the YP-80F carbon electrodes, and the addition of even layers blocks the ion transport. The reason for this lies on the similar uniformity of the first and second coatings and their opposite charge polarity, creating an antagonistic effect on ion transport (neither favoured nor blocked) due to charge compensation. For these carbon electrodes, the three-layer configuration provides the highest ion adsorption and efficiency values, reaching 2.3 mg g−1 and 68%, respectively. These figures are 1.6 mg g−1 and 30% for uncoated YP80.
A theoretical model for the multiple-layer configurations has been presented, which determines the temporal evolution of each ion species concentration while considering ion transport from the feed solution to the micropores. It is notable to mention the qualitative agreement between the theoretical predictions of this model and the experimental results if the proposed hypothesis about the density of the PE layers is considered.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
Financial support of this investigation by FEDER/Junta de Andalucía-Consejería de Transformación Económica, Industria, Conocimiento y Universidades, Spain (Grant No. P20_00233) and Consejería de Conocimiento, Investigación y Universidad, Junta de Andalucía, Spain (Grant No. A-FQM-492-UGR20) is gratefully acknowledged. Thanks are also due for the grant TED2021-131855B-I00/AEI/10.13039/501100011033/Unión Europea NextGenerationEU/PRTR.References
-
J. W. Blair and G. W. Murphy, Advances in Chemistry Series Number 27, American Chemical Society, Washington, DC, 1960 Search PubMed
.
-
Lewabrane, Principles of Reverse Osmosis Membrane Separation, Lanxess Deutschland GmbH, Köln, Germany, 2013 Search PubMed
.
-
A. Delgado, Interfacial electrokinetics and electrophoresis, Elsevier, New York, 2002 Search PubMed
.
- A. V. Delgado, M. L. Jiménez, G. R. Iglesias and S. Ahualli, Curr. Opin. Colloid Interface Sci., 2019, 44, 72–84 CrossRef CAS
.
- A. D. Khawaji, I. K. Kutubkhanah and J. Wie, Desalination, 2008, 221, 47–69 CrossRef CAS
.
- S. Ahualli, G. Iglesias, M. M. Fernández, M. L. Jiménez and A. V. Delgado, Environ. Sci. Technol., 2017, 51, 5326–5333 CrossRef CAS PubMed
.
- S. Porada, R. Zhao, A. Van Der Wal, V. Presser and P. M. Biesheuvel, Progress in Materials Science, 2013, 58(8), 1388–1442 CrossRef CAS
.
-
R. Zhao, Theory and operation of capacitive deionization systems, Wageningen University and Research, Netherlands, 2013 Search PubMed
.
- S. Ahualli, S. Orozco-Barrera, M. M. Fernández, A. V. Delgado and G. R. Iglesias, Polymers, 2019, 11(10), 1556 CrossRef CAS PubMed
.
- G. Decher, Science, 1997, 277, 1232–1237 CrossRef CAS
.
- J. J. Richardson, M. Björnmalm and F. Caruso, Science, 2015, 348, 6233 CrossRef PubMed
.
- J. J. Richardson, J. Cui, M. Björnmalm, J. A. Braunger, H. Ejima and F. Caruso, Chem. Rev., 2016, 116(23), 14828–14867 CrossRef CAS PubMed
.
- A. V. Delgado, S. Ahualli, M. M. Fernández, M. A. González, G. R. Iglesias, J. F. Vivo-Vilches and M. L. Jiménez, Environ. Chem., 2017, 14(5), 279–287 CrossRef CAS
.
- S. Nadakatti, M. Tendulkar and M. Kadam, Desalination, 2011, 268(1–3), 182–188 CrossRef CAS
.
- S. Ahualli, M. L. Jiménez, M. M. Fernández, G. Iglesias, D. Brogioli and A. V. Delgado, Phys. Chem. Chem. Phys., 2014, 16, 25241–25246 RSC
.
- M. E. Suss, S. Porada, X. Sun, P. M. Biesheuvel, J. Yoon and V. Presser, Energy Environ. Sci., 2015, 8(8), 2296–2319 RSC
.
- R. Zhao, P. M. Biesheuvel, H. Miedema, H. Bruning and A. Van der Wal, J. Phys. Chem. Lett., 2009, 1(1), 205–210 CrossRef
.
- P. Długołęcki, P. Ogonowski, S. J. Metz, M. Saakes, K. Nijmeijer and M. Wessling, J. Membr. Sci., 2010, 349(1–2), 369–379 CrossRef
.
- J. Chang, K. Tang, H. Cao, Z. Zhao, C. Su, Y. Li, F. Duan and Y. Sheng, Sep. Purif. Technol., 2018, 207, 387–395 CrossRef CAS
.
- W. Tang, P. Kovalsky, B. Cao, D. He and T. D. Waite, Environ. Sci. Technol., 2016, 50(19), 10570–10579 CrossRef CAS PubMed
.
- P. M. Biesheuvel, B. van Limpt and A. van der Wal, J. Phys. Chem. C, 2009, 113(14), 5636–5640 CrossRef CAS
.
- P. M. Biesheuvel and A. van der Wal, J. Membr. Sci., 2010, 346(2), 256–262 CrossRef CAS
.
- T. Kim, J. E. Dykstra, S. Porada, A. van der Wal, J. Yoon and P. M. Biesheuvel, J. Colloid Interface Sci., 2015, 446, 317–326 CrossRef CAS PubMed
.
- S. Porada, L. Borchardt, M. Oschatz, M. Bryjak, J. S. Atchison, K. J. Keesman, S. Kaskel, P. M. Biesheuvel and V. Presser, Energy Environ. Sci., 2013, 6(12), 3700–3712 RSC
.
- R. Zhao, M. van Soestbergen, H. H. M. Rijnaarts, A. van der Wal, M. Z. Bazant and P. M. Biesheuvel, J. Colloid Interface Sci., 2012, 384, 38–44 CrossRef CAS PubMed
.
- B. Kastening and M. Heins, Electrochim. Acta, 2005, 50(12), 2487–2498 CrossRef CAS
.
- W. Tang, P. Kovalsky, D. He and T. D. Waite, Water Res., 2015, 84, 342–349 CrossRef CAS PubMed
.
- A. Hemmatifar, M. Stadermann and J. G. Santiago, J. Phys. Chem. C, 2015, 119(44), 24681–24694 CrossRef CAS
.
- M. E. Suss, J. Electrochem. Soc., 2017, 164(9), E270–E275 CrossRef CAS
.
| This journal is © the Owner Societies 2023 |