Quasi-classical trajectory study of the OH⁻ + CH₃I reaction: theory meets experiment

Abstract

Regarding OH⁻ + CH₃I, several studies have focused on the dynamics of the reaction. Here, high-level quasi-classical trajectory simulations are carried out at four different collision energies on our recently developed potential energy surface. In all, more than half a million trajectories are performed, and for the first time, the detailed quasi-classical trajectory results are compared with the reanalysed crossed-beam ion imaging experiments. Concerning the previously reported direct dynamics study of OH⁻ + CH₃I, a better agreement can be obtained between the revised experiment and our novel theoretical results. Furthermore, in the present work, the benchmark geometries, frequencies and relative energies of the stationary points are also determined for the OH⁻ + CH₃I proton-abstraction channel along with the earlier characterized S_N2 channel.

---

I. Introduction

Moving further to larger systems, the investigations of bimolecular nucleophilic substitutions (S_N2) have become more and more complex over the last few decades.^1–9 The most thoroughly studied seven-atomic S_N2 reactions are OH⁻ + CH₃Y (Y = F, Cl, Br, I). In these cases, the S_N2 reaction profile differs from the traditional X⁻⋯CH₃Y → [X⋯CH₃⋯Y]⁻ → XCH₃⋯Y⁻ path.^10–15 For Y = Cl, Br and I, in the entrance channel, a H-bonded HO⁻⋯HCH₂Y complex and a H-bonded transition state are located, and for Y = I, the typical X⁻⋯CH₃Y ion-dipole pre-reaction complex and the [X⋯CH₃⋯Y]⁻ Walden-inversion transition state cannot be found. Moreover, instead of the XCH₃⋯Y⁻ post-reaction complex, a H-bonded CH₃OH⋯Y⁻ complex is situated in the product channel, which happens to be the global minimum for the OH⁻ + CH₃Y reactions. It should be noted that, by front-side attack¹⁶ and double-inversion¹⁷ mechanisms, retention of the initial configuration may also occur in the OH⁻ + CH₃Y S_N2 reaction.¹⁵

In 2002, Hase and co-workers investigated the reaction between OH⁻ and CH₃F using direct dynamics classical trajectory simulations, and revealed that the reaction rather takes place through a direct route by avoiding the deep CH₃OH⋯F⁻ well in the exit channel.¹² The stationary points of the OH⁻ + CH₃F Walden-inversion pathway were characterized by Sun et al.¹³ at HF, MP2 and CCSD(T) levels of theory and by Gonzales et al.^18,19 using density functional theory and the focal-point approach. Recently, based on the results of Hase and co-workers, several reaction analysis methods were applied for the reaction of OH⁻ and CH₃F.^20–24 Furthermore, dynamics simulations uncovered a novel oxide ion substitution for the reaction: in the post-reaction CH₃OH⋯F⁻ complex the leaving F⁻ may remove the proton of the hydroxyl group, which leads to the products of HF + CH₃O⁻.^25,26 The existence of the oxide ion substitution for OH⁻ + CH₃F was also confirmed by Li and co-workers,²⁷ and Ji et al. completed a detailed mapping of the possible proton abstraction-involved channels for the Y⁻(H₂O)_n + CH₃I (Y = F, Cl, Br, I) reactions, where n = 1 or 2, taking into account an oxide ion substitution leading to the CH₃O⁻ + HY + HI + (n − 1)H₂O products.²⁸ The OH⁻ + CH₃Cl S_N2 reaction was examined by various studies as well. The stationary points were identified by Evanseck et al.,¹⁰ and later the results were recalculated by Tachikawa et al.,¹¹ Souza et al.,²⁹ Laloo et al.³⁰ and Zhao et al.³¹ using DFT, HF, MP2 and CCSD(T) methods; moreover, direct dynamics simulations were also conducted at the HF/3-21+G(d) and B3LYP/aug-cc-pVDZ levels of theory.^31,32 Wang and co-workers performed QM/MM calculations for the OH⁻ + CH₃Y (Y = F, Cl and Br) S_N2 reactions in aqueous solution.^33–35

For the OH⁻ + CH₃I reaction, numerous experimental and theoretical investigations were carried out in the last decade.^14,36–43 Cross-beam imaging techniques were employed to analyse the dynamics of the reactions of OH⁻, OH⁻(H₂O) and OH⁻(H₂O)₂ with CH₃I at collision energies (E_coll) of 11.5, 23.1, 34.6 and 46.1 kcal mol⁻¹.³⁷ Considering the I⁻ velocity vector distributions, three different S_N2 reaction mechanisms were observed, and their occurrences were dependent on the presence of the water molecules. The stationary points of the latter reactions were studied, as well, using DFT and MP2 methods.^14,38,39,41 The crossed-beam and selected ion flow tube experiments were supported by the direct dynamics simulations of Hase and co-workers in order to describe the dynamics and kinetics of the reaction.^14,38,40,42 These findings, along with others, showed that the dynamics of the S_N2 reactions had to be rethought, because the picture is more complex than the traditional one.⁴⁴ For that reason, in 2018, we characterized the Walden-inversion, front-side attack and double-inversion mechanisms of the OH⁻ + CH₃Y (Y = F, Cl, Br, I) S_N2 reactions with high-level ab initio methods.¹⁵ In 2020, for the title reaction, several global analytical potential energy surfaces (PESs) were developed utilizing the in-house ROBOSURFER program package.^45,46 The final choice of the ab initio method was not evident: quasi-classical trajectory (QCT) simulations on the PESs unveiled that the gold-standard CCSD(T) method provides unphysically negative energies at some regions of the PES, and therefore a composite ab initio method was applied to obtain the energies of the structures.

In this work, we report a more detailed dynamical study of the OH⁻ + CH₃I reaction. At first, for the title reaction, we determine the benchmark geometries, frequencies and energies of the stationary points of the proton-abstraction pathway using the modern explicitly correlated CCSD(T)-F12b method in order to explore the energetics of the competing S_N2 and proton-abstraction channels. Then, utilizing our previously constructed PES,⁴⁵ in total more than half a million QCT computations are run at E_coll of 11.5, 23.1, 34.6 and 46.1 kcal mol⁻¹ providing the integral cross-sections (ICSs) of the possible reaction mechanisms, the scattering angle distributions and the translational and internal energy distributions of the S_N2 and proton-abstraction products, as well. Last but not least, the QCT results are compared with the reanalysed crossed-beam imaging experiments for the OH⁻ + CH₃I reaction. The details of the theoretical and experimental methods are given in Section II. The results are described and discussed in Section III, and in Section IV, the summary of the work can be found.

II. Computational and experimental methods

For the ab initio characterization of the OH⁻ + CH₃I → H₂O + CH₂I⁻ reaction, the same process is implemented as for the S_N2 channel discussed in ref. 15: the stationary points are searched at the MP2/aug-cc-pVDZ level of theory,⁴⁷ then, for the more accurate energies, structures and frequencies, the modern explicitly correlated coupled cluster singles, doubles and perturbative triples CCSD(T)-F12b method⁴⁸ is employed with the correlation-consistent aug-cc-pVDZ and aug-cc-pVTZ basis sets.⁴⁹ The benchmark classical energies are obtained utilizing the CCSD(T)-F12b method with the aug-cc-pVQZ basis set at the CCSD(T)-F12b/aug-cc-pVTZ geometries, and considering the post-CCSD(T) correlation effects^50–52 and the core correlation corrections. Taking account of the zero-point energy (ZPE) of the corresponding stationary point, the adiabatic energy is determined. For I, a small-core relativistic effective core potential⁵³ is applied with the aug-cc-pVnZ-PP (n = 2, 3, 4) and aug-cc-pwCVTZ-PP basis sets. Most of the ab initio calculations are performed using the MOLPRO program package,⁵⁴ except for CCSDT and CCSDT(Q) where the MRCC program is used.^55,56 A more detailed description of the ab initio computations is given in ref. 15.

On our previously developed PES, QCT simulations are carried out for the reaction of OH⁻ + CH₃I at 11.5, 23.1, 34.6 and 46.1 kcal mol⁻¹E_coll. In ref. 45, the interested reader may find the details about the PES development. It should be noted that the energy points of the PES are computed at the CCSD-F12b/aug-cc-pVTZ + BCCD(T)/aug-cc-pVDZ − BCCD/aug-cc-pVDZ composite level of theory⁵⁷ to resolve the failure of the CCSD(T)-F12b method. With regard to the conditions of the simulations, the vibrational ground states of the reactants (ν = 0) are prepared by normal-mode sampling,^58,59 and the rotational angular momenta are set to zero. The initial orientations of the reactants are randomly sampled, and the initial distance of OH⁻ and CH₃I is 40 bohr with a given impact parameter (b). At each b, 5000 trajectories are propagated and b is scanned from 0 to b_max (where the probability of the reaction becomes 0) with a step size of 0.5 bohr. Each trajectory is run with a time step of 0.0726 fs until the largest interatomic distance becomes larger by 1 bohr than the largest initial one. The opacity function (P(b)) is defined by the reaction probability as a function of b. At each E_coll, the ICS of each reaction channel is determined by a b-weighted numerical integration of the corresponding P(b):

which is expressed by the trapezoidal rule of the numerical integration. The scattering angle (θ) is the angle of the relative velocity vectors of the centre of masses of the OH⁻ and CH₃I reactants and the relevant products. The distributions of θ are attained by binning the cosine of the θ into 10 (for S_N2) and 20 (for proton abstraction) equidistant bins from −1 to 1, where cos(θ) = 1 corresponds to forward scattering. For the ICS of proton abstraction, two types of ZPE constraints are applied: (1) soft: reject trajectory if the sum of the classical vibrational energies of the CH₂I⁻ and H₂O products is smaller than the sum of their ZPEs on the PES, (2) hard: reject trajectory if the vibrational energy of either product is less than its ZPE on the PES. The product channels of the OH⁻ + CH₃I reaction are differentiated by determining the relevant bond distances of the corresponding products similarly as for the case of NH₂⁻ + CH₃I.⁶⁰ Note that, the distinction of the four different channels of proton abstraction with dissociation is based on the different C–I, O–I and C–O distances.

The experimental data on the OH⁻ + CH₃I reaction have been obtained using crossed-beam velocity map imaging, as described in earlier publications.^14,36,37 In brief, the negative ions were produced in a pulsed plasma discharge, mass-selected by time-of-flight, and stored in an octupole ion trap at about 100 K to cool the translational and rotational motion. After extraction from the trap, the ions were crossed with a supersonic neutral jet of CH₃I seeded in helium with relative collision energies selected between 11.5 and 46.1 kcal mol⁻¹ (0.5 and 2.0 eV). Product ions were mapped by a velocity map imaging spectrometer onto a position- and time-sensitive detector and for each reactive event the detector information was transformed into a product mass and velocity vector in the centre-of-mass frame. From the three-dimensional velocity distribution, the angular and internal energy distributions are integrated after multiplication with an appropriate Jacobian. During re-evaluation of the data, we noticed that for the integration of the relative translational energy distributions shown in Fig. 6 of ref. 14, an incorrect Jacobian was used, which is corrected in the present work.

III. Results and discussion

The stationary points of S_N2 and proton-abstraction channels of the OH⁻ + CH₃I reaction are shown in Fig. 1 with the corresponding benchmark classical relative energies and PES values. The detailed ab initio energies are summarized in Table 1 and the structures of the stationary points are given in Fig. S1 (ESI†). Similar to the back-side attack Walden-inversion (HMIN → HTS → PostHMIN), proton abstraction is also a submerged pathway, although S_N2 is much more exothermic with a reaction energy of 66.64 kcal mol⁻¹. In the entrance channel of S_N2 the Y⋯OH⁻-bonded front-side complex is below HMIN and the global minimum of the reaction is in the product channel of S_N2 (PostHMIN) with a classical energy of −78.78 kcal mol⁻¹. In the case of proton abstraction, involving the same H-bonded complex (HMIN) in the reactant channel as for S_N2, four minima and three transition states can be found: HMIN → TS1′/TS1′′ → MIN1′/MIN1′′ → TS2 → MIN2. As it can be seen in Fig. 1 and Fig. S1 (ESI†), TS1′ and TS1′′, as well as, MIN1′ and MIN1′′ are conformational isomers, due to the torsional motion of OH⁻: For TS1′ and MIN1′, the torsion angle of I–C⋯O–H⁻ is 180° (trans arrangement), while for TS1′′ and MIN1′′ the value is 0° (cis arrangement). The energies of the isomers are similar, TS1′ is below TS1′′ by 0.98 kcal mol⁻¹ and MIN1′ is above MIN1′′ by 1.32 kcal mol⁻¹, without ZPE corrections (Fig. 1). It should be emphasised that, considering ZPE effects, an energy of −17.45 and −18.74 kcal mol⁻¹ can be observed for TS1′ and TS1′′, respectively, and since the benchmark adiabatic energy is −18.07 kcal mol⁻¹ for HMIN, the barrier of TS1′′ vanishes (Table 1). For the stationary points of proton abstraction, the post-CCSD(T) effects are small, whereas, for S_N2, more significant post-CCSD(T) effect can be determined, especially for FSTS (−0.90 kcal mol⁻¹). Generally, the post-CCSD(T) and the core correlation effects cancel each other, however, in some cases, accumulation of the effects still appears with the highest values of 1.06 and 0.60 kcal mol⁻¹ for the S_N2 and proton-abstraction products, in order. The ZPE effects are usually between ±0.7 kcal mol⁻¹, except for PostHMIN, TS1′′, I⁻ + CH₃OH and CH₂I⁻ + H₂O, where much higher effects occur: 4.49, −1.93, 3.98 and −1.33 kcal mol⁻¹, respectively. The DFT energies of the stationary points provided by Xie et al.³⁸ are in a qualitative agreement with our benchmark results, although the energy differences for several cases are larger than 2 kcal mol⁻¹, especially for TS1′′, showing a deviation of −2.96 kcal mol⁻¹. This latter energy discrepancy shows that by employing DFT method, TS1′′ happens to be below TS1′, and the barrier heights of TS1′′ and TS1′ remarkably diminish (0.30 and 0.44 kcal mol⁻¹) compared to the benchmark classical values (1.68 and 0.70 kcal mol⁻¹, in order). As seen in Fig. 1, for the S_N2 pathway, the PES reproduces the benchmark energies of the stationary points within the chemical accuracy (±1 kcal mol⁻¹), while in the case of proton abstraction, PES provides slightly lower relative energies for MIN1′, MIN1′′, TS2, MIN2 and CH₂I⁻ + H₂O than the corresponding benchmark values, with differences of 1.16, 1.17, 1.53, 1.39 and 1.62 kcal mol⁻¹, respectively.

Fig. 1 The schematic potential energy surfaces of the S_N2 and proton-abstraction pathways for the OH⁻ + CH₃I reaction showing the classical benchmark relative energies (kcal mol⁻¹) of the stationary points with the corresponding PES values, relative to OH⁻(eq.) + CH₃I(eq.). In the case of the S_N2 channel, the benchmark energies and PES values are derived from ref. 15 and 45, respectively.

Table 1 Benchmark classical and adiabatic energies (kcal mol⁻¹) of the stationary points, relative to the OH⁻(eq.) + CH₃I(eq.) reactants, for the S_N2 and proton-abstraction pathways of the OH⁻ + CH₃I reaction. For the OH⁻ + CH₃I S_N2 reaction, the benchmark classical and adiabatic ab initio energies are adapted from ref. 15

SN2	DZ^a	TZ^b	QZ^c	δT^d	δ(Q)^e	Δcore^f	Classical^g	ΔZPE^h	Adiabatic^i
a CCSD(T)-F12b/aug-cc-pVDZ. b CCSD(T)-F12b/aug-cc-pVTZ. c CCSD(T)-F12b/aug-cc-pVQZ. d CCSDT/aug-cc-pVDZ – CCSD(T)/aug-cc-pVDZ. e CCSDT(Q)/aug-cc-pVDZ – CCSDT/aug-cc-pVDZ. f AE-CCSD(T)/aug-cc-pwCVTZ – FC-CCSD(T)/aug-cc-pwCVTZ. g QZ + δT + δ(Q) + Δcore. h ΔZPE(CCSD(T)-F12b/aug-cc-pVTZ). i QZ + δT + δ(Q) + Δcore + ΔZPE.
HMIN	−18.89	−18.64	−18.48	−0.02	0.00	0.02	−18.49	0.42	−18.07
HTS	−16.74	−16.69	−16.57	−0.04	−0.04	0.01	−16.65	0.50	−16.15
PostHMIN	−79.30	−79.08	−79.43	0.09	0.27	0.29	−78.78	4.49	−74.29
FSMIN	−24.09	−24.10	−24.05	0.07	−0.23	0.51	−23.69	0.68	−23.01
FSTS	17.19	17.03	17.10	−0.11	−0.79	0.42	16.62	0.58	17.20
DITS	−4.20	−4.13	−4.05	0.07	−0.01	0.15	−3.85	0.18	−3.67
I^− + CH3OH	−67.16	−67.08	−67.71	0.08	0.31	0.67	−66.64	3.98	−62.67

---

ABS	DZ^a	TZ^b	QZ^c	δT^d	δ(Q)^e	Δcore^f	Classical^g	ΔZPE^h	Adiabatic^i
TS1′	−18.19	−17.92	−17.76	−0.04	−0.02	0.02	−17.79	0.33	−17.45
TS1′′	−17.38	−17.11	−16.93	0.01	−0.02	0.14	−16.81	−1.93	−18.74
MIN1′	−19.60	−19.49	−19.36	−0.02	0.04	0.32	−19.03	0.33	−18.70
MIN1′′	−20.89	−20.80	−20.69	−0.03	0.04	0.32	−20.35	0.53	−19.82
TS2	−10.65	−10.60	−10.57	−0.06	0.06	0.41	−10.15	−0.08	−10.23
MIN2	−13.14	−13.13	−13.07	−0.06	0.05	0.35	−12.73	0.56	−12.16
CH2I^− + H2O	−1.77	−1.96	−2.08	−0.07	0.11	0.56	−1.49	−1.33	−2.82

---

In order to characterize the dynamics of the title reaction, QCT computations are carried out at several E_coll (11.5, 23.1, 34.6 and 46.1 kcal mol⁻¹) on our earlier constructed analytical PES⁴⁵ (see Computational and experimental methods). The ICSs of the possible reaction channels at each E_coll are presented in Fig. 2 and in Table S1 (ESI†). As it is expected for barrierless reactions, with increasing E_coll, the ICSs of proton abstraction and S_N2 are decreasing. The largest ICSs are obtained for proton abstraction at each E_coll, peaking at a value of 169.8 bohr² at E_coll = 11.5 kcal mol⁻¹, and even with soft ZPE restriction, the ICSs of proton abstraction are larger than the corresponding values of the S_N2 channel. Using hard ZPE restriction for proton abstraction, the reaction probability suffers a significant decrease, as its ICSs are 23.9 and 14.8 bohr² at E_coll = 11.5 and 23.1 kcal mol⁻¹, respectively, while in the case of soft ZPE restriction, ICSs of 100.0 and 40.1 bohr² are determined. For S_N2, no ZPE violation can be obtained. The opacity functions of S_N2 and proton abstraction are shown in Fig. S2 (ESI†). Since the four hydrogen atoms can be distinguished during the course of a simulation, two additional pathways can be identified within S_N2: besides inversion, retention of the initial CH₃I configuration can also take place (S_N2 with retention), on the other hand, a proton exchange is feasible between the OH⁻ and CH₃I reactants followed by the traditional Walden inversion (S_N2 with proton exchange). Within proton abstraction, two other paths can be separated as well: following proton abstraction, a dissociation of the C–I bond may occur (proton abstraction with dissociation), and analogously to S_N2 with proton exchange, proton abstraction with proton exchange can proceed. Likewise for the NH₂⁻ + CH₃I reaction,⁶⁰ the formation of the products of iodine abstraction ([I⋯OH]⁻ + CH₃) is viable, although with a significantly lower probability, and in some cases, as for OH⁻ + CH₃F,²⁶ proton exchange between OH⁻ and CH₃I may eventuate resulting products apparently similar to reactants: OH⁻ + CH₂H′I → HOH′ + CH₂I⁻ → OH′⁻ + CH₂HI. Regarding the channels involving proton exchange, at lower E_coll, their ICSs are in the range of 0.3–1.2 bohr², whereas, at higher E_coll, these paths are almost negligible. Fig. 3 shows that proton abstraction with dissociation can be separated into four different channels with the largest probability of the CH₂ + I⁻ + H₂O product formation.

Fig. 2 Integral cross-sections for (A) S_N2, proton abstraction with soft and hard restriction; (B) S_N2 with proton exchange, proton abstraction with proton exchange and proton abstraction with dissociation; and (C) iodine abstraction, S_N2 with retention and proton exchange pathways of the OH⁻ + CH₃I reaction as a function of collision energy.

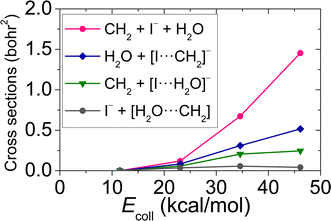Fig. 3 Integral cross-sections for the different types of the proton abstraction with dissociation pathway of the OH⁻ + CH₃I reaction as a function of collision energy.

Performing crossed-beam ion imaging experiments for the OH⁻ + CH₃I reaction, the following product ions are detected: I⁻, CH₂I⁻ and [I⋯H₂O]⁻/[I⋯OH]⁻. The latter product ions cannot be resolved individually, because the masses of the ions are almost equivalent (145 u/144 u), thus the time-of-flight peaks of [I⋯H₂O]⁻ and [I⋯OH]⁻ overlap. The experimental and theoretical branching ratios of these ions are shown in Table 2 at E_coll = 11.5, 23.1 34.6 and 46.1 kcal mol⁻¹. In QCT simulations, I⁻ is provided by three different reaction channels: S_N2 (I⁻ + CH₃OH) and two pathway-types of proton abstraction with dissociation (CH₂ + I⁻ + H₂O and I⁻ + [CH₂⋯H₂O]). CH₂I⁻ is formed as a result of proton abstraction, and note that, for the branching ratios, the soft ZPE-restricted proton abstraction is taken into account. The product of [I⋯H₂O]⁻ is generated by one of the pathways of proton abstraction with dissociation, while [I⋯OH]⁻ occurs as a result of iodine abstraction, as seen in Fig. 2 and 3. At 11.5 kcal mol⁻¹E_coll, experiment assesses a slightly higher ratio for I⁻ than theory with a difference of ∼1.4%, while at E_coll = 23.1 kcal mol⁻¹, a reversed situation appears, the formation of the I⁻ is overestimated by theory emerging a ∼4.3% deviation. As a consequence, at low E_coll, the computed and measured ratios of the CH₂I⁻ product ion also differ from each other. Nevertheless, the agreement between theory and experiment is still impressive, almost quantitative, at these low collision energies. Furthermore, at higher E_coll, an excellent, clearly quantitative, agreement can be identified between the experimental and theoretical branching ratios of I⁻ and CH₂I⁻: the differences of the corresponding ratios are below ∼0.4%. At each E_coll, experiment reveals a more significant prevalence of the [I⋯H₂O]⁻/[I⋯OH]⁻ product ions, for instance at 46.1 kcal mol⁻¹E_coll, a value of 2.58% is measured, whilst theory provides only 0.91%. It should be highlighted that, in the case of proton abstraction with dissociation, QCT simulations unveil another product ion, [I⋯CH₂]⁻ (see Fig. 3), which may be detected by the crossed-beam technique as I⁻ if the complex dissociates during the time scale of the experiment or as CH₂I⁻ if the complex remains stable. Therefore, we do not consider the small fraction of [I⋯CH₂]⁻ (0%, 0.1%, 0.8% and 1.8% at E_coll = 11.5, 23.1 34.6 and 46.1 kcal mol⁻¹, respectively) at the branching ratio computations. Nonetheless, the direct dynamics simulations performed by Xie et al. gave branching ratios of 31%, 38% and 36%, for I⁻, and 69%, 62% and 63% for CH₂I⁻ at E_coll = 11.5, 34.6 and 46.1 kcal mol⁻¹.¹⁴

Table 2 The experimental and theoretical branching ratios (%) of the product anions of I⁻, CH₂I⁻ and [I⋯H₂O]⁻/[I⋯OH]⁻ for the OH⁻ + CH₃I reaction at different collision energies. Note that for the theoretical branching ratios, soft ZPE-restricted proton abstraction is considered^a

E coll (kcal mol^−1)	I^−		CH2I^−		[I⋯H2O]^−/[I⋯OH]^−
	Exp.	Sim.^b	Exp.	Sim.^c	Exp.^d	Sim.^e
a 100% = ICSSN2 + ICSABS soft + ICSABS dissociation + ICSIodine ABS + ICSProton exch. b I^− originates from SN2, and two channels of the proton abstraction with dissociation leading to CH2 + I^− + H2O or I^− + [CH2⋯H2O]. c CH2I^− originates from the soft-restricted proton abstraction. d The [I⋯H2O]^− and [I⋯OH]^− ions cannot be distinguished from each other experimentally. e The sum of the branching ratios of the [I⋯H2O]^− and [I⋯OH]^− product ions. [I⋯H2O]^− originates from one of the channels of proton abstraction leading to the CH2 + [I⋯H2O]^− products, while [I⋯OH]^− is generated in iodine abstraction.
11.5	45.38	44.01	53.79	55.76	0.84	0.03
23.1	32.54	36.83	66.66	62.81	0.80	0.13
34.6	36.49	36.31	62.00	62.22	1.51	0.60
46.1	40.49	40.75	56.93	56.57	2.58	0.91

---

For the products of OH⁻ + CH₃I S_N2 and the proton-abstraction reaction, the experimental and theoretical internal energy as well as scattering angle distributions are compared at several E_coll in Fig. 4 and 5. As we can distinguish the products of proton abstraction in each simulation, the internal energy contributions of CH₂I⁻ and H₂O can be determined, which is presented in Fig. 6. The theoretical translational energy distributions of the S_N2 and proton-abstraction products are shown in Fig. 7. In the case of the products of proton abstraction, with increasing E_coll, translational energies are more affected, than internal energies and the dominance of the forward-scattering becomes more and more favoured. These tendencies support a prevalence of the direct stripping mechanism at each E_coll for proton abstraction, and it should also be emphasised that experiment and theory are in accordance with each other. As it can be expected, the internal energy contributions of the CH₂I⁻ product ion are more substantial than that of H₂O declaring that H₂O is more responsible for the hard-restricted proton-abstraction trajectories than CH₂I⁻. In contrast, the dynamics of S_N2 has a different character: on the one hand, upon increasing E_coll, the CH₃OH internal energy is more impacted than translational energy showing an indirect feature. On the other hand, the scattering angle distributions of CH₃OH display forward and/or backward preference besides the isotropic character signifying direct stripping and/or rebound pathways as well as complex-forming indirect dynamics. As seen in Fig. 4 and 5, the experimental and theoretical CH₃OH internal energy distributions are in good agreement at E_coll = 11.5 and 23.1 kcal mol⁻¹, whilst theory underestimates internal energies at E_coll = 34.6 and 46.1 kcal mol⁻¹. Regarding the scattering angle distributions of the S_N2 products, a pleasant agreement can be identified, as well, except at E_coll of 23.1 kcal mol⁻¹, where experiment shows the preference of a dual forward-backward scattering; however computations reveal an isotropic feature. Concerning the direct dynamics computations of Xie et al., for proton abstraction and S_N2, as well, a forward-scattered distribution is reported at E_coll = 11.5, 34.6 and 46.1 kcal mol⁻¹.¹⁴

Fig. 4 Experimental and theoretical (ZPE-corrected) internal energy distributions of the products of the S_N2 (CH₃OH) and proton-abstraction (CH₂I⁻ + H₂O) channels of the OH⁻ + CH₃I reaction at different collision energies.

Fig. 5 Experimental and theoretical normalized scattering angle distributions of the products of the S_N2 (CH₃OH + I⁻) and proton-abstraction (CH₂I⁻ + H₂O) channels of the OH⁻ + CH₃I reaction at different collision energies.

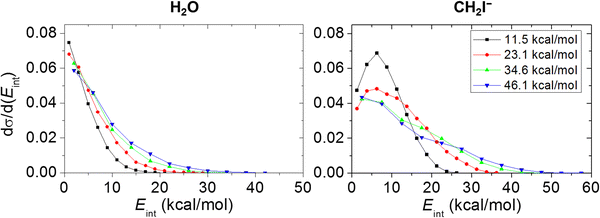Fig. 6 Theoretical ZPE-corrected internal energy distributions of the products of the proton-abstraction channel (H₂O and CH₂I⁻) of the OH⁻ + CH₃I reaction at different collision energies.

Fig. 7 Theoretical relative translational energy distributions of the products of the S_N2 (CH₃OH + I⁻) and proton-abstraction (CH₂I⁻ + H₂O) channels of the OH⁻ + CH₃I reaction at different collision energies.

IV. Summary and conclusions

In this paper, the dynamics of the OH⁻ + CH₃I reaction has been investigated performing QCT simulations at E_coll of 11.5, 23.1, 34.6 and 46.1 kcal mol⁻¹ on our high-level ab initio PES.⁴⁵ Utilizing the explicitly correlated CCSD(T)-F12b method, the stationary points of the proton-abstraction channel have been explored and presented with the previously characterized S_N2 channel.¹⁵ The theoretical analysis for the title reaction has been compared with the revised crossed-beam ion imaging experiments. Briefly, in the case of the branching ratios of the product ions, the internal energy distributions of the S_N2 and proton-abstraction products, as well as the scattering angle distributions of the proton-abstraction products, a pleasant agreement has been found. For proton abstraction, a dominance of the direct stripping mechanism is unveiled, in contrast for S_N2, a rather indirect character is found. The most notable difference between theory and experiment is observed for the scattering angle distributions of CH₃OH at E_coll = 23.1 kcal mol⁻¹, where a mixed backward–forward character is measured, while simulations show an isotropic feature. The earlier reported direct dynamics study of Xie et al.¹⁴ could not describe the dynamics of the OH⁻ + CH₃I reaction as accurate as our present QCT simulations, underlining the importance of the accuracy of the PES to provide well comparable results with experiments.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

The authors at the University of Szeged are thankful for the financial support from the National Research, Development and Innovation Office–NKFIH, Grant No. K-125317; the Ministry of Human Capacities, Hungary, Grant No. 20391-3/2018/FEKUSTRAT; Project No. TKP2021-NVA-19, provided by the Ministry of Innovation and Technology of Hungary from the National Research, Development and Innovation Fund, financed under the TKP2021-NVA funding scheme; the National Young Talent Scholarship (Grant No. NTP-NFTÖ-22-B-0050 for D. A. T.); and the Momentum (Lendület) Program of the Hungarian Academy of Sciences. The work at the University of Innsbruck has been supported by the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement no. 885479).

References

1. S. S. Shaik, H. B. Schlegel and S. Wolfe, Theoretical Aspects of Physical Organic Chemistry: The S_N2 Mechanism, Wiley, New York, 1992.
2. A. H. Maulitz, F. C. Lightstone, Y. J. Zheng and T. C. Bruice, Proc. Natl. Acad. Sci. U. S. A., 1997, 94, 6591.
3. J. K. Laerdahl and E. Uggerud, Int. J. Mass Spectrom., 2002, 214, 277.
4. G. Vayner, K. N. Houk, W. L. Jorgensen and J. I. Brauman, J. Am. Chem. Soc., 2004, 126, 9054.
5. J. M. Gonzales, W. D. Allen and H. F. Schaefer, J. Phys. Chem. A, 2005, 109, 10613.
6. T. A. Hamlin, M. Swart and F. M. Bickelhaupt, ChemPhysChem, 2018, 19, 1315.
7. R. Wester, Mass Spectrom. Rev., 2022, 41, 627.
8. T. Hansen, P. Vermeeren, L. De Jong, F. M. Bickelhaupt and T. A. Hamlin, J. Org. Chem., 2022, 87, 8892.
9. X. Lu, C. Shang, L. Li, R. Chen, B. Fu, X. Xu and D. H. Zhang, Nat. Commun., 2022, 13, 4427.
10. J. D. Evanseck, J. F. Blake and W. L. Jorgensen, J. Am. Chem. Soc., 1987, 109, 2349.
11. H. Tachikawa, M. Igarashi and T. Ishibashi, J. Phys. Chem. A, 2002, 106, 10977.
12. L. Sun, K. Song and W. L. Hase, Science, 2002, 296, 875.
13. L. Sun, K. Song, W. L. Hase, M. Sena and J. M. Riveros, Int. J. Mass Spectrom., 2003, 227, 315.
14. J. Xie, R. Sun, M. R. Siebert, R. Otto, R. Wester and W. L. Hase, J. Phys. Chem. A, 2013, 117, 7162.
15. D. A. Tasi, Z. Fábián and G. Czakó, J. Phys. Chem. A, 2018, 122, 5773.
16. H. B. Schlegel, K. Mislow, F. Bernardi and A. Bottoni, Theor. Chim. Acta, 1977, 44, 245.
17. I. Szabó and G. Czakó, Nat. Commun., 2015, 6, 5972.
18. J. M. Gonzales, R. S. Cox, S. T. Brown, W. D. Allen and H. F. Schaefer, J. Phys. Chem. A, 2001, 105, 11327.
19. J. M. Gonzales, C. Pak, R. Sidney Cox, W. D. Allen, H. F. Schaefer, A. G. Császár and G. Tarczay, Chem. – Eur. J., 2003, 9, 2173.
20. T. Tsutsumi, Y. Ono, Z. Arai and T. Taketsugu, J. Chem. Theory Comput., 2018, 14, 4263.
21. T. Tsutsumi, Y. Ono, Z. Arai and T. Taketsugu, J. Chem. Theory Comput., 2020, 16, 4029.
22. T. Tsutsumi, Y. Ono and T. Taketsugu, Chem. Commun., 2021, 57, 11734.
23. T. Tsutsumi, Y. Ono and T. Taketsugu, Top. Curr. Chem., 2022, 380, 19.
24. S. R. Hare, L. A. Bratholm, D. R. Glowacki and B. K. Carpenter, Chem. Sci., 2019, 10, 9954.
25. Y. G. Proenza, M. A. F. de Souza and R. L. Longo, Chem. – Eur. J., 2016, 22, 16220.
26. D. A. Tasi and G. Czakó, Chem. Sci., 2021, 12, 14369.
27. J. Qin, Y. Liu and J. Li, J. Chem. Phys., 2022, 157, 124301.
28. X. Ji and J. Xie, Phys. Chem. Chem. Phys., 2022, 24, 7539.
29. A. C. B. De Souza and G. F. Bauerfeldt, J. Braz. Chem. Soc., 2014, 25, 340.
30. J. Z. A. Laloo, L. Rhyman, O. Larrañaga, P. Ramasami, F. M. Bickelhaupt and A. de Cózar, Chem. – Asian J., 2018, 13, 1138.
31. S. Zhao, G. Fu, W. Zhen, L. Yang, J. Sun and J. Zhang, Phys. Chem. Chem. Phys., 2022, 24, 24146.
32. H. Tachikawa and M. Igarashi, Chem. Phys., 2006, 324, 639.
33. H. Yin, D. Wang and M. Valiev, J. Phys. Chem. A, 2011, 115, 12047.
34. Y. Xu, T. Wang and D. Wang, J. Chem. Phys., 2012, 137, 184501.
35. J. Chen, Y. Xu and D. Wang, J. Comput. Chem., 2014, 35, 445.
36. R. Otto, J. Xie, J. Brox, S. Trippel, M. Stei, T. Best, M. R. Siebert, W. L. Hase and R. Wester, Faraday Discuss., 2012, 157, 41.
37. R. Otto, J. Brox, S. Trippel, M. Stei, T. Best and R. Wester, Nat. Chem., 2012, 4, 534.
38. J. Xie, S. C. Kohale, W. L. Hase, S. G. Ard, J. J. Melko, N. S. Shuman and A. A. Viggiano, J. Phys. Chem. A, 2013, 117, 14019.
39. J. Xie, R. Otto, R. Wester and W. L. Hase, J. Chem. Phys., 2015, 142, 244308.
40. J. Xie, J. Zhang and W. L. Hase, Int. J. Mass Spectrom., 2015, 378, 14.
41. J. Xie, X. Ma, J. Zhang, P. M. Hierl, A. A. Viggiano and W. L. Hase, Int. J. Mass Spectrom., 2017, 418, 122.
42. J. Xie, J. Zhang, R. Sun, R. Wester and W. L. Hase, Int. J. Mass Spectrom., 2019, 438, 115.
43. X. Ji, C. Zhao and J. Xie, Phys. Chem. Chem. Phys., 2021, 23, 6349.
44. J. Xie and W. L. Hase, Science, 2016, 352, 32.
45. D. A. Tasi, T. Győri and G. Czakó, Phys. Chem. Chem. Phys., 2020, 22, 3775.
46. T. Győri and G. Czakó, J. Chem. Theory Comput., 2020, 16, 51.
47. C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618.
48. T. B. Adler, G. Knizia and H. J. Werner, J. Chem. Phys., 2007, 127, 221106.
49. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007.
50. K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479.
51. J. Noga and R. J. Bartlett, J. Chem. Phys., 1986, 86, 7041.
52. M. Kállay and J. Gauss, J. Chem. Phys., 2005, 123, 214105.
53. K. A. Peterson, D. Figgen, E. Goll, H. Stoll and M. Dolg, J. Chem. Phys., 2003, 119, 11113.
54. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, et al., Molpro, version 2015.1, a package of ab initio programs, see http://www.molpro.net.
55. M. Kállay, P. R. Nagy, D. Mester, Z. Rolik, G. Samu, J. Csontos, J. Csóka, P. B. Szabó, L. Gyevi-Nagy, B. Hégely, I. Ladjánszki, L. Szegedy, B. Ladóczki, K. Petrov, M. Farkas, P. D. Mezei and Á. Ganyecz, J. Chem. Phys., 2020, 152, 074107.
56. MRCC, a quantum chemical program suite written by M. Kállay, P. R. Nagy, D. Mester, Z. Rolik, G. Samu, J. Csontos, J. Csóka, P. B. Szabó, L. Gyevi-Nagy, B. Hégely, I. Ladjánszki, L. Szegedy, B. Ladóczki, K. Petrov, M. Farkas, P. D. Mezei and Á. Ganyecz. See http://www.mrcc.hu.
57. K. A. Brueckner, Phys. Rev., 1954, 96, 508.
58. W. L. Hase, Encyclopedia of Computational Chemistry, Wiley, New York, 1998, pp. 399–407.
59. S. Pratihar, X. Ma, Z. Homayoon, G. L. Barnes and W. L. Hase, J. Am. Chem. Soc., 2017, 139, 3570.
60. D. A. Tasi and G. Czakó, J. Chem. Phys., 2022, 156, 184306.

---

Footnote

† Electronic supplementary information (ESI) available: Integral cross sections (bohr²) of the possible pathways, structures of the stationary points for the S_N2 and proton-abstraction pathways with the most important bond lengths (Å) and angles (deg) obtained on the PES compared to the CCSD(T)-F12b/aug-cc-pVTZ values, opacity functions of the S_N2 and proton-abstraction pathways, Cartesian coordinates (Å) and energies (E_h) of the stationary points for the proton-abstraction channel obtained at the CCSD(T)-F12b/aug-cc-pVTZ level of theory. See DOI: https://doi.org/10.1039/d2cp05553h

---