 Open Access Article
Open Access ArticleUsing molecular dynamics to simulate realistic structures of nitrocellulose of different nitration levels†
Catriona
Gibbon
 a,
Poppy
Di Pietro
b,
Mark
Storr
b,
Duncan
Broughton
b and
Chris-Kriton
Skylaris
a,
Poppy
Di Pietro
b,
Mark
Storr
b,
Duncan
Broughton
b and
Chris-Kriton
Skylaris
 *a
*a
aSchool of Chemistry, University of Southampton, Highfield, Southampton, SO17 1BJ, UK. E-mail: C.Skylaris@soton.ac.uk
bAWE Aldermaston, Reading, Berkshire, RG7 4PR, UK
First published on 26th December 2022
Abstract
Nitrocellulose is a reactive derivative of cellulose, one of the most commonly occurring natural materials. Nitration of cellulose decreases the stability of the structure, meaning less is understood about its structure and reactions. Although cellulose is often found in fully crystalline forms, nitrocellulose is more commonly paracrystalline, or amorphous. We present a protocol based on molecular dynamics simulations for creating realistic structures of nitrocellulose, particularly focusing on the crystallinity of the systems being created. We will also provide a detailed analysis of the geometric and dynamical parameters used to quantify the degree of crystallinity for the structures created here, with nitration levels varying from 0–14.14 wt% nitrogen content. Paracrystalline cellulose was not created using the protocol designed here, although it was found that the more nitrated a nitrocellulose system, the more the structure tends to paracrystallinity. This is due to a decrease in the number of hydrogen bonds present, and an increase in the size of the functional groups pushing the chains apart and weakening the interactions between the chains of the structure. The structures created are representative of realistic systems, which in the future will be able to be used to build further understanding of long-term storage of nitrocellulose.
Nitrocellulose has a wide range of uses. Although best known for its use in explosives, it is also used for propellants, coatings, films and printing inks.1
Nitrocellulose is formed from the nitration of cellulose, through the following esterification reaction, which is reversible and highly exothermic.2
| R–OH + H–ONO2 ⇌ R–ONO2 + H2O | (1) |
The nitration level of nitrocellulose has a strong influence on the properties, such as the viscosity, and most importantly, the stability – the more nitrated the nitrocellulose, the less stable it is.4,5 Any nitrocellulose compound containing higher than 12 wt% of nitrogen is considered to be explosive.2
In this paper, we will use the “level of substitution” to refer to the number of positions of the dimer structure that have been nitrated. This means that the nitrate content can be calculated using the following formula:
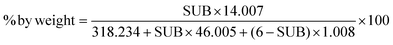 | (2) |
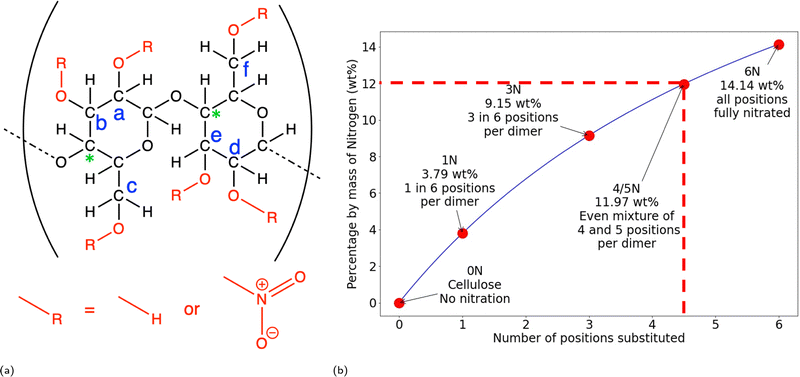 | ||
| Fig. 1 (a) Structure for cellulose and nitrocellulose. The red groups show the positions that can be nitrated, the blue letters are the labels used to refer to these positions and the green * show the carbons being used to measure the RDF discussed in Fig. 4a and b. For cellulose all R groups are hydrogen, and when these are replaced by nitrate groups the cellulose becomes nitrocellulose. (b) Nitration levels for nitrocellulose structures with different levels of substitution, where the number of positions substituted is the number of red –R group positions in (a) that are changed to nitrate groups. The 5 levels of substitution being simulated in this project are highlighted on this graph. The dotted line highlights 12 wt% nitrogen, the accepted limit of explosiveness. | ||
Most of the time cellulose is found in crystalline forms, with chains built up to structures that can contain up to 300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 residues.7 Non-crystalline cellulose is more reactive due to its more disordered structure. Cellulose has multiple crystal forms known as cellulose I, II, III and IV.3
000 residues.7 Non-crystalline cellulose is more reactive due to its more disordered structure. Cellulose has multiple crystal forms known as cellulose I, II, III and IV.3
There are conflicting views on what sort of cellulose model best portrays cellulose crystals, whether it is fully crystalline, or that it contains a combination of crystalline regions and amorphous regions.8 The way that calculations are run depend on the choice of how to model cellulose.
Previous studies such as that by Meader et al. in 1978, have modelled cellulose as several different helix parameters, and the best model they found was a 52 helical conformation.9 The spatial periodicity is 2.54 nm, with 5 glucose rings per period.
If the depolymerisation of cellulose is being studied, amorphous cellulose is important to look at. It is more ‘open’, the flexibility of the chain allowing more access to the glycosidic bonds which are the bonds that break in this process.10
Many cellulose computational chemistry studies use microfibril structures as this is the most commonly occurring natural form. Microfibrils are fibres that occur naturally in wood pulp, and they can be up to 3 × 3 nm in cross-section, and up to several micrometers in length.11 These are often simulated using a limited number of ‘infinitely’ long chains, using periodic boundary conditions. It has been found that the ‘degree of polymerisation’ used here, or the length of the chains in the simulation cell before being repeated through the boundary conditions does affect results, as shown in ref. 12 and 13.
It is known that most nitrocellulose created experimentally is not fully crystalline.14 This means that to create a realistic structure of nitrocellulose, paracrystallinity must be added to the system. The creation of paracrystalline and amorphous cellulose using molecular dynamics has been the subject of many previous studies.10–13,15–17
This study aims to use molecular dynamics simulations to create paracrystalline nitrocellulose systems, and to test how the level of nitration affects the crystallinity.
1 Computational setup
For this study, 5 different nitration levels are simulated, 0 wt% nitrogen (cellulose), 3.49 wt% nitrogen (1 position nitrated per dimer), 6.76 wt% nitrogen (3 positions nitrated per dimer), 12 wt% nitrogen (an even mix of dimers with 4 and 5 positions nitrated, which represents the explosive threshold) and 14.14 wt% nitrogen (fully nitrated nitrocellulose). These will henceforth be referred to based on the level of substitution, 0N, 1N, 3N, 4/5N and 6N respectively.The nitrocellulose unit cells were created by adding nitrate groups to crystalline cellulose Iβ unit cells based on crystallographic data from Nishiyama et al.18 using Avogadro. Coordinates for the atoms and instructions for how to build a unit cell of a specified nitration are available in the ESI.† The dimensions of the cellulose Iβ are shown in Table 1. Large crystal models were built using Moltemplate, a molecule-building tool for LAMMPS.19 The aim was then to perform molecular dynamics on these structures to make them paracrystalline.
| Length (Å) | Angle (°) | Lattice vector (Å) |
|---|---|---|
| a = 8.01 | α = 90 | (8.01, 0.00, 0.00) |
| b = 8.17 | β = 90 | (−1.04, 8.10, 0.00) |
| c = 10.36 | γ = 97.3 | (0.00, 0.00, 10.36) |
These unit cells were then repeated to form the simulation cells. Different sized systems were created, from 4 × 4 × 4 (approximately 6500 atoms), up to 10 × 10 × 10 (approximately 102![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms) and it was found that the size of the system had little effect on the final crystallinity. The systems used for the results presented here are 8 × 8 × 8 systems, containing around 50
000 atoms) and it was found that the size of the system had little effect on the final crystallinity. The systems used for the results presented here are 8 × 8 × 8 systems, containing around 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms.
000 atoms.
All calculations were run using LAMMPS (Large-scale Atomic/Molecular Massively Parallel Simulator).20 LAMMPS is a classical molecular dynamics code used for materials modelling which has previously been used to study cellulose.12
The OPLS (Optimized Potentials for Liquid Simulations) All-Atom force field was used, as this is a well-defined force field within LAMMPS.21 The bonding parameters of this force field have been either based on the values in the AMBER-all atom force field, or found through comparison to ab initio molecular calculations using RHF/6-31G*//RHF/6-31G* on over 50 molecules and the non-bonded parameters are based on Monte Carlo statistical mechanics simulations.22 The original OPLS (Optimized Potentials for Liquid Simulations) used a united-atom model, where only hydrogens attached to aliphatic carbons are considered implicitly. In the all-atom (AA) variation, all hydrogens are defined, which increases the computational cost (a propanol molecule becomes 12 sites to be considered, as opposed to 5), but reduces the error of calculations considerably. OPLS-AA has been used as a basis for studies on nitrocellulose, although extra parameterisation was required for the nitrate groups.23,24
These parameters were found using LigParGen, a web server that can be used to generate OPLS-AA force field parameters for a structure inputted through SMILES or PDB.25 The atoms that needed parameterising were those in the –ONO2 groups. These were found by using LigParGen to give parameters for a molecule of HNO3.
A parameter of importance for the accurate representation of the HNO3 group is the improper dihedral which can be described as the “out-of-plane bending” (Fig. 2).26 If it is not set correctly the nitrogen might not be trigonal planar, as it should be, and instead be trigonal pyramidal, as if there is a lone pair on the carbon.
The improper parameters provided by LigParGen are in a different ‘style’ from the default style in the OPLS-AA file provided on the Moltemplate GitHub, meaning that the style had to be changed from harmonic to CVFF (Constant Valence Force Field), meaning the potential is defined using 3 factors, shown in eqn (3)
E = K[1 + d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) cos(nϕijkl)] cos(nϕijkl)] | (3) |
| E = K(χijkl − χ0) | (4) |
• An energy minimization was performed on the structure, using the conjugate gradient method.
• The initial pressure was found. Due to the method used to make the nitrocellulose – adding nitrate groups into a cellulose structure without making a change to the size of the simulation cell – the density of the structures is going to be unnaturally high, increasing the initial pressure calculated. These initial pressures vary based on the nitration level and are shown in Fig. 2.
• The pressure was then brought down to 1 atm at a rate of 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atm per ns using NPT simulations, which seems fast, but was chosen to be compatible with all of the timescales needed, based on the initial pressures shown in Table 2.
000 atm per ns using NPT simulations, which seems fast, but was chosen to be compatible with all of the timescales needed, based on the initial pressures shown in Table 2.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atm per ns
000 atm per ns
| Structure name | P 0 (atm) | Time (ns) |
|---|---|---|
| Note: 0N is from experimental data, and it is not equilibrated in the OPLSAA forcefield, so it will still have a higher initial pressure than room pressure. | ||
| 0N | 100 | 0.001 |
| 1Na | 41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
0.415 |
| 1Nb | 42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
0.421 |
| 1Nc | 41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
0.416 |
| 1Nd | 41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 800 |
0.418 |
| 1Ne | 43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
0.431 |
| 1Nd | 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700 |
0.317 |
| 3Ncfa | 234![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
2.34 |
| 3Ncfb | 199![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
1.99 |
| 3Ncfd | 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
2.00 |
| 3Ncfe | 214![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
2.14 |
| 4/5N | 403![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
4.03 |
| 6N | 703![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
7.03 |
• 10 ns of NPT were run on the structures, and then an analysis of the crystallinity was run.
In some cases, either where paracrystalline structures had not been formed, or further simulation was chosen to be performed, annealing cycles were run to see if further heating and cooling would help break the crystallinity.16
• Heat to 700 K at a rate of 100 K per 1 ns (4 ns)
• 1 ns at constant 700 K and 1 atm
• 2 ns at constant 300 K and 1 atm
An example of the analysis of annealing cycles on cellulose is included in the ESI.†
All LAMMPS calculations were run using 0.5 fs timestep, Nosé-Hoover thermostat and barostat, with the temperature relaxation time set to 100 timesteps (50 ps) and the pressure relaxation time set to 1000 timesteps (500 ps). All of the calculations are NPT, and they were run using the triclinic setting in LAMMPS, meaning that all 6 of the parameters of the simulation cell – x, y, z and xy, xz, yz are all able to change independently.
1.1 Characterisation techniques
Several techniques can be used to look at different aspects of the simulation and to assess the crystallinity of the structures. | (5) |
After a calculation reaches an equilibrium, the variation of the structure should settle down, meaning that the RMSD can be used to show that an equilibrium has been reached.
 | ||
| Fig. 4 (a) Shows the RDF between the fourth carbon of each monomer within cellulose structures. The d labels here show regions of peaks representing specific distances, illustrated in (b), with the d1 and d2 demonstrated on two dimer sections of cellulose. The carbons between which the RDF is being measured are shown in green (illustrated by a green * on the structure shown in Fig. 1a). Other carbon atoms are shown in grey, oxygen atoms in red and hydrogen atoms in white. The profiles here are plotted from results obtained in this paper, using the RDF for the initial crystalline structure of 0N, and the final structures for 6N and 45N respectively. | ||
There are still two very clear peaks in the paracrystalline RDF shown in Fig. 4a, at around 5 Å and 10 Å. This is to be expected, as they represent the distances along the chain, which are not going to be subject to much variation as the periodic boundary conditions will prevent the folding of chains.
Cellulose and nitrocellulose have been studied under many different conditions and states, so there are many different literature density values. The structures created for this study are based on cellulose Iβ. In 2014 Kulasinski et al.11 studied cellulose, and found two values for the density, experimentally it was 1.656 g cm−3, and through simulation 1.501 g cm−3, implying that the structure experimentally is less pure crystalline than the simulations. 1.58 g cm−3 is often said to be the “commonly accepted” density value for nitrocellulose,14 although in the book “Explosives” by27 it specifies that for 13.3 wt% nitrocellulose the density is 1.67 g cm−3.27 In 2017 the effect of the nitration level on the density was studied by He et al.,28 and it was found that the density increases as the nitration level increases.
Using NPT molecular dynamics on the structures allows the dimensions of the simulation cell to change, and therefore the density of the structures can adapt. If the structures we simulate have comparable densities to experimentally measured values, this gives us some confidence in our results.
Also looked at the lattice parameters to compare structures obtained through simulation to those expected based on experimental results.
2 Results
2.1 RMSD
Before analysing how crystalline the structures produced are, we must ensure that the simulation has equilibrated. Looking at the RMSD, every structure reached an equilibrium within the first 2 ns of the 10 ns production phase.The RMSD was also used to validate that the periodic boundary conditions were being applied appropriately. Fig. 5 shows the RMSD graph for the 4/5N structure during the 10 ns production phase. In particular, this graph plots the RMSD for four specific chains within the structure, and the fact that all 4 of these show similar levels of variation, regardless of their starting position, implies that the periodic boundary conditions have been correctly applied.
2.2 Densities
After the simulations had been run as discussed on the 13 different structures described above, the average densities were collected in Fig. 6. | ||
| Fig. 6 Average densities of all of the structures generated calculated over the full 10 ns of the NPT production phase plotted relative to their nitrogen content. Also shown in black are three literature values with specific nitrogen content values for comparison. All of the structures simulated are within a realistic range of densities and follow the general trend stated in ref. 28 that as the nitration level increases, so does the density. The simulated density value quoted here was found by simulations run with GROMACS and a different forcefield and protocol, which is why it has a different density from the structure simulated in this paper.11 | ||
The density of the cellulose simulated here can be seen to be somewhere between that of experimental cellulose and cellulose simulated in previous work.11 The densities for the other structures follow the expected trend of increasing density as the nitration level increases, as is expected based on the literature.28 The highest energy density fits fairly well with the density given in ref. 27 for 13.3 wt%.
For the 1N structures, the density values show the densities have approximately paired up, with the positions at corresponding positions on the two rings of the dimer giving similar densities.
In the simulation of the 3Ncfe, there was a phase change during the 10 ns production phase, from paracrystalline to crystalline. More information about this can be found in the ESI.† This phase change also resulted in the structure having a different density, seen in Fig. 6.
2.3 Visualisations and RDF
For every structure the RDF was calculated. The more paracrystalline the structure is, the “smoother” the RDF will be. The smoothness can be considered as a combination of two factors – a smooth line will have fewer, wider peaks. Fig. 7 shows these two measures for each of the structures. | ||
| Fig. 7 The number of peaks in the RDF over the 10 ns production phase, at over g(r) = 0.05 intensity. The widths of the peaks are measured from half way up the peak prominence. | ||
The cellulose structure was still crystalline, even after the protocol had been performed on it, as can be seen in the visualisations in Fig. 8. The RDF shown in Fig. 8c has 11 narrow peaks with a prominence of g(r) > 0.05, making it the most crystalline of any of the structures (Fig. 7).
The cellulose structure was further tested with annealing cycles, and the results are discussed in the ESI.†
Fig. 9 shows the RDF graphs for all 6 singly nitrated structures and the visualisations of some of the structures created, and the RDF over the 10 ns NPT production phase. Looking at the RDF graphs in Fig. 9 it can be seen that the position of the single nitrogen can affect the crystallinity of the structure, and all of the structures created are at least somewhat paracrystalline.
Here, as with the densities, we can see a slight pairing based on the nitration position, especially in the visualisations. It can be seen that 1Nb and 1Ne look the most compact and crystalline, and in Fig. 7 they are further right and lower than the other 1N structures, 1Na and 1Nd are less regular, and 1Nc and 1Nf are the most irregular and paracrystalline, closer to the top left of Fig. 7, with much more twisting of the chains. The fact that 1Nc and 1Nf are the two most paracrystalline structures supports the suggestion that the reason these structures lose crystallinity during the simulation time, unlike cellulose, is that the added nitrate groups are affecting the inter-chain interactions – the off-ring nitrate positions are able to disrupt this to a greater extent.
The triple nitrated structures were created based on the observations made from the single nitrated structures, with the two off-ring positions, c and f, nitrated, as they would have the greatest chance of producing paracrystalline structures. Four structures were made, each one with a third position nitrated, one of the four remaining positions.
All of the RDF graphs and visualisations (Fig. 10) for the triple nitrated structures exhibited less paracrystallinity than expected, compared to the single nitrated structures. Particularly given that 1Nc and 1Nf both were paracrystalline, a structure containing both of these positions nitrated would be expected to be more paracrystalline.
The 12 wt% structure of nitrocellulose was made through alternating dimers that are 4 nitrated (at positions acdf) and 5 nitrated (at positions acdef), and the 6N structure was created by nitrating every possible position.
Looking at the visualisations and RDF in Fig. 11 both of the structures created are paracrystalline.
Another potential way in which the RDF data could be used to try to quantify the crystallinity of the structure is to study the position of the second peak. In Fig. 4a (d2) represents the distances between the chains, so when comparing structures of the same level of nitration, the r of the second peak can give information on how far apart the chains are. This cannot be used for comparison between differently nitrated structures, as the steric effects will also have a large influence on this.12
The intensity of the second peaks can also give a little information on the crystallinity of the structure – in Fig. 8c, the second peak of the crystalline cellulose is a lot higher (g(r) = 4.09) than the second peak of the 4/5N structure (g(r) = 1.14), where the distance between the chains is much less discrete.
2.4 Lattice parameters
In 2014 Kulasinski et al.11 used the fact that there was a large change in the lattice dimensions as proof that a change in crystallinity had occurred. For the structures being created in this study, however, this cannot be used as concrete evidence of a change to being paracrystalline – all of the structures are starting unnaturally dense, and so the lattice parameters are changing to account for this.In the ESI† there are some graphs showing how the lattice parameters change during the simulation, and how they vary between the different nitration levels.
2.5 Hydrogen bonds
When considering the hydrogen bonding of a system it becomes more important to consider the positions that have not been nitrated, as the –OH groups are where the hydrogen bonds form. It is impractical to compare the hydrogen bonding of structures with different levels of nitration. The number of hydroxyl oxygen atoms affects both the number of donors and the number of acceptors, so the number of bonds cannot be scaled proportionally to the number of –OH groups.However, structures of the same nitration levels can be compared. For example, Fig. 12 shows the number of hydrogen bonds in the single nitrated structures. The relative number of hydrogen bonds show a similar trend to the densities and RDF graphs – assuming the more crystalline the structure, the more hydrogen bonds it contains, the structures nitrated at position c and f are the most paracrystalline, and positions b and e the least.
Over the other structures, the trend is that the more nitrated the structure, the fewer hydrogen bonds there are, as expected. This does suggest another reason for why the nitrated structures break crystallinity more easily than the cellulose – not only do the nitrate groups require more space, so push the chains apart more, but there are fewer hydrogen bonds able to form, meaning that there is less rigidity.
3 Conclusions
We have presented a protocol for creating paracrystalline nitrocellulose of varying degrees of nitration, to reflect realistic systems. We were unable to create paracrystalline cellulose, even after using annealing cycles – suggesting that the addition of nitrate groups helps to break the crystallinity.The single and triply nitrated structures created became more paracrystalline than the initial crystal structure, although the effect of adding more groups was not as great as expected – the triple nitrated structures were a similar level of paracrystallinity to the single nitrated. It was found that the nitration of the off-ring positions of the nitrocellulose caused a more significant difference than the on-ring positions, further supporting the suggestion that interference of the nitrate groups with the interchain interactions is what causes this ability to become paracrystalline.
However, by following the protocol we developed, we were able to create fully paracrystalline structures for the 12 wt% and fully nitrated nitrocellulose. Although fully nitrated nitrocellulose is too reactive to be created experimentally, the 12 wt% is representative of the nitrocellulose that is often used in propellants and explosives, and therefore could be used to study other properties of the substance, such as viscosities, and effects of solvents.
There are two reasons why increasing the number of nitrate groups may increase the paracrystallinity – firstly the nitrate groups are sterically bulky, causing more space to be required between the chains. Secondly, adding nitrate groups removes hydrogen bonds, which are responsible for maintaining the crystallinity, as we have confirmed with a detailed analysis of hydrogen bonding.
Further use of the results from this paper will be to look at specific reactions within the context of these large-scale systems. Over time the bonds to the nitrate groups will break down, and the nitrocellulose will decompose. This has implications for the long-term storage of the material. Density Functional Theory (DFT) can be used to study specific reactions happening in a system, but is computationally expensive, scaling cubically as the number of atoms is increased, so previously these tests have not gone beyond monomers and dimers.29 However, with the use of ONETEP, a linear scaling DFT program, the option of using DFT to study these reactions in a larger scale system, which more accurately represents bulk nitrocellulose, is now available.30 The structures created here can be used as the basis for these calculations to find out how the context of a large system affects the results.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the use of the IRIDIS 5 High-Performance Computing Facility and associated support services at the University of Southampton in the completion of this work. C. G. would also like to thank the CDT for Next Generation Computational Modelling and AWE for financial support in the form of a PhD studentship.Notes and references
- R. Wei, S. Huang, Z. Wang, X. Wang, C. Ding, R. Yuen and J. Wang, J. Therm. Anal. Calorim., 2018, 136, 651–660 CrossRef.
- M. á Fernández de la Ossa, M. López-López, M. Torre and C. García-Ruiz, TrAC, Trends Anal. Chem., 2011, 30, 1740–1755 CrossRef.
- R. Ergun, J. Guo and B. Huebner-Keese, Encyclopedia of Food and Health, 2015, pp. 694–702 Search PubMed.
- A. J. Lai, PhD thesis, University College London, 2020.
- J. Brandrup, E. H. Immergut and E. A. Grulke, Polymer Handbook, Wiley & Sons, Ltd. Publications, Chichester, 4th edn, 1999, pp. 135–158 Search PubMed.
- K. Cieślak, K. Gańczyk-Specjalska, K. Drożdżewska-Szymańska and M. Uszyński, J. Therm. Anal. Calorim., 2021, 143, 3459–3470 CrossRef.
- R. M. Brown, Cellulose: Molecular and Structural Biology, Springer, 2007, ch. 15-Cellu, pp. 257–284 Search PubMed.
- Q. Wang, H. Song, S. Pan, N. Dong, X. Wang and S. Sun, Sci. Rep., 2020, 10, 1–18 CrossRef PubMed.
- D. Meader, E. Atkins and F. Happey, Polymer, 1978, 19, 1371–1374 CrossRef CAS.
- W. Chen, G. C. Lickfield and C. Q. Yang, Polymer, 2004, 45, 1063–1071 CrossRef CAS.
- K. Kulasinski, S. Keten, S. V. Churakov, D. Derome and J. Carmeliet, Cellulose, 2014, 21, 1103–1116 CrossRef CAS.
- J. L. Bregado, A. R. Secchi, F. W. Tavares, D. de Sousa Rodrigues and R. Gambetta, Fluid Phase Equilib., 2019, 491, 56–76 CrossRef CAS.
- G. Srinivas, X. Cheng and J. C. Smith, J. Chem. Theory Comput., 2011, 7, 2539–2548 CrossRef CAS PubMed.
- D. M. French, J. Appl. Polym. Sci., 1978, 22, 309–313 CrossRef CAS.
- K. Mazeau and L. Heux, J. Phys. Chem. B, 2003, 107, 2394–2403 CrossRef CAS.
- S. Neyertz, A. Pizzi, A. Merlin, B. Maigret, D. Brown and X. Deglise, J. Appl. Polym. Sci., 2000, 78, 1939–1946 CrossRef CAS.
- A. P. Heiner, J. Sugiyama and O. Teleman, Carbohydr. Res., 1995, 273, 207–223 CrossRef CAS.
- Y. Nishiyama, J. Sugiyama, H. Chanzy and P. Langan, J. Am. Chem. Soc., 2003, 125, 14300–14306 CrossRef CAS PubMed.
- A. I. Jewett, D. Stelter, J. Lambert, S. M. Saladi, O. M. Roscioni, M. Ricci, L. Autin, M. Maritan, S. M. Bashusqeh, T. Keyes, R. T. Dame, J. E. Shea, G. J. Jensen and D. S. Goodsell, J. Mol. Biol., 2021, 433, 166841 CrossRef CAS PubMed.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in’t Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- W. L. Jorgensen and J. Tirado-Rives, J. Am. Chem. Soc., 1988, 110, 1657–1666 CrossRef CAS PubMed.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- L. A. Richards, A. Nash, M. J. S. Phipps and N. H. De Leeuw, New J. Chem., 2018, 42, 17420–17428 RSC.
- L. A. Richards, A. Nash, A. Willetts, C. Entwistle and N. H. De Leeuw, RSC Adv., 2018, 8, 5728–5739 RSC.
- L. S. Dodda, I. C. De Vaca, J. Tirado-Rives and W. L. Jorgensen, Nucleic Acids Res., 2017, 45, W331–W336 CrossRef CAS PubMed.
- A. R. Leach, Molecular Modelling Principals and Applications, Pearson Education Limited, 2nd edn, 2001, ch. 4, pp. 165–252 Search PubMed.
- R. Meyer, J. Köhler and A. Homburg, Explosives, Wiley-VCH, 6th edn, 2007, vol. 377 Search PubMed.
- Y. He, Y. He, J. Liu, P. Li, M. Chen, R. Wei and J. Wang, J. Hazard. Mater., 2017, 340, 202–212 CrossRef CAS PubMed.
- M. K. Shukla and F. Hill, Struct. Chem., 2012, 23, 1905–1920 CrossRef CAS.
- J. C. Prentice, J. Aarons, J. C. Womack, A. E. Allen, L. Andrinopoulos, L. Anton, R. A. Bell, A. Bhandari, G. A. Bramley, R. J. Charlton, R. J. Clements, D. J. Cole, G. Constantinescu, F. Corsetti, S. M. Dubois, K. K. Duff, J. M. Escartín, A. Greco, Q. Hill, L. P. Lee, E. Linscott, D. D. O'Regan, M. J. Phipps, L. E. Ratcliff, Á. R. Serrano, E. W. Tait, G. Teobaldi, V. Vitale, N. Yeung, T. J. Zuehlsdorff, J. Dziedzic, P. D. Haynes, N. D. Hine, A. A. Mostofi, M. C. Payne and C. K. Skylaris, J. Chem. Phys., 2020, 152, 174111 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Additional parameters of OPLS-aa, Moltemplate input file including coordinates, sample LAMMPS input file, average density values for structures created, investigation of lattice parameters, investigation of 3Ncfe phase change, analysing annealing cycles on 0N. See DOI: https://doi.org/10.1039/d2cp05550c |
| This journal is © the Owner Societies 2023 |








