Infrared action spectroscopy of the deprotonated formic acid trimer, trapped in helium nanodroplets

Abstract

Hydrogen bonding interactions are essential in the structural stabilization and physicochemical properties of complex molecular systems, and carboxylic acid functional groups are common participants in these motifs. Consequently, the neutral formic acid (FA) dimer has been extensively investigated in the past, as it represents a useful model system to investigate proton donor–acceptor interactions. The analogous deprotonated dimers, in which two carboxylate groups are bound by a single proton, have also served as informative model systems. In these complexes, the position of the shared proton is mainly determined by the proton affinity of the carboxylate units. However, very little is known about the nature of the hydrogen bonding interactions in systems containing more than two carboxylate units. Here we report a study on the deprotonated (anionic) FA trimer. IR spectra are recorded in the 400–2000 cm⁻¹ spectral range by means of vibrational action spectroscopy of FA trimer ions embedded in helium nanodroplets. Characterization of the gas-phase conformer and assignment of the vibrational features is achieved by comparing the experimental results with electronic structure calculations. To assist in the assignments, the ²H and ¹⁸O FA trimer anion isotopologues are also measured under the same experimental conditions. Comparison between the experimental and computed spectra, especially the observed shifts in spectral line positions upon isotopic substitution of the exchangeable protons, suggests that the prevalent conformer, under the experimental conditions, exhibits a planar structure that resembles the crystalline structure of formic acid.

---

1 Introduction

Hydrogen bonding interactions are essential in many areas of physics, chemistry and biology,^1–3 and because of their unique physicochemical properties, they are central in many important processes such as, for example, single and double proton transfer reactions in nucleobases,^4,5 formation of low-barrier hydrogen bonds in proteins,^6–8 and proton-coupled electron transfer reactions in electrocatalysis.^9,10 In addition, the strength of the interactions within the hydrogen bonding network is vital to maintain the structural and thermodynamic stability of the system.^11–14 The challenges in understanding these interactions are often related to the complexity of the systems studied. To gain fundamental insight, it is useful to investigate small model systems, as their small size and minimal complexity permits precision spectroscopy experiments as well as high-level quantum chemical calculations that can yield a better understanding of the hydrogen bond interactions.^15–29

Particularly interesting are carboxylic acid systems. Carboxylate or carboxylic acid groups play an important role for hydrogen bonding in biological systems and are decisive in determining, for example, the structures and properties of peptides and proteins. In those systems, O–H⋯O interactions are of special importance. However, for formic and acetic acid, the much weaker C–H⋯O hydrogen bond plays an important role as well and for those acids in their solid form, the balance between O–H⋯O and C–H⋯O hydrogen bonds is determining the structure.^30–32

In a bottom up approach, small neutral carboxylic acid complexes, such as the formic acid (FA) dimer, have been extensively investigated. For carboxylic acid dimers, the proton affinity of the two units has a major influence on the proton location, as well as the ground-state structural motif of the complex. For small homo-dimers, in which the proton affinity of both carboxylic acids is equal, a cyclic double hydrogen-bonded complex is most likely to be formed.^33–35 For carboxylic acid hetero-dimers, instead, antisymmetric hydrogen bonding, as well as other structural motifs, may be observed when the difference between the proton affinity of the two acids is high enough.^36–39

When a proton is removed from the carboxylic acid moiety of a double hydrogen-bonded complex, a carboxylic dimer anion is formed, and the competition between the proton affinities of the units, possible additional hydrogen bonds, and electrostatic interactions will ultimately determine the position of the proton shared between the conjugate bases. Such shared-proton motifs are found in many different chemical environments, ranging from small complexes like water clusters to complex systems like proteins.^40–46 Recently, the ground-state structure of the proton-bound formate dimer anion was characterized by means of cryogenic-ion IR action spectroscopy, showing that the lowest energy conformer corresponds to a symmetrical motif in which the proton is equally shared between the two carboxylates.⁴⁷

Although many experimental and theoretical studies have examined carboxylic acid dimers, very little is known about the structure and properties of larger carboxylic acid clusters, such as trimers or tetramers. Although the energetic stability of the neutral FA_n and FA_n·H₂O_n cluster series growth has been investigated in the past,^48–50 there are only a very few spectroscopic studies of such systems.^50–52

Infrared (IR) action spectroscopy of isolated gas-phase ions has proven to be a very effective experimental technique for the characterization of small molecular complexes. Whereas spectral broadening often limits room-temperature spectroscopic approaches, cryogenic-ion IR spectroscopy methods, in which the ion of interest is cooled down to temperatures ranging from 10–100 K prior to spectroscopic interrogation, can significantly reduce the vibrational congestion and thus enable the acquisition of highly resolved IR spectra. Such experimental techniques, together with high level theoretical calculations, were successfully applied in the past to study the structure and properties of systems ranging from small carboxylic acid clusters to complex biomolecules.^{40,47,53–68}

Here we report the first gas-phase IR spectrum of the deprotonated (anionic) FA trimer complex in the 400–2000 cm⁻¹ range, utilizing IR action spectroscopy of ions trapped in helium nanodroplets. This system is expected to exhibit highly anharmonic behavior, resulting in complex spectra that are challenging to interpret. To gain additional information about the vibrational character of the observed bands, the deprotonated ²H-FA trimer and ¹⁸O-FA trimer isotopologues were also measured. For comparison to the experimental data, IR spectra were calculated within the harmonic approximation for a set of candidate structures. Our results indicate that among several conformers, the second-lowest energy structure, which resembles the crystalline form of formic acid, is the one observed under the experimental conditions.

2 Experimental and computational methods

2.1 Experimental section

The experimental setup for ion infrared action spectroscopy in helium droplets has been described in previous publications,^47,69–71 and only specific details are provided herein. The ions of interest are generated from a nanoelectrospray ionization (nESI) source using in-house-fabricated Pd/Pt-coated borosilicate capillaries. Samples with 10% of either FA (99.9% – Sigma-Aldrich Merck – Darmstadt, Germany) or d₂-FA (99.9% – Sigma-Aldrich Merck – Darmstadt, Germany) in a 1 : 1 H₂O : CH₃OH mixture are utilized to generate the ions in the gas phase. In the case of ¹⁸O-FA a 20% ¹⁸O-sodium formate (95% – Cambridge Isotope Laboratories – Massachusetts, United States) in a 1 : 1 H₂O : CH₃OH mixture is used instead. Deuterium substitution of the acid protons is carried out by bubbling N₂ through D₂O and flowing this gas trough the space between the cone and the inlet of the nESI source.

After ions are transferred into vacuum, the species of interest is isolated by a quadrupole mass filter, deflected 90° by a quadrupole ion bender and finally injected and accumulated in a hexapole ion trap. A 2.0 s duration pulse of He buffer gas is introduced before the entry of the ions to the hexapole ion trap to collisionally cool and effectively trap the ions. Moreover, in order to reduce the water partial pressure and possible ion-molecule reactions, the hexapole ion trap housing is cooled to ca. 90 K. After an additional 1.5 s pump-down period, helium droplets are allowed to traverse the trap.

Helium droplets are generated using an Even–Lavie pulsed valve⁷² that operates at a temperature of 23 K and at a helium backing pressure of ca. 70 bar. The He droplets pass through the trap and can pick up an ion. As the kinetic energy of the droplets is much larger than the longitudinal trap potential, ion-doped droplets can exit the trap and travel further downstream in the instrument. Previous measurements indicate that under the described experimental conditions, ion-doped droplets containing ∼20 000 He atoms are produced.⁷³ Ion-doped droplets reaching the subsequent interaction region are irradiated with infrared photons generated by the Fritz-Haber-Institut Free-Electron Laser (FHI-FEL).⁷⁴ Photons that are resonant with vibrational transitions of the ion can be absorbed, and the energy is rapidly dissipated via evaporation of helium atoms and associated re-cooling of the ion and the droplet. Several cycles of photon absorption and energy dissipation results in bare ions, void of any helium solvation shell, which are then monitored by a time-of-flight (TOF) mass analyzer. Ion infrared action spectra are then obtained by measuring the TOF ion signal as a function of IR wavelength.

The FHI-FEL radiation consists of laser macropulses of 10 μs duration, with each macropulse composed of micropulses of ca. 5 ps and energy of ca. 10 μJ at a repetition rate of 1 GHz. In the experiment, at each IR wavelength position, the ion trap is first filled, after which TOF signals from 25 laser pulses at a frequency of 10 Hz are measured before the FHI-FEL is set to a new wavelength. The IR spectrum obtained is then corrected by dividing the ion intensity by the photon fluence. The final spectrum is the average of at least three individual scans. As the output wavelength of the FHI-FEL is tunable only over a limited range for a given electron energy,⁷⁴ the spectra are collected in separate experiments in the 400–1100 and 850–2000 cm⁻¹ photon-energy ranges. The relative intensity of each partial spectrum is scaled on the basis of the intensity of the spectral lines found in the overlapping measurement regions.

2.2 Theoretical section

Candidate structures are obtained by performing a conformational search using the Conformer-Rotamer Ensemble Sampling Tool (CREST)⁷⁵ within the xTB molecular modeling program.⁷⁶ For a better sampling of the conformational space, the sampling of noncovalent complexes and aggregates feature (NCI) is used within the GFN2-xTB force field.⁷⁷ The resulting unique conformers are then optimized at the B3LYP-D3(BJ)/aug-cc-pVTZ level of theory^78,79 by using the Gaussian 16 software package,⁸⁰ and the most stable conformers obtained are reoptimized with very tight convergence criteria, followed by the calculation of the harmonic IR spectrum. To evaluate the relative energies of the conformers, harmonic zero-point energy (ZPE) correction to the total energy was taken into account at the B3LYP-D3(BJ)/aug-cc-pVTZ, DSDPBEP86/aug-cc-pVTZ and MP2/aug-cc-pVTZ levels of theory. All conformers were reoptimized prior to the harmonic frequency calculations at each level of theory. CCSD(T) single-point calculations were performed using the optimized structures at MP2/aug-cc-pVTZ, with zero-point energy corrections at the same level of theory. In addition, relative energies of the three lowest energy conformers were calculated at MP2 level using a complete basis set (CBS) extrapolation scheme⁸¹ with the aug-cc-pVnZ (n = 3, 4, 5) basis sets and a correction for the difference in correlation energy between CCSD(T) and MP2, with the aug-cc-pVTZ basis set.⁸² The experimental spectra of the complexes are compared to theoretical spectra calculated at B3LYP-D3(BJ)/aug-cc-pVTZ level of theory that are convoluted with Gaussian functions having a Full-Width at Half-Maximum (FWHM) of 0.4% of the wavenumber. The frequencies of all spectra that are calculated within the harmonic approximation are scaled by a factor of 0.98. Anharmonic corrections to calculated infrared spectra are performed using generalized second-order vibrational perturbation theory (GVPT2)^83–85 at the B3LYP-D3(BJ)/aug-cc-pVTZ level of theory.

3 Results and discussion

3.1 Experimental spectra of the deprotonated FA complex

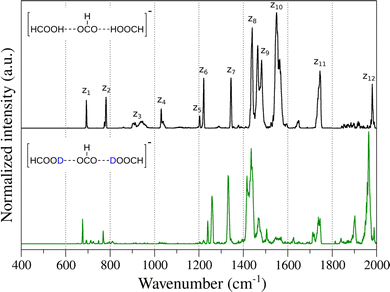
Fig. 1 shows the experimental IR spectrum obtained for the deprotonated FA trimer complex embedded in helium droplets (black). Of the five hydrogens in the complex, the three hydrogen atoms connected to the carbon atoms are non-exchangeable, whereas the two acidic protons can be exchanged with deuterium. Fig. 1 also shows the spectrum of the complex containing two deuterons (green). Both spectra were recorded in the 400–2000 cm⁻¹ spectral range. The main vibrational features are marked as z_n for discussion purposes.

Fig. 1 Experimental IR action spectra of the deprotonated FA trimer complex (black) and with the two exchangeable protons substituted by deuterons (green). For discussion purposes, relevant features are marked with numbered letters above the spectrum.

In the case of the unsubstituted deprotonated FA trimer complex, two very narrow bands can be observed between 700 cm⁻¹ and 800 cm⁻¹ (z₁, z₂), which may stem from low-frequency carboxyl (–COOH) motion, as was previously observed for the FA monomer.^19,86–89 Higher in energy, broad and weak bands appear between 900 cm⁻¹ and 1100 cm⁻¹ (z₃ and z₄). The position, intensity and width of these features suggests that they are related to COH and OCH bending displacements.¹⁹ Between 1200 cm⁻¹ and 1400 cm⁻¹, the sharp bands z₅, z₆ and z₇ may be associated with ν(C–OH) stretching vibrations of FAs and symmetric ν(COO⁻) stretching of the formate. Similar features were observed previously in carboxylate and carboxylic acid complexes.^59,90,91 Between 1400 cm⁻¹ and 1600 cm⁻¹, a set of broad and intense bands is observed. In this spectral region, it is expected to find δ(COH) and δ(OCH) bending modes, as well as the antisymmetric ν(COO⁻) stretching mode of formate.^20,86,91,92 The vibrational band at 1743 cm⁻¹ (z₁₁) can be related to the carbonyl ν(C=O) stretching mode. Finally, the band z₁₂ located at 1980 cm⁻¹ could be associated with either a combination or overtone feature or a very red-shifted ν(OH) stretching vibration in which the proton is most likely shared between the carboxylates.

In the case of the deprotonated FA trimer complex with two deuterons, similar features are observed in the vibrational spectrum (Fig. 1). Small red-shifts are observed for the majority of the vibrational bands, i.e. z_1,2, z₇ and z_11,12, as expected. Interestingly, the bands z_5,6 show a peculiar blue-shift, similar to observations on related systems.¹⁹ The largest differences upon isotopic substitution are observed for bands z_3,4 and for the set of bands in the 1400–1600 cm⁻¹ range. In the case of bands z₃ and z₄, large red-shifts are expected as they may correspond to δ(COH) bending modes. The weak vibrational features appearing in the 600–800 cm⁻¹ region could be related to δ(COD) bending modes. In the case of the δ(OCH) bending modes, even though little to no red-shift is expected when exchanging the mobile protons, however, their weak intensity may preclude these to be observed experimentally. For the complex vibrational structure in the 1400–1600 cm⁻¹ region, the changes caused by the isotope exchange are drastic. Bands z₉ and z₁₀ vanish upon substitution, and only a shoulder to the right of band z₈ appears. No other new features are observed at lower photon energies, indicating that these bands are apparently not directly associated with proton displacements. The shifts and changes in intensity of these bands may be related to changes in the vibrational coupling of the modes upon substitution and/or the presence of Fermi resonances involving combination or overtone modes in the spectrum of the unsubstituted species. Finally, a new feature appears at ∼1900 cm⁻¹ after isotopic exchange of the mobile protons that may correspond to a combination or overtone band, as no fundamental band is expected in this region.

3.2 Lowest energy conformers

Seven different candidate structures of the deprotonated FA trimer complex were found with the methodology employed in this work. All conformers, together with relevant O–H and O–O bond lengths, are shown in Fig. S1 (ESI†). Of those seven conformers, three are within ca. 3–5 kJ mol⁻¹ (depending on the level of theory) of the lowest energy structure (see Table 1). The four remaining structures are >10 kJ mol⁻¹ higher in energy than the lowest energy structure. Because of this large energy gap, discussion and analysis are focused on only the three lowest energy structures. Fig. 2 (bottom) shows the three lowest energy conformers, and Table 1 shows their respective relative energy calculated at different levels of theory. As a reductionist approach for discussion purposes, all conformers will be treated as two cis or trans FA molecules interacting with a deprotonated formate molecule via hydrogen bonds with different O–H⋯O⁻ bond lengths.

Table 1 Relative energies with zero-point energy correction (EE + ZPE) of the lowest energy conformers of the deprotonated FA trimer calculated at the CCSD(T)/aug-cc-pVTZ, MP2/aug-cc-pVTZ, DSDPBEP86/aug-cc-pVTZ and B3LYP-D3(BJ)/aug-cc-pVTZ levels of theory. In addition, energies at the MP2 level were also computed using the complete basis set extrapolation scheme (CBS) with MP2/aug-cc-pVnZ (n = 3, 4 and 5) and a correction for the difference in correlation energy between CCSD(T) and MP2 with the aug-cc-pVTZ basis set. In the case of CCSD(T) and MP2/CBS, the zero-point energy corrections at the MP2/aug-cc-pVTZ level were used. All values are in kJ mol⁻¹

Conformer	CCSD(T) + ZPEMP2	MP2/CBS(ΔCCSD(T)-MP2) + ZPEMP2	MP2	DSDPBEP86	B3LYP-D3(BJ)
a	0.00	0.00	0.00	0.00	0.00
b	2.38	2.49	2.21	2.10	1.88
c	5.16	4.01	4.10	4.04	3.07

---

Fig. 2 Relative energy and dipole moment values and vectors of the cis and trans formic acid monomers (top) and the lowest energy structures of the deprotonated FA trimer complex (bottom), calculated at the B3LYP-D3(BJ)/aug-cc-pVTZ level of theory.

The energy differences between the conformers may be explained by a competition between stabilization from hydrogen bonding, cis or trans conformations in the FA molecules, and the electrostatic interactions between the FA molecules and the formate anion. Previous works have reported that the dipole moment of the cis FA is larger (3.79 D)⁹³ than the one observed for trans FA (1.42 D).⁹³Fig. 2 (top) shows the dipole moment vectors of both rotamers of the FA molecule, calculated at B3LYP-D3(BJ)/aug-cc-pVTZ level of theory, which are in agreement with the values reported in literature.⁹³ Dipole moment values calculated at all levels of theory can be found in Table S2 (ESI†). In competition to the electrostatic interaction is the energy difference between the FA rotamers, with the cis rotamer being +16.72 kJ mol⁻¹ higher in energy than the trans rotamer, calculated at the B3LYP-D3(BJ)/aug-cc-pVTZ level of theory, very close to the experimental value of ΔE_cis–trans = +16.33 kJ mol⁻¹ determined by rotational spectroscopy.⁹³

Conformer (a) is predicted to be the lowest energy conformer at all levels of theory considered in this work. Here, two FA molecules in cis orientation interact with the formate anion, mimicking the structural motifs of the two lowest energy conformers previously found for the proton-bound formate dimer under similar experimental conditions.⁴⁷ For this conformer, a large interaction energy is expected as a result of the high dipole moment of the cis FA molecules interacting with the formate anion. The second lowest energy conformer (Fig. 2(b)) resembles the crystalline structure of formic acid^30–32 and is predicted to be 2.38 kJ mol⁻¹ higher in energy than conformer (a) at the CCSD(T) + ZPE_MP2/aug-cc-pVTZ level of theory. It has a planar structure (C_s symmetry point group) that differs from conformer (a) by one of the FA molecules being in trans orientation. The energy difference between conformers (a) and (b) may arise primarily from the lower dipole moment of the trans FA in comparison with the cis FA, which is apparently only partially compensated by the lower energy of the trans FA moiety and the additional interaction between the methyl hydrogen of the formate anion and the carbonyl oxygen of one formic acid. A potential energy curve along the dihedral coordinate for interconversion of conformer (a) to conformer (b) (∠(H1–C2–O5–H14), Fig. S2, ESI†) shows that the height of the barrier for this process is ca. 35 kJ mol⁻¹, very close to the height of the barrier for the cis → trans isomerisation of the FA monomer.^93,94 Also, the acidic protons in conformer (b) are slightly more shared between the carboxylates, compared to conformer (a), meaning that an elongation of the O–H bond is observed (Fig. S1, ESI†). Finally, conformer (c) lies +5.16 kJ mol⁻¹ above the lowest energy conformer at the CCSD(T) + ZPE_MP2/aug-cc-pVTZ level of theory and exhibits a motif, in which the two FA molecules are cis oriented and interacting symmetrically with the formate anion (C₂ symmetry point group). The difference in energy between conformer (c) and (a) may arise primarily from the additional in-plane interaction between the formate anion and the methyl hydrogen of one of the FA units in (a).

3.3 Experimental and theoretical spectra comparison

Shown in Fig. 3 are the experimental IR spectra in comparison to the theoretical spectra for conformer (a), (b) and (c). Traces in black correspond to the spectra of the unsubstituted deprotonated FA trimer (i.e. the complex with all hydrogens), and traces in green correspond to the spectra of the deuterated deprotonated FA trimer complex in which the two exchangeable protons were substituted by deuterons. As in Fig. 1, the main features in the theoretical spectra are marked with numbered letters for discussion purposes. Spectral lines corresponding to exchangeable proton displacement modes are also marked with an asterisk. Table 2 also shows a tentative assignment of the experimental features related to the carboxyl group displacement of the deprotonated FA trimer by using the computed harmonic frequencies at B3LYP-D3(BJ)/aug-cc-pVTZ level of theory of conformers (a) to (c). The assignment of the computed frequencies for all conformers can be found in Table S4 in the ESI.†

Fig. 3 Comparison between experimental and theoretical IR spectra of the deprotonated FA trimer with deuterium isotopic exchange, in the 400–2000 cm⁻¹ spectral region. Black and green traces correspond to the IR spectra of the deprotonated FA trimer with two protons and two deuterons, respectively. The experimental spectra is shown in the upper panel, while the theoretical spectra of conformers (a), (b) and (c) are shown in the lower panels, respectively. The relative energy of each isotopologue at the CCSD(T) + ZPE_MP2/aug-cc-pVTZ level of theory are shown on the left side of the spectra. For discussion purposes, relevant features are marked with numbered letters. Vibrational modes related to the exchangeable proton displacement are also marked with an asterisk. All theoretical spectra were computed at the B3LYP-D3(BJ)/aug-cc-pVTZ level of theory and scaled by a factor of 0.98.

Table 2 Tentative assignment of the experimental features related to the carboxyl (–COOH) and carboxylate (–COO⁻) groups displacements for the deprotonated FA trimer in comparison with the calculated harmonic frequencies at B3LYP-D3(BJ)/aug-cc-pVTZ level of theory, for conformers (a), (b) and (c). All values are in cm⁻¹. Numbered letters shown parentheses refer to the numbered letters in Fig. 3

Vibrational mode	Experiment	Structure
		(a)	(b)	(c)
ν(C=O)	1745 (z11)	1749/1745 (a13)	1741/1690 (b12)	1750/1749 (c9)
ν as(COO^−)	—	1604 (a12)	1536 (b11)	1600 (c8)
ν sym(COO^−)	1344 (z7)	1349 (a8)	1318 (b8)	1359 (c5)
ν(C–OH)	1221/1202 (z5,6)	1217/1204 (a6,7)	1262/1207 (b5,7)	1218/1217 (c4)
δ(COO^−)	781 (z2)	772 (a2)	789 (b2)	789 (c2)
δ(COOH)	693 (z1)	694/694 (a1)	717/695 (b1)	695/693 (c1)

---

For the unsubstituted conformer (a) in the 600–800 cm⁻¹ region, two bands labeled a₁ and a₂ are predicted, which correspond to carboxyl and carboxylate bending modes (Table 2). Similar bands are also calculated for conformers (b) and (c). They agree quite well in position and relative intensity with the experimental bands z₁ and z₂. Also for the unsubstituted complex, theory predicts quite well the position of some vibrational bands related to the carboxyl group displacements (ν(C–OH) – a_5,6 and ν_sym(COO⁻) – a₇ stretching modes). However, the vibrational structure between 1400–1600 cm⁻¹ and the band z₁₂ are not reproduced by this conformer. In particular, the intense feature a₁₂ (1604 cm⁻¹), corresponding to the ν_as(COO⁻) stretching vibration, is not observed experimentally. Clear discrepancies are also observed when comparing the theoretical spectrum for the substituted complex of a) with the corresponding experimental spectrum (green traces). In the 1400–1600 cm⁻¹ range, only a red-shift of the a₁₂ band is predicted, which clearly does not match the experimental observation.

In the case of conformer (c), a smaller number of bands is predicted, as expected for a structure of higher symmetry (C₂ point group). In the case of the unsubstituted complex, the relative intensities of bands z₁ and z₂ are not well reproduced by bands c₁ and c₂. Further, neither the vibrational structure between 1400–1600 cm⁻¹ nor the band z₁₂ is reproduced. An intense band is also predicted at 1600 cm⁻¹ (c₈), corresponding to the ν_as(COO⁻) stretching vibration, which is not observed experimentally. Upon isotopic substitution, a similar behavior as for conformer (a) is observed. Small red- and blue-shifts are predicted for bands involving atomic motion in the carboxyl group, and in general, a poor agreement with the experimental spectra is observed.

For the unsubstituted conformer (b), the position and relative intensities of the features b₁ and b₂ at 695 cm⁻¹ and 789 cm⁻¹ are in good agreement with the experimental bands z₁ and z₂. Some other bands related to motion in the carboxyl groups, namely b_5,7,8, are predicted slightly shifted in comparison with the experimental spectra, but are also in good agreement. Bands b₁₂ result from ν(C=O) stretching vibrations, and it is predicted as a doublet due to coupling of one of two ν(C=O) with the ν_as(COO⁻). Although this is not observed experimentally, the broad feature z₁₁ may include several spectral lines. Band b₁₃, corresponds to a very red-shifted ν(OH) stretching vibration and is predicted at 1968 cm⁻¹, in very good agreement with the experimentally observed band z₁₂ at 1980 cm⁻¹. However, as for conformer (a) and (c), for the unsubstituted complex of conformer (b), the 1400–1600 cm⁻¹ region is not reproduced by the calculated spectrum.

It is interesting to compare the calculated spectrum of the deuterated complex of conformer (b) with its experimental counterpart. Near 2000 cm⁻¹, an apparent blue-shift of the band b₁₃ to 1975 cm⁻¹ is calculated. The vibrational modes involved show that band b₁₃ in the unsubstituted complex corresponds to a very red-shifted ν(OH) stretching vibration of the proton at position H₁₄ (ν(O–H₁₄) (see structure in Fig. S2, ESI†)). However, upon isotopic substitution, this vibrational mode is shifted to 1222 cm⁻¹ (black dot line in Fig. 3(b)). Analyzing the band calculated at 1975 cm⁻¹ shows that it stems from the ν(O–D₄) stretching vibration, predicted at 2670 cm⁻¹ for the unsubstituted complex (Table S4, ESI†), which is in good agreement with the band observed experimentally at 1965 cm⁻¹. A clearer picture is obtained when analyzing the ν(O–H/O–D) bands after single isotopic substitutions, shown in Fig. S10 (ESI†). In case the substitution occurs in the H₄ position, a double peak is observed in this region, corresponding to the coupled symmetric and anti-symmetric ν(OH/OD) stretching vibrations. This is also observed experimentally for the singly substituted species. Interestingly, in contrast to the calculated spectra for conformer (a) and (c), the calculated spectrum of the doubly deuterated conformer (b) matches the experimental spectrum also very well in the 1400–1600 cm⁻¹ region. The intense band at 1424 cm⁻¹ is very close to the broad experimental feature at ∼1400 cm⁻¹. This band is predicted as a strongly coupled δ(OCH) bending and ν(OH) stretching mode.

The differences in spectra of the unsubstituted and deuterated species in the 1400–1600 cm⁻¹ region are surprising. As mentioned above, the unexpectedly large number of bands in the case of the unsubstituted complex might be the result of Fermi resonances. Also, anharmonic effects are expected to be less pronounced in the substituted species due to an effective lowering of the energy levels on the potential energy surface, thereby reducing the anharmonic character of the fundamental transitions, as was observed previously.⁹⁵ In the unsubstituted complex, fundamental transitions such as COH bending modes and/or the ν_as(COO⁻) stretching mode may couple to overtones or combination bands, causing transfer of intensity to otherwise dark modes as well as band shifting. Strong resonances involving in-plane and out-of-plane COH bending modes together with low frequency δ(COOH) bending modes have been observed previously in carboxylic acid monomers.^19,86 Standard harmonic calculations intrinsically do not take such couplings into account. Anharmonic calculations, such as VPT2, do include Fermi resonances. However, the strength of the coupling strongly depends on the frequency difference of the bands that couple, and we therefore do not expect that affordable and relatively low-level calculations are of sufficient accuracy (see also Fig. S7, ESI†). Upon isotopic substitution, the fundamental and/or dark modes undergo frequency shifts, and the Fermi resonances disappear. Simple harmonic calculations can then reproduce the experimental spectrum, yielding improved agreement between experiment and theory, as observed for the computed spectrum of the deuterated conformer (b).

The data presented here suggests that the observed structure of the deprotonated FA trimer in He-droplets is conformer (b), rather than conformers (a) or (c). If (a) or (c) would be present as well, we would expect to observe for the deuterated species a band predicted around 1550 cm⁻¹, which is not the case. The apparent exclusive observation of (b) is in contrast to the calculated energetics, which predicts conformer (a) to be the lowest energy conformer at all levels of theory. The reason for this discrepancy is unclear. Although the difference in relative energy between conformers (a) and (b) (∼200 cm⁻¹) may be on the order of the net error of the harmonic ZPE, possible effects might also include the kinetics and dynamics of the complex formation or its interaction with the helium environment. When comparing the two structures (a) and (b), as shown in Fig. 2, one can see that the two molecular units to the left side in each structure are essentially the same, with only the unit on the right side being different. Besides its orientation, it is apparent that the formic acid molecule on the right side is, in the case of (a), in cis configuration and, in the case of (b), in trans configuration. For the free formic acid molecule, the trans configuration is 16.7 kJ mol⁻¹ lower in energy than the cis configuration, implying that at room temperature, almost all monomer molecules are in trans configuration. One possibility is therefore that the formation of the trimer proceeds via adding a neutral trans monomer to a pre-formed dimer and due to kinetic constraints, rearrangement to structure (a) does not take place and conformer (b) becomes kinetically trapped. Another possibility is that, although in its free form conformer (a) is more stable, in the helium environment differences in solvation energy cause (b) to become lower in energy. Although the solvation energies are difficult to estimate, it is likely that they are quite small. Further, the differences in solvation energy between such very similar structures are expected to be negligible. In addition, if (a) would be lower in energy in the gas phase and (b) lower in energy in the droplet, a structural conversion at low droplet temperatures would have to take place. In Fig. S2 (ESI†), a scan of the respective reaction coordinate is shown and the corresponding barrier is more than 30 kJ mol⁻¹, which clearly cannot be passed at low temperatures. An alternative to this would be if the conversion happens by a tunneling process, but even in the case of the monomer, the tunneling rate constant for trans/cis conversion is expected to be very small.⁹⁴

3.4 Experimental IR spectra of deprotonated ²H-FA and deprotonated ¹⁸O-FA isotopologues

In order to strengthen the assignment of vibrational bands and gain more information about the origin of the experimental features, the IR spectra of the deprotonated (methyl deuterated) ²H-FA trimer and the deprotonated ¹O-FA trimer isotopologues were also measured. Fig. 4 shows the comparison between deprotonated ²FA, ²H-FA and ¹⁸O-FA trimer complexes. The experimental spectra of the deprotonated ¹⁸O-FA trimer were only measured between 900–1800 cm⁻¹ because the main vibrational bands related to carboxyl displacements are found within this range.

Fig. 4 Experimental IR spectra of the deprotonated FA trimer (black) in comparison with the experimental IR spectra of the deprotonated ²H-FA trimer (red) and deprotonated ¹⁸O-FA trimer (green) in the 400–2000 cm⁻¹ and 900–1800 cm⁻¹ spectral region, respectively. In the upper-left corner of each spectrum the hydrogens or oxygen substituted are shown in blue and red, respectively. For discussion purposes, relevant features are marked with numbered letters in each graph.

Small shifts are observed when exchanging the methyl hydrogens by deuteriums, as observed in Fig. 4. Vibrational features related to the carboxyl group displacements (ν(C–OH) – z_5,6 and ν_sym(COO⁻) z₇ stretching modes) experience almost no shift upon substitution, which support their assignment. In contrast, the ν(C=O) stretching vibration (band z₁₁) experiences a red-shift of ∼25 cm⁻¹. Similar shifts were already observed for the FA monomer in liquid-jet Raman spectroscopy experiments.¹⁹ Also of interest are the spectral lines in the 1400–1600 cm⁻¹ region, where one can observe changes in shape and intensity of the band labeled z₉. These changes could be related to a Fermi resonance involving δ(OCH) bending vibrations that is modulated by the slight shift in band positions upon methyl hydrogen substitution.

In the case of the deprotonated ¹⁸O-FA trimer spectrum, major red-shifts are observed for bands associated with the carboxyl group displacements. The ν_sym(COO⁻) and the ν(C–OH) stretching modes (bands z₇ and z₆, respectively), experience a strong red-shift upon ¹⁶O/¹⁸O exchange, which supports their assignment. The same is observed for z₁₁, assigned to the carbonyl ν(C=O) stretching mode, which experiences a red-shift of ca. 30 cm⁻¹ upon substitution. In addition, as observed for the ²H-FA trimer, band z₉ changes in shape and relative intensity, suggesting that oxygen atom movement contributes to the modes of the postulated Fermi resonance as well.

Finally, deuterium substitution of the exchangeable protons in the deprotonated ²H-FA and ¹⁸O-FA trimer complexes yields vibrational spectra that exhibit the same behavior as for the deprotonated ²FA complex. Specifically, bands z₉ and z₁₀ are observed to shift to lower photon energies and change in intensity (Fig. S12 and S13, ESI†). The comparison with the theoretical spectra of the conformers again shows that an agreement is only observed for conformer (b), supporting the conclusion that this is the prevalent structure of the deprotonated FA trimer in the He-droplet (Fig. S14–S19, ESI†).

4 Conclusions

The infrared spectra of the deprotonated formic acid trimer complex in helium nanodroplets was recorded in the 400–2000 cm⁻¹ spectral region, together with their ²H-FA and ¹⁸O-FA isotopologues in the 400–2000 cm⁻¹ and 900–1800 cm⁻¹ spectral region, respectively. In addition, the spectra of the complexes with the exchangeable protons substituted by deuterons were also recorded under the same experimental conditions.

Theoretical calculations at different levels of theory show that the lowest energy conformer consists of two cis-formic acid molecules in different planes interacting with the formate anion by hydrogen bonds. The second lowest energy structure, very close in energy, differs from conformer (a) in the rotation of one formic acid moiety, resulting in a planar structure that resembles the crystalline structure of formic acid.

Among the conformers considered, the behaviour upon isotopic exchange of a set of vibrational features in the 1400–1600 cm⁻¹ and a very red-shifted OH stretching vibration, are only predicted by the second lowest energy conformer (b). These observations may be explained by the presence of Fermi resonances and strongly coupled vibrational modes related to COH/OCH bending and COO⁻ stretching motions that change when exchangeable proton are substituted by deuterons.

Our results suggest that the prevalent structure of the deprotonated ²FA trimer in He droplets, at experimental conditions, is a planar structure that resembles the crystalline state of the formic acid. Given the highly anharmonic nature of these systems, a more detailed theoretical study is necessary to precisely reproduce and understand the origin of the features related to the vibrational modes that are strongly coupled with shared proton motion.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

M. T. acknowledge the support of the Alexander von Humboldt Foundation. Open Access funding provided by the Max Planck Society.

Notes and references

1. S. Scheiner, J. Indian Inst. Sci., 2020, 100, 61–76.
2. D. Herschlag and M. M. Pinney, Biochemistry, 2018, 57, 3338–3352.
3. S. C. C. van der Lubbe and C. Fonseca Guerra, Chem. – Asian J., 2019, 14, 2760–2769.
4. D. Jacquemin, J. Zúñiga, A. Requena and J. P. Céron-Carrasco, Acc. Chem. Res., 2014, 47, 2467–2474.
5. R. Srivastava, Front. Chem., 2019, 7, 536.
6. S. Dai, L.-M. Funk, F. R. von Pappenheim, V. Sautner, M. Paulikat, B. Schröder, J. Uranga, R. A. Mata and K. Tittmann, Nature, 2019, 573, 609–613.
7. M. T. Kemp, E. M. Lewandowski and Y. Chen, Biochim. Biophys. Acta, Proteins Proteomics, 2021, 1869, 140557.
8. J. P. Klinman, ACS Cent. Sci., 2015, 1, 115–116.
9. T. Wang, Y. Zhang, B. Huang, B. Cai, R. R. Rao, L. Giordano, S.-G. Sun and Y. Shao-Horn, Nat. Catal., 2021, 4, 753–762.
10. N. Berg, S. Bergwinkl, P. Nuernberger, D. Horinek and R. M. Gschwind, J. Am. Chem. Soc., 2021, 143, 724–735.
11. G. A. Jeffrey and W. Saenger, The Importance of Hydrogen Bonds, Springer Berlin Heidelberg, Berlin, Heidelberg, 1991, pp. 3–14.
12. G. Vladilo and A. Hassanali, Life, 2018, 8, 1.
13. E. D. Głowacki, M. Irimia-Vladu, S. Bauer and N. S. Sariciftci, J. Mater. Chem. B, 2013, 1, 3742–3753.
14. V. Vennelakanti, H. W. Qi, R. Mehmood and H. J. Kulik, Chem. Sci., 2021, 12, 1147–1162.
15. H. Liu, J. Cao and W. Bian, J. Phys. Chem. A, 2020, 124, 6536–6543.
16. R. Kalescky, E. Kraka and D. Cremer, J. Chem. Phys., 2014, 140, 084315.
17. J. A. Davies, M. W. D. Hanson-Heine, N. A. Besley, A. Shirley, J. Trowers, S. Yang and A. M. Ellis, Phys. Chem. Chem. Phys., 2019, 21, 13950–13958.
18. Q.-R. Huang, R. Shishido, C.-K. Lin, C.-W. Tsai, J. A. Tan, A. Fujii and J.-L. Kuo, Angew. Chem., Int. Ed., 2021, 60, 1936–1941.
19. A. Nejad, M. A. Suhm and K. A. E. Meyer, Phys. Chem. Chem. Phys., 2020, 22, 25492–25501.
20. C. K. Nandi, M. K. Hazra and T. Chakraborty, J. Chem. Phys., 2005, 123, 124310.
21. P. Rodziewicz and N. L. Doltsinis, J. Phys. Chem. A, 2009, 113, 6266–6274.
22. A. Martín Santa Daría, G. Avila and E. Mátyus, Phys. Chem. Chem. Phys., 2021, 23, 6526–6535.
23. H. Tachikawa, J. Phys. Chem. A, 2020, 124, 3048–3054.
24. J. Zaklika, L. Komorowski and P. Ordon, J. Phys. Chem. A, 2019, 123, 4274–4283.
25. C. Qu and J. Bowman, Faraday Discuss., 2018, 212, 33–49.
26. S. Giri, R. Parida, M. Jana, S. Gutiérrez-Oliva and A. Toro-Labbe, J. Phys. Chem. A, 2017, 121, 9531–9543.
27. P. Farfán, A. Echeverri, E. Diaz, J. D. Tapia, S. Gómez and A. Restrepo, J. Chem. Phys., 2017, 147, 044312.
28. S. Fathi, P. Blaise, A. Ceausu-Velcescu and S. Nasr, Chem. Phys., 2017, 492, 12–22.
29. W. Li, L. Evangelisti, Q. Gou, W. Caminati and R. Meyer, Angew. Chem., Int. Ed., 2019, 58, 859–865.
30. F. Holtzberg, B. Post and I. Fankuchen, J. Chem. Phys., 1952, 20, 198.
31. S. Nasr, M.-C. Bellissent-Funel and R. Cortès, J. Chem. Phys., 1999, 110, 10945–10952.
32. S. Imberti and D. T. Bowron, J. Phys.: Condens. Matter, 2010, 22, 404212.
33. N. Lumbroso-Bader, C. Coupry, D. Baron, D. Clague and G. Govil, J. Magn. Reson., 1969, 1975(17), 386–392.
34. A. Apelblat, Can. J. Chem., 1991, 69, 638–647.
35. D. Di Tommaso and K. L. Watson, J. Phys. Chem. A, 2014, 118, 11098–11113.
36. C. Ngaojampa, T. Kawatsu, Y. Oba, N. Kungwan and M. Tachikawa, Theor. Chem. Acc., 2017, 136, 30.
37. A. M. Daly, K. O. Douglass, L. C. Sarkozy, J. L. Neill, M. T. Muckle, D. P. Zaleski, B. H. Pate and S. G. Kukolich, J. Chem. Phys., 2011, 135, 154304.
38. J. W. Keller, J. Phys. Chem. A, 2004, 108, 4610–4618.
39. D. J. Frurip, L. A. Curtiss and M. Blander, J. Am. Chem. Soc., 1980, 102, 2610–2616.
40. N. Heine, T. I. Yacovitch, F. Schubert, C. Brieger, D. M. Neumark and K. R. Asmis, J. Phys. Chem. A, 2014, 118, 7613–7622.
41. A. B. McCoy, X. Huang, S. Carter and J. M. Bowman, J. Chem. Phys., 2005, 123, 064317.
42. D. Peláez and H.-D. Meyer, Chem. Phys., 2017, 482, 100–105.
43. E. G. Diken, J. M. Headrick, J. R. Roscioli, J. C. Bopp, M. A. Johnson and A. B. McCoy, J. Phys. Chem. A, 2005, 109, 1487–1490.
44. M. T. Kemp, E. M. Lewandowski and Y. Chen, Biochim. Biophys. Acta, Proteins Proteomics, 2021, 1869, 140557.
45. R. Tripathi, H. Forbert and D. Marx, J. Phys. Chem. B, 2019, 123, 9598–9608.
46. J. Lin, E. Pozharski and M. A. Wilson, Biochemistry, 2017, 56, 391–402.
47. D. A. Thomas, M. Marianski, E. Mucha, G. Meijer, M. A. Johnson and G. von Helden, Angew. Chem., Int. Ed., 2018, 57, 10615–10619.
48. L. Baptista, D. P. P. Andrade, A. B. Rocha, M. L. M. Rocco, H. M. Boechat-Roberty, E. F. da Silveira, E. C. da Silva and G. Arbilla, J. Phys. Chem. A, 2008, 112, 13382–13392.
49. L. Baptista, D. P. P. Andrade, A. B. Rocha, M. L. M. Rocco, H. M. Boechat-Roberty and E. F. d Silveira, J. Phys. Chem. A, 2010, 114, 6917–6926.
50. S. Heinbuch, F. Dong, J. J. Rocca and E. R. Bernstein, J. Chem. Phys., 2007, 126, 244301.
51. Y. Inokuchi and N. Nishi, J. Phys. Chem. A, 2002, 106, 4529–4535.
52. Y. Inokuchi and N. Nishi, J. Phys. Chem. A, 2003, 107, 11319–11323.
53. V. Scutelnic and T. R. Rizzo, J. Phys. Chem. A, 2019, 123, 2815–2819.
54. E. Carrascosa, R. P. Pellegrinelli, T. R. Rizzo and M. A. Muyskens, J. Phys. Chem. A, 2020, 124, 9942–9950.
55. C. Kirschbaum, K. Greis, E. Mucha, L. Kain, S. Deng, A. Zappe, S. Gewinner, W. Schöllkopf, G. von Helden, G. Meijer, P. B. Savage, M. Marianski, L. Teyton and K. Pagel, Nat. Commun., 2021, 12, 1201.
56. C. Kirschbaum, E. M. Saied, K. Greis, E. Mucha, S. Gewinner, W. Schöllkopf, G. Meijer, G. von Helden, B. L. J. Poad, S. J. Blanksby, C. Arenz and K. Pagel, Angew. Chem., Int. Ed., 2020, 59, 13638–13642.
57. E. Mucha, M. Marianski, F.-F. Xu, D. A. Thomas, G. Meijer, G. von Helden, P. H. Seeberger and K. Pagel, Nat. Commun., 2018, 9, 4174.
58. Y. Yang, O. Kühn, G. Santambrogio, D. J. Goebbert and K. R. Asmis, J. Chem. Phys., 2008, 129, 224302.
59. J. A. DeVine, S. Debnath, Y.-K. Li, L. M. McCaslin, W. Schöllkopf, D. M. Neumark and K. R. Asmis, Mol. Phys., 2020, 118, e1749953.
60. C. H. Duong, N. Yang, M. A. Johnson, R. J. DiRisio, A. B. McCoy, Q. Yu and J. M. Bowman, J. Phys. Chem. A, 2019, 123, 7965–7972.
61. F. S. Menges, E. H. Perez, S. C. Edington, C. H. Duong, N. Yang and M. A. Johnson, J. Am. Soc. Mass Spectrom., 2019, 30, 1551–1557.
62. F. Schinle, C. R. Jacob, A. B. Wolk, J.-F. Greisch, M. Vonderach, P. Weis, O. Hampe, M. A. Johnson and M. M. Kappes, J. Phys. Chem. A, 2014, 118, 8453–8463.
63. A. B. Wolk, C. M. Leavitt, E. Garand and M. A. Johnson, Acc. Chem. Res., 2014, 47, 202–210.
64. A. F. DeBlase, S. R. Kass and M. A. Johnson, Phys. Chem. Chem. Phys., 2014, 16, 4569–4575.
65. C. M. Leavitt, A. F. DeBlase, C. J. Johnson, M. van Stipdonk, A. B. McCoy and M. A. Johnson, J. Phys. Chem. Lett., 2013, 4, 3450–3457.
66. E. Garand, M. Z. Kamrath, P. A. Jordan, A. B. Wolk, C. M. Leavitt, A. B. McCoy, S. J. Miller and M. A. Johnson, Science, 2012, 335, 694–698.
67. M. Z. Kamrath, E. Garand, P. A. Jordan, C. M. Leavitt, A. B. Wolk, M. J. Van Stipdonk, S. J. Miller and M. A. Johnson, J. Am. Chem. Soc., 2011, 133, 6440–6448.
68. E. I. Obi, C. M. Leavitt, P. L. Raston, C. P. Moradi, S. D. Flynn, G. L. Vaghjiani, J. A. Boatz, S. D. Chambreau and G. E. Douberly, J. Phys. Chem. A, 2013, 117, 9047–9056.
69. D. A. Thomas, E. Mucha, M. Lettow, G. Meijer, M. Rossi and G. von Helden, J. Am. Chem. Soc., 2019, 141, 5815–5823.
70. E. Mucha, A. I. González Flórez, M. Marianski, D. A. Thomas, W. Hoffmann, W. B. Struwe, H. S. Hahm, S. Gewinner, W. Schöllkopf, P. H. Seeberger, G. von Helden and K. Pagel, Angew. Chem., Int. Ed., 2017, 56, 11248–11251.
71. A. I. González Flórez, E. Mucha, D.-S. Ahn, S. Gewinner, W. Schöllkopf, K. Pagel and G. von Helden, Angew. Chem., Int. Ed., 2016, 55, 3295–3299.
72. U. Even, EPJ Tech. Instrum., 2015, 2, 17.
73. A. I. González Flórez, PhD thesis, Freie Universität, Berlin, Germany, 2015.
74. W. Schöllkopf, S. Gewinner, H. Junkes, A. Paarmann, G. von Helden, H. P. Bluem and A. M. M. Todd, Advances in X-ray Free-Electron Lasers Instrumentation III, 2015, pp. 238–250.
75. P. Pracht, F. Bohle and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192.
76. C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671.
77. S. Spicher and S. Grimme, Angew. Chem., Int. Ed., 2020, 59, 15665–15673.
78. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
79. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
80. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision C.01, Gaussian Inc., Wallingford CT, 2016.
81. A. Halkier, T. Helgaker, P. Jørgensen, W. Klopper and J. Olsen, Chem. Phys. Lett., 1999, 302, 437–446.
82. M. O. Sinnokrot, E. F. Valeev and C. D. Sherrill, J. Am. Chem. Soc., 2002, 124, 10887–10893.
83. V. Barone, J. Chem. Phys., 2005, 122, 014108.
84. V. Barone, J. Bloino, C. A. Guido and F. Lipparini, Chem. Phys. Lett., 2010, 496, 157–161.
85. J. Bloino and V. Barone, J. Chem. Phys., 2012, 136, 124108.
86. K. A. E. Meyer and A. Nejad, Phys. Chem. Chem. Phys., 2021, 23, 17208–17223.
87. I. Reva, A. Plokhotnichenko, E. Radchenko, G. Sheina and Y. Blagoi, Spectrochim. Acta, Part A, 1994, 50, 1107–1111.
88. F. Ito, J. Mol. Struct., 2015, 1091, 203–209.
89. E. M. Maçôas, J. Lundell, M. Pettersson, L. Khriachtchev, R. Fausto and M. Räsänen, J. Mol. Spectrosc., 2003, 219, 70–80.
90. S. Lopes, R. Fausto and L. Khriachtchev, J. Chem. Phys., 2018, 148, 034301.
91. M. M. Nolasco, A. M. Amado and P. J. A. Ribeiro-Claro, J. Raman Spectrosc., 2009, 40, 394–400.
92. K. A. E. Meyer and M. A. Suhm, J. Chem. Phys., 2018, 149, 104307.
93. W. H. Hocking, Z. Naturforsch., A: Phys., Phys. Chem., Kosmophys., 1976, 31, 1113–1121.
94. M. Pettersson, E. M. S. Maçôas, L. Khriachtchev, J. Lundell, R. Fausto and M. Räsänen, J. Chem. Phys., 2002, 117, 9095–9098.
95. C. T. Wolke, A. F. DeBlase, C. M. Leavitt, A. B. McCoy and M. A. Johnson, J. Phys. Chem. A, 2015, 119, 13018–13024.

---

Footnote

† Electronic supplementary information (ESI) available: O–H and O–O bond lengths, vibrational modes assignment and comparison of additional experimental and theoretical spectra. See DOI: https://doi.org/10.1039/d2cp05409d

---