Structural analysis of potassium borate solutions

Abstract

In this work, H/D isotopic substitution neutron diffraction was combined with empirical potential structure refinement (EPSR) and DFT-based quantum calculations to study the interactions between B(OH)₃ boric acid molecules, B(OH)₄⁻ metaborate ions, water molecules, and potassium cations in borate solutions. The results show that the solute ions and molecules have a marked effect on the second coordination shell of the water molecules, causing a greater deviation from a tetrahedral structure than is observed for pure water. Potassium ions and trans-B(OH)₃ tend to form a monodentate contact ion pair (MCIP) with a K–B distance ∼3.8 Å, which remains constant upon changing the solution concentration. Potassium ions and cis-B(OH)₃ form both a MCIP at K–B ∼3.8 Å and a bidentate contact ion pair (BCIP) at K–B ∼3.4 Å. As the solution concentration increases, there is a BCIP to MCIP transformation. Boric acid molecules can undergo hydration in one of three ways: direct hydration, interstitial hydration, and axial hydration. The energetic hydration preference is direct hydration → interstitial hydration → axial hydration. Nine water molecules are required when all water molecules directly interact with the –OH groups of B(OH)₄⁻, and a tenth water molecule is located at an interstitial position. The hydrogen bonding between boric acid molecule/metaborate ion and water molecules is stronger than that between water molecules in the hydration layer.

---

Introduction

Boron-containing compounds have important applications in medical treatment, agriculture, and chemical products,^1–4 and they also have significant academic research value. The electron-deficient B atom has two structural units, BO₃ and BO₄ in borate anions, which can transform between themselves upon changing the atomic and molecular stoichiometry of the solution, or the species of cation within the mixture. Wright et al.^5,6 defined five basic structural units of BO₃ and BO₄ according to the bonding between the oxygen atoms and the boron atom. They also defined superstructural units for boron-containing cyclic species. This diversity of borate structures leads to a variety of interesting properties of borate materials.

A unique property of borate solutions is that a variety of boron-containing species can coexist in water. A significant amount of research has been performed using various techniques, including Raman spectroscopy,^7,8 nuclear magnetic resonance (NMR),^9,10 X-ray diffraction,^11,12 and near-edge X-ray absorption fine structure (NEXAFS).¹³ There are at least six boron-containing species in borate solutions: B(OH)₃, B(OH)₄⁻, B₃O₃(OH)₄⁻, B₃O₃(OH)₅²⁻, B₄O₅(OH)₄²⁻, and B₅O₆(OH)₄⁻.^14,15 New borate species have also been discovered in recent studies. For example, diborate [B₂O(OH)₅]⁻ was shown to exist in solution using Raman spectroscopy and quantitative calculations,^16,17 and the pentaborate ion [B₅O₆(OH)₄]⁻ was also shown to exist. The hexaborate [B₆O₇(OH)₆]²⁻ ion has also been found in magnesium borate solutions.¹⁸ Researchers have suggested that the cation greatly influences the structure of ion clusters in highly-concentrated solutions.^19,20 For example, a complex ion cluster is composed of two potassium ions and one metaborate ion, B(OH)₄⁻, in potassium metaborate solutions, while complex ion clusters dissociate into a sodium ion and two metaborate ions in sodium metaborate solutions. X-ray diffraction has recently been used to study the structure of borate solutions, the hydration number, and the distance between borate ions and water.^11,12,21 Although X-ray diffraction can provide direct structural information, it has certain limitations when used to study the hydration structure of borate solutions because of the weaker scattering power of lightweight atoms such as H and B.

Recently, Pye et al.²² studied the structure and vibrational frequencies of boron-containing species and proposed the most stable structures of their isomers, and a variety of boric acid isomers were proposed. It was pointed out that the most stable boric acid molecules had C_3h and C_s symmetries (trans-B(OH)₃ and cis-B(OH)₃), with similar energies. The species distribution map also showed that polyborate ions hydrolyzed to B(OH)₄⁻ and B(OH)₃ in dilute solutions.²³ This hints that the two B(OH)₃ isomers may coexist in borate solutions, but few experiments have reported these two structures. For this reason, we used quantitative calculation methods to study the hydrolysis mechanism of polyborate ions^24,25 and found that B₅O₆(OH)₄⁻ has two hydrolysis pathways: water-poor and water-rich. During water-poor hydrolysis, the products are B(OH)₃ and [B₃O₃(OH)₄]⁻. [B₃O₃(OH)₄]⁻ further hydrolyzes to B(OH)₄⁻ and B(OH)₃ in a water-rich process, and all boric acid molecules are cis-B(OH)₃. [B₄O₅(OH)₄²⁻] finally hydrolyzes to cis-B(OH)₃ and trans-B(OH)₃ in a 1 : 1 molar ratio. This was the first time that these two isomers were found in borate solutions.

Researchers^26–29 have studied the structures of boric acid molecules and B(OH)₄⁻ using quantitative calculations. The bond length, bond angle, Raman spectra, and water number of boric acids that formed Lewis bases were given, but few studies have shown whether trans-B(OH)₃ and cis-B(OH)₃ molecules coexist in solution, and their structure details remain unclear. The hydration structure of boric acid molecules and metaborate ions was studied using NEXAFS¹³ and it was found that the hydrated structure of borates had little effect on their spectra. The K-edge NEXAFS spectrum of B was not very sensitive to hydrogen bonds, solution environment, or interactions between solute and water molecules; therefore, the interaction between solute and water molecules should be further studied using other techniques.

Here, neutron diffraction measurements with hydrogen/deuterium (H/D) isotopic substitution^30,31 (NDIS) were analysed using empirical potential structure refinement (EPSR) simulations to obtain atomic-scale information on aqueous borate solutions. The effects of solution concentration, type, and structure of boron species on the hydration structure are discussed. H/D substitution is used to change the scattering ability of hydrogen atoms and hence to obtain more structural information related to the hydrogen atoms in the borate solutions. Replacing natural boron with ¹¹B eliminates the strong neutron absorption of ¹⁰B, which otherwise would be a great experimental handicap. The ¹¹B neutron scattering length is 6.06 fm, which is comparable to the O scattering length of 5.80 fm.³¹ This study provides a method to accurately analyze the hydration structure of borate species. DFT-based quantum calculations are also used to reveal the structural details of hydration of borate species.

Neutron diffraction experiment and data analysis

Sample preparation

The first stage of the sample preparation was to make hydrous K¹¹BO₂·1.33H₂O and K₂¹¹B₄O₇·4H₂O crystals by evaporation from solution, using information from the B₂O₃–K₂O–H₂O ternary phase diagram,³² and full details of the sample preparation are given in the ESI.† The crystals were then dehydrated, yielding anhydrous powders of K¹¹BO₂ and K₂¹¹B₄O₇ respectively. The solutions were made from these crystals with the aim of ensuring that the K : B ratio and the concentrations of potassium and boron in the solutions were as intended.

Hydrogen–deuterium isotopic substitution was used to obtain the structural information about hydrogen bonding.³³ Potassium borate solutions were prepared by dissolving the above anhydrous crystals in H₂O (double-distilled water), D₂O (Sigma-Aldrich 99.9 atom %D), and a 1 : 1 mixture of H₂O and D₂O. Solution densities were measured using a digital display instrument (Anton Paar) (Table 1) calibrated using pure water. The concentrations of the samples are specified by their water-salt molar ratio (WSR). The relationship between WSR and concentration (mol L⁻¹) is shown in Fig. S4 (ESI†). The detailed composition information is shown in Table 1.

Table 1 Compositions of aqueous potassium borates solutions

System	WSR	K^11BO2 (g)	K2^11B4O7 (g)	D2O (g)	H2O (g)	Density/g cm^−3
K[B(OH)4]_20	20	0.8494	0	4.1554	0	1.2993
	20	0.8488	0	2.1876	1.9758	1.2396
	20	0.9282	0	0	4.0791	1.1957
K[B(OH)4]_60	60	0.3192	0	4.6980	0	1.1751
	60	0.3206	0	2.4660	2.2179	1.1186
	60	0.3532	0	0	4.6550	1.0695
K2B4O7_60	60	0	0.8156	4.2124	0	1.2624
	60	0	0.8164	2.2091	1.9901	1.2028
	60	0	0.8918	0	4.1139	1.1582
K2B4O7_100	100	0	0.5239	4.4770	0	1.2038
	100	0	0.5231	2.3570	2.1280	1.1466
	100	0	0.5756	0	4.4317	1.0988
	WSR: the molar ratio of water to salt.

---

Neutron diffraction experiments

For neutron diffraction measurements, samples of volume ∼1.4 cm³ were transferred to a Ti_0.677Zr_0.323 null alloy container with internal dimensions of 1 mm thickness × 35 mm width × 40 mm height. The composition of the alloy was chosen so that ideally coherent scattering from the container is eliminated, because the average coherent scattering length of the alloy is zero (b̄_Ti = −3.438 fm and b̄_Zr = 7.16 fm³¹). Filled cells were loaded onto an automatic sample changer on the small-angle neutron diffractometer for amorphous and liquid samples (SANDALS) at the ISIS pulsed neutron source of the Rutherford Appleton Laboratory, UK.³⁴ The temperature of each sample was controlled to 25 ± 0.1 °C. The experimental data were corrected for background scattering, absorption, and multiple scattering using the Gudrun routines.³⁵ Finally, the diffraction data were normalized with reference to the measured scattering from a V-Nb null alloy plate. The corrected interference differential scattering cross-sections, F(Q), and pair distribution functions, G(r), are shown in Fig. 1.

Fig. 1 Experimentally-determined (blue points) and EPSR simulated (red solid line) F(Q) and G(r) for borate solutions. WSR 100 (a) and 60 (b) for K₂B₄O₇ solutions; WSR 60 (c) and 20 (d) for K[B(OH)₄] solutions.

Data analysis

The total differential scattering cross-section of a sample contains structural information about pair correlations between the constituent atoms of the sample, and is expressed as the total structure factor, F(Q), defined by eqn (1), in which Q is the magnitude of the momentum transfer vector of the scattering process:where S_αβ(Q) is the partial structure factor for correlations between atom types α and β, and δ_αβ is the Kronecker delta to prevent double-counting interactions between the same type of atoms. c_α and b̄_α are the atomic concentration and the Q-independent coherent neutron scattering length of each atom type.

The partial structure factors are related to the partial pair distribution functions, g_αβ(r), via a Fourier transform weighted by the atomic density of the system, ρ, defined by eqn (2):

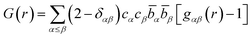The relationship between the total pair distribution function G(r) and the partial pair distribution functions is expressed by eqn (3):

The EPSR program is a tool for extracting structural information from the measured F(Q).^36,37 EPSR first performs a standard Monte Carlo simulation of a system using the intramolecular structure, the bulk atomic density, and a set of Lennard-Jones atomic reference potentials. It is predicted from the equilibrium constants that the metaborate ion B(OH)₄⁻ is the dominant ion for metaborate solutions,³⁸ and these predictions are supported by experimental results from Raman spectroscopy and X-ray diffraction.³⁹ Therefore the only borate anions in the EPSR models of metaborate solutions were B(OH)₄⁻. Equal numbers of B(OH)₄⁻ and B(OH)₃ anions were used in the EPSR modelling of K₂B₄O₇ solutions because DFT calculations²⁴ show that the tetraborate anion [B₄O₅(OH)₄²⁻] finally hydrolyses to equal numbers of B(OH)₄⁻ and B(OH)₃. The relative numbers of trans-B(OH)₃ and cis-B(OH)₃ are not known, and thus they were assumed to be equal in the EPSR modelling of these solutions. The details of the structural models and simulation box are shown in Table S3 (ESI†) and Table 2. EPSR modelling was performed using the three experimental structure factor measurements for each composition up to a maximum momentum transfer of 30 Å⁻¹, and the minimum momentum transfer of the structure factor measurements was 0.125 Å⁻¹. Fig. 1 shows the experimentally-determined and EPSR-simulated F(Q) and G(r) functions for potassium borate solutions. There is good agreement between the experimental and simulated data, which indicates that the simulated structures are close to the real structures.

Table 2 Cubic box details, Lennard-Jones parameters and effective atomic charges of EPSR refinements

WSR	Number of K^+	Number of [B(OH)4^−]	Number trans-[B(OH)3]	Number of cis-[B(OH)3]	Number of water molecules	Length of box (Å)	Number density (atoms A^−3)
Owater and Hwater refer to oxygen and hydrogen sites in water molecules, and the subscripts 4, trans and cis refer respectively to atom sites in B(OH)4^−, trans-[B(OH)3], and cis-[B(OH)3]; the charge parameters are the Mulliken charge from DFT calculation at m062x/6-311++g(2df,2pd); WSR: molar ratio of water to salt.a Aqueous K2B4O7 solution.
20	150	150	0	0	3000	47.2	0.099853
60	50	50	0	0	3000	45.6	0.10019
60^a	112	112	56	56	2968	47.6	0.10021
100^a	64	64	32	32	2976	46.4	0.10026

---

Atom	ε (kJ mol^−1)	σ (Å)	q (e)	Mass [amu]
K^40	0.5000	3.000	1.0000	39.0981
B4^41	0.3970	3.5180	0.71101	10.810
O4^41	0.7200	3.1200	−0.6594	15.9990
H4^41	0.000	0.000	2.000	0.2316
Btrans	0.7113	3.5000	0.8505	10.810
Otrans	0.8803	3.1000	−0.5706	15.9990
Htrans	0	0	0.2871	2.0
Bcis	0.8000	3.2000	0.7500	10.810
Ocis	0.6500	3.100	−0.5000	15.9990
Hcis	0	0	0.2500	2.0
Owater^42	0.6500	3.160	−0.8476	16.0
Hwater^42	0	0	0.4238	2.0

---

Computational methods for hydrated clusters

Density functional theory (DFT) is an effective method for studying boron-containing systems.^{11,12,19,20,24,25} The M06-2X method^43–45 and 6-311++G(2df,2pd) Pople-style basis set⁴⁶ were used to optimize hydrated structures in the gas phase, with as many initial structures as possible. Then, the optimized equilibrium structures were further optimized in the liquid phase to obtain the final equilibrium structure. Single-point energy calculations and frequency calculations were conducted on these structures using the same basis set to determine the zero-point energy (ZPE) values and to confirm that the optimized structures had reached a local minimum (zero imaginary frequency). Furthermore, self-consistent field (SCF) energy, zero-point vibrational energy (ZPE) and energy correction terms associated with the basis set superposition error (BSSE) were also involved in the definition of the calculated total energies of the hydrated clusters. After this, the optimized isomers were ranked in order of energy, and the low energy structures were chosen for discussion. The hydration shape of the chosen structures is similar to the spatial density functions and their hydration distance B–O(W) is close to the NDIS result. The optimized structures and their energy data are shown in Fig. S5 and Table S4 (ESI†). The Raman spectrum of the boric acid molecule was also calculated under the same conditions. The calculated Raman spectrum was compared with the Raman spectrum of boric acid solution, as shown in Fig. S6 (ESI†), showing that the calculated frequency of the stretching vibration of the boric acid molecule is close to the experimental value. Therefore, although the acidity medium was not considered during the DFT calculation, the results can support our experimental conclusion. All calculations were carried out using the Gaussian16 package.⁴⁷ The electrostatic potentials and average reduced density gradient analysis were performed using Multiwfn 3.6 (dev).⁴⁸

Results and discussion

Structure around water molecules

Fig. 2 shows the intermolecular pair distribution functions for O_water⋯O_water (g_{Owater…Owater}) (a), H_water⋯O_water (g_{Hwater⋯Owater}) (b), and H_water⋯H_water (g_{Hwater⋯Hwater}) (c) between pairs of atoms in pure water and different water molecules in the solutions. Fig. 2 and Table 3 show that the O_water⋯O_water distances (r_{Owater⋯Owater}) are in the range 2.2–3.3 Å. The peak position of ∼2.71 Å remains constant, and the coordination number (4.1–3.6) has an inverse relationship with the concentration. The peak r_{Owater⋯Owater} distance 2.71 Å is slightly shorter than the distance 2.73 Å obtained by Soper for pure water.⁴⁹ Using X-ray diffraction, Zhou et al.^11,12 reported that r_{Owater⋯Owater} is in the range 2.76–2.82 Å in sodium/potassium metaborate solution, which is larger than the hydration distance observed in this study. This difference probably arises from the superior ability of neutron diffraction with H/D substitution to locate the atoms in an aqueous solution. Skinner et al.⁵⁰ reported that the coordination number of the first hydration layer is 4.3 ± 0.1 in pure water when the cutoff value of the O_water⋯O_water pair distribution function is 3.3 Å, which is close to the value of 4.1 ± 1.1 found in this work. Zhou et al.^11,12 reported that the O_water⋯O_water coordination numbers were 4.9 ± 1.1 and 4.7 ± 1.4 in pure water and dilute sodium/potassium metaborate solutions, respectively, which are higher than the values in pure water and in this work. Again this difference may be due to the advantageous use of NDIS. The second hydration distance (O_water⋯O_water) in the solutions is about 3.8 Å (Fig. 2), shorter than the distance of 4.5 Å for pure water,⁵¹ and there is greater shortening of the distance as the potassium borate concentration increases.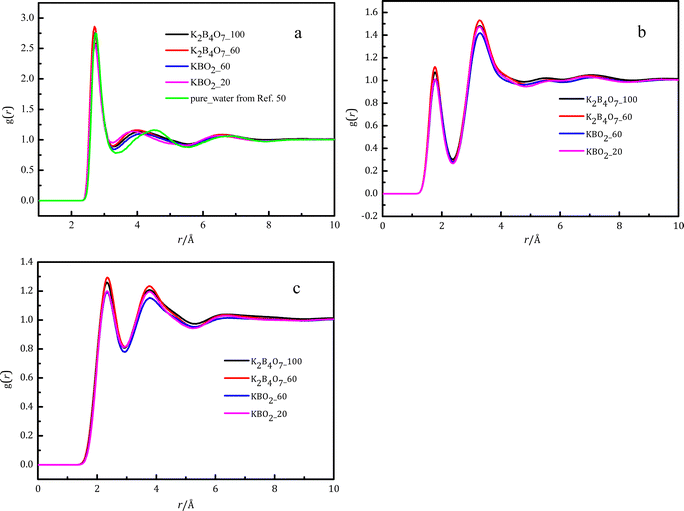

Fig. 2 Intermolecular pair distribution functions at various concentrations, obtained by EPSR modeling: O_water–O_water (a), H_water⋯O_water (b), and H_water⋯H_water (c).

Table 3 Positions and the average coordination number of the atom pairs in aqueous borate solutions. r/Å denotes the peak position and its range, whilst CN denotes the average coordination number of the first shell. The notation used for the systems is defined in Table 1

	K2B4O7_100			K2B4O7_60			K[B(OH)4]_60			K[B(OH)4]_20
	r peak	r min–rmax	CN	r peak	r min–rmax	CN	r peak	r min–rmax	CN	r peak	r min–rmax	CN
Owater–Owater	2.71	2.2–3.3	4.1 ± 1.2	2.71	2.2–3.25	3.6 ± 1.2	2.71	2.2–3.3	4.1 ± 1.1	2.71	2.2–3.3	3.6 ± 1.2
Hwater–Owater	1.77	1–2.3	1.1 ± 0.7	1.77	1–2.3	1.0 ± 0.7	1.77	1–2.4	1.1 ± 0.7	1.77	1–2.4	1.0 ± 0.7
Otrans–Owater	3.12	2.3–4.2	6.1 ± 2.5	3.12	2.3–4.1	4.6 ± 2.2
Ocis–Owater	3.12	2.3–4.1	6.1 ± 2.3	3.12	2.3–4.1	5.0 ± 2.1
OB–Owater	2.79	2.3–3.6	3.7 ± 1.2	2.79	2.3–3.6	3.5 ± 1.4	2.79	2.3–3.75	4.5 ± 1.3	2.79	2.2–3.75	4. 3 ± 1.4
Btrans–Owater	3.98	2.6–5.2	13.6 ± 4.4	4.02	2.6–5.2	12.2 ± 3.7
Bcis–Owater	3.85	2.6–5.2	12.9 ± 3.5	3.85	2.6–5.2	15.1 ± 4.6
B–Owater	3.56	2.6–4.8	11.6 ± 2.7	3.56	2.6–4.8	10.9 ± 2.3	3.56	2.7–4.55	15.1 ± 2.5	3.56	2.7–4.75	12.1 ± 1.9
K–Btrans	3.93	2.6–4.6	0.1 ± 0.2	3.95	2.6–4.6	0.1 ± 0.4
K–Bcis	3.42	2.6–4.6	0.2 ± 0.4	3.93	2.6–4.6	0.2 ± 0.4
K–B	3.32	2.6–4.6	0.8 ± 0.9	3.31	2.6–4.6	0.9 ± 0.8	3.30	2.6–4.6	0.4 ± 0.6	3.31	2.6–4.6	1.2 ± 0.8
K–Otrans	2.82	2–3.5	0.23 ± 0.6	2.79	2–3.5	0.17 ± 0.4
K–Ocis	2.80	2–3.4	0.05 ± 0.2	2.80	2–3.4	0.1 ± 0.4
K–O	2.68	2–3.4	1.1 ± 1.5	2.70	2–3.4	1.3 ± 1.4	2.70	2–3.5	0.5 ± 0.9	2.68	2.2–3.5	1.8 ± 1.6
K–Owater	2.63	2–3.45	5.6 ± 1.8	2.63	2–3.4	5.2 ± 1.5	2.63	2–3.5	6.2 ± 1.2	2.63	2–3.45	5.1 ± 1. 4

---

The EPSR simulations show that the ratio of the second to first oxygen-oxygen distances in the borate solutions are 1.52 and 1.48 (in K₂B₄O₇ solution with WSR = 100 and 60), and 1.52 and 1.43 (in KBO₂ solution with WSR = 60 and 20), compared to a value of 1.66 for pure water.⁵¹ The higher the concentration of the solutions, the more deviation from the ratio of pure water. This indicates that the dissolved ions distort the tetrahedral structure of water. The second coordination shell of water molecules is disrupted by the metal ion as the solution concentration increases, which causes water molecules in this outer shell to move to the first (inner) coordination shell. Soper and Ricci reported that external pressure caused the second hydration shell to move to smaller r in pure water.⁵¹ This implies the second shell is collapsing into some of the free space in a non-bonded fashion. Recently Woutersen et al.⁵² investigated three-dimensional structural density plots of the H-bond acceptor atoms (water O, TFA O, and hydrazinium N) in the first and second coordination shells of a water molecule in neat water at 1 bar, in neat water at 6 kbar, and in N₂H₅ TFA solution at 1 bar. The three-dimensional structural density surface of pure water at normal pressure is different from that under 600 MPa pressure and the N₂H₅ TFA solution under normal pressure. This is similar to that in pure water and in salt solutions reported by Soper et al.^42,53 These phenomena again demonstrate that environmental pressure and added ions have the same effect on the second hydration shell of a water molecule. g_{Hwater⋯Owater} and g_{Hwater⋯Hwater} are shown in Fig. 2(b and c). Their first peak positions are at 1.77 Å and 2.33 Å, and their coordination numbers are 1.0 and 1.1.

Fig. 3 shows the spatial density function (SDF) of water molecules in aqueous K₂B₄O₇ solutions for WSR = 100. The SDFs for other samples are shown in Fig. S7 (ESI†). The figure shows that the inner hydration layer has a tetrahedral structure and is less affected by concentration, which is consistent with r_{Owater⋯Owater} remaining constant at various concentrations. There is a slight difference in the SDF surfaces of the outer sphere (Fig. 3) because the dissolved ions in the solutions damage the second hydration layer. The B(OH)₃ and B(OH)₄⁻ species have –OH groups and prefer to form a tetrahedral structure. Therefore, this may reduce the disruption of the second hydration layer to some extent. Moreover, the H_water⋯O_water and H_water⋯H_water distances of the second hydration layer remained nearly unchanged. These phenomena also confirm that the disruption of the second hydration layer is small, and this shell is resilient to change.

Fig. 3 Spatial density functions of neighbouring water molecules with respect to the central water molecule of aqueous K₂B₄O₇ solutions for WSR = 100. The dark blue lobes represent the first coordination sphere, and the light green and semitransparent lobes/green lobes represent the second sphere. The red and white balls in the centre represent the O and H atoms of H₂O, respectively. (a) side view; (b) top view; (c) side view of the second hydration sphere of water; (d) top view of the second hydration sphere of water.

Ion pair structures. Fig. S8 (ESI†) displays the first layer hydration distance r_K–O(W) of potassium ions. The distance r_K–Owater remained at 2.63 Å, regardless of solution concentration. The hydration number ranged from 6.2 to 5.1 as the concentration decreased, indicating that a small number of borate ions enters the first hydration layer of potassium ions to form contact ions. Our results are similar to previous work.^12,54,55

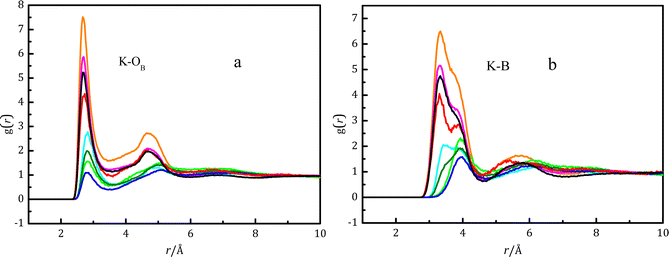
Fig. 4(a) shows the pair distribution function g_K–OB between potassium ions and oxygen atoms in various boron-containing species, whilst Fig. 4(b) shows the g_K–B between potassium ions and boron atoms in various boron-containing species. The intensity of g_K–OB for B(OH)₄⁻ is greater than B(OH)₃ due to strong electrostatic interactions between ions. is shorter than r_{K–B[B(OH)3]}, which is also caused by the strong electrostatic attraction between anions and cations. In Fig. 4(b), there is a strong peak at 3.3 Å with a shoulder at 3.85 Å in g_K–B for B(OH)₄⁻. The main peak at 3.3 Å in g_K–B of cis-B(OH)₃ gradually weakened, and the shoulder at 3.85 Å increased with the potassium borate concentration. For trans-B(OH)₃, only a peak at 3.85 Å was observed. We have previously studied the structure of potassium metaborate solutions and found that the peak at 3.85 Å is caused by the K–B distance of a monodentate ion pair (MCIP), while the peak at 3.3 Å is caused by a bidentate ion pair (BCIP).¹²Fig. 4(b) shows that the K–B distance (r_K–B) is ∼3.8 Å in K–B(trans-B(OH)₃), and the distance does not change with potassium borate concentration. When a contact ion pair is formed between the potassium ion and cis-B(OH)₃, the peak at ∼3.4 Å is the dominant peak in dilute solutions, and the peak at ∼3.8 Å becomes the dominant one in concentrated solutions.

Fig. 4 Pair distribution functions for various K–O_B pairs (a) and K–B pairs (b) at various concentrations obtained using EPSR modeling. cis-B(OH)₃ in K₂B₄O₇ solution with WSR = 100; B(OH)₄⁻ in K₂B₄O₇ solution with WSR = 100; trans-B(OH)₃ in K₂B₄O₇ solution with WSR = 100; cis-B(OH)₃ in K₂B₄O₇ solution with WSR = 60; B(OH)₄⁻ in K₂B₄O₇ solution with WSR = 60; trans-B(OH)₃ in K₂B₄O₇ solution with WSR = 60; B(OH)₄⁻ in KBO₂ solution with WSR = 60; B(OH)₄⁻ in KBO₂ solution with WSR = 20.

The DFT-based ab initio calculations were used to verify the above ion–pair structure. The structure and energy of the contact ion pair between a potassium ion and a boric acid molecule is shown in Fig. S9 and Table S5 (ESI†). Many initial models containing MCIPs and BCIPs were built to optimize their structures, but the BCIPs for trans-B(OH)₃ transformed to MCIPs during the optimization process. Thus, a BCIP between K⁺ and trans-B(OH)₃ cannot be found in Fig. S9 (ESI†). The lack of BCIPs for trans-B(OH)₃ provides an explanation of the results from EPSR modelling of the NDIS data shown in Fig. 4b; in this figure the K–B functions for trans-B(OH)₃ have a single peak at ∼4.0 Å, which is explained as arising solely from MCIPs (in the DFT calculations, the K–B distance for trans-B(OH)₃ MCIPs is predicted to be ∼3.8 Å, see Table S5, ESI†). For cis-B(OH)₃, BCIPs also transformed to a MCIP during the optimization process, except for n = 1. As shown in Table S5 (ESI†), for cis-B(OH)₃ and n = 1 the enthalpy for a BCIP (−21.0 kJ mol⁻¹) is lower than that of a MCIP (−17.1 kJ mol⁻¹), which shows that the BCIP is more stable than the MCIP. The Gibbs energy for a BCIP (7.1 kJ mol⁻¹) is lower than that of a MCIP (22.6 kJ mol⁻¹), which also shows that the BCIP is relatively more stable. Nevertheless, a BCIP may transform to a MCIP with the addition of water molecules. For cis-B(OH)₃, the K–B functions from EPSR modelling of the NDIS diffraction data shown in Fig. 4b have two peaks at ∼3.5 Å and ∼4.0 Å, and meanwhile the DFT calculations (Table S5, ESI†) predict that cis-B(OH)₃ has K–B distances of ∼3.3 Å and ∼3.85 Å for a BCIP and a MCIP respectively. This shows that K⁺ and cis-B(OH)₃ tend to form both monodentate and bidentate pairs in the solution. The DFT calculated K–O(B) distance r_K–O is 2.8 Å, which is consistent with the EPSR result, but longer than r_K–OW. The weaker interactions between K⁺ and boric acid molecules and stronger interactions between K⁺ and water cause this phenomenon. The small coordination numbers (see the CN values for K–O_trans and K–O_cis in Table 3) for K–O(B) and K–B also confirm the weaker interactions between K⁺ and boric acid. Duffin et al.¹³ also reported that increasing the concentration of cations (Na⁺, K⁺) did not significantly affect the NEXAFS spectra of boric acid aqueous solutions.

Hydration of borate anions

The hydration of trans-B(OH)₃ and cis-B(OH)₃. Hydrogen bonds are formed between boric acid molecules and water molecules. There is a broad peak in the B–O_water pair distribution function of boric acid molecules (g_B–Owater, see Fig. 5), and the intensity of this peak is weaker than that of the hydrated metaborate ion, B(OH)₄⁻, indicating that hydrated boric acid molecules are more disordered than hydrated metaborate ions. The metaborate ion has an explicit negative charge excess that enhances the interactions with the solvating water molecules, compared to the electrically neutral boric acid molecular unit. The first peak in g_B–Owater for B(OH)₃ ions ranges from 2.6 to 5.2 Å (Fig. 5(a)), and the peak value is at ∼3.9 Å, which coincides roughly with the shoulder on the long distance side of the first peak of g_B–O(W) of the hydrated metaborate ion, indicating more weakly hydrated boric acid molecules. The hydration number of boric acid is larger than for the metaborate ion (see the CN values in Table 3 for B_trans–O_water, B_cis–O_water and B–O_water), which is mainly caused by its broader g_B–Owater peak width. Tachikawa et al.²⁶ and Stefani et al.²⁷ studied the hydration of cis- and trans-B(OH)₃, but they did not provide the hydrated distance in their articles. Duffin et al.¹³ reported that the broadened B–O_water peak of the boric acid molecule was located at ∼4.1 Å, which is consistent with the conclusion of this study, but no specific structural details of the hydration of B(OH)₃ were given.

Fig. 5 Pair distribution functions for various atom pairs: B–O_water (a), O_B⋯O_water (b) and O_B⋯H_water (c) for various borate species in various solutions obtained using EPSR modeling. cis-B(OH)₃ in K₂B₄O₇ solution with WSR = 100; B(OH)₄⁻ in K₂B₄O₇ solution with WSR = 100; trans-B(OH)₃ in K₂B₄O₇ solution with WSR = 100; cis-B(OH)₃ in K₂B₄O₇ solution with WSR = 60; B(OH)₄⁻ in K₂B₄O₇ solution with WSR = 60; trans-B(OH)₃ in K₂B₄O₇ solution with WSR = 60; B(OH)₄⁻ in KBO₂ solution with WSR = 60; B(OH)₄⁻ in KBO₂ solution with WSR = 20.

Fig. 5(b and c) shows the pair distribution functions O_B⋯O_water (g_OB⋯Owater) and O_B⋯H_water (g_{Owater⋯Hwater}) between borate units and water. For boric acid molecules, g_OB⋯Hwater is weaker than that between metaborate ions and water, and the O⋯H_water distance of 2.1 Å is 0.2 Å longer than that of metaborate ions (Fig. 5(c)). Duffin et al.¹³ also reported that the interaction between boric acid and water molecules is weak. The peak of g_OB⋯Owater for boric acid molecules is at 3.1 Å (Fig. 5(b)), which is weaker than that of metaborate ions, and the O_B⋯H_water peak (Fig. 5(c)) is especially weak, further demonstrating the weak interactions between boric acid and water molecules.

Fig. 6(a–d) shows the SDF of the first hydration layer of boric acid isomers in solution, and different views of the SDFs are shown in Fig. S10 (ESI†). The blue area represents the SDF surfaces where the hydration distance between boric acid molecules and water molecules ranges from 2.6–4.5 Å. The hydration within this distance range is referred to as direct hydration. The green part represents interstitial hydration, and the hydration distance between boric acid molecules and water molecules ranges from 4.6–5.2 Å. The difference between the SDF surfaces of these two hydrated boric acid isomers is mainly in the direct hydration layer due to their different symmetries. There is a clear separation between the axial and equatorial hydrated SDF surfaces in dilute solutions, and the two SDF surfaces merge together as the solution concentration increases. This situation is similar to the SDF surfaces between water molecules when an external pressure is applied to a pure water system.⁵⁶ Both boric acid molecules have axial hydration, and the axially-hydrated SDF area decreases as the solution concentration increases. Axial hydration is mainly caused by water molecules in the empty 2p_z orbital, which is perpendicular to the plane of the boric acid molecule. This is the first time that axial and interstitial hydration water molecules have been observed in hydrated boric acid molecules. Researchers have also observed axial hydration of the Pd(II) aqua ion in solution.^40,57

Fig. 6 SDF surfaces showing the probability density for correlations of hydration water molecules with respect to the central [B(OH)₃] and [B(OH)₄⁻] moieties. The blue and semitransparent lobes represent water molecules in the first (direct) hydration shell, whilst the green lobes represent water molecules in the second (indirect) hydration shell. For the first and second hydration shells, the isosurfaces have been selected to show the distribution of neighbours with the threshold selected to show the most probable 30% and 20% of neighbour locations respectively. (a and b) The cis-B(OH)₃ in aqueous K₂B₄O₇ solutions with WSR = 100 and 60; (c and d) the trans-B(OH)₃ in aqueous K₂B₄O₇ solutions with WSR = 100 and 60; (e and f) the B(OH)₄⁻ anion in aqueous K₂B₄O₇ solutions with WSR= 100 and 60; (g and h) the B(OH)₄⁻ anion in aqueous KBO₂ solutions with WSR = 60 and 20; the pink, red, and white balls in the center respectively represent B, O, and H atoms of B(OH)₃ or B(OH)₄⁻. The first (direct) hydration shell of B(OH)₃⁻ is in the range 2.6 to 4.5 Å, and the second shell is in the range 4.6 to 5.2 Å. The first (direct) hydration shell of B(OH)₄⁻ is in the range 2.6 to 3.9 Å, and the second shell is in the range 3.7 to 4.8 Å.

The hydration of [B(OH)₄⁻]. We have previously studied alkali (Na⁺, K⁺, Rb⁺, Cs⁺) metaborate solutions using X-ray diffraction and found that r_B–O(W) is ∼3.6 Å, and 12 water molecules are located in the hydration layer of metaborate ions.^11,12,21,58Fig. 5(a) shows that the hydration distance of B(OH)₄⁻ ranges from 2.6 to 4.8 Å, with a peak at 3.56 Å, which is consistent with the X-ray diffraction experiment. The g_B–Owater functions for B(OH)₄⁻ at different concentrations are similar, and indicate that the solution concentration has a small effect on the hydration structure in the studied concentration range. Fig. 5(b and c) shows the functions g_OB⋯Owater and g_OB⋯Hwater for B(OH)₄⁻, and the positions and full width at half maximum of the first peaks in these functions at different concentrations are similar. This indicates that the concentration and metal ions have little effect on the structure of the first hydration layer of borate ions. The first peaks of g_OB⋯Owater and g_OB⋯Hwater are at 2.79 and 1.82 Å (Fig. 5(b) and (c)), respectively, whilst the corresponding distances between water molecules are 2.71 and 1.77 Å (Table 3), respectively. This shows that the hydrogen bond strength between water molecules is stronger than between B(OH)₄⁻ and water molecules. In general, the B–O_water distance is shorter for B(OH)₄⁻ than for B(OH)₃, therefore, the hydration ability of B(OH)₄⁻ is stronger than that of boric acid molecules, which is consistent with the conclusion of Duffin et al.¹³ The O_B⋯O_water coordination numbers are 4.5 and 4.3 for potassium metaborate solutions, while these values are 3.7 and 3.4 in dilute K₂B₄O₇ solutions. This shows that some of the water molecules in the mixed solution were hydrated to form boric acid, which reduced the hydration number in the B(OH)₄⁻ layer. A broad shoulder peak and hydration peak at 3.85 Å have also been observed through X-ray diffraction experiments, but the details of the hydration structure of metaborate ions were not further studied.¹²

Fig. 6(e–h) shows the SDF of hydration water molecules with respect to a central boric acid molecule and [B(OH)₄⁻], and the SDFs with a different view are shown in Fig. S10 (ESI†). The blue block represents the SDF map with a B–O_water distance of cis/trans-B(OH)₃ in the range 2.6–4.5 Å, and the green block represents the SDF map with a hydration distance range 4.6–5.2 Å. The blue block of the B(OH)₄⁻ SDF map (Fig. 6(e–h)) is in the range of 2.6–3.9 Å, and the green block is in the range of 3.7–4.8 Å. Therefore, there are two types of hydration in the hydration sphere of B(OH)₄⁻: direct and interstitial hydration layers. The details of these hydration clusters were further studied using DFT calculation.

DFT study of hydration structure

Hydration structure of B(OH)₃. The structural details of hydrated boric acid molecules and hydrated metaborate ions were further studied using DFT calculations. The DFT results show when the hydration number n ≤ 6 of trans-B(OH)₃ (Fig. 7 and Fig. S6, ESI†), the water directly interacts with boric acid in the in-plane direction. These water molecules were marked as direct hydration water molecules. When the hydration number is in the range 7 ≤ n ≤ 9, there is a water molecule between these direct hydration water molecules, but this water does not directly interact with the boric acid molecule, and it is referred to as an “interstitial hydrated water molecule”. Two typical isomers of hydrated trans-B(OH)₃, (n₁₀), are obtained when n = 10. One isomer is hydrated at an equatorial position (n_10A), and the other isomer is hydrated at an axial position of the boric acid molecule (n_10B). The energy of n_10B is 30.2 kJ mol⁻¹ higher than that of n_10A. As shown in Table 4, the distance r_{B–Owater-dir} between boron and the direct hydration water molecule remains at ∼3.6 Å before and after axial hydration, while the distance r_{B–Owater-indir} between water molecule and the indirect water molecule shortens from 4.44 Å to 4.17 Å. The distance r_{B–Owater-dir} is within the distance range of the direct hydration layer of the SDF diagram (2.6–4.5 Å). The distance r_{B–Owater-axis} between boron and the axial water molecule is ∼2.7 Å. Although the distance r_{B–Owater-axis} is within the distance range of the axial hydration layer of the SDF diagram (2.6–4.5 Å), this distance is too short compared with that of 4.4 Å for cis-B(OH)₃(H₂O)_n. Different models of trans-B(OH)₃(H₂O)₁₀ with B–O(1) distance ∼4.2 Å were built and optimized using DFT calculation, but these values finally decreased to ∼2.72 Å. We think this phenomenon is caused by the hydrogen bonding from the central water molecule to its surrounding water molecules. As an example, consider the model shown in Fig. S11 and Table S7 (ESI†): the initial B–O(1) distance is 4.24 Å, and the initial hydrogen bond lengths for O(4)⋯H(2), O(5)⋯H(3), and O(1)⋯H(6) are 2.38, 2.36, and 2.0 Å. These values decreased during the optimization, and B–O(1) finally decreased to 2.73 Å. The final angles 1-2-4, 1-3-5, and 1-6-7 were larger than 160°, and the hydrogen bond lengths for O(4)⋯H(2), O(5)⋯H(3), and O(1)⋯H(6) decreased to 1.88, 1.86, and 1.77 Å in the final optimization step. The central water molecule prefers to form a strong hydrogen bond in the energy minimum configuration. On the other hand, if the B–O(1) distance is ∼4.2 Å, the structure cannot reach a minimum energy configuration. Therefore, hydrogen bonding between axial water and interstitial hydration waters is a reason for such short axial hydration distance for trans-B(OH)₃. The other reason may be there is a local energy minimum structure, but we cannot find such a structure.

Fig. 7 Hydration structure diagram and RDG diagram of trans-B(OH)₃. The value of sign(λ₂) × ρ in surface is represented by the filling colour according to the colour bar below the figures. sign is the symbol (±) of the eigenvalue; λ₂ is the second eigenvalue of three eigenvalues. sign(λ₂) is the sign of the second largest eigenvalue of the electron density Hessian matrix at position r. ρ(r) is the electron density at position r, which reflects the interaction intensity.

Table 4 Interatomic distances (Å) in hydrated boric acid molecules and tetrahydroxyborate ions from DFT calculations

Species	n	B–O	B–Owater-dir	B–Owater-indir	B–Owater-axial	OB–Owater	Owater–Owater
trans-B(OH)3(H2O)n	6	1.367	3.653			2.721	2.715
	9	1.367	3.625	4.446		2.753	2.786
	10A	1.367	3.619	4.167	2.729	2.755	2.782
	10B	1.367	3.628	4.576		2.757	2.824
cis-B(OH)3(H2O)n	5	1.367	3.630			2.798	2.791
	8	1.369	3.489	3.884		2.755	2.782
	9A	1.368	3.521	4.191	4.401	2.795	2.802
	9B	1.368	3.478	4.21
B(OH)4^−(H2O)n	9	1.473	3.488			2.810	2.841
	10	1.473	3.482	4.595		2.812	2.839

---

As shown in Fig. 8 and Fig. S6 (ESI†), the hydrated structure of cis-B(OH)₃ is similar to that of trans-B(OH)₃. Five water molecules directly interact with cis-B(OH)₃. The hydration number of cis-B(OH)₃ is one less than trans-B(OH)₃ because the two hydrogen atoms in cis-B(OH)₃ simultaneously provide protons to water molecules. The similarity of the two isomers is that they have all three kinds of hydration modes in their first layers (direct hydration, interstitial hydration, and axial hydration). When the hydration number is in the range 6 ≤ n ≤ 8, the interstitial hydration layer appears. A ninth water molecule is found to hydrate the axial position of the trans-B(OH)₃ molecule according to the energy difference of n_9A and n_9B (Table S5, ESI†). The B(OH)₃ molecule is a planar structure, so it has an axial position both below and above the plane. The interstitial hydration occludes the axial position from one side, breaking the molecular symmetry. Therefore, only one of these sites is occupied. Table 4 shows that the distances r_{B–Owater-dir} and r_{B–Owater-indir} are roughly constant at ∼3.5 Å and ∼4.2 Å, respectively. r_{B–Owater-dir} is within the distance range of the direct hydration layer of the SDF diagram (2.6–4.5 Å), whilst r_{B–Owater-indir} is close to the range of the interstitial hydration layer of the SDF diagram (4.6–4.2 Å).

Fig. 8 Hydration structure diagram and RDG diagram of cis-B(OH)₃. The value of sign(λ₂) × ρ in surface is represented by the filling colour according to the colour bar below the figures. sign is the symbol (±) of the eigenvalue; λ₂ is the second eigenvalue of three eigenvalues. sign(λ₂) is the sign of the second largest eigenvalue of the electron density Hessian matrix at position r. ρ(r) is the electron density at position r, which reflects the interaction intensity.

The r_B–Owater distance for various borate ions in solution is ∼3.6 Å,^11,12,21,57 as measured using X-ray diffraction. This shows that only direct interaction information can be obtained using X-ray diffraction, whereas more hydration information can be extracted using NDIS. The NDIS and DFT results show that the energetic hydration preference of water molecules around boric acid is: direct hydration > interstitial hydration > axial hydration. As shown in Table 4, the DFT calculations show that the O_B⋯O_water distance between boric acid and water molecules is shorter than the O_water⋯O_water distance between water molecules of the hydration layer. This indicates that the hydrogen bonding between boric acid and water is stronger than that between water molecules in the hydration layer. This is why r_{B–Owater-dir} is less affected by solution concentration. Neutron diffraction experiments (Table 3) show that the peak for O_water–O_water distances between free water molecules is at 2.71 Å, which is shorter than O_B⋯O_water. This shows that the hydrogen bonding between free water molecules is the strongest, then the hydrogen bonding between boric acid molecules and water is second strongest, whilst the hydrogen bonding between water molecules in the hydration layer is relatively the weakest.

The reduced density gradient (RDG)⁵⁹ diagram in Fig. 7 shows the distribution and size of various weak interactions in hydrated clusters. The definition of RDG is shown in the ESI.† Since there is no axial hydration in n₆ and n₉, the effect of steric hindrance is small, while the situation in n_10A is the opposite. The interaction between the boron atom and the axial water molecules are van der Waals interactions, which are weaker than hydrogen bonds. The hydrogen bond between boric acid and water molecules is the strongest in n_10A and n_9A, both appearing (dark blue circles) in the RDG diagrams, while the hydrogen bonds between interstitial hydrated water molecules are weaker (light blue circles).

Hydration structure of B(OH)₄⁻. As shown in Fig. 9, each –OH of B(OH)₄⁻ forms hydrogen bonds with 3 water molecules; therefore, 12 water molecules interact with the first shell of B(OH)₄⁻. The direct interaction between water molecules and metaborate ions reaches saturation when 9 water molecules hydrate B(OH)₄⁻, and the tenth water molecule hydrates at the interstitial position. The NDIS data show that the hydration number of B(OH)₄⁻ ranged from 11 to 15 upon changing the concentration. This shows that water molecules occur in interstitial positions, as well as interacting directly with B(OH)₄⁻. The DFT calculations show that r_{B–Owater-dir} for B(OH)₄⁻ ions is about 3.5 Å, which is close to our neutron diffraction result of 3.56 Å (Table 3) and previous X-ray diffraction results.^11,12,21,57 The distance r_{B–Owater-indir} for metaborate ions, 4.6 Å, is also within the distance range of the interstitial hydration layer of the SDF diagram (3.7–4.8 Å). As seen in the RDG diagram, more steric hindrance exists between the water and B(OH)₄⁻, which weakens the hydration bonds that mainly exist as weak hydrogen bonds or van der Waals interactions. Table 4 shows that the O_B–O_water distance is shorter than the O_water–O_water distance, which indicates that the hydrogen bonding between B(OH)₄⁻/B(OH)₃ and water is slightly stronger than the hydrogen bonding between hydration water molecules in the hydration sphere. There is a delicate balance between various types of water molecules in solution. When this balance is affected by changing the concentration, B(OH)₄⁻ and boric acid molecules will polymerize to polyborate ions.²⁴

Fig. 9 Hydration structure diagram and RDG diagram of boric acid molecules and metaborate ions. The value of sign(λ₂) × ρ in surface is represented by the filling colour according to the colour bar below the figures. sign is the symbol (±) of the eigenvalue; λ₂ is the second eigenvalue of three eigenvalues. sign(λ₂) is the sign of the second largest eigenvalue of the electron density Hessian matrix at position r. ρ(r) is the electron density at position r, which reflects the interaction intensity.

Conclusions

In this work, neutron diffraction experiments were combined with quantum calculations to study interactions between boric acid molecules, metaborate ions, water molecules, and cations in borate solutions. The boric acid molecule has three hydration modes: direct hydration, interstitial hydration, and axial hydration. The distance r_B–Owater was in the range 2.6–3.9 Å for direct hydration, and the main hydration peak was at ∼3.6 Å, while it is in the range 4.0–4.8 Å for interstitial hydration with the main peak at ∼4.4 Å. The distance between boron and the axial hydration water molecules is 2.73 Å for trans-B(OH)₃ and 4.4 Å for cis-B(OH)₃. Hydrogen bonding between axial water and interstitial hydration waters is a reason for such a short axial hydration distance for trans-B(OH)₃. The energetic hydration preference of water molecules around boric acid is: direct hydration > interstitial hydration > axial hydration. DFT-based calculations indicated that the hydrogen bonds between boric acid and water molecules were stronger than those between interstitial hydration water molecules. Axial hydration water and B atoms mainly underwent van der Waals interactions. The hydrated B(OH)₄⁻ has spherical symmetry, and 9 water molecules directly interacted with –OH of B(OH)₄⁻, in which each –OH group form a four-coordinate hydration structure that is similar to water molecules. A tenth water molecule is located at the interstitial position. The hydrogen bond between B(OH)₄⁻ and water is stronger than the hydrogen bond between water molecules in the hydration layer.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

We thank the Natural Science Foundation of Qinghai (No. 2020-HZ-811), the Qinghai Provincial Program for High-Level Innovative Talents (No. E240HX1001), and the National Natural Science Foundation of China (No. U1607106) for financial support. We also thank the Science and Technology Facilities Research Council (STFC) for beam-time on SANDALS (DOI: http://10.5286/ISIS.E.RB1910244).

References

1. M. T. Sabatini, L. T. Boulton and T. D. Sheppard, Sci. Adv., 2017, 3, e1701028.
2. M. Mutailipu, M. Zhang, Z. H. Yang and S. L. Pan, Acc. Chem. Res., 2019, 52, 791–801.
3. X. L. Li, S. C. Wu, G. Q. Dong, S. Q. Chen, Z. L. Ma, D. Liu and C. Q. Sheng, ACS Med. Chem. Lett., 2020, 11, 439–444.
4. Q. Qin, R. H. Guo, E. H. Ren, X. X. Lai, C. Cui, H. Y. Xiao, M. Zhou, G. Yao, S. X. Jiang and J. W. Lan, ACS Sustainable Chem. Eng., 2020, 8, 10335–10344.
5. A. C. Wright, Phys. Chem. Glasses: Eur. J. Glass Sci. Technol., Part B, 2010, 51, 1–39.
6. A. C. Wright and N. M. Vedishcheva, Phys. Chem. Glasses: Eur. J. Glass Sci. Technol., Part B, 2013, 54, 147–156.
7. L. Maya, Inorg. Chem., 1976, 15, 2179–2184.
8. R. Janda and G. Heller, Spectrochim. Acta, Part A, 1980, 36, 997–1001.
9. A. K. Covington, J. Inorg. Nucl. Chem., 1973, 35, 3257–3262.
10. C. G. Salentine, Inorg. Chem., 1983, 22, 3920–3924.
11. Y. Q. Zhou, S. Higa, C. H. Fang, W. Q. Zhang and T. Yamaguchi, Phys. Chem. Chem. Phys., 2017, 19, 27878–27887.
12. F. Y. Zhu, T. Yamaguchi, K. Yoshida, W. Q. Zhang, Ho. Y. Liu, Y. Q. Zhou and C. H. Fang, Analyst, 2020, 145, 2245–2255.
13. A. M. Duffin, C. P. Schwartz, A. H. England, J. S. Uejio, D. Prendergast and R. J. Saykally, J. Chem. Phys., 2011, 134, 154503.
14. M. Maeda, J. Inorg. Nucl. Chem., 1979, 41, 1217–1220.
15. P. Wang, J. J. Kosinski, M. M. Lencka, A. Anderko and R. D. Springer, Pure Appl. Chem., 2013, 85, 2117–2144.
16. L. M. S. G. A. Applegarth, C. C. Pye, J. S. Cox and P. R. Tremaine, Ind. Eng. Chem. Res., 2017, 56, 13983–13996.
17. S. Sasidharanpillai, H. Arcis, L. Trevani and P. R. Tremaine, J. Phys. Chem. B, 2019, 123, 5147–5159.
18. J. Y. Peng, B. Zhang, J. Chen, Y. P. Dong and W. Li, Chin. J. Inorg. Chem., 2019, 35, 1821–1833.
19. F. Y. Zhu, W. Q. Zhang, H. Y. Liu, X. F. Wang, Y. Q. Zhou, C. H. Fang and Y. H. Zhang, Spectrochim. Acta, Part A, 2020, 224, 117308.
20. F. Y. Zhu, W. Q. Zhang, H. Y. Liu, Y. Q. Zhou, X. F. Wang and Y. H. Zhang, Spectrochim. Acta, Part A, 2020, 230, 118039.
21. F. Y. Zhu, C. H. Fang, Y. Fang, Y. Q. Zhou, H. W. Ge and H. Y. Liu, J. Mol. Struct., 2015, 1083, 471–479.
22. C. C. Pye, Prog. Theor. Chem. Phys., 2018, 31, 143–177.
23. H. W. Ge, Y. Fang, C. H. Fang, Y. Q. Zhou, F. Y. Zhu, H. Y. Liu, Z. X. Yang and Y. L. Tang, J. Chem. Eng. Data, 2014, 59, 4039–4048.
24. H. X. Zhou, F. Y. Zhu, H. Y. Liu, W. Q. Zhang, Y. Q. Zhou and C. H. Fang, Int. J. Quantum Chem., 2020, 120, e26118.
25. H. X. Zhou, F. Y. Zhu, H. Y. Liu, W. Q. Zhang, Y. Q. Zhou, C. H. Fang and H. B. Li, Chem. Phys. Lett., 2020, 739, 136930.
26. M. Tachikawa, J. Mol. Struct.: THEOCHEM, 2004, 710, 139–150.
27. D. Stefani, I. Pashalidis and A. V. Nicolaides, J. Mol. Struct.: THEOCHEM, 2008, 853, 33–38.
28. M. A. Beckett, R. A. Davies and C. D. Thomas, Comput. Theor. Chem., 2014, 1044, 74–79.
29. Y. Q. Zhou, Y. Fang, C. H. Fang, F. Y. Zhu, H. W. Ge and H. Y. Liu, Chem. Phys. Lett., 2015, 636, 97–102.
30. A. C. Wright, A. C. Hannon, R. N. Sinclair, W. L. Johnson and M. Atzmon, J. Phys. F: Met. Phys., 1984, 14, L201–L205.
31. V. F. Sears, Neutron News, 1992, 3, 26–37.
32. P. Toledano and A. Benhassaine, Rev. Chim. Miner., 1970, 7, 287–291.
33. M. D. Gioacchino, M. A. Ricci, S. Imberti, N. Holzmann and F. Bruni, J. Mol. Liq., 2020, 301, 112407.
34. (2019) for information: https://www.isis.stfc.ac.uk/Pages/sandals.aspx.
35. A. K. Soper and >Rutherford Appleton Laboratory Technical Report, RAL-TR-2011-013, 2011.
36. A. K. Soper, Chem. Phys., 1996, 202, 295–306.
37. A. K. Soper, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 104204.
38. F. Y. Zhu, C. H. Fang, Y. Fang, Y. Q. Zhou, H. W. Ge and H. Y. Liu, J. Mol. Struct., 2014, 1070, 80–85.
39. C. H. Fang, F. Y. Zhu, Y. Fang, Y. Q. Zhou, S. Tao and S. Xu, Phys. Chem. Liq., 2013, 51, 218–232.
40. D. T. Bowron, E. C. Beret, E. Martin–Zamora, A. K. Soper and E. S. Marcos, J. Am. Chem. Soc., 2012, 134, 962–967.
41. F. Bruni, S. Imberti, R. Mancinelli and M. A. Ricci, J. Chem. Phys., 2012, 136, 064520.
42. R. Mancinelli, A. Botti, F. Bruni, M. A. Ricci and A. K. Soper, Phys. Chem. Chem. Phys., 2007, 9, 2959–2967.
43. Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2006, 110, 5121–5129.
44. H. J. Zhang, W. Wang, H. Li, R. Gao and Y. S. Xu, RSC Adv., 2022, 12, 5501–5508.
45. T. Shinkai, P. J. Hsu, A. Fujii and J. L. Kuo, Phys. Chem. Chem. Phys., 2022, 24, 12631–12644.
46. M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265–3269.
47. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian, Gaussian 16, Revision A. 03, Gaussian, Inc., Wallingford CT, 2016.
48. T. Lu and F. W. Chen, J. Comput. Chem., 2012, 33, 580–592.
49. A. K. Soper, Chem. Phys., 2000, 258, 121–137.
50. L. B. Skinner, C. J. Benmore, J. C. Neuefeind and J. B. Parise, J. Chem. Phys., 2014, 141, 214507.
51. A. K. Soper and M. A. Ricci, Phys. Rev. Lett., 2000, 84, 2881–2884.
52. S. Woutersen, B. Ensing, M. Hilbers, Z. F. Zhao and C. A. Angell, Science, 2018, 359, 1127–1131.
53. A. K. Soper, Chem. Phys., 2000, 258, 121–137.
54. P. E. Mason, L. Tavagnacco, M. L. Saboungi, T. Hansen, H. E. Fischer, G. W. Neilson, T. Ichiye and J. W. Brady, J. Phys. Chem. B, 2019, 123, 10807–10813.
55. H. Ohtaki and N. Fukushima, J. Solution Chem., 1992, 21, 23–38.
56. S. Imberti, A. Botti, F. Bruni, G. Cappa, M. A. Ricci and A. K. Soper, J. Chem. Phys., 2005, 122, 194509.
57. J. M. Martinez, F. Torrico, R. R. Pappalardo and E. S. Marcos, J. Phys. Chem. B, 2004, 108, 15851–15855.
58. W. Q. Zhang, C. H. Fang, W. Li, Y. Q. Zhou, F. Y. Zhu and H. Y. Liu, J. Mol. Struct., 2019, 1194, 262–270.
59. E. R. Johnson, S. Keinan, P. Mori-Sanchez, J. Contreras-Garcia, A. J. Cohen and W. T. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp05331d

‡ Current address: Miltenyi Biotec B.V. & Co. KG, (R&D Engineering, Biophysics), Friedrich-Ebert-Straße 68, 51429 Bergisch Gladbach, Germany.

---