Open Access Article
Open Access ArticleInsights into the molecular structure and infrared spectrum of the prebiotic species aminoacetonitrile†
Ningjing
Jiang
 a,
Mattia
Melosso
a,
Mattia
Melosso
 *b,
Silvia
Alessandrini
*b,
Silvia
Alessandrini
 ac,
Luca
Bizzocchi
a,
Marie-Aline
Martin-Drumel
ac,
Luca
Bizzocchi
a,
Marie-Aline
Martin-Drumel
 d,
Olivier
Pirali
de and
Cristina
Puzzarini
d,
Olivier
Pirali
de and
Cristina
Puzzarini
 *a
*a
aDipartimento di Chimica “Giacomo Ciamician”, Università di Bologna, Via F. Selmi 2, 40126 Bologna, Italy. E-mail: cristina.puzzarini@unibo.it
bScuola Superiore Meridionale, Largo San Marcellino 10, 80138 Naples, Italy. E-mail: mattia.melosso@unina.it
cScuola Normale Superiore, Piazza dei Cavalieri 7, 56126 Pisa, Italy
dUniversité Paris-Saclay, CNRS, Institut des Sciences Moléculaires d'Orsay, 91405 Orsay, France
eSOLEIL Synchrotron, AILES beamline, l'Orme des Merisiers, 91190 Saint-Aubin, Gif-sur-Yvette, France
First published on 19th January 2023
Abstract
Aminoacetonitrile is an interstellar molecule with a prominent prebiotic role, already detected in the chemically-rich molecular cloud Sagittarius B2(N) and postulated to be present in the atmosphere of the largest Saturn's moon, Titan. To further support its observation in such remote environments and laboratory experiments aimed at improving our understanding of interstellar chemistry, we report a thorough spectroscopic and structural characterization of aminoacetonitrile. Equilibrium geometry, fundamental bands as well as spectroscopic and molecular parameters have been accurately computed by exploiting a composite scheme rooted in the coupled-cluster theory that accounts for the extrapolation to the complete basis set limit and core-correlation effects. In addition, a semi-experimental approach that combines ground-state rotational constants for different isotopic species and calculated vibrational corrections has been employed for the structure determination. From the experimental side, we report the analysis of the three strongest fundamental bands of aminoacetonitrile observed between 500 and 1000 cm−1 in high-resolution infrared spectra. More generally, all computed band positions are in excellent agreement with the present and previous experiments. The only exception is the ν15 band, for which we provide a revision of the experimental assignment, now in good agreement with theory.
1 Introduction
Over the past 50 years, a wide number of interstellar amino acids have been discovered in extraterrestrial objects, including meteorites,1–5 asteroids,6 and comets.7,8 However, despite extensive and dedicated searches, no evidence of amino acids in the gas phase of the interstellar medium (ISM) has been found to date.9,10 Yet, several molecular precursors of amino acids – and progenitors of biological species in general – have been discovered in the ISM in recent years, including for example aminoacetonitrile,11 glycolaldehyde,12 ethenediol,13 ethanolamine,14 hydroxylamine,15 urea,16,17 formamide,18 and many others. Among these, aminoacetonitrile is one of the closest glycine precursors and has been observed in the high-mass star-forming region Sagittarius B2(N).11,19,20Aminoacetonitrile is regarded as a prebiotic species because it is formed as intermediate in the second step of the Strecker synthesis of glycine, a chemical process based on simple reactants such as ammonia, formaldehyde, and hydrogen cyanide.21 The efficiency of this process in producing aminoacetonitrile even in astrophysical-like conditions has been demonstrated by Danger et al.,22 who monitored the products released during the warm-up of interstellar ice-analogues containing the ingredients of the Strecker synthesis without the involvement of VUV photons or any energetic particles. A subsequent experimental study, though, has shown that the hydrolysis of aminoacetonitrile to glycine (i.e. the last two steps of the Strecker synthesis) is unfeasible under the same conditions,23 as already predicted computationally.24 Moreover, aminoacetonitrile has been shown to be photoresistant to VUV radiation and to possess a high desorption energy, thus making it one of the most important reservoir of interstellar glycine.23 Nonetheless, this reservoir could have been present in asteroids and delivered to the aqueous phase of the early Earth during the late heavy bombardment period,25 where the hydrolysis process of aminoacetonitrile could have taken place and formed glycine.
In addition to the Strecker synthesis, the formation of aminoacetonitrile in interstellar conditions has been observed during the VUV irradiation of an acetonitrile/ammonia ice mixture26 as well as after the heating of acetonitrile-rich ices previously irradiated by X-rays,27 in accordance with chemical models.28 Furthermore, aminoacetonitrile has been identified among the components of Titan aerosol analogs produced in the laboratory by discharging a 95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 mixture of N2 and CH4 in a high vacuum reaction chamber at 195 K.29 This result points out the importance of aminoacetonitrile not only in hot molecular cores but also in Titan's atmosphere.
5 mixture of N2 and CH4 in a high vacuum reaction chamber at 195 K.29 This result points out the importance of aminoacetonitrile not only in hot molecular cores but also in Titan's atmosphere.
Given its importance in a variety of astrophysical objects, it is evident that a thorough spectroscopic characterization of aminoacetonitrile is mandatory in order to support its observation. If, on the one hand, ISM detections typically rely on the observation of rotational transitions at centimeter-/millimeter-wavelengths,30 on the other hand observations of planetary atmospheres and many laboratory studies (such as those mentioned above) are mainly based on the identification of vibrational features in the infrared domain.
The rotational spectrum of aminoacetonitrile has been investigated extensively. Previous works include the study of the vibrational ground state31–33 and several excited states34,35 of the main isotopic species, the observation of some isotopologues,31,33,34,36 the analysis of the hyperfine structure produced by the two nitrogen nuclei,37 and the determination of dipole moment components.36 Conversely, the vibrational spectrum has been studied mainly at low resolution, either in the gas phase38 or in Ar matrix,39 with only three fundamental bands analyzed at high resolution.20 Moreover, the vibrational analysis is still ambiguous and suffers from a limited support by quantum chemistry, so far restricted to low-level calculations.39–41
More generally, no study has properly addressed a complete structural and spectroscopic characterization of aminoacetonitrile using high-level quantum-chemical calculations. Here, we want to fill this gap and to expand the knowledge of the high-resolution ro-vibrational spectrum of aminoacetonitrile in the region between 500 and 1000 cm−1. To reach our goals, we combined a high-level quantum-chemical characterization of its structure and spectroscopic properties with the analysis of high-resolution infrared spectra recorded at the AILES beamline of SOLEIL synchrotron. More specifically, the goals of our work can be summarized as follows: (i) to derive a semi-experimental equilibrium structure of aminoacetonitrile and compare it with our best theoretical estimate; (ii) to carry out a theoretical rotational spectroscopic characterization; (iii) to predict the position of all fundamental bands with high accuracy and compare it with experimental data; (iv) to analyze the rotational structure of three new fundamental bands supported by computed vibration–rotation interaction constants.
2 Experimental details
The gas-phase infrared spectrum of aminoacetonitrile has been recorded between 500 and 1500 cm−1 using the Bruker IFS 125 FT interferometer located at the AILES beamline of the SOLEIL synchrotron facility.42 For this purpose, the spectrometer has been equipped with a White-type cell adjusted to attain an optical path length of about 150 m,43,44 a globar lamp as infrared radiation source, a KBr beamsplitter, and a MCT detector.45 The iris aperture was set to 1.15 mm, thus allowing for a spectral resolution of 0.0015 cm−1 in the entire frequency range (the Doppler broadening at these wavenumbers is smaller than 3 × 10−4 cm−1). Two diamond windows were used to isolate the cell from the interferometer, which was kept evacuated under continuous pumping to limit the absorption of atmospheric water. Aminoacetonitrile has been injected inside the cell at a pressure of 3 μbar to limit the saturation of the intense ν9 band at ∼790 cm−1.The final spectrum consists of 112 individual scans, co-added in order to improve its signal-to-noise ratio. After the baseline removal, the spectrum was calibrated using infrared bands of two interfering species, namely HCN and CO2. The HCN frequencies were taken from the HITRAN2020 database,46 while those of the CO2 band around 670 cm−1 were taken from ref. 47. No apodization functions were applied to the interferograms.
3 Computational details
Quantum-chemical calculations have been performed at different levels of theory, with the aim of obtaining the best possible estimates for the molecular geometry, vibrational frequencies, rotational and centrifugal distortion constants, electric dipole moment, and nuclear quadrupole coupling constants. The computational methodology employed is summarized in the following.The so-called CBS+CV scheme48–51 has been employed for an accurate determination of the equilibrium structure and harmonic force field. This approach involves calculations at the coupled cluster (CC) singles and doubles with perturbative triples corrections (CCSD(T)) level52 and relies on the additivity approximation:
| pbest = p∞(HF − SCF) + Δp∞(CCSD(T)) + Δp(CV), | (1) |
From the equilibrium structure, the equilibrium rotational constants are straightforwardly derived.57,58 While accurate CBS+CV equilibrium rotational constants and harmonic frequencies are invaluable information, for their exploitation in the field of rotational and ro-vibrational spectroscopy one needs to move from equilibrium to a realistic representation of the molecular system. This implies the incorporation of vibrational effects for rotational constants and anharmonicity for vibrational frequencies.
The vibrational dependence of the rotational constant on the vibrational state can be modelled using vibrational perturbation theory to second order (VPT2):59
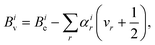 | (2) |
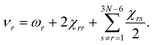 | (3) |
The so-called semi-experimental (SE) approach can be used to derive an accurate equilibrium geometry (rSEe). This is obtained by a least-squares fit of experimental vibrational ground state rotational constants (B0) of different isotopic species computationally corrected for the vibrational contribution (ΔBivib).57,62,63 In fact, according to eqn (2), one obtains the following expression when the vibrational ground state is considered:
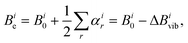 | (4) |
MP2 calculations have been performed using Gaussian 16,64 while for all the remaining calculations the CFOUR package65,66 has been employed. While the results of all CCSD(T) calculations are reported in the main text, geometry and harmonic frequencies computed at the HF-SCF level as well as the vibration–rotation interaction constants from MP2 calculations are only provided in the ESI.†
4 Results and discussion
4.1 Molecular structure
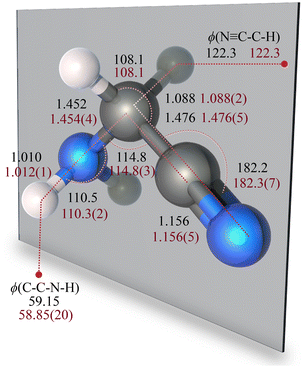
Previous experimental studies have shown that aminoacetonitrile only exists in the trans form, with the NH2 moiety being opposite to the CH2 group (see Fig. 1). For this reason, only this form has been investigated in this work. In its equilibrium configurations, all four heavy atoms of aminoacetonitrile lies on the same plane (the ab plane in its principal inertia system), with the pairs of hydrogen nuclei lying symmetrically out of this plane (see Fig. 1). Therefore, the molecule belongs to the Cs point group. The existence of a σh symmetry element is confirmed experimentally. For example, the absence of any c-type transitions in its rotational spectrum, which is instead dominated by a- and b-type transitions,36 demonstrates that the dipole moment component along the c axis is null.The molecular structure of aminoacetonitrile has already been investigated in the literature, both experimentally and theoretically. For what concerns experiment, the available determination only relies on the rotational constants of three different isotopologues (namely the main, –NHD, and –ND2 isotopic species, which means a total of nine parameters) and does not take into account how the vibrational effects alter the molecular structure.36 As far as computational studies are concerned, the equilibrium structure has only been calculated at low levels of theory.40,41
In the present study, to obtain an accurate determination of the equilibrium geometry of aminoacetonitrile, as explained in Section 3, we have carried out high-level quantum-chemical calculations and derived a semi-experimental equilibrium structure using a larger set of rotational constants with respect to previous experimental evaluations. For the rSEe determination, five isotopologues have been considered, namely the main, –NHD, –ND2,33 –13CH2, and –13C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N34 isotopic species. These provide 15 ground-state rotational constants, that are suitable for the derivation of an almost complete rSEe. Due to the lack of spectroscopic data for the –CHD and –CD2 isotopologues, the C–H bond length and the CCH angle have been kept fixed to our best-estimated computed values, while all the remaining structural parameters have been determined during the least-squares fit. As can be seen from inspection of Table 1, the rSEe values and our best-estimated CBS+CV structural parameters well agree within the statistical uncertainties of the former. Table 1 also collects the equilibrium geometries computed at different levels of theory. A monotonic trend for the CCSD(T) results by enlarging the basis set is evident, with CBS values (from the two right-hand terms of eqn (1)) being also provided in Table 1. From the comparison of the CBS and CBS+CV parameters, the importance of the CV contribution for obtaining an accuracy of about 0.001 Å for bond lengths is also apparent. For angles, the error affecting the CBS+CV structure is about 0.1°. The quality of the rSEe geometry is well assessed not only by the small uncertainties, but also by the fact that the experimental rotational constants of all isotopologues are reproduced with a standard deviation of 1.6 MHz for the A constant and of 0.1 MHz for B and C.
N34 isotopic species. These provide 15 ground-state rotational constants, that are suitable for the derivation of an almost complete rSEe. Due to the lack of spectroscopic data for the –CHD and –CD2 isotopologues, the C–H bond length and the CCH angle have been kept fixed to our best-estimated computed values, while all the remaining structural parameters have been determined during the least-squares fit. As can be seen from inspection of Table 1, the rSEe values and our best-estimated CBS+CV structural parameters well agree within the statistical uncertainties of the former. Table 1 also collects the equilibrium geometries computed at different levels of theory. A monotonic trend for the CCSD(T) results by enlarging the basis set is evident, with CBS values (from the two right-hand terms of eqn (1)) being also provided in Table 1. From the comparison of the CBS and CBS+CV parameters, the importance of the CV contribution for obtaining an accuracy of about 0.001 Å for bond lengths is also apparent. For angles, the error affecting the CBS+CV structure is about 0.1°. The quality of the rSEe geometry is well assessed not only by the small uncertainties, but also by the fact that the experimental rotational constants of all isotopologues are reproduced with a standard deviation of 1.6 MHz for the A constant and of 0.1 MHz for B and C.
| Parameter | CCSD(T) | CBS | CBS+CV | r SEe | |||
|---|---|---|---|---|---|---|---|
| fc/cc-pVTZ | fc/cc-pVQZ | fc/cc-CVTZ | ae/cc-pCVTZ | ||||
| Bond-lengths are in Å, angles in degrees, rotational constants in MHz; fc and ae stand for frozen-core and all-electron, respectively (see text). Values in parentheses represent standard errors in unit of the last quoted digits. | |||||||
r(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N) N) |
1.163 | 1.160 | 1.162 | 1.160 | 1.158 | 1.156 | 1.156(5) |
| r(C–C) | 1.484 | 1.481 | 1.483 | 1.481 | 1.479 | 1.476 | 1.476(5) |
| r(C–H) | 1.090 | 1.090 | 1.090 | 1.089 | 1.089 | 1.088 | 1.088(2) |
| r(C–N) | 1.461 | 1.457 | 1.460 | 1.458 | 1.454 | 1.452 | 1.454(4) |
| r(N–H) | 1.014 | 1.012 | 1.014 | 1.012 | 1.011 | 1.010 | 1.012(1) |
∠(C–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N) N) |
182.4 | 182.3 | 182.4 | 182.3 | 182.2 | 182.2 | 182.3(7) |
| ∠(C–C–N) | 114.9 | 114.9 | 114.8 | 114.9 | 114.8 | 114.8 | 114.8(3) |
| ∠(C–N–H) | 109.5 | 110.0 | 109.5 | 109.6 | 110.4 | 110.5 | 110.3(2) |
| ∠(C–C–H) | 108.1 | 108.1 | 108.1 | 108.1 | 108.1 | 108.1 | 108.1 |
| ϕ(C–C–N–H) | 57.96 | 58.54 | 57.95 | 58.11 | 59.02 | 59.15 | 58.85(20) |
ϕ (N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–C–H) C–C–H) |
122.2 | 122.2 | 122.2 | 122.3 | 122.2 | 122.3 | 122.3 |
| A e | 30110.4 | 30263.4 | 30127.5 | 30228.5 | 30344.4 | 30439.4 | 30355.9 |
| B e | 4741.25 | 4757.06 | 4745.78 | 4760.21 | 4766.52 | 4781.44 | 4785.27 |
| C e | 4296.40 | 4312.59 | 4300.38 | 4313.90 | 4322.28 | 4336.05 | 4337.40 |
Finally, in Table 1, the equilibrium rotational constants corresponding to the various structures reported are provided. These data allow us to point out the importance of applying a composite scheme to reproduce experimental rotational constants.
4.2 Rotational parameters
The rotational spectrum of the main isotopologue of aminoacetonitrile has been investigated extensively in the literature. Although experimental studies span from the centimeter-wave region to the millimeter-wave and THz domains, the spectroscopic parameters of aminoacetonitrile have never been compared to computed data. Currently, rotational, centrifugal distortion, and nuclear quadrupole coupling constants as well as electric dipole moment components can be evaluated with high precision and can provide a good reference for supporting the analysis of rotational spectra.57,67 Therefore, the present investigation allows us to benchmark the accuracy obtainable by exploiting the strategy presented in Section 3. The comparison is reported in Table 2.| Constant | Unit | Experimenta | Best estimatesb |
|---|---|---|---|
| Numbers in parentheses are standard errors and apply to the last significant digits.a Obtained from the analysis of all literature data. Dipole moments are taken from ref. 36.b Obtained as explained in Section 3. | |||
| A | MHz | 30246.4909(9) | 30331.332 |
| B | MHz | 4761.0626(1) | 4757.100 |
| C | MHz | 4310.7486(1) | 4309.318 |
| D J | kHz | 3.0669(1) | 3.0576 |
| D JK | kHz | −55.295(1) | −55.809 |
| D K | kHz | 714.092(7) | 704.828 |
| d 1 | kHz | −0.67355(4) | −0.66398 |
| d 2 | kHz | −0.02993(1) | −0.02793 |
| H J | mHz | 9.56(3) | 9.894 |
| H JK | Hz | −0.1249(4) | −0.1261 |
| H KJ | Hz | −2.714(4) | −2.728 |
| H K | Hz | 53.27(2) | 51.17 |
| h 1 | mHz | 3.88(1) | 3.923 |
| h 2 | mHz | 0.476(6) | 0.4578 |
| h 3 | mHz | 0.0503(8) | 0.0523 |
| χ aa (NH2) | MHz | −2.77(4) | −3.088 |
| χ bb (NH2) | MHz | 1.20(9) | 1.158 |
| χ aa (CN) | MHz | −3.48(3) | −3.552 |
| χ bb (CN) | MHz | 1.50(6) | 1.472 |
| μ a | D | 2.577(7) | 2.590 |
| μ b | D | 0.575(1) | 0.567 |
First of all, Table 2 shows that the computed rotational constants agree remarkably well with the experimental ones: the mean absolute percentage error (MAPE) is around 0.1%, in line with benchmark results available in the literature for molecules of similar size.49,57,58,68,69 This is a further confirmation that our best-estimated CBS+CV equilibrium structure is very close to the actual equilibrium geometry of aminoacetonitrile. Moving to the centrifugal distortion constants, a similar agreement is observed for both the quartic and sextic terms, the MAPE being 2.1% and 2.5%, respectively. The error obtained for the quartic terms is in line with the expected uncertainty range of about 2–3%,57,70 while the MAPE achieved on the sextic constants is well below the typical uncertainty of 5–7%.57,70,71 Such small errors seem to indicate that aminoacetonitrile is rather rigid, but also that the centrifugal distortion analysis performed in ref. 33 is robust, as demonstrated by the large number of distortion terms determined.
Finally, there are two first-order properties that can be compared to experimental data, namely the nuclear quadrupole coupling constants of the nitrogen nuclei and the electric dipole moment components. The former have been determined during the analysis of the hyperfine structure performed by Brown et al.,37 while the latter have been determined using Stark effect measurements.36 For these quantities, the MAPE is found to be 4.7% on the quadrupole coupling constants and 0.9% for the dipole moments. The overall good agreement points out the quality of our ab initio calculations as well as the reliability of the rotational studies available in the literature.
4.3 Infrared spectrum
Aminoacetonitrile possesses 18 vibrational modes that can be classified – according to the irreducible representations of the Cs point group – into 11 normal modes of A′ symmetry and 7 of A′′ symmetry. At present, the knowledge of the mid-infrared spectrum of aminoacetonitrile relies on the works by Bak et al.38 and Bernstein et al.39 The former provided the first tentative assignment of each normal mode from the analysis of a gas-phase spectrum recorded at low resolution with an accuracy of ca. 1 cm−1, while the latter reported the infrared spectrum obtained in a low-temperature matrix isolation experiment. Both studies were guided by low-level harmonic force-field calculations.In this work, we have computed the position of each fundamental band by correcting the CBS+CV harmonic frequencies with the anharmonic contributions evaluated at the ae-MP2/cc-pCVTZ level, thus leading to a hybrid approach denoted as CBS + CV/MP2. Similar approaches have been used successfully in the past49,50,72–74 and provided good results for species similar in size. Based on dedicated benchmark studies, we expect that this hybrid approach is able to provide a solid base for reviewing the vibrational analysis, with a relative mean error better than 1% and maximum errors not exceeding 3%.75–78
Our best-estimated CBS+CV/MP2 predictions for the band centers of the 18 fundamental bands of aminoacetonitrile are provided in the third last column of Table 3 (denoted as Hybrid). By comparing these values with those reported by Bak et al.38 and Melosso et al.,20 an overall good agreement is noted, with only one exception. In fact, the feature lying at 1297(1) cm−1 was assigned to the ν15 band in ref. 38, which is instead predicted to lie at 1173 cm−1 by our calculations. This would result in a deviation of 124 cm−1 and relative percentage error of about 10%, which is much larger than the average percentage error of the remaining fundamentals, which is around 1%. This discrepancy casts some doubt on the correct assignment of the ν15 vibrational mode by Bak et al.38 The hypothesis of a wrong assignment is further supported by the detection of a weak feature around 1160 cm−1 in the vibrational spectra recorded in this work. Therefore, we propose a new assignment for the ν15 band.
| Mode | CCSD(T) | CBS | CBS+CV | Anharm. corr. | Hybrid | Experimental | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| fc-pVTZ | fc-pVQZ | fc-CVTZ | ae-CVTZ | MP2/ae-CVTZ | Low res.a | High res.b | ||||
| Vibrational frequencies are expressed in cm−1. Values in parentheses represent standard errors in unit of the last quoted digits.a Low resolution data from Bak et al.38b High resolution data from Melosso et al.20 (below 500 cm−1) or from this work (above 500 cm−1). | ||||||||||
| ν 1 | 3505 | 3514 | 3504 | 3511 | 3523 | 3530 | −152 | 3378 | 3367(1) | — |
| ν 2 | 3078 | 3079 | 3078 | 3083 | 3082 | 3087 | −135 | 2952 | 2950(1) | — |
| ν 3 | 2275 | 2283 | 2277 | 2285 | 2288 | 2296 | −42 | 2254 | 2236(1) | — |
| ν 4 | 1674 | 1674 | 1674 | 1676 | 1675 | 1677 | −60 | 1617 | 1642(1) | — |
| ν 5 | 1482 | 1482 | 1483 | 1484 | 1483 | 1485 | −39 | 1446 | 1444(1) | — |
| ν 6 | 1369 | 1370 | 1370 | 1373 | 1371 | 1374 | −36 | 1338 | 1348(1) | — |
| ν 7 | 1123 | 1123 | 1123 | 1122 | 1122 | 1124 | −38 | 1086 | 1077(1) | — |
| ν 8 | 949 | 943 | 949 | 950 | 937 | 937 | −39 | 898 | 901(1) | 901.4(1) |
| ν 9 | 849 | 845 | 849 | 851 | 842 | 843 | −32 | 811 | 790(1) | 790.95908(7) |
| ν 10 | 560 | 562 | 561 | 563 | 563 | 565 | −6 | 559 | 558(1) | 556.56467(2) |
| ν 11 | 211 | 211 | 211 | 212 | 211 | 212 | −1 | 211 | 216(1) | 210.575842(5) |
| ν 12 | 3587 | 3597 | 3584 | 3592 | 3608 | 3616 | −168 | 3448 | 3431(1) | — |
| ν 13 | 3122 | 3125 | 3123 | 3128 | 3129 | 3134 | −143 | 2991 | 2975(1) | — |
| ν 14 | 1398 | 1396 | 1398 | 1400 | 1395 | 1397 | −37 | 1360 | 1331(1) | — |
| ν 15 | 1203 | 1201 | 1204 | 1206 | 1200 | 1203 | −30 | 1173 | 1297(1) | 1160.(1) |
| ν 16 | 895 | 894 | 896 | 897 | 893 | 895 | −11 | 884 | — | — |
| ν 17 | 381 | 379 | 382 | 383 | 377 | 379 | −9 | 370 | 370(1) | 368.104657(3) |
| ν 18 | 266 | 261 | 266 | 267 | 255 | 256 | −8 | 248 | 247(1) | 244.891525(3) |
Concerning the ν16 band – not identified by Bak et al.38 – our calculations predict an anharmonic intensity smaller than 0.001 km mol−1, which makes this band impossible to be observed using the present experimental setup. Hence, our computed frequency should be used as best estimate for such fundamental band.
Table 3 also reports the harmonic frequencies at different levels of theory. It is noted that the CV contribution is small (on average 0.2%) and that the fc-CCSD(T)/cc-pVQZ level of theory provides results nearly converged to the CBS limit.
4.4 Ro-vibrational analysis of the ν8, ν9, and ν10 bands
In our previous work, we have recorded at high-resolution and analyzed the three strongest fundamentals that dominate the frequency region below 500 cm−1, namely the ν11, ν17, and ν18 bands20 (see Table 3 for the experimental band centers). Here, we investigate the region between 500 and 1000 cm−1, where the three strongest features are the ν8, ν9, and ν10 bands. However, due to the greater congestion of the spectra and to the higher number of resonances that occur moving at higher energies, the present study is limited in terms of both assigned transitions and spectral analysis with respect to that of ref. 20. Yet, our ro-vibrational analysis is able to provide accurate band centers and a solid base for a more detailed study of these bands in the future.All these three fundamentals show the typical structure of an a-type band, i.e. strong P and R branches with a less pronounced Q branch. To guide the analysis of the rotational structure of each band, spectral simulations have been obtained by combining the ground state spectroscopic constants from ref. 20 and a set of vibrational excited state parameters obtained from our computed band centers and vibration–rotation interaction constants. The spectral simulation has been performed with the PGOPHER package,79 while the assignment procedure has been carried out using the graphical tools offered by the Loomis-Wood for Windows program.80 Moreover, the correctness of the assigned transitions has been checked using the ground-state combination differences method and the MARVEL (Measured Active Rotational-Vibrational Energy Levels) software.81 At the end of the assignment procedure, the spectral analysis has been performed using the SPFIT subroutine of the CALPGM suite of program82 and employing a S-reduced Watson-type Hamiltonian for a semi-rigid nearly-prolate rotor.83
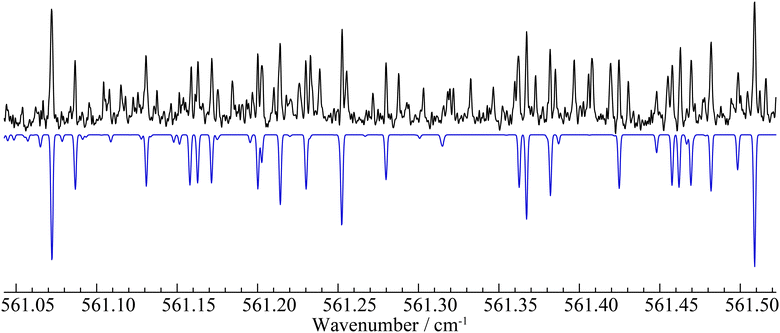
For the ν10 band – observed in the 534–577 cm−1 range – we were able to assign and successfully analyze 1180 distinct transitions, which involve energy levels with J and Ka values up to 75 and 10, respectively. A sub-set of 147 transitions having high values for both quantum numbers (including all the Ka = 11 transitions identified) have been discarded from the analysis because they show deviations at least five times larger than the assumed experimental uncertainty of 2 × 10−4 cm−1. The root-mean-square (rms) error of the final fit is 2.6 × 10−4 cm−1, which is in line with the expected frequency accuracy. The experimental rotational constants of the v10 = 1 state have been obtained with good precision and the corresponding vibration–rotation interaction constants αA10 = 382 MHz, αB10 = −8.6 MHz, and αC10 = −7.9 MHz agree very well with both the computed values (αA10 = 386 MHz, αB10 = −8.0 MHz, and αC10 = −7.5 MHz) and those determined in a millimeter-wave study (αA10 = 384 MHz, αB10 = −8.6 MHz, and αC10 = −7.9 MHz).34 Moreover, the centrifugal distortion constants of the vibrational excited state are very similar to those of the ground state, which seems to indicate that the v10 = 1 state is not strongly perturbed by another vibrational state. The band center, predicted at 560 cm−1, is found to be 556.56467(2) cm−1. Finally, we estimate that the b-type component of this band is at least 10 times weaker than the a-type component. Therefore, the unassigned features in this portion of the spectrum (see Fig. 2) belong mainly to hot-bands arising from low-lying energy states, e.g. v11 = 1, v17 = 1, v18 = 1.
The analysis of the ν9 band was slightly more problematic. In this case, we were able to assign a smaller number of transitions (707 lines in the 775–804 cm−1 range, 623 of which were included in the analysis and 84 were discarded) whose maxima values of J and Ka are 47 and 7, respectively. A root-mean-square error of 7.1 × 10−4 cm−1 together with anomalous values obtained for DK and d2 point out the existence of a moderate perturbation for the v9 = 1 state. This is also supported by the large difference found between the theoretical αA9 of 60 MHz and its experimental value of 204 MHz. The interaction occurs most likely with the v8 = 1 and v16 = 1 states, but many other overtone and combination states can produce accidental degeneracy and thus perturb the v9 = 1 energy levels. Given the difficulty in obtaining a thorough knowledge of the complete manifold of the vibrational excited states of aminoacetonitrile, we limit the present investigation to an effective and partial analysis. Still, the origin of this band has been determined at 790.95908(7) cm−1 with good accuracy and compare well with our predicted value of 812 cm−1. A good agreement is also obtained between our experimental α values for B and C (αB9 = −22.0 MHz and αC9 = −11.8 MHz) and those computed at the MP2 level (αB9 = −22.5 MHz and αC9 = −15.9 MHz). As last remark, we note that the tentative assignment made for this state by Kolesnikova et al.34 in their pure rotational study is correct, as demonstrated by the similar vibration–rotation interactions constants derived (αA9 = 194 MHz, αB9 = −19.9 MHz, and αC9 = −12.2 MHz).
The ν8 band was even more difficult to analyze. For this band, only 82 distinct lines corresponding to 168 transitions with J ≤ 21 and Ka values between 5 and 8 could be assigned safely. Attempts to derive a consistent set of spectroscopic constants and to search for further transitions – especially those with lower Ka values – were unsuccessful. Presumably, the resonances affecting the v8 = 1 state are much more pronounced due to its proximity to the v16 = 1 state, whose energy levels are unknown at present. In this case, we could only estimate the band center to be 901.4(1) cm−1, a value that reproduces roughly the shape of the Q branches (see Fig. 3) and is in excellent agreement with our computed value of 898 cm−1.
The spectroscopic constants determined from the analysis of the ν10 and ν9 bands are listed in Table 4, while the list of all the assigned transitions is provided in the ESI.†
| Constant | Unit | v 10 = 1 | v 9 = 1 |
|---|---|---|---|
| Numbers in parentheses are standard errors and apply to the last significant digits. | |||
| E vib | cm−1 | 556.56467(2) | 790.95908(7) |
| A | MHz | 30628.15(4) | 30450.1(2) |
| B | MHz | 4752.461(2) | 4739.10(5) |
| C | MHz | 4302.8854(8) | 4298.94(5) |
| D J | kHz | 3.0541(3) | 2.517(10) |
| D JK | kHz | −55.89(2) | −54.4(3) |
| D K | kHz | 748.3(4) | 512.(5) |
| d 1 | kHz | −0.6712(2) | −0.72(4) |
| d 2 | kHz | −0.02976(6) | −0.09(3) |
| No. of lines | 1180 | 623 | |
| J, Ka max | 75, 10 | 47, 7 | |
| rms × 103 | cm−1 | 0.26 | 0.71 |
5 Conclusions
The importance of aminoacetonitrile in astrochemistry demands for a deep knowledge of its spectroscopic properties. In this work, we presented the first thorough computational characterization of the structure and rotational/ro-vibrational spectra of aminoacetonitrile carried out by employing accurate quantum-chemical methods. This was accompanied by the determination of a semi-experimental equilibrium structure and the partial analysis of the three strongest vibrational bands observed between 500 and 1000 cm−1.As far as the molecular structure is concerned, the derived semi-experimental equilibrium geometry agrees very well with our best-estimated computational counterpart obtained by exploiting the CBS+CV composite scheme, thus confirming the accuracy of both approaches. Because of the close relationship between structure and physico-chemical properties, we recommend to use our newly determined geometry as reference for future spectroscopic studies. Focusing on the infrared spectrum, the CBS+CV harmonic frequencies combined with an accurate treatment of anharmonicity allowed us to predict very accurate positions for all fundamental bands, in good agreement with previous vibrational analyses.38,39 Moreover, the anomalous large discrepancy between the computed position of the ν15 band and the experimental frequency attributed by Bak et al.38 gave us the opportunity to point out the wrong experimental assignment and to re-assign this band to a feature observed at 1160 cm−1 in our infrared spectra.
In addition to the theoretical characterization, we have recorded and analyzed three ro-vibrational bands observed in the 500–1000 cm−1 range, namely the ν8, ν9, and ν10 bands. While the spectral analysis of the ν10 band was satisfactory and the determined spectroscopic constants are in line with those computed here and previous rotational studies,34 the analysis of the ν8 and ν9 bands revealed the presence of strong perturbations. Still, the correct assignment of more than 2000 ro-vibrational transitions has been validated using the MARVEL algorithm and should provide a solid base for future investigations.
In general, the experimental/theoretical characterization of the molecular structure and spectroscopic properties of aminoacetonitrile provided in this work can be used to assist both astronomical observations and laboratory experiments concerning the important role played by this species in interstellar environments.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been supported by MIUR (PRIN Grant Number 202082CE3T) and by the University of Bologna (RFO funds). N. J. thanks the China Scholarships Council (CSC) for financial support. We would like to thank the AILES beamline staff for their assistance in data acquisition.Notes and references
- K. Kvenvolden, J. Lawless, K. Pering, E. Peterson, J. Flores, C. Ponnamperuma, I. R. Kaplan and C. Moore, Nature, 1970, 228, 923–926 CrossRef CAS PubMed.
- J. G. Lawless, K. A. Kvenvolden, E. Peterson, C. Ponnamperuma and C. Moore, Science, 1971, 173, 626–627 CrossRef CAS PubMed.
- D. P. Glavin, J. L. Bada, K. L. Brinton and G. D. McDonald, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 8835–8838 CrossRef CAS PubMed.
- D. P. Glavin, A. D. Aubrey, M. P. Callahan, J. P. Dworkin, J. E. Elsila, E. T. Parker, J. L. Bada, P. Jenniskens and M. H. Shaddad, Meteorit. Planet. Sci., 2010, 45, 1695–1709 CrossRef CAS.
- D. P. Glavin, J. E. Elsila, A. S. Burton, M. P. Callahan, J. P. Dworkin, R. W. Hilts and C. D. Herd, Meteorit. Planet. Sci., 2012, 47, 1347–1364 CrossRef CAS.
- E. Nakamura, K. Kobayashi, R. Tanaka, T. Kunihiro, H. Kitagawa and C. Potiszil, et al. , Proc. Jpn. Acad., Ser. B, 2022, 98, 227–282 CrossRef CAS PubMed.
- J. E. Elsila, D. P. Glavin and J. P. Dworkin, Meteorit. Planet. Sci., 2009, 44, 1323–1330 CrossRef CAS.
- K. Altwegg, H. Balsiger, A. Bar-Nun, J.-J. Berthelier, A. Bieler, P. Bochsler, C. Briois, U. Calmonte, M. R. Combi and H. Cottin, et al. , Sci. Adv., 2016, 2, e1600285 CrossRef PubMed.
- J. M. Hollis, J. Pedelty, L. E. Snyder, P. R. Jewell, F. J. Lovas, P. Palmer and S.-Y. Liu, Astrophys. J., 2003, 588, 353 CrossRef CAS.
- L. E. Snyder, F. J. Lovas, J. Hollis, D. N. Friedel, P. Jewell, A. Remijan, V. V. Ilyushin, E. Alekseev and S. Dyubko, Astrophys. J., 2005, 619, 914 CrossRef CAS.
- A. Belloche, K. Menten, C. Comito, H. Müller, P. Schilke, J. Ott, S. Thorwirth and C. Hieret, Astron. Astrophys., 2008, 482, 179–196 CrossRef CAS.
- J. M. Hollis, F. J. Lovas and P. R. Jewell, Astrophys. J., 2000, 540, L107 CrossRef CAS.
- V. M. Rivilla, L. Colzi, I. Jiménez-Serra, J. Martn-Pintado, A. Megías, M. Melosso, L. Bizzocchi, A. López-Gallifa, A. Martínez-Henares and S. Massalkhi, et al. , Astrophys. J., Lett., 2022, 929, L11 CrossRef.
- V. M. Rivilla, I. Jiménez-Serra, J. Martn-Pintado, C. Briones, L. F. Rodrguez-Almeida, F. Rico-Villas, B. Tercero, S. Zeng, L. Colzi and P. de Vicente, et al. , Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2101314118 CrossRef CAS PubMed.
- V. M. Rivilla, J. Martn-Pintado, I. Jiménez-Serra, S. Martn, L. F. Rodrguez-Almeida, M. A. Requena-Torres, F. Rico-Villas, S. Zeng and C. Briones, Astrophys. J., Lett., 2020, 899, L28 CrossRef CAS.
- A. Belloche, R. Garrod, H. Müller, K. Menten, I. Medvedev, J. Thomas and Z. Kisiel, Astron. Astrophys., 2019, 628, A10 CrossRef CAS.
- I. Jiménez-Serra, J. Martn-Pintado, V. M. Rivilla, L. Rodrguez-Almeida, E. R. Alonso Alonso, S. Zeng, E. J. Cocinero, S. Martn, M. Requena-Torres and R. Martn-Domenech, et al. , Astrobiology, 2020, 20, 1048–1066 CrossRef PubMed.
- R. Rubin, G. Swenson Jr, R. Benson, H. Tigelaar and W. Flygare, Astrophys. J., 1971, 169, L39 CrossRef CAS.
- C. Richard, A. Belloche, L. Margulès, R. Motiyenko, K. Menten, R. Garrod and H. Müller, J. Mol. Spectrosc., 2018, 345, 51–59 CrossRef CAS.
- M. Melosso, A. Belloche, M.-A. Martin-Drumel, O. Pirali, F. Tamassia and L. Bizzocchi, et al. , Astron. Astrophys., 2020, 641, A160 CrossRef CAS.
- A. Strecker, Justus Liebigs Ann. Chem., 1850, 75, 27–45 CrossRef.
- G. Danger, F. Borget, M. Chomat, F. Duvernay, P. Theulé, J.-C. Guillemin, L. L. S. dHendecourt and T. Chiavassa, Astron. Astrophys., 2011, 535, A47 CrossRef.
- F. Borget, G. Danger, F. Duvernay, M. Chomat, V. Vinogradoff, P. Theulé and T. Chiavassa, Astron. Astrophys., 2012, 541, A114 CrossRef.
- A. Rimola, M. Sodupe and P. Ugliengo, Phys. Chem. Chem. Phys., 2010, 12, 5285–5294 RSC.
- C. Chyba and C. Sagan, Nature, 1992, 355, 125–132 CrossRef CAS PubMed.
- G. Danger, J.-B. Bossa, P. De Marcellus, F. Borget, F. Duvernay, P. Theulé, T. Chiavassa and L. dHendecourt, Astron. Astrophys., 2011, 525, A30 CrossRef.
- G. A. Carvalho and S. Pilling, Spectrochim. Acta A, 2022, 267, 120495 CrossRef CAS PubMed.
- R. T. Garrod, Astrophys. J., 2013, 765, 60 CrossRef.
- C. He and M. A. Smith, Icarus, 2014, 238, 86–92 CrossRef CAS.
- B. A. McGuire, Astrophys. J., Suppl. Ser., 2022, 259, 30 CrossRef.
- J. MacDonald and J. Tyler, J. Chem. Soc., Chem. Comm., 1972, 17, 995 RSC.
- M. Bogey, H. Dubus and J. Guillemin, J. Mol. Spectrosc., 1990, 143, 180–182 CrossRef CAS.
- Y. Motoki, Y. Tsunoda, H. Ozeki and K. Kobayashi, Astrophys. J., Suppl. Ser., 2013, 209, 23 CrossRef.
- L. Kolesniková, E. Alonso, S. Mata and J. Alonso, Astrophys. J., Suppl. Ser., 2017, 229, 26 CrossRef.
- C. Degli Esposti, L. Dore, M. Melosso, K. Kobayashi, C. Fujita and H. Ozeki, Astrophys. J., Suppl. Ser., 2017, 230, 26 CrossRef.
- H. M. Pickett, J. Mol. Spectrosc., 1973, 46, 335–340 CrossRef CAS.
- R. Brown, P. Godfrey, A. Ottrey and J. Storey, J. Mol. Spectrosc., 1977, 68, 359–366 CrossRef CAS.
- B. Bak, E. Hansen, F. Nicolaisen and O. Nielsen, Can. J. Phys., 1975, 53, 2183–2188 CrossRef CAS.
- M. P. Bernstein, C. W. Bauschlicher Jr and S. A. Sandford, Adv. Sp. Res., 2004, 33, 40–43 CrossRef CAS.
- G. M. Chaban, J. Phys. Chem. A, 2004, 108, 4551–4556 CrossRef CAS.
- M. Naganathappa and A. Chaudhari, Int. J. Quant. Chem., 2011, 111, 2064–2071 CrossRef CAS.
- J.-B. Brubach, L. Manceron, M. Rouzières, O. Pirali, D. Balcon, F. Kwabia-Tchana, V. Boudon, M. Tudorie, T. Huet, A. Cuisset and P. Roy, WIRMS 2009, 2010, pp. 81–84 Search PubMed.
- O. Pirali, V. Boudon, J. Oomens and M. Vervloet, J. Chem. Phys., 2012, 136, 024310 CrossRef CAS PubMed.
- O. Pirali, M. Goubet, T. R. Huet, R. Georges, P. Soulard, P. Asselin, J. Courbe, P. Roy and M. Vervloet, Phys. Chem. Chem. Phys., 2013, 15, 10141–10150 RSC.
- M. Faye, M. Bordessoule, B. Kanouté, J.-B. Brubach, P. Roy and L. Manceron, Rev. Sci. Instrum., 2016, 87, 063119 CrossRef PubMed.
- I. E. Gordon, L. S. Rothman, R. J. Hargreaves, R. Hashemi and E. V. Karlovets, et al. , J. Quant. Spectrosc. Radiat. Transfer, 2021, 107949 Search PubMed.
- V. M. Horneman, R. Anttila, S. Alanko and J. Pietila, J. Mol. Spectrosc., 2005, 234, 238–254 CrossRef CAS.
- C. Puzzarini, J. Phys. Chem. A, 2009, 113, 14530–14535 CrossRef CAS PubMed.
- V. Barone, M. Biczysko, J. Bloino and C. Puzzarini, Phys. Chem. Chem. Phys., 2013, 15, 10094–10111 RSC.
- V. Barone, M. Biczysko, J. Bloino and C. Puzzarini, J. Chem. Phys., 2014, 141, 034107 CrossRef PubMed.
- C. Puzzarini, Int. J. Quant. Chem., 2016, 116, 1513–1519 CrossRef CAS.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483 CrossRef CAS.
- D. Feller, J. Chem. Phys., 1993, 98, 7059–7071 CrossRef CAS.
- T. Helgaker, W. Klopper, H. Koch and J. Noga, J. Chem. Phys., 1997, 106, 9639–9646 CrossRef CAS.
- T. H. Dunning Jr., J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- D. E. Woon and T. H. Dunning Jr., J. Chem. Phys., 1995, 103, 4572 CrossRef CAS.
- C. Puzzarini, J. F. Stanton and J. Gauss, Int. Rev. Phys. Chem., 2010, 29, 273–367 Search PubMed.
- C. Puzzarini, J. Heckert and J. Gauss, J. Chem. Phys., 2008, 128, 194108 CrossRef PubMed.
- I. M. Mills, Molecular Spectroscopy: Modern Research, ed. K. N. Rao and C. W. Matthews, 1972 Search PubMed.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622 CrossRef.
- M. Piccardo, J. Bloino and V. Barone, Int. J. Quantum Chem., 2015, 115, 948–982 CrossRef CAS PubMed.
- P. Pulay, W. Meyer and J. E. Boggs, J. Chem. Phys., 1978, 68, 5077–5085 CrossRef CAS.
- Equilibrium Molecular Structures: From Spectroscopy to Quantum Chemistry, ed. J. Demaison, J. E. Boggs and A. G. Császár, CRC Press, Taylor & Francis Group, Boca Raton, FL, US, 2011 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision B.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- J. F. Stanton, J. Gauss, M. E. Harding and P. G. Szalay, A. A. Auer, R. J. Bartlett, U. Benedikt, C. Berger, D. E. Bernholdt, Y. J. Bomble, O. Christiansen, F. Engel, M. Heckert, O. Heun, C. Huber, T.-C. Jagau, D. Jonsson, J. Jusélius, K. Klein, W. J. Lauderdale, F. Lipparini, D. Matthews, T. Metzroth, L. A. Mück, D. P. O'Neill, D. R. Price, E. Prochnow, C. Puzzarini, K. Ruud, F. Schiffmann, W. Schwalbach, S. Stopkowicz, A. Tajti, J. Vázquez, F. Wang, J. D. Watts, and the integral packages MOLECULE (J. Almlöf and P. R. Taylor), PROPS (P. R. Taylor), ABACUS (T. Helgaker, H. J. Aa. Jensen, P. Jø rgensen, and J. Olsen), and ECP routines by A. V. Mitin and C. van Wüllen, CFOUR. A quantum chemical program package, 2016. For the current version, see https://www.cfour.de Search PubMed.
- D. A. Matthews, L. Cheng, M. E. Harding, F. Lipparini, S. Stopkowicz, T.-C. Jagau, P. G. Szalay, J. Gauss and J. F. Stanton, J. Chem. Phys., 2020, 152, 214108 CrossRef CAS PubMed.
- V. Barone, S. Alessandrini, M. Biczysko, J. R. Cheeseman, D. C. Clary, A. B. McCoy, R. J. DiRisio, F. Neese, M. Melosso and C. Puzzarini, Nat. Rev. Methods Primers, 2021, 1, 1–27 CrossRef.
- C. Puzzarini, Phys. Chem. Chem. Phys., 2013, 15, 6595–6607 RSC.
- S. Alessandrini, J. Gauss and C. Puzzarini, J. Chem. Theory Comput., 2018, 14, 5360–5371 CrossRef CAS PubMed.
- C. Puzzarini, G. Cazzoli and J. Gauss, Chem. Phys., 2012, 137, 154311 Search PubMed.
- R. Boussessi, N. Tasinato, A. Pietropolli Charmet, P. Stoppa and V. Barone, Mol. Phys., 2020, 118, e1734678 CrossRef.
- V. Barone, M. Biczysko, J. Bloino, P. Cimino, E. Penocchio and C. Puzzarini, J. Chem. Theory Comput., 2015, 11, 4342–4363 CrossRef CAS PubMed.
- C. Degli Esposti, L. Dore, C. Puzzarini, M. Biczysko, J. Bloino, L. Bizzocchi, V. Lattanzi and J.-U. Grabow, Astron. Astrophys., 2018, 615, A176 CrossRef.
- C. Puzzarini, N. Tasinato, J. Bloino, L. Spada and V. Barone, Phys. Chem. Chem. Phys., 2019, 21, 3431–3439 RSC.
- C. Puzzarini, M. Biczysko and V. Barone, J. Chem. Theory Comput., 2010, 6, 828–838 CrossRef CAS PubMed.
- J. Bloino, M. Biczysko and V. Barone, J. Chem. Theory Comput., 2012, 8, 1015–1036 CrossRef CAS PubMed.
- I. Carnimeo, C. Puzzarini, N. Tasinato, P. Stoppa, A. Pietropolli Charmet, M. Biczysko, C. Cappelli and V. Barone, J. Chem. Phys., 2013, 139, 074310 CrossRef PubMed.
- C. Puzzarini, J. Bloino, N. Tasinato and V. Barone, Chem. Rev., 2019, 119, 8131–8191 CrossRef CAS PubMed.
- C. M. Western, J. Quant. Spectrosc. Radiat. Transfer, 2017, 186, 221–242 CrossRef CAS.
- W. Lodyga, M. Krkeglewski, P. Pracna and V. Urban, J. Mol. Spectrosc., 2007, 243, 182–188 CrossRef CAS.
- T. Furtenbacher, A. G. Császár and J. Tennyson, J. Mol. Spectrosc., 2007, 245, 115–125 CrossRef CAS.
- H. M. Pickett, J. Mol. Spectrosc., 1991, 148, 371–377 CrossRef CAS.
- J. K. G. Watson, in Vibrational Spectra and Structure, ed. J. Durig, Elsevier, Amsterdam, 1977, vol. 6, pp. 1–89 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: List of the transitions assigned for the ν8, ν9, ν10 bands; geometry and harmonic frequencies at the HF-SCF level; vibration–rotation interaction constants at the MP2 level. See DOI: https://doi.org/10.1039/d2cp05179f |
| This journal is © the Owner Societies 2023 |