Is a thin mechanism appropriate for aromatic nitration?

Abstract

The mechanism of toluene nitration by NO₂BF₄ in dichloromethane solution is investigated by performing advanced ab initio MD simulations of the reaction trajectories, including at full quantum mechanical level the effects of both the solvent and of the counterion. The time evolution of the encounter complex, as well as that of the associated electronic structure, for different trajectories reveals that a single electron transfer step fastly occurs after reactants are accommodated in a common solvation shell, always preceding the formation of the σ-complex. The present results strongly suggest that the regioselectivity of the reaction is spin-density driven and that a thin mechanism, one based on reaction intermediates and transition states, can be appropriate to describe aromatic nitration.

---

1 Introduction

Aromatic nitration has played a central role in the development of a mechanistic theory of aromatic reactivity,^1–3 but, despite the huge body of experimental and theoretical data accumulated in many decades, many facets of its mechanism are far from being completely understood; the reaction mechanism is still elusive and subject of active research.^4–8

Ingold's pioneering work showed beyond any reasonable doubt that in reaction media composed of nitric acid (in acetic anhydride or nitromethane), the nitrating agent is the highly reactive nitronium ion and proposed the text-book two-step mechanism¹:

It was soon realized that the two-step mechanism was too simple to account for the very peculiar kinetic features of aromatic nitration. Indeed, it was shown that, for aromatics more reactive than benzene, nitration occurs at encounter limited rate, still exhibiting a high selectivity toward the substitution site.^3,9 Such a behavior suggests that the electrophilic species involved in nitration should be different from the nitronium ion, which does not show substrate selectivity.⁹ Similar conclusions were reached by Olah and Kuhn, who developed an efficient procedure for aromatic nitration by using stable nitronium salts (NO₂BF₄ and NO₂PF₆) in organic solvents.¹⁰ In those conditions, the use of the competitive method for benzene and toluene substrates resulted in a ratio of rate constants k_Tol/k_Benz ≈ 2, which, combined with the observed high positional selectivity of the products (ortho : meta : para = 66 : 3 : 31), led to the paradoxical conclusion that the meta carbons of toluene are sevenfold less reactive than a benzene carbon. Olah proposed that the first reaction step consists of the formation of a weakly bound π -complex between the two reactants, responsible for substrate selectivity. The second, faster step, leading to the Wheland intermediate, would account for positional selectivity.¹⁰

Olah's argumentations were criticized, the competitive method being considered inappropriate because the high reactivity of nitronium salts could not allow differentiation between the rates of different substrates; in other words, the low substrate selectivity could be simply the consequence of a reaction occurring before uniform mixing of the reagents.^11,12 However, variation of the toluene/benzene mole ratio led to no significant changes in either positional or substrate selectivity,¹² showing that the above results were not an experimental artifact but rather represented a new and important phenomenon: A chemical reaction showing low substrate but high positional selectivity. Such a rare event could be explained by resorting to the involvement of an intermediate species. The chemical nature of this intermediate has been described variously in the literature, e.g. as an encounter pair,^9,13,14 a π -complex,^10,15 a charge transfer complex,^16,17 and a radical ion pair originated by single electron transfer (SET) step from aromatics to NO₂⁺,¹⁸ but remains elusive.

Among the various hypotheses, the involvement of a radical pair in the mechanism of aromatic nitration gained popularity, because gas-phase ionization potentials and electrochemical anodic half-wave potentials show that an electron transfer step is thermodynamically favoured for all the aromatics more reactive than toluene, even in a polar solvent such as acetonitrile.¹⁸ Furthermore, the attacking species would be no longer the highly reactive nitronium ion, which exhibits no intramolecular selectivity, but the radical NO₂˙, the latter being compatible with intramolecular selectivity, since the formation of the Wheland intermediate is necessarily a spin-density driven reaction.

The hypothesis that a SET step could be of relevance in the mechanism of aromatic nitration has been substantiated by Kochi and coworkers who used time-dependent spectroscopy to show that various ArH:NO₂ electron-donor acceptor complexes, when thermally or photochemically activated, lead to nitration of the aromatic substrate, with identical regiospecificity of the conventional reaction,^19–21 and by several theoretical works, which, however did not account for the effect of the solvent and/or the counterion.^20–29

More recently, the possible occurrence of a SET mechanism in solution has been questioned.^4,5,30 Calculations based on density functional theory (DFT) predict that SET takes place in the gas-phase, whereas in mixed acid solution, including a sulphate counterion, no appreciable charge transfer is envisaged.⁵ Quinones and Singleton have questioned both the importance of a SET intermediate and the involvement of transition states.⁴ Those authors carried out a thorough analysis of the ground state potential energy hypersurface for toluene nitration by NO₂BF₄ in dichloromethane and found that the regiochemistry of the reaction is accurately predicted only from trajectories in explicit solvent, while approaches based on transition state theory fail to account for selectivity. The observed product regioselectivity is achieved only when both explicit solvent and counterion are included in trajectory computations, ruling out the possibility that a conventional mechanism, i.e. one based on transition states and/or reaction intermediates, can explain experimental observations.⁴

Herein, we reconsider the possibility of a SET step in CH₂Cl₂ solution by carrying out advanced ab initio MD simulations, which include at a full quantum mechanical level the effects of both the solvent and of the counterion. The time evolution of the encounter complex, as well as that of the associated electronic structure, for different trajectories reveals that SET always precedes the formation of the σ-complex.

2 Results and discussion

The energetics of a redox process in solution from periodic DFT-based simulations requires the use of adequate density functionals, devoid of the self-interaction error, which affects semi-local methods.^31,32 While the use of hybrid DFT generally leads to improved results,^33,34 most standard methods still suffer from this spurious interaction, thus undermining the accuracy of the calculated electronic properties.³⁵ In fact, since (i) the total energy of the exact exchange–correlation functional is a linear function of the number of electrons between integer values³⁶ and (ii) the variation of the total energy with respect to an orbital occupation is equal to the eigenvalue of that orbital (Janak theorem³⁷), it follows that the energy level associated with a single-particle state should not change upon its occupation (generalized Koopmans' theorem³⁶). In this context, nonempirical hybrid functionals in which the fraction of Fock exchange α is set to comply with the generalized Koopmans' theorem have proved do be particularly successful in simulating the electronic properties (e.g. band gap, band edges, polaron binding energies) of both solids and liquids, as well as reproducing redox levels in aqueous solution from MD simulations.^38–45 For the latter, accurate values of the energy gap and the band edges of the solvent are paramount for a proper description of the solutes energy level and to avoid the occurrence of unphysical dynamics,⁴⁶ in perfect analogy with defects and polarons in crystalline materials.^33,47–49

Therefore, the first step of our study is aimed at constructing a Koopmans' compliant density functional for liquid dichloromethane. In particular, we consider the PBE0(α) family of functionals, in which a single parameter, the fraction of Fock exchange α, needs to be determined.^50,51 For the determination of the α required for the fulfillment of Koopmans' condition, α_K, we employ the probe method recently developed by Bishoff et al. and successfully applied to various materials.^43,44 Within this technique, a hydrogen (proton) atom is inserted in the material [cf.Fig. 1(a)] and then the single-particle occupied (empty) energy level of the induced localized state is inspected. α_K is then given by the intersection between the α-dependent linear evolution of occupied and unoccupied energy levels [cf.Fig. 1(b)].⁴² Employing this method, we here achieve α_K = 49.8% (cf. Computational details).

Fig. 1 (a) Stick&ball visualization of a representative configuration of the hydrogen probe (blue) inserted in a periodic supercell of liquid CH₂Cl₂ along with the isodensity representation of the corresponding highest occupied molecular orbital. H atoms in white, C in grey, and Cl in green. (b) Occupied (blue, full circles) and unoccupied (red, empty circles) single-particle energy levels of the interstitial hydrogen as a function of the fraction of Fock exchange used in the PBE0 functional. Energies are referred to the average electrostatic potential of the system. Since these energy levels generally evolve linearly with the mixing parameter,⁴² the point of intersection between the lines achieved considering three values, corresponds to the value α_K enforcing the generalized Koopmans' condition, denoted with a dashed black line.

We then calculate the band gap, E_g, of liquid CH₂Cl₂ from the linear extrapolation of the wing of the respective near-edge density of states (DOS),³³ which is achieved from the average of 100 equally-spaced structural configurations extracted from classical MD simulation (cf. Fig. S1, ESI†). Such a methodology is analogous to that usually adopted in the experimental determination of the electronic structure of liquids (e.g. liquid water in ref. 52,53). We here obtain E_g = 8.95 eV, this being, to the best of our knowledge, the first ab initio estimate of the band gap for liquid dichloromethane. Inspection of the density of states (cf. Fig. S2, ESI†) reveals that both the valence band edge and the conduction band edge states are mainly constituted by the 3p orbitals of chlorine, a result consistent with the nature of the 3b₁ and 10a₁ molecular orbitals of the CH₂Cl₂ molecule.^54,55 Overall, the calculated wide band gap ensures a correct definition of localized states arising from solutes with no spurious resonant energy levels due to band gap underestimation.^33,46

Finally, in order to properly capture intermolecular interactions in condensed-phase CH₂Cl₂, we include non-local electron correlation in our functional self-consistently via the rVV10 scheme, developed by Vydrov and Van Voorhis,^56,57 in line with a previous study.⁵⁸ The constructed PBE0(α_K) + rVV10 functional is found to deliver energetics of CH₂Cl₂ dimers in excellent agreement with CCSD(T) calculations^59,60(cf. Fig. S3 and Table S1, ESI†), thus ensuring that both structural and electronic properties of liquid CH₂Cl₂ and its solutions will be adequately described in MD simulations.

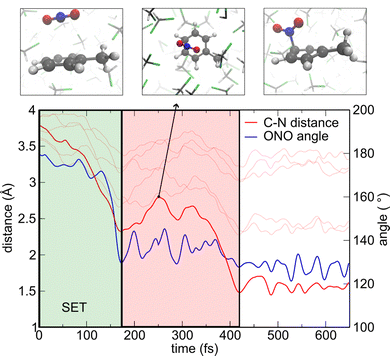
Having set up the appropriate computational protocol, we first investigate toluene nitration in CH₂Cl₂ solution, considering complete dissociation of NO₂BF₄ and evolving trajectories starting from a casual NO₂⁺-toluene encounter complex, in which the N atom is initially on top of the aromatic carbon in para position at a C–N distance of 3.5 Å (cf.Fig. 2).²⁹ The simulation cell is prepared starting from the structural configuration of a previously performed ab initio MD simulation. The NO₂⁺-toluene complex is then inserted in the centre of the supercell and four CH₂Cl₂ molecules are removed, to accommodate the complex preserving solvent density. The system, having a net charge of +1, is then subjected to DFT-based MD simulation in the NVT ensemble at 300 K (cf. Computational details) with the PBE0(α_K) + rVV10 functional. We note that, in order to properly capture the physics of electron transfer phenomena possibly occurring within the simulation time, we need to employ the unrestricted DFT method, even if the total number of electrons in the system is even, for it allows the possible localization of a pair of electrons on different orbitals, as a consequence of SET. First, the solvent surrounding the complex is equilibrated via a 5-ps MD simulation in which two constraints are applied: (i) the distance between N and the ortho C of toluene is preserved to its original value and (ii) the O–N–O angle is kept to 180°, i.e. for the nitronium cation. Then, the constraints are released and the simulation is carried out until C–N bond formation of the σ-complex.

Fig. 2 Evolution (i) of the distance between the para C atom of toluene and the N atom of the nitronium cation (red) and (ii) of the ONO angle upon MD simulation (blue). The simulation is initiated from a solvated NO₂⁺-toluene encounter complex with N lying directly above the para C atom (top left), proceeds via electron transfer (green shaded area, top middle for an illustrative configuration along with the isodensity representation of the lowest unoccupied molecular orbital and the Hirshfeld charges for the two moieties) and is concluded with formation of the σ-complex in para position (top right). H atoms in white, C in grey, Cl in green, N in blue, and O in red.

By studying the evolution of the structural parameters involved in the reaction, namely the C–N distance and O–N–O angle, it is possible to capture the key features of the reaction mechanism. In fact, the C–N distance is rapidly shrunk and formation of the σ-complex is observed in less than 1 ps. Furthermore, the O–N–O angle, which is the crucial parameter for defining the transition from nitronium cation to neutral NO₂, is accordingly reduced (cf.Fig. 2). The region of steep descent within the first 200 fs is of particular interest because the molecule is already sizably bent while the C–N distance is still well above bond formation. Moreover, hole localization on the aromatic molecule is confirmed by both inspection of the hole wavefunction and analysis of Hirshfeld charges (cf.Fig. 2 for a representative configuration). Overall, our analysis supports the occurrence of SET, in accord with the “rigid” approach in implicit solvent employed in ref. 29 predicting the NO₂/ArH⁺ complex to be more stable than the NO₂⁺/ArH one for C–N distances shorter than ≈ 2.7 Å. We again remark that the use of unrestricted DFT is fundamental to properly describe the SET mechanism, as evidenced by the time-dependent evolution of the lowest unoccupied molecular orbitals for α and β electrons, which clearly shows occupation of different orbitals occurring in the simulation (cf. Fig. S4, ESI†).

To ensure that the occurrence of SET is not affected by the initial geometry of the encounter complex, we have repeated the simulation starting from a configuration in which the nitronium cation lies above the centre of the aromatic ring, the C–N distances being essentially equal for all the aromatic C atoms.²⁹ From Fig. 3, we observe again a fast narrowing of the NO₂ angle within the first 200 fs of MD, accompanying the SET, in line with the previous simulation. However, the C–N bond is not immediately formed. In fact, while some C–N distances are rapidly shrunk towards SET at distances ≤2.5 Å the formed NO₂ radical is found to roam above the aromatic molecule between para and meta positions for other ∼250 fs, before finally forming the σ-complex, again in para position. Overall, the outcome of this simulation not only confirms the SET mechanism but also distinctly reveals that the radical NO₂ is the actual reactant and therefore points to a spin-density driven mechanism. These results are confirmed by a supplementary trajectory initiated from a nitronium cation on top of the ipso C atom, with the σ-complex forming in ortho position (cf. Fig. S5, ESI†), which confirms that the observed higher reactivity of para and ortho position is satisfactorily captured by simulations.

Fig. 3 Evolution of (i) the distances between the aromatic C atoms of toluene and the N atom of the nitronium cation (red) and (ii) the ONO angle upon MD simulation (blue). The bolder red line indicates the distance with the para C atom. The simulation is initiated from a solvated NO₂⁺-toluene encounter complex with N above the center of the aromatic ring (top left), then proceeds via electron transfer (green shaded area) and subsequent roaming of the NO₂ radical between para and meta positions (red shaded area, top middle for an indicative configuration) and is concluded with formation of the σ-complex in para position (top right). H atoms in white, C in grey, Cl in green, N in blue, and O in red.

Finally, we investigate the effect of the counterion on the mechanism of aromatic nitration in CH₂Cl₂, which has been recently postulated.⁴ In fact, the source of NO₂⁺ for the reaction is a nitronium salt, usually NO₂BF₄, which is known to be scarcely soluble in organic solvents⁶¹ and it is thought to form ion pairs in solution.⁶² On this basis and from MD simulations, it has been inferred that BF₄⁻ affects the reaction as its concerted displacement along with that of reactants and solvent molecules is required.⁴ In this regard, we note that, to the best of our knowledge, no measured value of the dissociation degree for NO₂BF₄ is available. In the worst-case scenario of a negligible fraction of dissociated ion pairs, does the counterion affect the nature of the proposed SET mechanism? To answer this question, we perform two extra MD simulations in which BF₄⁻ has been included. In particular, we consider the encounter complex of Fig. 2 and included the counterion in two different positions: (i) above the nitronium cation or (ii) on the side, closer to the toluene molecule, with the shortest B–C distance below 4 Å (P1 and P2, respectively, cf.Fig. 4).

Fig. 4 Time-dependent evolution of selected structural parameters for MD simulation initiated from solvated BF₄⁻–NO₂⁺–toluene complexes. The starting configurations involve a NO₂⁺–toluene complex having N above the center of the aromatic ring and with the counterion (a) on top or (b) on the side of the nitronium cation, closer to toluene, P1 and P2 respectively in the main text. The green shaded area in panel (a) highlights the region in which the NO₂ moiety is bent enough to allow for electron transfer (cf. inset for a representative configuration), while in panel (b) indicates the time frame for SET. H atoms in white, C in grey, N in blue, O in red, B in brown, and F in purple.

MD simulations reveal a drastically different time-evolution of the two configurations. In fact, for P1 we do not observe any nitration event during a 5 ps MD run, while for P2 the reaction is concluded within ≤1 ps, in fair agreement with previous simulations not including BF₄⁻. In fact, in P1, the Coulomb attraction between NO₂⁺ and BF₄⁻ appears to hinder electron transfer, resulting in a continuous oscillation of the C–N and B–N distances [cf.Fig. 4(a)]. In particular, the distance between the para C atom and N varies between 3.5 and 2.7 Å, well above that pertinent to bond formation, and is somewhat correlated with the B–N one, i.e. smaller values for the former correspond to larger ones for the latter and vice versa. Shortest values of the C–N distance coincide to a sensibly bent NO₂ moiety, which in turn indicates tendency towards electron transfer, which is however only transient. At variance with this, dynamics of the P2 structure mimics that of the analogous complex in absence of the counterion, with swift completion of the reaction via formation of the bent NO₂ radical already at C–N distances of ∼2.7 Å [cf.Fig. 4 (b)]. It is worth noticing that the time-dependent energy profiles of the two simulations are remarkably different with the P2 structure forming the σ-complex being more stable than the P1 one by more than 1 eV, on average (cf. Fig. S6, ESI†). Overall, the present results clearly indicate that considering the ion pair as the reactant, although requiring a favourable structural arrangement with the toluene molecule to overcome Coulomb interaction, does not change the nature of the SET-based mechanism, which is resumed in Fig. 5.

Fig. 5 Schematic representation of the proposed reaction mechanism for the nitration of toluene by NO₂BF₄ in dichloromethane solution.

3 Conclusions

The results reported above are largely in line with the analysis of Quinones and Singleton,⁴ but for the remarkable fact that involvement of a SET step has been systematically found in each reactive trajectory. The question now is at what extent SET is significant in the mechanism of aromatic nitration? Can NO₂˙ be considered as a true reaction intermediate, even if its life time is short? In our opinion it is, the positive answer being mainly based on the comparison between the reactive and non-reactive trajectories of Fig. 4, which clearly indicate that SET makes it possible the almost barrierless approach of the nitronium ion to the aromatic substrate. Furthermore, it has been longly known that the peculiar kinetics of aromatic nitration is more convincingly described by a three-step mechanism,^9,15 and that the paradox of high positional and low substrate selectivity can find a rationale if the attacking species is different from nitronium ion, which does not show substrate selectivity.^9,15,18 All these points make us confident that a thin mechanism, one based on reaction intermediates and/or transition states, can be appropriate to aromatic nitration.

Computational details

The initial configuration for liquid CH₂Cl₂ is obtained through the software Packmol,⁶³ by constructing a cubic box of side 20 Å containing 75 CH₂Cl₂ and corresponding to the experimental density of liquid CH₂Cl₂ (1.33 g cm⁻³). Then, we perform classical MD simulations with the Gromacs 2020.5 software⁶⁴ using the All-atom Optimised Potentials for Liquid Simulations (OPLS) force field.⁶⁵ We adopt periodic boundary conditions and take into account long range electrostatic effects through the PME algorithm.⁶⁶ Classical MD simulations are carried out in the NVT ensemble, adopting a modified Berendsen thermostat,⁶⁷ with a target temperature of 300 K. The computational protocol consists of an initial steepest descent minimisation, followed by a equilibration run over 100 ps and a subsequent production run of 1 ns. DFT calculations are here performed using the freely available CP2K/QUICKSTEP package.⁶⁸ This suite of programs features a combined atomic basis set/plane-wave approach in which atom-centered Gaussian-type basis functions are used to describe the orbitals, while an auxiliary plane-wave basis set is employed to re-expand the electron density. In particular, we use a triple-zeta correlation-consistent polarized basis set (cc-pVTZ)⁶⁹ and a cutoff of 800 Ry for the plane waves. We employ the analytical Goedecker-Teter-Hutter pseudopotentials.⁷⁰ Furthermore, for the calculation of exchange integrals required for hybrid functional calculations, we adopt the auxiliary density matrix method, as implemented in CP2K, with the cFIT auxiliary basis set.^71,72 For the determination of α_K, we consider ten structural configurations extracted from the classical MD simulation. For each structure, we insert a single hydrogen atom in a void [cf.Fig. 1(a)], we calculate the single-particle energy levels for the occupied (q = 0) and unoccupied (q = +1) states for three different values of α [cf.Fig. 1(b)]. From the average of ten configurations, we achieve α_K = 49.8% ± 0.1. We note that such a value is consistent with that of 49.5% estimated from the inverse high frequency dielectric constant ,^48,73 considering the experimental value of ε_∞ = 2.02 for dichloromethane.⁷⁴ We also pinpoint that the energy of the Kohn–Sham levels for the charged supercell suffers from an electrostatic finite-size error, arising from periodic boundary conditions.⁷⁵ Therefore, we employ the correction term derived in ref. 76 for Kohn–Sham levels, in analogy with the Freysoldt–Neugebauer–Van de Walle (FNV) scheme commonly employed for total energies.^75,77 This correction amounts to 0.81 eV for the employed supercell, considering the experimental high-frequency dielectric constant of liquid dichloromethane (2.02),⁷⁴ as calculations are performed without relaxing the positions of the nuclei. Unrestricted-DFT based Born-Oppenheimer MD simulations in the NVT ensemble are carried out in a periodic cubic cell of length 20 Å as previously described. The target temperature, controlled by a Nosé–Hoover thermostat,^78,79 is set to 300 K and a time-step of 0.50 fs is employed.

Author contributions

Francesco Ambrosio: conceptualization, data curation, formal analysis, visualization, investigation and writing – original draft. Amedeo Capobianco: conceptualization, supervision, writing – review & editing. Alessandro Landi: data curation, investigation, writing – review & editing. Teodoro Pizza: investigation. Andrea Peluso: conceptualization, writing – original draft, writing – review & editing, funding acquisition and supervision.

Conflicts of interest

There is no conflict to declare.

Acknowledgements

We thank Dr Attila Bende for kindly providing us with the coordinates of the dichloromethane dimers. We acknowledge financial support from the Università di Salerno, grants: FARB 2020 and FARB 2021.

References

1. C. K. Ingold, Structure and Mechanism in Organic Chemistry, Cornell Univ. Press, Ithaca, 2nd edn, 1986.
2. T. H. Lowry and K. S. Richardson, Mechanism and Theory in Organic Chemistry, Harper & Row, New York, 1981.
3. K. Schofield, Aromatic Nitration, Cambridge University Press, Cambridge, 1980.
4. Y. Nieves-Quinones and D. A. Singleton, J. Am. Chem. Soc., 2016, 138, 15167–15176.
5. G. Koleva, B. Galabov, B. Hadjieva, H. F. Schaefer III and P. v R. Schleyer, Angew. Chem., Int. Ed., 2015, 54, 14123–14127.
6. L. Lu, H. Liu and R. Hua, Org. Lett., 2018, 20, 3197–3201.
7. B. A. Steele, M.-X. Zhang and I.-F. W. Kuo, J. Phys. Chem. A, 2022, 126, 5089–5098.
8. A. Kroflič, M. Huš, M. Grilc and I. Grgíc, Environ. Sci. & Technol., 2018, 52, 13756–13765.
9. R. G. Coombes, R. B. Moodie and K. Schofield, J. Chem. Soc. B, 1968, 800–804.
10. G. A. Olah, Acc. Chem. Res., 1971, 4, 240–248.
11. W. S. Tolgyesi, Can. J. Chem., 1965, 43, 343–355.
12. G. A. Olah and N. A. Overchuk, Can. J. Chem., 1965, 43, 3279–3293.
13. L. M. Stock, Progress in Physical Organic Chemistry, Wiley-Interscience, New York, 1976.
14. J. H. Ridd, Acc. Chem. Res., 1971, 4, 248–253.
15. G. A. Olah, S. C. Narang, J. A. Olah and K. Lammertsma, Proc. Natl. Acad. Sci. U. S. A., 1982, 79, 4487–4494.
16. R. D. Brown, J. Chem. Soc., 1959, 2224–2232.
17. S. Fukuzumi and J. K. Kochi, J. Am. Chem. Soc., 1981, 103, 7240–7252.
18. C. L. Perrin, J. Am. Chem. Soc., 1977, 99, 5516–5518.
19. J. K. Kochi, Acc. Chem. Res., 1992, 25, 39–47.
20. S. V. Rosokha and J. K. Kochi, J. Org. Chem., 2002, 67, 1727–1737.
21. S. V. Rosokha and J. K. Kochi, New J. Chem., 2002, 26, 851–860.
22. A. Peluso and G. Del Re, J. Phys. Chem., 1996, 100, 5303–5309.
23. R. A. Albunia, R. Borrelli and A. Peluso, Theor. Chem. Acc., 2000, 104, 218.
24. S. R. Gwaltney, S. V. Rosokha, M. Head-Gordon and J. K. Kochi, J. Am. Chem. Soc., 2003, 125, 3273–3283.
25. P. M. Esteves, J. W. de, M. Carneiro, S. P. Cardoso, A. G. H. Barbosa, K. K. Laali, G. Rasul, G. K. S. Prakash and G. A. Olah, J. Am. Chem. Soc., 2003, 125, 4836–4849.
26. J. F. Queiroz, J. Walkimar, M. Carneiro, A. A. Sabino, R. Sparrapan, M. N. Eberlin and P. M. Esteves, J. Org. Chem., 2006, 71, 6192–6203.
27. X. F. Xu, S. Zilberg and Y. Haas, J. Phys. Chem. A, 2010, 114, 4924–4933.
28. K. Shopsowitz, F. Lelj and M. J. MacLachlan, J. Org. Chem., 2011, 76, 1285–1294.
29. A. Capobianco, A. Landi and A. Peluso, Chemistry, 2021, 3, 1286–1301.
30. V. D. Parker, T. Kar and D. Bethell, J. Org. Chem., 2013, 78, 9522–9525.
31. J. P. Perdew and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048–5079.
32. Y. Zhang and W. Yang, J. Chem. Phys., 1998, 109, 2604–2608.
33. F. Ambrosio, G. Miceli and A. Pasquarello, J. Chem. Phys., 2015, 143, 244508.
34. J. Cheng and M. Sprik, Phys. Chem. Chem. Phys., 2012, 14, 11245–11267.
35. V. Atalla, I. Y. Zhang, O. T. Hofmann, X. Ren, P. Rinke and M. Scheffler, Phys. Rev. B, 2016, 94, 035140.
36. J. P. Perdew, R. G. Parr, M. Levy and J. L. Balduz, Phys. Rev. Lett., 1982, 49, 1691–1694.
37. J. F. Janak, Phys. Rev. B: Condens. Matter Mater. Phys., 1978, 18, 7165–7168.
38. G. Miceli, W. Chen, I. Reshetnyak and A. Pasquarello, Phys. Rev. B, 2018, 97, 121112.
39. N. P. Brawand, M. Govoni, M. Vörös and G. Galli, J. Chem. Theory Comput., 2017, 13, 3318–3325.
40. H. Zheng, M. Govoni and G. Galli, Phys. Rev. Mater., 2019, 3, 073803.
41. F. Ambrosio, J. Wiktor, F. De Angelis and A. Pasquarello, Energy Environ. Sci., 2018, 11, 101–105.
42. T. Bischoff, I. Reshetnyak and A. Pasquarello, Phys. Rev. B, 2019, 99, 201114.
43. T. Bischoff, J. Wiktor, W. Chen and A. Pasquarello, Phys. Rev. Mater., 2019, 3, 123802.
44. T. Bischoff, I. Reshetnyak and A. Pasquarello, Phys. Rev. Res., 2021, 3, 023182.
45. H. Ouhbi, F. Ambrosio, F. De Angelis and J. Wiktor, J. Phys. Chem. Lett., 2021, 12, 5339–5343.
46. F. Ambrosio and A. Pasquarello, Phys. Chem. Chem. Phys., 2018, 20, 30281–30289.
47. A. Alkauskas, P. Broqvist and A. Pasquarello, Phys. Rev. Lett., 2008, 101, 046405.
48. A. Alkauskas, P. Broqvist and A. Pasquarello, Phys. Status Solidi B, 2011, 248, 775–789.
49. H.-P. Komsa, P. Broqvist and A. Pasquarello, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 205118.
50. J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982–9985.
51. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
52. B. Winter, M. Faubel, I. V. Hertel, C. Pettenkofer, S. E. Bradforth, B. Jagoda-Cwiklik, L. Cwiklik and P. Jungwirth, J. Am. Chem. Soc., 2006, 128, 3864–3865.
53. R. Seidel, S. Thürmer and B. Winter, J. Phys. Chem. Lett., 2011, 2, 633–641.
54. K. F. Alcantara, W. Wolff, A. H. A. Gomes, L. Sigaud, S. Soriano, V. Oliveira, A. B. Rocha and A. C. F. Santos, J. Phys. B, 2011, 44, 165205.
55. A. C. F. Santos, D. N. Vasconcelos, M. A. MacDonald, M. M. Sant'Anna, B. N. C. Tenório, A. B. Rocha, V. Morcelle, N. Appathurai and L. Zuin, J. Chem. Phys., 2018, 149, 054303.
56. O. A. Vydrov and T. Van Voorhis, J. Chem. Phys., 2010, 133, 244103.
57. R. Sabatini, T. Gorni and S. de Gironcoli, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 041108.
58. F. Ambrosio, G. Miceli and A. Pasquarello, J. Phys. Chem. B, 2016, 120, 7456–7470.
59. L. Almásy and A. Bende, J. Mol. Liq., 2011, 158, 205–207.
60. L. Almásy and A. Bende, Molecules, 2019, 24, 1810.
61. L. L. Ciaccio and R. A. Marcus, J. Am. Chem. Soc., 1962, 84, 1838–1841.
62. G. Oláh, S. Kuhn and A. Mlinká, J. Chem. Soc., 1956, 4257–4258.
63. L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164.
64. Lindahl, Abraham, Hess and van der Spoel, GROMACS 2020.5 Source code, 2021 DOI:10.5281/zenodo.4420785.
65. W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236.
66. M. F. Crowley, T. A. Darden, T. E. Cheatham III and D. W. Deerfield II, J. Supercomput., 1997, 11, 255–278.
67. B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472.
68. J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103–128.
69. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023.
70. C. Hartwigsen, S. Goedecker and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 3641–3662.
71. M. Guidon, F. Schiffmann, J. Hutter and J. VandeVondele, J. Chem. Phys., 2008, 128, 214104.
72. M. Guidon, J. Hutter and J. VandeVondele, J. Chem. Theory Comput., 2010, 6, 2348–2364.
73. M. A. L. Marques, J. Vidal, M. J. T. Oliveira, L. Reining and S. Botti, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 035119.
74. C. Wohlfarth and B. H. Book, Optical Constants: Supplement to Volume III/47, Springer, 2017.
75. C. Freysoldt, J. Neugebauer and C. G. Van de Walle, Phys. Rev. Lett., 2009, 102, 016402.
76. W. Chen and A. Pasquarello, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 115104.
77. H.-P. Komsa, T. T. Rantala and A. Pasquarello, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 045112.
78. S. Nosé, J. Chem. Phys., 1984, 81, 511–519.
79. W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp05176a

---