Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The performance of CCSD(T) for the calculation of dipole moments in diatomics
Xiangyue
Liu
 a,
Laura
McKemmish
b and
Jesús
Pérez-Ríos
a,
Laura
McKemmish
b and
Jesús
Pérez-Ríos
 *cd
*cd
aFritz-Haber-Institut der Max-Planck-Gesellschaft, Faradayweg 4-6, 14195 Berlin, Germany
bSchool of Chemistry, UNSW Sydney, Sydney, NSW 2052, Australia
cDepartment of Physics and Astronomy, Stony Brook University, Stony Brook 11794, New York, USA. E-mail: jesus.perezrios@stonybrook.edu
dInstitute for Advanced Computational Science, Stony Brook University, Stony Brook, NY 11794-3800, USA
First published on 21st December 2022
Abstract
This work analyzes the accuracy of the coupled cluster with single, double, and perturbative triple excitation [CCSD(T)] method for predicting dipole moments. In particular, we benchmark CCSD(T) predictions for the equilibrium bond length, vibrational frequency, and dipole moment versus accurate experimental data. As a result, we find that CCSD(T) leads to accurate dipole moments. However, in some cases, it disagrees with the experimental values, and the disagreement can not be satisfactorily explained via relativistic or multi-reference effects. Therefore, our results indicate that benchmark studies for energy and geometry properties do not accurately describe other electron density magnitudes.
1 Introduction
Coupled cluster with single, double, and perturbative triple excitations [CCSD(T)] is one of the most popular methods in electronic structure theory. Indeed, it serves as a benchmark reference in developing other electronic structure theory methods, such as density functional theory (DFT). It is size-consistent, and as a member of the coupled cluster family, it is systematically improvable. When utilized in combination with specific corrections, it is considered to approach sub-chemical accuracy in properties such as bond energies1 at the complete basis set (CBS) limit.2 DFT benchmarking studies most commonly focus on energetic properties.1,3–17 Nevertheless, recently there has been increased interest in understanding the performance of other aspects of the wavefunction such as the electric dipole moment.18–23Most of the literature about benchmarking dipole moments is typically based on CCSD(T) performance, focusing on molecules consisting of light main-group elements. Nevertheless, molecules involving elements from the third row and heavier (Z > 18), especially transition-metal compounds, play an essential role in modern applications like catalysis and material synthesis due to their electronic and magnetic properties.24–26 Many of these applications rely on an accurate description of the energetic properties and electron densities, so CCSD(T) is becoming popular among the different quantum chemistry methods. On the other hand, CCSD(T) generally relies on single Slater-determinant Hartree-Fock references. As a result, its performance can sometimes be questionable in systems with multi-reference nature.15,27 Another concern is the accuracy of the approximations that can be applied in CCSD(T) calculations. For example, frozen-core approximation is a popular choice when calculating systems with heavy elements. However, the computational cost of the CCSD(T) core-core and core-valence correlations quickly becomes impractical with an increasing number of electrons in the systems with effective core potentials (ECPs) applied.
Therefore, since the CCSD(T) method is central to modern quantum chemistry and for benchmarking other computational chemistry methods, it is necessary to compare its performance with that of other methods. In particular, it is possible to benchmark the performance of CCSD(T) against available experimental data on spectroscopic constants or molecular properties, such as the dipole moment. Fortunately, reliable experimental data regarding spectroscopic and molecular properties are increasing. In this regard, although small, diatomic molecules can be extremely effective benchmarking model systems as they show a wide variety of different bonding and spin configurations, they are expected to reflect some trends of polyatomic systems.7 Indeed, experimental diatomic test sets have become an attractive choice in various benchmarks for DFT and wavefunction methods for properties such as equilibrium geometries and bond energies.1,3–17 However, investigations focusing on the performance of CCSD(T) against experimental dipole moments are still minimal for dipole moments.9,28
This work extensively studies the accuracy and limitations of the performance of CCSD(T) regarding dipole moments of diatomics. First, our study compares the performance of CCSD(T) methods with different basis sets against experimentally measured dipole moments collected recently in ref. 29. Second, and in line with the previous point, the equilibrium bond length and harmonic frequency are tested against the experimental data. The dataset consists of 32 diatomic molecules involving both main-group and transition metal elements with divergent bond natures. The dipole moments are obtained from well-controlled experimental measurements such as microwave spectroscopy, with reported uncertainties typically below 0.05 D.
2 Methodology
2.1 Computational approach
Our computations are performed at the core-correlated CCSD(T) level of theory using the CFOUR package30 by means of unrestricted Hartree-Fock (UHF) orbitals as a reference. For elements with Z > 36, we use effective core potentials. The basis sets employed in this work include the augmented Dunning's weighted core-valence basis set aug-cc-pwCVT/QZ(-PP) to account for core-correlations2,31–46 and a computationally much cheaper basis set, the segmented def2-QZVPP series basis sets developed by Ahlrichs et al.47–49 In the case of closed-shell molecules with def2-QZVPP basis, the results are provided via the Molpro package.50,51In this paper, we report the equilibrium dipole moment μe and the zero-point vibrational corrected dipole moment μ0. To calculate μ0, for each molecule, we compute the potential energy curve in a point-wise manner using a grid of points ranging between 0.4 × Re(Exp) and 3 × Re(Exp).† The spin states of molecules are determined as the spin state whose potential energy curve has the lowest energies compared with other spin states. The obtained spin states are consistent with experiments. Next, the equilibrium bond length Re and harmonic vibrational frequency ωe are obtained by fitting the potential energy curve. The electric dipole moments μ are calculated from analytic gradients at every single-point geometry, leading to the dipole moment at the equilibrium bond length μe and the zero-point vibrational corrected dipole moment μ0. The latter includes vibrational average corrections, using the discrete variable representation (DVR) method for the vibrational wavefunctions,‡ and the overlap obtained by numerical integration. In this work, only the magnitude (not the direction) of the dipole moments is discussed.
For Dunning basis sets, the CBS limits are predicted using the standard two-point extrapolation scheme52–54 as
 | (1) |
For elements calculated with the aug-cc-pwCVT/QZ-PP basis set, the relativistic effects have already been considered in the effective core potentials, showing that these have a minimal effect.55 Nevertheless, a scalar relativistic effect correction has been obtained by the second-order Douglas–Kroll–Hess approximation (DK) implemented in Molpro for selected molecules when (aug-)cc-p(w)CVT/QZ-DK(3) basis sets56 are available.
2.2 Dataset
Experimentally, the equilibrium bond length, harmonic frequency, and dipole moment have been measured in more than 100 diatomic molecules.29 We selected 32 molecules to explore in depth with high-level quantum chemistry that was representative of the diatomics’ chemical diversity; see Table 1 for molecules considered. We divide them into six classes to aid interpretation, with the number of molecules of each class shown in Fig. 1, following the same graphical representative, we will use in this paper to show results. The dataset includes various main-group metal and non-metal compounds showing covalent and ionic bonds. In particular, the dataset contains 8 transition metal compounds.| Classes of molecules | Molecules |
|---|---|
| Metal/metalloid–halogen | AlF (X1Σ+), GaF (X1Σ+), InCl (X1Σ+), InF (X1Σ+) |
| Metal/metalloid/nonmetal-metal/metalloid | GeTe (X1Σ+), GeO (X1Σ+), GeS (X1Σ+), PbO (X1Σ+), PbS (X1Σ+), SiO (X1Σ+), SiS (X1Σ+) SnO (X1Σ+), SnS (X1Σ+) |
| Nonmetal/halogen–halogen | BrO (X2Π3/2), CF (X2Π), IBr (X1Σ+) |
| Nonmetal-nonmetal | CN (X2Σ+), CO (X1Σ+), CS (X1Σ+), CSe (X1Σ+), NO (X2Π1/2), PN (X1Σ+), PO (X2Π), SO (X3Σ−) |
| Transition metal–halogen | AgBr (X1Σ+), AgF (X1Σ+), AgI (X1Σ+), CuF (X1Σ+), YF (X1Σ+) |
| Transition metal-nonmetal | HfO (X1Σ+), ScO (X2Σ+), ZrO (X1Σ+) |
 | ||
| Fig. 1 Number of molecules in the present dataset classified by classes of their constituent elements. | ||
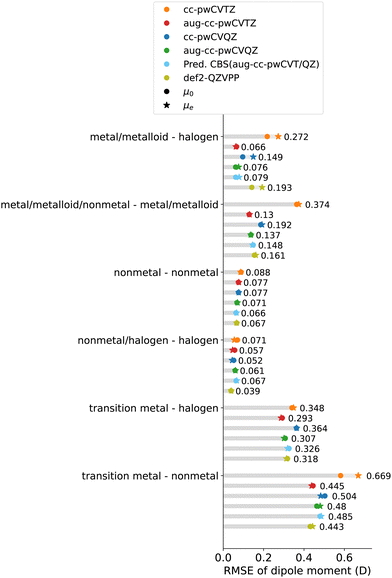
The accuracy of the experimentally measured electric dipole moments depends on determining the magnitude of the applied electric field and its homogeneity. In constructing the current dataset, focus on molecules with dipole moments determined by high-resolution spectroscopic measurements, especially microwave spectroscopy and molecular beam electric resonance, excluding molecules with considerable uncertainty in dipole moments such as BF and RbI. As shown in Fig. 2, in this dataset, typical error bars of 0.1–5% are found, which translates into errors less than 0.05 D for most of the molecules under consideration. PbO, AgF, InCl, PbS, SnS and SnO are labeled in the figure since they show uncertainties over 0.1 D.
3 Results and discussions
The performance of CCSD(T) on the equilibrium bond length, Re, harmonic vibrational frequency, ωe, of diatomic molecules has been exhaustively investigated in the literature by comparing with experiments. Not only the accuracy of basis set families,31,33,41 but also that of the conjunct relativistic pseudopotentials has been discussed and compared with full-electron relativistic treatments.36–40,42,43,57 Recently, it has been found that by using non-HF orbitals, the accuracy of CCSD(T) ωe can be further improved for diatomic molecules consisting of row 2 and row 3 elements.17 For transition metal diatomic molecules, the accuracy of CCSD(T) on Re and ωe, as well as the influence of relativistic effect and multi-reference character have been investigated based on a dataset of 60 molecules.55 Nevertheless, we first report the calculated Re and ωe for the dataset employed in this work. Then, we present and discuss the theoretical predictions of dipole moments compared to their experimental values for the molecules in the dataset.The performance of computations versus experimental data is tested via:
• Residuals defined as the difference between the experimental value of a molecular property and its computed value, xi(Exp.) − xi(CCSD(T)), where xi is the experimental or calculated properties for molecule i.
• Root mean squared error (RMSE) defined as
 | (2) |
We present the results in two formats for each computational method investigated and molecular property under consideration. First, we present residual errors of all molecules, labeling molecules with significant errors. Second, we perform a statistical analysis of the errors by presenting the RMSE grouped by molecular class as designated in Table 1. In addition, when needed, we report the relative error rE as
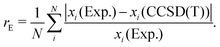 | (3) |
Finally, we show results based on the aug-cc-pwCVQZ and def2-QZVPP basis sets. The def2-QVPP basis set has just over half the number of basis functions as auc-cc-pwCVQZ (actually very similar in size to aug-cc-pwCVTZ).
3.1 Equilibrium bond length
When analyzing Re, both aug-cc-pwCVQZ and def2-QZVPP basis sets give very accurate predictions, showing an RMSE ≲ 0.008 Å (rE ≲ 0.2%), as shown in Fig. 3. In this figure, it is observed that non-metal diatomics, metal/metalloid/nonmetal-metal/metalloid molecules show the smallest RMSE ≃ 0.002 Å (rE ≃ 0.1–0.2%), while some transition-metal-containing diatomics display more significant errors, with RMSE ≃ 0.01 Å (rE ≃ 0.5%). Furthermore, some outliers are noticeable, such as CuF, AgBr and AgI.In the case of CuF, Aoto et al. have shown that the error of Re is reduced by including relativistic corrections,55 and our results confirm these findings, as discussed in Section 3.3.3. In contrast, for some other transition–metal-containing molecules, for example, ScO or AgF, the scalar relativistic effect correction is negligible. Another source of discrepancy may be due to multi-reference effects; on that front, it has been shown that using multi-reference coupled-cluster theory for ScO and AgF leads to results similar to the single-reference results.55 On the other hand, silver–halogen molecules have received little attention, except for AgF and AgCl, showing a negligible relativistic effect on the equilibrium bond length prediction. Therefore, in light of these results, we think that relativistic effects could not explain the significant error in the predictions of Re for AgBr and AgI.
Our def2-QZPP calculations show systematically large Re values further from the experiment than aug-cc-pwCVQZ calculations. For the aug-cc-pwCV basis set, increasing the number of basis functions usually improves the predictions of Re towards experimental values. From the aug-cc-pwCVTZ basis set to the quadruple-ζ level, the RMSE for most classes of molecules can be significantly reduced to around 50%. Exceptions are the transition metal-containing molecules, for which the aug-cc-pwCVT/QZ basis set gives similar RMSEs. However, the reduction of basis functions in the def2-QZVPP basis sets does not necessarily worsen the Re predictions. The RMSEs with the def2-QZVPP basis set are generally comparable with the aug-cc-pwCVQZ basis set for most molecules studied, except metal/metalloid halides. In particular, for transition metal halides, the def2-QZVPP basis set can be much closer to the experimental results than the aug-cc-pwCVQZ basis set.
3.2 Vibrational harmonic frequency
The CCSD(T) performance for the vibrational harmonic frequency versus experimental data is shown in Fig. 4, where we can identify the absolute error of CCSD(T) calculations and its RMSE for each molecular class. The relative errors of CCSD(T) were compared to experimental rE ≲ 2% for most molecules. The RMSEs with the predicted CBS(aug-cc-pwCVT/QZ) and def2-QZVPP basis sets are 24.7 and 16.3 cm−1, respectively. We find that the calculations of ωe of diatomics involving main-group metal elements are very accurate with both basis sets, leading to an RMSE ≲ 10 cm−1. These findings align with those of Aoto et al., showing that the main-group nonmetal diatomics have large errors,55 and the most significant outliers include CN and NO. These are correlated to the poor UHF reference. It has been recently shown that these errors can be healed by using non-HF.17For most molecules, the predictions of ωe are already close to experiments at the aug-cc-pwCVTZ level. The difference between the RMSEs from the aug-cc-pwCVTZ and aug-cc-pwCVQZ basis sets is only ∼2.5 cm−1. Similar to Re, the RMSE of the def2-QZVPP basis set is very close to that of the aug-cc-pwCVQZ basis set, sometimes even slightly better than that of the latter. However, for nonmetal diatomic molecules, the employment of the aug-cc-pwCV basis set significantly improves the results.
3.3 Dipole moment
3.3.1.1 Vibrational corrections on dipole moment predictions. Experimental dipole moments usually deviate from the theoretical ones at the equilibrium bond length due to the anharmonicity of the molecular interaction. Vibrational corrections have been shown to be important for accurate dipole moment calculations versus experimental values.28,58–61 The importance of vibrational corrections depends on the anharmonicity of the underlying potential energy curve. In the case of dipole moment, as a first-order molecular property, it can be important to count for the deviation between the equilibrium bond length (given by the potential energy curve) and the most probable interatomic distance given by the ground state vibrational wave function. Therefore, apart from reporting the dipole moment at the equilibrium bond length, μe, we calculate the vibrational average dipole moment μ0 by numerically averaging the radial-dependent dipole moment with the vibrational ground state wavefunction of the molecule under consideration. In particular, we use a DVR approach to solve the single-channel Schrödinger equation associated with the vibrational degrees of freedom over the obtained Born-Oppenheimer potential energy curve.
Fig. 5 and 6 show the residuals of CCSD(T) calculations on the dipole moments for the molecules of our dataset for the def2-QZVPP and CBS(aug-cc-pwCVT/QZ) basis set. As a result, we notice a trivial influence of the vibrational average on the dipole moment and consistent differences from the vibrational average with the two basis sets (∼0.01 D, 2%). However, we find a few outliers: diatomics with light elements and short bond lengths such as CO (∼20%), NO (∼10%), CF (∼10%), AlF (∼4%), GaF (∼3%), and YF (∼2%). Indeed, for these outliers, the difference introduced by vibrational average correction correlates with their harmonic vibrational frequency. Finally, due to the slightly better performance of the vibrational average dipole moment, we will use μ0 when referring to dipole moments from now on.
 | ||
| Fig. 5 Dipole moment errors calculated with def2-QZVPP basis set versus experimental results, with or without vibrational average corrections. | ||
 | ||
| Fig. 6 Dipole moment errors calculated with aug-cc-pwCVQZ basis set versus experimental results, with or without vibrational average corrections. | ||
3.3.1.2 Basis set family and size. A detailed study on the role of basis sets on the dipole moment is shown in Fig. 7 and 8, shown as the residuals of the calculated dipole moment with respect to the experiments. In particular, we investigate the performance of CCSD(T) dipole moments calculated with cc-pwCV, aug-cc-pwCV, and def2-QZVPP basis sets. For most molecules with larger basis sets, the predicted magnitude of the dipole moment increases.
In the case of the cc-pwCV basis set, we observe a significant basis set size effect. For most molecules, increasing the size of the basis set from cc-pwCVTZ to cc-pwCVQZ reduces the underestimation of the dipole moment, improving the RMSE from 0.30 D to 0.24 D. In particular, when using the cc-pwCV basis set, molecules containing metal/metalloid elements are sensitive to the size of the basis set. For molecules with main-group metal/metalloid elements, increasing the size of the basis set from cc-pwCVTZ to cc-pwCVQZ halves the RMSE. In contrast, for the nonmetal-nonmetal and nonmetal/halogen-halogen molecules, the improvement of the dipole moment from the triple-ζ to quadruple-ζ level is less than 0.02 D. Therefore, it is sufficient to use the cc-pwCVTZ basis set for molecules with nonmetal elements.
With the aug-cc-pwCV basis set, it is noticed that dipole moments are almost converged at the aug-cc-pwCVTZ level. As a result, the benefits of using the larger aug-cc-pwCVQZ basis set are ≲0.01 D, while in some cases, especially for diatomics with metal atoms, the aug-cc-pwCVTZ predictions are slightly more accurate than those of the aug-cc-pwCVQZ level. The role of augmented functions will be discussed in Section 3.3.1.3.
Furthermore, and surprisingly enough, for most molecules, using the def2-QZVPP basis set leads to a similar accuracy to that of the aug-cc-pwCVQZ basis set, even though the latter is computationally much more expensive. For some molecules, the def2-QZVPP basis set yields a dipole moment closer to the experimental one than the CBS(aug-cc-pwCVT/QZ).
3.3.1.3 Influence of diffuse functions. It has been shown that for dipole moments, diffuse functions augmented to the basis set play an important role in hybrid and double-hybrid density functionals, and wave function-based methods can be applied to get closer dipole moment predictions to CCSD(T).22,62 To further explore if diffuse functions help CCSD(T) predictions to approach experiments, the cc-pwCVT/QZ basis sets have been used to calculate the dipole moments and compared to the results from augmented basis sets, shown in Fig. 8. As discussed in Section 3.3.1.2, from the cc-pwCVTZ to the quadruple-ζ level, the prediction of the dipole moment's magnitude increases. Adding the augmentation functions further increases the dipole moment's magnitude, leading, in some cases, to its overestimation. Molecules containing metal elements are more sensitive to augmentation than nonmetal molecules because of the longer-range nature of the wave function. On average, the RMSE can be reduced by 0.10 D by augmenting the cc-pwCVTZ basis set, while at the quadruple-ζ level, the overall improvement from augmentation is only 0.03 D, much smaller than the triple-ζ level. Therefore, the improvement from including augmented functions is negligible at the quadruple-ζ level for dipole moments of most molecules. Exceptions are metal/metalloid halides (metal/metalloid-halogen and transition metal-halogen molecules), for which the improvement of RMSE by employing diffuse functions at the quadruple-ζ level is ∼0.07 D. Therefore, for these molecules, it is suggested to use augmented basis sets.
 | ||
| Fig. 9 The errors of dipole moment calculated with def2-QZVPP and aug-cc-pwCVQZ basis sets. The error bars of experimental measurements are shown in gray. | ||
In particular, diatomics containing main-group elements, especially non-metal elements, are well described with rE ≲ 5%: RMSE ≲ 0.08 D for nonmetal-nonmetal molecules and RMSE ≲ 0.5 D for nonmetal halides. For molecules containing main-group metals/metalloids, the RMSE becomes larger (≲0.15 D), but still close to the experimental uncertainty, except SnO and PbS.
However, in stark contrast to the main-group molecules, larger errors are observed in systems involving transition metals. In particular, with the predicted CBS(aug-cc-pwCVT/QZ), we observe an RMSE of 0.32 D (rE = 5.5%) and 0.51 D (rE = 6.9%) for transition metal halides and other transition metal-non metal diatomics, respectively, much larger than the experimental uncertainty.
The source of the discrepancy between CCSD(T) and experiments can be various. As the predicted CBS is obtained from a relatively large basis set, we believe the errors are not associated with the size of the basis set. Another source is the possible multi-reference character of the molecules. However, in the current dataset, the transition–metal-containing molecules or their analogs are generally dominated by singe-reference characters.55,63 Besides, we notice that the residuals of CCSD(T) predictions from experiments are not explicitly correlated with the experimental uncertainties. Although for some molecules, for example, PbO and InCl, the residual is closer to the experimental uncertainty, for other molecules, like PbS, the residual is much larger than the experimental uncertainty. In the following section, the possible sources of errors will be explored further in detail.
 | ||
| Fig. 10 Errors of dipole moments as a function of errors of Re with def2-QZVPP and predicted CBS(aug-cc-pwCVT/QZ). | ||
As noticed in Fig. 9, there are a few outliers that require some extra discussion. Naturally, one would expect that the error resides in the single-reference nature of CCSD(T) calculations. However, it has been previously shown that the molecules displaying significant errors on dipole moments show a dominant single-reference nature.55
Another possible source of errors is the non-relativistic treatment. We perform CCSD(T) calculations, including the scalar relativistic correction, to investigate the role of the relativistic effect. In particular, we focus on 9 molecules showing significant errors in the dipole moment. The dipole moments μe calculated at experimental geometry, with or without relativistic correction, are summarized in Table 2. We notice that the inclusion of the relativistic effect slightly decreases the magnitude of the predicted dipole moment. The difference of μe introduced by the relativistic effect is commonly tiny, 0.01–0.07 D (0.3–1.5%), except CuF, for which the difference is 0.14 D (2.7%). For the molecules whose dipole moments are overestimated by non-relativistic CCSD(T) treatments (e.g., PbS, AgI, CuF), the relativistic dipole moment becomes closer to the experiment. In contrast, for other molecules, the underestimation of the dipole moment is further aggravated by the relativistic correction. Overall, including the relativistic correction, the RMSE of the 9 molecules can be slightly improved from 0.252 D to 0.235 D.
| Molecule | μ 0 (Exp.) (D) | Non-relativistic | Scalar relativistic | ||
|---|---|---|---|---|---|
| μ e (D) | Basis set | μ e (D) | Basis set | ||
| AgF | 6.22(20) | 5.991 | Ag:cc-pwCVTZ-PP; F:cc-pVQZ | 5.956 | Ag:cc-pwCVTZ-DK; F:cc-pVQZ-DK |
| AgBr | 5.62(3) | 5.789 | Ag:cc-pwCVTZ-PP; Br:cc-pVQZ | 5.716 | Ag:cc-pwCVTZ-DK; Br:cc-pVQZ-DK |
| AgI | 4.55(5) | 5.139 | Ag:cc-pwCVTZ-PP; I:cc-pwCVTZ-PP | 5.087 | Ag:cc-pwCVTZ-DK; I:cc-pwCVTZ-DK3 |
| CuF | 5.26(2) | 5.420 | Cu:aug-cc-pwCVQZ; F:aug-cc-pwCVQZ | 5.278 | Cu:aug-cc-pwCVQZ-DK; F:aug-cc-pwCVQZ-DK |
| InCl | 3.79(19) | 3.629 | In:aug-cc-pwCVQZ-PP; Cl:aug-cc-pwCVQZ | 3.616 | In:aug-cc-pwCVQZ-DK3; Cl:aug-cc-pwCVQZ-DK |
| PbO | 4.64(30) | 4.479 | Pb:aug-cc-pwCVQZ-PP; O:aug-cc-pCVQZ | 4.460 | Pb:aug-cc-pwCVQZ-DK3; O:aug-cc-pCVQZ-DK |
| PbS | 3.59(10) | 3.726 | Pb:aug-cc-pwCVQZ-PP; S:aug-cc-pCVTZ | 3.669 | Pb:aug-cc-pwCVQZ-DK3; S:aug-cc-pCVTZ-DK |
| SnO | 4.32(10) | 4.106 | Sn:aug-cc-pwCVQZ-PP; O:aug-cc-pCVQZ | 4.074 | Sn:aug-cc-pwCVQZ-DK3; O:aug-cc-pCVQZ-DK |
| SnS | 3.18(10) | 3.190 | Sn:aug-cc-pwCVQZ-PP; S:aug-cc-pCVQZ | 3.147 | Sn:aug-cc-pwCVQZ-DK3; S:aug-cc-pCVQZ-DK |
To further investigate the origin of the errors, in the following paragraphs, we analyze individual molecules with the most significant errors, including ScO, CuF and AgI.
In the case of CuF, the dipole moment is overestimated by 0.28 D at the CCSD(T)/CBS(aug-cc-pwCVT/QZ) level compared to the experimental value of 5.26(2) D, taken from the recent supersonic molecular beam high-resolution optical Stark spectrum.73 Furthermore, we observe a small divergence of 0.02 Å between experimental Re and CCSD(T)/aug-cc-pwCVQZ prediction. At experimental Re, the predicted dipole moment μe is 5.420 D with CCSD(T)/aug-cc-pwCVQZ. Interestingly, when applying DK relativistic corrections to CCSD(T) with the corresponding relativistic-contracted Douglas–Kroll basis sets (Cu:aug-cc-pwCVQZ-DK; F:aug-cc-pwCVQZ-DK), the experimental Re is perfectly reproduced with an error of 0.001 Å, and the dipole moment obtained is 5.28 D, which is consistent with previous reports87 and perfectly reproduces experimental values. This finding aligns with the previous studies on CuH, AgH, and AuH,88 where small changes in the predicted Re by the inclusion of relativistic effect have been observed to cause considerable change in μe(Re).
The analysis of the Stark effect on the rotational spectrum of AgI shows a dipole moment of 4.55(5) D.66 However, our predicted CBS(aug-cc-pwCVT/QZ) gives 5.15 D, including the vibrational average correction, which overestimates the experimental measurement. However, it is in close agreement with previous theoretical predictions.89 In contrast, for AgF (isovalent analogues of AgI), CCSD(T) underestimates the dipole moment. Furthermore, silver-halogen molecules, experimentally, show a drastic decrease in the dipole moment as the halogen element becomes heavier, whereas, theoretically, the decrease is less steep, as shown in Fig. 11. The disagreement between CCSD(T) calculations and experimental results can not be healed by including a scalar relativistic effect. The difference of dipole moment obtained by relativistic CCSD(T)/(Ag:cc-pwCVTZ-DK; I:cc-pwCVTZ-DK) and non-relativistic CCSD(T)/(Ag:cc-pwCVTZ-PP; I:cc-pwCVTZ-PP) is only 0.05 D at the experimental Re. Additionally, we notice that there is an earlier measurement from the same group, giving μ0 = 5.10(15) D,90 which agrees with our CCSD(T)/(aug-cc-pwCVT/QZ) predictions. Therefore, the disagreement calls for revision.
4 Conclusions
In this work, we have benchmarked the performance of CCSD(T) for predicting dipole moments by comparing computational results based on large basis sets with accurate experimental results. In particular, we study 32 diatomic molecules with diverse bonding and elemental composition whose experimental dipole moments are available. Thus, we use experimental information to benchmark a computational approach directly. We also consider the accuracy of the equilibrium bond length and vibrational harmonic frequency and compare them to the accuracy of the dipole moment prediction.We find that single-reference CCSD(T) calculations, using the def2- and aug-cc-pwCVX (where X = T and Q) family of basis set, satisfactorily describe the dipole moment of most of the molecules in the dataset, with errors usually less than 0.15 D, especially for molecules containing only main-group elements. However, this accuracy is contingent on selecting the most appropriate basis sets depending on the molecule under consideration. For instance, we have shown that for the cc-pwCV basis set at the triple-ζ level, diffuse functions play an essential role in molecules containing metal elements. However, augmentation with diffuse functions slightly improves the dipole moment predictions at the quadruple-ζ level where the basis set is already large enough. Similarly, the basis set incompleteness error is evident at the triple-ζ level when employing the cc-pwCV basis set, while the augmented counterpart gives almost converged results. Surprisingly, the def2-QZVPP basis set shows good comparable performance compared to the much larger aug-cc-pwCVQZ basis set. Therefore, the def2-QZVPP basis set should be the choice to predict dipole moments in larger systems.
Non-relativistic predictions are generally accurate enough for most molecules. Although, for some molecules like CuF, scalar relativistic corrections may have an essential role in the dipole moment calculations. For some molecules, e.g., ScO, AgI, we observe significant divergence with experiments that can not satisfactorily be explained by the multi-reference or relativistic effect. We recommend for these unusual molecules a careful consideration of both experimental and theoretical (e.g., multi-reference coupled-cluster) results to ensure a better understanding of dipole moment in these systems. Furthermore, an extension of the current dataset, e.g., alkali metal molecules, would be desirable for future benchmarks.
Finally, we have shown that errors in the prediction of the dipole moment do not correlate with the accuracy of the equilibrium bond length, showing that errors in the dipole moment must be explained by errors in the electron distribution, not just differing bond lengths and reinforcing the fact that different properties are predicted with different accuracies with computational approximations. Therefore, benchmark studies on methods regarding energetic and geometric properties do not guarantee strong performance for other properties.
Conflicts of interest
There are no conflicts to declare.Appendices
Appendix: Experimental versus calculated equilibrium bond length Re, harmonic vibrational frequency ωe and electric dipole moment μ
Table 3 lists the experimental electric dipole moments employed in this work, including the pertinent references. Similarly, it includes the calculated dipole moments employing different basis sets.| Molecule | State | Exp. | μ e (cc-pwCVTZ) | μ 0 (cc-pwCVTZ) | μ e (cc-pwCVQZ) | μ 0 (cc-pwCVQZ) | μ e (aug-cc-pwCVTZ) | μ 0 (aug-cc-pwCVTZ) | μ e (aug-cc-pwCVQZ) | μ 0 (aug-cc-pwCVQZ) | μ e [CBS(aug-cc-pwCVT/QZ)] | μ 0 [CBS(aug-cc-pwCVT/QZ)] | μ e (def2-QZVPP) | μ 0 (def2-QZVPP) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AgBr | X1Σ+ | 5.62(3)64 | 5.574 | 5.594 | 5.473 | 5.493 | 5.509 | 5.530 | 5.548 | 5.569 | 5.631 | 5.652 | ||
| AgF | X1Σ+ | 6.22(20)65 | 5.767 | 5.803 | 5.877 | 5.916 | 5.935 | 5.977 | 5.922 | 5.964 | 5.927 | 5.969 | 5.898 | 5.940 |
| AgI | X1Σ+ | 4.55(5)66 | 5.161 | 5.178 | 5.191 | 5.208 | 5.015 | 5.030 | 5.082 | 5.098 | 5.145 | 5.161 | 5.144 | 5.160 |
| AlF | X1Σ+ | 1.515(4)67 | 1.343 | 1.401 | 1.423 | 1.484 | 1.496 | 1.560 | 1.476 | 1.540 | 1.471 | 1.535 | 1.478 | 1.540 |
| BrO | X2Π3/2 | 1.76(4)68 | 1.690 | 1.673 | 1.710 | 1.693 | 1.747 | 1.734 | 1.729 | 1.737 | 1.717 | 1.728 | 1.727 | 1.709 |
| CF | X2Π | 0.65(5)68 | 0.700 | 0.635 | 0.687 | 0.619 | 0.662 | 0.591 | 0.680 | 0.611 | 0.685 | 0.613 | 0.694 | 0.625 |
| CN | X2Σ+ | 1.45(8)69 | 1.362 | 1.335 | 1.415 | 1.390 | 1.413 | 1.387 | 1.431 | 1.407 | 1.444 | 1.421 | 1.426 | 1.407 |
| CO | X1Σ+ | 0.112(5)70 | 0.143 | 0.121 | 0.127 | 0.104 | 0.114 | 0.090 | 0.119 | 0.094 | 0.129 | 0.104 | 0.123 | 0.144 |
| CS | X1Σ+ | 1.958(5)71 | 1.983 | 1.954 | 1.972 | 1.943 | 1.961 | 1.932 | 1.960 | 1.932 | ||||
| CSe | X1Σ+ | 1.99(4)72 | 2.146 | 2.123 | 2.165 | 2.142 | 2.186 | 2.163 | 2.171 | 2.147 | 2.155 | 2.131 | 2.140 | 2.116 |
| CuF | X1Σ+ | 5.26(2)73 | 5.144 | 5.180 | 5.256 | 5.294 | 5.561 | 5.603 | 5.524 | 5.566 | 5.513 | 5.555 | 5.446 | 5.488 |
| GaF | X1Σ+ | 2.45(5)74 | 2.176 | 2.235 | 2.318 | 2.381 | 2.431 | 2.498 | 2.417 | 2.483 | 2.416 | 2.482 | 2.230 | 2.295 |
| GeO | X1Σ+ | 3.2824(1)75 | 3.012 | 3.028 | 3.202 | 3.220 | 3.295 | 3.315 | 3.303 | 3.323 | 3.314 | 3.334 | 3.198 | 3.217 |
| GeS | X1Σ+ | 2.00(6)76 | 1.952 | 1.969 | 2.056 | 2.074 | 2.057 | 2.076 | 2.084 | 2.103 | 2.114 | 2.133 | 1.981 | 1.999 |
| GeTe | X1Σ+ | 1.06(7)77 | 1.063 | 1.073 | 1.140 | 1.151 | 1.086 | 1.096 | 1.146 | 1.157 | 1.192 | 1.204 | 0.995 | 1.006 |
| HfO | X1Σ+ | 3.431(5)78 | 3.258 | 3.280 | 3.330 | 3.352 | 3.396 | 3.420 | 3.381 | 3.405 | 3.376 | 3.400 | 3.473 | 3.496 |
| IBr | X1Σ+ | 0.726(3)79 | 0.687 | 0.811 | 0.647 | 0.651 | 0.630 | 0.634 | 0.624 | 0.628 | 0.685 | 0.688 | ||
| InCl | X1Σ+ | 3.79(19)79 | 3.465 | 3.518 | 3.581 | 3.637 | 3.672 | 3.728 | 3.650 | 3.707 | 3.646 | 3.703 | 3.497 | 3.555 |
| InF | X1Σ+ | 3.40(7)74 | 3.066 | 3.124 | 3.227 | 3.288 | 3.378 | 3.445 | 3.358 | 3.425 | 3.358 | 3.424 | 3.219 | 3.285 |
| NO | X2Π1/2 | 0.1595(15)80 | 0.126 | 0.115 | 0.135 | 0.121 | 0.144 | 0.132 | 0.149 | 0.134 | 0.156 | 0.139 | 0.143 | 0.128 |
| PN | X1Σ+ | 2.7514(6)81 | 2.634 | 2.626 | 2.722 | 2.715 | 2.758 | 2.751 | 2.771 | 2.764 | 2.780 | 2.773 | 2.757 | 2.750 |
| PO | X2Π | 1.88(7)82 | 1.946 | 1.959 | 1.966 | 1.983 | 1.962 | 1.978 | 1.958 | 1.976 | 1.959 | 1.979 | 1.984 | 2.001 |
| PbO | X1Σ+ | 4.64(30)76 | 3.990 | 4.004 | 4.289 | 4.305 | 4.470 | 4.489 | 4.467 | 4.486 | 4.471 | 4.490 | 4.373 | 4.389 |
| PbS | X1Σ+ | 3.59(10)76 | 3.614 | 3.629 | 3.780 | 3.796 | 3.833 | 3.849 | 3.849 | 3.866 | 3.872 | 3.889 | 3.792 | 3.809 |
| SO | X 3Σ− | 1.55(2)83 | 1.566 | 1.566 | 1.564 | 1.568 | 1.574 | 1.581 | 1.559 | 1.566 | 1.552 | 1.559 | 1.578 | 1.584 |
| ScO | X2Σ+ | 4.55(8)84 | 3.419 | 3.567 | 3.727 | 3.685 | 3.793 | 3.779 | 3.721 | 3.748 | 3.713 | 3.721 | 3.788 | 3.809 |
| SiO | X1Σ+ | 3.0982(10)75 | 2.871 | 2.886 | 3.025 | 3.041 | 3.099 | 3.118 | 3.106 | 3.125 | 3.114 | 3.133 | 3.082 | 3.100 |
| SiS | X1Σ+ | 1.73(6)85 | 1.608 | 1.626 | 1.681 | 1.701 | 1.683 | 1.703 | 1.699 | 1.720 | 1.723 | 1.744 | 1.695 | 1.716 |
| SnO | X1Σ+ | 4.32(10)76 | 3.675 | 3.688 | 3.939 | 3.955 | 4.079 | 4.097 | 4.085 | 4.103 | 4.098 | 4.116 | 3.995 | 4.011 |
| SnS | X1Σ+ | 3.18(10)76 | 2.974 | 2.990 | 3.125 | 3.142 | 3.153 | 3.170 | 3.180 | 3.197 | 3.210 | 3.227 | 3.125 | 3.143 |
| YF | X1Σ+ | 1.82(8)86 | 1.711 | 1.749 | 1.800 | 1.840 | 1.848 | 1.890 | 1.848 | 1.890 | 1.853 | 1.895 | 1.830 | 1.871 |
| ZrO | X1Σ+ | 2.551(11)78 | 2.370 | 2.395 | 2.445 | 2.471 | 2.521 | 2.549 | 2.502 | 2.530 | 2.500 | 2.530 | 2.478 | 2.505 |
Table 4 lists the experimental and calculated equilibrium bond length Re and harmonic vibrational frequency ωe, employing different basis sets.
| Molecule | State | R e (Exp.) | R e (aug-cc-pwCVTZ) | R e (aug-cc-pwCVQZ) | R e (def2-QZVPP) | ω e (Exp.) | ω e (aug-cc-pwCVTZ) | ω e (aug-cc-pwCVQZ) | ω e [CBS(aug-cc-pwCVT/QZ)] | ω e (def2-QZVPP) |
|---|---|---|---|---|---|---|---|---|---|---|
| AgBr | X1Σ+ | 2.393 | 2.394 | 2.387 | 2.397 | 247.7 | 246.4 | 248.6 | 250.2 | 246.9 |
| AgF | X1Σ+ | 1.983 | 1.982 | 1.979 | 1.982 | 513.5 | 512.0 | 515.7 | 518.1 | 515.0 |
| AgI | X1Σ+ | 2.545 | 2.542 | 2.536 | 2.541 | 206.5 | 208.9 | 209.7 | 210.2 | 210.1 |
| AlF | X1Σ+ | 1.654 | 1.660 | 1.656 | 1.660 | 802.3 | 793.9 | 801.5 | 804.9 | 804.1 |
| BrO | X2Π3/2 | 1.717 | 1.728 | 1.726 | 1.714 | 778.7 | 767.5 | 762.8 | 631.2 | 743.0 |
| CF | X2Π | 1.272 | 1.277 | 1.273 | 1.272 | 1308.1 | 1304.5 | 1299.7 | 1269.4 | 1307.2 |
| CN | X2Σ+ | 1.172 | 1.170 | 1.167 | 1.168 | 2068.6 | 2160.4 | 2175.5 | 2181.2 | 2108.1 |
| CO | X1Σ+ | 1.128 | 1.132 | 1.129 | 1.129 | 2169.8 | 2153.4 | 2170.3 | 2177.5 | 2174.4 |
| CS | X1Σ+ | 1.535 | 1.539 | 1.536 | 1.537 | 1285.1 | 1279.1 | 1288.5 | 1293.7 | 1292.9 |
| CSe | X1Σ+ | 1.676 | 1.678 | 1.674 | 1.678 | 1035.4 | 1033.1 | 1041.4 | 1045.8 | 1052.4 |
| CuF | X1Σ+ | 1.745 | 1.773 | 1.769 | 1.756 | 622.7 | 595.3 | 599.7 | 603.3 | 605.6 |
| GaF | X1Σ+ | 1.774 | 1.778 | 1.775 | 1.769 | 622.2 | 615.4 | 621.0 | 623.7 | 634.7 |
| GeO | X1Σ+ | 1.625 | 1.627 | 1.623 | 1.626 | 985.5 | 979.8 | 989.0 | 994.9 | 997.7 |
| GeS | X1Σ+ | 2.012 | 2.019 | 2.012 | 2.013 | 575.8 | 571.1 | 577.1 | 581.3 | 584.2 |
| GeTe | X1Σ+ | 2.340 | 2.343 | 2.335 | 2.332 | 323.9 | 322.7 | 326.1 | 328.7 | 331.7 |
| HfO | X1Σ+ | 1.723 | 1.719 | 1.715 | 1.735 | 974.1 | 970.1 | 976.0 | 980.7 | 952.5 |
| IBr | X1Σ+ | 2.469 | 2.478 | 2.464 | 2.463 | 268.6 | 269.2 | 276.1 | 279.5 | 279.7 |
| InCl | X1Σ+ | 2.401 | 2.413 | 2.404 | 2.392 | 317.4 | 313.6 | 316.4 | 318.6 | 319.2 |
| InF | X1Σ+ | 1.985 | 1.988 | 1.984 | 1.974 | 535.4 | 530.1 | 534.5 | 536.3 | 549.9 |
| NO | X2Π1/2 | 1.151 | 1.152 | 1.149 | 1.148 | 1904.2 | 1883.7 | 1912.5 | 1928.7 | 1927.6 |
| PN | X1Σ+ | 1.491 | 1.496 | 1.491 | 1.493 | 1337.2 | 1332.5 | 1345.6 | 1352.8 | 1346.4 |
| PO | X2Π | 1.476 | 1.482 | 1.477 | 1.479 | 1233.3 | 1232.0 | 1242.9 | 1250.8 | 1243.7 |
| PbO | X1Σ+ | 1.922 | 1.924 | 1.919 | 1.922 | 721.0 | 732.8 | 739.9 | 745.1 | 746.1 |
| PbS | X1Σ+ | 2.287 | 2.297 | 2.288 | 2.286 | 429.4 | 433.2 | 439.9 | 444.6 | 445.3 |
| SO | X3Σ− | 1.481 | 1.486 | 1.481 | 1.482 | 1149.2 | 1152.9 | 1161.3 | 1167.7 | 1162.7 |
| ScO | X2Σ+ | 1.668 | 1.674 | 1.663 | 1.670 | 965.0 | 968.6 | 979.6 | 936.3 | 932.9 |
| SiO | X1Σ+ | 1.510 | 1.515 | 1.511 | 1.514 | 1241.6 | 1231.6 | 1242.3 | 1248.6 | 1241.0 |
| SiS | X1Σ+ | 1.929 | 1.939 | 1.931 | 1.933 | 749.6 | 741.1 | 752.6 | 759.2 | 753.1 |
| SnO | X1Σ+ | 1.833 | 1.832 | 1.827 | 1.826 | 814.6 | 821.6 | 829.9 | 835.6 | 842.3 |
| SnS | X1Σ+ | 2.209 | 2.215 | 2.206 | 2.204 | 487.3 | 484.2 | 491.4 | 496.5 | 492.9 |
| YF | X1Σ+ | 1.926 | 1.935 | 1.930 | 1.936 | 631.3 | 628.9 | 634.4 | 637.7 | 629.2 |
| ZrO | X1Σ+ | 1.712 | 1.719 | 1.714 | 1.715 | 969.8 | 977.9 | 981.4 | 981.6 | 979.8 |
Acknowledgements
The authors thank Dr Adam Wasserman and Yuming Shi for their insight and suggestions on this work and Dr Stefan Truppe for fruitful discussions. X. Liu acknowledges the support of the Deutsche Forschungsgemeinschaft (DFG – German Research Foundation) under grant number PE 3477/2 – 493725479, and J. P.-R. thanks the Simons Foundations for support.References
- Z. Fang, M. Vasiliu, K. A. Peterson and D. A. Dixon, J. Chem. Theory Comput., 2017, 13, 1057–1066 CrossRef CAS PubMed.
- T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- C. J. Barden, J. C. Rienstra-Kiracofe and H. F. Schaefer III, J. Chem. Phys., 2000, 113, 690–700 CrossRef CAS.
- S. Yanagisawa, T. Tsuneda and K. Hirao, J. Chem. Phys., 2000, 112, 545–553 CrossRef CAS.
- G. L. Gutsev and C. W. Bauschlicher, J. Phys. Chem. A, 2003, 107, 4755–4767 CrossRef CAS.
- N. E. Schultz, Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2005, 109, 4388–4403 CrossRef CAS PubMed.
- F. Furche and J. P. Perdew, J. Chem. Phys., 2006, 124, 044103 CrossRef PubMed.
- M. Bühl and H. Kabrede, J. Chem. Theory Comput., 2006, 2, 1282–1290 CrossRef PubMed.
- K. P. Jensen, B. O. Roos and U. Ryde, J. Chem. Phys., 2007, 126, 014103 CrossRef PubMed.
- E. Goll, H. Stoll, C. Thierfelder and P. Schwerdtfeger, Phys. Rev. A: At., Mol., Opt. Phys., 2007, 76, 032507 CrossRef.
- C. J. Cramer and D. G. Truhlar, Phys. Chem. Chem. Phys., 2009, 11, 10757–10816 RSC.
- A. Sorkin, D. G. Truhlar and E. A. Amin, J. Chem. Theory Comput., 2009, 5, 1254–1265 CrossRef CAS.
- W. Jiang, N. J. DeYonker, J. J. Determan and A. K. Wilson, J. Phys. Chem. A, 2012, 116, 870–885 CrossRef CAS PubMed.
- W. Zhang, D. G. Truhlar and M. Tang, J. Chem. Theory Comput., 2013, 9, 3965–3977 CrossRef CAS PubMed.
- X. Xu, W. Zhang, M. Tang and D. G. Truhlar, J. Chem. Theory Comput., 2015, 11, 2036–2052 CrossRef CAS PubMed.
- L. Cheng, J. Gauss, B. Ruscic, P. B. Armentrout and J. F. Stanton, J. Chem. Theory Comput., 2017, 13, 1044–1056 CrossRef CAS PubMed.
- L. W. Bertels, J. Lee and M. Head-Gordon, J. Chem. Theory Comput., 2021, 17, 742–755 CrossRef CAS PubMed.
- D. Hait and M. Head-Gordon, J. Chem. Theory Comput., 2018, 14, 1969–1981 CrossRef CAS PubMed.
- D. Hait and M. Head-Gordon, J. Chem. Phys., 2018, 148, 171102 CrossRef PubMed.
- A. I. Johnson, K. P. Withanage, K. Sharkas, Y. Yamamoto, T. Baruah, R. R. Zope, J. E. Peralta and K. A. Jackson, J. Chem. Phys., 2019, 151, 174106 CrossRef PubMed.
- R. Grotjahn, G. J. Lauter, M. Haasler and M. Kaupp, J. Phys. Chem. A, 2020, 124, 8346–8358 CrossRef CAS PubMed.
- J. C. Zapata and L. K. McKemmish, J. Phys. Chem. A, 2020, 124, 7538–7548 CrossRef CAS PubMed.
- D. Hait, Y. H. Liang and M. Head-Gordon, J. Chem. Phys., 2021, 154, 074109 CrossRef CAS PubMed.
- Z. W. Seh, J. Kibsgaard, C. F. Dickens, I. Chorkendorff, J. K. Nørskov and T. F. Jaramillo, Science, 2017, 355, eaad4998 CrossRef PubMed.
- F. Calle-Vallejo, J. Tymoczko, V. Colic, Q. H. Vu, M. D. Pohl, K. Morgenstern, D. Loffreda, P. Sautet, W. Schuhmann and A. S. Bandarenka, Science, 2015, 350, 185–189 CrossRef CAS PubMed.
- W. Wang, X. Liu and J. Pérez-Ros, J. Phys. Chem. A, 2021, 125, 5670–5680 CrossRef CAS PubMed.
- J. T. Margraf, A. Perera, J. J. Lutz and R. J. Bartlett, J. Chem. Phys., 2017, 147, 184101 CrossRef PubMed.
- A. Halkier, H. Larsen, J. Olsen, P. Jo/rgensen and J. Gauss, J. Chem. Phys., 1999, 110, 734–740 CrossRef.
- X. Liu, G. Meijer and J. Pérez-Ríos, Phys. Chem. Chem. Phys., 2020, 22, 24191–24200 RSC.
- J. F. Stanton, J. Gauss, L. Cheng, M. E. Harding, D. A. Matthews and P. G. Szalay, CFOUR, Coupled-Cluster techniques for Computational Chemistry, a quantum-chemical program package, With contributions from A. Asthana, A. A. Auer, R. J. Bartlett, U. Benedikt, C. Berger, D. E. Bernholdt, S. Blaschke, Y. J. Bomble, S. Burger, O. Christiansen, D. Datta, F. Engel, R. Faber, J. Greiner, M. Heckert, O. Heun, M. Hilgenberg, C. Huber, T.-C. Jagau, D. Jonsson, J. Jusélius, T. Kirsch, M.-P. Kitsaras, K. Klein, G. M. Kopper, W. J. Lauderdale, F. Lipparini, J. Liu, T. Metzroth, L. A. Mück, D. P. O'Neill, T. Nottoli, J. Oswald, D. R. Price, E. Prochnow, C. Puzzarini, K. Ruud, F. Schiffmann, W. Schwalbach, C. Simmons, S. Stopkowicz, A. Tajti, J. Vázquez, F. Wang, J. D. Watts, C. Zhang, X. Zheng, and the integral packages MOLECULE (J. Almlöf and P. R. Taylor), PROPS (P. R. Taylor), ABACUS (T. Helgaker, H. J. Aa. Jensen, P. Jørgensen, and J. Olsen), and ECP routines by A. V. Mitin and C. van Wüllen. For the current version, see https://www.cfour.de.
- N. B. Balabanov and K. A. Peterson, J. Chem. Phys., 2005, 123, 064107 CrossRef PubMed.
- R. A. Kendall, T. H. Dunning Jr and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- K. A. Peterson and T. H. Dunning Jr, J. Chem. Phys., 2002, 117, 10548–10560 CrossRef CAS.
- A. K. Wilson, D. E. Woon, K. A. Peterson and T. H. Dunning Jr, J. Chem. Phys., 1999, 110, 7667–7676 CrossRef CAS.
- D. E. Woon and T. H. Dunning Jr, J. Chem. Phys., 1993, 98, 1358–1371 CrossRef CAS.
- D. Figgen, G. Rauhut, M. Dolg and H. Stoll, Chem. Phys., 2005, 311, 227–244 CrossRef CAS.
- D. Figgen, K. A. Peterson, M. Dolg and H. Stoll, J. Chem. Phys., 2009, 130, 164108 CrossRef PubMed.
- B. Metz, H. Stoll and M. Dolg, J. Chem. Phys., 2000, 113, 2563–2569 CrossRef CAS.
- K. A. Peterson, J. Chem. Phys., 2003, 119, 11099–11112 CrossRef CAS.
- K. A. Peterson, D. Figgen, E. Goll, H. Stoll and M. Dolg, J. Chem. Phys., 2003, 119, 11113–11123 CrossRef CAS.
- K. A. Peterson, B. C. Shepler, D. Figgen and H. Stoll, J. Phys. Chem. A, 2006, 110, 13877–13883 CrossRef CAS PubMed.
- K. A. Peterson, D. Figgen, M. Dolg and H. Stoll, J. Chem. Phys., 2007, 126, 124101 CrossRef PubMed.
- K. A. Peterson and K. E. Yousaf, J. Chem. Phys., 2010, 133, 174116 CrossRef PubMed.
- D. Feller, J. Comput. Chem., 1996, 17, 1571–1586 CrossRef CAS.
- K. L. Schuchardt, B. T. Didier, T. Elsethagen, L. Sun, V. Gurumoorthi, J. Chase, J. Li and T. L. Windus, J. Chem. Inf. Model., 2007, 47, 1045–1052 CrossRef CAS PubMed.
- B. P. Pritchard, D. Altarawy, B. Didier, T. D. Gibson and T. L. Windus, J. Chem. Inf. Model., 2019, 59, 4814–4820 CrossRef CAS PubMed.
- F. Weigend, F. Furche and R. Ahlrichs, J. Chem. Phys., 2003, 119, 12753–12762 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- D. Rappoport and F. Furche, J. Chem. Phys., 2010, 133, 134105 CrossRef PubMed.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, et al., MOLPRO, version 2019.2, a package of ab initio programs, 2019, see https://www.molpro.net Search PubMed.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253 CAS.
- A. Halkier, W. Klopper, T. Helgaker and P. Jorgensen, J. Chem. Phys., 1999, 111, 4424–4430 CrossRef CAS.
- F. Neese and E. F. Valeev, J. Chem. Theory Comput., 2011, 7, 33–43 CrossRef CAS PubMed.
- F. Weigend, A. Köhn and C. Hättig, J. Chem. Phys., 2002, 116, 3175–3183 CrossRef CAS.
- Y. A. Aoto, A. P. de Lima Batista, A. Kohn and A. G. de Oliveira-Filho, J. Chem. Theory Comput., 2017, 13, 5291–5316 CrossRef CAS PubMed.
- W. A. De Jong, R. J. Harrison and D. A. Dixon, J. Chem. Phys., 2001, 114, 48–53 CrossRef CAS.
- D. P. Tew, W. Klopper, M. Heckert and J. Gauss, J. Phys. Chem. A, 2007, 111, 11242–11248 CrossRef CAS PubMed.
- D. M. Bishop, Rev. Mod. Phys., 1990, 62, 343 CrossRef CAS.
- M. Brieger, Chem. Phys., 1984, 89, 275–295 CrossRef CAS.
- A. M. Teale, O. B. Lutnæs, T. Helgaker, D. J. Tozer and J. Gauss, J. Chem. Phys., 2013, 138, 024111 CrossRef PubMed.
- V. E. Ingamells, M. G. Papadopoulos and S. G. Raptis, Chem. Phys. Lett., 1999, 307, 484–492 CrossRef CAS.
- A. Halkier, H. Koch, O. Christiansen, P. Jørgensen and T. Helgaker, J. Chem. Phys., 1997, 107, 849–866 CrossRef CAS.
- E. Miliordos and A. Mavridis, J. Phys. Chem. A, 2010, 114, 8536–8572 CrossRef CAS PubMed.
- K. Nair and J. Hoeft, Chem. Phys. Lett., 1983, 102, 438–439 CrossRef CAS.
- J. Hoeft, F. Lovas, E. Tiemann and T. Törring, Zeitschrift für Naturforschung A, 1970, 25, 35–39 CrossRef CAS.
- K. Nair and J. Hoeft, Phys. Rev. A: At., Mol., Opt. Phys., 1984, 29, 1889 CrossRef CAS.
- S. Truppe, S. Marx, S. Kray, M. Doppelbauer, S. Hofsäss, H. C. Schewe, N. Walter, J. Pérez-Ros, B. G. Sartakov and G. Meijer, Phys. Rev. A, 2019, 100, 052513 CrossRef CAS.
- C. Byfleet, A. Carrington and D. Russell, Mol. Phys., 1971, 20, 271–277 CrossRef CAS.
- R. Thomson and F. Dalby, Can. J. Phys., 1968, 46, 2815–2819 CrossRef CAS.
- C. A. Burrus, J. Chem. Phys., 1958, 28, 427–429 CrossRef CAS.
- G. Winnewisser and R. L. Cook, J. Mol. Spectrosc., 1968, 28, 266–268 CrossRef CAS.
- J. McGurk, H. Tigelaar, S. Rock, C. Norris and W. Flygare, J. Chem. Phys., 1973, 58, 1420–1424 CrossRef CAS.
- F. Wang and T. C. Steimle, J. Chem. Phys., 2010, 132, 054301 CrossRef PubMed.
- J. Hoeft, F. Lovas, E. Tiemann and T. Törring, Zeitschrift für Naturforschung A, 1970, 25, 1029–1035 CrossRef CAS.
- J. W. Raymonda, J. S. Muenter and W. A. Klemperer, J. Chem. Phys., 1970, 52, 3458–3461 CrossRef CAS.
- J. Hoeft, F. Lovas, E. Tiemann, R. Tischer and T. Törring, Zeitschrift für Naturforschung A, 1969, 24, 1217–1221 CrossRef CAS.
- J. Hoeft, F. Lovas, E. Tiemann and T. TöING, Zeitschrift Naturforschung Teil A, 1970, 25, 539 CAS.
- R. Suenram, F. Lovas, G. Fraser and K. Matsumura, J. Chem. Phys., 1990, 92, 4724–4733 CrossRef CAS.
- W. M. Haynes, CRC handbook of chemistry and physics, CRC press, 2014 Search PubMed.
- Y. Liu, Y. Guo, J. Lin, G. Huang, C. Duan and F. Li, Mol. Phys., 2001, 99, 1457–1461 CrossRef CAS.
- F. Wyse, E. Manson and W. Gordy, J. Chem. Phys., 1972, 57, 1106–1108 CrossRef CAS.
- H. Kanata, S. Yamamoto and S. Saito, J. Mol. Spectrosc., 1988, 131, 89–95 CrossRef CAS.
- F. Powell and D. R. Lide Jr, J. Chem. Phys., 1964, 41, 1413–1419 CrossRef CAS.
- J. Shirley, C. Scurlock and T. Steimle, J. Chem. Phys., 1990, 93, 1568–1575 CrossRef CAS.
- J. Hoeft, F. Lovas and T. Törring, Zeitschrift für Naturforschung A, 1969, 24, 1422–1423 CrossRef CAS.
- J. Shirley, C. Scurlock, T. Steimle, B. Simard, M. Vasseur and P. Hackett, J. Chem. Phys., 1990, 93, 8580–8585 CrossRef CAS.
- C. Koukounas and A. Mavridis, J. Phys. Chem. A, 2008, 112, 11235–11250 CrossRef CAS PubMed.
- A. Avramopoulos, V. E. Ingamells, M. G. Papadopoulos and A. J. Sadlej, J. Chem. Phys., 2001, 114, 198–210 CrossRef CAS.
- E. Goll, H. Stoll, C. Thierfelder and P. Schwerdtfeger, Phys. Rev. A: At., Mol., Opt. Phys., 2007, 76, 032507 CrossRef.
- J. Hoeft and K. Nair, J. Mol. Struct., 1983, 97, 347–350 CrossRef CAS.
- K. P. Huber and G. Herzberg, Molecular Spectra and Molecular Structure, Springer-Verlag, Berlin, Germany, 1979 Search PubMed.
- B. M. Smirnov, Reference Data on Atomic Physics and Atomic Processes, Springer-Verlag, Berlin, Germany, 2008 Search PubMed.
Footnotes |
| † In particular, we use the points −0.4x, −0.35x, −0.3x, −0.24x, −0.18x, −0.12x, −0.08x, −0.04x, −0.02x, 0, 0.02x, 0.04x, 0.08x, 0.12x, 0.2x, 0.28x, 0.36x, 0.45x, 0.5x, 0.6x, 0.8x, 1.0x, 1.5x, 2.0x, 3.0x, where x = Re(Exp). |
| ‡ We use 200 DVR points to guarantee convergence on the vibrational energies better than 0.1%. |
| This journal is © the Owner Societies 2023 |