 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
First principles study of layered scandium disulfide for use as Li-ion and beyond-Li-ion batteries†
Conor Jason
Price
 *,
Joe
Pitfield
*,
Joe
Pitfield
 ,
Edward Allery David
Baker
,
Edward Allery David
Baker
 and
Steven Paul
Hepplestone
and
Steven Paul
Hepplestone
 *
*
Department of Physics, University of Exeter, Stocker Road, Exeter, EX4 4QL, UK. E-mail: cjp225@exeter.ac.uk; S.P.Hepplestone@exeter.ac.uk
First published on 3rd January 2023
Abstract
The growing demand for high efficiency portable batteries has prompted a deeper exploration for alternative cathode materials. Due to low Earth abundance, scandium has not received much attention, however its low atomic mass makes it ideal for high gravimetric capacity electrodes. Here we have performed a comprehensive first-principles study to assess the performance of layered ScS2 as a potential cathode for lithium-ion and beyond-lithium-ion batteries. We have explored the configuration space of ScS2 and its intercalated compounds using a mix of machine learning and ab initio techniques, finding the ground state geometry to be layered in nature. This layered structure is found to have a high voltage, reaching above 4.5 V for Group I intercalants, ideal volume expansions below 10% for lithium and magnesium intercalation, is electronically conductive, and is ductile once intercalated. Of the intercalants considered, we find that lithium is the best choice for cathode applications, for which we have used a combination of thermodynamic phase diagrams, ab intio phonon calculations, and evaluation of the elastic tensor to conclude that ScS2 possesses a reversible capacity of 182.99 mA h g−1, on par with current state of the art cathode materials such as LiCoO2, NMC, and NCA. Finally, we substitute foreign metal species into the ScS2 material to determine their effect on key cathode properties, but find that these are overall detrimental to the performance of ScS2. This does, however, highlight the potential for improvement if scandium were mixed into other layered systems such as the layered transition metal oxides.
1 Introduction
As the demand for rechargeable batteries rises, the need for both better and a wider range of cathode materials rises with it. Whereas for anodes there are a wealth of materials available and the key challenge is competing with the abundance of hard carbons, for cathodes the range of materials is much lower with leading contenders being the phosphates,1–3 the ubiquitous NMC and its variants,4–9 and spinel oxides such as LiMn2O4.10–13There has been some interest in the use of other intercalant species14 due to the safety issues associated with lithium, its high cost of production, and the rising concern for the sustainability of lithium deposits. Other Group I elements15–17 offer the same chemistry as lithium and so there is hope they would be able to match the performance of lithium. Alternatively, Group II elements have also been considered18–20 as they possess two valence electrons and so the available charge transfer (and hence electrode energy storage) should in principle be twice that of the Group I elements.
For intercalation electrodes, layered materials such as the TMDCs,21–23 NMC,5,24 and the MXenes25 are highly attractive as their van der Waals gaps allow for low diffusion barriers and hence fast intercalant transport. Recent works have started to note the potential of scandium, where the doping of metal oxides with scandium has been shown to increase particle size without affecting the crystal structure,26 provide a comparable capacity whilst improve cycling stability,26,27 and significantly lower the surface energy of nanoparticles.28 With these clear structural and energetic improvements, as well as the fact that scandium is one of the lightest available metals, it raises the question as to how good scandium-based materials themselves would perform as electrode materials.
Transition metal oxides have been widely investigated and used for intercalation cathodes as they display high voltages and capacities. Lithium scandium dioxide (LiScO2) has been experimentally verified to exist in only one form, a fractional cationic ordered rock-salt structure, with the I41/amd space group.29,30 This is similar to the anatase structure of TiO2 but with lithium filling the voids. However, this material was found to have poor ionic conductivity, requiring substitutional doping with transition metals in place of the scandium atoms.30 This lack of ionic conductivity prevents its exploitation as a cathode material. Alternative, layered structures have therefore been considered,31,32 but are unfeasible as the structure is energetically unfavourable compared to the rock-salt phase.
Layered sulfides are closely related to the oxides, and have the added benefit of being compatible with sulfide-electrolytes. Sulfide electrolytes are chemically unstable with high-voltage oxides due to the difference in electronegativity of oxygen and sulfur.33 Thus, scandium-sulfide materials could offer the optimal properties for cathodes whilst allowing the use of sulfide-electrolytes. The bulk properties of the TMDC T- and H-phases of ScS2 have been shown to be conducting,34 however, the monolayer form of the H-phase is insulating.34–36 For intercalation electrodes, the intercalated form of ScS2 is of interest. LiScS2, NaScS2, and KScS2 have all been synthesised,37,38 and were found to have the layered α-NaFeO2 structure with space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) M. Unfortunately, theoretical investigations of this structure have been limited to monolayers,39,40 though these have suggested high capacities of over 400 mA h g−1 with lithium intercalation. However, monolayers are significantly more difficult to synthesise compared to their bulk counterpart, and do not provide an accurate representation of the dimensions of electrodes being utilised in functional devices. To the best of our knowledge there are currently no studies investigating the potential of bulk ScS2 for electrodes, and so the questions of how well the bulk material would perform as an intercalation electrode remains.
M. Unfortunately, theoretical investigations of this structure have been limited to monolayers,39,40 though these have suggested high capacities of over 400 mA h g−1 with lithium intercalation. However, monolayers are significantly more difficult to synthesise compared to their bulk counterpart, and do not provide an accurate representation of the dimensions of electrodes being utilised in functional devices. To the best of our knowledge there are currently no studies investigating the potential of bulk ScS2 for electrodes, and so the questions of how well the bulk material would perform as an intercalation electrode remains.
In this work we explore the potential of intercalated ScS2 compounds as a cathode material for lithium, sodium, potassium, and magnesium batteries using a range of theoretical techniques built upon first principles calculations. We explore the phase space of these materials to determine the lowest energy structures, determine the relevant properties for cathode performance, and evaluate their dynamic and thermodynamic stabilities to obtain a reversible intercalation capacity. Finally, we consider how the substitution of other metallic species in place of scandium affects these key properties for electrode applications.
2 Methods
2.1 First-principles methods
In this work, first principles techniques based on density functional theory were used to determine structural and energetic properties of layered scandium disulfide (ScS2) intercalated with varying levels of lithium, sodium, potassium, and magnesium. These calculations were done using the Vienna Ab initio Simulation Package (VASP).41–44 The valence electrons included for each species were Sc 3d2 4s1, S 3s2 3p4, Li 1s2 2s1, Na 2p6 3s1, K 3p6 4s1, and Mg 2p6 3s2. All other electrons were effectively contained within the used pseudopotentials. The projector augmented wave method45 was used to describe the interaction between core and valence electrons, and a plane-wave basis set was used with an energy cutoff of 700 eV. van der Waals interactions have been addressed using the zero damping DFT-D3 method of Grimme.46Three different phases of the ScS2 structure were considered: the T-phase, the Hc-phase,47,48 and the α-NaFeO2-like37,38 structure which is here referred to as the α-phase. The T- and α-phases have the same in-plane structure but differ in the relative stacking of layers, leading to the α-structure containing three ScS2 layers in the primitive unit cell, compared to the one in the primitive unit cell of T-ScS2. The Hc-phase has a different layer structure, and possesses two layers of ScS2 in its primitive unit cell. To consider intercalation with the different species, supercells of (2 × 2 × 2), (2 × 2 × 1), and (2 × 2 × 1) were used for the T-, Hc-, and α-phases, respectively. These supercells provided eight different intercalation sites for the T- and Hc-phases, and twelve sites for the α-phase. These allowed for various filling configurations, which were explored, the details are in the ESI† Section S1. Whilst other phases are possible for the TMDCs, such as 3R and distorted T structures, their intercalation environments are similar to that of the T-, Hc-phase, or α-phases, and so have not been explicitly considered here. It was found through two different methods (the details of which are presented in the ESI,† Section S1) that the favoured intercalation site in all three phases of ScS2 is the octahedrally-coordinated site. Consequently, this site has been used in the following study.
All structural relaxations were completed using the Perdew–Burke–Ernzerhof (PBE)49 functional form of the generalised gradient approximation (GGA), using the conjugate gradient algorithm and converged to a force tolerance of 0.01 eV per atom, while electronic self-consistency is considered to an accuracy of 10−7 eV. Of these, only the most energetically favourable structures at each level of lithium intercalation were considered. To account for the inaccurate calculation of exchange in GGA functionals, the HSE06 hybrid functional50–52 was also used for a selection of systems. Monkhorst-Pack grids53 of k-points equivalent to a 6 × 6 × 6 grid in the supercells are used throughout.
Phonon band structures were obtained using the frozen-phonon method employed with Phonopy.54 For these, the primitive unit cells of the pristine and intercalated structures were geometrically relaxed to a force tolerance of 0.0001 eV per atom, and electronic convergence of 10−8 eV. From these, the unique displacements were generated in supercells of 6 × 6 × 1. Elastic properties were determined using these primitive cell for the pristine and interalated T-phase ScS2. The elastic and internal strain tensors were computed from the second order derivatives of the total energy with respect to the position of the ions and changes to the size and shape of the unit cell, as employed in VASP. From the elastic tensor, various elastic moduli were computed, as outlined in the ESI† Section S2.
One possible method commonly used to modify the properties of electrodes is through the introduction of other elements, in particular substitution with transition metals55–57 or lithium.13 We consider the substitution of these metals in place of the scandium, which can be achieved through additional precursor materials. For low quantities of alternative metals this results in a substitutional doping,4 and for higher concentrations this results in metal mixing akin to how cobalt in lithium cobalt oxide is replaced with nickel and manganese in NMC. Seeing the effects of doping and metal mixing in other materials, it offers the natural question as to whether it can be employed to enhance the properties of ScS2. Here, we consider the metals Co, Cr, Fe, Hf, Mn, Nb, Ni, Sn, Ta, Ti, V, and Zr for this substitution, which were chosen to ensure a sufficient spread of species from across the transition metal block. We have also considered lithium as substitutions could occur during synthesis or cycling.
Due to the number of possible concentrations (and the configurations of each of those concentrations) available for metal mixing in the α-phase, we have limited this part of our study to the T-phase. Different concentrations of substitutions were considered, with all unique configurations being considered for each concentration of mixed metals. For Sc1−xMxS2, concentrations of 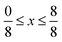 in increments of
in increments of  were considered, with
were considered, with 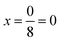 corresponding to the ScS2 composition and
corresponding to the ScS2 composition and  corresponding to the MS2 composition. The configurations of mixing used are equivalent to the different configurations used for lithium intercalation, with the same indexing being used for the metal species instead of the intercalated lithium. Once the Sc1−xMxS2 compound is synthesised, the metal species M becomes ‘locked’ in the host structure due to bonding with the sulfur atoms. It is thus more difficult for the metal species to reconfigure into a lower energy configuration than it would be for intercalated species such as lithium. As such, we consider a random configuration of metal mixing by taking the average of the different configurations considered.
corresponding to the MS2 composition. The configurations of mixing used are equivalent to the different configurations used for lithium intercalation, with the same indexing being used for the metal species instead of the intercalated lithium. Once the Sc1−xMxS2 compound is synthesised, the metal species M becomes ‘locked’ in the host structure due to bonding with the sulfur atoms. It is thus more difficult for the metal species to reconfigure into a lower energy configuration than it would be for intercalated species such as lithium. As such, we consider a random configuration of metal mixing by taking the average of the different configurations considered.
2.2 Methods for material evaluation
To compare ScS2 intercalated with different amounts of a metal (M = Li, Na, K, Mg), the voltage, V, can be calculated using,58,59 | (1) |
In some situations, however, taking the difference between two equivalent structures of different lithium contents does not always give the most accurate representation of what happens in reality. For example, intercalants have been found to cluster into domains for some materials rather than distributing evenly throughout the host.61,62 In these cases, it is more accurate to consider combinations of different lithium concentrations; for example, it might be favourable for lithium to fill one cell to LiScS2 and leave an adjacent cell empty, rather than filling a single cell to Li0.5ScS2. This would be indicative of clustering/domain separation, and so has been considered in the voltage calculation.
For the following discussion, we will use lithium (Li) as the stand-in for Group I intercalants, and magnesium (Mg) for Group II intercalants. The stability of TMDCs for lithium intercalation depends heavily on the formation of Li2S. Generally, when this compound forms the reaction becomes difficult to reverse due to the loss of the layered structure and the required separation of the lithium and sulfur. By assessing the relative stability of the Li2S phase against the intercalated structure, one can construct phase diagrams63 to indicate the thermodynamic stability of the intercalated structure at different intercalant concentrations. In terms of the chemical potential, we express this limit as,
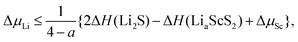 | (2) |
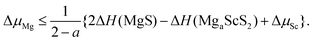 | (3) |
| ΔμLi,Mg,Sc,S ≤ 0, | (4) |
 | (5) |
3 Results
3.1 Determination of structure
We explore the phase space of LiScS2 using our random structure search RAFFLE, details of which are presented in the ESI,† Section S4. Of the over 800 structures generated and structurally relaxed, the 20 lowest-energy systems are presented in Fig. 1a Of these, the eight lowest-energy systems are are all T-phase structures with hexagonal symmetry, with the differences in energy arising from different coordination of the lithium with the ScS2 layers, relative shifts of the ScS2 layers, and small structural fluctuations arising from the tolerances of the search. These are indicated in Fig. 1b, where the structures with octahedrally-coordinated lithium are lower in energy23,60,62,64 than the equivalent systems with tetrahedrally-coordinated lithium due to the higher coordination between lithium and sulfur (see ESI,† Section S1). There is then a large jump of 42.1 meV per atom to the next group of structures, which have orthorhombic unit cells. As this energy exceeds typical values associated with thermal energy, it is safe to conclude that the layered structure will preferentially form.As the structure search shows that layered structures are the most favourable, we explicitly investigate them further. As with all partially heuristic methods of structure searching, the result is never guaranteed to be the true ground state. So, to ensure that we do not limit our investigation to the results of the random structure search, further layered polymorphs of intercalated ScS2 were also considered. Specifically, we focused on the TMDC 1T-phase (following the results of the random structure search), the TMDC 2Hc-phase, and the α-ScS2 phase (following experimental evidence37,38). The results of this are presented in Fig. 1c, where we show the energies (per formula unit) of each of the considered phases of LiaScS2. This allows for easy comparison of the different phases and indicates which phases are energetically preferred for different intercalation concentrations. For visual aid we have included a linear fit, which allows us to determine that the T-phase is the lowest in energy for low intercalant concentrations (a < 0.15 in LiaScS2), whereas for higher concentrations the α-phase is preferred. These two structures are presented in Fig. 1d, where the relative shift of the ScS2 layers can be seen. We see the same results for the other intercalant species, the results of which are presented in the ESI,† Section S5. Further discussion of how the functional choice, zero-point energy and finite temperature corrections affect this ordering are discussed in the ESI,† Section S6.
To further ensure we have not missed the preferred intercalation site we have also carried out NEB calculations with a lithium intercalant, further discussion of which are in ESI,† Section S1. The results of this are shown in Fig. 2, where we have considered diffusion between two equivalent octahedral sites (Route A), between adjacent octahedral and tetrahedral sites (Route B) and between two equivalent tetrahedral sites (Route C), and are shown in Fig. 2b for the T-phase and Fig. 2d for the α-phase. These results show that the most favourable intercalation site for each of the phases is the octahedral-coordination (O) site, which is the site of intercalation used throughout this work. This is in agreement with other TMDC investigations,23,60,62,64 as well as the results of the structure search. These NEB results also allow us to comment on the diffusion properties of intercalants in ScS2. As the rate of diffusion follows an Arrhenius equation, the height of the activation barriers is a key parameter for characterizing electrode materials. For both T- and α-phases we see that, whilst Route A offers the most direct path between two octahedral sites, diffusion along Route B has a lower activation energy. Route A in the T-phase demonstrates a barrier height of 0.58 eV, and 0.37 eV (0.12 eV) along Route B. These compare very well with the 0.67 eV and 0.34 eV see for lithium diffusion along monolayer T-ScS2.40 We see the same for the α-phase ScS2, though we do note significantly larger barriers of 1.87 eV along Route A and 1.55 eV (0.01 eV) along Route B. These larger barriers are partially caused by the particular methods used for generating these NEB barriers. However a more significant cause is due to the relative layer shift seen for the α-phase compared to the T-phase resulting in an ‘interlocking’ of layers, and hence a sulfur of one layer protrudes into the void space of the next. Thus we see a larger barrier to ionic movement.
We are also interested in the structure of ScS2 when the intercalants are removed, and so we have investigated a range of Sc–S stoichiometries to determine the stability of ScS2. As the data available within literature and on databases such as the ICSD and Materials Project65 for scandium-sulfide compounds is fairly limited, we have also used the structures of scandium-oxide analogues. The results of this are presented in ESI,† Section S7. For the composition ScS2, the layered T-structure is found to be the lowest in energy, though it lies 0.37 eV above the convex hull, and a mixture of Sc2S3 and S would be preferred.
3.2 Properties of ScS2 cathodes
 | ||
Fig. 3 (a) Resents the voltage profiles for α-ScS2 intercalated with Li, Na, K, and Mg. (b) Shows the percentage volume change  of T-ScS2 and α-ScS2 caused by intercalation. (c) Shows a schematic phase diagram, described by eqn (2)–(5). (d) Shows the resultant phase diagram for α-ScS2 intercalated with different concentrations of Li, and the inset presents the the values of EIS for α-ScS2 intercalated with each of the considered intercalants. of T-ScS2 and α-ScS2 caused by intercalation. (c) Shows a schematic phase diagram, described by eqn (2)–(5). (d) Shows the resultant phase diagram for α-ScS2 intercalated with different concentrations of Li, and the inset presents the the values of EIS for α-ScS2 intercalated with each of the considered intercalants. | ||
For magnesium intercalation the voltage behaviour is different from that of the Group I elements. The average voltage is 1.474 V for α-ScS2, but changes considerably by 2.5 V across the range. This is due to the double valency of magnesium allowing for two changes in oxidation state of the host material. This behaviour is also present in the T- and Hc-phases. All phases, when fully intercalated (a = 1), decrease to voltages below 0.6 V.
It is important to make a careful choice of exchange–correlation functional in first-principles calculations, as it can lead to discrepancies in the electronic structure66–68 and material energetics.69–71 We compare our PBE results with those obtained from the HSE06 functional for a limited number of cases (see ESI† Section S10) to determine the sensitivity of the results to functional choice. Using the hybrid functional we obtain higher voltages of 4.440 V (Li), 4.420 V (Na), 3.953 V (K), and 1.719 V (Mg). These are higher than the PBE voltages by 0.463 V, 0.546 V, 0.154 V, and 0.245 V, respectively. However, the voltage ordering is maintained and thus both functionals indicate that the ScS2 would be very suitable for a cathode material.
 , where V0 is the volume of the unintercalated bulk material. From the figure, we see that as the size of the intercalant is increased from Li to Na to K, the expansion increased by a larger percentage accordingly. For example, the volume change from intercalating with lithium to LiScS2 is 6.51%, which is comparable to the 8% observed for NMC.72 However, for NaScS2 the expansion exceeds 20%, and for KScS2 is exceeds 40%. Interestingly, intercalation with magnesium leads to a volume expansion of 7.53%, comparable to that arising from intercalation with lithium, which is due to the larger nuclear charge on the Mg resulting in a reduced ionic radius.
, where V0 is the volume of the unintercalated bulk material. From the figure, we see that as the size of the intercalant is increased from Li to Na to K, the expansion increased by a larger percentage accordingly. For example, the volume change from intercalating with lithium to LiScS2 is 6.51%, which is comparable to the 8% observed for NMC.72 However, for NaScS2 the expansion exceeds 20%, and for KScS2 is exceeds 40%. Interestingly, intercalation with magnesium leads to a volume expansion of 7.53%, comparable to that arising from intercalation with lithium, which is due to the larger nuclear charge on the Mg resulting in a reduced ionic radius.
The phase diagram for α-ScS2 intercalated with Li is presented in Fig. 3d, and the resultant values of EIS for each of the intercalants is presented in the inset. It is clear to see that, for the range of intercalation concentrations presented here, ScS2 has a sizeable window of stability with EIS values in excess of 3 eV. This means that ScS2 has a total capacity of 243.99 mA h g−1 (487.98 mA h g−1) at full intercalation for the Group I intercalants (Mg). For the Group I intercalants, EIS remains relatively unchanged with intercalant concentration.
The thermodynamic stability behaviour for magnesium intercalation is different from that of the Group I intercalants. It has very favourable energetics for low intercalation, but for higher concentrations EIS dramatically reduces. This arises from a significant upward shift of the phase boundary between ScS2 and MgaScS2, given by eqn (5). This behaviour is not dependent on the phase of the ScS2. This can be seen in the ESI,† Section S3, where equivalent phase diagrams for the intercalation stability of T-ScS2 and Hc-ScS2 are presented and similar trends are observed.
To further validate our approach, we have compared the HSE06 and PBE functionals for this system. We see the value of EIS using HSE06 is a more favourable than compared to PBE. This improvement to EIS arises from a downward shift of the horizontal line described by eqn (5), and very little change in the diagonal line described by eqn (2). We see that the stability trends hold for both functionals, and that the more accurate exchange is only important for the comparison between ScS2 and intercalated ScS2.
Our results show that LiScS2 is phonon stable, and at some point, as the concentration of lithium is decreased, the phonon-stability is lost. The evaluation of the phonon band structures for intermediate lithium concentrations allows us to determine the lowest concentration of lithium we can access before the intercalated layered structure becomes dynamically unstable. For the α-phase, the instability is also seen up to and including  . Similarly for T-ScS2,
. Similarly for T-ScS2, 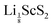 is unstable whereas
is unstable whereas  is not. We can therefore conclude that the lowest concentration of lithium that can be reached (corresponding to the depth of discharge and hence the maximum reversible capacity) in ScS2 lies in the range 0.125 < a < 0.25. Taking the range of intercalation to be 0.25 < a < 1, corresponding to 75% of the theoretical capacity, this gives a charge capacity of 182.99 mA h g−1, which is comparable to the ∼200 mA h g−1 of other materials.1–9 The 75% of the maximum capacity compares well with the 60–80% available in NMC materials.5
is not. We can therefore conclude that the lowest concentration of lithium that can be reached (corresponding to the depth of discharge and hence the maximum reversible capacity) in ScS2 lies in the range 0.125 < a < 0.25. Taking the range of intercalation to be 0.25 < a < 1, corresponding to 75% of the theoretical capacity, this gives a charge capacity of 182.99 mA h g−1, which is comparable to the ∼200 mA h g−1 of other materials.1–9 The 75% of the maximum capacity compares well with the 60–80% available in NMC materials.5
 | ||
| Fig. 5 Elastic properties of T-ScS2 in its pristine and intercalated forms. The bulk and shear moduli were calculated using the Voigt scheme. | ||
The elastic stability conditions for specific crystal types have been outlined elsewhere,75 which have been used here to assess the stability of the T- and α-phases. We find that the elements of the elastic tensor for both T- and α-phases (see ESI,† Section S2) break the requirements of c44 > 0 and  and so the pristine material is not elastically stable. However, each of the intercalated phases meet all of the conditions, and so are elastically stable.
and so the pristine material is not elastically stable. However, each of the intercalated phases meet all of the conditions, and so are elastically stable.
Equivalent data for the intercalated ScS2 structures can also be found in the ESI,† Section S11, which show that the addition of the Group I intercalants provides electrons, filling the previously unoccupied sulfur p-orbitals, shifting the Fermi level (located mid-band in ScS2) upwards. This is also shown with the charge analysis presented in the ESI,† Section S9. Upon intercalation to the point of MScS2 with Group I metals, the intercalated structure develops a semiconducting nature with an occupied valence band separated from the conduction band by an moderate band gap of size ∼1 eV (PBE). Specifically for LiScS2, the PBE band gap is 1.36 eV and the HSE06 Bang gap is 2.32 eV, though we note from previous work that the HSE06 functional generally overestimates the band gap of TMDC structures.68,76 This gives a limit on the intercalation potential obtainable for practical uses: the insulating nature at this point would inhibit electronic conduction during cycling, and any intercalation past this point would require ScS2 to be mixed with conductive additives to account for the insulating behaviour.
Magnesium intercalated into ScS2 has different conducting behaviour compared to the group I elements, due to its double valency. Whilst the unintercalated system is conducting, intercalating to Mg0.5ScS2 fills the unoccupied sulfur p-orbitals and results in the structure losing its conductive nature, possessing a band gap of over 1.5 eV using the PBE functional. This would provide a practical limit during cycling, and would require conductive additives to be used to help facilitate intercalation past this point. However, past this the added magnesium provides electrons that begin to fill the unoccupied scandium d-states above the band gap.
Of the intercalant metals presented, lithium is the smallest and lightest, presents the highest (average) voltage of nearly 4 V, and has the lowest volumetric expansion. As such, lithium is identified as the best ion for ScS2 to be used as an intercalation electrode. We summarise the key electrode properties in Table 1, along with the properties of other presently practiced electrode materials for lithium-ion batteries, where it is clear to see that ScS2 offers a serious competitor to these materials. Below, we focus on lithium for exploring intercalation beyond the LiScS2 composition, and for considering the effect of substitution of different transition metals for the scandium site in ScS2.
3.3 Intercalation beyond a = 1
The intercalated LiScS2 structures show both dynamic stability (with no imaginary phonon modes) and thermodynamic stability against conversion (with positive values of EIS), and so the question as to the maximum possible lithium capacity still remains. As each of the octahedral sites is occupied at LiScS2, any further addition of lithium results in the occupation of the tetrahedrally-coordinated sites (see ESI,† Section S1). For the supercell sizes considered, the first step of intercalation past LiScS2 resulted in a stoichiometry of . As this compound still possesses a sizeable value of EIS = 3.209 eV, it is still remarkably stable against conversion reactions and demonstrates a robustness in this material to lithium intercalation beyond the usual limit considered for layered materials. However, there is a dramatic decrease in the intercalation voltage (with respect to the LiScS2 structure) to 0.436 V, which indicates a clear cutoff in the practical uses for ScS2 as a cathode material. These larger lithium contents align with the lithium concentrations used in the study of monolayer ScS2,40 where a drop in the voltage of over 2 V was also seen for concentrations beyond LiScS2.
. As this compound still possesses a sizeable value of EIS = 3.209 eV, it is still remarkably stable against conversion reactions and demonstrates a robustness in this material to lithium intercalation beyond the usual limit considered for layered materials. However, there is a dramatic decrease in the intercalation voltage (with respect to the LiScS2 structure) to 0.436 V, which indicates a clear cutoff in the practical uses for ScS2 as a cathode material. These larger lithium contents align with the lithium concentrations used in the study of monolayer ScS2,40 where a drop in the voltage of over 2 V was also seen for concentrations beyond LiScS2.
With further intercalation we find the value of EIS to drop, reaching a value of −0.735 eV at Li2ScS2. At these relatively high lithium concentrations the large repulsion between these positively charged ions results in the intercalated structure being destabilised and becoming more susceptible to conversion. A similar drop in EIS could be expected for the monolayer system, along with further instability arising from a separation of the ScS2 layers.
3.4 Metal mixing
One possible method commonly used to modify the properties of electrodes is through the introduction of other elements (M), in particular transition metals55,56 or with excessive lithium,13 resulting in the LiSc1−xMxS2 compound. We first consider the formation energy of metal mixing, using,| Eform = [E(Sc1−xMxS2) + xE(Sc)] − [E(ScS2) + xE(M)]. | (6) |
Our results, presented in Fig. 7, show that for low concentrations (x < 0.25), the energetic cost is very low or even negative, with lithium showing the highest formation energy of 0.61 eV at x = 0.125. The Group IV metals (Ti, Zr and Hf) have negative formation energies, and so it is energetically favourable to perform this substitution. We also see negative values of Eform for Group V elements Nb and Ta for mixing values of x < 0.5, whilst the other metals considered here (and x > 0.5 for Nb and Ta) demonstrate positive values of formation energy.
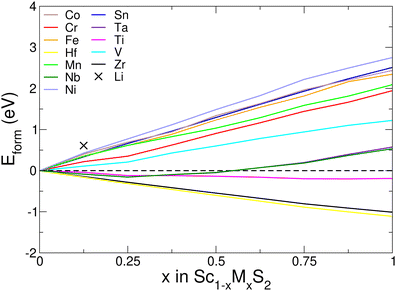 | ||
| Fig. 7 Formation energy of substituting scandium with different metal species, given by eqn (6). | ||
In general, our results show (see ESI,† Section S12) that there is a reduction in both the intercalation potential and the values of EIS as the proportion of scandium is reduced. The exception to this is demonstrated with lithium where, for a mixing concentration of x = 0.125, the average voltage is increased past the 3.655 V of ScS2 to 3.668 V. In general, the voltage and EIS values for the mixed materials falls below the weighted average of the two component materials. The greatest difference from the weighted average result is most dramatically show with Sc0.5Ta0.5S2. For voltage, the average of the two components is 2.706 V, whereas the actual voltage obtained is 2.264 V. Similarly for the value of EIS, the average of the ScS2 and TaS2 materials is 1.857 eV, whereas the value obtained is 1.381 eV.
The energetic cost of formation of ScS2 can be reduced by the inclusion of other metals, Sc1−xMxS2. However, we see that this results in both a decrease in the obtainable voltage and a decrease in the the thermodynamic stability indicated by EIS. whilst the mixing of these systems reduces the suitability of ScS2 as a cathode, the mixing of scandium into other materials for cathodes could be highly beneficial.
4 Conclusion
In this work, we have presented a thorough first-principles study into the performance of layered ScS2 as a potential cathode electrode material. We have applied a random structure search to demonstrate that the ground state phase for the intercalated material is a layered structure, agreeing with experimental studies and supporting its use as an electrode. From this, different layered-phases of the material were investigated and intercalated with different metal species. It was found that the T- and α-phases are energetically preferred, though they are not dynamically stable (determined through analysis of the phonon band structures) for low intercalation concentrations. The lowest achievable intercalant concentration is thus determined to be a = 0.25, and so a capacity corresponding to 75% of the theoretical capacity is predicted, corresponding to a charge capacity of 182.99 mA h g−1.For Group I intercalants, ScS2 is found to have a high voltage of nearly 3.5 V which is ideal for cathodes. Whilst this is reduced to 1.5 V for intercalation with magnesium (a Group II metal), the double valency offers a larger range of charge transfer and hence a comparable energy density. This low voltage also offers some promise for an anode. Thermodynamic phase diagrams were constructed to evaluate the stability of the layered ScS2 material against the conversion reaction forming Li2S (or equivalent compound), a reaction commonly seen for TMDC sulfides when intercalated. ScS2 was found to have a remarkably large window of stability, particularly when compared to the related TMDC materials. Beyond this, ScS2 was shown to have a Fermi level which lies within a band, indicating a conductive nature that is convenient for device cycling. It also has a low volumetric expansion (below 10%) when intercalated with lithium or magnesium, something that is essential for extended device lifetime.
To explore methods that could offer some improvement to the core properties of ScS2 material, we also considered metal mixing (substitutionally swapping out scandium atoms with transition metal elements, similar to what is done with NMC). With mixing of other metals, we find a gradual drop in both the voltage and the size of the phase diagram window of stability which suggests that this would be detrimental to the performance of a ScS2 electrode. However, this does highlight the potential advantage scandium could provide if mixed into other layered systems such as the layered transition metal oxides.
Our study highlights that ScS2 shows potential as a cathode material for lithium-ion batteries, with theoretical estimates of the capacity comparable with NMC and similar materials. We hope that our study encourages further development of this material for lithium-ion batteries.
Author contributions
C. J. Price: conceptualization, data curation, formal analysis, methodology, writing – original draft, review and editing. J. Pitfield: data curation, formal analysis, methodology, writing – original draft, review and editing. E. A. D. Baker: data curation, formal analysis, writing – original draft, review and editing. S. P. Hepplestone: conceptualization, funding acquisition, supervision, writing – original draft, review and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to acknowledge financial support from the EPSRC (United Kingdom), (Grant No. EP/L015331/1) and the Materials Chemistry Consortium, (EP/L000202, EP/R029431). The authors acknowledge the use of the University of Exeter HPC facility. We wish to acknowledge the use of the EPSRC funded Physical Sciences Data-science Service hosted by the University of Southampton and STFC under grant number EP/S020357/1.References
- A. S. Andersson, Electrochem. Solid-State Lett., 2000, 3, 66 CrossRef.
- L. Liao, P. Zuo, Y. Ma, X. Chen, Y. An, Y. Gao and G. Yin, Electrochim. Acta, 2012, 60, 269–273 CrossRef.
- B. Lung-Hao Hu, F. Y. Wu, C. T. Lin, A. N. Khlobystov and L. J. Li, Nat. Commun., 2013, 4, 1–7 Search PubMed.
- D. Y. Wan, Z. Y. Fan, Y. X. Dong, E. Baasanjav, H.-B. Jun, B. Jin, E. M. Jin and S. M. Jeong, J. Nanomater., 2018, 2018, 1–9 CrossRef.
- J. Kasnatscheew, S. Röser, M. Börner and M. Winter, ACS Appl. Energy Mater., 2019, 2, 7733–7737 CrossRef.
- G. W. Nam, N. Y. Park, K. J. Park, J. Yang, J. Liu, S. C. Yoon and K.-Y. Sun, ACS Energy Lett., 2019, 4, 2995–3001 CrossRef.
- W. Li, S. Lee and A. Manthiram, Adv. Mater., 2020, 32, 2002718 CrossRef CAS PubMed.
- N. D. Phillip, A. S. Westover, C. Daniel and G. M. Veith, ACS Appl. Energy Mater., 2020, 3, 1768–1774 CrossRef CAS.
- R. N. Ramesha, D. Bosubabu, M. G. Karthick Babu and K. Ramesha, ACS Appl. Energy Mater., 2020, 3, 10872–10881 CrossRef CAS.
- X. Li and Y. Xu, Appl. Surf. Sci., 2007, 253, 8592–8596 CrossRef CAS.
- X. Li, Y. Xu and C. Wang, J. Alloys Compd., 2009, 479, 310–313 CrossRef CAS.
- Y. Liu, J. Lv, Y. Fei, X. Huo and Y. Zhu, Ionics, 2013, 19, 1241–1246 CrossRef CAS.
- H. Ji, J. Wu, Z. Cai, J. Liu, D. H. Kwon, H. Kim, A. Urban, J. K. Papp, E. Foley, Y. Tian, M. Balasubramanian, H. Kim, R. J. Clément, B. D. McCloskey, W. Yang and G. Ceder, Nat. Energy, 2020, 5, 213–221 CrossRef CAS.
- Y. Ding, Q. Deng, C. You, Y. Xu, J. Li and B. Xiao, Phys. Chem. Chem. Phys., 2020, 22, 21208–21221 RSC.
- V. V. Kulish, O. I. Malyi, C. Persson and P. Wu, Phys. Chem. Chem. Phys., 2015, 17, 13921–13928 RSC.
- X. Zou, P. Xiong, J. Zhao, J. Hu, Z. Liu and Y. Xu, Phys. Chem. Chem. Phys., 2017, 19, 26495–26506 RSC.
- D. Wang, Y. Zhao, R. Lian, D. Yang, D. Zhang, X. Meng, Y. Liu, Y. Wei and G. Chen, J. Mater. Chem. A, 2018, 6, 15985–15992 RSC.
- B. Zhou, H. Shi, R. Cao, X. Zhang and Z. Jiang, Phys. Chem. Chem. Phys., 2014, 16, 18578–18585 RSC.
- J. Wu and G. Gao, Phys. Chem. Chem. Phys., 2019, 21, 4947–4952 RSC.
- D. Ni, J. Shi, W. Xiong, S. Zhong, B. Xu and C. Ouyang, Phys. Chem. Chem. Phys., 2019, 21, 7406–7411 RSC.
- M. Chhowalla, H. S. Shin, G. Eda, L.-J. Li, K. P. Loh and H. Zhang, Nat. Chem., 2013, 5, 263–275 CrossRef PubMed.
- S. J. McDonnell and R. M. Wallace, Thin Solid Films, 2016, 616, 482–501 CrossRef CAS.
- S. Fan, X. Zou, H. Du, L. Gan, C. Xu, W. Lv, Y. B. He, Q. H. Yang, F. Kang and J. Li, J. Phys. Chem. C, 2017, 121, 13599–13605 CrossRef CAS.
- Y. Wei, J. Zheng, S. Cui, X. Song, Y. Su, W. Deng, Z. Wu, X. Wang, W. Wang, M. Rao, Y. Lin, C. Wang, K. Amine and F. Pan, J. Am. Chem. Soc., 2015, 137, 8364–8367 CrossRef CAS PubMed.
- Q. D. Chen, S. F. Yuan, J. H. Dai and Y. Song, Phys. Chem. Chem. Phys., 2021, 23, 1038–1049 RSC.
- P. Luo and Z. Huang, Solid State Ionics, 2019, 338, 20–24 CrossRef CAS.
- S. Bhuvaneswari, U. Varadaraju, R. Gopalan and R. Prakash, Electrochim. Acta, 2019, 301, 342–351 CrossRef CAS.
- K. Nakajima, F. L. Souza, A. L. Freitas, A. Thron and R. H. Castro, Chem. Mater., 2021, 33, 3915–3925 CrossRef CAS.
- C. J. M. Rooymans, Z. Anorg. Allg. Chem., 1961, 2, 234–235 CrossRef.
- G. Zhao, I. Muhammad, K. Suzuki, M. Hirayama and R. Kanno, Mater. Trans., 2016, 57, 1370–1373 CrossRef CAS.
- Z. Liu, H. Deng, S. Zhang, W. Hu and F. Gao, J. Mater. Chem. A, 2018, 6, 3171–3180 RSC.
- Z. Liu, H. Deng, S. Zhang, W. Hu and F. Gao, Phys. Chem. Chem. Phys., 2018, 20, 22351–22358 RSC.
- Z. M. Xu, S. H. Bo and H. Zhu, ACS Appl. Mater. Interfaces, 2018, 10, 36941–36953 CrossRef CAS PubMed.
- H. Zhang, X. Lin and Z.-K. Tang, Solid State Commun., 2015, 220, 12–16 CrossRef CAS.
- C. Ataca, H. Åžahin and S. Ciraci, J. Phys. Chem. C, 2012, 116, 8983–8999 CrossRef CAS.
- J. A. Reyes-Retana and F. Cervantes-Sodi, Sci. Rep., 2016, 6, 24093 CrossRef CAS PubMed.
- M. van Dijk and C. Plug, Mater. Res. Bull., 1980, 15, 103–106 CrossRef CAS.
- L. Havlák, J. Fábry, M. Henriques and M. Dušek, Acta Crystallogr., Sect. C: Struct, Chem, 2015, 71, 623–630 CrossRef PubMed.
- D. Chakraborty, M. Pandey and P. Johari, arXiv, 2021, preprint, arXiv:2201.02268 [cond-mat.mtrl-sci] DOI:10.48550/arXiv.2201.02268.
- A. Al Roman, M. M. Rahman, K. Hossain, S. Das and F. Ahmed, Solid State Commun., 2022, 352, 114828 CrossRef.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- H. Katzke, P. Tolédano and W. Depmeier, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 1–8 CrossRef.
- J. Ribeiro-Soares, R. M. Almeida, E. B. Barros, P. T. Araujo, M. S. Dresselhaus, L. G. Cançado and A. Jorio, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 115438 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, Erratum: Hybrid functionals based on a screened Coulomb potential, J. Chem. Phys., 2003, 118, 8207, DOI:10.1063/1.2204597.
- J. Paier, M. Marsman, K. Hummer, G. Kresse, I. C. Gerber and J. G. Angyán, J. Chem. Phys., 2006, 124, 154709 CrossRef PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192 CrossRef.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- A. Bhaskar, D. Mikhailova, N. Kiziltas-Yavuz, K. Nikolowski, S. Oswald, N. N. Bramnik and H. Ehrenberg, Prog. Solid State Chem., 2014, 42, 128–148 CrossRef CAS.
- H. H. Sun, U. H. Kim, J. H. Park, S. W. Park, D. H. Seo, A. Heller, C. B. Mullins, C. S. Yoon and Y. K. Sun, Nat. Commun., 2021, 12, 1–11 CrossRef.
- P. Wen, H. Wang, X. Wang, H. Wang, Y. Bai and Z. Yang, Phys. Chem. Chem. Phys., 2022, 24, 14877–14885 RSC.
- M. K. Aydinol, A. F. Kohan, G. Ceder, K. Cho and J. Joannopoulos, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 1354–1365 CrossRef CAS.
- M. Mayo, K. J. Griffith, C. J. Pickard and A. J. Morris, Chem. Mater., 2016, 28, 2011–2021 CrossRef CAS.
- A. N. Enyashin and G. Seifert, Comput. Theor. Chem., 2012, 999, 13–20 CrossRef CAS.
- Q. Zhang, R. Li, M. Zhang, B. Zhang and X. Gou, Electrochim. Acta, 2014, 115, 425–433 CrossRef CAS.
- P. Gao, L. Wang, Y. Y. Zhang, Y. Huang, L. Liao, P. Sutter, K. Liu, D. Yu and E. G. Wang, Nano Lett., 2016, 16, 5582–5588 CrossRef CAS PubMed.
- Y. Koyama, H. Arai, I. Tanaka, Y. Uchimoto and Z. Ogumi, J. Mater. Chem. A, 2014, 2, 11235–11245 RSC.
- Z. Liu, H. Deng and P. P. Mukherjee, ACS Appl. Mater. Interfaces, 2015, 7, 4000–4009 CrossRef CAS PubMed.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- B. Amin, N. Singh and U. Schwingenschlögl, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 1–6 CrossRef.
- F. Khan, M. Idrees, C. Nguyen, I. Ahmad and B. Amin, RSC Adv., 2020, 10, 24683–24690 RSC.
- F. H. Davies, C. J. Price, N. T. Taylor, S. G. Davies and S. P. Hepplestone, Phys. Rev. B: Condens. Matter Mater. Phys., 2021, 103, 1–10 CrossRef.
- F. Zhou, M. Cococcioni, C. A. Marianetti, D. Morgan and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 1–8 Search PubMed.
- F. Zhou, C. A. Marianetti, M. Cococcioni, D. Morgan and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 1–4 Search PubMed.
- V. L. Chevrier, S. P. Ong, R. Armiento, M. K. Chan and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 1–11 CrossRef.
- M. Woodcox, R. Shepard and M. Smeu, J. Power Sources, 2021, 516, 230620 CrossRef CAS.
- S. Shang, Y. Wang, P. Guan, W. Y. Wang, H. Fang, T. Anderson and Z.-K. Liu, J. Mater. Chem. A, 2015, 3, 8002–8014 RSC.
- Y. Qi, L. G. Hector, C. James and K. J. Kim, J. Electrochem. Soc., 2014, 161, F3010–F3018 CrossRef.
- F. Mouhat and F.-X. Coudert, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 224104 CrossRef.
- E. A. D. Baker, J. Pitfield, C. J. Price and S. P. Hepplestone, J. Phys.: Condens. Matter, 2022, 34, 375001 CrossRef PubMed.
- Y. Lyu, X. Wu, K. Wang, Z. Feng, T. Cheng, Y. Liu, M. Wang, R. Chen, L. Xu, J. Zhou, Y. Lu and B. Guo, Adv. Energy Mater., 2021, 11, 2000982 CrossRef.
- J. Luo, C. Dai, Z. Wang, K. Liu, W. Mao, D. Fang and X. Chen, Measurement, 2016, 94, 759–770 CrossRef.
- A. Yamada, S. C. Chung and K. Hinokuma, J. Electrochem. Soc., 2001, 148, A224 CrossRef CAS.
- J. Barker, Electrochim. Acta, 1999, 45, 235–242 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp05055b |
| This journal is © the Owner Societies 2023 |




