Metallic bonds and thermal vibration in brass

Abstract

Nature of the metallic bond and thermal vibration in brass alloy is investigated from the local structural and thermodynamical points of view by the temperature-dependent Cu and Zn K-edge extended X-ray absorption fine structure spectroscopy and the path-integral effective classical potential theoretical simulation. It is unexpectedly found that the thermal vibrational amplitude around Zn is a little but meaningfully smaller than that around Cu, although it is usually believed that Zn is a much softer metal than Cu in terms of various thermodynamical physical quantities of elemental metals. Moreover, it is found that the nearest neighbor distance around Zn is almost equivalent to that around Cu (only ∼0.01 Å difference), although the metallic radius of Zn commonly used is considerably larger than that of Cu (∼0.06–0.09 Å difference). These peculiar findings can be interpreted as a result of confinement of Zn atoms in a smaller space than usual and a significantly larger repulsive potential of Zn than Cu.

---

Introduction

It is well known that in the local structural point of view, mixed crystals and alloys exhibit different interatomic distances depending on the atom pairs, even though the materials provide distinct X-ray diffraction patterns as if the atoms in the material were perfectly configured to form a quite simple lattice such as fcc and bcc in the case of alloys. It is interesting and fundamentally important to understand the nature of the chemical bonds in the metallic alloys both form the local and periodic points of view. The CuZn alloy called brass is one of the most familiar alloys. Cu and Zn exhibit significantly different thermodynamical properties in elemental metals from each other: the boiling points T_b and the melting points T_m are T_b(Cu) = 2571 °C, T_b(Zn) = 907 °C, T_m(Cu) = 1083 °C, and T_b(Zn) = 419.5 °C, respectively, and the adhesive energy (heat of sublimation) E_c and the bulk moduli B are E_c(Cu) = 338.32 kJ mol⁻¹, E_c(Zn) = 130.73 kJ mol⁻¹, B(Cu) = 137.8 GPa, and B(Zn) = 72 GPa. All of these thermodynamic quantities indicate much larger potential stiffness in Cu than in Zn. Correspondingly, the interatomic distances R are significantly shorter in fcc Cu (2.548 Å, the coordination number N = 12) than in hcp Zn [2.660 Å (N = 6 within the ab plane) and 2.876 Å (N = 6 along the c axis)].

Local structure of mixed crystals and random alloys is investigated mainly by extended X-ray-absorption fine structure (EXAFS) spectroscopy. Many EXAFS studies have been reported to reveal local structural properties of mixed crystals and alloys.^1–10 Moreover, temperature dependent EXAFS analysis provides local thermodynamical information on the Debye–Waller factors (mean square relative displacements) and thermal expansion, and a lot of EXAFS works have been performed to develop the EXAFS methodology and clarify interesting structural and thermodynamical properties.^11–27 For instance, in the study on the FeNi Invar alloy,⁶ it was found that the interatomic distances and thermal expansion around Fe and Ni are meaningfully different from each other, although the X-ray diffraction looks as if the alloy formed perfect fcc lattice. On the other hand, from the theoretical point of view, the path-integral effective classical potential method (PIECP)^{6–9,28–33} is regarded as one of the most appropriate methods to investigate the interatomic distance, the mean square relative displacements, and thermal expansion including the quantum fluctuation, which is essentially important to describe the harmonic and anharmonic thermal properties at low temperature.

In the present work, local structural and thermal vibrational properties of the brass alloy were investigated by analysing temperature dependent Cu and Zn K-edge EXAFS spectra and conducting the theoretical PIECP simulations. The average interatomic distance R, the second-order cumulant C₂ = 〈(r − R)²〉 (mean square relative displacement), the third-order cumulant C₃ = 〈(r − R)³〉, and the fourth-order cumulant C₄ = 〈(r − R)⁴〉 − 3C₂² were obtained.¹² The PIECP methodology was newly developed in this work. In the previous works,^6–9 the normal vibrational analysis has been performed by assuming the average potentials even in the alloy to evaluate the effective classical potentials. This approximation was found to work rather well but was not easy to be justified strictly. In the present work, to avoid the previous ambiguity, the normal vibrational analysis was conducted for the assumed large superlattice directly, yielding much more reliable and reasonable results. Surprisingly, it is found that the Debye temperature estimated from the mean square relative displacements obtained by the EXAFS analysis and the PIECP simulations is slightly but meaningfully higher around Zn and that the interatomic distance is not very different between Cu and Zn. These findings apparently contradict with the above simple consideration concerning the thermodynamical properties of elemental Cu and Zn metals but can be interpreted as a result of confinement of Zn atoms in a smaller space than usual and a significantly larger repulsive potential of Zn than Cu.

EXAFS analysis

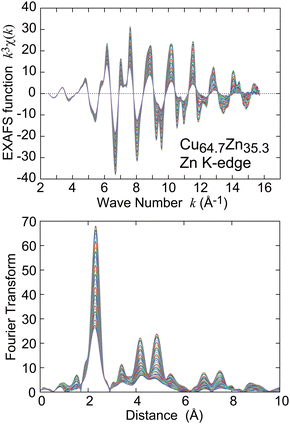
The Cu and Zn K-edge EXAFS spectra of a commercially available brass foil (Cu_64.7Zn_35.3, Takeuchi Kinzoku-Haku Kogyo Co. Ltd, Tokyo, Japan) with thickness of 10 μm were recorded at Beamline 9C³⁴ of Photon Factory (top-up operation, the electron storage ring energy of 2.5 GeV and the ring current of ∼450 mA) in High Energy Accelerator Research Organization (KEK-PF) with the transmission mode using a Si(111) double crystal monochromator. Ionization chambers filled with pure N₂ (17 cm in length) and pure Ar (31 cm) were used to measure the incident and transmitted X-ray intensities, respectively. The samples were cooled down using a He gas-circulating refrigerator and the measurement temperature range was 21–300 K. Typical EXAFS and XANES (X-ray absorption near edge structure) spectra of the brass foil are depicted in Fig. S1 and S2 in the ESI.†

The EXAFS oscillation functions k³χ(k) (k the photoelectron wave number) were obtained based on the standard procedures as the pre-edge baseline and the post-edge background subtractions and the subsequent normalization with atomic absorption coefficients. The k³χ(k) functions were subsequently Fourier transformed, Fourier filtered for the peaks of interest, and were finally curve fitted in k space. In the present study, the first- to fourth-nearest neighbor (NN) shells were quantitatively analysed. The Cu and Zn K-edge EXAFS functions k³χ(k) and their Fourier transforms are depicted in Fig. 1 and 2, respectively, and the k and R spaces employed in the analysis are summarized in Table S1 in the ESI.†

Fig. 1 Cu K-edge EXAFS oscillation functions k³χ(k) and their Fourier transforms at temperatures from 21 to 300 K. Typical fcc features are found and the curve-fitting analysis from the first- to fourth-NN shells were performed.

Fig. 2 Zn K-edge EXAFS oscillation functions k³χ(k) and their Fourier transforms at temperatures from 21 to 300 K. Typical fcc features are again found and the curve-fitting analysis from the first- to fourth-NN shells were performed.

The single-shell EXAFS formula employed is given as¹²

where N is the coordination number, S²₀ the intrinsic reduction factor due to the many-electron effect, F(k) the backscattering amplitude including the inelastic scattering loss factor, and ϕ(k) the total phase shift between the X-ray absorbing and photoelectron scattering atoms.

For the curve-fitting analysis to obtain the structural parameters, theoretical standards were at first calculated using FEFF8.4.³⁵ Here, we assumed randomly distributed clusters with the perfect fcc lattice constant of 3.6782 Å^36,37 (the number of the fcc unit lattices of 4³), where the composition ratio of brass was assumed to be Cu₇₂Zn₃₆. Ten random alloy clusters were evaluated and the average EXAFS spectra were obtained as consequent theoretical standards. Although static lattice strains are actually expected in this alloy, the FEFF simulations were conducted with the assumption that all the atoms are distributed at ideal fcc lattice positions. The curve-fitting analysis of the experimental EXAFS spectra at the lowest temperature was performed using the FEFF standards obtained above. Here, the one-shell and two-shell analyses for the first-NN shell were tried. In the Cu (Zn) K-edge EXAFS of the brass alloy, there exist Cu–Cu and Cu–Zn (Zn–Cu and Zn–Zn) X-ray-absorber and photoelectron scatterer atom pairs in the first-NN shells. In the one-shell analysis, the average quantities between the two different pairs were obtained. The parameters fitted were S²₀, R, ΔE₀ (edge energy shift), and C₂ with fixed parameters of N = 12, C₃ = 0 and C₄ = 0, while in the two-shell analysis, S²₀ was also fixed at the values obtained in the one-shell analysis. Note here that the Cu and Zn K-edge EXAFS spectra were analysed separately without restriction of equivalence for the Cu–Zn interatomic distance between Cu and Zn K edges. Goodness of the curve fitting is plotted in Fig. S3 (ESI†) and the detailed analysis results are summarized in Table S2 in the ESI.†

It is consequently found that the one-shell analysis is much more reliable because of the following reasons. First, the interatomic distances of the two different pairs in the two-shell analysis are not different enough to be analysed separately: R(Cu–Cu) = 2.557 Å, R(Cu–Zn) = 2.601 Å, R(Zn–Cu) = 2.598 Å, and R(Zn–Zn) = 2.606 Å. Especially, the difference between the Zn–Cu and Zn–Zn distances is less than 0.01 Å. Second, C₂ of the Cu–Zn and Zn–Cu pairs deviate noticeably from each other [C₂(Cu–Zn) = 0.181 × 10⁻² Ų and C₂(Zn–Cu) = 0.655 × 10⁻² Ų], although the two atom pairs are identical and their C₂ values should be equivalent. Third, the reliability factors χ²_v of the one-shell analysis are meaningfully smaller than those of the two-shell analysis both in the Cu and Zn K-edge EXAFS. It is thus concluded that all the first-NN Cu–Cu, Cu–Zn, and Zn–Zn pairs exhibit similar interatomic distances, although the inherent metallic radii of Cu and Zn are believed to be quite different. It is here noted that Reinhard et al.³⁸ reported a partial short-range order in α-brass through the elastic diffuse neutron scattering and proposed the DO₂₃ ordered structure from the Monte Carl simulation. In the present EXAFS study, it is practically impossible to distinguish the presence or absence of the short-range order, because the backscattering amplitudes and the first-NN interatomic distances between the two atom pairs of Cu–Cu and Cu–Zn for Cu K-edge analysis (or Zn–Cu and Zn–Zn for Zn K-edge analysis) are almost identical with each other. Even in the presence of such a kind of the short-range order, the present results and conclusions is not affected due to almost equivalence of the interatomic distances between the two atom pairs.

Temperature dependence of the EXAFS spectra was subsequently analysed by the empirical analysis method, where the lowest-temperature data (21 K) were used as empirical standards. Here, S²₀, N, and ΔE₀ were assumed to be identical to those of the lowest temperature, while R, C₂, C₃, and C₄ are fitting variables. The analysis of the higher-NN (second, third, and fourth) shell was similarly performed. Here, the three shells were simultaneously analysed. In the analysis of higher NN shells in fcc metals, especially the fourth-NN shell, the multiple-scattering effect should be taken into account. In the present analysis, the fourth-NN contributions including the multiple scattering paths were summed up and treated as an average single-shell contribution, and the curve-fitting analysis in which the fourth-NN shell was regarded as a one-shell contribution was performed. For the second- and third-NN shells, the multiple scattering effect was neglected, because the FEFF simulations yielded sufficiently small multiple scattering effect using appropriate Debye–Waller factors. In the lowest-temperature data analysis, the FEFF standards were employed to fit S²₀, R, ΔE₀, and C₂, while in the temperature dependence analysis, the empirical standard method was used to fit R and C₂. Note here that higher-order cumulants in the second-, third-, and fourth-NN shells are known to be neglected with high accuracy because of the absence of the chemical bonds that induces anharmonicity,¹⁸ as in the central limit theorem that random distribution without correlation approaches Gaussian distribution. The analysis results are given in Table S3 and Fig. S4 and S5 in the ESI.† The results will be discussed combining the following PIECP results.

PIECP simulation

To investigate temperature dependent structural properties of brass theoretically, PIECP^28–31 Monte Carlo (MC) simulations were conducted under a constant number of particles, pressure, and temperature (NPT) condition. Detailed PIECP formalism for the application to EXAFS is described in the literature.¹⁰ The normal vibrational analysis should be carried out prior to the MC simulation because the quantum and classical mean square relative displacements parallel and perpendicular to the bond direction of each NN atom pairs¹⁰ are necessary to evaluate the effective classical potentials that modify the classical potentials so that the quantum mechanical fluctuation can approximately but appropriately be taken into account. In the previous works,^6–9 the normal vibrational analysis was conducted by assuming the average interatomic potentials in the alloy, although each atom pair had a different interatomic potential because of different atom pairs. This approximation worked quite well in the previous studies but was hardly able to be justified satisfactorily. More reliable and reasonable description is employed in the present work; namely, the appropriate normal vibrational analysis for the assumed sufficiently large superlattice is strictly performed. This treatment is the most important improvement in the theoretical PIECP simulations conducted in the present work.

The interatomic potentials of Cu and Zn are based on the empirical embedded-atom method (EAM).^39–41 The numerical parameters^42,43 are tabulated in Table S4 in the ESI.† The compositions of the brass alloy in the simulations were assumed to be Cu₁₇₁Zn₈₅. The total number of atoms was 256 (4³ fcc cubic unit cells), and the distributions of Cu and Zn were chosen randomly. In a similar manner to the FEFF evaluations, ten types of the superlattices were simulated and the results were averaged to provide consequent physical quantities. In each superlattice, up to the second-NN force constants were taken into consideration (totally 41 472 force constants), and the dynamical matrices (Hermitian with 768 dimension) were diagonalized over the first Brillouin zone (21³ = 9261 k points) to evaluate the eigen-frequencies and eigenvectors for all the vibrational modes. Totally 13 824 types of the mean square relative displacements along and normal to the bond direction up to the fourth-NN shells were obtained in the temperature range of 1–400 K (21 temperatures). It should be noted that although the computational load was much larger than in the previous works, much more reliable evaluations were successfully achieved.

To verify that the size of the superlattice is sufficiently large, similar PIECP MC simulations for the 108 atom systems (Cu₇₂Zn₃₆) were conducted, and the results were found to be essentially equivalent to those for the 256-atom system. The phonon dispersion curves are plotted in Fig. S6 (ESI†). Since there exist many kinds of metallic bonds in the present superlattice, the phonon modes are almost continuously dispersed except the acoustic modes at low frequency. After the presently developed normal vibrational analysis of the superlattice, the PIECP MC simulations were performed based on the conventional Metropolis method, where 2 00 000 MC steps were calculated with 256 times trials of the atom movement and one trial of the lattice constant variation in each MC step. In the calculations of thermodynamical quantities, the results before the system reaches sufficient equilibrium (∼20 000 MC steps) were excluded. The temperatures considered in the present simulations were in the range of 1–400 K (21 temperatures).

Results and discussion

Fig. 3 shows the mean square relative displacements C₂ for the first-NN shells obtained by the experimental EXAFS analysis and the theoretical PIECP simulation. It is at first found that the absolute C₂ values are noticeably larger in the EXAFS results than in the PIECP simulation, indicating much larger static disorder in the real alloy sample. The EXAFS static disorders σ²_s are estimated to be σ²_s(Cu) = 0.166 × 10⁻² Ų and σ²_s(Zn) = 0.238 × 10⁻² Ų, while the PIECP ones are 0.040 × 10⁻² Ų around Cu and 0.054 × 10⁻² Ų around Zn, respectively. More importantly, the EXAFS results show slightly smaller temperature dependence around Zn than around Cu, this yielding the Debye temperatures of Θ_D(Cu) = 295 K and Θ_D(Zn) = 302 K. The PIECP results agree with the EXAFS finding at least qualitatively [Θ_D(Cu) = 329 K and Θ_D(Zn) = 348 K]. This consequence is rather surprising since it seems to be essentially contradictory to the simple prediction based on the potential stiffness (Cu should be stiffer than Zn) mentioned above. It is also noted that the PIECP Debye temperatures are comparatively higher than the EXAFS ones, implying that the potential function employed in the present work is slightly too stiff.

Fig. 3 Mean square relative displacements for the first-NN pairs obtained by the one-shell EXAFS analysis (with error bars; Cu: red; Zn: green) and the PIECP simulations (average Cu: magenta; average Zn: light blue; solid line: quantum; dashed line: classical), respectively. The corresponding Debye temperatures are also given in the figure.

The above finding that the thermal vibrational amplitude is meaningfully smaller around Zn than around Cu is really unexpected, and let us further confirm the finding using the results of the normal vibration analysis. Fig. 4 shows the theoretically evaluated mean square relative displacements C₂ of Cu₁₇₁Zn₈₅ obtained by the normal vibrational analysis for the ideal fcc lattice (all the first-NN interatomic distances are identical) and the relaxed fcc like lattice (structurally optimized within the superlattice), and by the PIECP simulations, respectively. In Fig. 4(a and b), the perpendicular components 1/2〈u²_⊥〉 are also depicted. The sequence of the vibrational amplitude is found to be Zn–Zn < Cu–Zn < Cu–Cu in all the results, being consistent with the consequence from Fig. 3. Interestingly, the difference in the thermal vibrational amplitude among the Zn–Zn, Cu–Zn, and Cu–Cu atom pairs gradually becomes smaller from the ideal fcc lattice to the relaxed lattice and the PIECP simulated one. It is satisfactorily confirmed that the sequence of the Debye temperature is Θ_D(Cu–Cu) < Θ_D(Cu–Zn) < Θ_D(Zn–Zn).

Fig. 4 Theoretical mean square relative displacements C₂ for the first-NN pairs in Cu₁₇₁Zn₈₅ evaluated by the normal vibrational analysis assuming (a) the ideal fcc lattice and (b) the relaxed (structurally optimized) superlattice, together with the perpendicular components 1/2〈u²_⊥〉, and (c) those evaluated by the PIECP simulations. The quantum mechanical parallel components are given as filled circles and solid lines, the classical parallel component as dashed lines (Cu–Cu: red; Cu–Zn: green; Zn–Zn: blue), and the perpendicular components are depicted as dot-dashed lines in (a and b). In (c), the average C₂ for Cu, Zn, and total are also plotted. The corresponding Debye temperatures are given in the figure.

Fig. 5 shows temperature dependence of the interatomic distance R, the third- and fourth-order cumulants, C₃ and C₄, for the first-NN shells obtained by the EXAFS and PIECP. The experimentally obtained anharmonic parameters C₃ and C₄ are found to be sufficiently small (C₃ < 10⁻³ ų and C₄ < 10⁻⁴ Å⁴), this indicating sufficient reliability of the present cumulant expansion analysis. For both the EXAFS and PIECP results shown in Fig. 5(a), the interatomic distance around Zn is slightly longer than that around Cu, as expected by the simple consideration based on the metallic radii of Cu and Zn. It is noted, however, that the difference between Cu and Zn is quite small (∼0.01 Å) as mentioned above in the EXAFS analysis. The experimental⁴⁴ and PIECP-simulated thermal expansion coefficients for the lattice constant a₀ around 300 K are 1.68 × 10⁻⁵ and 1.39 × 10⁻⁵ K⁻¹, respectively, the agreement being satisfactorily good. On the contrary, the EXAFS results are found to be much smaller [1.02 × 10⁻⁵ K⁻¹ around Cu and 0.56 × 10⁻⁵ K⁻¹ around Zn] than the PIECP results of 1.85 × 10⁻⁵ K⁻¹ (Cu) and 1.92 × 10⁻⁵ K⁻¹ (Zn). More detailed PIECP results for the interatomic distance and the mean square relative displacement are depicted in Fig. S7 and S8 in the in the ESI.†

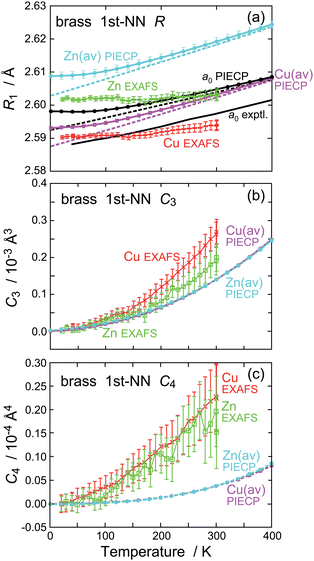Fig. 5 Temperature dependence of (a) the interatomic distance R, (b) third- and (c) fourth-order cumulants, C₃ and C₄, for the first-NN pairs obtained by the EXAFS analysis (with error bars; Cu: red; Zn: green) and the PIECP simulations (average Cu: magenta; average Zn: light blue). The lattice constant (a₀/√2) are also plotted in (a), where the experimental thermal expansion coefficient was referred to from the literature.⁴⁴

To interpret the discrepancy concerning thermal expansion between the EXAFS and PIECP, we will see temperature dependence of C₃ in Fig. 5(b). Although the PIECP simulation slightly underestimates, the agreement in C₃ between the EXAFS and PIECP results is fairly good. The EXAFS C₃(Zn) seems to be a little smaller than C₃(Cu), and temperature dependence of PIECP C₃(Zn) also looks slightly smaller than the PIECP C₃(Cu), implying consistency between the EXAFS and PIECP results at least qualitatively. This indicates that the EXAFS C₃ has been obtained appropriately. If the EXAFS C₃ would be much smaller than the PIECP one, the EXAFS result would be less reliable, because too small EXAFS thermal expansion should often be associated with erroneous estimation or neglect of C₃. It is thus supposed that the present underestimation of thermal expansion in EXAFS originates from the presence of considerably large static disorder observed in EXAFS. When the static disorder is significantly large and there exist many different pairs in the first NN shell, the contribution from the atom pairs with a longer distance and a larger Debye–Waller factor may be underestimated compared to the ones with a closer distance and a smaller Debye–Waller factor. This would be an intrinsic problem in EXAFS and here we may conclude that thermal expansion estimated by the present EXAFS analysis might be less reliable. In Fig. 5(c), temperature dependence of C₄ obtained by the EXAFS and PIECP is also shown, and the EXAFS results are found to be much larger than the PIECP ones. This may be attributed to the EAM potential parameters employed in this study; namely, the present EAM potential is a little too stiff to estimate C₄, as is already found in the estimation of the Debye temperatures.

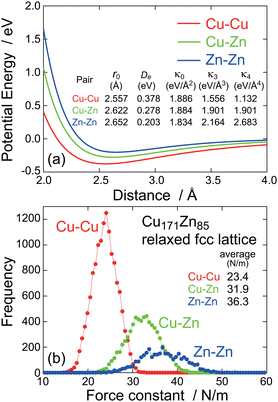
The most important finding in the present study is that the thermal vibrational amplitude around Zn is slightly but meaningfully smaller than that around Cu, which is clarified by the EXAFS analysis and also by the PIECP simulation. Since this finding seems contradictory with our simple prediction, the origin should be clarified. Fig. 6(a) shows the two-body interatomic potential for each atom pair. Although the EAM potential is inherently of many body, the two-body potential can approximately be evaluated.⁴⁰ As mentioned above, the Zn–Zn potential is actually the shallowest, while the Cu–Cu potential is the deepest. On the contrary, Fig. 6(b) shows the frequency distribution of the first-NN force constants in the present Cu₁₇₁Zn₈₅ superlattices, and it is clearly found that the Zn–Zn atom pair gives a larger force constant than the Cu–Cu pair. The reason for a larger force constant in Zn–Zn atom pair is not straightforwardly recognized but is probably ascribed to a steeper repulsive potential at a shorter distance side in the Zn–Zn pair. When the system is really diatomic, the Zn–Zn distance is hardly contracted due to the steep repulsive potential and is easily elongated, resulting in large anharmonic vibrational amplitude in the diatomic Zn₂ molecule. On the contrary, in a closed packed solid like fcc, the Zn–Zn distance is hardly elongated due to the existence of other atoms at the opposite side, leading to confinement of the Zn atom. This is coincident to the interatomic distance determined by the EXAFS analysis. It is expected that the first-NN interatomic distance around Zn would be significantly larger than that around Cu, while the EXAFS analysis reveals that the first-NN interatomic distances are not very different from each other (only ∼0.01 Å difference between Cu and Zn). This indicates that the Zn atoms in brass are likely to be confined in a space that is a little too small for Zn and are hardly movable.

Fig. 6 (a) Two-body interatomic potentials of Cu–Cu, Cu–Zn, and Zn–Zn pairs estimated the EAM method. Numerical potential indicators are given in the figure. (b) Frequency distribution of the first-NN Cu–Cu, Cu–Zn, and Zn–Zn force constants in ten types Cu₁₇₁Zn₈₅ superlattices. The average force constant values for the Cu–Cu, Cu–Zn, and Zn–Zn pairs are given in the figure.

Summary

In summary, local thermal vibration in brass was investigated by the temperature dependent Cu and Zn K-edge EXAFS measurements and the theoretical PIECP simulation. It is unexpectedly found that the thermal vibrational amplitude around Zn is meaningfully smaller than that around Cu and that the first-NN interatomic distances are nearly equivalent between Zn and Cu. Although brass is one of the most familiar alloys, the fundamental thermal properties are still not easily predicted. The experimental EXAFS and theoretical PIECP techniques have successfully settle the problem in the present work and will remain useful techniques for future works.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

I would like to thank beamline staffs (Prof. Hitoshi Abe, Prof. Masao Kimura, Dr Hiroaki Nitani, and Mr Yasuhiro Niwa) in KEK-PF for their technical helps in the EXAFS measurements. I am also grateful for the partial financial support of Grant-in-Aid for Scientific Research (A) (No. 21H04677) from Japan Society for the Promotion of Science (JSPS). The EXAFS measurements at Photon Factory have been performed under the approval of Photon Factory Program Advisory Committee (PF-PAC proposal No. 2022G017).

References

1. J. B. Boyce and J. C. Mikkelsen Jr., Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 6903.
2. A. Balzarotti, N. Motta, A. Kisiel, M. Zimnal-Starnawska, M. T. Czyyk and M. Podgórny, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 7526.
3. R. A. Mayanovic, W.-F. Pong and B. A. Bunker, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 42, 11174.
4. T. Yokoyama, F. Takamatsu, K. Seki, K. Miyake, T. Tani and T. Ohta, Jpn. J. Appl. Phys., 1990, 29, L1486.
5. H. Sato, T. Yokoyama, I. Ono, K. Kaneyuki and T. Ohta, Jpn. J. Appl. Phys., 1992, 31, 1118.
6. T. Yokoyama and K. Eguchi, Phys. Rev. Lett., 2011, 107, 065901.
7. T. Yokoyama and K. Eguchi, Phys. Rev. Lett., 2013, 110, 075901.
8. T. Yokoyama, A. Koide and Y. Uemura, Phys. Rev. Mater., 2018, 2, 023601.
9. T. Yokoyama and S. Chaveanghong, Phys. Rev. Mater., 2019, 3, 033607.
10. T. Yokoyama, Microstructures, 2021, 1, 2021003.
11. P. Eisenberger and G. S. Brown, Solid State Commun., 1979, 29, 481.
12. G. Bunker, Nucl. Instrum. Methods, 1983, 207, 437.
13. J. M. Tranquada and R. Ingalls, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 28, 3520.
14. T. Yokoyama, T. Satsukawa and T. Ohta, Jpn. J. Appl. Phys., 1898, 28, 1905.
15. L. Wenzel, D. Arvanitis, H. Rabus, T. Lederer, K. Baberschke and G. Comelli, Phys. Rev. Lett., 1990, 64, 1765.
16. A. Di Cicco, A. Filipponi, J. P. Itié and A. Polian, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 9086.
17. H. Wende, D. Arvanitis, M. Tischer, R. Chauvistre, H. Henneken, F. May and K. Baberschke, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 5920.
18. T. Yokoyama, T. Ohta and H. Sato, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 11320.
19. G. Dalba, P. Fornasini, R. Grisenti and J. Purans, Phys. Rev. Lett., 1999, 82, 4240.
20. A. Filipponi, A. Di Cicco and S. De Panfilis, Phys. Rev. Lett., 1999, 83, 560.
21. S. a Beccara, G. Dalba, P. Fornasini, R. Grisenti, A. Sanson and F. Rocca, Phys. Rev. Lett., 2002, 89, 025503.
22. A. Di Cicco, A. Trapananti, S. Faggioni and A. Filipponi, Phys. Rev. Lett., 2003, 91, 135505.
23. P. Fornasini, S. A. Beccara, G. Dalba, R. Grisenti, A. Sanson, M. Vaccari and F. Rocca, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 174301.
24. P. Fornasini and R. Grisenti, J. Synchrotron Radiat., 2015, 22, 1242.
25. J. Purans, P. Fornasini, S. E. Ali, G. Dalba, A. Kuzmin and F. Rocca, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 014302.
26. P. Fornasini, R. Grisenti, M. Dapiaggi, G. Agostini and T. Miyanaga, J. Chem. Phys., 2017, 147, 044503.
27. P. Fornasini, R. Grisenti, T. Irifune, T. Shinmei, O. Mathon, S. Pascarelli and A. Rosa, J. Phys.: Condens. Matter, 2018, 30, 245402.
28. A. Cuccoli, V. Tognetti, A. A. Maradudin, A. R. McGurn and R. Vaia, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 8839.
29. A. Cuccoli, V. Tognetti, A. A. Maradudin, A. R. McGurn and R. Vaia, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 7015.
30. A. Cuccoli, R. Giachetti, V. Tognetti, R. Vaia and P. Verrucchi, J. Phys.: Condens. Matter, 1995, 7, 7891.
31. A. Cuccoli, V. Tognetti, R. Vaia and P. Verrucchi, Phys. Rev. Lett., 1996, 77, 3439.
32. T. Fujikawa, T. Miyanaga and T. Suzuki, J. Phys. Soc. Jpn., 1997, 66, 2897.
33. T. Yokoyama, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 3423.
34. https://pfxafs.kek.jp/beamlies/bl-9c/ .
35. A. L. Ankudinov, A. I. Nesvizhskii and J. J. Rehr, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 115120.
36. H. M. Otte, J. Appl. Phys., 1962, 33, 1436.
37. J. H. L. Voncken and Th. W. Verkroost, Powder Diffr., 1997, 12, 228.
38. L. Reinhard, B. Schönfeld and G. Kostorz, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 1727.
39. M. S. Daw and M. I. Baskes, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 29, 6443.
40. S. M. Foiles, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 32, 3409.
41. M. I. Baskes, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 2727.
42. B.-J. Lee, J.-H. Shim and M. I. Baskes, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 144112.
43. H.-S. Jang, K.-M. Kim and B.-J. Lee, Calphad, 2018, 60, 200.
44. G. Bianchini, M. Barucci, E. Pasca and G. Ventura, Meas. Sci. Technol., 2006, 17, 689.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp05035h

---