Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A method to capture the large relativistic and solvent effects on the UV-vis spectra of photo-activated metal complexes†
Joel
Creutzberg
 *a and
Erik Donovan
Hedegård
*a and
Erik Donovan
Hedegård
 ab
ab
aDivision of Theoretical Chemistry, Lund University, Lund, Sweden. E-mail: joel.creutzberg@teokem.lu.se
bDepartment of Physics, Chemistry and Pharmacy, Campusvej 55, 5230 Odense, Denmark. E-mail: erdh@sdu.dk
First published on 20th January 2023
Abstract
We have recently developed a method based on relativistic time-dependent density functional theory (TD-DFT) that allows the calculation of electronic spectra in solution (Creutzberg, Hedegård, J. Chem. Theory Comput.18, 2022, 3671). This method treats the solvent explicitly with a classical, polarizable embedding (PE) description. Furthermore, it employs the complex polarization propagator (CPP) formalism which allows calculations on complexes with a dense population of electronic states (such complexes are known to be problematic for conventional TD-DFT). Here, we employ this method to investigate both the dynamic and electronic effects of the solvent for the excited electronic states of trans-trans-trans-[Pt(N3)2(OH)2(NH3)2] in aqueous solution. This complex decomposes into species harmful to cancer cells under light irradiation. Thus, understanding its photo-physical properties may lead to a more efficient method to battle cancer. We quantify the effect of the underlying structure and dynamics by classical molecular mechanics simulations, refined with a subsequent DFT or semi-empirical optimization on a cluster. Moreover, we quantify the effect of employing different methods to set up the solvated system, e.g., how sensitive the results are to the method used for the refinement, and how large a solvent shell that is required. The electronic solvent effect is always included through a PE potential.
I. Introduction
Platinum(II) complexes have been used in cancer treatment since the 1970s. The prototypical complex for cancer treatment is cis-[Pt(NH3)2Cl2], but several complexes with similar motifs are in use today.2–4 Unfortunately, treatments cause severe side effects.5 The side effects occur since cis-[Pt(NH3)2Cl2] reacts with other bio-molecules in the body rather than the target molecules inside the cancer cells. To circumvent these side effects, it has been suggested to use a so-called pro-drug.3 A pro-drug is inactive (and thus harmless for the body) until activation at the site of the tumor. Octahedral Pt(IV) complexes have been investigated as pro-drugs over the last few years.3,4,6 These complexes are kinetically stable d6 complexes until they are photo-activated. The use of photo-activation combined with a pro-drug has been coined photo-activated anti-cancer therapy (PACT).6,7Different octahedral Pt(IV) complexes have been investigated for use in PACT. A class of complexes that have received considerable attention is diazido Pt(IV) complexes.6,8 One of the most simple of these complexes is shown in Fig. 1. The advantage of diazido complexes is their inertness with respect to bio-reducing agents (such as glutathione).9
 | ||
| Fig. 1 Lewis structures of trans-trans-trans-[Pt(N3)2(OH)2(NH3)2] (trans-Pt) investigated in this paper. | ||
These complexes are known to decompose after irradiation, but the mechanistic pathways of this decomposition are still not understood.6 A more complete understanding of the photo-physical properties of Pt(IV) pro-drugs is the next step to further develop PACT.
Theoretical methods based on time-dependent density functional theory (TD-DFT) can help unravel the photo-physical properties.10 Investigations by Salassa et al.11 employed this method to understand and characterize the UV-vis spectrum of cis-trans-cis-[Pt(N3)2(OH)2(NH3)2]. They found that excitations are mainly of a ligand-to-metal-charge-transfer (LMCT) character, involving orbitals on azide ligands and platinum. The resulting excited states were found to be dissociative with respect to N3−. Triplet states were also speculated to be involved in decomposition. In a later paper by Sokolov et al.12, similar results were obtained for both trans-trans-trans-[Pt(N3)2(OH)2(NH3)2] and cis-trans-cis-[Pt(N3)2(OH)2(NH3)2], albeit with the difference that excitation facilitated the release of two azide radical ligands.
Calculations of the excited state manifold of platinum complexes are generally expected to require relativistic effects. These effects have mostly been included with either scalar relativistic Douglas–Kroll–Hess (DKH) to second order12 or effective core potentials (ECPs).11 None of these methods include spin–orbit coupling (SOC) explicitly. In a recent investigation, we investigated the effect of SOC on the calculated UV-vis spectra of the Pt(IV) complexes trans-trans-trans-[Pt(N3)2(OH)2(NH3)2] and cis-trans-cis-[Pt(N3)2(OH)2(NH3)2], employing a four-component linear response framework.13 One of our main findings was that the SOC led to a much denser manifold of electronic states and many of these states were of mixed singlet–triplet character. Similar findings were also observed in a recent study by Freitag and González, using a relativistic DMRG-SCF method to study the excited state dissociation reactions.14
Thus, the explicit inclusion of SOC is important to correctly access the excited state manifold of the Pt(IV) complexes used in PACT. Yet, even with the inclusion of SOC, the solvent (usually water) employed in the experimental work may also have a large impact on the excited states and UV-vis spectra. Accordingly, the next step is to investigate the effect of the solvent: although we will not study the full dissociation mechanism here, we note that there are strong indications that the decomposition mechanisms of the Pt(IV) complexes are solvent dependent.15–17 However, previous theoretical studies either ignored12–14 the solvent or included it through continuum models,11 which are known to be inaccurate for solvents prone to form hydrogen bonds.
Over the last few years, we and others have developed models that explicitly include the solvent, employing a polarizable embedding (PE) model.18–23 The PE model includes the environment classically with multipoles and polarizabilities, allowing mutual polarization between the quantum mechanical and classical subsystems. Within non-relativistic frameworks, the PE models have been shown to work well for electronic spectroscopy.24–28 The PE models were only recently introduced to a relativistic framework1,29,30 and applications of this methodology have therefore been rare. The initial calculations have demonstrated that the electronic solvent effect on trans-trans-trans-[Pt(N3)2(OH)2(NH3)2] is substantial.1 However, the structural and/or dynamical effects of the solvent have not been investigated. In this investigation, we undertake a more systematic investigation of solvent effects on the trans-trans-trans-[Pt(N3)2(OH)2(NH3)2] complex. We will mainly address how the structural changes in the environment influence the spectra by performing molecular dynamics simulations. The dynamics are obtained through classical simulations, but since no force field exists for the platinum complexes, we have constructed one based on calculated charges and the molecular Hessian. We have set up a method in which snapshots extracted from the classical simulation are refined by cluster calculations, employing first a semi-empirical method and then DFT. Part of this paper is also devoted to quantifying to what degree the calculated UV-vis spectra depend on the QM methods employed in this setup. Finally, we also investigate the effect of including water molecules explicitly in the QM region.
II. Theory
In the PE model, the system is divided into a region that is treated using methods from quantum chemistry (QM), and a region treated classically. The classical region is parameterized by electrostatic multipoles and point polarizabilties, calculated from a quantum mechanical method by fragmenting the solvent into individual molecules. The total energy expression is then| E = EQM + Ees + Eind + Eenv, | (1) |
 | (2) |
In eqn (2), we have used a second quantization formalism. Thus, Dpq is an element of the one-electron reduced density matrix, hpq is an integral over the kinetic energy and nuclear attraction one-electron operators, and jpq contains the Coulomb integral for electron repulsion (and scaled exchange integrals if hybrid functionals are used). Finally, Exc[ρ] and Enn contain the correlation–exchange functional and nuclear repulsion, respectively. For brevity, the former is only a functional of the density, ρ. We refer to the literature for explicit expressions31 of the terms involved in eqn (2). Note that in the second-quantization formalism, non-relativistic, two- or four-component frameworks are formally equivalent and the form of eqn (2) is therefore similar in all three cases. However, the form of the integrals will differ between non-relativistic, two- or four-component frameworks and modifications of the Exc[ρ] term are also required in a relativistic framework. The largest difference is seen in one-electron integrals, hpq, where the integrals in a four-component framework are over the operator
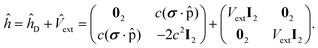 | (3) |
 | (4) |
The energy Ees in eqn (1) accounts for the interaction between the electrostatic multipoles in the environment and the QM density, whereas the energy, Eind, accounts for the mutual polarization of the QM and MM densities (the latter through the point polarizabilities). These two energies can be represented by the operators, ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) es and
es and ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) ind, that are added to the vacuum Kohn–Sham operator
ind, that are added to the vacuum Kohn–Sham operator
 | (5) |
In this formalism, μind is a vector containing the induced dipole moments calculated as34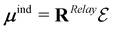 . The definition of RRelay can be found in the literature (see e.g. ref. 30) whereas
. The definition of RRelay can be found in the literature (see e.g. ref. 30) whereas  is the total electric field, here given for a specific site s in the environment
is the total electric field, here given for a specific site s in the environment
 | (6) |
The total electric field has components from nuclei in the QM region,  , electrons in the QM region,
, electrons in the QM region,  , and the multipoles on the remaining sites,
, and the multipoles on the remaining sites,  , where we again refer to the literature for details.35 In the following, we will use the short-hand form
, where we again refer to the literature for details.35 In the following, we will use the short-hand form ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) ind for the term involving the induced dipoles.
ind for the term involving the induced dipoles.
In this work, we employ linear response theory36,37 to calculate UV-vis spectra. The linear response formalism is often denoted as TD-DFT. In this formalism, we solve the equation
| κz= −(E[2]−zS[2])−1EX[1]. | (7) |
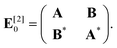 | (8) |
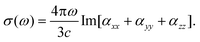 | (9) |
The calculation of the signal cross section is performed using an input-defined frequency, ω, meaning that the CPP method has the same cost in all frequency ranges. This is unlike traditional response solvers, which obtain the frequency by solving for a number of roots, starting from the lowest ones (thus the total number of roots may become very high for regions with a dense population of electronic states).
We have previously shown how the modification of eqn (7) due to the PE framework leads to the modified linear response equations for both the regular linear response18,30 and the CPP model.1,43 In short, these changes are
 | (10) |
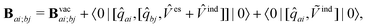 | (11) |
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) es and Vind are defined in eqn (5) and Ṽind is a transformed form of Vind (a more detailed derivation can be found in the literature).1,30,38,44 The first term accounts for the effect due to the multipoles and ground-state polarization. The second term accounts for the change in the solvent response due to the change of electron density in the QM system during electronic excitation.
es and Vind are defined in eqn (5) and Ṽind is a transformed form of Vind (a more detailed derivation can be found in the literature).1,30,38,44 The first term accounts for the effect due to the multipoles and ground-state polarization. The second term accounts for the change in the solvent response due to the change of electron density in the QM system during electronic excitation.
Finally, we introduce effective external field (EEF) effects.45,46 This contribution arises as the external magnetic field that induces an electronic transition, also induces a field, 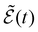 , within the environment. This can be accounted by modifying the total induced field in eqn (6) to
, within the environment. This can be accounted by modifying the total induced field in eqn (6) to  within the linear response framework. The result is that the property gradients are modified (see e.g. ref. 30 for a derivation)
within the linear response framework. The result is that the property gradients are modified (see e.g. ref. 30 for a derivation)
 | (12) |
The last term, containing  , is responsible for the EEF effect.
, is responsible for the EEF effect.
III. Computational details
Static structures and potentials of the trans-Pt complex in water
Since the structures obtained during MD simulations are purely classical, we refine these structures through quantum mechanical optimizations on smaller clusters (more details are given in the next subsection). We initially employed a fast semi-empirical method for this refinement to save computer time. The structures were subsequently refined using DFT. We decided to employ a single structure to investigate the effect of the additional DFT refinement on the calculated UV-vis spectrum, before embarking on optimizing a large number of snapshots. Rather than employing a random snapshot from the classical MD, the structure was taken from our previously optimized solvated trans-trans-trans-[Pt(N3)2(OH)2(NH3)2] (trans-Pt) complex.1 We recapitulate the optimization here: we employed QM/MM in a box (35 × 35 × 35 Å) of explicit (frozen) water molecules, optimizing only the trans-trans-trans-[Pt(N3)2(OH)2(NH3)2] complex. This optimization was followed by two subsequent optimizations. First, we made a cutout including the water molecules within 6 Å from the platinum complex. Structure optimizations of this cluster were then carried out relaxing the platinum complex and all water molecules within 4 Å, while the rest were kept frozen. This was performed using the PBEh-3c47 method. Next, we refined this optimization using the BP86 functional48 and a def2-sv(p)49,50 basis set. We chose this functional since it is computationally efficient and has been shown to provide structures similar to B3LYP in accuracy for transition metal complexes.51 These calculations were performed in ORCA.52 Finally, a 6 Å sphere was re-inserted into the original box and a 10 Å sphere was cut out (see Fig. 2; the PBEh-3c systems are shown as examples). The largest cluster of 10 Å contains 282 water molecules, whereas the 6 Å cluster contains 79 water molecules. Since we also employed these structures in ref. 1 we can re-use previously obtained PE potentials.1Force field for trans-Pt
We developed a force field (bonded model) for the trans-pt complex, employing the MCPB.py program.53 This program extracts bonding parameters from the molecular Hessian and employs the RESP model for the electrostatics. The structure optimization, force constants, and Merz–Kollman RESP charges were obtained from calculations using the B3LYP48,54,55 functional in Gaussian 16.56 The 6-31G*57,58 basis set was employed for the ligands while the effective core potential SDD59 was employed for the platinum atom. Default radii were used for all atoms. A final adjustment of the force field parameters was performed by setting the angle between the nitrogen atoms in the N3− ligands to 180 degrees, in order to ensure that they were kept linear during simulations.Dynamics and polarizable embedding potentials
Using the constructed force field, the complex was solvated in a box (10 × 10 × 10 Å) of explicit TIP3P water molecules. Minimization was then performed preceded by two MDs to ensure that the platinum complex maintained a reasonable structure: first a MD for 20 fs at a constant pressure using SHAKE.60 After ensuring the integrity of the platinum complex, we continued this MD for 1 ns. Thereafter, an equilibration simulation was performed at constant pressure for 2 ns before the final production MD was performed for 20 ns (also at a constant pressure). All calculations were performed using AMBER 16.61 From the trajectory, 49 structures were extracted with a minimum time separation of 0.2 ns. After this, the same QM optimization procedure as for the first single structure (trans-Pt complex in water) was carried out on 6 Å sphere cutouts from the structures, but no re-insertion into the original box was performed. Thus, the final systems are all 6 Å, which (as we show below) is sufficient.Embedding potentials were calculated for the snapshots described above, using the B3LYP functional with the A-6-31PGP basis set and included multipole moments up to quadropoles and anisotropic polarizabilities. Fragmentation of the environment was carried out using the PyFrame62 script, where each fragment in the environment consisted of a water molecule. The localized multipoles and polarizabilities were obtained from the LoProp method63 as implemented in DALTON64,65 (the level of theory employed for the potentials is identical to the potentials from ref. 1).
Frequency dependent polarizabilities
CPP calculations were carried out in DIRAC66 in the UV-vis range (6–2 eV) using the CAM-B3LYP67 functional and a γ value of 1000 cm−1 (0.124 eV). We employed the following Hamiltonians: Levy-Leblond (non-relativistic limit), Dyall's spinfree Hamiltonian (scalar relativistic) and X2C. We also initially carried out linear response calculations using both four-component Dirac–Kohn–Sham and X2C Hamiltonians employing 80 roots with a conventional linear response solver. This was performed in order to ensure that X2C was sufficient to reproduce four-component results. Seeing that larger errors are expected from the choice of the functional or setup of the environment, we have not included the four-component calculations in the paper (they are provided in the ESI†). Polarizable embedding (PE) was included in the calculations using the PeLib library (which is interfaced to DIRAC); moreover, effective external field (EEF) calculations were included. All calculations employed the dyall.v2z68 basis set for the platinum atom, while the ligands employed the def2-sv(p) basis set. For a few snapshots, we additionally performed CPP calculations using B3LYP (and the same double-zeta basis sets as above) or CAM-B3LYP and triple zeta basis sets (the results from these calculations are shown in Fig. S4 and S5, ESI†). The basis sets were always used uncontracted.We will not discuss the non-relativistic results in the following since they (as expected) were quite different from the X2C calculations.
IV. Results and discussion
We first discuss the effect of optimizing the Pt(IV) complex in a small cluster of water molecules after the initial solvation. We next compare the spectra (and solvent shifts) resulting from employing the X2C and scalar relativistic Hamiltonians for the PE regions of different sizes. We additionally investigate the effects of extending the QM region with selected water molecules. These initial investigations will serve to justify the method used for the dynamics, which is performed in the last subsection.A. Structural solvent effects from the method employed in refinement
We start by comparing the spectra obtained from a PBEh-3c optimized structure to those optimized using BP86. To appropriately separate the structural and electronic solvent effects, we first compare the two spectra without a PE description of the environment, i.e., a vacuum calculation on the two structures (Fig. 3a). Since we previously showed that the electronic effect due to PE can significantly change the spectrum, we repeated the comparison while including a PE environment within 6 and 10 Å spheres (Fig. 3b). Yet, both vacuum and solvated UV-vis spectra show that the spectra obtained for the BP86 optimized structure are significantly red-shifted in comparison to the PBEh-3c spectra (peak positions for the individual calculations are given in Table 1): in the vacuum case, the red-shifts are 0.61 and 0.41 eV, respectively. When including the electronic solvent effect with PE, the corresponding shifts are both 0.48 eV for the 6 Å system, whereas they are 0.41 and 0.54 eV for the 10 Å system. The absorption cross-sections also change significantly from vacuum to solvent and this is discussed further in the next subsection. Here, we only note that for the absorption cross-sections in a vacuum, the first peak is 0.24 a.u. higher for the PBEh-3c structure than the first peak of the BP86 structure, while the second peak of PBEh-3c is 0.42 a.u. lower than that of BP86 (see Fig. 3a and Table 1). When including the 6 Å environment, similar changes are observed, with the first peak from the PBEh-3c structure being 0.56 a.u. higher and the second peak being 0.26 a.u. lower when compared to the peaks of the spectra from the BP86 structure (Fig. 3b and Table 1). For the 10 Å environment, the PBEh-3c structure again has a higher absorption cross-section for the first peak (0.52 a.u.), and lower (0.29 a.u.) for the second peak compared to BP86 (Fig. 3b and Table 1).| Method | Environment | ΔE1 [σ(ω)] | ΔE2 [σ(ω)] |
|---|---|---|---|
| PBEh-3c | vac | 4.38 (1.557) | 5.13 (1.315) |
| BP86 | vac | 3.97 (1.319) | 4.52 (1.740) |
| PBEh-3c | solv. (6 Å) | 4.93 (3.243) | 5.74 (0.599) |
| BP86 | solv. (6 Å) | 4.45 (2.685) | 5.27 (0.858) |
| PBEh-3c | solv. (10 Å) | 4.93 (3.297) | 5.67 (0.597) |
| BP86 | solv. (10 Å) | 4.38 (2.779) | 5.27 (0.885) |
In conclusion, both the underlying structure and the electronic contribution of the solvent have large effects on the resulting UV-vis spectra. These large effects prompted us to investigate the underlying structures. These are shown as overlays in Fig. 4. In this figure, some of the water molecules can be seen to overlap exactly and these correspond to the ones kept frozen during the optimizations. However, both water molecules close to the trans-Pt complex and the complex itself show significant structural changes after optimization with BP86. One of the goals of employing a semi-empirical method for the refinement was to investigate whether the snapshots obtained from the classical dynamics can be refined in a computationally cheap manner. Unfortunately, the changes in the structures combined with accompanying shifts in both energies and cross sections strongly indicate that this is not the case. Thus, we here employ the higher level of theory, e.g., BP86. We note for the particular structure employed here, the highest peak of the BP86 result in Fig. 3b is only 0.03 eV off from the experimental peak at 4.35 eV,69 while that of PBEh-3c predicts a peak that is 0.58 eV (33 nm) shifted from the experiment. One of the peaks in the vacuum spectrum of PBEh-3c is also at 4.38 eV, but seeing that the results shift to 4.93 eV due to the electronic effect of the solvent, this result is likely fortitous. In fact, we show in a section below that the result from BP86 (including PE) also is likely to be fortuitous, since including dynamical effects will move the result slightly away from the experimental maximum.
 | ||
| Fig. 4 Solvated trans-Pt system optimized with PBEh-3c (green) or BP86. Only parts of the full 6 Å systems are shown. | ||
B. Solvent shifts with different choices of Hamiltonian
In the next series of calculations, we compared the environmental effect obtained by different choices of the underlying Hamiltonian: we either included only scalar relativistic effects (SR) or employ X2C. Systems with both 6 Å and 10 Å solvation spheres are investigated (but we exclusively use the structure refined with BP86). The resulting UV-vis spectra are shown in Fig. 5(a) and (b) and the peak positions are provided in Table 2. From vacuum to solvent, it is seen that the inclusion of PE yields a significant change in the spectra, but this change is qualitatively similar for SR and X2C Hamiltonians: the two distinct peaks in the vacuum spectra around 3.5–4.5 eV become a single peak, whereas a new peak appears at higher energies in the solvated spectra. Thus, we can conclude that the difference is not related to the inclusion of SOC, but exclusively an effect of the solvent. To understand the observed difference, we analyzed the transitions in the response vectors, employing the 10 Å system. All peaks are LMCT transitions involving donor orbitals on the N3− ligands and acceptor orbitals on the Pt center. The d-orbitals contributing to both peaks in the X2C spectra are along the Pt–N3− bond axis. Meanwhile, the vacuum spectra have contributions from the d-orbital along the Pt–OH− axis and the d-orbital in the N3−–NH3 plane. The difference between the contributing d-orbitals can explain the differences between the vacuum and PE spectra (the SR and X2C calculations employ the same structure for the trans-Pt complex).| Method | Environment | ΔE1 [σ(ω)] | ΔE2 [σ(ω)] |
|---|---|---|---|
| SR | vac | 3.97 (1.456) | 4.52 (1.964) |
| SR | solv. (6 Å) | 4.38 (3.356) | 5.20 (1.043) |
| SR | solv. (10 Å) | 4.38 (3.487) | 5.12 (1.075) |
| X2C | vac | 3.97 (1.319) | 4.52 (1.740) |
| X2C | solv. (6 Å) | 4.45 (2.685) | 5.27 (0.858) |
| X2C | solv. (6 Å) + EEF | 4.45 (2.367) | 5.27 (0.785) |
| X2C | solv. (10 Å) | 4.38 (2.779) | 5.27 (0.883) |
| X2C | solv. (10 Å) + EEF | 4.38 (2.412) | 5.27 (0.795) |
Due to the rather dramatic effect of PE on the spectra, it is not meaningful to compare the solvent shift from the vacuum to the PE environment of the SR and X2C Hamiltonians. However, we can compare the final, solvated excitation energies and peak maxima: the excitation energies (taken as the energy of the peak maxima) are not very different between SR and X2C Hamiltonians. However, the absorption cross-sections at peak maxima change between the Hamiltonians. For the 6 Å system, the cross-sections are 22–25% lower for the X2C Hamiltonian. Interestingly, the inclusion of a larger environment does not induce any significant changes, as seen when moving from the 6 Å solvation sphere to the 10 Å solvation sphere, with only the second peak being slightly shifted to 0.07 eV and the absorption cross-section increases around 4%.
We have also investigated how taking the EEF effects into account changes the spectra (this investigation was only carried out for X2C). As expected, the excitation energies are not changed, while the absorption cross-sections decrease with 9 and 13% for the 10 Å solvation sphere (see Fig. 6 and Table 2). For the 6 Å solvation sphere, the corresponding changes in the absorption cross-sections for the peaks are a decrease with 9% and 11% when including EEF effects (see Table 2). Thus, we conclude that we can safely employ a 6 Å sphere to study the solvent effects, but an EEF should be included. In the next subsection, we will additionally attempt to include a few solvent molecules in the QM region.
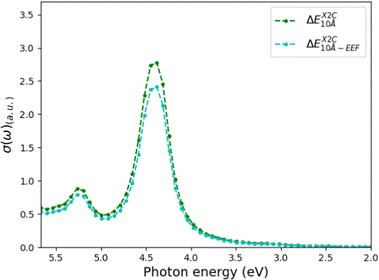 | ||
| Fig. 6 UV-vis spectra calculated using CAM-B3LYP and X2C with and without EEF effects included. The total system was 10 Å, using the BP86 refined structure. | ||
C. Inclusion of water molecules in the QM region
From the structure optimized with BP86, we included the five water molecules closest to the trans-Pt complex in the QM region (all water molecules within a 4.2 Å distance from the Pt atom). The corresponding UV-vis spectra are shown in Fig. 7(a), while the QM region is shown in Fig. 7(b). For the most intense peak, which is the only one seen experimentally, the effect of including QM water is much smaller than the effect of using a PBEh-3c refined structure. A slightly larger effect is seen for the higher energy peak, but the effect is still much smaller than the effect of using the refined structure. We carefully analyzed the response vectors to ensure that none of the excitations contained underlying transitions from the water molecules to the platinum complex (or vice versa). While this was not the case within the investigated frequency window, this will likely occur further into the high-energy region.D. Dynamic effects: conformations from MD
We have thus far only investigated the solvent effects for a single conformation. While this did provide insight into how a solvent can influence the features of UV-vis absorption spectra, dynamic effects are required to mimic experimental conditions. From a series of snapshots obtained from the classical MD simulation with subsequent refinement through QM optimizations, we obtained 49 spectra with X2C. The spectra of the various snapshots are shown in Fig. S2 (ESI†); they generally have one peak (all peak positions are reported in Table S3, ESI†). We here show only the mean spectrum, as well as the spectra with peak maxima mostly red- and blue-shifted from the mean, respectively (Fig. 8a). The corresponding absorption cross-sections and excitation energies at peak maxima are provided in Table 3. From the spectra that display the largest difference in the position of the peak maxima, the span of potential peak maxima ranges from 4.31 to 5.13 eV, i.e., 0.8 eV. This demonstrates the importance of dynamic solvent effects. | ||
| Fig. 8 (a) Average spectra and the spectra of the structures that are shifted the most compared to the average peak. (b) Comparison of the averaged spectra of PE with EEF and only PE. | ||
| Peak | Energy [eV] | σ(ω) [a.u.] |
|---|---|---|
| Mean max. | 4.79 ± 0.23 | 2.33 ± 0.52 |
| ΔEmax(+) | 5.13 | 2.72 |
| ΔEmax(−) | 4.31 | 2.10 |
All spectra calculations were carried out both with and without EEF effects. We mainly consider the values including the EEF effects, but note that the absorption cross-section decreases with 24% when we include the EEF effect. The mean spectra with and without EEF are shown in Fig. 8(b).
Previous investigations employing range-separated functionals found that these calculations provide excellent agreement with experimental results for both the shape of the spectra and the energy at the absorption maximum.12,13 However, these investigations were carried out without the inclusion of dynamic and electronic solvent effects. In light of our present results, it is clear that benchmarking should include these effects. Yet, the inclusion of dynamics does not bring the computed spectra closer to the peak maximum of the experimental spectrum. The computed mean peak position is 4.79 ± 0.23 eV, compared to the experimental 4.35 eV.69 Several underlying causes for this apparent discrepancy may be found: one of them being the choice of functional. To investigate this possibility, we computed the spectra for 5 structures using B3LYP, employing 5 randomly selected snapshots (see Fig. S4, ESI†). We found that the peaks of the CAM-B3LYP spectra are blue-shifted compared to those of B3LYP. The average blue-shift is calculated to be 0.27 eV. If the calculated average of 4.79 eV from Table 3 is shifted with 0.27 eV, the calculated result is within the experimental results (including the uncertainty). Thus, the discrepancy is likely caused at least partially by a tendency for CAM-B3LYP to blue shift excitation energies, and this blue shift likely cancels with the lack of the dynamical and electronic solvent effects in previous studies.12,13 Moreover, a blueshift of CAM-B3LYP has been observed previously: a benchmark study of vertical excitation energies for TD-DFT against CC2 found that several functionals (among them CAM-B3LYP) overestimated vertical excitation energies with 0.2–0.3 eV.70 Another benchmark study (focusing on transition metal complexes) yielded a similar conclusion.71 For three of the five snapshots used to compare B3LYP and CAM-B3LYP, we also investigated the effect of extending the basis set to the triple-zeta quality, but this cannot explain the blue shift (see Fig. S5, ESI†).
We also note that some of the deviations from the experiment in the present investigation may be caused by inaccuracies in the sampled structures from the subsequent restricted QM refinement. We investigated if the blueshift could be correlated with a simple structural parameter. In the ESI† (Fig. S6), we show how the peak maximum depends on the Pt–N3 bond distance for the considered snapshots. This distance was chosen due to the LMCT nature of the transition and the involvement of orbitals located on the azide ligands. The peak maxima are indeed sensitive to this distance, and distances smaller than the average usually result in transitions energies above the average. However, since we do not have a reference structure, it is not possible to isolate the blueshift to be an issue caused by the structure alone. We therefore leave this matter here. A reference structure may be obtained from ab initio MD, although it will come at the price of reduced sampling times or significantly increased computational demands. Despite the blueshift compared to experiment, our present results serve to quantify the importance of environment interactions on calculations of molecular properties, and therefore further emphasize the need for an explicit treatment of the environment.
Finally, we discuss whether our results are converged with respect to the sampling of solvent configurations. We have investigated the convergence in Table S2 (ESI†), where the average peak maxima and excitation energies are compiled in blocks of 10, 20, 30 (and so forth) snapshots. The calculated mean excitation energies and absorption cross-sections are converged after 20 snapshots. Thus, we do not expect significant errors due to the employed sampling method.
V. Conclusion
In this study, we have investigated the UV-vis absorption spectra of the trans-trans-trans-[Pt(N3)2(OH)2(NH3)2] (trans-Pt) complex embedded in various aqueous environments, using the relativistic CPP method combined with the PE model. The first part of the study involves a single structure based on trans-Pt optimized in water, employing either PBEh-3c or BP86 to refine the structure. The underlying structures have a large effect on the resulting spectra, and we chose here the theoretically best method (BP86). Thus, the following analysis employs structures obtained at the BP86 level. We also found that the spectrum computed without electronic solvent effects is rather different, compared to those including PE. However, extending the environment from 6 Å to 10 Å only has a minor effect on the spectra, leading to the conclusion that a smaller solvation sphere of 6 Å is sufficient. Extending the QM region by including the nearest five water molecules likewise has only a benign effect on the calculated spectrum.Regarding the inclusion of dynamics (with subsequent QM optimizations), we found that the individual snapshots lead to rather different spectra. While this emphasizes that the explicit treatment of the environment is required, the resulting average excitation energy (taken as the average peak maximum positions) is somewhat blue-shifted, compared to the experiment. Yet, the excellent agreement with the experiment in previous investigations with range-separated functionals12,13 is in light of our present results likely to be somewhat fortuitous due to the lack of dynamic (and electronic) solvent effects. Indeed, employing global hybrid functionals such as B3LYP yields spectra that are systematically red-shifted compared to CAM-B3LYP. This shows the importance of including a realistic solvent environment in functional benchmarking. Finally, the EEF effects significantly alter the absorption cross-sections and should be included.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
E. D. H. thanks The Villum Foundation, Young Investigator Program (grant no. 29412), the Swedish Research Council (grant no. 2019-04205), and the Independent Research Fund Denmark (grants no. 0252-00002B and no. 2064-00002B) for support.References
- J. Creutzberg and E. D. Hedegård, Polarizable Embedding Complex Polarization Propagator in Four- and Two-Component Frameworks, J. Chem. Theory Comput., 2022, 18(6), 3671–3686 CrossRef CAS PubMed.
- B. Rosenberg, L. Vancamp, J. Trosko and V. Mansour, Platinum Compounds: a New Class of Potent Antitumour Agents, Nature, 1969, 05(222), 385–386 CrossRef PubMed.
- T. C. Johnstone, K. Suntharalingam and S. J. Lippard, The next generation of platinum Drugs: targeted Pt(II) agents, nanoparticle delivery, and Pt(IV) prodrugs, Chem. Rev., 2016, 116, 3436–3486 CrossRef CAS PubMed.
- M. Imran, W. Ayub, I. S. Butler and Zu Rehman, Photoactivated platinum-based anticancer drugs, Coord. Chem. Rev., 2018, 376, 405–429 CrossRef CAS.
- R. Oun, Y. E. Moussa and N. J. Wheate, The side effects of platinum-based chemotherapy drugs: a review for chemists, Dalton Trans., 2018, 47(19), 6645–6653 RSC.
- C. Imberti, P. Zhang, H. Huang and P. J. Sadler, New Designs for Phototherapeutic Transition Metal Complexes, Angew. Chem., Int. Ed., 2020, 59, 61–73 CrossRef CAS PubMed.
- S. Bonnet, Why develop photoactivated chemotherapy?, Dalton Trans., 2018, 47, 10330–10343 RSC.
- H. Shi, C. Imberti and P. J. Sadler, Diazido platinum(iv) complexes for photoactivated anticancer chemotherapy, Inorg. Chem. Front., 2019, 6(7), 1623–1638 RSC.
- N. A. Kratochwil, Z. Guo, P. del Socorro Murdoch, J. A. Parkinson, P. J. Bednarski and P. J. Sadler, Electron-Transfer-Driven Trans-Ligand Labilization: A Novel Activation Mechanism for Pt(IV) Anticancer Complexes, J. Am. Chem. Soc., 1998, 120(32), 8253–8254 CrossRef CAS.
- E. D. Hedegård and J. Creutzberg, New relativistic quantum chemical methods for understanding light-induced therapeutics, Dalton. Trans., 2022, 51, 16055–16064 RSC.
- L. Salassa, H. I. A. Phillips and P. J. Sadler, Decomposition pathways for the photoactivated anticancer complex cis,trans,cis-[Pt(N3)2(OH)2(NH3)2]: insights from DFT calculations, Phys. Chem. Chem. Phys., 2009, 11, 10311–10316 RSC.
- A. Y. Sokolov and H. F. Schaefer III, Ground and excited state properties of photoactive platinum (IV) diazido complexes: Theoretical considerations, Dalton Trans., 2011, 40, 7571–7582 RSC.
- J. Creutzberg and E. D. Hedegård, Investigating the inuence of relativistic effects on absorption spectra for platinum complexes with light-activated activity against cancer cells, Phys. Chem. Chem. Phys., 2020, 22(46), 27013–27023 RSC.
- L. Freitag and L. González, The Role of Triplet States in the Photodissociation of a Platinum Azide Complex by a Density Matrix Renormalization Group Method, J. Phys. Chem. Lett., 2021, 12(20), 4876–4881 CrossRef CAS PubMed.
- H. I. A. Phillips, L. Ronconi and P. J. Sadler, Photoinduced Reactions of cis,trans,cis-[PtIV (N3)2(OH)2(NH3)2] with 1-Methylimidazole, Chem. – Eur. J., 2009, 15, 1588–1596 CrossRef CAS PubMed.
- L. Ronconi and P. J. Sadler, Unprecedented carbon-carbon bond formation induced by photoactivation of a platinum(iv)-diazido complex, Chem. Commun., 2008, 235–237 RSC.
- L. Ronconi and P. J. Sadler, Photoreaction pathways for the anticancer complextrans,trans,trans-[Pt(N3)2(OH)2(NH3)2], Dalton Trans., 2011, 40, 262–268 RSC.
- J. M. Olsen, K. Aidas and J. Kongsted, Excited states in solution through polarizable embedding, J. Chem. Theory Comput., 2010, 6, 3721–3734 CrossRef CAS.
- K. Sneskov, T. Schwabe, J. Kongsted and O. Christiansen, The polarizable Coupled Cluster method, J. Chem. Phys., 2011, 134, 104108 CrossRef PubMed.
- E. D. Hedegård, N. H. List, H. J. A. Jensen and J. Kongsted, The multi-configuration self-consistent field method within a polarizable embedded framework, J. Chem. Phys., 2013, 139, 044101 CrossRef PubMed.
- E. D. Hedegård, J. M. H. Olsen, S. Knecht, J. Kongsted and H. J. A. Jensen, Polarizable embedding with a multiconfiguration short-range density functional theory linear response method, J. Chem. Phys., 2015, 114, 1102–1107 Search PubMed.
- E. D. Hedegård and M. Reiher, Polarizable Embedding Density Matrix Renormalization Group, J. Chem. Theory Comput., 2016, 12, 4242–4253 CrossRef.
- C. Steinmann, P. Reinholdt, M. S. Nørby, J. Kongsted and J. M. H. Olsen, Response properties of embedded molecules through the polarizable embedding model, Int. J. Quantum Chem., 2018, 119(1), e25717 CrossRef.
- M. Bondanza, M. Nottoli, L. Cupellini, F. Lipparini and B. Mennucci, Polarizable embedding QM/MM: The future gold standard for complex (bio)systems?, Phys. Chem. Chem. Phys., 2020, 22, 14433–14448 RSC.
- L. V. Slipchenko, Solvation of the excited states of chromophores in polarizable environment: Orbital relaxation versus polarization, J. Phys. Chem. A, 2010, 114, 8824–8830 CrossRef CAS PubMed.
- K. Sneskov, T. Schwabe, O. Christiansen and J. Kongsted, Scrutinizing the effects of polarization in QM/MM excited state calculations, Phys. Chem. Chem. Phys., 2011, 13, 18551–18560 RSC.
- A. Defusco, N. Minezawa, L. V. Slipchenko, F. Zahariev and M. S. Gordon, Modeling solvent effects on electronic excited states, J. Phys. Chem. Lett., 2011, 2, 2184–2192 CrossRef CAS.
- M. T. P. Beerepoot, A. H. Steindal, K. Ruud, J. M. H. Olsen and J. Kongsted, Convergence of environment polarization effects in multiscale modeling of excitation energies, Comput. Theory Chem., 2014, 1040–1041, 304–311 CrossRef CAS.
- K. Krause, M. Bauer and W. Klopper, Approaching Phosphorescence Lifetimes in Solution: The Two-Component Polarizable-Embedding Approximate Coupled-Cluster Method, J. Chem. Theory Comput., 2016, 12(6), 2853–2860 CrossRef CAS PubMed.
- E. D. Hedegård, R. Bast, J. Kongsted, J. M. H. Olsen and H. J. A. Jensen, Relativistic polarizable embedding, J. Chem. Theory Comput., 2017, 13, 2870–2880 CrossRef PubMed.
- T. Saue and T. Helgaker, Four-component relativistic Kohn-Sham theory, J. Comput. Chem., 2002, 23, 814–823 CrossRef CAS PubMed.
- T. Saue, R. Bast, A. S. P. Gomes, H. J. A. Jensen, L. Visscher and I. A. Aucar, et al., The DIRAC code for relativistic molecular calculations, J. Chem. Phys., 2020, 152, 204104 CrossRef CAS PubMed.
- T. Saue, Relativistic hamiltonians for chemistry: A primer, ChemPhysChem., 2011, 12, 3077–3094 CrossRef CAS PubMed.
- J. Applequist, J. R. Carl and K. K. Fung, An atom dipole interaction model for molecular polarizability. Application to polyatomic molecules and determination of atom polarizabilities, J. Am. Chem. Soc., 1972, 94, 2952–2960 CrossRef CAS.
- E. D. Hedegård, N. H. List, H. J. A. Jensen and J. Kongsted, The multi-configuration self-consistent field method within a polarizable embedded framework, J. Chem. Phys., 2013, 139(4), 044101 CrossRef PubMed.
- J. Olsen and P. Jørgensen, Linear and non-linear response functions for an exact state and foran MCSCF state, J. Chem. Phys., 1985, 82, 3235–3264 CrossRef CAS.
- T. Helgaker, S. Coriani, P. Jørgensen, K. Kristiansen, J. Olsen and K. Ruud, Recent advances inwave function based methods of molecular-property calculations, Chem. Rev., 2012, 112, 543–631 CrossRef CAS PubMed.
- P. Salek, T. Helgaker and T. Saue, Linear response at the 4-component relativistic densityfunctional level: application to the frequency-dependent dipole polarizability of Hg, AuHand PtH2, Chem. Phys., 2005, 311, 187–201 CrossRef CAS.
- S. Villaume, T. Saue and P. Norman, Linear complex polarization propagator in a fourcomponent Kohn-Sham framework, J. Chem. Phys., 2010, 133(6), 064105 CrossRef PubMed.
- P. Norman, D. M. Bishop, Aa Jörgen, H. Jensen and J. Oddershede, Near-resonant absorption in the time-dependent self-consistent field and multiconfigurational self-consistent field approximations, J. Chem. Phys., 2001, 115(22), 10323–10334 CrossRef CAS.
- K. Kristensen, J. Kauczor, T. Kjærgaard and P. Jørgensen, Quasienergy formulation of damped response theory, J. Chem. Phys., 2009, 131(4), 044112 CrossRef PubMed.
- J. Kauczor and P. Norman, Efficient Calculations of Molecular Linear Response Properties for Spectral Regions, J. Chem. Theory Comput., 2014, 10(6), 2449–2455 CrossRef CAS PubMed.
- M. N. Pedersen, E. D. Hedegård, J. M. H. Olsen, J. Kauczor, P. Norman and J. Kongsted, Damped Response Theory in Combination with Polarizable Environments: The Polarizable Embedding Complex Polarization Propagator Method, J. Chem. Theory Comput., 2014, 10, 1164–1171 CrossRef CAS PubMed.
- T. Saue and H. J. A. Jensen, Linear response at the 4-component relativistic level: Application to the frequency-dependent dipole polarizabilities of the coinage metal dimers, J. Chem. Phys., 2003, 118(2), 522–536 CrossRef CAS.
- L. Jensen, M. Swart and P. T. van Duijnen, Microscopic and macroscopic polarization within a combined quantum mechanics and molecular mechanics model, J. Chem. Phys., 2005, 122(3), 034103 CrossRef CAS PubMed.
- N. H. List, H. J. A. Jensen and J. Kongsted, Local electric fields and molecular properties in heterogeneous environments through polarizable embedding, Phys. Chem. Chem. Phys., 2016, 18(15), 10070–10080 RSC.
- S. Grimme, J. G. Brandenburg, C. Bannwarth and A. Hansen, Consistent structures and interactions by density functional theory with small atomic orbital basis sets, J. Chem. Phys., 2015, 143(5), 054107 CrossRef PubMed.
- A. D. Becke, Density-functional exchange-energy approximation with correct asymptotic behavior, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7(18), 3297–3305 RSC.
- F. Weigend, Accurate Coulomb-fitting basis sets for H to Rn, Phys. Chem. Chem. Phys., 2006, 8(9), 1057–1065 RSC.
- M. Bühl, C. Reimann, D. A. Pantazis, T. Bredow and F. Neese, Geometries of Third-Row Transition-Metal Complexes from Density-Functional Theory, J. Chem. Theory Comput., 2008, 4, 1449–1459 CrossRef PubMed.
- F. Neese, Software update: the ORCA program system, version 4.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8(1), e1327 Search PubMed.
- P. Li and K. M. Merz, MCPB.py: A Python Based Metal Center Parameter Builder, J. Chem. Inf. Model., 2016, 56(4), 599–604 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb and J. R. Cheeseman, et al., Gaussian∼16 Revision C.01. Gaussian Inc.Wallingford CT, 2016 Search PubMed.
- G. A. Petersson, A. Bennett, T. G. Tensfeldt, M. A. Al-Laham, W. A. Shirley and J. Mantzaris, A complete basis set model chemistry. I. The total energies of closed-shell atoms and hydrides of the first-row elements, J. Chem. Phys., 1988, 89(4), 2193–2218 CrossRef CAS.
- G. A. Petersson and M. A. Al-Laham, A complete basis set model chemistry. II. Open-shell systems and the total energies of the first-row atoms, J. Chem. Phys., 1991, 94(9), 6081–6090 CrossRef CAS.
- D. Andrae, U. Häußermann, M. Dolg, H. Stoll and H. Preuß, Energy-adjustedab initio pseudopotentials for the second and third row transition elements, Theor. Chim. Acta, 1990, 77, 123–141 CrossRef CAS.
- J. P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes, J. Comput. Phys., 1977, 23(3), 327–341 CrossRef CAS.
- D. Case, R. Betz, D. S. Cerutti, T. Cheatham, T. Darden and R. Duke, et al., Amber 16, University of California, San Francisco, 2016 Search PubMed.
- J. M. H. Olsen and P. Reinholdt, contributors. PyFraME: Python framework for Fragment-based Multiscale Embedding (version 0.4.0), 2021 Search PubMed.
- L. Gagliardi, R. Lindh and G. Karlström, Local properties of quantum chemical systems: The LoProp approach, J. Chem. Phys., 2004, 121(10), 4494–4500 CrossRef CAS PubMed.
- O. Vahtras LoProp for Dalton, 2014 Search PubMed.
- J. M. H. Olsen, S. Reine, O. Vahtras, E. Kjellgren, P. Reinholdt and K. O. Hjorth Dundas, et al., Dalton Project: A Python platform for molecular- and electronic-structure simulations of complex systems, J. Chem. Phys., 2020, 152, 214115 CrossRef CAS PubMed.
- DIRAC, a relativistic ab initio electronic structure program, Release DIRAC22 (2022), written by H. J. Aa. Jensen, R. Bast, A. S. P. Gomes, T. Saue and L. Visscher, with contributions from I. A. Aucar, V. Bakken, C. Chibueze, J. Creutzberg, K. G. Dyall, S. Dubillard, U. Ekströom, E. Eliav, T. Enevoldsen, E. Faßhauer, T. Fleig, O. Fossgaard, L. Halbert, E. D. Hedegård, T. Helgaker, B. Helmich-Paris, J. Henriksson, M. van Horn, M. Iliaš, R. Ch.Jacob, S. Knecht, S. Komorovský, O. Kullie, J. K. Lærdahl, C. V. Larsen, Y. S. Lee, N. H. List, H. S. Nataraj, M. K. Nayak, P. Norman, G. Olejniczak, J. Olsen, J. M. H. Olsen, A. Papadopoulos, Y. C. Park, J. K. Pedersen, M. Pernpointner, J. V. Pototschnig, R. di Remigio, M. Repisky, K. Ruud, P. Sałek, B. Schimmelpfennig, B. Senjean, A. Shee, J. Sikkema, A. Sunaga, A. J. Thorvaldsen, J. Thyssen, J. van Stralen, M. L. Vidal, S. Villaume, O. Visser, T. Winther, S. Yamamoto and X. Yuan.
- T. Yanai, D. P. Tew and N. C. Handy, A new hybrid exchange-correlation functional using the Coulomb-attenuating method (CAM-B3LYP), Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- A. Severo Pereira Gomes, K. Dyall and L. Visscher, Relativistic double-zeta, triple-zeta, and quadruple-zeta basis sets for the lanthanides La-Lu, Theor. Chem. Acc., 2010, 11(127), 369–381 Search PubMed.
- F. S. Mackay, J. A. Woods, H. Moseley, J. Ferguson, A. Dawson and S. Parsons, et al., A photoactivated trans-diammine platinum complex as cytotoxic as cisplatin, Chem. – Eur. J., 2006, 12, 3155–3161 CrossRef CAS PubMed.
- Y. Shao, Y. Mei, D. Sundholm and V. R. I. Kaila, Benchmarking the Performance of Time-Dependent Density Functional Theory Methods on Biochromophores, J. Chem. Theory Comput., 2020, 16(1), 587–600 CrossRef PubMed.
- C. Latouche, D. Skouteris, F. Palazzetti and V. Barone, TD-DFT Benchmark on Inorganic Pt(II) and Ir(III) Complexes, J. Chem. Theory Comput., 2015, 11(7), 3281–3289 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp04937f |
| This journal is © the Owner Societies 2023 |