Dynamic domain boundaries: chemical dopants carried by moving twin walls

Abstract

Domain walls and specifically ferroelastic twin boundaries are depositaries and fast diffusion pathways for chemical dopants and intrinsic lattice defects. Ferroelastic domain patterns act as templates for chemical structures where the walls are the device and not the bulk. Several examples of such engineered domain boundaries are given. Moving twin boundaries are shown to carry with them the dopants, although the activation of this mechanism depends sensitively on the applied external force. If the force is too weak, the walls remain pinned while too strong forces break the walls free of the dopants and move them independently. Several experimental methods and approaches are discussed.

---

1. Introduction

Domain boundaries typically constitute only a minute fraction of the total volume of a crystal. However, a special (but not unusual) situation can occur in which the domain boundary energy becomes very small. Specifically, the domain size is sometimes miniaturized to near-atomic scales and the domain boundary density becomes extremely high.^1–5 In such cases, the properties of the crystal become dominated by a combination of both the domains and the domain boundaries. In this perspective article we focus on a specific property of domain boundaries, namely that they allow much faster chemical diffusion inside domain walls than in the bulk. This makes it possible to modify the composition of domain walls without changing the composition of the bulk.^6–10 Domain boundary dominated systems also differ from most bulk dominated materials because the motion of the domain boundaries dominates the response to external forces. Novel emergent phenomena are then expected. Typical examples for high-density domain boundaries include tweed-like structures^11,12 (e.g. in morphotropic phase boundary piezoelectric crystals^13,14) conventional and ferromagnetic shape memory alloys,^15,16 and pre-martensitic states.¹⁷ In these materials, the properties of the twin boundaries represent the principal contributors to the functionality of the sample.

Besides twin boundaries the effect of dislocations and surfaces for the electronic properties and conductivity has been investigated in great detail in SrTiO₃ and zirconia.^18–20 The effect of impurities and defects was already highlighted by several authors e.g.^21,22 while in this paper we focus on the effect of twin boundaries while being well aware that similar developments exist for other microstructures. Even when only few twin boundaries exist in a crystal, their properties can still dominate specific applications. A typical example is the race-track technology,²³ based on the controlled movement of domain walls in magnetic nanowires by short pulses of spin-polarized current. They are projected to serves as nonvolatile memory devices with the high performance and reliability of conventional solid-state memory but at the low cost of conventional magnetic disk drive storage. The racetrack memory is an array of magnetic nanowires arranged horizontally or vertically on a silicon chip with 10 to 100 domain walls per nano-wire.

Often it is possible to isolate the domain boundary-related properties from bulk properties also in non-magnetic materials. Such emerging local properties include highly conducting interfaces,^24,25 polarity,²⁶ memory effects,²⁷ photovoltaic signals,^28,29 domain wall transistors,³⁰ superconducting domain walls for Josephson junctions,³¹ memristor devices in neuromorphic computation,³² and creating pliable materials with highly reduced elastic stiffnesses of otherwise hard materials, such as special alloys.³³ Several of these features were already predicted in 2010³⁴ and these ideas were expanded in 2022.³⁵ In fact, it seems that we are at the verge of developments that could result in tailoring functional properties for a desired outcome. The term ‘domain boundary engineering’ was first coined for this endeavour, which describes particularly the design of novel chemical properties inside twin boundaries that are not the properties of the domains. An additional feature of domain boundary engineering, which only came to light during the last decade, is that their dynamics differs greatly from predictions of continuous processes like the drift of domains under a constant field. This idea was already understood in the development of ‘Barkhausen jumps’ in magnetic materials but was revived to great depth by the seminal paper of Sethna et al.³⁶ with the introduction of the notion of ‘crackling noise’ for the sudden changes of domain structures. In domain dominated system the concrete origin of such noise is the sudden movement of domain walls³⁷ which is directly correlated with the dynamics behaviour of avalanches.³⁸ Defects play a crucial role in such domain movements, and we will discuss this aspect below.

Looking forward, domain boundaries offer hence an important aspect for enhancing the properties of the bulk and create unique properties where the twin boundary is the device (and not the bulk).

In this perspective article, the focus is on the chemical modifications of twin boundaries. Two main properties of twin boundaries are at the core of the argument. Firstly, a domain wall cannot just stop in the middle of a crystal. Any domain wall ends at an interface or the surface of the crystal, join with another domain wall (forming a needle domain or a 90° configuration in ferroelastics), or on itself (forming a bubble domain). Domain walls are nanoscopically thin and macroscopically long, providing a continuous path between different interfaces of a crystal irrespective of how big the crystal is. This “topologically protected” percolation path is most useful for transport applications.^39–41 Secondly, domain walls are mobile; they shift their position as domains grow or shrink in response to external fields. This mobility sets domain walls apart from other types of interfaces as the required fields are usually very weak.^42–44 The high mobility means that domain walls need not only be regarded as just a transport medium but also as a “container” of chemical compounds that can itself be moved into and out of specific nano-scale locations, carrying with it whatever wall-specific physical property is of interest, such as, e.g. internal magnetization or polarization.⁴⁵ Such processes may be relevant to medical applications⁴⁶ where field induced healing processes may occur in bones. Twin boundaries can also be preferential sites for precipitation of new phases.^47,48 It is the purpose of this paper to briefly discuss the multitude of issues related with abovementioned functionalities of domain walls:

– Transport of dopants and intrinsic defects along immobile twin boundaries (their transport applications);

– Container-type behaviour of the twin boundaries;

– Transport of dopants and intrinsic defects by moving twin boundaries.

A large body of theoretical work relates to the transport in networks as described in this paper. It is generally accepted that diffusing ions migrate along a network of sites that have different energies and that are separated by configuration dependent activation barriers as considered in ref. 49 using first-principles calculation of the diffusion coefficient in solids exhibiting configurational disorder. The formalism involves the implementation of a local cluster expansion to describe the configuration dependence of activation barriers. Local cluster expansions were used to obtain the activation barrier for migration in any configuration. A study of the activation barriers in LiCoO₂ within the local density approximation shows that the migration mechanism and activation barriers depend strongly on the local lithium-vacancy arrangement around the migrating lithium ion.⁵⁰ The strain effect for oxygen anion diffusivity in Y₂O₃ stabilized ZrO₂ (YSZ) was calculated⁵¹ by density functional theory (DFT) and nudged elastic band (NEB) methods. These authors found that the oxygen diffusivity exhibits an exponential increase up to a critical value of tensile strain. At the strain states higher than the critical strain, the diffusivity decreases. This is attributed to the local relaxations at large strain states beyond a limit of elastic bond strain, resulting in the strengthening of the local oxygen–cation bonds that increases the migration barrier. In this article we use simple Landau–Ginzburg approaches for the structure of the domain walls and their effect on defect migration. We refer the reader for further information to other reviews of more technical coverage on charged domain walls,⁵² other topological structures in ferroics^53,54 and details on the interplay of ferroelectric and magnetic domain walls in multiferroics.⁵⁵

The structure of the paper is as follows.

First, the experimental methods, mostly the acoustic properties, which are especially sensitive to the mobility of twin boundaries, will be introduced in Section 2. The most relevant basic ingredients of dopant/intrinsic defect interactions with twin boundaries will be mentioned in Section 3. Finally, ideas and examples of applications of twin boundaries for different modes of transport of dopants will be given in Section 4.

2. A brief sketch of spectroscopy methods

Our main interest is the segregation of the dopants onto twin boundaries and the twin boundary motion, especially together with segregated dopants or other localized lattice defects.

Two strategies to observe and characterize the segregation of dopants and intrinsic defects onto twin boundaries are commonly used. The first employs measurements of bulk property which are sensitive to the concentration of point defects (e.g. electrical conductivity, positron annihilation, optical methods, internal friction studies). The downside of this approach is that it does not seem to be reliable when only a small fraction of defects interact with twin boundaries and when materials contain several types of defects. The second way is to characterize the properties of twin boundaries directly by methods sensitive to their state, including direct observations by means of various types of microscopy. Once it is established that twin boundaries move, their position can be determined by optical inspection^56,57 or by atomic force microscopy, AFM.⁵⁸ Using direct observations, the twin boundary patterns can be established, usually by standard micro-manipulators.

A parameter directly related to the movement of twin boundaries is the anelastic strain. If a periodic stress is applied to a twinned crystal, moving twin boundaries provoke apparent modulus softening (modulus defect) and absorption of elastic energy (internal friction). Studying of these parameters, e.g. in ferroics, is the subject of so-called ‘mechanical spectroscopy’.⁵⁹ The motion of twin boundaries is hindered by the dopants or intrinsic lattice defects and the related anelastic response of the crystal may become non-linear. Often non-linearity exclusively relates to domain walls and then serves as a highly selective method of tracking domain wall dynamics.

To measure the pinning power of the dopants and investigate the change of the internal structure of the twin boundaries, several spectroscopic techniques were previously developed. Among these methods are Resonance Ultrasonic Spectroscopy (RUS),^60–62 Resonant Piezoelectric Spectroscopy (RPS),⁶² and Acoustic Emission Spectroscopy (AE) [ref. 63–66]. In all three cases an external force is applied to a sample, either as a weak mechanical force in form of acoustic waves in RUS, a weak electric force to interact with local sample polarities in RPS, or strong mechanical, electrical or magnetic forces in AE, which lead to moving domain boundaries on a much larger scale. When domain boundaries clash with defects, other domain boundaries or surfaces, they emit acoustic signals in AE. In contrast to RUS and RPS, the Piezoelectric Ultrasonic Composite Oscillator Technique (PUCOT)^67–69 is a method of continuous scanning the dynamics of the twin boundaries over a wide range of oscillatory stresses, covering several orders of magnitude. Linear and non-linear responses of twin boundaries and the transition between them can be studied in detail by this technique. Some typical experimental arrangements are shown in Fig. 1.

Fig. 1 (a) Schematic of RPS measurements. The sample is lightly held between two transducers. A voltage VAC = 1–20 V is applied across the sample and the resonances are detected with the piezoelectric detector. (b) Three component piezoelectric composite oscillator containing drive and gauge quartz transducers and a sample for measurements of the absorption and effective elastic modulus over a wide range of strain amplitudes. (c) Electric field induced movement of domain boundaries are measured by a piezoelectric sensor (a microphone) on the samples surface. The external electric field in (c) is replaced by stresses or magnetic fields if needed. Modified after.^62,63,70

Very promising for future studies of domain wall dynamics is the Acoustic Coupling Technique (ACT).⁶⁸ ACT consists of the simultaneous application of low-frequency periodic bias stresses and pulse-echo ultrasonic measurements of the absorption and elastic modulus defect. This method was initially developed to identify different modes of interaction between dopants and dislocations: it yields absorption characteristics of various mechanisms that impede the motion of dislocations such as Peierls relief, dopant pinning, depinning and dragging of defects at sufficiently high temperatures.⁶⁸ Another possible novel way to pursue in spectroscopy experiments can be a combination of the PUCOT and RPS to study the intrinsic and domain wall-related polarization over a wide range of applied stresses. This method proved to be efficient in ferro- and antiferromagnetic materials^71,72 where it is referred to as mechanomagnetic spectroscopy.⁷³

3. Elements of twin boundary – point-like defect interaction

We focus on atomic scale obstacles such as dopants, intrinsic defects, and Peierls relief and will not discuss the interactions of twin boundaries with heterophase inclusions, tweed, dislocations, and effects of phonon viscosity. First, one may ask why twin walls are not (always) pinned by the lattice Peierls potential. Computer simulations have shown that pinning by the crystal lattice is possible if the twin boundaries are extremely thin but that Peierls pinning disappears when the wall thickness is comparable to or larger than the lattice spacings when the twin boundaries slide through the crystal lattice with very little interaction.^74,75 A key indicator for pinning is, thus, the thickness of twin boundaries. Most ferroelastic walls are too thick to experience the Peierls effect so that dopants and defects become the main pinners. Model calculations were undertaken by He et al.⁷⁶ using a generic ferroelastic model where the double well Landau potential is represented by anharmonic and harmonic springs between atoms (Fig. 2). The potential for these simulations is composed of the nearest neighbour interaction U_NN = 20 (r − 1)² (0.8 < r < 1.2), the second nearest neighbour interaction is a Landau spring with U_NNN = −10 (r − 2^1/2)² + 2000 (r − 2^1/2)⁴ (1.207 < r < 1.621) and the third nearest neighbour interaction U_NNNN = −(r − 2)⁴ (1.8 < r < 2.2), where r is the relevant inter-atomic distance.

Fig. 2 Interatomic potential for generic ferroelastic toy-model. The model with nearest-neighbour (black springs), next-nearest-neighbour (yellow Landau springs), and third-nearest-neighbour (green springs) interactions. This model ensures an appropriate shear angle with respect to the cubic unit cell.

The attractive forces which pull defects onto twin boundaries to lower the energy by some several milli-electronvolts. The energy range is rather large even in the same material because twin boundaries are not homogeneous. They contain topological defects like kinks and junctions between domain boundaries. Three configurations are shown in Fig. 3 whereby the interatomic distances in a simple monoatomic lattice are calibrated to be 0.1 nm per unit cell. The twin boundaries potentials decay to the bulk value after distances slightly larger than one unit cell while kink energies extend to >2 unit cells and junction energies to >4 unit cells. The local strains are more delocalized (Fig. 3a). The binding energy for vacancies at twin boundaries, kinks and junctions are ΔEVa-TB = −0.014 eV, ΔEVa-kink = −0.051 eV and ΔEVa-junction = −0.114 eV at the core of the defects (r = 0) as simulated for a simple model by He et al.⁷⁶ Thermal movements overcome the binding energies at sufficiently high temperatures (Fig. 3c). The relevant temperature scale is given by the background relaxation⁷⁷ where the stress induced domain relaxation follows a Vogel–Fulcher relaxation over a very wide temperature interval. The simulations⁷⁶ show that wall attractions disappear at temperatures above 3T_VF. As a typical example, the Vogel–Fulcher temperature in LaAlO₃ is ca. 230 K so that the wall attraction is no longer relevant above 700 K which is well below the phase transition temperature of 813 K.⁷⁸ The calculated binding energies of vacancies and domain boundaries are of the same order of magnitude as those obtained by experiments and density functional theory (DFT). For example, the binding energy of oxygen interstitials and vacancies with neutral twin boundaries are 30 meV⁷⁹ and 100 meV to 140 meV⁸⁰ in YMnO₃. Similar binding energies of oxygen vacancies in BaTiO₃ and PbTiO₃ are 23 meV and 299 meV, respectively.⁸¹ The equivalent twin boundary energies range between 10 mJ m⁻² and 300 mJ m⁻² for most twinned materials with wall thicknesses of a few nanometers.⁸²

Fig. 3 (a) The atomistic configurations for vacancies at twin boundary (left), kinks (middle) and junctions (right). The atoms are coded according to the potential energy. The upper inset of each image shows twin boundary, kink and junction with colours coded by local shear angles. (b) The variation of binding energy of vacancy at twin boundary, kink and junction as a function to the core site of corresponding defects. The binding energy is defined as the potential energy difference of a vacancy at the twin boundary, kink and junction sites and the reference in the bulk. Specifically, the binding energies at the core position of defects are ΔEVa-TB = 0.014 eV (green data), ΔEVa-kink = 0.051 eV (blue and red data), and ΔEVa-junction = 0.114 eV (grey, purple and black data) at r = 0 Å, respectively. Due to the orientation-dependent distribution of the binding energy, we show the change of ΔEVa-kink along 0° and 45° directions, and ΔEVa-junction along 0°, 45° and 120° directions. (c) The effect of temperature on the binding energy of vacancy at twin boundary (blue points) and junctions (red points). When the temperature is above 3.0T_VF, the trapping ability of twin boundary almost vanishes (after He et al.⁷⁶).

A compilation of wall thicknesses and energies of twin boundaries is found in ref. 83. These two energies are very similar for simple models (1 eV = 1.6 × 10⁻¹⁹ J, i.e. wall energies are 16 J m⁻² if the wall is one atomic diameter thick), so that the dopants do not change the absolute values of wall energies too much. The relevant mechanism is hence the pinning of domain boundary movements rather than the increase of the effective mass of defects in a twin boundary. The vacancy concentration ρ_VA in domain boundaries (=number of vacancy positions relative to the total number of atoms) for a total vacancy concentration of 500 ppm diminishes with temperature (Fig. 4). The ratio decreases to ∼2.45 at T = 0.8T_VF, indicating that twin boundaries only weakly trap vacancies at high temperatures while the trapping is very strong at low temperatures.

Fig. 4 Enrichment of vacancies concentration in twin boundaries relative to the total vacancy concentration as function of temperature (after He et al.⁷⁶).

3.1. Stress-temperature phase diagram with “pinning–depinning and dragging”

In this section we will focus on the results of recent MD simulation of complex twin structure interacting with vacancies⁸³ and detailed experimental study of linear and non-linear anelasticity in SrTiO₃.⁸⁴ If stress is used to move ‘loaded’ domain boundaries, one finds that there is a critical stress-amplitude when twin boundaries start to break away from junctions and pinning and depinning becomes the dominant process.⁸³ Twin boundary movements appear ballistic after depinning. Pinning and de-pinning decrease and increase the total energy of a sample. The energy loss due to de-pinning can be measured as internal friction (IF). The dissipated energy of mechanical oscillations eventually transforms into the energy of phonons. Macroscopically, the ballistic movement of rather complex domain patterns is dominated by the progression and retraction of needle domains and, for larger forces, by the sideways movement of twin walls.⁸³

The efficiency of dopant or intrinsic defect transport by moving twin boundaries depends on several factors: temperature, applied stress and frequency in case of periodic excitation. Detailed experimental data for SrTiO₃⁸⁴ are used to construct a schematic temperature–stress amplitude “phase diagram” of pinning–depinning–dragging modes of twin boundary-dopant interactions and find the conditions for efficient defect transport by twin boundaries. First, even the ‘cleanest’ samples of SrTiO₃ contain defects due to variations of oxygen^85–88 based on an extensive study by Chan et al.⁸⁹ who found several 100 ppm per formula unit of chemical impurities including Mg, Cl, Ca and Fe. The defect concentration is hence similar to the one considered by He et al.⁷⁶ The temperature evolution of the conventional IF registered at low oscillatory strain amplitude ε₀ ≈ 10⁻⁷ and of the Young's modulus is shown in Fig. 5.⁸⁴ On cooling, strong softening of the Young's modulus marks the transition range around 110 K. The dependence of damping on strain amplitude taken below T_C, Fig. 6, identifies temperature intervals of different modes of twin boundary motion. Perfectly linear twin boundary dynamics over a broad range of strain amplitudes, Fig. 6a, forms broad and high damping maximum due to the dragging of obstacles between T_C at ca. 80 K. Lower temperatures between ca. 80 and 40 K lead to a competition between dragging and depinning modes. On cooling, twin boundaries become gradually pinned since obstacles become less mobile and cannot be dragged by twin boundaries. The depinning is characterized by the nonlinearity of the strain amplitude dependence, Fig. 6b and c. Between 80 and 40 K the critical depinning strain amplitude decreases notably from 4 × 10⁻⁷ to ca. 10⁻⁷. Limited ability of twin boundaries to move obstacles at lower temperatures is the origin of the strain amplitude hysteresis when the damping during increasing and decreasing strain amplitude do not coincide. Another characteristic feature of dragging–depinning mode is the macroscopically jerky damping behaviour beyond depinning strain amplitude, Fig. 6b and c. At even lower temperatures the boundaries move collectively due to stronger wall–wall couplings. These regimes are called, depending on the strength of the interactions, either a quantum domain glass or a quantum domain solid.⁸⁴ The transition to the glassy state is marked, firstly, by an abrupt switch from jerky to continuous domain dynamics. Secondly, the low-amplitude range of linear (independent of strain amplitude) anelastic response disappears, Fig. 6c and d. The damping below 40 K is nonlinear over the entire strain amplitude range down to 2 × 10⁻⁸. This property is typical for glassy dynamics^90,91 due to divergence of the barrier height with decreasing strain amplitudes.^92,93 The observed onset of the glassy dynamics coincides with the high polarity of the twin boundaries and the onset of the glassy twin dynamics seen by electric field driven experiments.³²

Fig. 5 Temperature spectra of low-amplitude (ε₀ ∼ 10⁻⁷) ultrasonic internal friction δ (a) and Young's modulus E (b) for several cooling–heating scans below T_c ≈ 106 K in SrTiO₃. Cooling and Heating 2 scans are performed with the cryocompressor switched on, Heating 1 and Heating 3—with the compressor switched off. During Heating 3, strain amplitude dependences of the internal friction were measured at selected temperatures. The inset in (b) shows, on an expanded scale, the internal friction δ and Young's modulus E below 40 K during the Heating 1 scan. For the Heating 2 scan (green curve) only each fourth experimental point is shown above 90 K in (a) and (b) to make the points of Heating 1 scan (black curve) visible. After ref. 84.

Fig. 6 Strain amplitude dependence of the internal friction δ measured at temperatures between 72 and 108 K (a), 46 and 72 K (b), and 18 and 46 K (c) during heating from 18 K. Solid lines connect experimental points in panels (a), (b), and (c). All strain amplitude dependences include direct and reverse runs (increasing and decreasing strain amplitude). The jerks during increasing and decreasing strain amplitudes are seen in (b) and (c). Arrows in (c) (for jerky curves at 42 and 46 K) indicate increase and decrease of the strain amplitude, mark the difference between the data for direct and reverse runs, and indicate the strain amplitude hysteresis between ca. 40 and 70 K. Panel (d) shows the strain amplitude dependences between 18 and 36 K on an expanded scale. Solid lines are their fittings with power law. The inset shows the glassy strain exponent μ vs. temperature; the dotted line in the inset is a guide to the eye. After ref. 84.

Data from Fig. 5 and 6 are used to construct a “pinning–depinning–dragging” stress amplitude-temperature phase diagram,⁹⁴Fig. 7. The temperature T-stress amplitude σ₀ plane is separated by a dotted vertical line at a temperature T = T₁ into two temperature domains wherein the dopants or intrinsic defects are immobile and start to move together with twin boundaries. The position of this line is frequency-dependent. The solid line divided into Sections I–IV shows the variation of the frequency-dependent critical depinning stress with temperature. Small lower panels show selected strain amplitude dependences of damping from Fig. 6 representative of each mode of twin boundary motion. Sections IV and III fall within the range of transport of dopants/intrinsic defects by twin boundaries. The most efficient transport occurs below the critical depinning stress in Section IV of pure dragging. It is quite remarkable that, over the range of transport by pure dragging, twin boundary dynamics remains linear and no depinning occurs. That is, the pure dragging range corresponds to the unusual increase of the critical depinning stress with temperature. In domain III of dragging–depinning stage, the motion of dopants with twin boundaries is intermittent of the stick-slip type. Of course, new portions of defects participate in each stick-slip event. Dragging-depinning mode can be activated at rather low temperatures. As a characteristic value, typical “signatures” of this effect are detected in ferroelastic Cu–Al–Be martensite starting from ca. 15 K.⁹⁵

Fig. 7 Stress amplitude – temperature, σ₀–T, diagram showing temperature dependence of the critical depinning stress σ^Cr₀(T,ω) in acoustic experiments and delineating different Sections I–IV of the twin boundary dynamics. A set of small panels below the main plot show stress amplitude dependences of the internal friction (IF) characteristic of each type of twin boundary dynamics: pure dragging, competition between pinning and dragging, glassy and pinned states. Dotted part of the line indicates schematically the high-temperature approximation when thermal energy becomes comparable with the binding energy.

Twins in SrTiO₃ are very easily depinned: the critical depinning strain is ε^Cr₀ ≈ (2–3) × 10⁻⁷ between 40 and 70 K. Data in Fig. 5 indicate that the vibration of a cryomotor during the course of the experiment is sufficient to depin twin boundaries.⁸⁴ SrTiO₃ is an example of weak pinning. Other ferroelastics with weak pinning effect are several Cu-base shape memory alloys.^96–98 Weakly pinned twin boundaries in complex twin structures are prone to depin at sufficiently low temperatures due to the thermal stresses induced in multidomain structures. As far as we are aware, all thermally depinned twin boundaries show glassy dynamics at low temperatures, domain II in Fig. 7.^84,96–98 LaAlO₃ shows the opposite scenario with strong pinning effect with critical depinning strains ε^Cr₀ ≈ 10⁻⁴,⁷⁰i.e. ca. 500 times higher than in SrTiO₃. Here, thermal stresses are not sufficient to depin twin boundaries and they remain pinned down to the lowest temperatures. This scenario is represented in Fig. 7 by the low-temperature mode I.

3.2. Transport along (immobile) twin boundaries

Transport along twin boundaries can be related to local strains and more open crystalline structure, allowing atoms to migrate more easily, Fig. 8.

Fig. 8 Two boundaries in a simple model where the bulk of the sample is in an antiferrodistortive (left) or twinned state (right). In both cases, the pink regions (i.e. the domain walls) tend to have larger interatomic distances across the boundary and hence smaller densities. This effect commonly favors faster transport along the boundaries rather than through the bulk (modified after Viehland and Salje¹).

Another potential reason is higher concentration of vacancies or dopants^74,99 affecting diffusion along twin boundaries. Space charge-zones or dipole moments localized at twin boundaries affect strongly ionic transport. The most common emerging property of a domain wall, namely domain wall polarity, is sketched in Fig. 9.

Fig. 9 Sketch of of a simple two-atomic, twinned bulk material. The repetition unit of the bulk (thin black lines) is smaller than the unit cells (green) along the horizontal twin wall. The red atoms inside the green unit cells are not constraint by symmetry with shifts along the horizontal twin boundary. The red atoms commonly shift whith respect to the centre of gravity of the beige atoms. If the atoms are charged, this shift generates an electric dipole (here towards the apex of the twin boundary) which influences chemical transport along the twin boundary.

Extra mobility of dopants along twin boundaries as compared to the bulk stems from the difference in corresponding diffusion constants. As an example, activation energies for Li migration in LiCoO₂ were determined using first pricinples calculations based on density functional theory.⁵⁰ For a sufficiently high vacancy concentration to activate double vacancy mechanism of Li migration, the activation energy for diffusion along a twin boundary is 0.2 eV lower than across the same (11̄04̄) twin boundary.⁵⁰ This activation energy difference corresponds to an increase of the diffusion constant along twin boundaries by a factor of ca. 10³.

3.3. On the role of avalanches

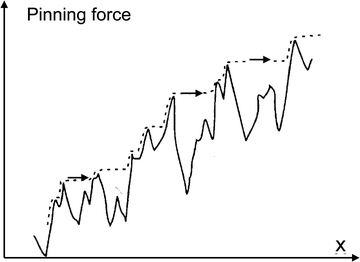
Dragging a domain wall through a complex energy landscape leads to jumps, splitting of domain walls and the creation of new domain walls. It is then impossible to describe, with a sufficient degree of generality, the movement of one domain wall. Instead, it is more meaningful to focus on the statistical properties of all domain walls. Their energies of movements are conveniently described by avalanches where the probability of sudden movements (∼jerks) is power law distributed
where ε is the all-important energy exponent which takes specific values in the range between 1.33 and 3 in most materials. The typical values for moving twin walls are between the mean field values 4/3 and 5/3 and values close to 2 in martensitic compounds.³⁷ Besides energies, other avalanche parameters, like their amplitudes, durations and aftershock probabilities can be derived from experimental observations.³⁷ Defects delay the domain boundary movements so that the avalanche related translational motion of twin boundaries dominates when the pinning potential is strong: the periods of rather low-velocity slow twin boundary motion are intercalated with jumps in avalanches. Slowly moving twin boundaries can then accumulate dopants during the intervals of their slow motion but leave the defects behind once the jump is activated (and often at the jump position, Fig. 10). An important consequence of the intermittence of the twin boundary motion in complex structures is the heterogeneous distribution of dopants in the volume swept by twin boundaries. This feature is crucial for the formation of large number of nanoprecipitates through low-temperature ageing, for example in Ni–Ti.^100,101

Fig. 10 Schematic sketch of the trajectory (dotted line) of intermittent motion of a twin boundary over random profile of resistance forces under a uniform external field. Horizontal arrows indicate some avalanche-type fast displacements of twin boundaries.

4. Examples and prospects of applications

4.1. Transport along (immobile) twin boundaries

Chemical turnstile. A hypothetical device application is the ‘chemical turnstile’³⁹ which is depicted in Fig. 11. Fast diffusion along twin boundaries can be turned on and off by moving the boundaries by external stress, electric field etc. Such devices are plausible for medical applications where a reservoir of medication is connected to the blood stream. The administration of the medication can then be controlled from outside the body electrically or mechanically without further operative interventions.

Fig. 11 A ‘chemical turnstile’. The white twin boundary acts as a fast diffusion pathway and its position can be switched by external forces. In (a) the diffusion connects the two surfaces. In (b) the twin boundary has been rotated and is now parallel to the surface. No fast diffusion across the crystal is possible because the twin boundary is situated parallel to the surface. The device can hence allow fast diffusion in (a) or not in (b) by switching the orientation of twin boundaries.

Memristors and neuromorphic computation. This application was first proposed by Chaudhary et al.,¹⁰² Chanthbouala et al.,¹⁰³ and McConville et al.¹⁰⁴ in the field of neuromorphic computing. The memristor-type formation of filaments inducing conduction spikes near a percolation point^105–107 can, potentially, be replaced by injected ions in domain walls. This has several advantages. First, the chemical changes are strongly confined to the interfaces because their diffusivity perpendicular to the domain wall is very small. The ‘loading’ of the domain walls can be identified by spectroscopy methods as introduced above. Even though percolations will presumably generate Schottky barriers near junction areas, these barriers are limited to atomic size patches and will relax even at high operating frequencies. Moreover, ferroelectric walls and highly conducting walls can help to overcome the bottleneck between memory and synaptic data transfer. Neuromorphic computers imitate the functionality of brain neurons and connecting synapses, where the synapses combine logical operations with memory effects. For this purpose, the dual functionality of the domain walls may be the key ingredient. Injected defects can stop transport currents in domain walls. Furthermore, synapses are dynamical elements, which is also the case for mobile domain walls.

The path of the electrical current can be switched at the percolation point. The percolation point is modified by shifting the position of the domain wall or of defects, which blocks the transport of atoms along the domain walls. Defect movements by electric fields can greatly change the ionic current.¹⁰⁸ The changes occur rapidly because the wall movements proceed by jerks which are extremely fast.¹⁰⁹ Equally, the connection and the blocking of atomic transport can occur over extremely short time intervals.^33,110–112 The work by Sharma et al.¹¹⁰ is particularly important and gives much hope for future developments. These authors demonstrated that by using nanofabricated electrodes and scanning probe techniques, a prototypic non-volatile ferroelectric memory element can be constructed which is entirely based on the transport inside domain boundaries. The element was scalable to below 100 μm. The binary memory element is the conductivity which is present or absent in the boundary. They demonstrated that the device could be read non-destructively at less than 3 V with an on–off ratio of ∼1000.

Much work has been directed into such use of ferroelectric domain boundary engineering in neuromorphic computation over the last decade, but several key issues remain obscure. First, ferroelectric and ferroelastic domains and domain walls generate many complex domain patterns¹¹³ so that choosing the most appropriate domain configuration and producing it reproducibly is extremely challenging. Each domain boundary may carry specific chemical loading, which can be tailored to change the percolation point for the memristive carrier transport. Even additional magnetic interactions, generated by the polar and rough domain boundaries, have been postulated¹¹⁴ but not confirmed experimentally.

Ion transport, some examples. Not all domain walls are fast ionic connectors (such as the case of quartz where the c-axis transport in the twin wall is slower than in the bulk⁷) while in most cases they are. CaTiO₃ is a good example of a perovskite material which contains oxygen vacancies. The trapping energies for oxygen vacancies were determined in ref. 6 and 9 for all potential wall positions and compared with the bulk. It was found that the defects have local potential energies which are ca. 0.8 eV lower than the bulk potentials so that even without external forces, the oxygen vacancies accumulate in the twin boundaries. Under sufficiently strong external electric fields, the accumulated defects will then move along the twin boundaries.

Nie et al. have shown that the presence of (101̄) twin boundaries in anode SnO₂ nanowires strongly enhances lithiation processes.⁹⁹ The presence of twins changes the scenario of lithiation through the enhancement of lattice strain and formation of Sn vacancies at the twin boundary. This potential application is an example of smart domain engineering of electrodes for high-rate batteries.

4.2. Twin boundaries as sinks for dopants and intrinsic defects

Segregation of dopants to twin boundaries in WO₃. A typical doping arrangement is shown in Fig. 12. A twinned WO₃ sample (left) shows two types of twin boundaries, namely related to the twinning transitions between the tetragonal and the orthorhombic phase (TO) and between the orthorhombic phase and the monoclinic room temperature phase (OM). The sample is then sealed into a quartz glass tube (middle) and exposed to Na vapour. The vapour covers the sample surface and penetrates the sample along the domain boundaries. The sample is then cleaved to eliminate the surface-near regions and the Na content is measured using a microprobe (right). Very strong enrichment of Na is seen at the twin boundaries. No significant difference between the two domain boundary types was observed.

Fig. 12 Tetragonal–orthorhombic (TO) and orthorhombic–monoclinic (OM) domain walls in WO₃. The OM walls correspond to the dark lines shown in the SEM photograph and the TO walls divide regions of parallel OM walls. The scale bar is 100 μm. The sodium vapour reaction was carried out in a sealed evacuated U-shape silica tube. The cleaved crystal (a) with orthorhombic-tetragonal walls reacted with sodium vapor. The white line (of length 25 μm) corresponds to the position of the microprobe line-scan shown in Fig. 4b. (b) Microprobe line-scan showing measured Na:W atom ratios at 1 μm steps. (Modified after Aird and Salje^8,31).

The same experiment was undertaken by heating the sample for several hours which lead to loss of oxygen. The outwards diffusion of oxygen was strongest along the twin boundaries.¹¹⁵ The ease with which boundaries can be doped suggests that samples which were subjected to vapour or liquid with different chemical compositions are, in their majority, doped. This situation is likely to be widely encountered in minerals in a metamorphic environment¹¹⁶ so that geochemical characterisation of global chemical compositions can be misleading. A better way to determine compositional characterizations for geochronological processes would be to analyse the dopants in twin boundaries. Alas, this has not yet been done because of technical difficulties to restrict the chemical analysis to small enough regions in the crystal. Future work in this field is highly desirable. On the other hand, so-called ‘ghost domain walls’ have been well documented.¹¹⁷ They occur when external forces are applied to material which are strong enough to move the twin boundaries. In some cases, the moving boundary leaves the segregated dopants behind as a ‘ghost’ wall, which is easily seen in transmission electron microscopy.

Preferential precipitation along habit plane twin boundaries in martensitic alloys. Castro et al.⁴⁷ studied precipitation in a Cu–Zn–Al martensitic shape memory alloy. Samples quenched into the low temperature twinned martensitic phase inherit high concentration of vacancies which promote diffusion. If quenched samples are aged in the high-temperature cubic phase, preferential precipitation is found along the positions of habit plane twin boundaries in the martensitic phase. This is an indication that nuclei of precipitates are formed in the twinned martensitic phase in habit plane twin boundaries.

4.3 Transport of dopants by moving domain walls

Strain ageing during deformation of twinned structures. Macroscopic deformation of twinned structures necessarily implies motion of twin boundaries. If deformation proceeds in the temperature interval wherein dopants or intrinsic defects can be dragged by twin boundaries, classical strain ageing effects can be observed. In order to detect strain ageing, measurements of linear and non-linear internal friction were performed in situ during deformation of quenched Cu–Al–Ni single crystals in the martensitic twinned state.¹¹⁸ Measurements in situ during deformation show jerky non-linear response of the crystal with strain-rate dependent critical depinning strain amplitude.

Kinetic stabilization of martensite. Examples of accumulation of dopants or intrinsic defects by moving twin boundaries can be extended to interphase boundaries moving during first order ferroelastic transitions. In quenched martensitic alloys with high density of quenched-in defects, the one-time effect similar to strain ageing in twinned structures is then transformed into blocking of the conventional thermoelastic transition into the high-temperature phase or stabilization of martensite.^119,120 This stabilization mode is found in Cu-based martensites and is referred to as kinetic stabilization.¹²¹ A necessary condition for intense kinetic stabilization is a high defect density, rather high phase transformation temperatures and low heating rates to activate the accumulation of defects.

Phase transition induced ageing effect. Dragging of vacancies or substitutional defects by interphase boundaries can affect functionality of the widely used Ni–Ti alloys. Conventional bulk diffusion in NiTi is negligible¹⁷ at ambient temperature. However, diffusion assistance by moving interphase boundaries can activate ageing at ambient temperature and affect functional properties of working elements suppressing the direct martensitic transformation.^48,100,101 This low-temperature ageing is thus a consequence of thermal cycling across the phase transition range where the activation of ageing requires thermal cycling with a low rate to permit defect-assisted diffusion. Strong ageing near martensitic transformation temperatures implies the creation of a large number of nanoscale precipitates. The high density of nuclei of precipitates is formed in the volume of a crystal due to the intermittent avalanche-like nature of the martensitic transformation.^65,66 A schematic model of thermal cycling and ageing is shown in Fig. 13. Initial quenching creates a homogeneous distribution of vacancies and substitutional atoms, Fig. 13a, since the quenching rate is high. During phase transitions, interphase boundaries capture defects in those parts of the crystal where the motion of boundaries is slow. Segregated defects are left behind moving boundary when the boundary participates in an avalanche-like displacement, Fig. 13b. Segregated defects detached from the boundaries form nanoprecipitates during low-temperature ageing through short-range diffusion, Fig. 13c.

Fig. 13 Qualitative model of phase transition-induced low-temperature ageing of Ni-rich Ni–Ti alloys: (a) resistance force encountered by moving interphase boundaries (black line) and initial spatial distribution of point defects (blue line) in the initial state of the reverse martensitic transformation of as quenched sample; the trajectory of the interphase boundary motion is A-B-C-D-E-F-G; (b) the distribution of point defects after the first reverse martensitic transformation: the spikes in the defect density correspond to the peaks of the resistance force B, D, F etc., the zones of the reduced defect density (as compared to the initial one) correspond to the zones of the slow motion of interphase boundary (A-B, C-D, E-F) where sweeping up of point defects by interphase boundary occurs; (c) formation of the (nano) precipitates or their nuclei from the atmospheres of point defects left behind by moving interphase boundary as the result of short-range diffusion during low-temperature ageing.

5. Summary

Static twin boundaries are, in most materials, pathways for fast diffusion of chemical dopants. They also constitute reservoirs of dopants which are enriched in the twin boundaries relative to the bulk. Once a specific twin pattern is generated, it serves as template for chemical doping where boundaries are structurally and chemically very different from the bulk material. This can be the starting point for self-generated device structures where both the domain structure and the subsequent doping are equilibrium structures under appropriate boundary conditions.

We argue here that moving domain boundaries can be used as carriers to move dopants through a sample. Device materials can hence be modified, and dopants can be transported to assigned locations. This method is best understood for twin boundaries, where transport is very much dependent on the external strain and the strain rate. Weak strains do not sufficiently de-pin the walls while at very high strains the walls are totally de-pinned and loose the dopants. The useful interval for applicable strain rates is hence the intermediate interval which is easily accessible in most applications. Such applications extend from material sciences, medical applications to geochemistry and metamorphic petrology.

Applications are still hampered by experimental limitations, although much progress was made during the last decade. Further developments may include promising approaches, like the Acoustic Coupling Technique⁶⁸ to identify specific mechanisms of interaction of moving twin boundaries with dopants and intrinsic defects or the PUCOT⁶⁹ + RPS⁶⁰ technique to study non-linear dynamics of polarized domain walls. Insight into the atomic mechanism was initially based on simple analytical models. Great progress was made by the development of simple toy models where the local mechanisms can be studied in systems with some 100 000 particles.^122–124 Future work needs now to extend the models to more realistic interatomic potentials and larger simulation boxes. Such work is under way.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

EKHS is grateful to EPSRC (EP/P024904/1) and the H2020 Marie-Sklodowska-Curie Actions (grant number 861153) for financial support. SK acknowledges the supported from MCIN/AEI/10.13039/501100011033 and “FEDER Una manera de hacer Europa, EU”, project RTI2018-094683-B-C51.

References

1. D. D. Viehland and E. K. H. Salje, Adv. Phys., 2014, 63, 267–326.
2. G. Catalan and N. Domingo, Physical Properties inside Domain Walls: Basic Principles and Scanning Probe Measurements, in Domain Walls: From Fundamental Properties to Nanotechnology Concepts, ed. D. Meier, J. Seidel, M. Gregg and R. Ramesh, Oxford University Press, 2020, pp. 1–22.
3. X. Ding, Z. Zhao, T. Lookman, A. Saxena and E. K. H. Salje, Adv. Mater., 2012, 24, 5385–5389.
4. E. K. H. Salje, X. Ding and O. Aktas, Phys. Status Solidi B, 2014, 251, 2061–2066.
5. E. K. H. Salje, X. Ding, Z. Zhao and T. Lookman, Appl. Phys. Lett., 2012, 100, 22905.
6. M. Calleja, M. T. Dove and E. K. H. Salje, J. Phys.: Condens. Matter, 2003, 15, 2301–2307.
7. M. Calleja, M. T. Dove and E. K. H. Salje, J. Phys.: Condens. Matter, 2001, 13, 9445–9454.
8. A. Aird and E. K. H. Salje, Eur. Phys. J. B, 2000, 15, 205–210.
9. L. Gonçalves-Ferreira, S. A. T. Redfern, E. Artacho and E. K. H. Salje, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 024109.
10. W. T. Lee, E. K. H. Salje and U. Bismayer, J. Phys.: Condens. Matter, 2003, 15, 1353–1366.
11. E. K. H. Salje, M. Alexe, S. Kustov, M. C. Weber, J. Schiemer, G. F. Nataf and J. Kreisel, Sci. Rep., 2016, 6, 27193.
12. E. K. H. Salje and K. Parlinski, Supercond. Sci. Technol., 1991, 4, 93–97.
13. B. Noheda, D. E. Cox, G. Shirane, J. Gao and Z. G. Ye, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 054104.
14. B. Noheda, D. E. Cox, G. Shirane, R. Guo, B. Jones and L. E. Cross, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 014103.
15. K. Ullakko, J. Mater. Eng. Perform., 1996, 5, 405–409.
16. A. N. Vasil’ev, V. D. Buchelnikov, T. Takagi, V. V. Khovailo and E. I. Estrin, Phys.-Usp., 2003, 46, 559–588.
17. K. Otsuka and X. Ren, Prog. Mater. Sci., 2005, 50, 511–678.
18. K. Szot, W. Speier, G. Bihlmayer and R. Waser, Nat. Mater., 2006, 5, 312–320.
19. X. Guo, E. Vasco, S. B. Mi, K. Szot, E. Wachsman and R. Waser, Acta Mater., 2005, 53, 5161–5166.
20. T. Menke, P. Meuffels, R. Dittmann, K. Szot and R. Waser, J. Appl. Phys., 2009, 105, 066104.
21. C. Rossel, G. I. Meijer, D. Bremaud and D. Widmer, J. Appl. Phys., 2001, 90, 2892–2898.
22. S. Tsui, A. Baikalov, J. Cmaidalka, Y. Y. Sun, Y. Q. Wang, Y. Y. yue, C. W. Chu, L. Chen and A. J. Jacobson, Appl. Phys. Lett., 2004, 85, 317–319.
23. S. S. P. Parkin, M. Hayashi and L. Thomas, Science, 2008, 320, 190–194.
24. S. M. Wu, S. A. Cybart, P. Yu, M. D. Rossell, J. X. Zhang, R. Ramesh and R. C. Dynes, Nat. Mater., 2010, 9, 756–761.
25. J. Seidel, L. W. Martin, Q. He, Q. Zhan, Y. H. Chu, A. Rother, M. E. Hawkridge, P. Maksymovych, P. Yu, M. Gajek, N. Balke, S. V. Kalinin, S. Gemming, F. Wang, G. Catalan, J. F. Scott, N. A. Spaldin, J. Orenstein and R. Ramesh, Nat. Mater., 2009, 8, 229–234.
26. S. Van Aert, S. Turner, R. Delville, D. Schryvers, G. Van Tendeloo and E. K. H. Salje, Adv. Mater., 2012, 24, 523–527.
27. P. Sharma, Q. Zhang, D. Sando, C. H. Lei, Y. Y. Liu, J. Y. Li, V. Nagarajan and J. Seidel, Sci. Adv., 2017, 3, e1700512.
28. S. Y. Yang, J. Seidel, S. J. Byrnes, P. Shafer, C. H. Yang, M. D. Rossell, P. Yu, Y. H. Chu, J. F. Scott, J. W. Ager, L. W. Martin and R. Ramesh, Nat. Nanotechnol., 2010, 5, 143–147.
29. A. Bhatnagar, A. R. Chaudhuri, Y. H. Kim, D. Hesse and M. Alexe, Nat. Commun., 2013, 4, 2835.
30. X. J. Chai, J. Jiang, Q. H. Zhang, X. Hou, F. Q. Meng, J. Wang, L. Gu, D. W. Zhang and A. Q. Jiang, Nat. Commun., 2020, 11, 2811.
31. A. Aird and E. K. H. Salje, J. Phys.: Condens. Matter, 1998, 10, L377–L380.
32. E. K. H. Salje, APL Mater., 2021, 9, 010903.
33. E. K. H. Salje, X. F. Wang, X. D. Ding and J. F. Scott, Adv. Funct. Mater., 2017, 27, 1700367.
34. E. K. H. Salje, ChemPhysChem, 2010, 11, 940–950.
35. G. F. Nataf, M. Guennou, J. M. Gregg, D. Meier, J. Hlinka, E. K. H. Salje and J. Kreisel, Nat. Rev. Phys., 2020, 2, 634–648.
36. J. P. Sethna, K. A. Dahmen and C. R. Myers, Nature, 2001, 410, 242–250.
37. E. K. H. Salje and K. A. Dahmen, Ann. Rev. Condens. Matter Phys., 2014, 55, 233–254.
38. R. Harrison and E. K. H. Salje, Appl. Phys. Lett., 2010, 97, 021907.
39. W. T. Lee and E. K. H. Salje, Appl. Phys. Lett., 2005, 87, 143110.
40. J. Seidel, L. W. Martin, Q. Hel, Q. Zhan, Y.-H. Chu, A. Rother, M. E. Hawkridge, P. Maksymovych, P. Yu, M. Gajek, N. Balke, S. V. Kalinin, S. Gemming, F. Wang, G. Catalan, J. F. Scott, N. A. Spaldin, J. Orenstein and R. Ramesh, Nat. Mater., 2009, 8, 229–234.
41. M. Schroder, A. Haussmann, A. Thiessen, E. Soergel, T. Woike and L. M. Eng, Adv. Funct. Mater., 2012, 22, 3936–3944.
42. D. A. Allwood, G. Xiong, C. C. Faulkner, D. Atkinson, D. Petit and R. P. Cowburn, Science, 2005, 309, 1688–1692.
43. E. K. H. Salje and J. F. Scott, Appl. Phys. Lett., 2014, 105, 252904.
44. G. Catalan, J. Seidel, R. Ramesh and J. F. Scott, Rev. Mod. Phys., 2012, 84, 119–156.
45. J. Gonnissen, D. Batuk, G. F. Nataf, L. Jones, A. M. Abakumov, S. Van Aert, D. Schryvers and E. K. H. Salje, Adv. Funct. Mater., 2016, 26, 7599–7604.
46. F. Vasquez-Sancho, A. Abdollahi, D. Damjanovic and G. Catalan, Adv. Mater., 2018, 30, 1705316.
47. M. L. Castro, J. Pons and E. Cesari, J. Phys. IV, 2003, 112, 533–536.
48. S. Kustov, B. Mas, Z. Kuskarbaev, X. Wang and J. Van Humbeeck, Scr. Mater., 2016, 123, 166–168.
49. A. Van der Ven, G. Ceder, M. Asta and P. D. Tepesch, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 184307.
50. H. Moriwake, A. Kuwabara, C. A. J. Fisher, R. Huang, T. Hitosugi, Y. H. Ikuhara, H. Oki and Y. Ikuhara, Adv. Mater., 2013, 25, 618–622.
51. A. Kushima and B. Yildiz, J. Mater. Chem., 2010, 20, 4809–4819.
52. P. S. Bednyakov, B. I. Sturman, T. Sluka, A. K. Tagantsev and P. V. Yudin, npj Comput. Mater., 2018, 4, 65.
53. J. Seidel, R. K. Vasudevan and N. Valanoor, Adv. Electron. Mater., 2016, 2, 1500292.
54. J. Seidel, Nat. Mater., 2019, 18, 188–190.
55. D. Meier, J. Phys.: Condens. Matter, 2015, 27, 463003.
56. B. Casals, G. F. Nataf and E. K. H. Salje, Nat. Commun., 2021, 12, 345.
57. J. F. Scott, B. Casals, K. Luo, A. Haq, D. Mariotti, E. K. H. Salje and M. Arredondo, Sci. Rep., 2022, 12, 14818.
58. Y. Kim, M. Alexe and E. K. H. Salje, Nanoscale properties of thin twin walls and surface layers in piezoelectric WO_3−x, Appl. Phys. Lett., 2010, 96, 032904.
59. in Mechnical Spectroscopy Q-1 2001 with Applications to Materials Science, ed. R. Schaller, G. Fantozzi and G. Gremaud, 2001, Trans Tech Publ., Switzerland.
60. M. A. Carpenter, J. Phys.: Condens. Matter, 2015, 27, 263201.
61. A. Migliori, J. L. Sarrao, W. M. Visscher, T. M. Bell, M. Lei, Z. Fisk and R. G. Leisure, Phys. B, 1993, 183, 1–24.
62. O. Aktas, M. Kangama, G. Linyu, G. Catalan, X. D. Ding, A. Zunger and E. K. H. Salje, Phys. Rev. Res., 2021, 3, 043221.
63. E. K. H. Salje, D. Xue, X. Ding, K. A. Dahmen and J. F. Scott, Phys. Rev. Mater., 2019, 3, 014415.
64. G. F. Nataf, P. O. Castillo-Villa, J. Baro, X. Illa, E. Vives, A. Planes and E. K. H. Salje, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 022405.
65. M. C. Gallardo, J. Manchado, F. J. Romero, J. del Cerro, E. K. H. Salje, A. Planes, E. Vives and R. Romero, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 174102.
66. E. K. H. Salje, A. Planes and E. Vives, Phys. Rev. E, 2017, 96, 042122.
67. W. H. Robinson and A. Edgar, IEEE Trans. Sonics Ultrasonics, 1974, SU21, 98–105.
68. G. Gremaud, S. Kustov and Ø. Bremnes, Mater. Sci. Forum, 2001, 366–368, 652–666.
69. S. Kustov, S. Golyandin, A. Ichino and G. Gremaud, Mater. Sci. Eng., A, 2006, 442, 532–537.
70. S. Kustov, Iu Liubimova and E. K. H. Salje, Appl. Phys. Lett., 2018, 112, 042902.
71. S. Kustov, M. L. Corró, E. Cesari, J. I. Pérez-Landazábal and V. Recarte, J. Phys. D, 2010, 43, 175002.
72. M. L. Corró, A. el Hichou, E. Cesari and S. Kustov, J. Phys. D, 2016, 49, 015001.
73. S. Kustov, F. Masdeu and E. Cesari, Appl. Phys. Lett., 2006, 89, 061917.
74. W. T. Lee, E. K. H. Salje, L. Goncalves-Ferreira, M. Daraktchiev and U. Bismayer, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 214110.
75. E. K. H. Salje, Ann. Rev. Mater. Res., 2012, 42, 265–283.
76. X. M. He, S. Z. Li, X. D. Ding, J. Sun, S. M. Selbach and E. K. H. Salje, Acta Mater., 2019, 178, 26–35.
77. E. K. H. Salje and M. A. Carpenter, Appl. Phys. Lett., 2011, 99, 051907.
78. S. A. Hayward, F. D. Morrison, S. A. T. Redfern, E. K. H. Salje, J. F. Scott, K. S. Knight, S. Tarantino, A. M. Glazer, V. Shuvaeva, P. Daniel, M. Zhang and M. A. Carpenter, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 054110.
79. J. Schaab, S. H. Skjærvø, S. Krohns, X. Dai, M. E. Holtz, A. Cano, M. Lilienblum, Z. Yan, E. Bourret, D. A. Muller, M. Fiebig, S. M. Selbach and D. Meier, Nat. Nanotechnol., 2018, 13, 1028–1035.
80. S. H. Skjærvø, D. R. Småbråten, N. A. Spaldin, T. Tybell and S. M. Selbach, Phys. Rev. B, 2018, 98, 184102.
81. X. Li, Q. Yang, J. Cao, L. Sun, Q. Peng, Y. Zhou and R. Zhang, J. Phys. Chem. C, 2018, 122, 3091–3100.
82. J. Chrosch and E. K. H. Salje, J. Appl. Phys., 1999, 85, 722–727.
83. X. He, S. Li, X. D. Ding, J. Sun, S. Kustov and E. K. H. Salje, Acta Mater., 2022, 228, 117787.
84. S. Kustov, Iu Liubimova and E. K. H. Salje, Phys. Rev. Lett., 2020, 124, 016801.
85. P. C. Bowes, J. N. Baker, J. S. Harris, B. D. Behrhorst and D. L. Irving, Appl. Phys. Lett., 2018, 112, 022902.
86. R. Waser, J. Am. Ceram. Soc., 1991, 74, 1934–1940.
87. R. Merkle and J. Maier, Angew. Chem., Int. Ed., 2008, 47, 3874–3894.
88. I. Denk, W. Munch and J. Maier, J. Am. Ceram. Soc., 1995, 78, 3265–3272.
89. N.-H. Chan, R. K. Sharma and D. M. Smyth, J. Electrochem. Soc., 1981, 128, 1762–1769.
90. S. Kustov, E. Cesari and G. Gremaud, Mater. Sci. Eng., A, 2006, 442, 390–397.
91. S. Kustov, E. Cesari and G. Gremaud, Mater. Sci. Eng., A, 2008, 481–482, 28–35.
92. G. Blatter, M. V. Feigelman, V. B. Geshkenbein, A. I. Larkin and V. M. Vinokur, Rev. Mod. Phys., 1994, 66, 1125–1388.
93. G. D’Anna, W. Benoit and V. M. Vinokur, J. Appl. Phys., 1997, 82, 5983–5990.
94. G. Gremaud, Mater. Sci. Forum, 2001, 366–368, 178–246.
95. K. Sapozhnikov, S. Golyandin, S. Kustov and E. Cesari, Mater. Sci. Eng., A, 2008, 481–482, 532–537.
96. S. Kustov, S. Golyandin, K. Sapozhnikov, J. Van Humbeeck and R. De Batist, Acta Mater., 1998, 46, 5117–5126.
97. S. Kustov, S. Golyandin, K. Sapozhnikov, E. Cesari, J. Van Humbeeck and R. De Batist, Acta Mater., 2002, 50, 3023–3044.
98. S. Kustov, E. Cesari and G. Gremaud, Mater. Sci. Eng., A, 2008, 481–482, 28–35.
99. A. Nie, L.-Y. Gan, Y. Cheng, Q. Li, Y. Yuan, F. Mashayek, H. Wang, R. Klie, U. Schwingenschlogl and R. Shabazian-Yassar, Nano Lett., 2014, 15, 610–615.
100. X. Wang, J. Van Humbeeck, B. Verlinden and S. Kustov, Scr. Mater., 2016, 113, 206–208.
101. S. Kustov, K. Sapozhnikov and X. Wang, Funct. Mater. Lett., 2017, 10, 1740010.
102. P. Chaudhary, H. Lu, A. Lipatov, Z. Ahmadi, J. P. V. McConville, A. Sokolov, J. E. Shield, A. Sinitskii, J. M. Gregg and A. Guverman, Nano Lett., 2020, 20, 5873–5878.
103. A. Chanthbouala, V. Garcia, R. O. Cherifi, K. Bouzehouane, S. Fusil, X. Moya, S. Xavier, H. Yamada, C. Deranlot, N. D. Mathur, M. Bibes, A. Barthélémy and J. Grollier, Nat. Mater., 2012, 11, 860–864.
104. J. P. V. McConville, H. Lu, B. Wang, Y. Tan, C. Cochard, M. Conroy, K. Moore, A. Harvey, U. Bangert, L. Q. Chen, A. Gruverman and J. M. Gregg, Adv. Funct. Mater., 2020, 30, 2000109.
105. T. D. Dongale, A. A. Bagade, S. V. Mohite, A. D. Rananavare, M. K. Orlowski, R. K. Kamat and K. Y. Rajpure, J. Mater. Sci.: Mater. Electron., 2018, 29, 3231–3238.
106. M. Bibes and A. Barthélémy, Nat. Mater., 2008, 7, 425–426.
107. D. M. Evans, V. Garcia, D. Meier and M. Bibes, Phys. Sci. Rev., 2020, 5, 20190067.
108. G. Lu, S. Li, X. Ding, J. Sun and E. K. H. Salje, Phys. Rev. Mater., 2019, 3, 114405.
109. L. Zhang, E. K. H. Salje, X. Ding and J. Sun, Appl. Phys. Lett., 2014, 104, 162906.
110. P. Sharma, Q. Zhang, D. Sando, C. H. Lei, Y. Liu, J. Li, V. Nagarajan and J. Seidel, Sci. Adv., 2017, 3, e1700512.
111. J. Jiang, Z. L. Bai, Z. H. Chen, L. He, D. W. Zhang, Q. H. Zhang, J. A. Shi, M. H. Park, J. F. Scott, C. S. Hwang and A. Q. Jiang, Nat. Mater., 2018, 17, 49–56.
112. X. Chai, J. Jiang, Q. Zhang, H. Xu, F. Meng, J. Wang, L. Gu, D. W. Zhang and A. Q. Jiang, Nat. Commun., 2020, 11, 2811.
113. J. F. Scott, Turing patterns in ferroelectric domains, in: Non-Linear Instabilities in Domain Walls, ed. D. Meier, J. Seidel, M. Gregg and R. Ramesh, Oxford Science Publications, 2020, p. 185.
114. G. M. Lu, S. Z. Li, X. D. Ding, J. Sun and E. K. H. Salje, npj Comput. Mater., 2020, 6, 145.
115. Y. Kim, M. Alexe and E. K. H. Salje, Appl. Phys. Lett., 2010, 96, 032904.
116. E. K. H. Salje, Minerals, 2021, 11, 478.
117. S. A. Hayward, E. K. H. Salje and J. Chrosch, Mineral. Mag., 1998, 62, 639–645.
118. K. Sapozhnikov, S. Golyandin, S. Kustov, J. Van Humbeeck and R. De Batist, Acta Mater., 2000, 48, 1141–1151.
119. J. Janssen, J. Van Humbeeck, M. Chandrasekaran, N. Mwamba and L. Delaey, J. Phys., 1982, 43, C4–715–720.
120. A. Abu-Arab, M. Chandrasekaran and M. Ahlers, Scr. Metall., 1984, 18, 709–714.
121. S. Kustov, J. Pons, E. Cesari and J. Van Humbeeck, Acta Mater., 2004, 52, 3083–3096.
122. G. Lu, S. Li, X. Ding, J. Sun and E. K. H. Salje, npj Comput. Mater., 2020, 6, 145.
123. G. Lu, S. Li, X. Ding, J. Sun and E. K. H. Salje, Phys. Rev. Mater., 2020, 4, 074410.
124. G. Lu, S. Li, X. Ding and E. K. H. Salje, Appl. Phys. Lett., 2019, 114, 202901.

---