 Open Access Article
Open Access ArticleSimultaneous electrical impedance and optical absorption spectroscopy for rapid characterization of oxygen vacancies and small polarons in doped ceria
D.
Kalaev
 * and
H. L.
Tuller
* and
H. L.
Tuller

Department of Materials Science and Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: dkalaev@mit.edu; tuller@mit.edu
First published on 6th February 2023
Abstract
Mixed ionic–electronic conductors (MIECs) play a central role in emerging energy conversion and energy efficient computational technologies. However, it is both challenging and resource demanding to characterize MIECs over the broad range of experimental conditions of interest, thereby significantly limiting their study and applications. Here, a novel method of a simultaneous measurement of electrical conductivity and optical absorption of thin films in out-of-equilibrium state, i.e. during a reduction process, is employed for a comprehensive study of a MIEC oxide, PrxCe1−xO2−δ (PCO). It enables, orders of magnitude faster than by established techniques, characterization of the oxygen vacancy and small polaron formation and transport as a function of temperature (demonstrated here down to 200 °C), in a wide range of deviation from stoichiometry, δ. For instance, at 600 °C the PCO properties were obtained during a ten minute reduction process, in the pO2 range from 1 to 10−13 bar. The experimental results show that the oxygen vacancy mobility is constant while the small polaron mobility is linear in δ, in the whole pO2 range, which yields the total conductivity quadratic in δ. Furthermore, the method was applied to study the modification of PCO's transport properties with composition change. It was shown that increasing x from 0.1 to 0.2 suppresses the ionic mobility and, at the same time, enhances the small polaron mobility. Finally, the optically determined δ was used to define an instantaneous oxygen activity in PCO that can be accessed in the out-of-equilibrium experiments. This work opens up new possibilities to study the effects of microstructure, strain and other applied external stimuli on the transport and thermodynamic properties of PCO and similar types of MIEC materials.
1. Introduction
Ceria (CeO2) and its doped derivatives are increasingly being identified as promising materials in applications related to energy conversion1–3 and storage,4 catalysis,5 gas separation6 and gas sensing,7,8 ionic memory and tunable optical thin film devices.9–11 This is in part due to the redox activity of Ce4+/3+ cations that, together with high oxygen vacancies and electronic charge densities, promote surface reactivity12,13 and significant mixed ionic–electronic bulk transport properties.14 Chemical doping of ceria by transition and rare-earth cations provides an additional degree of freedom in tuning its properties, enabling adjustment of the extent of oxygen deficiency, thereby modifying its surface reactivity12 and bulk transport properties.1,6,15–18One particularly attractive rare-earth dopant is praseodymium, Pr, that possesses a closely matching cation size to that of cerium, favoring the formation of single phase Pr doped CeO2 (PCO), i.e. PrxCe1−xO2−δ. PCO is actively studied as a cathode material in solid oxide fuel cells.19 It has a well established point defect model6,20–22 and several previous studies on its bulk transport6,20 and surface oxygen exchange12,23 mechanisms. However, there are scarce quantitative data on PCO's mixed ionic–electronic transport properties as a function of oxygen stoichiometry and doping level, especially below 400 °C. The mixed ionic–electronic conductivity of PCO comes about by the enhanced formation of mobile oxygen vacancies (point defects) favored by a low reduction enthalpy of Pr4+ to Pr3+ (relative to the host Ce4+ cations) and the ability of the electrons localized on Pr sites, i.e. small polarons, to move by thermal hopping to adjacent empty Pr4+ cations.20,24 Additionally, PCO is a tunable optical material as Pr4+ dopants form in-gap states25 that strongly absorb in the visible spectrum (above ∼2 eV) and upon complete reduction of the Pr dopants from 4+ to 3+ valence state, become nearly transparent.10,11,22 The reduction state of PCO can be controlled by varying the deviation from oxygen stoichiometry, δ, providing means for active tuning of the optical (and electrical) properties of PCO by either exposure to reactive gases or by applying an electrical bias.10,11,26
To fully reveal the mechanisms underlying PCO's ionic and small polaron transport and optical properties, it needs to be studied as a function of the oxygen non-stoichiometry, δ, that at equilibrium depends on both temperature and oxygen partial pressure (pO2). Previously, the thermodynamic properties of point defects in PCO were examined by measuring the oxygen non-stoichiometry dependence on pO2 and temperature by thermogravimetry,12,20 coulometric titration,6 electrical impedance spectroscopy (IS),21 strain analysis,27 XPS28,29 and optical absorption spectroscopy.22 The ionic and electronic transport properties of PCO were studied by four probe,20 oxygen permeation,30 and more recently, IS and dynamic I-V analysis.31 In the above-mentioned studies, the PCO properties were probed in a limited number of discrete states, mainly under chemical and thermal equilibrium (or steady state) at each temperature and pO2. Given that bulk transport processes and oxygen exchange at interfaces in MIEC oxides, including PCO, are thermally activated, this leads to an exponential increase in required equilibration times, limiting accessible temperatures typically to above 400 °C, even when nanosized samples are used.21,22,32,33 Furthermore, the pO2 range that may be obtained in equilibrium experiments by mixtures of O2/Ar or reactive gases has an extended gap at intermediate pO2 conditions, for instance, between 10−5 to 10−13 bar at 700 °C, as a very fine control over gas concentrations in the mixture is required in that range.24,34 This leads to several major drawbacks that limit the experimentally accessible temperature, pO2 and thus δ ranges where PCO (and similar MIECs) can be characterized and utilized in applications.
To mitigate the above-mentioned limitations, in the present study we employ a novel concurrent total conductivity and optical absorption measurement method (σ–α method), for characterization of PCO's defect thermodynamics, transport and optical properties. The method is based on an analysis of the quadratic relation of the total conductivity on the optical absorption in MIECs characterized by electron hopping transport, with PCO as a representative example of this kind of material, as shown in the methods and theory section. We demonstrate that the σ–α method can be used under out-of-equilibrium conditions, with very large pO2 steps applied on PCO thin film samples that are surface kinetics limited, to access the PCO parameters continuously over the whole pO2 (and corresponding δ) range. Moreover, the out-of-equilibrium type of measurement enables orders of magnitude faster PCO characterization than equilibrium counterparts, thereby enabling a significant increase in the accessible temperature range, extended in this study down to 200 °C.
Furthermore, measurement of the absorption cross section of PCO, without additional calibration, enabled calculation of the instantaneous δ during the experiment. The in-plane transport in the PCO thin films (for x = 0.1 and 0.2) was characterized in detail, including decoupling of the ionic and small polaron components, studying their dependencies on δ and x, and extracting the corresponding activation energies and mobility constants. An explicit parabolic dependence of the small polaron conductivity on concentration, as predicted by theory,35,36 is shown in detail for the PCO compositions. Finally, we demonstrate that an effective pO2 in the PCO thin film can be derived based on the determination of δ from the optical absorption measurements, thereby enabling its instantaneous evaluation in the out-of-equilibrium experiment.
2. Methods and theory
In this section we briefly review the method taken to characterize the transport and optical properties of MIECs with hopping transport, in the special case of PCO. It employs a simultaneous measurement of total conductivity and optical absorption coefficient as a function of non-stoichiometry, thus we term it the “σ–α method”. A more general and detailed treatment of the method and the applicable MIEC materials will be given elsewhere. In PCO compounds, the total conductivity, σ, is composed of the sum of ionic and electronic components. Under thermodynamic conditions, where mainly Pr cations are reduced, the ionic conductivity (σion) is associated with the created mobile oxygen vacancies, VO, and the electronic conductivity (σe) with the excess electrons localized on Pr sites (forming a small polaron, Pr3+, by reducing Pr4+), that are able to move by hopping to adjacent Pr4+ cations.6,22,24 Note that the superscripts of absolute valence charges on the cations, i.e. 3+/4+, are used here in order to distinguish the different oxidation states only and they do not relate to the charge number of the small polaron, which is singly charged (for more details see Appendix A). Summing the two contributions yields| σ = σion + σe = |zi|qμi[VO] + qμe[Pr3+] | (1) |
 ). In the case considered here, i.e. relatively low doping levels with x ≤ 0.2 that is significantly lower than the number of the occupied oxygen sites, the μi dependence on the oxygen vacancy concentration can be omitted.36 The latter assumption is consistent with the experimental results, as shown below in the discussion related to the absolute values and temperature dependence of μi. Thus, the thermally activated ionic mobility, up to a pre-exponential factor, is given by
). In the case considered here, i.e. relatively low doping levels with x ≤ 0.2 that is significantly lower than the number of the occupied oxygen sites, the μi dependence on the oxygen vacancy concentration can be omitted.36 The latter assumption is consistent with the experimental results, as shown below in the discussion related to the absolute values and temperature dependence of μi. Thus, the thermally activated ionic mobility, up to a pre-exponential factor, is given by| μi ∼ T−1e−Ea,i/kBT | (2) |
| μe = μe,0Pr0−1[Pr4+] ∼ T−1e−Ea,e/kBTPr0−1[Pr4+] | (3) |
| σ = qμi(Pr0 − [Pr4+]) + qμe,0Pr0−1[Pr4+](Pr0 − [Pr4+]) | (4) |
| σ = C0 + C1α + C2α2 | (5) |
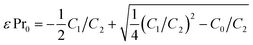 | (6) |
| qμiPr0 = C0 | (7) |
 | (8) |
3. Experimental section
3.1. Sample preparation
PCO powders with x = 0.1 and 0.2 doping levels (PCO10 and PCO20, respectively) were synthesized and used for making ceramic targets following a procedure described elsewhere.11 Thin films of PCO were grown by pulsed laser deposition (PLD) on top of interdigitated electrodes (IDEs) previously deposited onto a transparent c-cut single crystal sapphire square plate with 10 mm sides and 0.43 mm thickness. Deposition conditions included a base pressure ∼10−6 mbar; target to substrate distance 9 cm; substrate temperature during deposition of 500 °C (heating and cooling rates of 10 °C min−1); growth pressure of 2.7 × 10−2 mbar (in O2); laser energy of 0.4 J (∼5 J cm−2 energy density on the target); with substrate rotation during deposition to ensure thin film homogeneity. The IDEs were 90 nm thick sputtered Pt thin films prepared by a standard lift-off process, without use of an adhesion layer. Pt was chosen as the electrode material due to its high stability toward thermal and chemical stresses and a low diffusivity in doped ceria.37 The IDE patterns consist of repeating pairs of 8.4 mm long electrode fingers, connected in parallel, with widths equal to the electrode spacings, thereby leaving ∼0.5 of the substrate accessible to light passage through the deposited PCO film. For the PCO10 device, IDEs with electrode spacings of 50 μm and oxide thin film thickness of 170 ± 5 nm were used. For the PCO20 device, the parameters were 200 μm and 220 ± 5 nm, respectively. Additionally, test PCO thin films were deposited on bare sapphire substrates for XRD analysis. The latter was done with a Rigaku SmartLab diffractometer using a Cu Kα radiation source, a parallel beam configuration without a monochromator.3.2. Concurrent electrical and optical characterization in a controlled environment
Transmission spectrophotometry and electrical impedance spectroscopy (IS) measurements were performed in situ, in a specially designed gas flow cell (as detailed elsewhere10) that enables temperature and pO2 control. To induce chemical changes in the studied oxides, the pO2 in the flow cell is controlled in a range from 1 to 10−4 bar by changing the concentration of O2 in the O2/Ar gas mixture and below 10−8 bar (temperature dependent) by a reactive gas mixture of 1000 ppm CO in CO2. A nominal gas flush time constant, i.e. the ratio of the flow cell volume to the flow rate, was ∼2 s, in all experiments. The pO2 in the gas flow cell is monitored continuously by a Nernst sensor during the experiment. Two lock-in amplifiers (Stanford Research SR830), synchronized by a TTL trigger signal, were used for measuring the optical and electrical relaxation signals in the out-of-equilibrium experiments.4. Results and discussion
4.1. Preliminary characterization of PCO devices
Fig. 1a shows a schematic diagram of the simultaneous electrical and optical measurements performed on a PCO device with IDE electrodes (described above) for studying the PCO thin film properties by the σ–α method. Fig. 1b shows XRD patterns of PCO10 (top) and PCO20 (bottom) thin films, respectively. For both PCO compositions, the XRD analysis confirms the expected fluorite structure, with lattice parameters similar to that of undoped ceria, with preferred (111) orientation in the out of plane direction. This is consistent with previous reports on acceptor doped ceria thin films grown by PLD on sapphire substrates.38Preliminary optical transmission and electrical IS analyses were performed under equilibrium conditions, at several pO2 points, in order to choose appropriate experimental parameters, i.e., voltage frequency and specific wavelength for the σ and α measurements. Additionally, it was verified that there are no cross effects on the σ due to the light absorption in PCO, namely, that photoconductivity and heating by light are negligible. Fig. 1c shows the changes in the optical transmittance, T, of the PCO10 thin film with pO2 at several equilibrium states at 600 °C. The observed changes in the optical transmittance follow changes in the optically absorbing Pr4+ cation concentration with pO2, consistent with the PCO defect model (see also Appendix A).22 Previous studies show that Pr4+ cations exhibit broad optical absorption in the visible range, beginning from ∼2 eV and extending up to PCO's band gap energy of ∼3 eV.10,11,22 The latter observation enables some degree of freedom in choosing a single wavelength where α is proportional to [Pr4+] and thus can be used in the σ–α method. The absorption coefficient of the PCO10 device was calculated at a wavelength of 517 nm (2.4 eV) by using an approximate relationship α = −ln(T/T0)s−1,39 where s denotes the thin film thickness and T0 is the reference total transmittance at the most reduced state ([Pr4+] ∼ 0). Using the approximate relationship requires that the real part of the PCO refractive index does not change significantly within the studied pO2 range. The latter requirement can be verified here from the nearly constant positions of the interference fringes observed in the thin film transmittance, e.g. at transmittances in Fig. 1c near 1.6 eV in the most oxidized versus the most reduced states. Following the above guidelines, a 570 nm wavelength was chosen for the α measurements in the PCO20 device.
Fig. 1d shows representative electrical frequency dependent impedance spectroscopy (IS) spectra of the test PCO10 device (used in preliminary studies only) as a function of pO2, for several equilibrium states at 600 °C. The IS spectra exhibit single semicircles, for all conditions studied here, that correspond to an equivalent circuit of the total resistance of PCO, R, connected in parallel to a capacitor C (due to the IDE and the instrument's stray capacitances). The calculated below values of the ionic and electronic conductivities from the EIS and optical data indicate that there is no major contribution from the in-plane grain boundaries and the thin film exhibits properties similar to that of the bulk material. This observation is qualitatively consistent with the studies by Göbel et al. on the grain boundary regions in acceptor doped ceria.38,40 Fitting the semicircle by an impedance of the derived equivalent circuits (thin grey solid lines) provides the total resistance, that graphically corresponds to the distance between the crossings of the semicircle with the Zre axis at high and low frequencies. The PCO total conductivity is obtained from the reciprocal of the total resistance, σ = w/(sLN)R−1, where w is the spacing between the electrode fingers, and L and N are the length and the number of electrode fingers, respectively. For the out-of-equilibrium experiments, a high sampling rate of the total resistance is required in order to follow the rapid transients. A single frequency impedance was thus monitored that corresponded to the right-hand side (low frequency) crossing of the semicircle with the Zre axis, that given the negligible in-series resistance, nearly equals R (see Fig. 1d). The corresponding measurement frequency is chosen based on the equilibrium electrical IS spectra presented on a Bode plot, Fig. 1e. For example, a frequency of 100 Hz can be used for the test PCO10 sample because at that frequency the impedance has a negligible imaginary part (i.e. a nearly zero phase) and the real part closely corresponds to the total resistance, as was verified in the whole temperature range. For the PCO samples used in the actual experiment, a voltage signal frequency of 10 kHz was chosen for the total resistance measurement, based on a similar Bode plot analysis (not shown).
4.2. Characterizing PCO compositions by the σ–α method
For characterization of optical and mixed ionic–electronic transport properties as a function of a continuously varying oxygen deficiency, δ, in the designated PCO compositions, a series of experiments were conducted. Fig. 2a shows a representative example of an out-of-equilibrium measurement of the PCO10 thin film sample at 600 °C that is used in the following analysis. The top plot shows a pO2 reading of a Nernst sensor inside the flow cell during the experiment. Initially, the sample is equilibrated in pure O2. Then, at a subsequent time, it is exposed to a large pO2 step, from 1 to 10−13 bar, created by rapidly changing the gas flow composition to a reactive gas mixture of 1000 ppm CO in CO2. For the fast evolving, out-of-equilibrium experiment, the instantaneous oxygen sensor reading is not synchronized to the true momentary oxygen chemical activity inside the PCO10 thin film, and is thus not used for further analysis, but rather serves as a general indicator of the changes in pO2 occurring within the flow cell. The large pO2 step, spanning 13 orders of magnitude at 600 °C, is qualitatively divided into two parts. In the first part, the pO2 drops slowly by 4 orders of magnitude; at this stage the remnant background O2 gas concentration in the flow cell is higher or comparable to the reactive CO component. This is then followed by a rapid drop to the minimum pO2 value that initiates after the CO concentration in the flow cell becomes higher than the O2 concentration, and the new equilibrium state is approached. The middle and the bottom plots in Fig. 2a show relaxations, respectively, in the thin film optical absorption coefficient and the electrical conductivity, in response to the pO2 changes, that are being continuously and synchronously sampled. The concentrations of the charge carriers in the thin film remain homogeneously distributed during the relaxation given that the oxygen exchange kinetics are surface limited (s ≪ Dion/ks, where ks is the oxygen exchange coefficient), between the thin film and its surroundings.41 To confirm the latter assumption, control experiments were undertaken under equilibrium conditions, yielding very close σ–α datapoints to the ks limited, out-of-equilibrium, measurement (see also the discussion below). In general, the σ–α method is flexible to the choice of the stoichiometry variation direction with pO2. The latter can be changed also in, e.g. the reverse direction (oxidation of MIEC from a reduced state) or in a stepwise manner, yielding the same result. The change in the optical absorption coefficient (middle plot) provides information on the change in the concentration of Pr4+ with a sensitivity of about 0.1% (estimated from the noise level at the plateau region to the total change range in the absorption signal). The absorption of the thin film reaches a new steady state value, close to zero, after about 10 minutes, meaning that the concentration of Pr4+ decreased below the instrument's sensitivity limit. Importantly, nearly the full range of Pr4+ concentrations, between the initial value (close to Pr0) and zero, are swept through during the pO2 step. At this stage, it is not possible to do a quantitative analysis of the Pr4+ concentration as the absorption cross section, ε, is not known a priori and will be calculated explicitly at a later stage. The concurrently sampled relaxation in conductivity exhibits a more complicated shape, first going to a maximum near 560 seconds, then slightly decreasing to a new steady state value. The distinctive relaxation shape in conductivity reflects the quadratic dependence of the PCO10 conductivity on charge carrier concentrations, as described by eqn (4). Fig. 2b shows a representative example of an out-of-equilibrium measurement of the PCO20 thin film sample at the same temperature that appears qualitatively similar to the one for the PCO10 sample. | ||
| Fig. 2 PCO thin film sample characterization by the σ–α method in the pO2 range from 1 to ∼10−13 bar, at elevated temperatures. (a) Example of out-of-equilibrium measurement of relaxations in σ and α at 600 °C under a pO2 step for PCO10 and (b) PCO20 thin film samples. Top plots show Nernst sensor pO2 readings inside the flow cell during the pO2 step experiments. The middle and the bottom plots show the synchronously measured relaxations in the optical absorption coefficient and in the conductivity, respectively. (c) Conductivity versus the absorption coefficient, for PCO10 and (d) PCO20 thin film samples, measured at the same time steps in the out-of-equilibrium experiments at T = 500, 600 and 725 °C. The conductivity is quadratically dependent on the absorption coefficient with the quadratic fitting to eqn (5) shown by dashed black lines. The time span of experiments, at 600 °C, shown in plots (c and d) is the same as in plots (a and b), respectively. The equilibrium σ and α measurements at 600 °C (blue filled circles) are shown for comparison in plots (c and d). The equilibrium pO2 values are 1 (right-most point), 0.5, 0.3, 0.1, 10−2, 5 × 10−3, 2 × 10−3 and 5 × 10−4 bar. | ||
Proceeding with the σ–α method analysis of the out-of-equilibrium experiment on the PCO10 sample at 600 °C, the synchronized relaxations of conductivity and absorption coefficient are plotted on the y and x axes, respectively, as shown in Fig. 2c (green circles). The conductivity follows the absorption coefficient with the predicted quadratic dependence, eqn (5), as seen from the quadratic fit on the same plot (dashed black line). Eight equilibrium data points (blue filled circles), measured in a separate experiment for several pO2 levels (in the range from 1 to 5 × 10−4 bar) at the same temperature, are shown in Fig. 2c for comparison. The equilibrium data points closely correspond to the out-of-equilibrium measurements, supporting the initial assumption regarding the surface exchange limited kinetics of oxygen in the latter. The repeatability of the out-of-equilibrium type of measurement was verified (not shown) and while the σ and α time relaxations separately can exhibit somewhat different shapes, they yield the same σ–α curve at a given temperature. It is evident that the experimentally assessed range of Pr4+ concentrations (proportional to the change in α, e.g. ∼37%) in the equilibrium experiment is considerably more limited and cannot fully reveal the details of the mixed conductivity dependence on the oxygen stoichiometry. Moreover, the PCO characterization under equilibrium conditions for pO2 levels below 10−5 bar are challenging to achieve experimentally.24 In contrast, the out-of-equilibrium experiment, developed here, enables one to study the PCO properties over a much wider range of δ that corresponds, at its limits, to a complete reduction of the Pr cations. From the quadratic fitting of the σ versus α experimental data, one obtains the polynomial coefficients, Ck, that are used to calculate the ε, μi and μe,0 parameters from eqn (6), (7) and (8), respectively, and are discussed below. Expressions for the absorption cross section and the ionic conductivity, in terms of Ck, have a simple graphical meaning on the plot of σ as a function of α, e.g. the ones shown in Fig. 2c. The intercept points between the fitted theoretical conductivity on the σ and the α axes correspond at α = 0 to the maximum ionic conductivity, qμiPr0, and at σ = 0 to the theoretically maximum possible absorption coefficient, εPr0, respectively. Fig. 2c shows additional results for the same PCO10 device at 500 °C and 725 °C. From a qualitative graphical analysis of the corresponding fits (dashed black lines) at three different temperatures, it is apparent that the ionic and electronic mobilities increase noticeably with temperature, and the corresponding activation energies are calculated below.
The absorption cross section, ε, was found to equal 6.9 ± 0.1 × 10−18 cm2 (at 517 nm) at a temperature of 600 °C and exhibited a non-negligible temperature dependence above that temperature, increasing by ∼15% at 750 °C. The measured ε is similar (albeit higher) to previous reports for PCO10, at a slightly different wavelength (532 nm).22 Note that the method used here to calculate ε is self-consistent and does not require additional calibration procedures. Fig. 2d shows a σ–α method analysis of the out-of-equilibrium experiment for the PCO20 sample. The observed σ versus α dependency (green circles) is qualitatively similar to the PCO10 case, closely fitting the quadratic relation given by eqn (5) (dashed black lines). However, the quadratic term is more pronounced in the PCO20 case, for example, cf. conductivity at 600 °C in Fig. 2c and d. The latter indicates that the small polaron conductivity is now significantly higher than the ionic one, as discussed in more detail below. A control experiment under equilibrium conditions was performed at 600 °C and is shown in the same plot (blue filled circles). An excellent agreement between the out-of-equilibrium and the control experiments indicates that the oxygen kinetics are surface exchange limited in the PCO20 sample as well. Comparison between the equilibrium experiments on PCO10 and PCO20 shows that the latter is reduced more easily, under the same conditions. For instance, at pO2 of 5 × 10−4 bar, about 65% of the Pr cations are reduced in PCO20 (relative to the initial state in pure O2) and only ∼37% in PCO10. The absorption cross section ε, for PCO20 was found to be 5.2 ± 0.1 × 10−18 cm2 (at 570 nm) at a temperature of 600 °C, increasing by ∼8% at 750 °C. The lower absorption cross section in the PCO20 case is due to a longer wavelength chosen in the second experiment, while the comparison at the same 517 nm wavelength yields a PCO20 absorption cross section that is higher by a factor of ∼1.5 than in PCO10.
The optical and transport parameters of PCO10 and PCO20, derived by the σ–α method in out-of-equilibrium experiments, e.g. shown in Fig. 2a and b, enable one to evaluate partial ionic and electronic conductivities as a function of the deviation from oxygen stoichiometry (0 < δ < x/2), as illustrated in Fig. 3a and b for several temperatures. The partial ionic conductivity is calculated from eqn (1) and (7) while the electronic conductivity is calculated from eqn (1), (3) and (8). σion is linear with the oxygen vacancy concentration (and thus with δ), increasing from 0 to qμiPr0, between the fully oxidized and reduced states of the Pr dopants, respectively. In the same range of oxygen non-stoichiometry, σe has a parabolic form that vanishes in the most oxidized and the most reduced states and reaches a maximum at the point where  . The two components of the conductivity add up to the total conductivity that also has a parabolic form but with a maximum shifted towards the origin, where the magnitude of the shift is proportional to the ratio of mobilities (μi/μe,0). Fig. 3c and d show the ionic and electronic transference numbers, defined as a ratio of the corresponding partial conductivity to the total σ, associated with the mixed conductivity in PCO10 and PCO20, respectively. We have therefore been able to demonstrate that the σ–α method, when applied to thin film samples with IDEs, enables one to access the ionic and electronic transference numbers as a continuous function of δ, at an elevated temperature of 750 °C and at quite low temperatures of 250 °C and 350 °C for PCO10 and PCO20, respectively.
. The two components of the conductivity add up to the total conductivity that also has a parabolic form but with a maximum shifted towards the origin, where the magnitude of the shift is proportional to the ratio of mobilities (μi/μe,0). Fig. 3c and d show the ionic and electronic transference numbers, defined as a ratio of the corresponding partial conductivity to the total σ, associated with the mixed conductivity in PCO10 and PCO20, respectively. We have therefore been able to demonstrate that the σ–α method, when applied to thin film samples with IDEs, enables one to access the ionic and electronic transference numbers as a continuous function of δ, at an elevated temperature of 750 °C and at quite low temperatures of 250 °C and 350 °C for PCO10 and PCO20, respectively.
 | ||
| Fig. 3 Partial ionic and electronic conductivities and transference numbers versus deviation from oxygen stoichiometry, δ, derived by the σ–α method. (a) The total conductivity and the decoupled ionic and electronic counterparts of PCO10 and (b) PCO20 thin film samples at T = 500, 600 and 725 °C (see also Fig. 2c and d for the corresponding experimental total conductivities). (c) Ionic and electronic transference numbers for PCO10 at T = 250, 300, 450, 600 and 750 °C; and (d) for PCO20 at 350, 450, 600 and 750 °C. | ||
Next, we use the σ–α method results to derive the temperature dependence of the oxygen non-stoichiometry, δ, Fig. 4a, the oxygen vacancy mobility, Fig. 4b and c, and the electronic mobility, Fig. 4d, for the two PCO compositions. The non-stoichiometry of the PCO samples in the initial state, e.g. equilibrated in pure O2, was determined at each temperature after the corresponding ε was obtained from the out-of-equilibrium experiment at the same temperature. For instance, the oxidation state of PCO10 in O2 at 600 °C, shown in Fig. 2a, is calculated first, by dividing the initial absorption coefficient (right most green circle) by ε = 6.9 ± 0.1 × 10−18 cm2 to calculate [Pr4+]. Then, the corresponding [Pr3+] and [VO] are obtained as described in the methods and theory section. The latter yields δ that equals, in this example, 6.2 × 10−3. The logarithm of deviation from the oxygen stoichiometry, log(δ), shows a linear dependence on (kBT)−1 with activation energies of 0.54 ± 0.04 eV and 0.48 ± 0.03 eV for PCO10 and PCO20, respectively. The reduction level in PCO20 is about 3 times higher than in PCO10, over the whole temperature range. The change in δ (or in [VO]) with temperature yields the reduction enthalpy of PCO, Hr,Pr,20,24 which at a low oxygen vacancy concentration equals three times the activation energy, according to the PCO defect model (see Appendix A). The calculated reduction enthalpies are thus 1.62 ± 0.07 eV and 1.44 ± 0.05 eV, for PCO10 and PCO20, respectively. Comparison with the previous results by Chen et al.,21 measured by the chemical capacitance method in PCO10 thin film samples, was found to be in very close agreement above 550 °C, see Fig. 4a (green circles). Furthermore, the thermogravimetry analysis of PCO bulk samples, by Bishop et al.20 (PCO10) and by Schaube et al.12 (PCO20, for a slightly lower pO2 of 0.83 bar), yielded δ-s that are similar, but ∼20% lower than the values reported here.
 | ||
| Fig. 4 Thermally activated thermodynamic and transport properties of the PCO10 and PCO20 thin films, obtained by the σ–α method in out-of-equilibrium experiments. The corresponding activation energies and details on the comparison data are given in the legends. (a) Thermally activated change in the oxygen non-stoichiometry, δ, in PCO10 and PCO20 measured at pO2 of 1 bar (in pure O2) and the corresponding linear fittings (dashed lines). A comparison with previous published works is shown for PCO1020,21 and PCO2012 (a slightly lower pO2 of 0.83 bar was used in the latter study by Schaube et al.). (b) Arrhenius plot of ionic (oxygen vacancy) mobility measured in PCO10 (previously reported data20,24,31 is shown for a comparison) and (c) in PCO20. Ionic mobility in PCO20 bulk samples calculated from a study by Fagg et al.30 is shown for a comparison. (d) Arrhenius plot of concentration-independent electronic (small polaron) hopping mobility, i.e. for [Pr3+] ≪ Pr0 in eqn (3), and comparison with previous studies.20,24 | ||
Fig. 4b and c show the ionic mobilities of oxygen vacancy, calculated from eqn (7), multiplied by temperature on an Arrhenius plot for PCO10 and PCO20, respectively. The activation energies of the mobilities (see eqn (2)) for PCO10 and PCO20, are 0.71 ± 0.02 eV and 0.81 ± 0.02 eV, respectively. For the PCO10 activation energy calculation, data points in the temperature range 200–625 °C were used. At higher temperatures, reduction of Ce host ions begins to affect the total conductivity21,24 and introduces a systematic error to the σ–α method analysis. The same source of error in PCO20 has a less pronounced effect on the calculated ionic mobilities, that continue to follow a linear trend above 625 °C, as now the total conductivity is higher, thus the relative error is lower. The ability to calculate and use mobilities instead of conductivities provides more accurate transport activation energies, given that in the latter case, the carrier densities are thermally activated, implying a change in PCO's stoichiometric state with increasing temperature under the same pO2. The latter unwanted effect adds carrier formation energy contributions, e.g. the one found here for oxygen vacancies to be ∼0.5 eV, to the overall activation energy, and thus interfere significantly with extracting the activation energies associated with transport. For comparison, the ionic mobilities obtained from the literature20,24,30,31 were added to Fig. 4b and c, showing excellent agreement with the present data both in terms of absolute values and activation energies (see also the caption of Fig. 4). To enable extrapolation of the mobilities reported here, the natural logarithms of ionic mobility pre-exponential factors can be found from the y-intercept of the linear fits to the mobility data in Fig. 4b and c, yielding 5.9 ± 0.5 (PCO10) and 6.6 ± 0.3 (PCO20), where the mobilities and T are normalized in units of cm2 s−1 V−1 and K. Comparing the ionic mobilities in the PCO compositions, cf. linear fittings in Fig. 4b and c, shows that the ionic mobility in the PCO10 is higher by 2 to 5 times than that of PCO20 from 600 °C to 200 °C, respectively. That result aligns with previous studies on the effect of the doping level on the ionic mobility in ceria; the doping has an optimal value, after which, a further increase leads to a decrease in the ionic mobility.17 Finally, we find that the ionic mobilities examined in the PCO10 and PCO20 compositions remain constant with varying δ, that enables their evaluation by the σ–α method.
Fig. 4d shows the concentration-independent electronic (small polaron) mobilities multiplied by T, calculated from eqn (8), of PCO10 (black dots) and PCO20 (red diamonds) respectively. The thermal activation energies of the electronic mobilities were found to be 0.57 ± 0.01 eV and 0.50 ± 0.02 eV for PCO10 and PCO20, respectively. For the PCO10 sample, only data points in the 200–625 °C temperature range were used for evaluating the activation energy as at higher temperatures there is a change in the linear trend due to the same reason related to Ce reduction that was discussed above for the ionic mobility. The PCO10 electronic mobility values were compared against the previously reported values by Stefanik et al.20,24 (green dashed line) obtained from a model fitting to the measured total conductivity versus pO2 for a bulk sample. The electronic mobilities have the same activation energy and nearly overlap below 600 °C. To enable calculating extrapolated values, the natural logarithm of electronic mobility pre-exponential factors can be found from the y-intercept of the linear fits in Fig. 4d that yielded 4.7 ± 0.2 (PCO10) and 4.8 ± 0.3 (PCO20), where the mobilities and T are normalized in units of cm2 s−1 V−1 and K. To calculate the small polaron mobilities in a specific stoichiometric state, a concentration dependence should be taken into account using eqn (3). The doping level was found to have a significant effect on the electronic mobility as doubling of the dopant from PCO10 to PCO20 increases the mobility by ∼3 times in the latter. The large variations in electronic mobility can be explained by a small polaron transport mechanism that is exponentially dependent on the mean distance between the dopants which decreases with increasing doping density.35
4.3. Determination of an effective optical pO2 in PCO thin films
In the out-of-equilibrium experiments, as shown for instance in Fig. 2a and b, the pO2 inside the flow cell does not relate directly to the oxygen stoichiometry of the thin film (contrary to equilibrium conditions). Nevertheless, the effective pO2 inside the thin film can be calculated in the out-of-equilibrium experiment indirectly, if the dependence of the point defect concentration in the MIEC on the equilibrium pO2 is known from the defect model. We define an effective pO2 that at each moment uniquely corresponds to the homogeneously distributed δ (that is measured in the experiment) according to the thermodynamic defect model of the material system (see Appendix A). Note that under equilibrium, the effective pO2 coincides with the pO2 of the ambient that induces the same value of δ. In the present case, δ was measured optically as described in the methods and theory section. We refer to a pO2 defined in that way, and calculated from an optically measured δ, as an “effective optical pO2”. Next, the effective optical pO2 is used for studying the dependence of conductivity on oxygen activity in PCO.Fig. 5a shows a log–log plot of the total conductivity of PCO10, e.g. shown in Fig. 2c and d, as a function of the effective optical pO2 as calculated from eqn (A2). The qualitative shape of the experimental data (green circles) and the fitting lines (dashed lines) at different temperatures in Fig. 5a exhibits the expected electrolytic flat (pO2 independent) region at low pO2, followed by an asymmetric peak like shape (more pronounced below 450 °C) with a +1/4 slope on its left side and −1/6 slope on its right side in accordance with the defect model and eqn (4). A comparison with the equilibrium measurements at known pO2-s is shown at 600 °C, exhibiting a very close agreement with the calculated effective optical pO2 values (cf. purple crosses and green circles). From the latter comparison it is apparent that the out-of-equilibrium experiment enables continuous characterization of PCO over an extended pO2 range, that spans over ∼13 orders of magnitude, without a compromise in the measurement accuracy. Remarkably, the out-of-equilibrium experiment lasts less than 10 minutes and enables access to the intermediate pO2 conditions (<10−5 bar) that are challenging to achieve by regular means.34 Previously Stefanik24 used an electrochemical oxygen pumping technique to control pO2 in the 1 to 10−15 bar range, however the experimental temperature was bounded by a 600 °C lower limit at which it took about 20 days to characterize the PCO10 conductivity (Stefanik's results shown for comparison in Fig. 5a as blue squares). The effective optical pO2 can also be used to show the non-stoichiometry dependence of PCO on pO2, as illustrated in Fig. 5b for the δ (green dots) measured in the experiment at several temperatures.
 | ||
| Fig. 5 Transport and thermodynamic properties of the PCO10 thin film as a function of effective optical pO2 obtained by the σ–α method in the out-of-equilibrium experiments. (a) Total conductivity plotted against an effective optical pO2, at several different temperatures (indicated on plot). At 600 °C, the conductivity versus pO2 measurements, under equilibrium with a gas atmosphere (× – symbols) and from the literature24 (squares), are shown for reference. The effective optical pO2 (indicated on the x-axes with *) is calculated from the PCO10 defect model, using eqn (A2), and the oxygen vacancy concentration that is obtained in the experiment (see Appendix A and the methods and theory section for the details). (b) The deviation from the oxygen stoichiometry, δ, versus effective optical pO2, at several different temperatures (as indicated on the plot). The PCO10 defect model shown as a dashed curve, at higher pO2-s (lower δ), the slope of the linear part is −1/6. | ||
5. Conclusions
In this study, a concurrent conductivity and optical absorption measurement method, i.e. the σ–α method, was employed to characterize in detail the thermodynamic, optical and mixed ionic–electronic transport properties of the PCO10 and PCO20 non-stoichiometric oxides. By using thin film samples with surface exchange limited kinetics, we were able to apply the method under out-of-equilibrium conditions, for an extremely large step change in pO2. We demonstrated that this approach enables rapid characterization of the key ionic and electronic defects and their respective mobilities. The out-of-equilibrium experiment enables a direct and detailed observation of the quadratic dependence of the conductivity on the optical absorption coefficient in PCO over the whole range of oxidation levels of the Pr dopants. This is in accordance with a model of mixed ionic–electronic (small polaron) transport where both types of mobile species move via an activated hopping process. Fitting the model to out-of-equilibrium experiments enables one to calculate the optical absorption cross section (ε) of the Pr4+ cations and consequently, the δ under each experimental condition, in a novel manner, without prior calibration. The measured Arrhenius relationship of δ with temperature was then used to extract the reduction enthalpy of PCO. Furthermore, the mixed ionic–electronic transport for PCO10 in the 200–750 °C range and for PCO20 in the 350–750 °C range was characterized in a continuous manner as a function of oxygen deficiency, 0 < δ < x/2. The theoretical dependence of the electronic mobility on the concentration of available sites, due to hopping small polarons, was demonstrated and quantitatively characterized in the experiment. This, together with the extracted ionic mobility (independent of δ), enabled us to calculate the electronic and ionic partial conductivities and transference numbers as a continuous function of δ. The measured in-plane transport properties of the thin film, i.e. activation energies and absolute values of mobilities, were found to be in very close agreement with the previously reported results in the literature for PCO10 and PCO20 bulk samples, obtained at elevated temperatures and under equilibrium conditions. Finally, an “effective optical pO2” was introduced and employed to study the conductivity dependence on the instantaneous pO2 inside the thin film in the out-of-equilibrium experiments. The results based on the effective optical pO2 were shown to be consistent with the ones obtained under equilibrium pO2 conditions both in this study and with those previously reported in the literature.The demonstrated σ–α method for rapid characterization of the in-plane mixed ionic electronic conductivity in PCO thin films makes it feasible to systematically study the effects of varying external parameters (e.g. strain) on defect formation, ionic and small polaron transport in similar types of MIECs; a feature of great recent interest, but difficult to pursue by other means.
Conflicts of interest
The authors declare no conflict of interest.Appendix
A. Thermodynamic defect model of PCO compositions
A defect model describing the reduction reaction of PrCe1−xO2–δ was published previously in ref. 6, 20–22 and 24. The key mass action relationship describing this reaction is given (utilizing Kröger–Vink notation42) by | (A1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ] denote the concentration of the enclosed species;
] denote the concentration of the enclosed species;  (VO in the main text) is a positive double charged oxygen vacancy;
(VO in the main text) is a positive double charged oxygen vacancy;  and
and  are the negative single charged (reduced) and neutral Pr dopants, respectively;
are the negative single charged (reduced) and neutral Pr dopants, respectively;  is the regular oxygen ion activity in PCO (nearly constant); and K is the reaction constant. A dilute concentration of defects was assumed in deriving eqn (A1) that was shown to hold in PCO for a doping level as high as x = 0.1.20–22,24 For the total number of Pr sites conserved, and under local charge neutrality,
is the regular oxygen ion activity in PCO (nearly constant); and K is the reaction constant. A dilute concentration of defects was assumed in deriving eqn (A1) that was shown to hold in PCO for a doping level as high as x = 0.1.20–22,24 For the total number of Pr sites conserved, and under local charge neutrality, 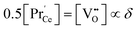 , the defect model can be expressed in terms of the oxygen vacancy concentration,
, the defect model can be expressed in terms of the oxygen vacancy concentration, | (A2) |
 . For that purpose, the constant K(T) = K0e−Hr,Pr/kBT is calculated at each temperature from calibration against some equilibrium pO2 value, e.g. in pure O2. For low oxygen vacancy concentrations,
. For that purpose, the constant K(T) = K0e−Hr,Pr/kBT is calculated at each temperature from calibration against some equilibrium pO2 value, e.g. in pure O2. For low oxygen vacancy concentrations,  , eqn (A2) is approximated by
, eqn (A2) is approximated by | (A3) |
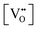 (or δ).
(or δ).
Acknowledgements
We thank the U.S. Department of Energy, Basic Energy Sciences Program: “Chemomechanics of Far-From-Equilibrium Interfaces” (COFFEI), project DE-SC0002633 for funding this research. We particularly thank Dr Han Gil Seo for assistance with PCO powder synthesis and the preparation of ceramic targets for PLD deposition. This work made use of the MRL Shared Experimental Facilities at MIT, supported by the National Science Foundation under award number DMR-1419807, and of the MIT.nano clean lab facilities.References
- M. Mogensen, N. M. Sammes and G. A. Tompsett, Solid State Ionics, 2000, 129, 63 CrossRef CAS.
- R. C. Pullar, R. M. Novais, A. P. F. Caetano, M. A. Barreiros, S. Abanades and F. A. C. Oliveira, Front. Chem., 2019, 7, 601 CrossRef CAS PubMed.
- H. Yahiro, K. Eguchi and H. Arai, Solid State Ionics, 1989, 36, 71 CrossRef CAS.
- W. C. Chueh and S. M. Haile, Philos. Trans. R. Soc., A, 2010, 368, 3269 CrossRef CAS PubMed.
- X. Huang, K. Zhang, B. Peng, G. Wang, M. Muhler and F. Wang, ACS Catal., 2021, 11, 9618 CrossRef CAS.
- D. P. Fagg, J. R. Frade, V. V. Kharton and I. P. Marozau, J. Solid State Chem., 2006, 179, 1469 CrossRef CAS.
- T. S. Stefanik and H. L. Tuller, J. Eur. Ceram. Soc., 2001, 21, 1967 CrossRef CAS.
- L. Liao, H. X. Mai, Q. Yuan, H. B. Lu, J. C. Li, C. Liu, C. H. Yan, Z. X. Shen and T. Yu, J. Phys. Chem. C, 2008, 112, 9061 CrossRef CAS.
- R. Schmitt, J. Spring, R. Korobko and J. L. M. Rupp, ACS Nano, 2017, 11, 8881 CrossRef CAS PubMed.
- D. Kalaev and H. L. Tuller, Adv. Opt. Mater., 2021, 2001934 CrossRef CAS.
- D. Kalaev, H. G. Seo and H. L. Tuller, Nanophotonics, 2022, 79, 3943 CrossRef.
- M. Schaube, R. Merkle and J. Maier, J. Mater. Chem. A, 2019, 7, 21854 RSC.
- J. Paier, C. Penschke and J. Sauer, Chem. Rev., 2013, 113, 3949 CrossRef CAS PubMed.
- S. Ackermann, J. R. Scheffe and A. Steinfeld, J. Phys. Chem. C, 2014, 118, 5216 CrossRef CAS.
- D. A. Andersson, S. I. Simak, N. V. Skorodumova, I. A. Abrikosov and B. Johansson, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 3518 CrossRef CAS PubMed.
- J. O. Nilsson, M. Leetmaa, O. Y. Vekilova, S. I. Simak and N. V. Skorodumova, Phys. Chem. Chem. Phys., 2017, 19, 13723 RSC.
- J. Koettgen, S. Grieshammer, P. Hein, B. O. H. Grope, M. Nakayama and M. Martin, Phys. Chem. Chem. Phys., 2018, 20, 14291 RSC.
- W. Lai and S. M. Haile, J. Am. Ceram. Soc., 2005, 88, 2979 CrossRef CAS.
- H. G. Seo, Y. Choi and W. C. Jung, Adv. Energy Mater., 2018, 8, 1 Search PubMed.
- S. R. Bishop, T. S. Stefanik and H. L. Tuller, Phys. Chem. Chem. Phys., 2011, 13, 10165 RSC.
- D. Chen, S. R. Bishop and H. L. Tuller, Chem. Mater., 2014, 26, 6622 CrossRef CAS.
- J. J. Kim, S. R. Bishop, D. Chen and H. L. Tuller, Chem. Mater., 2017, 29, 1999 CrossRef CAS.
- D. Chen, Z. Guan, D. Zhang, L. Trotochaud, E. Crumlin, S. Nemsak, H. Bluhm, H. L. Tuller and W. C. Chueh, Nat. Catal., 2020, 3, 116 CrossRef CAS.
- T. S. Stefanik, Electrical Properties and Defect Structure of Praseodymium-Cerium Oxide Solid Solutions, PhD thesis, MIT, 2004.
- W. J. Bowman, K. March, C. A. Hernandez and P. A. Crozier, Ultramicroscopy, 2016, 167, 5 CrossRef CAS PubMed.
- R. Waser, R. Dittmann, G. Staikov and K. Szot, Adv. Mater., 2009, 21, 2632 CrossRef CAS.
- Y. Ma and J. D. Nicholas, Phys. Chem. Chem. Phys., 2018, 20, 27350 RSC.
- Q. Lu, G. Vardar, M. Jansen, S. R. Bishop, I. Waluyo, H. L. Tuller and B. Yildiz, Chem. Mater., 2018, 30, 2600 CrossRef CAS.
- H. Borchert, Y. V. Frolova, V. V. Kaichev, I. P. Prosvirin, G. M. Alikina, A. I. Lukashevich, V. I. Zaikovskii, E. M. Moroz, S. N. Trukhan, V. P. Ivanov, E. A. Paukshtis, V. I. Bukhtiyarov and V. A. Sadykov, J. Phys. Chem. B, 2005, 109, 5728 CrossRef CAS PubMed.
- D. P. Fagg, A. L. Shaula, V. V. Kharton and J. R. Frade, J. Membr. Sci., 2007, 299, 1 CrossRef CAS.
- D. Kalaev, T. Defferriere, C. Nicollet, T. Kadosh and H. L. Tuller, Adv. Funct. Mater., 2020, 30, 1907402 CrossRef CAS.
- G. F. Harrington, D. Kalaev, B. Yildiz, K. Sasaki, N. H. Perry and H. L. Tuller, ACS Appl. Mater. Interfaces, 2019, 11, 34841 CrossRef CAS PubMed.
- N. H. Perry, J. J. Kim and H. L. Tuller, Sci. Technol. Adv. Mater., 2018, 19, 130 CrossRef CAS PubMed.
- A. Benisek and W. Sitte, J. Electrochem. Soc., 2005, 152, H157 CrossRef CAS.
- I. G. Austin and N. F. Mott, Adv. Phys., 1969, 18, 41 CrossRef CAS.
- I. Riess and J. Maier, J. Electrochem. Soc., 2009, 156, P7 CrossRef CAS.
- N. W. Kwak, D. K. Lim, S. J. Jeong, P. Byeon, S. Y. Chung and W. C. Jung, Adv. Mater. Interfaces, 2020, 7, 1 Search PubMed.
- M. C. Göbel, G. Gregori, X. Guo and J. Maier, Phys. Chem. Chem. Phys., 2010, 12, 14351 RSC.
- O. S. Heavens, Optical Properties of Thin Solid Films, Courier Corporation, 1991 Search PubMed.
- M. C. Göbel, G. Gregori and J. Maier, Phys. Chem. Chem. Phys., 2014, 16, 10175 RSC.
- R. Merkle and J. Maier, Angew. Chem., Int. Ed., 2008, 47, 3874 CrossRef CAS PubMed.
- F. A. Kröger and H. J. Vink, Solid State Phys., 1956, 307–435 Search PubMed.
| This journal is © the Owner Societies 2023 |

