The Malaprade reaction mechanism for ethylene glycol oxidation by periodic acid based on density functional theory (DFT)

Abstract

A general mechanism of the Malaprade oxidative carbon–carbon bond cleavage reaction of α-glycol in the presence of periodic acid has been proposed on the basis of density functional theory (DFT) computations. Ethylene glycol and periodic acid, both in their neutral forms, have been studied as noble substrate representatives in model reactions. The proposed reaction mechanism has been constructed based on and compared with previously published experimental kinetic, spectroscopic and temperature and pH-dependent studies. In the presented theoretical mechanistic considerations, four alternative molecular transformations have been analyzed from thermodynamic and kinetic points of view. Theoretically, the predicted activation energy barriers have been compared with experimental ones published elsewhere. The presented minimum energy pathway (MEP) unveiled the shape and conformation of the intermediate and transition state structures. The three-step reaction process involves the formation of a seven-membered quasi-ring assisted by an intramolecular hydrogen-bond intermediate structure forming one I–O bond (IC1_B), a cyclic ester intermediate forming two I–O bonds (IC2_C) and the final products formed at the two very last stages (HIO3, water and two formaldehyde molecules). The computed and energetically the most favourable reaction landscape proposed in this work uniforms and refines the mechanistic proposition given by Criegee for Malaprade type of reactions and further gives a detailed molecular understanding of the reaction rate and atomic connections en route the transformation. The molecular geometries of all stationary points (intermediate and transition state structures) lying on the potential energy hypersurface have been optimized at the four alternative DFT levels under the solvation model based on the density approximation: B3PW91, CAM-B3LYP, BMK, ωB97XD. The 6-311+G(2d,p) basis set for C, O, and H atoms and both the full (DGDZVP) and Ahlrichs-Weigend¹ (def2-TZVP) basis sets for iodine atoms were used during the computations.

---

1. Introduction

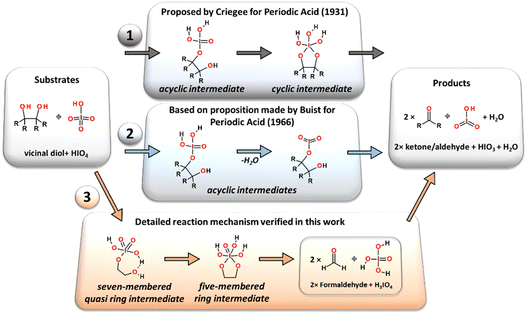
In 1928, Léon Malaprade published his explorative work,^2,3 in which the effective two-electron oxidative carbon–carbon bond cleavage reaction of α-glycols in the presence of periodic acid has been presented (Fig. 1). Since its discovery, the reaction has gained popularity and has become widely used in organic synthesis and industry. The formation of new carbonyl functional groups by effective oxidation of the two hydroxy moieties attached to adjacent carbon atoms has been demonstrated in a variety of structurally diverse carbohydrates,^4–10 from simple vicinal diols to molecularly complexed steroids or even as a key step in the total synthesis of natural products.^11,12

Fig. 1 The course of the Malaprade reaction between ethylene glycol and periodic acid.

The scope and detailed mechanistic course of the reaction was extensively studied in decades following the seminal work by Malaprade. In its pristine form the reaction proceeds in water solution with periodic acid, which enables fast substrate transformation with almost optimal efficiency. The room temperature, defined as 25 °C (77 °F), of the reacting solution is usually used in a classic synthetic procedure, without additional thermal stabilization.^2,3 The released thermodynamic degree of freedom allows the smooth equilibration of the reaction products and intermediates. This conclusion has been supported by the work of Duke and co-authors, who showed that cooling down the reaction decreases the reaction rate significantly.¹³ The influence of the pH value on reaction rates and reaction activation energy barriers for the oxidation reaction of 1,2-diols by periodic acid in aqueous solution were experimentally determined in a series of kinetic studies performed by Taylor, Charles and Duke, independently.^13–17 It was shown that the oxidation proceeds with the highest reaction rate constants within the range of 1–7 pH and was defined to be a second order process (depending on both substrate concentrations).¹⁵ This observation indicates that an excess of proton donors is required in the reaction mechanism to efficiently promote water elimination from the substrate atomic system. The importance of contiguous orientation of OH groups in the molecular carbon chain (vicinal diols) as a key structural feature allowing the C–C bond cleavage was suggested by Fleury in 1932.¹⁸

Very first implications on how the reaction proceeds on a molecular scale were made by Criegee,^19,20 who proposed that the cleavage reaction induced by HIO4 must involve the formation of the cyclic ester as an intermediate structure established in a reversible manner via an acyclic complex of substrates (periodic acid and glycol), (Path 1 in Fig. 2). The formation of the intermediate structure en route from the substrates to the final oxidation products has been detected by both pH¹⁵ and ultraviolet spectral changes.²¹ The authors maintained Criegee's^19,20 opinion that the intermediate complex between periodic acid and glycol might pose the cyclic diester or acyclic form, without direct identification of its geometrical structure. The steric hindrance and configurational isomerism of the diol substrate are also crucial for the performance of the reaction.¹³ It has been shown that the reaction rate is sensitive to the virtual orientation of the hydroxyl moieties and is significantly decreased for the trans-diols,¹⁵ while their cis-counterparts are cleaved more rapidly. Besides the fact that the molecular geometry of some trans-oriented vicinal diols prevents the possibility of the formation of cyclic reaction intermediates due to the limited flexibility of the C–C bond, they still undergo periodate oxidation.¹² As an alternative to the first reaction mechanism involving cyclic diester as an obligatory reaction intermediate the other transformation pathway running through only one acyclic intermediate complex was initially proposed for other types of oxidants (lead(IV) acetate) by Criegee²² and later adopted for periodate by Buist.²³ This reaction pathway can also be used to explain periodate oxidation under basic conditions (high pH values) or for the glycol molecular structures in which the direct formation of two O–I atomic bonds between the reductant and oxidizing agent is impossible due to geometry reasons.¹² Considering the abovementioned, at least one general mechanistic pathway undergoing via the acyclic intermediate can be considered in the case of the Malaprade type of reactions (Path 2 in Fig. 2).¹² The spectrometric studies of periodic acid in water solution published by Crouthamel and Martin^24,25 showed that the negatively charged IO₄⁻ ion dominates in the reaction solution over other iodates (H₄IO₆⁻, H₅IO₆⁻, and H₃IO₆⁻) below pH equal to 7, with almost constant concentration. However, it is more likely that in an acidic environment, a fully protonated form of periodate (HIO₄) should be expected as an active form of the oxidant and the reaction equilibrium that plays a key role in the process should be clearly shifted towards anion protonation.

Fig. 2 Potential reaction mechanisms proposed for the glycol oxidation reaction with periodic acid. Classic mechanism (CM) proposed by Criegee (1), reaction mechanism involving an acyclic intermediate structure proposed by Buist (2) and the reaction mechanism involving seven-membered quasi ring and five-membered ring intermediates described in this work (3).

Herein, we present the results of a theoretical investigation of the four alternative Malaprade reaction mechanisms. The pristine form of the oxidation reaction in water solution (solvation model based on density, SMD) has been examined using density functional theory. The simplified vicinal diol structure: ethane-1,2-diol (ethylene glycol) with minimum steric hindrance was used to elucidate the reaction mechanism without additional space factors. In a two-molecule reaction model, the periodic acid compound (HIO₄) acts as an oxidant. The atomic system imitates the reaction conditions where both substrates are in equal molar ratio and the balanced charge state conditions are preserved (protonated periodate).

2. Computational methods

The geometry optimization of all critical stationary points (transition states and local minima) was performed using the Gaussian 09²⁶ suite of programs and preparation of cartesian coordinates for all geometries were conducted using the GaussView 6²⁷ visualisation software. Four density functional theory (DFT) methods were applied to determine the kinetic and thermodynamic properties of the Malaprade reaction mechanism: B3PW91,^28,29 CAM-B3LYP,³⁰ BMK³¹ and ωB97XD.³² The unrestricted DFT computations were performed using a valence triple-ζ basis set (6-311+G(2d,p))[12] including diffuse and polarization functions for oxygen and carbon atoms and polarization functions for hydrogen. In addition, two alternative description strategies for iodine atoms have been performed in parallel. The full-electron type of basis set: DGDZVP^33,34 and Weigend's effective core potential (ECP) (def2-TZVP),^1,35 were applied for the iodine atom and its electrons (see the ESI† for method discussion). The implicit solvation model based on electron density (SMD)³⁶ was used in all computations to reflect the molecular properties in the water environment (dielectric constant for water: ε = 78.3553). The structures were pre-optimized at the B3PW91/6-311+G(2d,p) level of theory and then re-optimized using the other three functionals. No geometry restrictions have been applied. The thermal and zero-point vibrational energy (ZPE) corrections have been used in the calculations. Harmonic frequency analysis has been performed to confirm the proper position of the ground state (no imaginary frequencies) and transition state (one imaginary frequency) structures. In the case, when more than one transition state or local minimum has been found, the statistical contribution of energy has been calculated using standard Boltzmann equation. Intrinsic reaction coordinate (IRC)^37,38 calculations were also carried out, to verify the connectivity of the transition state structures. Quantum Theory Atoms in Molecules analysis (QTAIM)^39–45 was performed using the AIMAll program⁴⁶ with all default options. The geometries of intermediate (IC2_C) and transition state (TS3_C) structures optimized at the B3PW91/6-311+G(2d,p) (with 6-311+G(2d,p) basis set for C, O, H atoms and the full basis set (DGDZVP) for Iodine atom) level of theory were used to generate wave function files (WFN) in the Gaussian 09 software. The WFN files were then used to compute the electron density (ρ) at Bond Critical Points (BCPs) and the differences between corresponding values were used to describe the molecular behavior during the C–C bond cleavage.

3. Results and discussion

Four alternative reaction pathways were found (Fig. 3) for the oxidative substrate transformation leading to the formation of two formaldehyde molecules, water and iodic acid (IO₃). The first two reaction pathways (AM1, blue-colored structures and AM2, green-colored structures in Fig. 3) in their neutral charged form have been taken into consideration based on mechanistic suggestions published by Buist²³ in 1966 as an alternative for the acid/base-mediated reactions. In this case, many mechanistic and structural details have been uncovered based on quantum chemical computations, e.g. the formation of intramolecular hydrogen bonds between glycol hydroxyl groups and iodate proton acceptors stabilizing the proton-involved quasi-ring intermediates. The third and fourth reaction pathways (CM and AM3, orange and yellow colored structures in Fig. 3) were constructed as a theoretical model variation of the classic mechanistic picture of the Malaprade reaction presented by Criegee in 1938.^19,20,22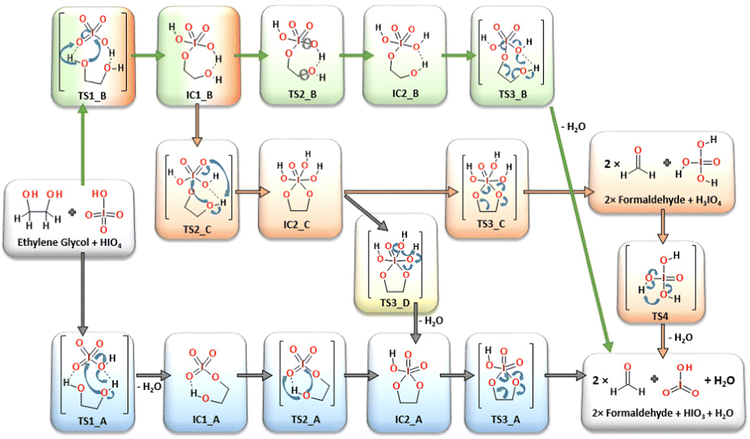

Fig. 3 All considered reaction pathways, including classic mechanism CM (orange) and three alternative reaction mechanisms: AM-1 (blue), AM-2 (green) and AM-3 (yellow), respectively.

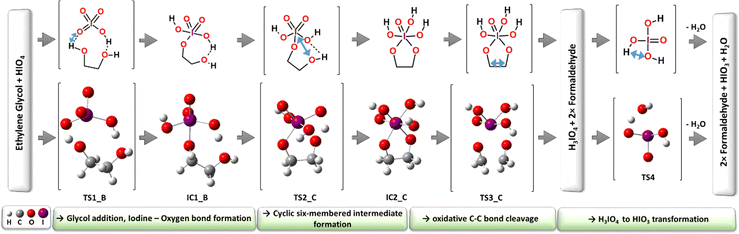
First, modeled mechanistic route (AM1) undergoes three transition state structures (TS1_A, TS2_A and TS3_A) and two intermediates (IC1_A and IC2_A). In the very first stage, the bimolecular system loses the water molecule as a result of the proton transfer from glycol to the OH moiety localized on the oxidant molecule (IO₄H). The formation of the seven-membered quasi-ring intermediate structure (IC1_A) via the transition state (TS1_A) requires an extra energy input of 149.1 kJ mol⁻¹ (Fig. 4). The second transition state structure corresponds to the new O–I bond formation process combined with the proton transfer from the glycol hydroxyl group and the iodate. The TS1_A energy barrier was computed to be at the 70.9 kJ mol⁻¹ level (Fig. 4). Consequently, the five-membered ring intermediate structure is formed (IC2_A) from which the key C–C bond cleavage occurs through the activation barrier of 19.9 kJ mol⁻¹ (TS3_A), leading to the formation of the final reaction products: two formaldehyde, HIO₃ and water molecules. In the second independent reaction pathway AM2 (green-colored structures in Fig. 3), at the very first step, the new O–I bond is formed together with the proton transfer from the glycol hydroxyl group and the oxidant. The first transition state (TS1_B), being the reaction rate-limiting step, has been located at 119.9 kJ mol⁻¹ energy level and leads to the formation of the seven-membered quasi ring intermediate (IC1_B). Then, in the next step, the smooth conformational change takes place via transition state TS2_B (63.5 kJ mol⁻¹), where the intramolecular hydrogen bonds are relocated to form intermediate IC2_B. From this point, the rate-limiting step of the AM2 route (TS3_B, 130.9 kJ mol⁻¹) takes place, where the C–C bond is cleaved leading to the final reaction products.

Fig. 4 Gibbs free energy profiles for all considered reaction pathways, computed at the B3PW91/6-311+G(2d,p) (SMD = water) level of theory.

Both mechanistic pathways proposed herein as AM1 and AM2 involve the formation of the quasi-ring posing intermediates, in which the intramolecular hydrogen bond plays a geometry-forming role. The presence of the intramolecular proton bridges has not been a part of the consideration under previous kinetic and mechanistic studies,^21,23,47 while it seems to be crucial for understanding the atomic reorganization during the oxidation process. In addition, in both cases (AM1 and AM2 pathways) the formation of the H₃IO₄ individuum as a direct water precursor has not occurred, since water elimination takes place from the glycol-periodate molecular system at earlier stages. In the AM1 route, the water molecule is eliminated in the very first step (TS1_A, 149.1 kJ mol⁻¹) and in the last step in the AM2 pathway (TS3_B, 130.9 kJ mol⁻¹). Each of the transition states is located at the highest energy points on each particular potential energy surface (PES) being the rate-limiting steps.

The classic reaction pathway constructed based on Criege's mechanistic remarks,^19,20,22 has been shown in both Fig. 3 and 4 in two congenial variations drawn as CM and AM4. The first step in both mechanisms undergoes via the transition state TS1_B, the formation of a new O–I bond within the seven-membered quasi-ring intermediate structure (IC1_B). Then, in the next step while the second glycol oxygen atom approaches the iodine atomic center to form the second O–I bond, the adjacent hydroxyl proton smoothly shifts to one of the deprotonated iodate oxygen atoms. As a consequence of the transition state TS2_C (126.6 kJ mol⁻¹), the five-membered cyclic ester intermediate structure IC2_C is formed. From this point, two alternative pathways can occur: CM and AM4. First, the CM route in the consequent step leads to the formation of two formaldehyde molecules and H₃IO₄ individuum via the transition state TS3_C (90.2 kJ mol⁻¹). The CM mechanism is the only one showing the possibility of forming an independent H₃IO₄ molecule, from which the water elimination process occurs far below the energetic regime of the main potential energy surface area, with the transition state TS4 located at −154.7 kJ mol⁻¹ energy level, with respect to the separate substrate molecules (glycol and oxidant). In addition, the performed computations clearly showed the formation of the cyclic ester intermediate (IC2_C) in the two-step reaction as postulated by Criegee in his mechanistic deliberations. The alternative AM4 route can take place starting at this point from the IC2_C intermediate structure, leading to the final products by incorporating the last step of the AM1 pathway and forming the IC2_A intermediate via the transition state TS3_D (94.3 kJ mol⁻¹).

One of the most crucial transformations occurring during the Malaprade reaction mechanism is the point where the carbon–carbon bond of the glycol molecule is ultimately cleaved. The intermediate structure (IC2_C) and consequent transition state (TS3_C) posing the five-membered atomic ring seems to be a great subject for topological studies and electronic structure analysis.[CYTOWANIE ANETKI] The Quantum Theory Atoms in Molecules analysis (QTAIM)^39–45 was used in order to determine the changes in electronic density values (ρ-BCP) at bond critical points (BCPs) before (in IC2_C structure) and at the cleavage “point” in the transition state TS3_C (Fig. 5). The following comparison of changes in the electron density and nominal bond length gives a chance to track the reorganization of the atomic bonds during the C–C tie disassembling.

Fig. 5 Molecular graphs of the intermediate (IC2_C) and transition state (TS3_C), the green circles represent the bond critical points (BCPs) indicating the localization of the lowest electronic charge density (ρ, a.u.) on the bond paths, the blue number represents the angle values in [°].

The electron density (ρ, a.u.) at each BCP in both structures was computed (for all parameters please see the ESI†). While the reaction proceeds within this part of the mechanism from the stable intermediate IC2_C to the first-order saddle point (transition state) TS3_C, the following bond reorganization can be observed. The very first and the most significant change in bond distance and electron density located at the BCP occurs between the key C8–C7 bond. The key carbon–carbon bond dissociation results in the reduction of the ρ-BCP of −0.1575 a.u from 0.2520 in IC2_C to 0.0944 a.u in TS3_C (Table 2). The same behavior can be observed while analyzing appropriate bond lengths. The interatomic distance increases by 0.3945 Å from 1.5185 in IC2_C to 1.9130 Å in TS3_C. The C–C bond breaking motion in TS3_C indicated by the computed imaginary frequency (−593.45 cm⁻¹) announces the further reaction direction followed by the infinite bond dissociation leading to two separate formaldehyde molecules and one H₃IO₄ individuum.

The electron density laying at the BCP between two hydroxylate oxygen (O6 and O5) atoms and Iodine (I1) and two carbon glycol atoms (C7 and C8) are significantly involved in final product formation. The strengthening of both O6–C7 and O5–C8 bonds can be observed by the increase of ρ-BCP of 0.0972 and 0.0950 a.u. from 0.2435 and 0.2449 in IC2_C to 0.3407 and 0.3399 a.u. in TS3_C (Table 2). The stabilization of the double bonds between these two carbon-oxygen bonds is significant and simultaneously manifested by shortening the interatomic distances from ca. 1.431 to 1.291 Å. At the same time, the weakening of two bonds I1–O5 and I1–O6 can be seen during the main C7–C8 bond cleavage. Dissociation of two separate formaldehyde molecules is preceded by the loss of electronic charge density at the BCP by −0.05 a.u. from ca. 0.13 to 0.07 a.u. The increase in the bond distances from c.a 2.0009 Å to 2.2777 Å at the fist-saddle point predicts the further complete dissociation of both I–O bonds. The opening of the five-membered ring (–I–O–C–C–O–) results in the cleavage of three bonds (two I–O and one C–C) and the stabilization of two carbon-oxygen bonds. The ring opening process can be tracked by the analysis of angle changes within the pentagon ring (please see the ESI† for more angle values). All the angle values increased except one between ∠O5–I1–O6, which decreased from 84.105 to 78.178° indicating that the main ring-breaking force is driven by the C8–C7 bond cleavage accompanied by elongation of two pair of O–I bonds.

Among all four considered reaction pathways, the classic reaction mechanism (CM) occurred to be the most energetically favourable (MEP-minimum energy pathway), with the rate-limiting step located at the fist-order saddle point TS2_C (126.6 kJ mol⁻¹, see Fig. 6). All alternative reaction steps, including the energetically most accessible CM reaction channel, have been analyzed and compared using four different functionals (Table 1). Among the tested method, the energy of the rate-limiting transition state (TS2_C) was computed to be within the range of 123–132 kJ mol⁻¹ (Table 1, please see the ESI† for more details). The available experimental data for glycol oxidation by periodate acidic agent varies between 97.5–167.4 kJ mol⁻¹ depending on the study and the reaction condition (Table 1).^13,14 The lowest found experimental energy value is 79.1 kJ mol⁻¹,¹⁷ which has not been shown in Table 1 refers to reaction rate measurements under specific reaction conditions. Based on the report, experimental model appears to be an ion–dipole type involving the monovalent periodate ion and the glycol molecule.¹⁷ The reported low reaction activation barrier refers to the subtle interplay of the oxidation agent anionic forms (IO₄⁻,H₃IO₆⁻, H₄IO₅⁻,H₄IO₆⁻), which seems to be predominant in the reaction chamber.

Fig. 6 Visualization of optimized structures lying on the minimum energy pathway (MEP) – the classic reaction mechanism (CM), blue arrow indicates displacement vectors of the normal mode with imaginary frequency.

Table 1 Experimental and computationally predicted activation energies for the model reaction between ethylene glycol and periodic acid

Method	Theoretical ΔG (kJ mol^−1)		Experimental ΔG (kJ mol^−1)
	Classic mechanism (CM) – TS2_C		Ref. 14	Ref. 13
	def2-TZVP^a	DGDZVP^b
a Effective core potential (ECP) def2-TZVP was used to describe iodine electrons and 6-311+G(2d,p) for other atoms. b The DGDZVP type of full basis set was used to describe iodine electrons and 6-311+G(2d,p) for other atoms.
B3PW91/6-311+G(2d,p) (SMD = water)	126.6	102.0	97.5	125.5–167.4
CAM-B3LYP/6-311+G(2d,p) (SMD = water)	123.2	93.9
BMK/6-311+G(2d,p) (SMD = water)	133.8	104.6
ωB97XD/6-311+G(2d,p) (SMD = water)	131.7	99.5

---

Table 2 Selected calculated bond distances (d, Å) and electron density at BCP (ρ, a.u.)

No.	Atoms	ρ-BCP(IC2_C) (a.u.)	ρ-BCP(TS3_C) (a.u.)	Δρ-BCP(TS3_C-IC2_C) (a.u.)	d-Bond dist.(IC2_C) (Å)	d-Bond dist.(TS3_C) (Å)	Δd-Bond dist.(TS3_C-IC2_C) (Å)
No.-sequence number; ρ-BCP-electron density at the bond critical point; Δρ-BCP(TS3_C-IC2_C)-electron density difference between corresponding two bond critical points of the transition state structure TS3_C and the intermediate structure IC2_C, d-bond dist.-bond Distance between the atoms in Å; Δd-bond dist.(TS3_C-IC2_C)-the difference between two corresponding bond distances of the transition state structure TS3_C and intermediate structure IC2_C.
1	I1–O5	0.1309	0.0773	−0.0536	2.0009	2.2777	0.2768
2	I1–O6	0.1302	0.0747	−0.0555	2.0020	2.2977	0.2957
3	C7–C8	0.2520	0.0944	−0.1575	1.5185	1.9130	0.3945
4	O6–C7	0.2435	0.3407	0.0972	1.4330	1.2904	-0.1426
5	O5–C8	0.2449	0.3399	0.0950	1.4315	1.2913	-0.1403

---

Considering the abovementioned and the neutral character (HIO₄ and glycol) of the model reaction substrates studied here by the theoretical approach, we are of the opinion that the computationally derived energy barrier should be compared with other experimental studies considering more similar process conditions.^13,14 When analizing experimental kinetic studies, the theoretical models seem to locate the computed reaction energies between the experimental measurements and shown to be a good quantitative representation of the potential energy surface that accompanies the molecular transformations. In addition, a detailed structure–energy relationship analysis of the MEP supported the Criegee mechanism proposition that on the course of the reaction, first, the H₃IO₄ structure is formed at the TS3_C energy point, after which the water molecule is eliminated from the separated H₃IO₄ molecule far below the main energy regime (Fig. 6). The alternative direct dissociation of HIO₃ from the glycol-oxidant complex as a consequence of previous water elimination shown to be energetically unfavorable and stays in contrast to the mechanistic proposition published by Buist.²³

4. Conclusions

As the Malaprade reaction mechanism has been a matter of extensive experimental consideration since its first report,^2,3 and due to its broad practical and synthetic value, the understanding of a detailed reaction mechanism based on a computational approach has been an essential mission. We utilized the DFT methods to explore the mechanism of the model reaction between ethylene glycol and periodic acid in the oxidative carbon–carbon bond cleavage process leading to the formation of HIO₃ and two formaldehyde molecules. According to our computational results, which comprise a comparison of four alternative mechanistic pathways, the most energetically favourable reaction route has been pointed out to have the rate-limiting first-order saddle point (depending on the level of theoretical approximation) between 107 and 134 kJ mol⁻¹ and stays in good agreement with experimentally derived values (98–167 kJ mol⁻¹).^13,14 Based on the results obtained from all the methods used in the study, with both the effective core potential (ECP) (def2-TZVP) and the full basis set (DGDZVP) describing the electronic structure of the iodine atom, the same mechanistic picture can be drawn and comparable trends along the potential energy surface, from substrates to products, are observed. The minimum energy pathway (MEP) has been described as a three-step process, involving the formation of three key intermediate structures and final products. The first intermediate is formed as a result of the addition of glycol alcohol to the iodine oxidizer atomic center leading to the formation of the seven-membered quasi ring assisted by the intramolecular hydrogen-bond intermediate structure forming one I–O bond. The first intermediate structure (IC1_B) is formed by crossing the rate-limiting activation barrier. The cyclic ester structure incorporating two newly formed symmetric I–O bonds (IC2_C) is the second defined stationary point structure that leads at the final stage to the formation of a H₃IO₄ molecule from which the water molecule is eliminated and forms the desired final products of HIO₃, water and two formaldehyde molecules. The reaction mechanism proposed in this work, constructed based on experimental presumptions and detailed theoretically predicted intimate visualization of molecular and atomic reorganization, verifies previous experimental mechanistic prepositions, giving, to our best knowledge, the first in silico drawn picture of the Malaprade-type reaction.

Author contributions

KB coordinated the study, conceived the methodology plan, prepared graphics and led its design, performed the computations, analyzed data, and prepared a draft of the manuscript, MB, AJ, KP and AK contributed to the formulation of the final conclusions, and helped to draft the manuscript. All authors read and approved the final manuscript.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

This work has been financed by the National Science Centre, Poland, grant SONATA 17 no. 2021/43/D/ST4/01679. We express our thanks to the Wroclaw Center for Networking and Supercomputing (WCSS) and Interdisciplinary Centre for Mathematical and Computational Modeling (ICM) in Warsaw (grant no. G50-2) for providing computer time and facilities.

References

1. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
2. L. Malaprade, Bull. Soc. Chim. Fr., 1928, 43, 683.
3. L. Malaprade, C. R. Hebd. Seances Acad. Sci., Ser. D, 1928, 186, 382.
4. A. S. Perlin, in Adv. Carbohydr. Chem. Biochem., ed. D. Horton, Academic Press, 2006, vol. 60, pp. 183–250.
5. K. A. Kristiansen, A. Potthast and B. E. Christensen, Carbohydr. Res., 2010, 345, 1264–1271.
6. C. Urakami and Y. Kakutani, Bull. Chem. Soc. Jpn., 1957, 379–381.
7. A. Amore, K. Wals, E. Koekoek, R. Hoppes, M. Toebes, T. N. M. Schumacher, B. Rodenko and H. Ovaa, ChemBioChem, 2013, 14, 123–131.
8. B. H. Nicolet and L. A. Shinn, J. Am. Chem. Soc., 1939, 61, 1615.
9. R. A. Harkness and K. Fotherby, Experientia, 1961, 17, 253–254.
10. A. J. Fatiadi, Synthesis, 1974, 229–272.
11. B. M. Trost, G. Dong and J. A. Vance, J. Am. Chem. Soc., 2007, 129, 4540–4541.
12. A.-K. C. Schmidt and C. B. W. Stark, Synthesis, 2014, 3283–3308.
13. F. R. Duke and V. C. Bulgrin, J. Am. Chem. Soc., 1954, 76, 3803–3806.
14. F. R. Duke, J. Am. Chem. Soc., 1947, 69, 3054–3055.
15. C. C. Price and M. Knell, J. Am. Chem. Soc., 1942, 64, 552–554.
16. C. C. Price and H. Kroll, J. Am. Chem. Soc., 1938, 60, 2726–2729.
17. J. E. Taylor, J. Am. Chem. Soc., 1953, 75, 3912–3916.
18. P. Fleury and J. Lange, C. R. Acad. Sci., 1932, 195, 1395.
19. R. Criegee, Berichte der deutschen chemischen Gesellschaft (A and B Series), 1931, 64, 260–266.
20. R. Criegee, L. Kraft and B. Rank, Justus Liebigs Ann. Chem., 1933, 507, 159–197.
21. G. J. Buist, C. A. Bunton and J. H. Miles, J. Chem. Soc., 1957, 4575–4579,  10.1039/JR9570004575.
22. R. Criegee, E. Höger, G. Huber, P. Kruck, F. Marktscheffel and H. Schellenberger, Justus Liebigs Ann. Chem., 1956, 599, 81–124.
23. G. J. Buist, C. A. Bunton and J. Lomas, Journal of the Chemical Society B: Physical Organic, 1966, 1099–1105,  10.1039/J29660001099.
24. C. E. Crouthamel, A. M. Hayes and D. S. Martin, J. Am. Chem. Soc., 1951, 73, 82–87.
25. C. E. Crouthamel, H. V. Meek, D. S. Martin and C. V. Banks, J. Am. Chem. Soc., 1949, 71, 3031–3035.
26. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, 2016.
27. R. Dennington, T. Keith and J. Millam, GaussView 6 Software, 2009.
28. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
29. A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100.
30. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
31. A. D. Boese and J. M. L. Martin, J. Chem. Phys., 2004, 121, 3405–3416.
32. J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
33. N. Godbout, D. R. Salahub, J. Andzelm and E. Wimmer, Can. J. Chem., 1992, 70, 560–571.
34. C. Sosa, J. Andzelm, B. C. Elkin, E. Wimmer, K. D. Dobbs and D. A. Dixon, J. Phys. Chem., 1992, 96, 6630–6636.
35. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
36. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396.
37. C. Gonzalez and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523–5527.
38. G. Carlos and S. Bernhard, J. Chem. Phys., 1989, 90, 2154–2161.
39. R. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, USA, 1994.
40. R. F. W. Bader, Chem. Rev., 1991, 91, 893–928.
41. R. F. W. Bader, J. Phys. Chem. A, 2007, 111, 7966–7972.
42. R. F. W. Bader, J. Phys. Chem. A, 1998, 102, 7314–7323.
43. R. F. W. Bader, Atoms in Molecules, A Quantum Theory; International Series of Monographs in Chemistry, OxfordUniversityPress, Oxford, 1990.
44. R. F. W. Bader, Monatshefte für Chemie, 2005, 819.
45. P. L. A. Popelier, Atoms in Molecules: An Introduction, PrenticeHall, England, 2000.
46. T. A. Keith, et al. , AIMAll Software, 2019.
47. G. J. Buist, C. A. Bunton and W. C. P. Hipperson, Journal of the Chemical Society B: Physical Organic, 1971, 2128–2142,  10.1039/J29710002128.

---

Footnote

† Electronic supplementary information (ESI) available: Cartesian coordinates and thermodynamic data for all intermediate and transition state structures, chosen structure topology parameters (electronic charge densities at BCPs, bond distances in angles in IC2_C and TS3_C geometries). See DOI: https://doi.org/10.1039/d2cp04764k

---