Determining nuclear quadrupole moments of Bi and Sb from molecular data

Abstract

An independent value of −422(3) millibarn (mb) is obtained for the nuclear quadrupole moment Q(²⁰⁹Bi) using experimental coupling constants for diatomic BiN, BiP, BiF, BiCl, and BiI, combined with full-Dirac CCSD-T calculations of the electric field gradient q. This value lies close to two other recently published molecular results, and a full-triplet CCSDT atomic result. Based on the same approach, we obtained Q(¹²¹Sb) = −541.7(0.8) mb and Q(¹²³Sb) = −690.6( 1.0) mb, in agreement with one recently published molecular result.

---

The nuclear quadrupole moment Q(²⁰⁹Bi) was one of the first moments determined.¹ The value, in 1936, was −400 mb [1 mb = 10⁻³¹ m²]. Interest in the Q value of the neutron deficient isotopes continues, due to the nuclear physics.² A common way to determine Q is to measure a nuclear quadrupole coupling constant (NQCC), B = eqQ/h, and to combine it with a theoretical determination of the electric field gradient (EFG), q, on the nuclear site in the system studied. This can be done for atomic, molecular, or solid-state systems and the results usually agree with each other, and with the main alternative approach of muonic or pionic systems. For a recent review see Pyykkö.³

A notable exception is Q(²⁰⁹Bi), where a 2001 atomic Q was −516(15) mb⁴ but a molecular value using the BiN and BiP diatomics by Teodoro⁵ was −420(8) mb. Both B experiments and both q calculations were expected to be quite accurate. Therefore the problem is still on the table (see below) and we want to have a further look at the ‘molecular’ Q(²⁰⁹Bi). Note that we here consider two series of molecules, the pnicogens BiN and BiP and the monohalides BiX (X = Cl, F, I) and that these series have opposite signs of B (Table 1).

Table 1 Available accurate experimental nuclear quadrupole coupling constants B_e at the equilibrium bond distance R_e in ²⁰⁹Bi and ¹²¹Sb diatomic molecules to lowest order

Molecule	B e (MHz)	R e (Å)	Ref.
a Experimental B0 given for BiCl and BiI. b This value of B has been calculated from the experimental results for ^123Sb^35Cl by using the ratio B(^123Sb)/B(^121Sb) = 1.27491(1).^17
BiN	905.066(88)	1.9349079(7)	11
BiP	903.031	2.2961520(80)	5 and 11
BiF	−1150.9632	2.034276(1)	12
BiCl	−1027(12)^a	2.47155(7)	13
BiI	−909.5(20)^a	2.80053(8)	14 and 15
SbN	649.669(9)	1.8356707(2)	16
SbP	620.35(1)	2.2054454(5)	16
SbF	−586.802(1)	1.917584(28)	17
SbCl	−515.124^b	2.335472(13)	17

---

The case of antimony still remains difficult. The reference value has fluctuated widely over the years. The old, atomic standard values for ^121,123Sb were −360(40) mb and −490(50) mb,⁶ respectively. Later, Voss et al. from an experimental and theoretical analysis of the configuration 5p² 6s supported a value of −440(30) mb for ¹²¹Sb.⁷ Solid-state calculations by Svane⁸ first suggested that the ¹²¹Sb value should be changed to −669 mb. Then molecular calculations by Demovič et al.⁹ and Haiduke et al.¹⁰ produced mutually consistent values of −556 mb and −543 mb, respectively. Both determinations were based on diatomic data for SbN, SbP, SbF and SbCl by Cooke and co-workers, reported in Table 1. This second series of four molecules has been studied in this work.

BiN, SbN, BiP and SbP are triple-bonded, closed-shell, short-bond systems with a substantial gap between the highest occupied and lowest empty molecular orbital. They are consequently easiest to describe with a single-configuration starting point. The monohalide BiX (X = F, Cl, I) and SbX (X = F, Cl) are, in a non-relativistic picture, open-shell ³∑⁻ states and were found to be a good example of Hund's case (b). In the relativistic picture, due to strong spin–orbit coupling, they are very near the Hund's case (c) limit, with the consequence of a ¹∑⁺ ground state, that could be considered as a relativistic closed-shell.

In a diatomic molecule, the total electric-field gradient q at the nucleus X can be decomposed into nuclear and electronic contributions.

q(X) = q_nucl(X) + q_el(X)

In this work, the electronic contribution has been calculated with the DIRAC program package¹⁸ using a relativistic coupled-cluster approach (CCSD-T) and the density functional theory (DFT) using the long-range corrected hybrid CAM-B3LYP* functional¹⁹ with a 4-component Dirac–Coulomb (DC) Hamiltonian including spin–orbit coupling (see ESI† for details). CCSD-T was first introduced by Deegan and Knowles²⁰ and differs from the standard CCSD(T) correction by an inclusion of more disconnected triples terms up to fifth order. Haiduke et al.¹⁰ pointed out, for example, that for Sb compounds, there could be a non-negligible difference between CCSD(T) and CCSD-T for Q(¹²¹Sb) and Q(¹²³Sb) and concluded that CCSD-T provided significantly better results.

All calculations were carried out applying CV3Z triple-zeta Dyall basis sets with core correlating functions (see ref. 21 and 22 and the appropriate references) in their fully uncontracted form. We used a Gaussian charge distribution model to describe the charge of nuclei. Furthermore, all the present calculations have been carried out at the experimental value of the equilibrium bond distances, R_e (Table 1). Note that the use of available experimental (B_e, R_e) takes care of the vibrational effects. Within the DFT framework, the electronic contribution to the q value is obtained from an analytic gradient formulation as implemented in the DIRAC program. For the CCSD-T approach, the electronic contribution to the q value is obtained by adding the q analytic HF value to the contribution of the electronic correlation to q (q_el(X) = q_el.,HF(X) + q_el.,corr.(X)). In order to get the correlation correction to q we used an approach proposed by Pernpointner et al.²³ fitting the correlation energy obtained at different field strengths (between ±1.0 × 10⁻⁶ a.u. and ±1.0 × 10⁻¹⁰ a.u.) to an nth order polynomial. The correlation correction to q is obtained from the first order response energy²³ (see ESI† for details). In a final step, Q was calculated from the indirect method introduced by Belpassi et al.²⁴ which corresponds to the calculation of slope from a least squares regression line through all (q,B) points of the Bi and Sb molecular series BIN, BiP, BiF, BiCl, BiI and SbN, SbP, SbF, SbCl according to: (B/MHz) = 0.2349647 (q/a.u.) (Q/mb) with B the experimental nuclear quadrupole coupling constant (see ESI† for details). This original approach combining on the one hand the polynomial determination of the correlation correction to q and on the other hand the indirect method to determine Q makes it possible to minimize the impact of errors in each stage of the evaluation of the Q value (see ESI† for details).

The graphs are reported in Fig. 1 and 2 for the Bi and Sb molecules, respectively, in a closed-shell ground-state picture.

Fig. 1 The experimental NQCC in MHz as a function of the calculated EFG in atomic units for bismuth-based molecules.

Fig. 2 The experimental NQCC in MHz as a function of the calculated EFG in atomic units for antimony-based molecules.

For the Bi-containing molecules, we obtained a good agreement between CAM-B3LYP* functional and the CCSD-T value. The determined Q(²⁰⁹Bi) value from the linear fit is −405(9) mb from the DFT/CAM-B3LYP* calculations and −422(3) mb from the CCSD-T calculation. Here the error limits are statistical standard errors. These values are in agreement with the recent determinations of Teodoro et al.⁵ at −420(8) mb based on the direct approach for each molecule BiN and BiP separately. Shee et al.²⁵ obtain from the same two molecules −415.1 mb. Skripnikov et al.²⁶ published a new ‘atomic’, FS-CCSDT Q(²⁰⁹Bi) of −418(6) mb. Our results are also consistent with recent work by Liu and Cheng²⁷ who obtained values in the range of −411 to −422 mb for the same five molecules using an atomic mean-field spin–orbit approach within the exact two-component theory (SOX2CAMF).

Commenting on the Q(²⁰⁹Bi) of −516 mb by Bieroń and Pyykkö in 2001,⁴ it was obtained by about 20 000 Configuration State Functions (CSF), thought at the time to be adequate. Single, some double and no triple substitutions were included. Currently over 4 million CSFs are possible and still don’t provide a complete convergence for the 5-valence-electron system Bi.²⁸

We compare our Q(Bi) determination with the (previous) Group-15 case of Q(Sb). The B_e and R_e are listed in Table 1. Concerning the Q(¹²¹Sb) we observed a significant deviation between the CAM-B3LYP* value at −474(3) mb and the CCSD-T value at −541.7(0.8) mb. In 2006, from a CCSD-T calculation, Haiduke et al.¹⁰ proposed a recommended value of −543(11) mb for ¹²¹Sb. Their values were calculated using only the SbN and SbP closed-shell molecule results due to too large errors in the SbF and SbCl open-shell calculations. In the same time, Demovič et al.⁹ recommended the value of (−556 ± 24) mb from direct method on the SbN, SbP, SbF, SbCl series with IOTC CCSD(T) calculations. In closed-shell picture, the Haiduke et al.¹⁰ value is in good agreement with our new value. We can also notice the quality of calculated EFGs confirmed by an R² of 1 and the intercept at origin that does not deviate substantially from zero. Any deviation from zero intercept would indicate a systematic error in the method applied. This consistency of values can also be seen as an argument in favor of relativistic closed-shell monohalides.

To go further and interpret the origin of calculated values, we performed an analysis of the electronic contributions to the q value of the individual orbitals. These results are illustrated in Fig. 3 and 4. These analyses are only possible from analytical calculation of the EFG. Hence they were done with DFT calculations with CAM-B3LYP* functional.

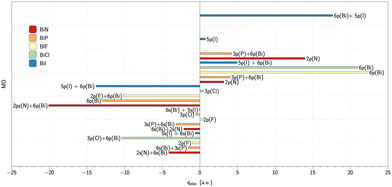Fig. 3 Electronic contribution from individual orbitals to q_el (CAM-B3LYP*/CV3Z) for bismuth-based molecules.

Fig. 4 Electronic contribution from individual orbitals to q_el (CAM-B3LYP*/CV3Z) for antimony-based molecules.

A first general comment is that the main contribution to EFG is due to valence electrons. This has already been outlined, e.g., by Neese et al.²⁹ for the HI and HAt compounds for which most of the observable field gradient comes from the valence region. The contribution from the 6s(Bi) is quite similar in BiN (6s(Bi)/2s(N) mixing) and BiP (6s(Bi)/3s(P) mixing). The negative overall value of q is due to the large negative contribution given by the mixing of 6p(Bi) and 2p(N) (σ bonding orbital) in BiN and by the 6p(Bi) orbital in BiP. In contrast, in BiF and BiCl, the 6p(Bi) π orbital provides a significant positive contribution to EFG that is partially counterbalanced by a negative EFG contribution from σ bonding orbitals (2p(F)/3p(Cl)/5p(I)) mixing with the 6p(Bi) orbitals resulting in a significant positive total EFG value. In SbN and in SbP the negative EFG value originates from the 5p(Sb)/2p(N) and 5p(Sb)/3p(P) mixing respectively (σ bonding orbitals). In the SbX series of molecules, the large positive value is due to the high contribution of the 5p(Sb) π orbital that is partly compensated, by negative contribution from the mixing of the 5p(Sb) with the 2p(F)/3p(Cl) (σ bonding orbitals).

In this work, from extensive ab initio and DFT calculations in the relativistic four-component framework, on a series of closed-shell states of molecules containing bismuth and antimony, we have estimated the nuclear quadrupole moment of ²⁰⁹Bi and ¹²¹Sb at the CCSD-T level, equal to −422 mb and −542 mb, respectively. Though there has been much debate on the subject, this is a further step towards a converged value of the nuclear quadrupole moment of ²⁰⁹Bi and ¹²¹Sb. The proposed methodology significantly improves the consistency of the results, minimizes the impact of systematic errors, and allows to discard unreliable results.

Additionally, an analysis of the electronic contributions to the q value of individual orbitals reveals a general layout along the Bi and Sb series of molecules. 6p(Bi) or 5p(Sb) σ orbitals have a significant negative contribution to EFG while 6p(Bi) or 5p(Sb) π orbitals have a significant positive contribution to EFG. The overall value can be modulated by the mixing of these orbitals with those of N, P, F, Cl or I.

In conclusion, our five new full-Dirac CCSD-T determinations using the coupling constants for diatomic BiN, BiP, BiF, BiCl and BiI yield a Q(²⁰⁹ Bi) of −422(3) mb, in close agreement with the molecular values of Teodoro et al.⁵ or Shee et al.,²⁵ and the new CCSDT atomic value by Skripnikov et al.²⁶ Our more approximate molecular DFT/CAM-B3LYP* Q(Bi) of −405(9) mb also lies close. Thus we fully support the ‘World average’ of −420(17) mb in Barzakh et al.² For the antimony isotopes we obtain Q(¹²¹Sb) = −541.7(0.8) mb and Q(¹²³Sb) = −690.6(0.8) mb using the ratio B(¹²³Sb)/B(¹²¹Sb) = 1.27491(1).¹⁷

We thank the referees for their careful work. J.-P. Dognon thanks the Finnish-French Maupertuis program for supporting his stays at Helsinki by travel grants.

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. H. Schüler and T. Schmidt, Z. Phys., 1936, 99, 717–728.
2. A. Barzakh, A. N. Andreyev, C. Raison, J. G. Cubiss, P. Van Duppen, S. Péru, S. Hilaire, S. Goriely, B. Andel, S. Antalic, M. Al Monthery, J. C. Berengut, J. Bieroń, M. L. Bissell, A. Borschevsky, K. Chrysalidis, T. E. Cocolios, T. Day Goodacre, J.-P. Dognon, M. Elantkowska, E. Eliav, G. J. Farooq-Smith, D. V. Fedorov, V. N. Fedosseev, L. P. Gaffney, R. F. Garcia Ruiz, M. Godefroid, C. Granados, R. D. Harding, R. Heinke, M. Huyse, J. Karls, P. Larmonier, J. G. Li, K. M. Lynch, D. E. Maison, B. A. Marsh, P. Molkanov, P. Mosat, A. V. Oleynichenko, V. Panteleev, P. Pyykkö, M. L. Reitsma, K. Rezynkina, R. E. Rossel, S. Rothe, J. Ruczkowski, S. Schiffmann, C. Seiffert, M. D. Seliverstov, S. Sels, L. V. Skripnikov, M. Stryjczyk, D. Studer, M. Verlinde, S. Wilman and A. V. Zaitsevskii, Phys. Rev. Lett., 2021, 127, 192501.
3. P. Pyykkö, Mol. Phys., 2018, 116, 1328–1338.
4. J. Bieroń and P. Pyykkö, Phys. Rev. Lett., 2001, 87, 133003.
5. T. Q. Teodoro and R. L. A. Haiduke, Phys. Rev. A: At., Mol., Opt. Phys., 2013, 88, 052504.
6. B. Buchholz, H. D. Kronfeldt, G. Müller, M. Voss and R. Winkler, Z. Phys. A: Hadrons Nucl., 1978, 288, 247–256.
7. M. Voss, W. Weiss, B. Buchholz and R. Winkler, Z. Phys. D: At., Mol. Clusters, 1986, 1, 151–156.
8. A. Svane, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 064422.
9. L. Demovič, V. Kellö, A. J. Sadlej and S. A. Cooke, J. Chem. Phys., 2006, 124, 184308.
10. R. L. A. Haiduke, A. B. F. da Silva and L. Visscher, J. Chem. Phys., 2006, 125, 064301.
11. S. A. Cooke, J. M. Michaud and M. C. L. Gerry, J. Mol. Struct., 2004, 695–696, 13–22.
12. E. H. Fink, K. D. Setzer, D. A. Ramsay, J. P. Towle and J. M. Brown, J. Mol. Spectrosc., 1996, 178, 143–156.
13. P. Kuijpers, T. Törring and A. Dymanus, Chem. Phys., 1976, 18, 401–416.
14. P. Kuijpers, T. Torring and A. Dymanus, Chem. Phys., 1976, 12, 309–313.
15. R. Tischer, K. Möller and T. Törring, Chem. Phys., 1981, 62, 115–121.
16. S. A. Cooke and M. C. L. Gerry, Phys. Chem. Chem. Phys., 2004, 6, 4579–4585.
17. S. A. Cooke and M. C. Gerry, J. Mol. Spectrosc., 2005, 234, 195–203.
18. DIRAC, a relativistic ab initio electronic structure program, Release DIRAC19 (2019), written by A. S. P. Gomes, T. Saue, L. Visscher, H. J. Aa. Jensen, and R. Bast, with contributions from I. A. Aucar, V. Bakken, K. G. Dyall, S. Dubillard, U. Ekström, E. Eliav, T. Enevoldsen, E. Faßhauer, T. Fleig, O. Fossgaard, L. Halbert, E. D. Hedegård, B. Heimlich-Paris, T. Helgaker, J. Henriksson, M. Iliaš, Ch. R. Jacob, S. Knecht, S. Komorovský, O. Kullie, J. K. Lærdahl, C. V. Larsen, Y. S. Lee, H. S. Nataraj, M. K. Nayak, P. Norman, G. Olejniczak, J. Olsen, J. M. H. Olsen, Y. C. Park, J. K. Pedersen, M. Pernpointner, R. di Remigio, K. Ruud, P. Sałek, B. Schimmelpfennig, B. Senjean, A. Shee, J. Sikkema, A. J. Thorvaldsen, J. Thyssen, J. van Stralen, M. L. Vidal, S. Villaume, O. Visser, T. Winther, and S. Yamamoto (available at DOI:10.5281/zenodo.3572669, see also http://www.diracprogram.org).
19. C. Thierfelder, P. Schwerdtfeger and T. Saue, Phys. Rev. A: At., Mol., Opt. Phys., 2007, 76, 034502.
20. M. J. Deegan and P. J. Knowles, Chem. Phys. Lett., 1994, 227, 321–326.
21. K. G. Dyall, Theor. Chem. Acc., 2012, 131, 1217.
22. K. G. Dyall, Theor. Chem. Acc., 2016, 135, 128.
23. M. Pernpointner and L. Visscher, J. Chem. Phys., 2001, 114, 10389–10395.
24. L. Belpassi, F. Tarantelli, A. Sgamellotti, H. M. Quiney, J. N. P. van Stralen and L. Visscher, J. Chem. Phys., 2007, 126, 064314.
25. A. Shee, L. Visscher and T. Saue, J. Chem. Phys., 2016, 145, 184107.
26. L. V. Skripnikov, A. V. Oleynichenko, A. V. Zaitsevskii, D. E. Maison and A. E. Barzakh, Phys. Rev. C, 2021, 104, 034316.
27. J. Liu and L. Cheng, J. Chem. Phys., 2018, 148, 144108.
28. J. Bieroń, 2022, private communication.
29. F. Neese, A. Wolf, T. Fleig, M. Reiher and B. A. Hess, J. Chem. Phys., 2005, 122, 204107.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp04747k

---