 Open Access Article
Open Access ArticleConnections between the accuracy of rotational constants and equilibrium molecular structures
Cristina
Puzzarini
 *a and
John F.
Stanton
*b
*a and
John F.
Stanton
*b
aDipartimento di Chimica “Giacomo Ciamician”, Università di Bologna, via F. Selmi 2, 40126, Bologna, Italy. E-mail: cristina.puzzarini@unibo.it
bDepartment of Chemistry, University of Florida, Gainesville, FL 32611, USA. E-mail: johnstanton@chem.ufl.edu
First published on 12th December 2022
Abstract
Rotational spectroscopy is the technique of choice for investigating molecular structures in the gas phase. Indeed, rotational constants are strongly connected to the geometry of the molecular system under consideration. Therefore, they are powerful tools for assessing the accuracy that quantum chemical approaches can reach in structural determinations. In this review article, it is shown how it is possible to measure the accuracy of a computed equilibrium geometry based on the comparison of rotational constants. But, it is also addressed what accuracy is required by computations for providing molecular structures and thus rotational constants that are useful to experiment. Quantum chemical methodologies for obtaining the “0.1% accuracy” for rotational constants are reviewed for systems ranging in size from small molecules to small polycyclic aromatic hydrocarbons. This accuracy for systems containing two dozen or so atoms opens the way towards future applications such as the accurate characterization of non-covalent interactions, which play a key role in several biological and technological processes.
1 Introduction
Quantum chemistry has currently reached such an advanced level that highly accurate results can be achieved for energies,1–8 equilibrium structures7,9–11 as well as molecular and spectroscopic properties11–17 of small (up to 6–10 atoms) to medium-sized (up to 15–20) isolated molecules. For these high-level calculations, the requirements are efficient treatment of electron correlation together with an effective reduction of the basis-set truncation error.18 The proper account of vibrational effects is often needed as well.19–22 The requirements above are usually fulfilled by exploiting the additivity approximation within the so-called composite schemes.3–5,10,12,14,23,24 By definition, these approaches compute the various contributions separately at the highest possible level and then combine them together by relying on the additivity approximation. The most widely used composite schemes employ coupled-cluster (CC) techniques with hierarchical series of basis sets, thus allowing the extrapolation to the complete basis-set (CBS) limit.25–27Quantum chemical composite approaches and methods are continuously under development in order to extend their applicability and/or their accuracy.7,28,29 Therefore, benchmarking the results they deliver with experiment is a crucial step in assessing their performance. On the other hand, advancements in gas-phase spectroscopic techniques have extended their use to larger and flexible systems (such as clusters,30–32 amino acids,33,34 DNA-scaffold ribosugars35) as well as to unstable species (obtained by flash vacuum pyrolysis36,37 or discharge38). Increasingly, complicated spectra have to be analyzed which strongly require theory for their interpretation.12,13,34,36,39–41 For isolated systems, rotational spectroscopy can serve to demonstrate the accuracy that can be reached by quantum chemistry and to show how much we need to push theory to obtain predictions useful to experiment. In this spectroscopic technique, rotational constants are the leading terms and strongly depend on the molecular structure.12,42–47 In fact, rotational constants are inversely proportional to the moments of inertia which in turn are related to the mass distribution of the molecule:
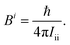 | (1) |
In the equation above (in frequency units, which are those considered along this manuscript), i refers to the intertial axis (a, b or c, these leading to Ba = A, Bb = B or Bc = C, respectively, with A ≥ B ≥ C), and Iii denotes the i-th diagonal element of the inertia tensor I:
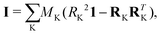 | (2) |
The focus of this contribution is on the accuracy that computational predictions should meet in order to support rotational spectroscopy. In the next section, the requirements for accuracy are introduced. Then, the relation existing between the error affecting structural parameters and the corresponding deviation in rotational constants is addressed. Finally, the performance of different computational approaches is discussed through some examples.
2 Definition of accuracy
In the context of this review, it is appropriate to consider some practical aspects of highly-precise equilibrium structure determinations. Specifically, what level of accuracy is needed in order to be useful for rotational spectroscopy? When one is looking for a “new” molecule (one not previously observed in the microwave or millimeter wave region of the spectrum), it is enormously helpful to have very accurate predictions of the location of its spectroscopic transitions in this region of the spectrum. Broadly speaking, the level of accuracy associated with predicted rotational constants should be at least 0.1% (corresponding to 10 MHz for a constant with magnitude 10000 MHz). However, there is a decided non-linearity in the degree to which a particular level of accuracy is useful; calculations accurate to 1% are not at all helpful for tasks such as analysis of pyrolysis or discharge products that contain tens of species, while accuracies of 0.01% (1 MHz) would be extraordinarily valuable. This motivates the following brief discussion of what is attainable, and what level of accuracy in the fundamental quantum chemical level of calculations is needed.As briefly mentioned in the Introduction, there are two principal contributions to rotational constants.12 The first and simplest is the so-called equilibrium constant Be, which is directly proportional to the reciprocal principal inertial moments of the equilibrium structure that is easily calculated by quantum chemistry (see eqn (1)). The second important contribution – which is much smaller in magnitude for semi-rigid molecules – comes from the interaction of vibration and rotation. This contribution is less straightforward to calculate than the equilibrium structure, and is usually approximated by means of vibrational perturbation theory carried out to second order (VPT2)48:
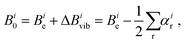 | (3) |
The magnitude of the vibrational contribution ΔBvib is typically 0.1% to 0.7% that of the corresponding equilibrium rotational constant, with 0.5% being the largely dominant case in semi-rigid systems. Its calculation by the methods of quantum chemistry requires evaluation of the harmonic and (cubic) anharmonic force fields, and the error in such computations can be estimated to be comparable to that of the force constants. For a high-quality coupled-cluster calculation with an appropriate basis set, errors in force constants are usually less than 5%. For low-level calculations, errors can increase up to 20%. Consequently, the error in the vibrational contribution to the rotational constants can be estimated to be no larger than about 0.05% of the total value of the ground state constants B0 (a maximum of 0.1% is estimated in the case of a vibrational contribution of 0.5% evaluated with an error of 20%).
It is the equilibrium rotational constant prediction that plays the most important role for the issue at hand. For a diatomic molecule, it is very easy to show that a change in the bond length re leads to a fractional change of the rotational constant according to43
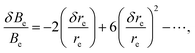 | (4) |
For polyatomic molecules, such an analysis is considerably more complicated. However, for bond lengths, the k fractional changes in equilibrium rotational constants (δkBe/Be) that arise from fractional changes in the corresponding different bond distances (δrk/rk) obey the surprisingly simple relationship
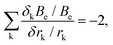 | (5) |
In summary, it is clear that equilibrium structure predictions are valuable to rotational spectroscopy only if they are done with an accuracy that demands a very high-level quantum chemical treatment (which usually means employing composite schemes). While an accuracy of 1% for ground-state rotational constants can be achieved with relative ease, it is not particularly useful for guided searches and spectra interpretation. At the other end, accuracy rivaling that of experiments (0.01%) is beyond the reach of computation. Realistic prospects lie somewhat intermediate between these regimes with 0.1% (and slightly better than that) an achievable but still challenging goal. For diatomic and small polyatomic molecules, the requisite level of accuracy can be achieved only by means of basis-set extrapolation and high-level correlation treatments, but similar calculations for larger systems are generally not possible at this time. In this context, for medium-sized molecules, reduced-cost composite schemes have been defined.7,10 However, for larger systems, alternatives to brute-force computation, such as the locality-exploiting “Lego-brick” approach,50–53 are likely to prove more valuable in the future.
3 Structure and rotational constants
As addressed in the previous section, rotational constants make sizeable any small variation in the geometrical parameters. To quantify this point, the equilibrium rotational constants of some diatomics have been considered (see Table 1). Having only one geometrical parameter, they allow for a direct correlation between the bond distance and the unique rotational constant. A couple of small polyatomic molecules (water and formaldehyde) have been selected to emphasize how the situation is considerably more complicated when there is more than one geometrical parameter (Table 2).| Moleculea | r e (Å) | B(re) (MHz) | B(re + 0.0001)c (MHz) | B(re + 0.001)c (MHz) | B(re + 0.002)c (MHz) |
|---|---|---|---|---|---|
| a CN and OH are radical species, both are doublet in the electronic ground state. b Equilibrium distances at the all-CCSD(T)/cc-pCVQZ level of theory. c r e + 0.0001, re + 0.001, and re + 0.002 mean equilibrium distance (re) augmented by 0.0001 Å, 0.001 Å, and 0.002 Å, respectively. In the second line, differences with respect to the equilibrium rotational constants are given in absolute and relative terms: [(B(re + Δr) − B(re))/B(re)] × 100. | |||||
| SiS | 1.9316 | 9077.97 | 9077.26 | 9068.57 | 9059.20 |
| −0.71 (−0.008%) | −9.40 (−0.10%) | −18.77 (−0.21%) | |||
| PN | 1.4913 | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 563.42 563.42 |
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 560.26 560.26 |
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 531.85 531.85 |
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500.34 500.34 |
| −3.16 (−0.013%) | −31.57 (−0.13%) | −63.08 (−0.27%) | |||
| CN | 1.1674 | 57![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 386.18 386.18 |
57![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 376.35 376.35 |
57![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 287.99 287.99 |
57![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 190.06 190.06 |
| −9.83 (−0.017%) | −98.19 (−0.17%) | −196.12 (−0.34%) | |||
| CO | 1.1289 | 57![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 841.66 841.66 |
57![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 831.41 831.41 |
57![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 739.32 739.32 |
57![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 637.25 637.25 |
| −10.25 (−0.018%) | −102.34 (−0.18%) | −204.41 (−0.35%) | |||
| HCl | 1.2736 | 318![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 069.32 069.32 |
318![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 019.38 019.38 |
317![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 570.42 570.42 |
317![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 072.69 072.69 |
| −49.94 (−0.016%) | −498.90 (−0.16%) | −996.63 (−0.31%) | |||
| OH | 0.9689 | 567![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 822.08 822.08 |
567![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 704.88 704.88 |
566![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 651.79 651.79 |
565![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485.1 485.1 |
| −117.20 (−0.021%) | −1170.29 (−0.21%) | −2336.96 (−0.41%) | |||
| HF | 0.9158 | 629![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 664.95 664.95 |
629![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 527.45 527.45 |
628![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 292.0 292.0 |
626923.6 |
| −137.50 (−0.021%) | −1372.92 (−0.22%) | −2741.34 (−0.44%) | |||
| Molecule | Parametersa | A e (MHz)b | B e (MHz)b | C e (MHz)b | ||
|---|---|---|---|---|---|---|
| a Equilibrium distances at the all-CCSD(T)/cc-pCVTZ level of theory. b Differences, in relative terms, with respect to the equilibrium rotational constants are given in parentheses (for definition, see footnote c of Table 1). | ||||||
| H2O | r(OH) | ∠(HOH) | ||||
| 0.9584 | 103.68 | 805![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 164.3 164.3 |
441![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 462.4 462.4 |
285![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 129.3 129.3 |
||
| +0.001 | — | 803![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 486.8 (−0.21%) 486.8 (−0.21%) |
440![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 542.6 (−0.21%) 542.6 (−0.21%) |
284![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 535.2 (−0.21%) 535.2 (−0.21%) |
||
| — | +0.1 | 806![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 956.4 (+0.22%) 956.4 (+0.22%) |
440![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 858.0 (−0.14%) 858.0 (−0.14%) |
285![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 101.0 (−0.01%) 101.0 (−0.01%) |
||
| +0.001 | +0.1 | 805![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 275.1 (+0.01%) 275.1 (+0.01%) |
439![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 939.4 (−0.34%) 939.4 (−0.34%) |
284![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 507.0 (−0.22%) 507.0 (−0.22%) |
||
| H2CO | r(CO) | r(CH) | ∠(HCO) | |||
| 1.2043 | 1.1008 | 121.78 | 286![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 354.8 354.8 |
38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 976.8 976.8 |
34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 307.1 307.1 |
|
| +0.001 | — | — | 286![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 354.8 (—) 354.8 (—) |
38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 919.0 (−0.15%) 919.0 (−0.15%) |
34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 262.3 (−0.14%) 262.3 (−0.14%) |
|
| — | +0.001 | — | 285![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 835.2 (−0.18%) 835.2 (−0.18%) |
38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 969.2 (−0.02%) 969.2 (−0.02%) |
34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 293.8 (−0.04%) 293.8 (−0.04%) |
|
| — | — | +0.1 | 286![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 975.9 (+0.22%) 975.9 (+0.22%) |
38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 953.4 (−0.06%) 953.4 (−0.06%) |
34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 297.9 (−0.03%) 297.9 (−0.03%) |
|
| +0.001 | +0.001 | — | 285![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 835.2 (−0.18%) 835.2 (−0.18%) |
38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 911.5 (−0.17%) 911.5 (−0.17%) |
34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 249.1 (−0.16%) 249.1 (−0.16%) |
|
| +0.001 | — | +0.1 | 286![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 975.9 (+0.22%) 975.9 (+0.22%) |
38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 895.7 (−0.21%) 895.7 (−0.21%) |
34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 253.1 (−0.16%) 253.1 (−0.16%) |
|
| — | +0.001 | +0.1 | 286![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 455.2 (+0.04%) 455.2 (+0.04%) |
38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 945.8 (−0.08%) 945.8 (−0.08%) |
34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 284.5 (−0.07%) 284.5 (−0.07%) |
|
| +0.001 | +0.001 | +0.1 | 286![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 455.2 (+0.04%) 455.2 (+0.04%) |
38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 888.1 (−0.22%) 888.1 (−0.22%) |
34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 239.8 (−0.20%) 239.8 (−0.20%) |
|
Table 1 collects data for seven diatomic molecules, three of them also containing third-row atoms (SiS, PN and HCl) and two of them being radical species (CN and OH). In this table, for each molecule, the equilibrium distance and the corresponding equilibrium constant are reported together with the rotational constants resulting from increasing the bond distance by 0.0001 Å, 0.001 Å, and 0.002 Å. For the latter constants, the absolute and relative deviations from the equilibrium one are provided. Although being of limited importance to the present discussion, we note that bond distances were optimized at the CCSD(T)/cc-pCVQZ level,54–56 with all electrons correlated (this level of theory has been chosen because of its accuracy57). Inspection of the results of Table 1 confirms the fractional change pointed out in eqn (4) and, thus, an accuracy of 0.001 Å on the bond distance leads to a deviation of 0.1% on the rotational constant for bond lengths of about 2 Å such as that of SiS and of 0.2% for distances of about 1 Å. This table makes also clear that for light molecules deviations of about 0.1% in the rotational constant mean, in absolute terms, deviations of hundreds or even thousands of MHz.
In Table 2, an analysis similar to that reported in Table 1 is extended to two simple polyatomic molecules: water and formaldehyde. In both cases, distances have been varied by 0.001 Å and angles by 0.1°. From this table, it is clear that the situation is much more complicated even for very simple molecules. In fact, we can have the variation of only one parameter, two of them or, in the case of H2CO, even three of them. For evident geometrical reasons, changing only one structural parameter affects differently the three rotational constants, and the variation of two might lead to a fortuitous cancellation of error. The concomitant variation of all geometrical parameters (which might be interpreted as a systematic error affecting the structural determination) determines different changes (and thus accuracy) on the three rotational constants. However, it is noted that, no matter how many parameters are modified, the maximum relative error on each rotational constant is in line with what observed for diatomics and confirms the conclusions of the previous section.
To address the impact of the deviations discussed above on the prediction of the rotational spectrum, a fictitious diatomic molecule with a rotational constant B of 100 GHz is considered within the rigid-rotor approximation. The frequency of a generic rotational transition (from the J to J + 1 rotational energy level) is then given by the simple expression
| ν = 2B(J + 1) | (6) |
4 How to meet the target accuracy
To obtain high accuracy in molecular structure determinations, one has to reduce as much possible as the errors due to the truncation of both the basis set and the wave function, that is, to reduce as much as possible the so-called one- and N-electron error, respectively.18 Along these directions, composite approaches have been developed and, as mentioned in the Introduction, they rely on the additivity approximation. This can be either exploited at an energy gradient level9,24,65,66 (gradient scheme) or directly applied to structural parameters7,10,44,67 (geometry scheme). Within the so-called gradient scheme, the energy gradient to be minimized in the geometry optimization procedure can be set up according to the accuracy required and the size of the system under consideration.9,24,45 The so-called geometry scheme is based on the assumption that the additivity approximation can be directly applied to geometrical parameters and that they show the same behavior as the energy.68 Different geometry optimizations are carried out in order to derive the contributions to be incorporated in the composite approaches.10,68In all approaches, to recover the error due to the basis-set truncation, an extrapolation to the CBS limit is performed, with different formula that can be used.25–27,41,68 If extrapolation to the CBS limit is carried out within the frozen-core (fc) approximation, then core-valence correlation (CV) effects need to be incorporated (as the difference of all-electron and fc calculations in the same basis set). To keep the N-electron error low, the CCSD(T) method is often used, whose good performance resulted in defining it as the “gold standard” for accurate quantum chemical calculations. Improvement in the description of energy correlation requires to go beyond the CCSD(T) model, and thus to incorporate corrections due to a full treatment of triples (fT) and quadruples (fQ). While different groups all around the world have developed and employed quantum chemical composite approaches to obtain accurate equilibrium geometries (with examples being provided by cited references along this manuscript), in the following we present results from the work of the authors and their groups.
To discuss the accuracy of different composite schemes in terms of accuracy of the corresponding rotational constants, in ref. 45, a statistical analysis was carried out for a significant set of small-sized molecular species (up to 6 atoms). Since equilibrium rotational constants only depend on the equilibrium structure, the corresponding statistical measures allows one to infer the accuracy of the computed geometries. Some of the results obtained in the framework of the analysis performed in ref. 45 are reported in Table 3, which collects the mean absolute error (MAE) and the standard deviation for different levels of theory. As well known from the literature (see, e.g., ref. 13, 69), the CCSD(T) method – within the fc approximation – in conjunction with a triple-zeta basis set does not provide accurate structures. The situation improves by enlarging the basis set and the “0.1% accuracy” target is reached once the extrapolation to the CBS limit (or a very large basis set) is combined with CV corrections. Incorporation of fT and fQ contributions further improves both the MAE and the standard deviation, but at the cost of very expensive quantum chemical computations and without reducing the error by one order of magnitude (thus still far from the 0.01% accuracy limit). Therefore, the CCSD(T)/CBS+CV approach (or simply CBS+CV)61 is the most cost effective scheme, among those entirely based on CC techniques, to meet the so-called “0.1% accuracy” for rotational constants for molecules up to 10 atoms.69
| Computational approachb | Mean absolute | Standard |
|---|---|---|
| Error | Deviation | |
| a Semi-experimental Be values are obtained from experimental B0 values by subtracting computed vibrational and electronic contributions. Data taken from ref. 45. b VnZ stands for cc-pVnZ; fc stands for frozen-core approximation. | ||
| fc-CCSD(T)/VTZ | 0.90 | 0.59 |
| fc-CCSD(T)/VQZ | 0.43 | 0.30 |
| fc-CCSD(T)/V5Z | 0.32 | 0.18 |
| fc-CCSD(T)/V6Z | 0.30 | 0.16 |
| fc-CCSD(T)/CBS | 0.28 | 0.14 |
| fc-CCSD(T)/V6Z + CV | 0.06 | 0.10 |
| fc-CCSD(T)/V6Z + CV + fT | 0.09 | 0.11 |
| fc-CCSD(T)/V6Z + CV + fT + fQ | 0.06 | 0.07 |
| fc-CCSD(T)/CBS + CV + fT + fQ | 0.04 | 0.07 |
To extend the application of composite schemes to medium-sized species such as buildings blocks of biomolecules, it is necessary to reduce the computational cost while keeping a good accuracy. In recent years, a very effective approach – denoted as “cheap” scheme (ChS) – has been introduced.7,10,70 Starting from fc-CCSD(T) calculations with a triple-zeta quality basis set, the ChS model incorporates the extrapolation to the CBS limit and the CV effects using Møller-Plesset second-order theory (MP2).71 MP2, CCSD(T) and ChS results for selected medium-sized molecules (up to 16 atoms), ranging from nucleobases to amino acids and dipeptide analogues, are collected in Table 4 and compared to the corresponding semi-experimental equilibrium rotational constants (namely experimental B0 values from which computed vibrational contributions have been subtracted), with the relative deviations being reported. For fc-CCSD(T)/cc-pVTZ calculations, the data of Table 4 are in line with the statistical measures given in Table 3. On average, MP2/cc-pVTZ performs better than CCSD(T)/cc-pVTZ, with MAE of 0.43% and 0.80%, respectively. This result is expected based on the considerations mentioned before: since basis set deficiencies tend to lead to long distances, while correlation deficiencies lead to systematically short distances, in fc-MP2/cc-pVTZ we observe a partial cancellation of errors. Moving to the ChS composite scheme, which means augmenting the fc-CCSD(T)/cc-pVTZ level by CBS and CV corrections using MP2, the MAE reduces to 0.13%, thus meeting the “0.1% accuracy”.
| fc-MP2/cc-pVTZ | fc-CCSD(T)/cc-pVTZ | ChS | Semi-experimentalb (equilibrium) | |
|---|---|---|---|---|
| a If applies, the conformer considered is specified in parentheses. b See also ref. 52. c Mean absolute error with respect to semi-experimental Be constants. | ||||
| Uracil10 | ||||
| A e | 3906.8 (−0.14%) | 3884.1 (−0.72%) | 3913.9 (+0.04%) | 3912.4 |
| B e | 2018.6 (−0.82%) | 2015.7 (−0.96%) | 2039.1 (+0.19%) | 2035.3 |
| C e | 1330.9 (−0.60%) | 1327.0 (−0.89%) | 1340.7 (+0.13%) | 1338.9 |
| Thiouracil58 | ||||
| A e | 3569.7 (−0.24%) | 3550.5 (−0.78%) | 3578.6 (+0.008%) | 3578.3 |
| B e | 1313.6 (−0.63%) | 1306.6 (−1.16%) | 1322.4 (+0.04%) | 1321.9 |
| C e | 960.3 (−0.53%) | 955.1 (−1.07%) | 965.6 (+0.002%) | 965.4 |
| Pyruvic acid (Tc)59 | ||||
| A e | 5502.9 (−1.01%) | 5501.8 (−1.03%) | 5564.5 (+0.09%) | 5559.3 |
| B e | 3625.6 (+0.11%) | 3602.4 (−0.53%) | 3611.4 (−0.29%) | 3621.5 |
| C e | 2214.9 (−0.33%) | 2206.3 (−0.72%) | 2219.6 (−0.13%) | 2222.4 |
| Glycolic acid (sSc)60 | ||||
| A e | 10699.3 (−0.90%) | 10701.9 (−0.88%) | 10801.2 (+0.04) | 10797.3 |
| B e | 4092.9 (−0.12%) | 4073.0 (−0.61%) | 4102.9 (+0.12%) | 4098.0 |
| C e | 3015.6 (−0.33%) | 3005.3 (−0.67%) | 3029.2 (+0.12%) | 3025.5 |
| Glycine (Ip)61 | ||||
| A e | 10328.0 (−0.87%) | 10328.2 (−0.86%) | 10396.6 (−0.21%) | 10418.2 |
| B e | 3905.0 (−0.05%) | 3884.4 (−0.58%) | 3901.1 (−0.15%) | 3906.9 |
| C e | 2926.2 (−0.28%) | 2915.0 (−0.66%) | 2930.4 (−0.14%) | 2934.4 |
| Glycine dipeptide analogue (C7)62 | ||||
| A e | 4369.5 (−1.70%) | 4417.3 (−0.63%) | 4456.6 (−0.26%) | 4445.2 |
| B e | 1236.1 (+0.29%) | 1220.2 (−1.00%) | 1228.9 (−0.29%) | 1232.5 |
| C e | 1097.6 (+0.26%) | 1087.1 (−0.70%) | 1096.5 (−0.16%) | 1094.8 |
| MAEc | 0.43% | 0.80% | 0.13% | |
For molecules larger than those discussed above such as small polycyclic aromatic hydrocarbons (PAHs) and their derivatives (up to about 30 atoms), the ChS and its variants7,10 are not computationally affordable. Usually, one has to resort to density functional theory (DFT), with double-hybrid functionals (such as B2PLYP72 and rev-DSDPBEP8664) providing the best results.52,73–77 To further improve the accuracy obtainable by DFT functionals in structural determinations, the so-called “template molecule” (TM) approach46 has been introduced. This model is based on the assumption that a molecular system can be seen as formed by smaller fragments for which a very accurate equilibrium structure is available and that the difference between the latter and the DFT determination can be directly applied to the larger system. Recently, this model has been extended to define the so-called “Lego-brick” approach (also denoted TM+LR or TM+LR_SE).51,53 Within this protocol, semi-experimental equilibrium structures are employed for the geometries of the fragments, the TM approach is exploited to account for the modifications occurring when going from the isolated fragment to the molecular system under investigation, and the “linear regression” (LR) model78 is used to correct the linkage between different fragments. Some results, taken from ref. 53, are reported in Table 5. This table collects computed ground-state rotational constants, which have been obtained by correcting the calculated Be values (straightforwardly derived from uncorrected DFT structures as well as from TM and TM+LR geometries) for vibrational contributions (calculated using the global hybrid B3LYP functional79,80 in conjunction with a double-zeta basis set). The comparison with the experimental counterparts is provided in terms of relative deviations. On average, the deviation from experiment of the double-hybrid rev-DSDPBEP86 functional64 is 0.4%, which reduces to about 0.1% when only the TM approach is applied. A further improvement, with a MAE of about 0.05%, is noted when moving to the complete TM+LR model.53 Overall, the results of ref. 53 demonstrate that the “Lego-brick” approach is robust, can be extended to systems of increasing size and is able to deal some degree flexibility.
| revDSD/mayTZb | TMc | TM+LRc | revDSD/mayTZb | TMc | TM+LRc | ||
|---|---|---|---|---|---|---|---|
| a B e values have been augmented by vibrational corrections at the B3LYP/jun-cc-pVDZ level.63 b B e values using the double-hybrid rev-DSDPBEP86 (revDSD) functional64 in conjunction with the may-cc-pVTZ (mayTZ) basis set.63 c B e values from the TM and TM+LR approaches (see text). Fragments employed in the TM approach: 9-cyanoanthracene: three benzene molecules and HCN; 9-cyanophenantrene: three benzene molecules and HCN; trans-2-naphthol: two benzene molecules and H2O; cis-1-naphthol: two benzene molecules and H2O; 2-ethynylpyridine: pyridine and HCN; cis-3-hydroxy-pyridine: pyridine and H2O; 4-hydroxy-pyridine: pyridine and H2O; Benzoic acid: benzene and trans formic acid. | |||||||
| 9-Cyanoanthracene | 9-Cyanophenantrene | ||||||
| A 0 | 981.590 (−0.43%) | 984.547 (−0.13%) | 985.342 (−0.05%) | A 0 | 842.512 (−0.43%) | 845.175 (−0.06%) | 845.507 (−0.07%) |
| B 0 | 449.739 (−0.32%) | 451.174 (−0.01%) | 451.174 (−0.01%) | B 0 | 484.613 (−0.36%) | 486.116 (−0.06%) | 486.248 (−0.03%) |
| C 0 | 308.490 (−0.36%) | 309.457 (−0.05%) | 309.535 (−0.03%) | C 0 | 307.726 (−0.39%) | 308.687 (−0.08%) | 308.784 (−0.05%) |
| trans-2-Naphthol | cis-1-Naphthol | ||||||
| A 0 | 2834.666 (−0.38%) | 2844.215 (−0.04%) | 2844.763 (−0.02%) | A 0 | 1939.026 (−0.44%) | 1944.532 (−0.15%) | 1946.589 (−0.05%) |
| B 0 | 822.384 (−0.38%) | 824.730 (−0.10%) | 825.329 (−0.03%) | B 0 | 1120.756 (−0.32%) | 1124.286 (+0.002%) | 1124.496 (+0.02%) |
| C 0 | 637.619 (−0.39%) | 639.512 (−0.09%) | 639.900 (−0.03%) | C 0 | 710.552 (−0.36%) | 712.709 (−0.05%) | 713.068 (+0.004%) |
| 2-Ethynylpyridine | cis-3-Hydroxy-pyridine | ||||||
| A 0 | 5840.592 (−0.29%) | 5861.682 (+0.07%) | 5861.683 (+0.07%) | A 0 | 5799.384 (−0.30%) | 5818.882 (+0.03%) | 5818.880 (+0.03%) |
| B 0 | 1575.320 (−0.40%) | 1579.432 (−0.14%) | 1581.163 (−0.03%) | B 0 | 2677.827 (−0.44%) | 2684.360 (−0.20%) | 2688.875 (−0.03%) |
| C 0 | 1240.423 (−0.38%) | 1243.924 (−0.10%) | 1244.999 (−0.01%) | C 0 | 1831.952 (−0.41%) | 1836.955 (−0.13%) | 1839.069 (−0.02%) |
| 4-Hydroxy-pyridine | cis-Benzoic acid | ||||||
| A 0 | 5969.478 (−0.35%) | 5990.387 (−0.001%) | 5990.389 (−0.001%) | A 0 | 3855.244 (−0.44%) | 3872.310 (+0.001%) | 3872.312 (+0.001%) |
| B 0 | 2621.113 (−0.41%) | 2627.396 (−0.17%) | 2631.857 (+0.001%) | B 0 | 1221.700 (−0.46%) | 1224.776 (−0.21%) | 1226.332 (−0.08%) |
| C 0 | 1821.369 (−0.40%) | 1826.347 (−0.12%) | 1828.504 (−0.01%) | C 0 | 928.230 (−0.46%) | 930.991 (−0.17%) | 931.889 (−0.07%) |
5 Conclusions
The strong connection between rotational constants and molecular structure is at the heart of this contribution. On the one hand, experimental rotational constants have been employed to benchmark the accuracy that can be obtained in structural determinations by quantum chemical calculations and, in particular, by composite schemes. On the other hand, we have addressed the accuracy that computational predictions should meet in order to be a useful support to experiment. The overall conclusion is that an accuracy of about 0.1% on rotational constants is suitable for guiding experiment in the field of rotational spectroscopy and that this can be obtained for small- and medium-sized molecules (i.e. up to 15–20 atoms) by exploiting quantum chemical composite schemes, with empirical strategies extending such an accuracy to larger systems (up to 30 atoms). From a structural point of view, the target “0.1% accuracy” on rotational constants implies bond distances that are affected by uncertainties of 0.0005–0.001 Å. For angles, any systematic conclusion is rather complicated, but a clear indication points to accuracy requirements of 0.1° or better.Section 4 provides an overview, based on the work carried out in our groups, on how to meet the target accuracy for rotational constants of 0.1% for molecular systems ranging in size from a few atoms to few dozen. However, several challenges still remain open and these mainly concern small biomolecules and large intermolecular complexes. In the last decade, we have witnessed crucial developments in the field of rotational spectroscopy. Introduction of chirped-pulsed microwave spectrometers81,82 have allowed for covering broadband spectral regions, and – once combined with fast-mixing nozzles – have permitted the investigation of non-covalent interactions in large systems.83–85 Furthermore, the introduction of the laser ablation technique – which allows laser to vaporize solids without decomposing molecules – has extended the field toward the investigation to solid compounds,86 and in particular to building blocks of biomolecules.33,87 However, the application of composite schemes to non-covalent intermolecular complexes is limited and still requires further extension,7,88,89 while the TM and TM+LR approaches have not been developed yet for non-covalent adducts. Furthermore, for flexible systems, interpretation of the experimental data often requires the accurate computational characterization of complex potential energy surfaces showing several low-energy minima and interconversion routes.34
Author contributions
Both authors equally contributed to this work.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been supported by MUR (PRIN Grant Number 202082CE3T) and by the University of Bologna (RFO funds).References
- A. Karton, E. Rabinovich, J. M. L. Martin and B. Ruscic, J. Chem. Phys., 2006, 125, 144108 CrossRef PubMed.
- A. Karton and J. M. L. Martin, J. Chem. Phys., 2012, 136, 124114 CrossRef PubMed.
- A. Tajti, P. G. Szalay, A. G. Császár, M. Kállay, J. Gauss, E. F. Valeev, B. A. Flowers, J. Vázquez and J. F. Stanton, J. Chem. Phys., 2004, 121, 11599–11613 CrossRef CAS PubMed.
- A. G. Császár, W. D. Allen and H. F. Schaefer III, J. Chem. Phys., 1998, 108, 9751–9764 CrossRef.
- K. A. Peterson, D. Feller and D. Dixon, Theor. Chem. Acc., 2012, 113, 1079 Search PubMed.
- A. Ganyecz, M. Kállay and J. Csontos, J. Chem. Theory Comput., 2017, 13, 4193–4204 CrossRef CAS PubMed.
- J. Lupi, S. Alessandrini, C. Puzzarini and V. Barone, J. Chem. Theory Comput., 2021, 17, 6974–6992 CrossRef CAS PubMed.
- P. Vermeeren, M. Dalla Tiezza, M. E. Wolf, M. E. Lahm, W. D. Allen, H. F. Schaefer, T. A. Hamlin and F. M. Bickelhaupt, Phys. Chem. Chem. Phys., 2022, 24, 18028–18042 RSC.
- M. Heckert, M. Kállay and J. Gauss, Mol. Phys., 2005, 103, 2109 CrossRef CAS.
- C. Puzzarini and V. Barone, Phys. Chem. Chem. Phys., 2011, 13, 7189–7197 RSC.
- W. J. Morgan, D. A. Matthews, M. Ringholm, J. Agarwal, J. Z. Gong, K. Ruud, W. D. Allen, J. F. Stanton and H. F. Schaefer, J. Chem. Theory Comput., 2018, 14, 1333–1350 CrossRef CAS PubMed.
- C. Puzzarini, J. F. Stanton and J. Gauss, Int. Rev. Phys. Chem., 2010, 29, 273–367 Search PubMed.
- C. Puzzarini, J. Bloino, N. Tasinato and V. Barone, Chem. Rev., 2019, 119, 8131–8191 CrossRef CAS PubMed.
- X. Huang and T. J. Lee, J. Chem. Phys., 2009, 131, 104301 CrossRef.
- Q. Cheng, R. C. Fortenberry and N. J. DeYonker, J. Chem. Phys., 2017, 147, 234303 CrossRef PubMed.
- J. P. Misiewicz, K. B. Moore, P. R. Franke, W. J. Morgan, J. M. Turney, G. E. Douberly and H. F. Schaefer, J. Chem. Phys., 2020, 152, 024302 CrossRef CAS PubMed.
- J. Bloino, M. Biczysko and V. Barone, J. Chem. Theory Comput., 2012, 8, 1015–1036 CrossRef CAS PubMed.
- T. Helgaker, P. Jørgensen and J. Olsen, Electronic-Structure Theory, Wiley: Chichester, 2000 Search PubMed.
- P. Pulay, W. Meyer and J. E. Boggs, J. Chem. Phys., 1978, 68, 5077–5085 CrossRef CAS.
- J. F. Stanton, C. L. Lopreore and J. Gauss, J. Chem. Phys., 1998, 108, 7190–7196 CrossRef CAS.
- J. Z. Gong, D. A. Matthews, P. B. Changala and J. F. Stanton, J. Chem. Phys., 2018, 149, 114102 CrossRef PubMed.
- P. Goel and J. F. Stanton, J. Chem. Phys., 2018, 149, 134109 CrossRef PubMed.
- A. D. Boese, M. Oren, O. Atasoylu, J. M. L. Martin, M. Kállay and J. Gauss, J. Chem. Phys., 2004, 120, 4129–4141 CrossRef CAS PubMed.
- M. Heckert, M. Kállay, D. P. Tew, W. Klopper and J. Gauss, J. Chem. Phys., 2006, 125, 044108 CrossRef PubMed.
- D. Feller, J. Chem. Phys., 1993, 98, 7059–7071 CrossRef CAS.
- T. Helgaker, W. Klopper, H. Koch and J. Noga, J. Chem. Phys., 1997, 106, 9639–9646 CrossRef CAS.
- D. Feller and K. A. Peterson, J. Chem. Phys., 1999, 110, 8384–8396 CrossRef CAS.
- G. Schmitz, C. Hättig and D. P. Tew, Phys. Chem. Chem. Phys., 2014, 16, 22167–22178 RSC.
- P. R. Nagy and M. Kállay, J. Chem. Theory Comput., 2019, 15, 5275–5298 CrossRef CAS PubMed.
- C. Pérez, M. T. Muckle, D. P. Zaleski, N. A. Seifert, B. Temelso, G. C. Shields, Z. Kisiel and B. H. Pate, Science, 2012, 336, 897–901 CrossRef PubMed.
- M. Chrayteh, E. Burevschi, D. Loru, T. R. Huet, P. Dréan and M. E. Sanz, Phys. Chem. Chem. Phys., 2021, 23, 20686–20694 RSC.
- R. Medel, A. Camiruaga, R. T. Saragi, P. Pinacho, C. Pérez, M. Schnell, A. Lesarri, M. A. Suhm and J. A. Fernández, Phys. Chem. Chem. Phys., 2021, 23, 23610–23624 RSC.
- I. León, E. R. Alonso, S. Mata, C. Cabezas and J. L. Alonso, Angew. Chem., Int. Ed., 2019, 58, 16002–16007 CrossRef PubMed.
- I. León, M. Fusè, E. R. Alonso, S. Mata, G. Mancini, C. Puzzarini, J. L. Alonso and V. Barone, J. Chem. Phys., 2022, 157, 074107 CrossRef PubMed.
- C. Calabrese, I. Uriarte, A. Insausti, M. Vallejo-López, F. J. Basterretxea, S. A. Cochrane, B. G. Davis, F. Corzana and E. J. Cocinero, ACS Cent. Sci., 2020, 6, 293–303 CrossRef CAS PubMed.
- M. Melosso, L. Bizzocchi, H. Gazzeh, F. Tonolo, J.-C. Guillemin, S. Alessandrini, V. M. Rivilla, L. Dore, V. Barone and C. Puzzarini, Chem. Commun., 2022, 58, 2750–2753 RSC.
- A. Melli, M. Melosso, L. Bizzocchi, S. Alessandrini, N. Jiang, F. Tonolo, S. Boi, G. Castellan, C. Sapienza, J.-C. Guillemin, L. Dore and C. Puzzarini, J. Phys. Chem. A, 2022, 126, 6210–6220 CrossRef CAS PubMed.
- M. C. McCarthy, K. L. K. Lee, P. B. Carroll, J. P. Porterfield, P. B. Changala, J. H. Thorpe and J. F. Stanton, J. Phys. Chem. A, 2020, 124, 5170–5181 CrossRef CAS PubMed.
- V. Barone, S. Alessandrini, M. Biczysko, J. R. Cheeseman, D. C. Clary, A. B. McCoy, R. J. DiRisio, F. Neese, M. Melosso and C. Puzzarini, Nat. Rev. Methods Primers, 2021, 1, 38 CrossRef CAS.
- E. M. Brás, T. L. Fischer and M. A. Suhm, Angew. Chem., Int. Ed., 2021, 60, 19013–19017 CrossRef PubMed.
- H. C. Gottschalk, A. Poblotzki, M. Fatima, D. A. Obenchain, C. Pérez, J. Antony, A. A. Auer, L. Baptista, D. M. Benoit, G. Bistoni, F. Bohle, R. Dahmani, D. Firaha, S. Grimme, A. Hansen, M. E. Harding, M. Hochlaf, C. Holzer, G. Jansen, W. Klopper, W. A. Kopp, M. Krasowska, L. C. Kröger, K. Leonhard, M. Mogren Al-Mogren, H. Mouhib, F. Neese, M. N. Pereira, M. Prakash, I. S. Ulusoy, R. A. Mata, M. A. Suhm and M. Schnell, J. Chem. Phys., 2020, 152, 164303 CrossRef CAS PubMed.
- W. Gordy and R. L. Cook, Microwave Molecular Spectra, Wiley: New York, 3rd edn, 1984 Search PubMed.
- F. Pawłowski, P. Jørgensen, J. Olsen, F. Hegelund, T. Helgaker, J. Gauss, K. L. Bak and J. F. Stanton, J. Chem. Phys., 2002, 116, 6482–6496 CrossRef.
- J. Demaison, Mol. Phys., 2007, 105, 3109–3138 CrossRef CAS.
- C. Puzzarini, J. Heckert and J. Gauss, J. Chem. Phys., 2008, 128, 194108 CrossRef PubMed.
- M. Piccardo, E. Penocchio, C. Puzzarini, M. Biczysko and V. Barone, J. Phys. Chem. A, 2015, 119, 2058–2082 CrossRef CAS PubMed.
- J. Demaison, J. E. Boggs and A. G. Császár, ed. Equilibrium Molecular Structures: From Spectroscopy to Quantum Chemistry, CRC Press, Taylor & Francis Group: Boca Raton, FL, US, 2011 Search PubMed.
- I. M. Mills, Molecular Spectroscopy: Modern Research, ed. K. N. Rao and C. W. Matthews, 1972 Search PubMed.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483 CrossRef CAS.
- C. Puzzarini and V. Barone, Acc. Chem. Res., 2018, 51, 548–556 CrossRef CAS PubMed.
- A. Melli, F. Tonolo, V. Barone and C. Puzzarini, J. Phys. Chem. A, 2021, 125, 9904–9916 CrossRef CAS PubMed.
- G. Ceselin, V. Barone and N. Tasinato, J. Chem. Theory Comput., 2021, 17, 7290–7311 CrossRef CAS PubMed.
- H. Ye, S. Alessandrini, M. Melosso and C. Puzzarini, Phys. Chem. Chem. Phys., 2022, 24, 23254–23264 RSC.
- T. H. Dunning Jr., J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- D. E. Woon and T. H. Dunning Jr., J. Chem. Phys., 1995, 103, 4572 CrossRef CAS.
- K. A. Peterson and T. H. Dunning Jr., J. Chem. Phys., 2002, 117, 10548–10560 CrossRef CAS.
- S. Coriani, D. Marchesan, J. Gauss, C. Hättig, T. Helgaker and P. Jørgensen, J. Chem. Phys., 2005, 123, 184107 CrossRef PubMed.
- C. Puzzarini, M. Biczysko, V. Barone, I. Peña, C. Cabezas and J. L. Alonso, Phys. Chem. Chem. Phys., 2013, 15, 16965–16975 RSC.
- V. Barone, M. Biczysko, J. Bloino, P. Cimino, E. Penocchio and C. Puzzarini, J. Chem. Theory Comput., 2015, 11, 4342–4363 CrossRef CAS PubMed.
- G. Ceselin, Z. Salta, J. Bloino, N. Tasinato and V. Barone, J. Phys. Chem. A, 2022, 126, 2373–2387 CrossRef CAS PubMed.
- V. Barone, M. Biczysko, J. Bloino and C. Puzzarini, Phys. Chem. Chem. Phys., 2013, 15, 10094–10111 RSC.
- C. Puzzarini, M. Biczysko, V. Barone, L. Largo, I. Peña, C. Cabezas and J. L. Alonso, J. Phys. Chem. Lett., 2014, 5, 534–540 CrossRef CAS PubMed.
- E. Papajak, J. Zheng, X. Xu, H. R. Leverentz and D. G. Truhlar, J. Chem. Theory Comput., 2011, 7, 3027–3034 CrossRef CAS PubMed.
- G. Santra, N. Sylvetsky and J. M. L. Martin, J. Phys. Chem. A, 2019, 123, 5129–5143 CrossRef CAS PubMed.
- W. D. Allen, A. L. L. East and A. G. Csaśzaŕ, in Structures and Conformations of Non-Rigid Molecules, ed. J. Laane, M. Dakkouri, B. van der Veken and H. E. Oberhammer, Kluwer: Dordrecht, 1993, p. 343 Search PubMed.
- A. L. L. East and W. D. Allen, J. Chem. Phys., 1993, 99, 4638 CrossRef CAS.
- J. M. Martin and T. J. Lee, Chem. Phys. Lett., 1996, 258, 129–135 CrossRef CAS.
- C. Puzzarini, J. Phys. Chem. A, 2009, 113, 14530–14535 CrossRef CAS PubMed.
- C. Puzzarini, Int. J. Quantum Chem., 2016, 116, 1513–1519 CrossRef CAS.
- S. Alessandrini, V. Barone and C. Puzzarini, J. Chem. Theory Comput., 2020, 16, 988–1006 CrossRef CAS PubMed.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622 CrossRef.
- S. Grimme, J. Chem. Phys., 2006, 124, 034108 CrossRef PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- L. Goerigk and S. Grimme, J. Chem. Theory Comput., 2011, 7, 291–309 CrossRef CAS PubMed.
- M. Biczysko, J. Bloino and C. Puzzarini, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1349 Search PubMed.
- V. Barone, G. Ceselin, M. Fusè and N. Tasinato, Front. Chem., 2020, 8, 584203 CrossRef CAS PubMed.
- D. Mester and M. Kállay, J. Chem. Theory Comput., 2022, 18, 865–882 CrossRef CAS PubMed.
- E. Penocchio, M. Piccardo and V. Barone, J. Chem. Theory Comput., 2015, 11, 4689–4707 CrossRef CAS PubMed.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS PubMed.
- G. G. Brown, B. C. Dian, K. O. Douglass, S. M. Geyer, S. T. Shipman and B. H. Pate, Rev. Sci. Instrum., 2008, 79, 053103 CrossRef PubMed.
- A. L. Steber, J. L. Neill, D. P. Zaleski, B. H. Pate, A. Lesarri, R. G. Bird, V. Vaquero-Vara and D. W. Pratt, Faraday Discuss., 2011, 150, 227–242 RSC.
- C. Pérez, J. L. Neill, M. T. Muckle, D. P. Zaleski, I. Peña, J. C. López, J. L. Alonso and B. H. Pate, Angew. Chem., Int. Ed., 2015, 54, 979–982 CrossRef PubMed.
- A. L. Steber, C. Pérez, B. Temelso, G. C. Shields, A. M. Rijs, B. H. Pate, Z. Kisiel and M. Schnell, J. Phys. Chem. Lett., 2017, 8, 5744–5750 CrossRef CAS PubMed.
- F. Xie, M. Fusè, S. Hazrah, A. W. Jaeger, V. Barone and Y. Xu, Angew. Chem., Int. Ed., 2020, 59, 22427–22430 CrossRef CAS PubMed.
- A. Lesarri, S. Mata, J. López and J. Alonso, Rev. Sci. Instrum., 2003, 74, 4799–4804 CrossRef CAS.
- J. L. Alonso and J. C. López, in Gas-Phase IR Spectroscopy and Structure of Biological Molecules, Springer; 2015, pp. 335–401 Search PubMed.
- J. Řezáč and P. Hobza, J. Chem. Theory Comput., 2013, 9, 2151–2155 Search PubMed.
- J. Řezáč, K. E. Riley and P. Hobza, J. Chem. Theory Comput., 2011, 7, 2427–2438 CrossRef PubMed.
| This journal is © the Owner Societies 2023 |


