B–H⋯π and C–H⋯π interactions in protein–ligand complexes: carbonic anhydrase II inhibition by carborane sulfonamides

Abstract

Among non-covalent interactions, B–H⋯π and C–H⋯π hydrogen bonding is rather weak and less studied. Nevertheless, since both can affect the energetics of protein–ligand binding, their understanding is an important prerequisite for reliable predictions of affinities. Through a combination of high-resolution X-ray crystallography and quantum-chemical calculations on carbonic anhydrase II/carborane-based inhibitor systems, this paper provides the first example of B–H⋯π hydrogen bonding in a protein–ligand complex. It shows that the B–H⋯π interaction is stabilized by dispersion, followed by electrostatics. Furthermore, it demonstrates that the similar C–H⋯π interaction is twice as strong, with a slightly smaller contribution of dispersion and a slightly higher contribution of electrostatics. Such a detailed insight will facilitate the rational design of future protein ligands, controlling these types of non-covalent interactions.

---

Introduction

C–H⋯π is a weak hydrogen bond between a non-classical donor (typically aliphatic or aromatic groups) and a non-classical acceptor (e.g. electron density of phenyl rings) that can stabilize crystals of small organic molecules or proteins.¹ This interaction may also involve inorganic compounds, e.g. C–H groups of carbon-substituted three-dimensional boron hydrides (carboranes).² In contrast, the B–H groups of carboranes act as hydrogen-bond acceptors due to the low electronegativity of boron. The hydridic nature of boron-attached hydrogens thus results in dihydrogen-bond formation.^3–7 Nevertheless, B–H groups can also form a weak dispersion-driven non-covalent contact with weak acceptors, referred to as B–H⋯π,^8,9 which has recently been observed by means of X-ray crystallography in the boron-hydride organometallic complex.¹⁰ Comparing the C–H⋯π and B–H⋯π interactions of neutral carboranes, the latter has been calculated to be two times weaker in model systems.⁹ In this work, we study these interactions in protein–ligand complexes by means of X-ray crystallography and quantum-mechanical computations. The protein studied is carbonic anhydrase II (CA II), and the ligands are sulfonamide inhibitors terminated with three isomers of carborane cages (ortho – compound 1, meta – compound 2 and para – compound 3; Fig. 1(A)).

Fig. 1 (A) The structural formulae of the carborane propyl-sulfonamide compounds 1, 2 and 3 and the values of the inhibition constant K_i for the inhibition of CA II. (B) Details of the crystal structure of compound 1 bound in the active site of CA II (PDB code 6YZT). Interacting residues are marked with sticks. The inhibitor and the residue Phe131 occupy two alternative conformations: the major conformation (an occupancy of 0.8) is depicted in stick representation, whereas the minor conformation (an occupancy of 0.2) is in line representation. Polar interactions are represented by blue dashed lines, while the black dashed line marks the potential B–H⋯π interaction between the carborane cage and Phe131.

Carbonic anhydrases (CAs) are metalloenzymes catalyzing the interconversion between CO₂ and bicarbonate. These enzymes participate in many physiological processes and some of their isoforms are involved in human pathologies, such as cancer development (isoform CA IX).^11,12 CAs have thus been targets for inhibitor development; dozens of diverse families of CA inhibitors (CAIs) have been prepared.¹³ Due to this wealth of gathered information, these systems are an attractive model for biophysical studies of protein–ligand binding.¹⁴ Human CAs can be efficiently and selectively inhibited by carboranes linked to a sulfamide or sulfonamide moiety.^15–18 More than 30 X-ray crystal structures of carborane-containing inhibitors with CA II or CA IX have been determined at high or even atomic resolution, which has provided insight into the structural basis of the interactions of carborane with enzyme active sites.¹⁵ Here, we focus on a series of carborane propyl-sulfonamides that differ in the geometric positions of carbon atoms within the carborane cage and on their affinities toward CA II (Fig. 1(A)). Some compounds have exhibited selective inhibitory activity toward CA IX over CA II,¹⁹ and the structural basis of this selectivity has been explained by a detailed crystallographic study of compound 1 in these complexes.¹⁷ Interestingly, the crystal structure of 1 in complex with CA II (PDB code 6YZT) has revealed that compound 1 has acquired two alternative binding orientations in the CA II active site and the minor conformation (with an occupancy factor of 0.2) is accompanied by a rearrangement of the Phe131 side chain (Fig. 1(B)). The mutual position and distance between the carborane cage and the side chain of Phe131 indicate a potential B–H⋯π interaction (the dashed black line in Fig. 1(B)).

Methods

Crystallization, structure determination and refinement

Complexes of CA II with compounds were prepared by the addition of a one- to twofold molar excess of the compounds (dissolved in 100% DMSO) to a 20–25 mg ml⁻¹ protein solution in 50 mM Tris–H₂SO₄, pH 7.8. The final concentration of DMSO in crystallization drops did not exceed 10%. Crystals were prepared by the hanging-drop vapor-diffusion method at 18 °C using EasyXtal® 15-well plates (Qiagen). Drops containing 2 μl of the complex solution were mixed with 1 μl of precipitant solution. Subsequently, these mixtures were equilibrated over a reservoir containing 1 ml of the precipitant solution. The precipitation solution consisted of 1.6 M sodium citrate and 50 mM tris–H₂SO₄, pH 7.8. Crystals formed within one to three weeks. Prior to data collection, the crystals were soaked for 10 s in the reservoir solution supplemented with 20% (v/v) sucrose and stored in liquid nitrogen. X-ray diffraction data at 100 K were collected on BL14.1 and BL14.2, operated by the Helmholtz-Zentrum Berlin (HZB) at the BESSY II electron storage ring (Berlin-Adlershof, Germany).²⁰ Diffraction data were processed using the XDS suite of programs.^21,22 Crystal parameters and data-collection statistics are summarized in the ESI† (Table S1).

The crystal structures of the CA II complexes with compounds 2 and 3 were determined by the difference Fourier technique. Coordinates from the 4Z1N entry in the PDB²³ were used as models for the CA II complexes. Atomic coordinates of inhibitor molecules were generated by quantum-mechanical (QM) optimizations in the Turbomole package²⁴ by means of the density functional theory (DFT) method augmented with empirical dispersion correction²⁵ using the B-LYP functional and the SVP basis set. The geometric library for the compounds was generated using the Libcheck program.²⁶ The Coot program²⁷ was used for inhibitor fitting, model rebuilding, and the addition of water molecules. Refinement was carried out with the Refmac5 program²⁸ with 5% of the reflections reserved for cross-validation. The structures were first refined with isotropic atomic-displacement parameters (ADPs). After the addition of solvent atoms and zinc ions, building inhibitor molecules in the active site, and several alternate conformations for a number of residues, anisotropic ADPs were refined for nearly all atoms. The refinement of ADPs was not carried out for spatially overlapping atoms in segments with alternate conformations or for oxygen atoms of water molecules with an unrealistic ratio of ellipsoid axes. The quality of the crystallographic model was assessed with MolProbity.²⁹ The final refinement statistics are summarized in the ESI† (Table S1). All the figures representing structures were created using PyMOL.³⁰ Contacts were analyzed using the Contact program included in the CCP4 suite.³¹ Structure factors and coordinates were deposited in the PDB under the accession codes 8AA6 and 8AAE for the CAII complex with 2 and 3, respectively.

Molecular modeling

The alignment of the three crystal structures of 1, 2 and 3 bound to CA II showed high similarity between the structures. The only larger difference concerned the Phe131 residue. To minimize the effects of the minor differences in the structures, we selected a single protein structure (the 1/CA II complex, PDB code 6YZT¹⁷), into which the other two inhibitors and Phe113 were seeded based on the alignment. All the rotamers of the carborane cages of 1 and 2 (including the two orientations of 1) were modeled because B–H and C–H groups are difficult to distinguish by X-ray crystallography.³² The most stable conformations obtained from QM/MM optimization (see below) were further used for scoring. Both alternative orientations were considered for compounds 1 and 3. The hydrogen atoms of the protein were added by the Reduce and Leap programs in AMBER 14,³³ with individual protonation of all the histidines assigned on the basis of the visual inspection of their surroundings. The H atoms of the inhibitors were added manually. The sulfonamide moiety binds to the Zn²⁺ of CA II and is thus considered in a deprotonated NH⁻ form.³⁴ The ff14SB force field³⁵ was used for the protein. A general AMBER force field (GAFF)³⁶ for the organic parts of the inhibitor was combined with the tested boron parameters from the universal force field (UFF) for the ligand.⁶ Hydrogen atoms were relaxed by annealing from 900 K to 0 K at the molecular mechanics (MM) level in AMBER 14. The cooling runs using a Berendsen thermostat were 4 ps long with a 1 fs step. The complexes were optimized employing the hybrid QM/MM methodology and mechanical embedding. The QM part comprised His94, His96, His119, Phe131, Thr198, Zn²⁺, and the inhibitor. The QM part was treated at the DFT-D3 level using B3LYP/TZVPP.²⁵ The rest of the system was treated at the MM level by AMBER. The environment was described by the generalized Born (IGB7) implicit solvent model.³³ The coupling between QM and MM was done by Cuby4³⁷ which uses Turbomole 7.0²⁴ for QM and AMBER 14³³ for MM. Residues farther than 5 Å from the inhibitor were frozen during the optimization.

The score was computed as the sum of the gas-phase interaction energy (ΔE_int), the interaction solvation free energy (ΔΔG_solv), and the change of the conformational “free” energy of the ligand and protein .³⁸ ΔE_int was computed using the QM/MM methodology described above. For solvation free-energy calculations, the implicit solvent IGB7 model was utilized. was computed as the “free”-energy change between the monomer taken from the optimized protein–ligand complex and the monomer structure optimized in solution by the same method. The “free” energy (G′) was defined as the sum of the gas-phase energy (E) and the solvation free energy (G).

The ΔE values of the selected motif were decomposed using the symmetry-adapted perturbation-theory (SAPT) methodology.³⁹ The simplest truncation of SAPT (SAPT0) decomposition was performed with the recommended jun-cc-pVDZ basis set using the PSI4 program.⁴⁰

Synthesis

For a synthesis using two different methods and detailed characterization of compounds 1, 2 and 3 see previous articles.^18,19

Results and discussion

X-ray crystal structures

To obtain structural information on the interaction of the other studied compounds with the CA II active site, the crystal structures of CA II in complex with 2 and 3 were determined in this work at a high resolution of 1.09 Å and 1.15 Å, respectively (Table S1, ESI†). Unlike compound 1 (Fig. 2(A)), compound 2 was modeled as a single conformation with full occupancy (Fig. 2(B)). Compound 3 was modeled in two alternative orientations within the CA II active site: conformations A and B with the occupancy of 0.7 and 0.3, respectively (Fig. 2(C)).

Fig. 2 The active site of CA II with the bound compounds 1 (panel A), 2 (B) and 3 (C). The inhibitor residue Phe131 occupies two alternative conformations. Major populations are depicted in stick representation, whereas minor conformations are shown in line representation. The 2Fo-Fc map is contoured on 1.2 sigma in blue (for OMIT difference maps see Fig. S1, ESI†). On this level, electron density is shown for the major conformation of the ligand and the side chain of Phe131. Panels D and E depict two inhibitor orientations in CA II active sites: orientations I and II exemplified by compound 3. Interacting residues are highlighted as sticks and labeled. The dashed lines have the same meaning as in Fig. 1.

A comparison of the crystal structures of all the three isomers (Fig. 2(A)–(C)) shows that the interaction of the sulfonamide head moiety with the catalytic zinc ion and residues at the bottom of the active-site cavity is conserved, with differences being located in the position of the carborane cage. For ligands 1 and 3, we can identify two possible ligand orientations: orientations I and II (Fig. 2(D) and (E)). Orientation I is characterized by the staggered position of the S–C and S=O bonds in the –CH₂–CH₂–SO₂–NH⁻ moiety, which enables the binding of the carborane cage to a preformed hydrophobic pocket formed by residues Val121 and Phe131. This orientation is more prevalent in our crystal structures and can be found in all three structures as: (a) the major conformation A of compound 1, (b) a single conformation of 2, and (c) the minor conformation B of compound 3. Orientation II has an extended propyl linker (eclipsed position of the S–C and S=O bonds in the –CH₂–CH₂–SO₂–NH⁻ moiety) and is only possible when the Phe131 side chain changes its rotamer position such that the phenyl ring is more exposed to the solvent (Fig. 2). This orientation occurs as: (a) the minor conformation B of compound 1 and (b) the major conformation A of compound 3.

Molecular modeling

The binding of the studied inhibitors to CA II has been examined by quantum mechanics-based scoring function,^38,41,42 which was shown previously to describe reliably the CA II metalloenzyme-carborane system.³⁴ Ranking was performed using the most stable (see Tables S2 and S3, ESI†) of the five possible rotamers for each orientation I or II of inhibitors 1 and 2 bound to CA II. Considering the more favorable scores of the two orientations of 1 and 3 (Table 1 in bold), the obtained ranking of the compounds (the scores of −10.6 > −12.0 > −13.3 kcal mol⁻¹ for compounds 1, 2 and 3, respectively) matched the order of experimental binding free energies (the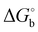 of −8.5, −9.0 and −9.2 kcal mol⁻¹, respectively, Table 1). It should be noted here that entropic effects, coming for example from two possible conformations of the propyl linker of bound 1 and 3, which are not treated in the present version of the scoring function, could add a higher penalty to the score of 2 with respect to those of 1 and 3. Compound 1, the weakest-binding inhibitor, had the least favorable score because of the least favorable interactions with the CA II active site as reflected in the least negative ΔE_int value of −194.5 kcal mol⁻¹ (Table 1). The score of 3 was the most favorable due to the strongest interactions with the protein (the most negative ΔE_int of −203.6 kcal mol⁻¹). Considering the conserved positions of the sulfonamide head moiety, the catalytic zinc ion and the residues of the active-site cavity in the modeled structures, the only difference was in the position of the C–H vertex of the carborane cage. The C–H vertex of 3 was oriented toward Phe131, thus replacing the B–H···π interaction of the 1:CA II complex with the C–H⋯π interaction, which implies that the latter is stronger. The stronger interaction (ΔE_int) is only partly offset (163.3 vs. 169.8 kcal mol⁻¹) by solvation (ΔΔG_solv; Table 1).

Table 1 The inhibition constant (K_i), experimental binding free energy () and scores. The total score was computed as the sum of the following terms: the interaction energy (ΔE_int), the interaction solvation free energy (ΔΔG_solv), and the change of the conformational ‘free’ energy of the ligand (L) and protein (P). The more favorable scores of the two orientations of 1 and 3 are in bold. All energies are in kcal mol⁻¹ and K_i in nM

Complex	Orientation	Occupancy in crystal	K i		Score	ΔEint	ΔΔGsolv	(L)	(P)
a As determined in ref. 15. b is derived from Ki values using .
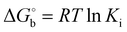1:CA II	I	0.8	622 ± 87	−8.47	−8.7	−190.1	168.0	5.6	7.8
	II	0.2			−10.6	−194.5	163.3	7.4	13.4
2:CA II	I	1.0	254 ± 23	−9.01	−12.0	−197.7	171.5	6.7	7.5
3:CA II	I	0.3	171 ± 17	−9.24	−10.1	−196.6	171.8	6.9	7.8
	II	0.7			−13.3	−203.6	169.8	7.2	13.3

---

Compound 2 only had a single conformation in orientation I in the crystal structure. In such an arrangement, the C–H vertex of 2 still interacted with the π ring of Phe131, albeit in a less favourable tilted arrangement (as opposed to an ideal perpendicular arrangement). In contrast to other inhibitors, orientation I of compound 2 enabled the formation of C–H^δ+⋯^δ−H–B dihydrogen bonds (Fig. 3), a typical non-covalent interaction of heteroboranes with proteins.³

Fig. 3 The models of the active site of CA II with the bound compounds 1 (A), 2 (B) and 3 (C) in orientation I (crystal structures of orientations II are shown in Fig. 2). B–H⋯π and C–H···π are shown as dot-dashed lines. Hydrogen contacts are shown as dashed lines. Hydrogen separations are in Å.

The applied scoring function did not rank correctly the orientations of 1. The orientation II with a minor occupancy of 0.2 had erroneously a more favorable score by 1.9 kcal mol⁻¹, which was due to more favorable interaction (ΔE_int) and desolvation (ΔΔG_solv) terms. This may be caused by inherent limitations of the methodology used, such as the lack of explicit solvation or dynamical treatment and entropy effects.

To gain an even deeper insight into the nature of the B–H⋯π and C–H⋯π interactions evidenced in CA II complexes with 1 and 3, we further dissected the gas-phase interaction energy ΔE into individual terms using the SAPT methodology on small models derived from the crystal structures.³⁹ The results showed favorable interactions of the carborane cages of both inhibitors with the side chain of Phe131 but more so for C–H⋯π (−3 kcal mol⁻¹) than for B–H⋯π (−1.6 kcal mol⁻¹) (Table 2). The leading term was dispersion (E_disp) as expected for weak hydrogen bonding.⁴³ It was more pronounced for B–H⋯π than for C–H⋯π (74 and 66% of the sum of all attractive terms, respectively). The second largest attractive term was electrostatics (E_elec), which was more important for C–H⋯π than for B–H⋯π (26 and 17% of the sum of all attractive terms, respectively). It is worth mentioning that the E_elec for B–H⋯π is attractive, which has confirmed the amphiphilic noncovalent bonding character of the B–H group.^9,44 In both cases, the induction term (E_ind) was of little importance (below 10% of the sum of all attractive terms). The exchange-repulsive term (E_exch) was more repulsive for B–H⋯π (3.1 kcal mol⁻¹) than for C–H⋯π (1.7 kcal mol⁻¹). The larger repulsion of B–H⋯π might be due to the smaller spatial requirement of the acidic H^δ+ atom of the C–H group in comparison with the hydridic H^δ− atom of the B–H group. Moreover, the C atom is also smaller than the B atom (van der Waals radius of C being smaller by 0.22 Å⁴⁵ than that of B), which overall reduces the spatial requirement of the entire C–H vertex.

Table 2 The results of interaction-energy decomposition by the SAPT0/jun-cc-pVDZ methodology. SAPT0 captures the classical electrostatic interaction of two charge densities (E_elec), exchange (Pauli repulsion, E_exch), electrostatic induction (the polarization of the molecular orbitals in the electric field of the interacting molecule, E_ind) and dispersion (E_disp). All energies are in kcal mol⁻¹. The relative values in parentheses show the contribution to the sum of all the attractive energy terms of SAPT0. Color coding: green – carbon, pink – boron, and white – hydrogen

Model
Interaction	C–H⋯π	B–H⋯π
E disp	−3.1 (66%)	−3.5 (74%)
E elec	−1.2 (26%)	−0.8 (17%)
E ind	−0.4 (8%)	−0.4 (9%)
E exch	1.7	3.1
Total	−3.0	−1.6

---

Conclusions

B–H⋯π and C–H⋯π non-covalent interactions have been examined in a series of carborane propyl-sulfonamide inhibitors binding to CA II using a combination of X-ray crystallography and quantum-chemical calculations. Based on the X-ray structures, the interactions of the sulfonamide moiety were conserved, while the carborane cages had different orientations and interactions. In the case of the ortho-carborane moiety (compound 1), the B–H⋯π interaction with Phe131 was minor and the affinity was the lowest in the series. In contrast, for para-carborane (compound 3), the C–H⋯π interaction with Phe131 was the major conformation, with the highest affinity attained. The difference in the affinities was a result of the difference in the strength of these two interactions as determined by quantum-mechanical calculations. A detailed understanding of B–H⋯π and C–H⋯π non-covalent interactions will be used for the future rational control over protein–ligand binding.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

This work was supported by the project ChemBioDrug CZ.02.1.01/0.0/0.0/16_019/0000729 from the European Regional Development Fund (OP RDE) and the project 2114409S from the Czech Science Foundation under a grant awarded to B. G and by project National Institute for Cancer Research (Programme EXCELES, ID Project No. LX22NPO5102) – Funded by the European Union – Next Generation EU.

References

1. G. R. Desiraju and T. Steiner, The weak hydrogen bond in structural chemistry and biology, Oxford University Press, Oxford, 2006, ISBN 9780198509707.
2. L. R. Raston and W. V. Cave, Chem. – Eur. J., 2004, 10, 279–282.
3. J. Fanfrlík, M. Lepšík, D. Hořínek, Z. Havlas and P. Hobza, ChemPhysChem, 2006, 7, 1100–1105.
4. N. V. Belkova, E. S. Shubina and L. M. Epstein, Acc. Chem. Res., 2005, 38, 624–631.
5. R. Custelcean and J. E. Jackson, Chem. Rev., 2001, 101, 1963–1980.
6. J. Fanfrlík, A. Pecina, J. Řezáč, M. Lepšík, M. B. Sárosi, D. Hnyk and P. Hobza, ChemPhysChem, 2020, 21, 2599–2604.
7. J. G. Planas, C. Viñas, F. Teixidor, A. Comas-Vives, G. Ujaque, A. Lledós, M. E. Light and M. B. Hursthouse, J. Am. Chem. Soc., 2005, 127, 15976–15982.
8. J. Grunenberg, Chem. – Eur. J., 2016, 22, 18678.
9. J. Fanfrlík, A. Pecina, J. Řezáč, R. Sedlak, D. Hnyk, M. Lepšík and P. Hobza, Phys. Chem. Chem. Phys., 2017, 19, 18194–18200.
10. X. Zhang, H. Dai, H. Yan, W. Zou and D. Cremer, J. Am. Chem. Soc., 2016, 138, 4334–4337.
11. S. Pastorekova and R. J. Gillies, Cancer Metastasis Rev., 2019, 38, 65–77.
12. S. Zamanova, A. M. Shabana, U. K. Mondal and M. A. Ilies, Expert Opin. Ther. Pat., 2008, 29, 509–533.
13. C. B. Mishra, M. Tiwari and C. T. Supuran, Med. Res. Rev., 2020, 40, 2485–2565.
14. V. M. Krishnamurthy, G. K. Kaufman, A. R. Urbach, I. Gitlin, K. L. Gudiksen, D. B. Weibel and G. M. Whitesides, Chem. Rev., 2008, 108, 946–1051.
15. M. Kugler, J. Nekvinda, J. Holub, S. E. Anwar, V. Das, V. Šícha, K. Pospíšilová, M. Fábry, V. Král and J. Brynda, et al. , ChemBioChem, 2021, 22, 2741–2761.
16. J. Brynda, P. Máder, V. Šícha, M. Fábry, K. Poncová, M. Bakardiev, B. Grüner, P. Cígler and P. Řezáčová, Angew. Chem., Int. Ed., 2013, 52, 13760–13763.
17. M. Kugler, J. Holub, J. Brynda, K. Pospisilova, S. E. Anwar, D. Bavol, M. Havranek, V. Kral, M. Fabry, B. Gruner and P. Rezacova, J. Enzyme Inhib. Med. Chem., 2020, 35, 1800–1810.
18. J. Dvořanová, M. Kugler, J. Holub, V. Šícha, V. Das, J. Nekvinda, S. E. Anwar, M. Havránek, K. Pospíšilová and M. Fábry, et al. , Eur. J. Med. Chem., 2020, 200, 112460.
19. J. Nekvinda, M. Kugler, J. Holub, S. E. Anwar, J. Brynda, K. Pospíšilová, Z. Růžičková, P. Řezáčová and B. Grüner, Chem. – Eur. J., 2020, 26, 16541–16553.
20. U. Mueller, R. Forster, M. Hellmig, F. U. Huschmann, A. Kastner, P. Malecki, S. Puhringer, M. Rower, K. Sparta and M. Steffien, et al. , Eur. Phys. J. Plus, 2015, 130, 141.
21. W. Kabsch, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2010, 66, 125–132.
22. W. Kabsch, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2010, 66, 133–144.
23. M. R. Buemi, L. De Luca, S. Ferro, E. Bruno, M. Ceruso, C. T. Supuran, K. Pospisilova, J. Brynda, P. Rezacova and R. Gitto, Eur. J. Med. Chem., 2015, 102, 223–232.
24. R. Ahlrichs, M. Bar, M. Haser, H. Horn and C. Kolmel, Chem. Phys. Lett., 1989, 162, 165–169.
25. J. Hostas and J. Rezac, J. Chem. Theory Comput., 2017, 13, 3575.
26. A. A. Vagin, G. N. Murshudov and B. V. Strokopytov, J. Appl. Crystallogr., 1998, 31, 98–102.
27. P. Emsley and K. Cowtan, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2004, 60, 2126–2132.
28. G. N. Murshudov, A. A. Vagin and E. J. Dodson, Acta Crystallogr., Sect. D: Biol. Crystallogr., 1997, 53, 240–255.
29. V. B. Chen, W. B. Arendall, J. J. Headd 3rd, A. D. Keedy, R. M. Immormino, G. J. Kapral, L. W. Murray, J. S. Richardson and D. C. Richardson, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2010, 66, 12–21.
30. W. DeLano, 2020 PyMOL. Retrieved from https://www.pymol.org/pymol or The PyMOL Molecular Graphics System, Version 2.0 Schrödinger, LLC.
31. M. D. Winn, C. C. Ballard, K. D. Cowtan, E. J. Dodson, P. Emsley, P. R. Evans, R. M. Keegan, E. B. Krissinel, A. G. Leslie and A. McCoy, et al. , Acta Crystallogr.; Sect. D: Biol. Crystallogr, 2011, 67, 235–242.
32. A. Welch, Crystals, 2017, 7, 234.
33. D. A. Case, V. Babin, J. T. Berryman, R. M. Betz, Q. Cai, D. S. Cerutti, T. E. Cheatham, T. A. Darden, R. E. Duke and H. Gohlke, et al., AMBER 14, University of California, San Francisco, San Francisco (USA), 2014.
34. A. Pecina, M. Lepšík, J. Řezáč, J. Brynda, P. Mader, P. Řezáčová, P. Hobza and J. Fanfrlík, J. Phys. Chem. B, 2013, 117, 16096–16104.
35. J. A. Maier, C. Martinez, K. Kasavajhala, L. Wickstrom, K. E. Hauser and C. Simmerling, J. Chem. Theory Comput., 2015, 11, 3696–3713.
36. J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174.
37. J. Řezáč, J. Comput. Chem., 2016, 37(13), 1230–1237.
38. A. Pecina, S. M. Eyrilmez, C. Köprülüoğlu, V. M. Miriyala, M. Lepšík, J. Fanfrlík, J. Řezáč and P. Hobza, ChemPlusChem, 2020, 85, 2362–2371.
39. B. Jeziorski, R. Moszynski and K. Szalewicz, Chem. Rev., 1994, 94, 1887–1930.
40. J. M. Turney, A. C. Simmonett, R. M. Parrish, E. G. Hohenstein, F. Evangelista, J. T. Fermann, B. J. Mintz, L. A. Burns, J. J. Wilke and M. L. Abrams, et al. , Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 556–565.
41. M. Lepšík, J. Řezáč, M. Kolář, P. Pecina, P. Hobza and J. Fanfrlík, ChemPlusChem, 2013, 78, 921–931.
42. J. Fanfrlík, A. K. Bronowska, J. Řezáč, O. Přenosil, J. Konvalinka and P. Hobza, J. Phys. Chem. B, 2010, 114, 12666–12678.
43. M. Nishio, Phys. Chem. Chem. Phys., 2011, 13, 13873–13900.
44. C. Esterhuysen, A. Hesselmann and T. Clark, ChemPhysChem, 2017, 18, 772–784.
45. M. Mantina, A. C. Chamberlin, R. Valero, Ch. J. Cramer and D. G. Truhlar, J. Phys. Chem. A, 2009, 113, 5806–5812.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp04673c

‡ These authors contributed equally to this work. The manuscript was written through contributions of all authors.

---