Prediction of parameters of group contribution models of mixtures by matrix completion†
Fabian
Jirasek
 *a,
Nicolas
Hayer
a,
Rima
Abbas
b,
Bastian
Schmid
b and
Hans
Hasse
a
*a,
Nicolas
Hayer
a,
Rima
Abbas
b,
Bastian
Schmid
b and
Hans
Hasse
a
aLaboratory of Engineering Thermodynamics (LTD), TU Kaiserslautern, Erwin-Schrodinger-Str. 44, 67663, Kaiserslautern, Germany. E-mail: fabian.jirasek@mv.uni-kl.de
bDDBST GmbH, Marie-Curie-Str. 10, 26129, Oldenburg, Germany
First published on 12th December 2022
Abstract
Group contribution (GC) methods are widely used for predicting the thermodynamic properties of mixtures by dividing components into structural groups. These structural groups can be combined freely so that the applicability of a GC method is only limited by the availability of its parameters for the groups of interest. For describing mixtures, pairwise interaction parameters between the groups are of prime importance. Finding suitable numbers for these parameters is often impeded by a lack of suitable experimental data. Here, we address this problem by using matrix completion methods (MCMs) from machine learning to predict missing group-interaction parameters. This new approach is applied to UNIFAC, an established group contribution method for predicting activity coefficients in mixtures. The developed MCM yields a complete set of parameters for the first 50 main groups of UNIFAC, which substantially extends the scope and applicability of UNIFAC. The quality of the predicted parameter set is evaluated using vapor–liquid equilibrium data of binary mixtures from the Dortmund Data Bank. This evaluation reveals that our approach gives prediction accuracies comparable with UNIFAC for data sets to which UNIFAC was fitted, and only slightly lower accuracies for data sets to which UNIFAC is not applicable.
1 Introduction
Methods for predicting thermodynamic properties are of paramount importance in chemical engineering, simply because there are too many relevant substances to study them all in experiments. The scale of this problem soars when going from pure components to mixtures, for simple combinatorial reasons. Also methodologically, predicting properties of mixtures is a demanding task. It can be tackled basically from two sides: on the one hand, one can look for similarities between substances (which is basically a data-driven approach), on the other hand, one can try to base predictions on physical theory.The most successful methods in the field combine these two aspects. Among these, methods that rely on the concept of group contributions (GC) play an important role. They are based on the idea that components can be characterized by the structural groups they contain and take advantage of the fact that the number of relevant structural groups is many orders of magnitude smaller than the number of relevant components. As a consequence, GC methods can be used for describing a very large number of components based on a relatively small number of group-specific parameters: any component that can be built from groups, for which parameters are available, can be modeled.
Basically all thermodynamic models of mixtures rely on describing pair interactions. Component-specific models, like UNIQUAC1,2 or NRTL,3 thereby describe the pairwise interactions between components using component-specific pair-interaction parameters, which need to be fitted to experimental data. Usually, data for binary mixtures are used for this purpose, which means that for modeling multi-component mixtures, binary mixture data are needed for all binary subsystems of the studied mixture. Unfortunately, due to the combinatorial problem, even data for binary mixtures are often missing, which strongly limits the applicability of the component-specific models.
GC methods circumvent this problem. By dividing components into structural groups, GC methods only rely on group-specific pair-interaction parameters, namely group-interaction parameters, which are fitted to experimental mixture data, whereby the amount of required training data compared to component-specific models is significantly reduced.
One of the most successful thermodynamic group contribution methods for mixtures is UNIFAC, which was first introduced in 19754 and has been significantly extended and refined since then.5–10 Also, several tailored versions of UNIFAC fitted for specific applications are available.11–13 And there is also a commercial version of UNIFAC, provided within the UNIFAC-Consortium, which is based on the same model equations as the public versions of UNIFAC, but whose parameter tables have been revised and extended on a regular basis since 199614 using both public data and non-public data provided or generated within the consortium. The scope of the commercial version is therefore larger than that of the public versions of UNIFAC. Since the commercial version is not freely accessible, we focus here on the most recent public version of UNIFAC,10 to which we refer simply as UNIFAC in the following for brevity. The authors have also access to the commercial version of UNIFAC, called UNIFAC-TUC in the following, but this version is used for comparisons only.
UNIFAC was derived from the component-specific lattice model UNIQUAC1,2 and describes the molar excess Gibbs energy gE of a mixture as a function of temperature T and composition x. Both energetic and entropic contributions to gE are considered in the model. All versions of UNIFAC use geometric parameters for the individual structural groups, which describe their volume and surface and determine the entropic contribution. Furthermore, parameters describing the pairwise energetic interactions between the different structural groups in the mixture are used. These group-interaction parameters play the central role in the model.
From the Gibbs excess energy gE, many properties that are essential in chemical engineering can be determined, most importantly the activity coefficients γi of the components i in the mixture, based on which phase equilibria can be predicted.15 Over the years, many structural groups have been included in the UNIFAC parameter tables, so that a huge number of components of practical interest can be modeled. UNIFAC presently considers 54 main groups, which are further divided into 113 sub groups.10 The difference between main and sub groups is that each sub group g has individual geometric parameters, namely the group volume Rg and group surface area Qg,16 while all sub groups that belong to the same main group G share the same group-interaction parameters. There are two distinct group-interaction parameters for each binary combination of different main groups (G, G′); they are generally labeled as AGG′ and AG′G, and have, as a result of the fit, usually different values, i.e., AGG′ ≠ AG′G.
While Qg and Rg are reported for 113 individual sub groups, there are still significant gaps regarding the group-interaction parameters AGG′ and AG′G between the 54 main groups: there are 1431 distinct binary combinations of unlike main groups (G ≠ G′), for which only for 635 (44%) group-interaction parameters have been reported yet. Fig. 1 schematically shows the publicly available set of group-interaction parameters between the first 50 main groups of UNIFAC.10 The first 50 main groups were chosen here since for all of these, group-interaction parameters with at least five other main groups are publicly available to date. This threshold was chosen since, as described in detail below, the missing group-interaction parameters were predicted based on information from the available parameters only. For the sake of completeness, Fig. S1 in the ESI† shows for which of the group combinations parameters are available in the commercial UNIFAC-TUC.
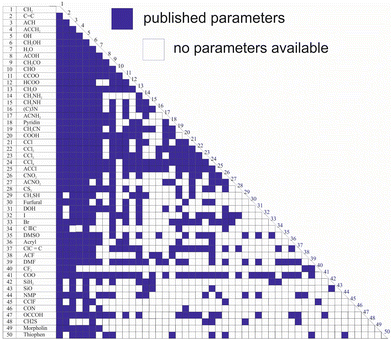 | ||
| Fig. 1 Matrix representing the availability of group-interaction parameters of UNIFAC10 up to main group 50. Blue: parameters available. | ||
Hence, the availability of the parameters describing the individual sub groups Rg and Qg generally poses no problem, whereas missing main group-interaction parameters AGG′ and AG′G significantly limit the applicability of all versions of UNIFAC. The main reason why these gaps still persist, after so many years of work on the development of UNIFAC, is that the data base for their determination is simply too narrow. There are structural groups that occur in many molecules, such as the methyl group or the hydroxyl group, and there are less common groups. It is particularly these less common groups for which the parameters are lacking. This is not to say that these groups do not occur in interesting components, but there are simply less data on binary mixtures containing components with these groups. It is evident that this causes problems in the parameterization of UNIFAC.
A further drawback is that fitting group-interaction parameters is still not a routine but rather artwork, in particular regarding the selection of the considered data sets, including their initial evaluation and consistency checking, and regarding the selection of a suitable objective function to be minimized during the fitting procedure. For a more detailed description of the fitting procedure of UNIFAC group-interaction parameters, we refer to the literature.15,17–19
In this work, we present a method for the prediction of the complete set of the group-interaction parameters of group contribution methods based on an existing parameter set, without requiring new experimental data. The basic idea is to consider the group-interaction parameters as entries of a squared matrix (which is only partially filled, as several parameters are missing), and to use a matrix completion method (MCM)20,21 to estimate the missing entries. To demonstrate the applicability of our approach, it is applied to UNIFAC,10 for which the complete set of the group-interaction parameters for the first 50 main groups is predicted. Fig. S2 in the ESI† gives an overview of our approach.
Following an idea developed in a recent paper,22 in which we have applied an MCM for estimating the component-specific pair-interaction parameters of UNIQUAC, we do not use the asymmetric group-interaction parameters (AGG′ ≠ AG′G) directly, but rather the symmetric group-interaction energies UGG′ = UG′G. The parameters of the two types (A and U) are connected by:
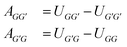 | (1) |
In a series of recent papers, we have demonstrated the capabilities of MCMs for predicting different types of thermodynamic data of mixtures using various component-based approaches.22–27 However, these component-based approaches are inherently limited regarding the number of components that are covered; the respective models complete a matrix spanned by the components that are part of the mixtures in the training set. This is not the case for the group contribution methods, which we consider in the present work: as the groups form building blocks from which components can be created flexibly, the scope of the group contribution methods for mixture properties is inherently extremely large – and it can now be extended substantially by using an MCM to complete the set of group-interaction parameters.
The approach we propose here should also be applicable to any other version of UNIFAC, and to other group contribution models for predicting thermodynamic properties of mixtures that are based on pair interactions. One advantage of our approach is that it can be put into practice, e.g., be integrated into existing process simulators, in a very simple and straightforward manner: one only has to replace the existing UNIFAC parameter set of the model implementation by the predicted one provided with our approach. For other machine-learning approaches, like artificial neural networks operating on molecular graphs28,29 or SMILES representations of the components,30 this might be more complicated in practice.
2 Method
We demonstrate the applicability of using MCMs for the prediction of group-interaction parameters of thermodynamic group contribution methods by applying it to UNIFAC.10 The resulting new version of UNIFAC (in which the predicted new parameters are used) is called UNIFAC-MCM in the following.The MCM that was used in the present work is based on Bayesian matrix factorization31 and similar to the ones used in our previous works.22–25,27 In principle, we could have applied the MCM directly to the matrix of the A-type parameters, i.e., the matrix containing the group-interaction parameters AGG′ and AG′G. However, this option was discarded for the following reasons: firstly, the available values for AGG′ and AG′G are inconsistent with eqn (1). Also, fitting AGG′ and AG′G to mixture data can give different combinations of these parameters yielding basically equivalent results for the physical properties to which they were fitted.32 This hinders an interpretation of these parameters and makes them poor candidates for applying an MCM. These problems were overcome by working with the group-interaction energies UGG′ as explained below. Furthermore, in applying the MCM to the A matrix, the target function would have been to achieve an optimal representation of the A-type parameters. However, with UNIFAC-MCM, we are rather interested in an optimal description of activity coefficients than in a representation of model parameters. UNIFAC-MCM was therefore trained on pseudo-data for activity coefficients as described in the next section.
2.1 Training data
As training data for UNIFAC-MCM, we have generated pseudo-data for the logarithmic activity coefficients ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γGG′ in hypothetical binary mixtures of the ‘pure main groups’ of UNIFAC (G and G′) at different temperatures and group mole fractions. Here, ln
γGG′ in hypothetical binary mixtures of the ‘pure main groups’ of UNIFAC (G and G′) at different temperatures and group mole fractions. Here, ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γGG′ represents the logarithmic activity coefficient of G in the binary mixture with G′. For any given temperature and mole fraction, there are two distinct values ln
γGG′ represents the logarithmic activity coefficient of G in the binary mixture with G′. For any given temperature and mole fraction, there are two distinct values ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γGG′ and ln
γGG′ and ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γG′G, respectively, which can be represented in a matrix. The diagonal elements of this matrix are occupied with ones by definition and were not considered here. For simplicity, we will simply speak of ln
γG′G, respectively, which can be represented in a matrix. The diagonal elements of this matrix are occupied with ones by definition and were not considered here. For simplicity, we will simply speak of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γGG′ in the following referring to that matrix, which includes the values from both triangular matrices, ln
γGG′ in the following referring to that matrix, which includes the values from both triangular matrices, ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γGG′ and ln
γGG′ and ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γG′G.
γG′G.
Specifically, we have calculated ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γGG′ for all binary combinations of the first 50 main groups of UNIFAC for which the required parameters were available, which holds for 619 combinations (or 50.5% of all possible binary combinations of these main groups). The grid was spanned by T ∈ {250, 300, 350, 400, 450} K for the temperature, which covers the temperature of most of the available experimental data, and xG ∈ {0.01, 0.2, 0.4, 0.6, 0.8, 0.99} mol mol−1 for the composition.
γGG′ for all binary combinations of the first 50 main groups of UNIFAC for which the required parameters were available, which holds for 619 combinations (or 50.5% of all possible binary combinations of these main groups). The grid was spanned by T ∈ {250, 300, 350, 400, 450} K for the temperature, which covers the temperature of most of the available experimental data, and xG ∈ {0.01, 0.2, 0.4, 0.6, 0.8, 0.99} mol mol−1 for the composition.
For generating the pseudo-data for ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γGG′, the UNIFAC equations (cf. eqn (S1)–(S11) in the ESI†) were used in the common manner for hypothetical components that were composed of a single main group in all cases. For main groups G with several sub groups g (with individual geometric parameters Qg and Rg), the values of Qg and Rg for one of the respective sub groups were selected, for details see Table S1 in the ESI.† In principle, UNIFAC-MCM could also be trained on data for the residual part of the activity coefficients alone, which describes the energetic interactions (cf. eqn (S7) in the ESI†), because the interaction parameters only occur in this term. We have also tested this option and found results very similar to those reported here, as expected.
γGG′, the UNIFAC equations (cf. eqn (S1)–(S11) in the ESI†) were used in the common manner for hypothetical components that were composed of a single main group in all cases. For main groups G with several sub groups g (with individual geometric parameters Qg and Rg), the values of Qg and Rg for one of the respective sub groups were selected, for details see Table S1 in the ESI.† In principle, UNIFAC-MCM could also be trained on data for the residual part of the activity coefficients alone, which describes the energetic interactions (cf. eqn (S7) in the ESI†), because the interaction parameters only occur in this term. We have also tested this option and found results very similar to those reported here, as expected.
2.2 Matrix factorization
At its heart, UNIFAC-MCM factorizes the matrix of group-interaction energies UGG′ between UNIFAC main groups G and G′. The unlike UGG′ (G ≠ G′) are modeled as the sum of two dot products:| UGG′ = UG′G = θG·βG′ + θG′·βG | (2) |
For training UNIFAC-MCM on the pseudo-data for ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γGG′, cf. section ‘Training data’, the matrix factorization of the group-interaction energies UGG′, cf.eqn (2), as well as eqn (1), which relates the UGG′ to the group-interaction parameters AGG′, were embedded in the UNIFAC equations, cf. eqn (S1)–(S11) in the ESI.† This establishes a generative probabilistic model for the ln
γGG′, cf. section ‘Training data’, the matrix factorization of the group-interaction energies UGG′, cf.eqn (2), as well as eqn (1), which relates the UGG′ to the group-interaction parameters AGG′, were embedded in the UNIFAC equations, cf. eqn (S1)–(S11) in the ESI.† This establishes a generative probabilistic model for the ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γGG′. The training data were hence modeled by:
γGG′. The training data were hence modeled by:
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γGG′(T, xG) = UNIFAC(T, xG, θG, θG′, βG, βG′, UGG, UG′G′) + εGG′ γGG′(T, xG) = UNIFAC(T, xG, θG, θG′, βG, βG′, UGG, UG′G′) + εGG′ | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γGG′ and the training data. The model parameters θG, θG′, βG, βG′, UGG, and UG′G′ were fitted in a Bayesian framework to minimize these deviations. For more details on the implementation of the model and the training procedure, we refer to the ESI.†
γGG′ and the training data. The model parameters θG, θG′, βG, βG′, UGG, and UG′G′ were fitted in a Bayesian framework to minimize these deviations. For more details on the implementation of the model and the training procedure, we refer to the ESI.†
2.3 Prediction of UNIFAC group-interaction parameters
UNIFAC-MCM only contains parameters for the ‘pure’ main groups, namely θG, βG, θG′, βG′, UGG, and UG′G′, which were fitted to the ‘group-mixture’ data, namely the pseudo-data for ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γGG′, during the training of the model as described above. Based on the learned parameters, the group-interaction energies UGG′ of all combinations of the considered main groups can be calculated based on eqn (2), from which, in turn, the commonly used group-interaction parameters of UNIFAC AGG′ and AG′G can be predicted from eqn (1). Hence, a complete parameterization of UNIFAC regarding the first 50 main groups is obtained by this procedure, which can be used for predicting temperature- and concentration-dependent activity coefficients ln
γGG′, during the training of the model as described above. Based on the learned parameters, the group-interaction energies UGG′ of all combinations of the considered main groups can be calculated based on eqn (2), from which, in turn, the commonly used group-interaction parameters of UNIFAC AGG′ and AG′G can be predicted from eqn (1). Hence, a complete parameterization of UNIFAC regarding the first 50 main groups is obtained by this procedure, which can be used for predicting temperature- and concentration-dependent activity coefficients ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γi of all components i in any (binary or multi-component) mixture, if all components that make up the mixture can be segmented using the first 50 main groups of UNIFAC. We report the predicted complete set of AGG′ (and of UGG′) as CSV file in the ESI.† Note that this set of AGG′ is consistent in terms of fulfilling eqn (1) as demanded by the lattice theory, which is in contrast to the previously available UNIFAC parameter tables that were obtained by fitting AGG′ individually.
γi of all components i in any (binary or multi-component) mixture, if all components that make up the mixture can be segmented using the first 50 main groups of UNIFAC. We report the predicted complete set of AGG′ (and of UGG′) as CSV file in the ESI.† Note that this set of AGG′ is consistent in terms of fulfilling eqn (1) as demanded by the lattice theory, which is in contrast to the previously available UNIFAC parameter tables that were obtained by fitting AGG′ individually.
The latter also explains why a direct matrix factorization of the reported AGG′ is not expedient, and instead the pseudo-data for ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γGG′ were used for training UNIFAC-MCM; the reported AGG′ matrix simply lacks structure that could be exploited by the MCM.
γGG′ were used for training UNIFAC-MCM; the reported AGG′ matrix simply lacks structure that could be exploited by the MCM.
3 Results and discussion
In the following, we evaluate the quality of UNIFAC-MCM by considering predictions of vapor–liquid equilibria (VLE), which is probably the most important field in which activity coefficients are applied. As basis for this evaluation, we have used all VLE data sets for binary mixtures from the Dortmund Data Bank (DDB)33–35 that comply with the following conditions:• both components of the mixture can be built from the first 50 main groups of UNIFAC;10
• the data set contains information on temperature, pressure, and composition of the liquid and vapor phase;
• the data set is labeled as ‘thermodynamically consistent’ in the DDB, i.e., it fulfills area and point-to-point test;36–38
• Antoine parameters for calculating the pure-component vapor pressure at the temperature of the VLE are available in the DDB for both components;
• the pressure is not higher than 10 bar to justify the assumption of an ideal gas phase.
In the present version of the DDB, such VLE data are available for 2246 distinct binary systems. We will call this complete set of binary systems ‘complete horizon’ in the following.
The VLE were predicted using extended Raoult's law assuming an ideal vapor phase and a pressure independence of the chemical potentials in the liquid phase:
| psi(T) xiγi(T, xi) = p yi | (4) |
For the calculations, the mole fractions xi in the liquid phase as well as either the pressure p (for isobaric data sets) or the temperature T (for isothermal data sets) were specified, the pure component vapor pressure psi was calculated with the Antoine equation using the parameters from the DDB, and the activity coefficients γi of the components in the liquid phase were predicted with UNIFAC-MCM. The mole fractions yi in the vapor phase and the pressure p (for isothermal data sets) or the temperature T (for isobaric data sets) were then calculated from the system of equations resulting from applying eqn (4) to both components. The results were compared to the experimental data from the DDB, with a focus on the gas phase mole fraction of the low-boiling component.
For comparison, the same calculations were also carried out with UNIFAC;10 albeit, this is only possible for a subset of 2068 systems from the complete horizon (‘UNIFAC horizon’). At a first glance, it may look disappointing that by using UNIFAC-MCM, with its substantially enlarged parameter table, only 178 additional systems for which data are available can be modeled. However, this is as expected: the lack of data on these systems has hindered the extension of the UNIFAC parameter table so far. Furthermore, we have also used the commercial version UNIFAC-TUC for comparison, which enabled predictions of VLE for 2237 of the studied systems (‘UNIFAC-TUC horizon’). We have included the results from UNIFAC-TUC in the comparison (even though it is not publicly available) for two reasons: firstly, it is the best available benchmark method and, secondly, it allows to evaluate the predictive performance of UNIFAC-MCM also on systems that can not be modeled by UNIFAC, which is the basis of UNIFAC-MCM.
The results are shown in Fig. 2, where the horizons in the three panels differ: in the left panel, it is the complete horizon, in the middle panel, it is the UNIFAC-TUC horizon, and in the right one, it is the smallest horizon, that of UNIFAC.10
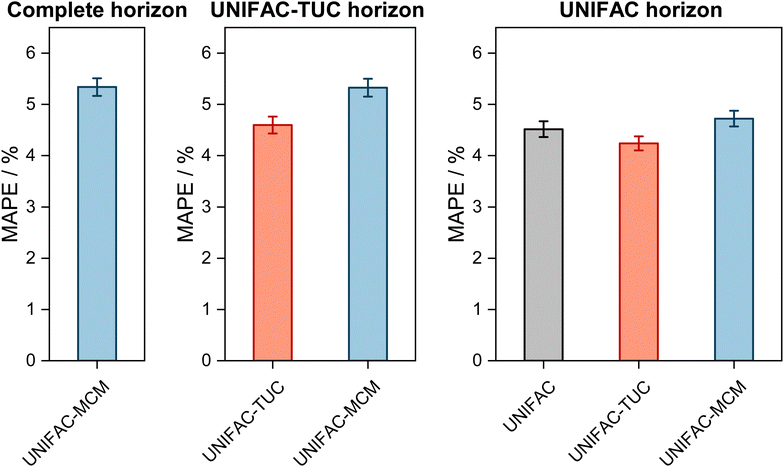 | ||
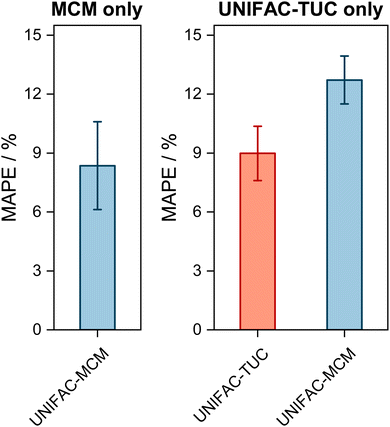
| Fig. 2 Mean Absolute Percentage Error (MAPE) of the predicted vapor-phase mole fraction of the low-boiling component in VLE with UNIFAC-MCM for the ‘complete horizon’ (2246 systems, left) and comparison to the commercial UNIFAC-TUC for the ‘UNIFAC-TUC horizon’ (2237 systems, middle), and to the public UNIFAC10 for the ‘UNIFAC horizon’ (2068 systems, right). Error bars denote standard errors of the means. | ||
The results obtained with UNIFAC-MCM on the complete horizon are shown in Fig. 2 (left), where the mean absolute percentage error (MAPE) in yi of the low-boiling component of the predictions with UNIFAC-MCM averaged over all 2246 systems is plotted, which was calculated by comparing the UNIFAC-MCM predictions system-wise to the respective experimental data from the DDB. As the results indicate, UNIFAC-MCM predicts the vapor-phase mole fractions for all 2246 studied binary systems with an average error of 5.3%, which is not much larger than the typical uncertainty of experimental data for vapor-phase mole fractions. The MAPE of UNIFAC-MCM in the pressure p, averaged over all isothermal data sets from the complete horizon, is 5.0 ± 0.2%; the MAPE in the absolute temperature T in K, averaged over all isobaric data sets from the complete horizon, is 0.48 ± 0.02%.
In the middle panel of Fig. 2, the performance of MCM-UNIFAC is compared to that of UNIFAC-TUC, and in the right panel, it is compared to UNIFAC10 as well as to UNIFAC-TUC. The highest accuracy among the three models is found for the commercial UNIFAC-TUC (MAPE of 4.6% on the UNIFAC-TUC horizon, cf. middle panel, and 4.2% on the UNIFAC horizon, cf. right panel), which is not surprising since a lot of effort has been put into refining its parameterization during the last decades. However, the scores of UNIFAC-MCM (MAPE of 5.3% on the UNIFAC-TUC horizon, cf. middle panel, and 4.7% on the UNIFAC horizon, cf. right panel) are only slightly worse than that of UNIFAC-TUC.
On the UNIFAC horizon, cf.Fig. 2 (right), the scores of UNIFAC-MCM (MAPE of 4.7%) and of the public UNIFAC (MAPE of 4.5%) are very similar. This demonstrates two things: first, that the additional flexibility of the UNIFAC model achieved by the inconsistent individual fitting of group-interaction parameters AGG′ and AG′G compared to the sole physical consideration of group-interaction energies UGG′ (including the like group-interaction energies UGG and UG′G′) is unnecessary; for the complete matrix of the considered 50 main groups of UNIFAC, there are 2450 distinct group-interaction parameters AGG′ and AG′G, but only 1275 distinct group-interaction energies UGG′ (including 50 like energies UGG). And second, the MCM, which is at the heart of UNIFAC-MCM, is able to capture the structure within the unlike group-interaction energies using six latent parameters for each main group.
It is interesting to also study the performance of UNIFAC-MCM and UNIFAC-TUC only for those systems that cannot be modeled with UNIFAC;10 this gives an impression of the performance of UNIFAC-MCM when applied for true predictions, namely for systems containing combinations of main groups for which no interaction parameters of UNIFAC are available, as it is unlikely that data on any of these systems were used in the development of UNIFAC,10 on which UNIFAC-MCM is based. In contrast, it may be assumed that basically all these additional VLE data were used for the development of UNIFAC-TUC, so that for UNIFAC-TUC, such a comparison shows basically only if the correlation of these additional data was successful. The respective results are presented in Fig. 3. Most of the systems within the complete horizon can be modeled not only with UNIFAC-MCM but also with UNIFAC-TUC. The few systems for which this is not the case, are treated separately in Fig. 3 (left panel).
The first message from Fig. 3 is that the deviations increase compared to the ones shown in Fig. 2, which holds both for UNIFAC-TUC and UNIFAC-MCM. Averaged over all systems that can be modeled by both models (but not by UNIFAC), cf.Fig. 3 (right), the MAPE for UNIFAC-TUC is now 9.0%, that for UNIFAC-MCM is 12.7%. However, considering that the results from Fig. 3 obtained with UNIFAC-MCM are bold predictions, while those from UNIFAC-TUC are basically only correlations, the difference between both methods is unexpectedly small.
Comparing the results from Fig. 3 with those from Fig. 2 is most informative when referring to Fig. 2 (right), where the UNIFAC horizon is shown, because it then gives an impression on the changes when carrying out the comparison for complementary data sets: the UNIFAC horizon, for which the results are shown in Fig. 2 (right), covers all systems that can also be modeled by the public UNIFAC; Fig. 3, on the other hand, shows the results for all remaining systems from our data set, i.e., for the ones that cannot be modeled by the public UNIFAC.
Carrying out this comparison for UNIFAC-TUC (for which the results are correlations in both cases) clearly shows that the systems studied in Fig. 3 are more difficult to describe than those studied in Fig. 2 (right). We are not going into the details of these additional difficulties, which can be related to different factors, including spotty and uncertain data (cf. also Fig. S3 in the ESI†) as well as to the fact that many of the respective systems contain components with special properties (highly halogenated or reactive components), which substantially complicates the accurate modeling with UNIFAC.
Hence, the results for UNIFAC-TUC indicate that most of the increase of the MAPE scores observed also for UNIFAC-MCM when going from Fig. 2 (right) to Fig. 3 is simply due to the increased difficulties in describing the data considered in Fig. 3, and, thus, cannot be attributed to a lack of predictive power. We only note here that the scope of the developed UNIFAC-MCM is much larger than we can demonstrate here, simply due to the fact that for many of the group-interaction parameters that can now be predicted, no experimental data for testing are available, cf. Fig. S3 in the ESI.† An alternative representation of the results of UNIFAC-MCM in the form of histograms is given in Fig. S4 in the ESI.†
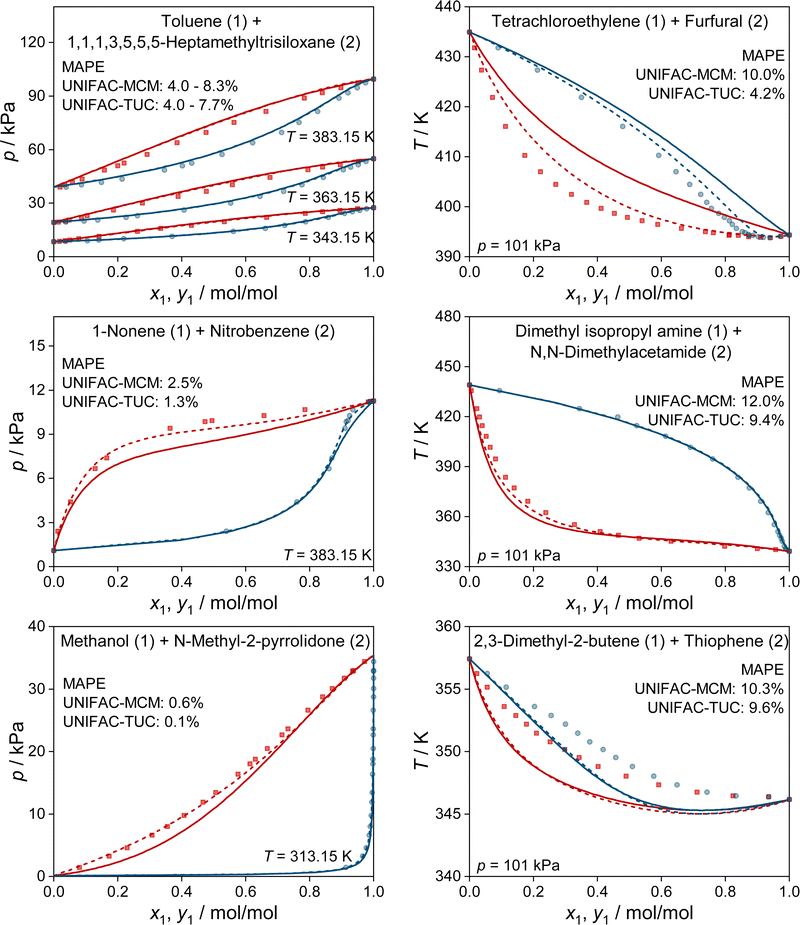
In Fig. 4, we show some typical examples for the prediction of vapor–liquid phase diagrams with UNIFAC-MCM and compare the results to those obtained with UNIFAC-TUC. Only systems that cannot be modeled by the public UNIFAC version were therefore chosen, such that the results of UNIFAC-MCM are true predictions. This is, again, not the case for UNIFAC-TUC, as the data shown in Fig. 4 were available for the development of the method. In all cases, UNIFAC-MCM represents the different types of phase behavior well.
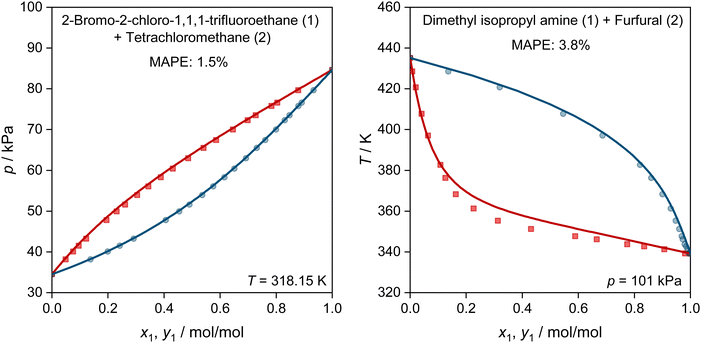
In Fig. 5, we show two further examples for the prediction of VLE phase diagrams with UNIFAC-MCM. The chosen systems can neither be modeled by the public UNIFAC, nor with the commercial UNIFAC-TUC due to missing group-interaction parameters in both models. We observe an almost perfect agreement of the predictions with UNIFAC-MCM and the experimental data, but note that we also find systems with poorer agreement, cf. Fig. S4 in the ESI.†
UNIFAC-MCM should in general be used in cases in which required group-interaction parameters of UNIFAC are missing, while in cases in which all parameters are available, we recommend using these. The reason is that UNIFAC-MCM is basically a derivate of UNIFAC, i.e., based on the available parameter tables, and it would only be by chance were it for certain systems better than its basis. However, we emphasize that the differences between UNIFAC and UNIFAC-MCM are not expected to be large, as shown in Fig. 2.
4 Conclusions
Group contribution methods for the prediction of thermophysical properties are highly important in chemical engineering. One of the most successful of these methods is UNIFAC. However, the applicability of UNIFAC is still substantially hampered by missing group-interaction parameters, which is in particular due to the lack of suitable mixture data for fitting the parameters. As a consequence, there are still significant gaps in the matrix in which these UNIFAC parameters are usually represented.In the present work, we present an approach to complete the group-interaction parameter set of UNIFAC using a matrix completion method (MCM) from machine learning. Our approach, called UNIFAC-MCM, was trained in a purely data-based manner solely on pseudo-data generated with UNIFAC, and approximately doubles the number of available group-interaction parameters.
We have evaluated the performance of UNIFAC-MCM for the prediction of vapor–liquid equilibria (VLE) of 2246 binary systems from the Dortmund Data Bank. This set can be divided into data that can be predicted with the public UNIFAC (2068 systems) and data for which this is not the case, but which can be predicted with the developed UNIFAC-MCM (169 systems). The latter set is comparatively small, as the missing groups in UNIFAC are rather uncommon ones, i.e., only present in components for which only few data have been measured.
Where a direct comparison is possible, UNIFAC and UNIFAC-MCM show a similar performance. This alone is astonishing since UNIFAC-MCM is based only on consistent group-interaction energies, whereas in UNIFAC the number of the parameters to describe the pairwise interactions has almost been doubled, simply to increase the flexibility, which is, however, not well founded in the physical lattice theory from which UNIFAC was derived. For the systems for which UNIFAC cannot be applied, the performance of UNIFAC-MCM is poorer but still acceptable, especially given the fact that this set contains basically only demanding systems, as also the commercial version UNIFAC-TUC, which we used for comparison here, shows significantly larger error scores.
This work has shown that working with consistent group-interaction energies is not only a feasible alternative to the common procedure of fitting UNIFAC parameters, but also a highly attractive one: a similar quality is obtained by a significantly smaller (approx. 50%) number of parameters, which promises a higher predictive performance and could be useful also for the fitting of new UNIFAC parameters in the future. The predicted parameters provided in this work might in general serve as valuable starting points for the future fitting of UNIFAC parameters to experimental data. In future work, it will be interesting to include further structural groups in the model, to transfer our approach to other group contribution methods for mixture properties, and to consider an end-to-end training, directly on experimental VLE data.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge financial support by Carl Zeiss Foundation in the frame of the project ‘Process Engineering 4.0’ and by Germany's Bundesministerium für Wirtschaft und Klimaschutz (BMWK) in the frame of the project ‘KEEN’.Notes and references
- D. S. Abrams and J. M. Prausnitz, AIChE J., 1975, 21, 116–128 CrossRef CAS.
- G. Maurer and J. Prausnitz, Fluid Phase Equilib., 1978, 2, 91–99 CrossRef CAS.
- H. Renon and J. M. Prausnitz, AIChE J., 1968, 14, 135–144 CrossRef CAS.
- A. Fredenslund, R. L. Jones and J. M. Prausnitz, AIChE J., 1975, 21, 1086–1099 CrossRef CAS.
- S. Skjold-Jorgensen, B. Kolbe, J. Gmehling and P. Rasmussen, Ind. Eng. Chem. Process Des. Dev., 1979, 18, 714–722 CrossRef.
- J. Gmehling, P. Rasmussen and A. Fredenslund, Ind. Eng. Chem. Process Des. Dev., 1982, 21, 118–127 CrossRef CAS.
- E. A. Macedo, U. Weidlich, J. Gmehling and P. Rasmussen, Ind. Eng. Chem. Process Des. Dev., 1983, 22, 676–678 CrossRef CAS.
- D. Tiegs, P. Rasmussen, J. Gmehling and A. Fredenslund, Ind. Eng. Chem. Res., 1987, 26, 159–161 CrossRef CAS.
- H. K. Hansen, P. Rasmussen, A. Fredenslund, M. Schiller and J. Gmehling, Ind. Eng. Chem. Res., 1991, 30, 2352–2355 CrossRef CAS.
- R. Wittig, J. Lohmann and J. Gmehling, Ind. Eng. Chem. Res., 2003, 42, 183–188 CrossRef CAS.
- T. Magnussen, P. Rasmussen and A. Fredenslund, Ind. Eng. Chem. Process Des. Dev., 1981, 20, 331–339 CrossRef CAS.
- G. Wienke and J. Gmehling, Toxicol. Environ. Chem., 1998, 65, 57–86 CrossRef CAS.
- W. Yan, M. Topphoff, C. Rose and J. Gmehling, Fluid Phase Equilib., 1999, 162, 97–113 CrossRef CAS.
- The UNIFAC Consortium, 2022, http://www.unifac.org.
- A. Fredenslund, J. Gmehling and P. Rasmussen, Vapor-liquid Equilibria using UNIFAC: a Group-contribution Method, Elsevier, 1977 Search PubMed.
- A. A. Bondi, Physical Properties of Molecular Crystals Liquids, and Glasses, Wiley, 1968 Search PubMed.
- A. Fredenslund, Vapor-liquid Equilibria using UNIFAC: a Group-contribution Method, Elsevier, 2012 Search PubMed.
- J. Gmehling, R. Wittig, J. Lohmann and R. Joh, Ind. Eng. Chem. Res., 2002, 41, 1678–1688 CrossRef CAS.
- B. Schmid, A. Schedemann and J. Gmehling, Ind. Eng. Chem. Res., 2014, 53, 3393–3405 CrossRef CAS.
- Y. Koren, R. Bell and C. Volinsky, Computer, 2009, 42, 30–37 Search PubMed.
- G. Takács, I. Pilászy, B. Németh and D. Tikk, IEEE Int. Conf. Data Min., 2008, 553–562 Search PubMed.
- F. Jirasek, R. Bamler, S. Fellenz, M. Bortz, M. Kloft, S. Mandt and H. Hasse, Chem. Sci., 2022, 13, 4854–4862 RSC.
- F. Jirasek, R. A. S. Alves, J. Damay, R. A. Vandermeulen, R. Bamler, M. Bortz, S. Mandt, M. Kloft and H. Hasse, J. Phys. Chem. Lett., 2020, 11, 981–985 CrossRef CAS PubMed.
- F. Jirasek, R. Bamler and S. Mandt, Chem. Commun., 2020, 56, 12407–12410 RSC.
- F. Jirasek and H. Hasse, Fluid Phase Equilib., 2021, 549, 113206 CrossRef CAS.
- J. Damay, F. Jirasek, M. Kloft, M. Bortz and H. Hasse, Ind. Eng. Chem. Res., 2021, 60, 14564–14578 CrossRef CAS.
- N. Hayer, F. Jirasek and H. Hasse, AIChE J., 2022, 68, e17753 CrossRef CAS.
- J. G. Rittig, K. B. Hicham, A. M. Schweidtmann, M. Dahmen and A. Mitsos, 2022, preprint, arXiv:2206.11776 DOI:10.48550/arXiv.2206.11776.
- E. I. S. Medina, S. Linke, M. Stoll and K. Sundmacher, Digital Discovery, 2022, 1, 216–225 RSC.
- B. Winter, C. Winter, J. Schilling and A. Bardow, Digital Discovery, 2022, 1, 859–869 RSC.
- R. Salakhutdinov and A. Mnih, Proceedings of the 25th International Conference on Machine Learning, 2008, pp. 880–887 Search PubMed.
- J. M. Prausnitz, F. Anderson and T. Anderson, Computer Calculations for Multicomponent Vapor-liquid and Liquid-liquid Equilibria, Prentice Hall, 1980 Search PubMed.
- U. Onken, J. Rarey-Nies and J. Gmehling, Int. J. Thermophys., 1989, 10, 739–747 CrossRef.
- J. Gmehling, Vak. Forsch. Prax., 2002, 14, 272–279 CrossRef CAS.
- Dortmund Data Bank (DDB), 2022, http://www.ddbst.com.
- O. Redlich and A. Kister, Ind. Eng. Chem., 1948, 40, 345–348 CrossRef.
- E. Herington, Nature, 1947, 160, 610–611 CrossRef CAS PubMed.
- H. C. Van Ness, S. M. Byer and R. E. Gibbs, AIChE J., 1973, 19, 238–244 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: UNIFAC equations, model details, additional results, completed UNIFAC parameter set. See DOI: https://doi.org/10.1039/d2cp04478a |
| ‡ For an N-component mixture, there are N2 – N asymmetric pair-interaction parameters of the A-type (the diagonal remains empty or is filled with zeros), while there are (N2 – N)/2 + N symmetric pair-interaction energies of the U-type (the diagonal is occupied by the pure-component energies, but only one of the triangular matrices has to be filled due to the symmetry). It is always possible to determine the A-parameters from the U-parameters, but not vice versa. |
| This journal is © the Owner Societies 2023 |