Character of intermolecular vibrations in the benzene–neon complex based on CCSD(T) and SAPT potential energy surfaces†
Leonid
Shirkov

Institute of Physics, Polish Academy of Sciences, Al. Lotników 32/46, 02-668 Warsaw, Poland. E-mail: leonid.shirkov@ifpan.edu.pl
First published on 21st November 2022
Abstract
The intermolecular potential energy surface of the benzene–neon complex is constructed using highly accurate electronic structure methods for the ground electronic state. The interaction energies have been calculated with the CCSD(T) (coupled cluster level including single and double excitations supplemented by triple excitation) method and symmetry-adapted perturbation theory based on the density functional and CCSD descriptions of monomer properties (DFT-SAPT and CCSD-SAPT) with augmented triple Dunning's basis set (aug-cc-pVTZ) supplemented by the midbond functions. The analytical PESs have been constructed using an analytical long-range part based on spherical multipole expansion and a short-range part based on many-body expansion. The potential is characterized by two symmetrically equivalent global minima located at the benzene C6 axis of symmetry and by local minima lying in the benzene plane on the axes connecting the benzene center of mass and the middle of CC bonds. The values of the equilibrium geometry parameters, the dissociation energy and vibrational energy have been extracted from these potentials and compared to their empirical counterparts derived previously from the microwave spectra. The complex is characterized by large-amplitude motion of the Ne atom which, however, can be studied with a theoretical approach with neglected tunneling motion through the monomer plane, when the lowest vibrational energy levels are considered.
1 Introduction
The complexes of aromatic molecules with rare gas atoms (AromRg) have been the subject of intensive research in the last few decades. Such interest is motivated by the fact that these complexes are exemplary models to study many phenomena at the microscopic level, for example, solvation and physisorption on surfaces,1–3 intramolecular vibrational redistribution (IVR) and vibrational predissociation (VP).4–6 The complexation of these complexes is mostly due to the domination of the dispersion component of the interaction energy and these complexes are considered as prototypical with dominating dispersion.Vast experimental data are available for AromRg, mostly involving Ar as the interaction partner. These complexes were studied by microwave spectroscopy (MW),7–11 one- and two-color resonance-enhanced two-photon ionization12–27 and stimulated Raman spectroscopic methods.28–31 The complexes with heavier rare gas atoms such as krypton and xenon were also studied by experiment.8,17,24,32,33
The experimental data available for complexes with the lighter Ne atom are relatively scarce. Previously, rotationally resolved spectra for the benzene–Ne (BzNe) complex were reported,8,12,23,33–36 but no direct measurement of intermolecular vibrations for the BzNe complex has been conducted by now. The other AromNe complexes such as pyrrole-Ne, pyridine-Ne, pentafluoropyridine-Ne and some others were also studied by different experimental methods,15,19,20,37–48 including the studies where intermolecular vibrations were measured. The experimental study of the intermolecular vibrations in AromNe complexes is more difficult when compared to the AromRg complexes with heavier Ar. This is because of lower dissociation energies and the higher cost of Ne gas. On the other hand, when a lighter atom than Ar is used such as Ne, the effect of large amplitude intermolecular motion of Ne is more visible in the infrared and microwave spectra. The dissociation energy D0 of AromNe is about three times less when compared to that of an analogous AromAr complex, and the equilibrium position of the Rg atom is closer to the aromatic ring by about 0.2 Å.
The theoretical study of molecular complexes requires the knowledge of potential energy surfaces (PESs). If the intramolecular motion of the monomer is neglected, then the potential is three-dimensional (3D) for AromRg complexes. Once the potential is known, it is possible not only to find the binding energy De and the equilibrium geometry of the complex, but also to calculate the dissociation energy D0 and the intermolecular rovibrational energy levels. Before the computer era, it was possible to use experimental data for the construction of an empirical potential. For example, empirical potentials that contain atom–atom terms of Lennard-Jones type were constructed,49,50 whose parameters can be tuned to reproduce experimental data.8,18,19,51 In order to confirm the accuracy of such potentials, the important physical quantities extracted from such potentials have to be compared to those calculated using a highly accurate ab initio potential or measured directly experimentally. One has to note that such calculations cannot be done as ‘blackbox’ and require a few steps and manual tuning of potentials in order to obtain reliable results.
Previously, the rotational spectra of benzene–Rg (BzRg) for Rg = Ne, Ar, Kr, and Xe were recorded and intermolecular motion were studied with a rovibrational Hamiltonian with empirical potentials derived from the MW spectra.8 The accuracy of the potentials has been already confirmed for Rg = Ar, Kr, and Xe by comparison with highly accurate ab initio potentials.52–55 It was shown that the lowest theoretical vibrational states up to 100 cm−1 agree within 1 cm−1 with their theoretical counterparts, while the empirical binding De and dissociation energies are overestimated by about 5%.
The previous theoretical study of the BzNe potential is rather poor compared to today's computational standards.56,57 The studies were limited to the calculation of potential in the vicinity of the global minimum using the Møller–Plesset perturbation theory (MP2). Then, the equilibrium geometry re, binding De and dissociation D0 energies as well as the stretching fundamental νz were calculated. MP2 was also used for the aniline–Ne complex,58 where a preliminary PES within rigid monomer approximation was reported, but also the coupling of the intermolecular bending mode with the inversion mode of the amino group of aniline was studied. The coupled cluster with single and double excitations including the connected triples theory [CCSD(T)]59 has been proven to be accurate for the series of complexes containing aromatic molecules with Rg atoms.53–55,60–65 The accuracy is confirmed by comparison with the experimental data, i.e., directly measured, or with the empirical one, i.e., derived from the potential constructed to reproduce the experimental data.
The goal of this work is the construction of an ab initio 3D PES for BzNe with all intermolecular degrees of freedom included. Then, this potential is applied to study the nuclear dynamics of the complex in the rigid monomer approximation. The binding, dissociation and vibrational energies extracted from the ab initio and available empirical potentials are compared. One can expect the complex BzNe to be floppier with larger amplitude vibrations when compared to other BzRg complexes with heavier Rg atoms. An open question if the employment of harmonic oscillator (HO) quantum numbers for the assignment of the vibrational states is applicable for BzNe as it had been done for the BzRg complexes with heavier Rg atoms.53–55
Additionally, the accuracy of the symmetry-adapted perturbation theory based on the density functional description of monomer properties (DFT-SAPT) for BzNe was studied,66–68 which was found to be very accurate for the series of AromAr complexes.64,69 However, it is not clear if DFT-SAPT will be that accurate for AromNe complexes. The DFT-SAPT calculations are accompanied by the benchmark CCSD-SAPT calculations,70 which will help to reveal possible inaccuracies of the DFT-SAPT terms.
The organization of the article is as follows. The computational methods used are introduced in Section 2, a description of the analytical potential is given in Section 3, the vibrational pattern is analyzed in Section 4, and a summary in Section 5.
2 Electronic structure methods
2.1 Geometry and intermolecular coordinates
The position of Ne with respect to the benzene monomer can be described by vector r in Cartesian (x,y,z) or spherical coordinates (r,θ,ϕ). The origin of the Cartesian coordinate system was placed at the center of the benzene monomer. The z-axis is the C6 symmetry axis of benzene, the x-axis goes through two carbon nuclei and y-axis is perpendicular to two of the six C–C bonds. In order to build an analytical potential based on electronic structure calculations, one has to calculate the interaction energy Eint at a finite set of positions of the Ne atom. One can expect that the position of the stationary points of BzNe is analogous to other BzRg complexes.53–55 Such potentials are characterized by the global minima Mz below and above the center of the monomer, and six symmetrically equivalent local minima My in the monomer plane. All the minima are connected to each other by minimum energy paths (MEPs) that go through the symmetrically equivalent saddle points – six in the monomer plane denoted as Sx and six above and below it denoted as Syz.In such a way, we first calculated Eint at a few Ne positions in the vicinity of the critical points Mz, My and Sx using different methods. That allowed us to find the accurate values of the coordinates and Eint at these points using local polynomial interpolation. The SAPT components are compared at one Ne position at ze = 3.32 Å in close vicinity of the global minimum Mz. This data is summarized in Tables 1 and 2 and the details of the electronic structure calculations are given in Sections 2.2 and 2.3.
| Method | Basis | M z (r = ze,0°,0°) | M y (r,90°,90°) | S x (r,90°,0°) |
|---|---|---|---|---|
| a M y is the saddle point in the MW potential. | ||||
| DFT-SAPT | avDz+ | (3.378, −136.2) | (4.849, −77.2) | (5.417, −40.4) |
| avTz+ | (3.359, −142.5) | (4.816, −83.2) | (5.406, −43.7) | |
| avQz+ | (3.354, −144.2) | (4.804, −86.4) | (5.385, −45.7) | |
| DFT-SAPT + δ(HF) | avDz+ | (3.325, −146.4) | (4.821, −80.7) | (5.390, −41.7) |
| avTz+ | (3.306, −153.3) | (4.783, −86.9) | (5.371, −45.8) | |
| avQz+ | (3.300, −155.4) | (4.772, −90.3) | (5.385, −48.0) | |
| DFT/CCSD-SAPT | avDz+ | (3.389, −139.5) | (4.831, −84.7) | (5.378, −48.5) |
| avTz+ | (3.352, −146.1) | (4.778, −91.6) | (5.345, −49.3) | |
| avQz+ | (3.334, −149.6) | (4.746, −96.5) | (5.311, −52.3) | |
| CCSD(T)/FC | avDz+ | (3.334, −152.5) | (4.759, −90.9) | (5.340, −51.5) |
| avTz+ | (3.331, −149.0) | (4.753, −91.2) | (5.325, −48.9) | |
| avQz+ | (3.320, −148.1) | (4.740, −93.0) | (5.307, −50.2) | |
| CCSD(T)/AE | acvQz+ | (3.318, −148.3) | (4.740, −93.0) | (5.306, −50.2) |
| MW | (3.299, −151.0) | (4.874, −50.4)a | (5.035, −42.6) | |
| Method | Basis | E (1)elst | E (1)ex | E (2)ind | E (2)ex-ind | E (1,2)non-disp | E (2)disp | E (2)ex-disp | δ(HF) | E 1 + E2 | E int |
|---|---|---|---|---|---|---|---|---|---|---|---|
| a The values with cumulant corrections are 235.51 and 84.73, respectively. b Found with DFT-SAPT dispersion and exhange-dispersion. | |||||||||||
| DFT-SAPT | avDz+ | −72.35 | 220.41 | −80.79 | 81.47 | 148.73 | −307.89 | 24.16 | −11.36 | −134.99 | −146.35 |
| avTz+ | −70.13 | 220.62 | −86.69 | 87.75 | 151.55 | −318.63 | 25.18 | −11.33 | −141.90 | −153.22 | |
| avQz+ | −68.37 | 220.69 | −85.73 | 86.82 | 153.41 | −322.94 | 25.78 | −11.47 | −143.75 | −155.23 | |
| CCSD-SAPT | avDz+ | −88.82 | 235.19 | −85.13 | 84.80 | 146.04 | — | — | −137.69b | ||
| avTz+ | −74.05 | 222.10a | −85.21 | 84.85a | 147.69 | — | — | −145.76b | |||
| avQz+ | −68.85 | 216.82 | −81.80 | 81.43 | 147.59 | — | — | −149.57b | |||
| CCSD(T) | avDz+ | −152.44 | |||||||||
| avTz+ | −148.94 | ||||||||||
| avQz+ | −148.09 | ||||||||||
We used the same benzene geometry as previously for BzKr and BzXe – the bond lengths were 1.3915 Å for CC and 1.080 Å for CH bonds.71
2.2 Supermolecular calculations
The conventional CCSD(T) with frozen core (FC) approximation with the counterpoise correction taken into account72 was used for ab initio calculations together with the Dunning's basis sets aug-cc-pVXZ (avXz, X = D, T, and Q).73,74 The basis sets were supplemented with 3s3p2d1f1g midbond functions.75,76 The exponents for the midbond functions are 0.9, 0.3, and 0.1 for s and p functions, 0.6 and 0.2 for d functions, and 0.3 for f and 0.25 for g functions. We use the notations avXz+ for such basis sets with midbonds. The basis set dependence of the coordinates of the critical points and Eint at these points is given in Table 1. As one can see, the basis set extension gives lower values of De = −Eint and the equilibrium coordinates ze.In order to check the core effects on Eint, we calculated a few single point energies with all orbitals correlated (AE) for a limited number of configurations in the vicinity of the critical points with the appropriate additional tight core-correlated functions in the basis set aug-cc-pCVTZ+ (acvTz+). Table 1 lists the results in acvQz+ basis sets that were estimated using the following formula:
| EAEint(avcQz+) = EFCint(avQz+) + (EAEint(avcTz+) − EFCint(avcTz+)). | (1) |
The results given in Table 1 suggest that the good compromise between accuracy and computation cost would be the FC CCSD(T)/avTz+ level of theory. We then used it for the calculation of Eint at around 300 positions of the Ne atom including the short-range and long-range regions up to r = 15.0 Å. The density of the grid was taken higher in the regions with high energy gradients of the potential well and in the vicinity of the global minimum Mz.
2.3 SAPT calculations
The general form of Eint decomposed into energy components within the SAPT theory is as follows:66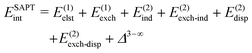 | (2) |
In this work, we used the same variety of DFT-SAPT as previously for the series of AromAr complexes.64,69 This version of DFT-SAPT employs the density fitting approximation with LPBE0ac exchange–correlation functional and adiabatic local-density approximation (ALDA) kernel,79,80 and gradient regulated asymptotic correction (AC) with Leeuwen and Baerends XC potential (GR-LB).81 The localized Hartree–Fock exchange part of Sala and Görling82 is used instead of the Hartree–Fock exchange of the PBE0 functional in this approach. The following values of the AC were taken (a.u.): 0.200 for Ne and 0.072 for benzene. These corrections were calculated as the difference between negative LPBE0 HOMO energies and the PBE0 ionization potentials. The orbitals basis sets avXz (X = D,T,Q) were used for these calculations. The density-fitting required the auxiliary basis sets – avXz-jkfit and avXz-mp2fit for SCF and response SAPT calculations, respectively.83,84 The dimer-centered basis was supplemented by 3s3p2d1f1g midbond functions with the same exponents as used for CCSD(T) calculations. The midbond functions for the auxiliary basis sets at midbond were taken as 5s5p5d4f3g with the exponents 1.8, 1.2, 0.6, 0.4 and 0.2 for s, p and d, 1.5, 0.9, 0.5 and 0.3 for f, and 1.5, 0.9 and 0.3 for g functions.
The SAPT components can be also calculated using CCSD properties based on the expectation theory,85–89 XCCSD. This method is considered as more accurate than the DFT-SAPT, but more expensive computationally, especially for the dispersion terms. We were able to calculate only the non-dispersion SAPT(CCSD) terms for BzNe. The exchange terms found with XCCSD include two parts, the larger noncumulant and much smaller cumulant corrections.
Table 2 contains the detailed comparison of the basis set dependence of the DFT-SAPT and CCSD-SAPT energies at a point ze = 3.32 Å close to the equilibrium configuration. It also contains the comparison of the total SAPT energies to the CCSD(T) benchmarks. Analysis of the SAPT results reveals that not all the terms can be considered as converged. However, the sum of the non-dispersion terms E(1,2)non-disp seems to be close to the convergence limit thanks to the cancellation of terms of different signs, at least for the CCSD terms. When compared to the CCSD(T) values, the DFT-SAPT yields underestimated values of |Eint| if only the first- and the second-terms are considered, and overestimated if the term δ(HF) is taken into account. However, E(1,2)non-disp(CCSD) taken with DFT-SAPT E(2)disp and E(2)exch-disp gives much better agreement for Eint found with CCSD(T) in the vicinity of the global minimum. Therefore, we used this hybrid DFT-CCSD-SAPT approach to calculate the energies at the same larger set of Ne positions as used for CCSD(T) for the construction of an analytical potential.
The interaction energy Eint in the long-range region of weakly bound complexes can be also reproduced using only the properties of single monomers such as multipole moments and static/polarizabilities as explained in Section 3. It is convenient to use the notation of spherical functions for the multipole moments and Qlm and polarizabilities 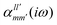 .90 We used two approaches to calculate these quantities, compatible with the dispersion and induction energies found with CCSD-SAPT and DFT-SAPT, XCCSD, and DFT response, respectively. We employed the avQz basis set for benzene and a triply augmented tav6z basis set was used for the Ne atom. We have to note that the values of DFT response polarizabilities of Ne were found without density-fitting approximation. The polarizabilities were calculated up to hexadecapole-hexadecapole terms, i.e. the
.90 We used two approaches to calculate these quantities, compatible with the dispersion and induction energies found with CCSD-SAPT and DFT-SAPT, XCCSD, and DFT response, respectively. We employed the avQz basis set for benzene and a triply augmented tav6z basis set was used for the Ne atom. We have to note that the values of DFT response polarizabilities of Ne were found without density-fitting approximation. The polarizabilities were calculated up to hexadecapole-hexadecapole terms, i.e. the 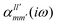 with l, l′ up to 4, and the value of multipole moments for benzene up to hexadecapole terms (l = 4).
with l, l′ up to 4, and the value of multipole moments for benzene up to hexadecapole terms (l = 4).
Molpro software package was used for all the electronic structure calculations.91 The calculated SAPT and CCSD(T) energy values and the monomer properties are available in the ESI.†
3 Analytical PES
The calculated single-point CCSD(T) and SAPT energies have been employed to reproduce an analytical potential whose general form can be written as follows:| V(r) = fsh(r)Vsh(r) + fln(r)Vln(r). | (3) |
Both the short-range Vsh(r) and the long-range Vln(r) parts of the potential in eqn (3) are multiplied by damping functions defined as fln(r) = (1 + e−γ(r−r0)/r)−1 and fsh(r) = (1 + eγ(r−r0)/r)−1 to provide the correct asymptotics of the potential at r → 0 and r → ∞.
The short-range part Vsh(r) was taken in the same many-body form as before for other BzRg complexes54,55
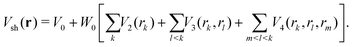 | (4) |
The term rk defines the distance between Ne and the kth atom of benzene. The two-body terms Vk are defined as follows:
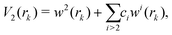 | (5) |
The three-body terms are defined in a similar manner,
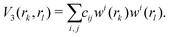 | (6) |
In order to describe the long-range part of the potential, it is convenient to use the spherical multipole series with the expansion coefficients Cl,mn,92,93 which has the following form in case of a non-linear molecule and an atom
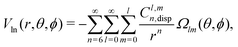 | (7) |
The set of the long-range Cl,mn coefficients can be found by fitting the calculated Eint to the functional form eqn (7). In such a way, we took the Eint for r ≥ 8 Å and found the fitted values of Cl,mn. These coefficients reproduce ab initio Eint with root mean square error (rmse) of an order of 0.001 cm−1.
There is another way to calculate the coefficients from the first principles using the calculated monomer properties – multipole moments and static/dynamic polarizabilities of the monomer. The approach described in Refs. 92 and 93 had been implemented in the POLCOR package.94 We used this software and the calculated monomer properties to obtain the sets of Cl,mn. Since the Ne atom does not have a permanent dipole moment, Cl,mn includes only the dispersion and inductions terms Cl,mn = Cl,mn,disp + Cl,mn,ind. The dispersion contribution is much larger than the induction one in the case of AromRg complexes. Coefficients found with such a method are compatible with SAPT E(2)disp and E(2)ind in the long-range region. The leading Cl,mn coefficients found by fitting to the calculated ab initio Eint and those found from the first principles are given in Table 3. As one can see, there is a very good agreement between the values found using completely different approaches.
| CCSD(T) | XCCSD | DFT resp. | |
|---|---|---|---|
| C 0,06 (×102) | 0.932 | 1.021 | 0.986 |
| C 2,06 (×101) | −2.622 | −2.995 | −2.859 |
| C 0,08 (×103) | 4.793 | 6.535 | 6.517 |
| C 2,08 (×104) | −1.440 | −1.705 | −1.698 |
The next stage of constructing an analytical potential included the calculation of the parameters given in eqn (4). The long-range part was kept fixed and the parameters were found using a non-linear optimization algorithm. We used the fitted Cl,mn coefficients for the CCSD(T) potential and calculated from the first principle for the SAPT one. We have to note that Eint extracted from the DFT response set of the coefficients Cl,mn is not exactly asymptotically equivalent to the DFT-SAPT dispersion energy, because different basis sets were used for the calculation of the monomer properties and for the SAPT energies. The same concerns XCCSD induction energy. However, the difference found between these two approaches is negligible. The final version of the fitted analytical potentials has 39 parameters γ, r0, ci and cij not counting the fixed Cl,mn, and reproduces Eint with rmse equal to 0.2 cm−1 in the energy range (−De, 100 cm−1) for both CCSD(T) and SAPT potentials. The higher energies up to 1000 cm−1 were also used in the fit with the lower weighting coefficients.
The isosurfaces of the CCSD(T) potential are presented in Fig. 1. The topology of the BzNe complex is typical for BzRg complexes with heavier Rg atoms. The potential is almost isotropic in the small vicinity of the global minimum Mz and becomes anisotropic when the Rg atom approaches the Syz saddle point. Two kinds of saddle points, Sx and Syz connect the minima Mz and My through the minimum energy path (MEP) shown as the dotted lines.
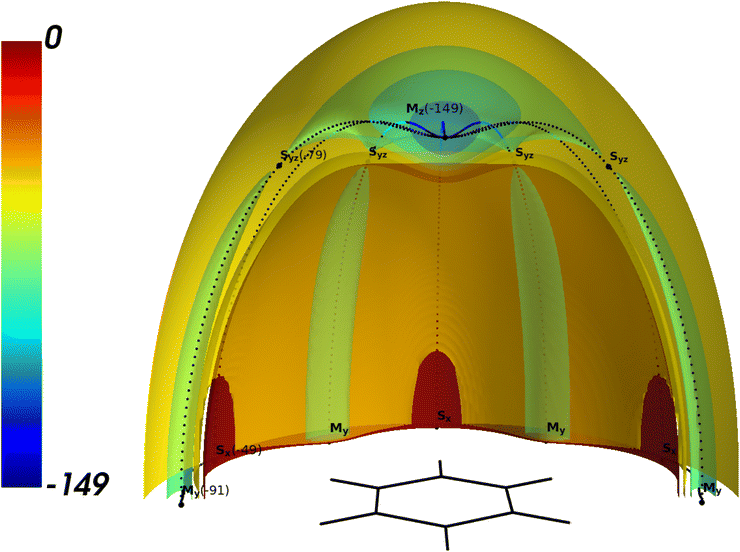 | ||
Fig. 1 3D the cut of the isopotential surfaces for BzNe for x > 0, z > 0. The energy values are in cm−1. The scale of the space coordinates is x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) y y![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) z = 2 z = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. 1. | ||
Similar to the other studied BzRg complexes, there is a potential barrier at Syz, which is equal to 70 cm−1 for BzNe. This value is 114 cm−1 smaller than for BzAr, for which it was proven that the tunneling motion of Ar between the minima Mz could be neglected for the lowest states localized around it.52 Therefore, one can expect stronger delocalization of the vibrational states for BzNe when compared to the BzRg complexes with heavier Rg atoms.
The ESI† contains the full sets of the long-range coefficients Cl,mn and a Python program for the calculation of the potential energy values at a given position of Ne for both of the potentials.
4 van der Waals vibrational states
In order to check if there is no physically meaningful splitting of the vibrational levels due to the ring-plane crossing, we employed two theoretical approaches. Within the first one, the motion of the Rg atom is described in Cartesian coordinates95 with neglected tunneling motion through the monomer plane. Such an approach was proved to be accurate for the series of AromRg complexes.54,55,64,65 However, none of these studies included AromNe complexes. Previous results for AromNe19,51 complexes employing the DVR method did not reveal tunneling motion for the lowest vibrational energies. Nevertheless, the results obtained with the first program were compared to another approach that uses spherical coordinates and describes the motion of an Rg atom in the whole space.8,55 Both approaches gave very close results for vibrational levels up to approximately 51 cm−1 above the ground state. The vibrational basis set was taken large enough to achieve the convergence below 0.01 cm−1 for these lowers levels. The splitting due to the ring-plane crossing was of order 10−5 cm−1 for the lowest states, which is below any available spectroscopic measurement accuracy.We will attempt to use the quantum numbers (ns,nb,l) of HO for the assignment of the lowest vibrational levels. For anharmonic motion, the stretching ns and the bending nb numbers are approximate. They describe the number of nodes of the vibrational wavefunction (WF) along the stretching z coordinate and bending angle θ, respectively. The vibrational angular momentum quantum number l is a good one if the potential is isotropic. However, unlike for heavier BzRg complexes, the part of the space, where the potential of BzNe is almost isotropic, is relatively less, because the saddle point Syz is located closer to the global Mz point than for the other BzRg. We will also employ an alternative set of quantum numbers vl = 2nb + l to describe the bending motion, which is convenient to describe the degenerate bending modes for 2D HO.
Besides the graphical analysis of WF, we will use a few additional quantities for the assignment. In particular, we will use the quantities like the mean values 〈q〉 and the amplitudes 〈Δq〉 = (〈q2〉 − 〈q〉2)1/2 of the vibrational Cartesian coordinates (x,y,z). It is convenient to use the quantities involving bending coordinate 〈ρ〉 = 〈Δρ〉 = 〈x2 + y2〉1/2, and the stretching one, 〈Δz〉 and 〈z〉. Additionally, the mean value of the vibrational angular momentum 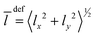 of Ne atoms will be used to identify the degenerate states. When the tunneling motion is neglected, one can use the C6v group to label the lowest states. For this symmetry, the states with l > 0 are degenerate, and the states with l = 3k are split as it takes place e.g. for (0 0 3)+ and (0 0 3)−.
of Ne atoms will be used to identify the degenerate states. When the tunneling motion is neglected, one can use the C6v group to label the lowest states. For this symmetry, the states with l > 0 are degenerate, and the states with l = 3k are split as it takes place e.g. for (0 0 3)+ and (0 0 3)−.
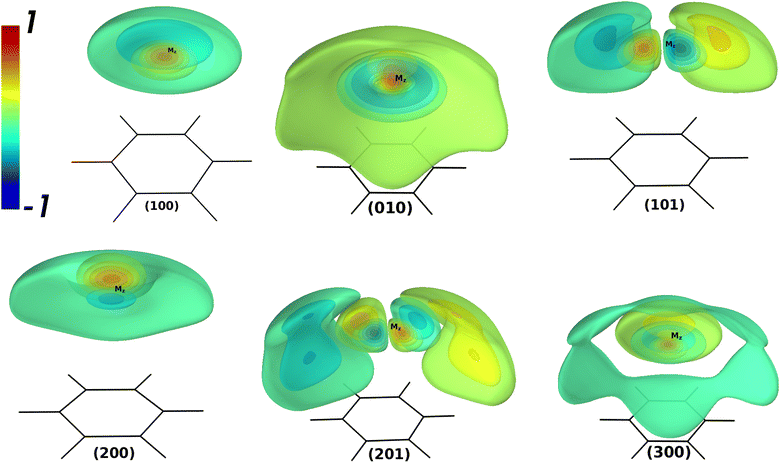
Table 4 contains the calculated vibrational energies up to 51 cm−1 above the ground state were found from the theoretical CCSD(T)/SAPT and empirical PESs. The vibrational 3D isosurfaces of the WF from the CCSD(T) potential for the selected states are shown in Fig. 2. The group of vibrational energies with the same number N = ns + 2nb + l are close in energy and called polyads. The vibrational energies found in the theoretical potentials exhibit completely different patterns than their empirical counterpart. Thus, the empirical PES is highly isotropical due to the absence of the saddle point Syz. Therefore, one can expect a good agreement between the empirical and CCSD(T)/SAPT only for the lowest vibrational energies. Indeed, the agreement is good up to the 2nd polyad. For the 3d polyad, the order of the states found from the empirical potential changes when compared to CCSD(T)/SAPT ones, and intermode mixing is present to a much less extent. Therefore, the empirical vibrational energies can not be considered as the benchmark for the theoretical values like in the case of AromRg with heavier Rg atoms.54,55,64 In contrast, the quantities extracted from the CCSD(T) PES can serve as the benchmark.
![[l with combining macron]](https://www.rsc.org/images/entities/i_char_006c_0304.gif) ≡ 〈
≡ 〈![[l with combining circumflex]](https://www.rsc.org/images/entities/i_char_006c_0302.gif) z2〉1/2 are given in ħ units found from the CCSD(T) potential
z2〉1/2 are given in ħ units found from the CCSD(T) potential
| n | N | Γ 6v | n s n b l | n s v l | Empir. | CCSD(T) | SAPT | 〈z〉 | 〈Δz〉 | 〈ρ〉 |
![[l with combining macron]](https://www.rsc.org/images/entities/i_char_006c_0304.gif)
|
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | A 1 | 000 | 000 | 42.5 | 43.1 | 44.1 | 3.447 | 0.181 | 0.567 | 0.002 |
| 1 | 1 | E 1 | 001 | 010 | 20.1 | 20.3 | 21.1 | 3.496 | 0.190 | 0.909 | 1.000 |
| 2 | A 1 | 100 | 100 | 25.8 | 26.1 | 25.9 | 3.564 | 0.279 | 0.955 | 0.024 | |
| 3 | 2 | E 2 | 002 | 020 | 36.8 | 36.5 | 37.6 | 3.529 | 0.205 | 1.324 | 2.001 |
| 4 | E 1 | 101 | 111 | 40.2 | 39.2 | 39.7 | 3.541 | 0.268 | 1.577 | 1.014 | |
| 5 | A 1 | 200 | 200 | 40.5 | 39.3 | 39.7 | 3.549 | 0.271 | 1.410 | 0.163 | |
| 6 | A 1 | 010 | 020 | 47.2 | 45.9 | 46.2 | 3.496 | 0.365 | 1.925 | 0.531 | |
| 7 | 3 | B 1 | 003+ | 03+3 | 50.1 | 47.2 | 47.9 | 3.428 | 0.310 | 2.174 | 3.023 |
| 8 | E 2 | 102 | 122 | 52.3 | 47.9 | 48.1 | 3.342 | 0.350 | 2.481 | 2.183 | |
| 9 | B 2 | 003− | 03−3 | 50.6 | 48.4 | 49.3 | 3.504 | 0.249 | 1.899 | 3.006 | |
| 10 | E 1 | 201 | 211 | 54.1 | 48.6 | 48.4 | 3.288 | 0.388 | 2.619 | 1.450 | |
| 11 | A 1 | 300 | 300 | 55.6 | 50.6 | 49.9 | 3.371 | 0.506 | 2.410 | 1.167 | |
| 12 | E 1 | 011 | 031 | 60.0 | 52.8 | 52.8 | 3.153 | 0.413 | 2.847 | 3.126 |
Analysis of the theoretical vibrational energies revealed the following. The shape of (1 0 0), which is the stretching fundamental, is quite regular for this state. However, it has a non-zero value of ![[l with combining macron]](https://www.rsc.org/images/entities/i_char_006c_0304.gif) and a large value of 〈ρ〉. The state (1 0 1) is also easily identifiable and is similar to the states of the assignment for the BzRg complexes with heavier Rg atoms, though much more delocalized around the global minimum Mz. The stretching overtone (2 0 0) reveals only one node along the z coordinate and exhibits a tendency to form a very flat node along the bending coordinate ρ. The value of
and a large value of 〈ρ〉. The state (1 0 1) is also easily identifiable and is similar to the states of the assignment for the BzRg complexes with heavier Rg atoms, though much more delocalized around the global minimum Mz. The stretching overtone (2 0 0) reveals only one node along the z coordinate and exhibits a tendency to form a very flat node along the bending coordinate ρ. The value of ![[l with combining macron]](https://www.rsc.org/images/entities/i_char_006c_0304.gif) = 0.055 ħ for this state for the empirical potential, which is three times as much for the CCSD(T) and SAPT ones. The state classified as (0 1 0) is strongly delocalized and has the value of 〈Δz〉 larger than for (2 0 0). The state (2 0 1) has still a recognizable pattern of the WF shape, though has the value of
= 0.055 ħ for this state for the empirical potential, which is three times as much for the CCSD(T) and SAPT ones. The state classified as (0 1 0) is strongly delocalized and has the value of 〈Δz〉 larger than for (2 0 0). The state (2 0 1) has still a recognizable pattern of the WF shape, though has the value of ![[l with combining macron]](https://www.rsc.org/images/entities/i_char_006c_0304.gif) = 1.450 ħ. The second stretching overtone (3 0 0) also has the value of
= 1.450 ħ. The second stretching overtone (3 0 0) also has the value of ![[l with combining macron]](https://www.rsc.org/images/entities/i_char_006c_0304.gif) > 0 typical for the states with excited bending modes. For higher states, the irregular behavior becomes more noticeable and the classification of the vibrational states in terms of the HO oscillator becomes meaningless. The vibrational energy levels found with the hybrid SAPT potential differ from the CCSD(T) benchmark within 1 cm−1 while the order of states is different for the 3d polyad.
> 0 typical for the states with excited bending modes. For higher states, the irregular behavior becomes more noticeable and the classification of the vibrational states in terms of the HO oscillator becomes meaningless. The vibrational energy levels found with the hybrid SAPT potential differ from the CCSD(T) benchmark within 1 cm−1 while the order of states is different for the 3d polyad.
The study of the higher states higher than 51 cm−1 above the ground state will be presented in a separate article.
5 Conclusions
We have presented the first detailed study of the AromNe complex based on CCSD(T) and SAPT potentials. We chose the prototypical BzNe complex for which the empirical potential derived from the MW spectra was used for the comparison. Besides that, we have shown that the DFT-SAPT approach underestimates the potential depth by about 4 cm−1 when used without the residual term δ(HF) and overestimates by 7 cm−1 if used with this term. However, a hybrid SAPT approach in which the non-dispersion terms are calculated with the CCSD-SAPT level and the dispersion ones with DFT-SAPT gives much better agreement with the CCSD(T) benchmark of Eint in the vicinity of the global minimum.We combined two analytical forms for the construction of an analytical potential – the many-body form for the short-range part, and the long-range part based on spherical multipole expansion. We then used the fitted Cl,mn coefficients for the CCSD(T) PES and found from the first principles for the SAPT PES, which reproduce E(2)ind and E(2)disp asymptotically in the long-range region.
The constructed theoretical potentials have been used to study intermolecular vibrational energies. It has been proved that there is no physically meaningful splitting of the lowest vibrational energy level due to ring-plane crossings of the Ne atom. Even the lowest vibrational states are characterized by large amplitude motion and strong intermode mixing which makes their assignment difficult. We attempted to label the lowest vibrational states using the 2D HO model, which was possible for the states up to the 3d polyad. The existing empirical potential derived from the MW spectra was accurate only for the lowest vibrational states up to the 2nd polyad. This can be explained by the simple analytical form of this potential which does not take into account the anisotropy of the potential in the correct form, which is important for the higher vibrational states.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The author thanks the PL-GRID project for granting access to their computational resources and the PL-GRID team for helpful software support. Professor Jan Makarewicz is acknowledged for stimulating the author's interest in the studied complex.Notes and references
- M. Y. Hahn and R. L. Whetten, Phys. Rev. Lett., 1988, 61, 1190–1193 CrossRef CAS PubMed.
- S. Leutwyler and J. Boesiger, Chem. Rev., 1990, 90, 489–507 CrossRef CAS.
- M. Schmidt, M. Mons and J. L. Calvé, Chem. Phys. Lett., 1991, 177, 371–379 CrossRef CAS.
- S. H. Kable, J. W. Thoman and A. E. W. Knight, J. Chem. Phys., 1988, 88, 4748–4764 CrossRef CAS.
- B. A. Jacobson, S. Humphrey and S. A. Rice, J. Chem. Phys., 1988, 89, 5624–5641 CrossRef CAS.
- P. M. Weber and S. A. Rice, J. Chem. Phys., 1988, 88, 6120–6133 CrossRef CAS.
- T. Brupbacher and A. Bauder, Chem. Phys. Lett., 1990, 173, 435–438 CrossRef CAS.
- T. Brupbacher, J. Makarewicz and A. Bauder, J. Chem. Phys., 1994, 101, 9736–9746 CrossRef CAS.
- R. M. Spycher, D. Petitprez, F. L. Bettens and A. Bauder, J. Chem. Phys., 1994, 98, 11863–11869 CrossRef CAS.
- R. Spycher, L. Hausherr-Primo, G. Grassi and A. Bauder, J. Mol. Struc., 1995, 351, 7–17 CrossRef CAS.
- W. Caminati, S. Melandri, A. Millemaggi and P. G. Favero, Chem. Phys. Lett., 1998, 294, 377–380 CrossRef CAS.
- T. A. Stephenson and S. A. Rice, J. Chem. Phys., 1984, 81, 1083–1101 CrossRef CAS.
- T. Weber, E. Riedle and H. J. Neusser, Z. Phys. D: At., Mol. Clusters, 1991, 20, 43–46 CrossRef CAS.
- T. Troxler and S. Leutwyler, J. Chem. Phys., 1991, 95, 4010–4023 CrossRef CAS.
- N. Ben-Horin, U. Even, J. Jortner and S. Leutwyler, J. Chem. Phys., 1992, 97, 5296–5315 CrossRef CAS.
- T. Troxler and S. Leutwyler, J. Chem. Phys., 1993, 99, 4363–4378 CrossRef CAS.
- H. Krause and H. J. Neusser, J. Chem. Phys., 1993, 99, 6278–6286 CrossRef CAS.
- M. Mandziuk, Z. Bačić, T. Droz and S. Leutwyler, J. Chem. Phys., 1994, 100, 52–62 CrossRef CAS.
- T. Droz, T. Bürgi and S. Leutwyler, J. Chem. Phys., 1995, 103, 4035–4045 CrossRef CAS.
- M. Becucci, G. Pietraperzia, N. Lakin, E. Castellucci and P. Bréchignac, Chem. Phys. Lett., 1996, 260, 87–94 CrossRef CAS.
- M. Mons, A. Courty, M. Schmidt, J. L. Calvé, F. Piuzzi and I. Dimicoli, J. Chem. Phys., 1997, 106, 1676–1686 CrossRef CAS.
- A. Bach, S. Leutwyler, D. Sabo and Z. Bačić, J. Chem. Phys., 1997, 107, 8781–8793 CrossRef CAS.
- K. Siglow, R. Neuhauser and H. J. Neusser, Chem. Phys. Lett., 1998, 293, 19–25 CrossRef CAS.
- K. Siglow, R. Neuhauser and H. J. Neusser, J. Chem. Phys., 1999, 110, 5589–5599 CrossRef CAS.
- U. Even, J. Jortner, D. Noy, N. Lavie and C. Cossart-Magos, J. Chem. Phys., 2000, 112, 8068–8071 CrossRef CAS.
- C. Kang, J. T. Yi and D. W. Pratt, J. Chem. Phys., 2005, 123, 094306 CrossRef PubMed.
- M. Hayashi and Y. Ohshima, Chem. Rev., 2013, 419, 131–137 CAS.
- V. A. Venturo, P. M. Maxton and P. M. Felker, Chem. Phys. Lett., 1992, 198, 628–636 CrossRef CAS.
- V. A. Venturo and P. M. Felker, J. Chem. Phys., 1993, 97, 4882–4886 CrossRef CAS.
- R. Neuhauser, K. Siglow and H. J. Neusser, Phys. Rev. Lett., 1998, 80, 5089–5092 CrossRef CAS.
- R. Neuhauser, J. Braun, H. J. Neusser and A. van der Avoird, J. Chem. Phys., 1998, 108, 8408–8417 CrossRef CAS.
- T. Weber, E. Riedle, H. Neusser and E. Schlag, Chem. Phys. Lett., 1991, 183, 77–83 CrossRef CAS.
- K. Siglow and H. J. Neusser, Farad. Discuss. Chem. Soc., 2000, 115, 245–257 RSC.
- T. Weber, E. Riedle, H. Neusser and E. Schlag, Struct., 1991, 249, 69–80 CAS.
- E. Arunan, T. Emilsson and H. S. Gutowsky, J. Chem. Phys., 1993, 99, 6208–6210 CrossRef CAS.
- K. Esteki, A. Barclay, A. McKellar and N. Moazzen-Ahmadi, Chem. Phys. Lett., 2018, 713, 65–70 CrossRef CAS.
- K. Yamanouchi, S. Isogai, S. Tsuchiya and K. Kuchitsu, Chem. Phys., 1987, 116, 123–132 CrossRef CAS.
- R. J. Wilson, S. A. Peebles, S. Antolínez, M. E. Sanz and R. L. Kuczkowski, J. Phys. Chem. A, 1998, 102, 10630–10635 CrossRef CAS.
- W. Caminati and P. G. Favero, Eur. J. Chem., 1999, 5, 811–814 CrossRef CAS.
- W. Caminati, S. Melandri, A. DellErba and P. G. Favero, PhysChemComm, 2000, 3, 1–4 RSC.
- J. J. Oh, I. Park, R. J. Wilson, S. A. Peebles, R. L. Kuczkowski, E. Kraka and D. Cremer, J. Chem. Phys., 2000, 113, 9051–9059 CrossRef CAS.
- A. Dell’Erba, S. Melandri, A. Millemaggi, W. Caminati and P. G. Favero, J. Chem. Phys., 2000, 112, 2204–2209 CrossRef.
- T. Jayasekharan and C. S. Parmenter, J. Chem. Phys., 2004, 120, 11469–11478 CrossRef CAS PubMed.
- B. Velino and W. Caminati, Spectrosc., 2008, 251, 176–179 CAS.
- L. Evangelisti, L. B. Favero, B. M. Giuliano, S. Tang, S. Melandri and W. Caminati, J. Phys. Chem. A, 2009, 113, 14227–14230 CrossRef CAS PubMed.
- R. Knochenmuss, R. K. Sinha and S. Leutwyler, J. Chem. Phys., 2018, 148, 134302 CrossRef PubMed.
- I. Peña and C. Cabezas, Phys. Chem. Chem. Phys., 2020, 22, 25652–25660 RSC.
- A. Macario, S. Blanco, I. Alkorta and J. C. López, Molecules, 2021, 27, 17 CrossRef PubMed.
- M. Coreno, S. Piccirillo, A. Guidoni, A. Mele, A. Palleschi, P. Bréchignac and P. Parneix, Chem. Phys. Lett., 1995, 236, 580–586 CrossRef CAS.
- F. Pirani, M. Albertí, A. Castro, M. M. Teixidor and D. Cappelletti, Chem. Phys. Lett., 2004, 394, 37–44 CrossRef CAS.
- T. Droz, S. Leutwyler, M. Mandziuk and Z. Bačić, J. Chem. Phys., 1995, 103, 4855–4868 CrossRef CAS.
- H. Koch, B. Fernández and J. Makarewicz, J. Chem. Phys., 1999, 111, 198–204 CrossRef CAS.
- S. B. Capelo, B. Fernández, H. Koch and P. M. Felker, J. Phys. Chem. A, 2009, 113, 5212–5216 CrossRef CAS PubMed.
- L. Shirkov and J. Makarewicz, J. Chem. Phys., 2015, 142, 204107 CrossRef PubMed.
- L. Shirkov, V. Sladek and J. Makarewicz, J. Chem. Phys., 2020, 152, 114116 CrossRef CAS PubMed.
- T. Brupbacher, H. Lüthi and A. Bauder, Chem. Phys. Lett., 1992, 195, 482–486 CrossRef CAS.
- W. Klopper, H. P. Lüthi, T. Brupbacher and A. Bauder, J. Chem. Phys., 1994, 101, 9747–9754 CrossRef CAS.
- I. López-Tocón, J. Otero, J. Soto, M. Becucci, G. Pietraperzia and E. Castellucci, Chem. Phys., 2004, 303, 143–150 CrossRef.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483 CrossRef CAS.
- S. Lee, J. S. Chung, P. M. Felker, J. L. Cacheiro, B. Fernández, T. B. Pedersen and H. Koch, J. Chem. Phys., 2003, 119, 12956–12964 CrossRef CAS.
- D. L. Crittenden, J. Phys. Chem. A, 2009, 113, 1663–1669 CrossRef CAS PubMed.
- H. Cybulski, B. Fernández, C. Henriksen and P. M. Felker, J. Chem. Phys., 2012, 137, 074305 CrossRef PubMed.
- H. Cybulski, A. Baranowska-Laczkowska, C. Henriksen and B. Fernández, J. Phys. Chem. A, 2014, 118, 10288–10297 CrossRef CAS PubMed.
- J. Makarewicz and L. Shirkov, J. Chem. Phys., 2016, 144, 204115 CrossRef PubMed.
- J. Makarewicz and L. Shirkov, J. Chem. Phys., 2019, 150, 074301 CrossRef PubMed.
- B. Jeziorski, R. Moszynski and K. Szalewicz, Chem. Rev., 1994, 94, 1887–1930 CrossRef CAS.
- K. Szalewicz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 2, 254–272 Search PubMed.
- T. M. Parker, L. A. Burns, R. M. Parrish, A. G. Ryno and C. D. Sherrill, J. Chem. Phys., 2014, 140, 094106 CrossRef PubMed.
- L. Shirkov and J. Makarewicz, J. Chem. Phys., 2019, 150, 074302 CrossRef PubMed.
- T. Korona, Mol. Phys., 2013, 111, 3705–3715 CrossRef CAS.
- J. Gauss and J. Stanton, J. Phys. Chem. A, 2000, 104, 2865–2868 CrossRef CAS.
- S. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- F.-M. Tao and Y.-K. Pan, J. Chem. Phys., 1992, 97, 4989–4995 CrossRef CAS.
- S. M. Cybulski and R. R. Toczyłowski, J. Chem. Phys., 1999, 111, 10520–10528 CrossRef CAS.
- K. Patkowski, K. Szalewicz and B. Jeziorski, J. Chem. Phys., 2006, 125, 154107 CrossRef PubMed.
- K. Patkowski, K. Szalewicz and B. Jeziorski, Theor. Chem. Acc., 2010, 127, 211–221 Search PubMed.
- A. Heßelmann, G. Jansen and M. Schütz, J. Chem. Phys., 2005, 122, 014103 CrossRef PubMed.
- A. Tekin and G. Jansen, Phys. Chem. Chem. Phys., 2007, 9, 1680–1687 RSC.
- M. Grüning, O. V. Gritsenko, S. J. A. van Gisbergen and E. J. Baerends, J. Chem. Phys., 2001, 114, 652 CrossRef.
- F. D. Sala and A. Görling, J. Chem. Phys., 2001, 115, 5718–5732 CrossRef.
- F. Weigend, A. Köhn and C. Hättig, J. Chem. Phys., 2002, 116, 3175–3183 CrossRef CAS.
- F. Weigend, Phys. Chem. Chem. Phys., 2002, 4, 4285–4291 RSC.
- R. Moszynski, P. S. Żuchowski and B. Jeziorski, Collect. Czech. Chem. Commun., 2005, 70, 1109–1132 CrossRef CAS.
- T. Korona, M. Przybytek and B. Jeziorski, Mol. Phys., 2006, 104, 2303–2316 CrossRef CAS.
- T. Korona, J. Chem. Phys., 2008, 128, 224104 CrossRef PubMed.
- T. Korona, Phys. Chem. Chem. Phys., 2008, 10, 6509 RSC.
- T. Korona, J. Chem. Theory Comput., 2009, 5, 2663–2678 CrossRef CAS PubMed.
- A. Stone, The Theory of Intermolecular Forces, Oxford University Press, 2013 Search PubMed.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, P. Celani, W. Györffy, D. Kats, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, K. R. Shamasundar, T. B. Adler, R. D. Amos, S. J. Bennie, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. Köppl, S. J. R. Lee, Y. Liu, A. W. Lloyd, Q. Ma, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, T. F. Miller III, M. E. Mura, A. Nicklass, D. P. O’Neill, P. Palmieri, D. Peng, K. Pflüger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson, M. Wang and M. Welborn, MOLPRO, version 2015.1, a package of ab initio programs, see https://www.molpro.net Search PubMed.
- A. van der Avoird, P. E. S. Wormer, F. Mulder and R. M. Berns, Topics in Current Chemistry, Wiley, 1980, vol. 93 Search PubMed.
- W. Rijks and P. E. S. Wormer, J. Chem. Phys., 1989, 90, 6507–6519 CrossRef CAS.
- P. E. S. Wormer and H. Hettema, POLCOR package, 1992 Search PubMed.
- J. Makarewicz and A. Bauder, Mol. Phys., 1995, 84, 853–878 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: The calculated and fitted Eint for CCSD(T) and DFT/CCSD-SAPT. The DFT-SAPT and CCSD-SAPT energy corrections. The Python program for the calculation of Eint for both potentials at the given position of Ne. The calculated multipole moments of benzene and dynamic polarizabilities of benzene and Ne found with DFT response and XCCSD. The sets of the long-range coefficients Cl,mn. See DOI: https://doi.org/10.1039/d2cp04369f |
| This journal is © the Owner Societies 2023 |