The structure of protic ionic liquids based on sulfuric acid, doped with excess of sulfuric acid or with water

Abstract

Neutron scattering with isotopic substitution was used to study the structure of concentrated sulfuric acid, and two protic ionic liquids (PILs): a Brønsted-acidic PIL, synthesised using pyridine and excess of sulfuric acid, [Hpy][HSO₄]·H₂SO₄, and a hydrated PIL, in which an equimolar mixture of sulfuric acid and pyridine has been doped with water, [Hpy][HSO₄]·2H₂O. Brønsted acidic PILs are excellent solvents/catalysts for esterifications, driving reaction to completion by phase-separating water and ester products. Water-doped PILs are efficient solvents/antisolvents in biomass fractionation. This study was carried out to provide an insight into the relationship between the performance of PILs in the two respective processes and their liquid structure. It was found that a persistent sulfate/sulfuric acid/water network structure was retained through the transition from sulfuric acid to PILs, even in the presence of 2 moles (∼17 wt%) of water. Hydrogen sulfate PILs have the propensity to incorporate water into hydrogen-bonded anionic chains, with strong and directional hydrogen bonds, which essentially form a new water-in-salt solvent system, with its own distinct structure and physico-chemical properties. It is the properties of this hydrated PIL that can be credited both for the good performance in esterification and beneficial solvent/antisolvent behaviour in biomass fractionation.

---

Introduction

Protic ionic liquids (PILs) derived from sulfuric acid and amines combine excellent performance across a number of chemical processes, with inherently lower costs than comparable aprotic ionic liquids. Even among PILs, these ionic liquids are amongst the least expensive since both sulfuric acid and triethylamine are cheap commodity chemicals. A technoeconomic assessment concluded that triethylammonium hydrogensulfate, [HN₂₂₂][HSO₄], could be produced for as little as US$0.78 kg⁻¹, comparable to many organic solvents in commercial use.^1–4 Ionic liquids formulated from di- and tri-alkylamines with excess sulfuric acid were postulated to be even cheaper,⁵ dispensing with the still-popular misconception that ionic liquids are, generically, too expensive for mainstream industrial use.⁶

Brønsted acidic sulfuric acid based PILS can act as potent acidic catalysts.^7–10 In esterification reactions, equilibria are strongly shifted towards the products because phase separation of esters from the acidic PIL phase is enhanced when compared to use of concentrated sulfuric acid.¹⁰ Hydrated PILs formulated from equimolar quantities of an amine and sulfuric acid, but with the addition of 10–40 wt% water, have been found to be excellent solvents for lignocellulosic biomass pre-treatment, enhancing the fractionation of cellulose, lignin and hemicellulose, leading to higher yields of sugars from subsequent saccharification of the carbohydrates.^11–13

In both of these examples, enhanced performance arises from doping of the simple hydrogensulfate salt, [Hbase][HSO₄], either with an excess of acid or with water, respectively, exemplifying a “4th generation” of ionic liquids,¹⁴ where molecular dopants are incorporated into the ionic liquid matrix, at quantities that preserve the key characteristics of an ionic liquid system (that is, without turning it into a concentrated solution of ions) while enhancing physico-chemical characteristics, viz. increased acidity, lowered viscosity or favourably modified phase behaviour. There are two characteristic features of these doped PILs: simplicity of the preparation, and potential complexity of the speciation/liquid structure of the resulting three-component mixtures that requires investigation and understanding.

There has been a history of debate surrounding the speciation in ionic liquids generated from proton transfer reactions, especially those with non-stoichiometric compositions, which could be described as network vs. cluster models. In 1981, Evans, Arnett and co-workers postulated that ethylammonium nitrate exhibited 3D hydrogen bonded network similar to that of water.¹⁵ The liquid network structure of ethylammonium nitrate was only confirmed, through far-infrared spectroscopy and DFT calculations, in 2009.¹⁶ This was followed by direct liquid structural investigations using neutron^17–20 and X-ray²¹ scattering that identified nanostructured polar/non-polar domains generated by the extensive hydrogen bonding interactions in the polar regions. Similar structure is also present in PILs formed from other primary alkylamines bearing a C_n alkyl chain (n = 2–4) and anions including hydrogen sulfate, thiocyanate, nitrate and formate.²² Weaker acids add further complexity of incomplete proton transfer. For example, mixtures of pyridine and acetic acid were shown to feature a hydrogen-bonded network, which consisted of charge-neutral molecules of acetic acid, with free pyridine sitting in pockets of this network, unprotonated even with a large excess of acid.²³

On the other hand, in PILs synthesised from amines and excess of hydrogen halides (χ_acid > 0.5, X = F⁻,^24–29 Cl⁻,³⁰ and Br⁻,³¹) discrete dimeric and oligomeric clusters, and chains of [X⋯H⋯X]⁻ have been identified, with ample crystallographic evidence in addition to liquid-phase studies. Complex anionic clusters have been proposed in other Brønsted acidic PILs.^10,32,33 For example, in mixtures of amines and trifluoroacetic acid (HTFA), where χ_HTFA > 0.5, was postulated to contain [TFA(HTFA)_x]⁻ clusters.³⁴

Doping ethylammonium nitrate with water resulted in gradual altering of the liquid structure, but even upon the addition of as much as six moles of water, the structure of the hydrated PIL remained ionic liquid-like, distinctly different from homogenous solution.³⁵ These results, along with numerous other contributions,³⁶ suggest that hydrated PILs form their own class of water-in-salt solvents, a sub-class of a wide family of solvent-doped ionic liquids.¹⁴ Consequently, macroscopic properties of hydrated PILs, and their liquids structures, are distinct from both the parent PIL and simple aqueous solution.

Considering the structure of PILs derived from sulfuric acid, a 3D networked structure could be postulated based on the structure of sulfuric acid. Neutron and X-ray scattering studies of H₂SO₄ have shown that sulfate moieties have an ordered, dense network of hydrogen bonds in concentrated liquid acid,^37–39 in the solid state,^40–44 and in aqueous solution.^45,46 With increasing dilution the structure trends to resemble water, albeit with nearest neighbour intermolecular r_O⋯O bond distances ca. 0.2 Å shorter than in pure H₂O.

On the other hand, discrete oligomeric hydrogen bonded anionic clusters have been reported to exist in the gas phase, in the Earth's stratosphere.^47–50 The first paper by our group reporting PILs derived from sulfuric acid¹⁰ also postulated the existence of anionic clusters, in analogy to earlier works on trifluoroacetate ionic liquids²⁵ and other strongly hydrogen bonding anions. FT-IR and NMR spectroscopic studies have been used to justify these assignments, but whereas these early results do show strong interactions between molecules of H₂SO₄ and [HSO₄]⁻, they could admittedly occur in both the cluster and the 3D network arrangement.

Here, neutron scattering has been used to compare the liquid structures of concentrated sulfuric acid and two pyridine/sulfuric acid PILs containing either excess of the acid or doped with water. The objective was to elucidate potential relationships between the local liquid structure, the effectiveness of these PILs as catalysts and solvents for esterification reactions^8–10 and for treatment of lignocellulosic biomass.^11–13

Experimental

Materials

Synthesis of ionic liquids. Three studied samples were: concentrated sulfuric acid, a Brønsted-acidic PIL formed from sulfuric acid and pyridine in 2 : 1 molar ratio, [Hpy][HSO₄]·H₂SO₄ and a hydrated PIL, formed from concentrated sulfuric acid, pyridine and water in 1 : 1 : 2 molar ratio [Hpy][HSO₄]·2H₂O. For each composition, isotopologues containing protiated (H), deuteriated (D) or equimolar mixture of protiated and deuteriated components (H/D) were prepared. A detailed synthetic procedure can be found in the ESI.†

All samples (Table 1) were homogeneous liquids at ambient temperature.

Table 1 Samples of sulfuric acid : pyridine : water, their compositions and corresponding levels of protiation and/or deuteration

Sample number	Theoretical formula (actual H2SO4 : py : H2O)	Sulfuric acid	py	water
1	Concentrated sulfuric acid H2SO4 (1 : 0 : 0.2)	H		H
2		H/D		H/D
3		D		D
4	Brønsted acidic PIL [Hpy][HSO4]·H2SO4 (2 : 1 : 0.4)	H	D	H
5		H/D	D	H/D
6		D	D	D
7		D	H	D
8		D	H/D	D
9		H	H	H
10		H	H/D	H
11	Hydrated PIL	H	D	H
12	[Hpy][HSO4]·2H2O (1 : 1 : 2.2)	H/D	D	H/D
13		D	D	D
14		D	H	D
15		D	H/D	D
16		H	H	H
17		H	H/D	H

---

Neutron scattering experiments. Neutron scattering data from the seventeen samples (Table 1) were recorded using the SANDALS spectrometer at the ISIS Pulsed Neutron and Muon Source at Rutherford Appleton Laboratory, Oxfordshire, UK. The instrument uses neutrons over a wavelength range 0.05–4.5 Å, giving an accessible Q range of 0.1–50 Å⁻¹. All samples were measured in quartz cells with 30 × 30 mm flat-plate geometry and with a path length of either 1 or 2 mm. 2 mm cells were used for samples with high deuteration levels (samples 2, 3, 5, 6, 8, 12–15 – Tables 1) and 1 mm cells were employed for the more hydrogenous samples (samples 1, 4, 7, 9, 10, 11, 16, 17 – Table 1) in order to avoid high levels of beam attenuation and multiple scattering. At least 1000 μA of data were collected on each sample. Prior to data collection, quartz cells filled with sample were weighed, placed in a Thermo Scientific vacuum oven (25 °C, <1 × 10⁻² mbar, 20 min), and weighed again, to ensure tightness of the seal against leakage in the instrument vacuum. Data were collected at 25 °C, with the temperature maintained using an FP50 Julabo heating circulator.

Total scattering data were reduced into a differential scattering cross section using the GUDRUN package.⁵¹ Data collected on a 3.1 mm vanadium-niobium alloy plate standard was used for calibration, while data recorded on the empty SANDALS instrument and an empty 1 mm quartz cell were used for background subtraction.⁵²

Reduced data were analysed using the Empirical Potential Structure Refinement (EPSR)^53,54 software to examine the time-averaged liquid structure. EPSR uses a Monte Carlo simulation approach coupled with Lennard-Jones potentials with atom-centred point charges, combined with basic structural information about the atoms or molecules and the total atomic densities present of the system.^53,54 Differences between the experimental and simulated data sets in Q space (i.e. the empirical perturbation potential) are determined, enabling iterative refinement to generate a self-consistent fit to the scattering cross sections obtained from isotopically distinct samples. Simulations were equilibrated over ca. 2000–3000 cycles before accumulating and averaging data. The EPSR refinements, in each case, were initialised using an equilibrated Monte Carlo simulation containing 500 or 1000 molecular moieties (pyridine, hydrogen sulfate, molecular sulfuric acid and water, with atomic sites labelled as shown in Fig. 1) depending on the sample.

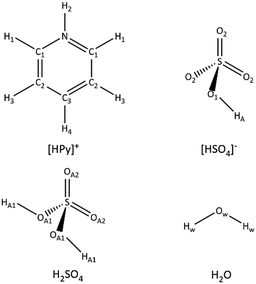Fig. 1 Atom types used in the EPSR simulation models for the pyridinium cation, hydrogen sulfate anion, molecular sulfuric acid and water.

The full set of reference potential parameters and constraints used in the EPSR simulation model, and the total number of pyridine, hydrogen sulfate and/or sulfuric acid and water and size of each simulation box, corresponding to the experimentally determined molecular densities of the fully protiated mixtures are shown in ESI.† Charges were scaled to ±0.8 e, in line with results from neutron diffraction and MD simulations of ILs.⁵⁵ Here reduced charges have been shown to reproduce experimental data more effectively. This better simulates effects of electronic polarisability captured when using more expensive polarisable force fields.⁵⁶

Results and discussion

Selection of samples

The experimental design included the study of concentrated sulfuric acid, a Brønsted acidic PIL formulated with two moles of H₂SO₄ per one mol of pyridine, [Hpy][HSO₄]·H₂SO₄ and a hydrated ionic liquid, [Hpy][HSO₄]·2H₂O. Adjusting for the actual water content from these idealised compositions, concentrated sulfuric acid (98%) was assumed to contain 0.2 M of either H₂O (in H₂SO₄) or D₂O (in D₂SO₄). This was confirmed by examination of the respective measured neutron scattering levels. As such, actual compositions of the examined samples used to model the neutron scattering data were: concentrated sulfuric acid (1 : 0.2, acid : water), Brønsted acidic PIL (2 : 1 : 0.4, acid : pyridine : water) and hydrated PIL (1 : 1 : 2.2, acid : pyridine : water), as summarised in Table 1.

The structure of concentrated sulfuric acid was used as a baseline to compare with the structures of both PILs. The composition of the Brønsted acidic PIL, [Hpy][HSO₄]·H₂SO₄, was one of the two standard acidic compositions used in our earlier catalytic studies.^5,8–10 The aim of this work was to elucidate its structure (3D network vs. discrete anionic clusters) and understand how differences in the liquid structure of this PIL and sulfuric acid account for their different miscibilities with the ester product. Finally, the hydrated PIL, [Hpy][HSO₄]·2H₂O, with a 1 : 1 : 2.2, acid : pyridine : water ratio (ca. 17 wt% of water), was close in composition to the 20 wt% water content, cited as the optimum composition for delignification of cellulosic biomass.^4,11–13,57 It was anticipated that particularly efficient biomass fractionation reported for this aqueous PIL composition could be tied to the speciation of water in the 1 : 1 : 2.2 mixture.

EPSR modelling and fit to experimental data

The data from sulfuric acid (samples 1–3) was modelled using molecular descriptions of the species present (H₂SO₄ and H₂O in a 1 : 0.2 molar ratio) – see Fig. 1. Although several more complex water species (H₃O⁺, H₅O₂⁺) have been reported as constituents of sulfuric acid hydrates,^40–44 descriptors were limited to the main moieties, enabling the examination of key associations in these already complex mixtures. This approach is aligned with EPSR analysis of neutron scattering data recorded for other ‘neat’ acids (acetic acid, formic acid),⁵⁸ in which molecular (undissociated) descriptions were used. The same strategy has been used in MD simulations of sulfuric acid : water mixtures⁵⁹ and other ‘neat’ acids, small molecules and mixtures.^52,58–66

The Brønsted acidic PIL (samples 4–10) and the hydrated PIL (samples 11–17) were modelled using fully protonated pyridinium cations [Py-H]⁺, anionic [HSO₄]⁻ and molecular H₂O. Additionally, the model of samples 4–10 contained molecular H₂SO₄.

Although pyridine in the presence of sulfuric acid can be considered fully protonated, based on both FT-IR spectroscopy⁶⁷ and crystallographic data for pyridinium hydrogen sulfate,⁶⁸ an alternative ‘free proton’ model,²³ (with discrete H⁺, labelled as H_F), [HSO₄]⁻ and H₂O components in the simulation box) was also examined. However, the degree of pyridine protonation found was significantly underestimated with an average N⋯H_F coordination number of only 0.2 ± 0.4 and with the maximum in the N⋯H_F correlation (corresponding to N–H bonds in pyridinium cations) overestimated at 1.6 Å. In consequence, the fully-protonated cationic pyridinium descriptor was used.

Comparisons of experimental and simulated total structure factors, F(R), and the corresponding Fourier transforms to real space G(r) for each of the isotopically distinct experimental mixtures (Fig. 2) show the quality of fit to the experimental data. With the exception of the region at Q ≤ 1 Å⁻¹, which is most susceptible to inconsistencies due to inelastic scattering contributions from hydrogen in the data, the fitted data aligns well with experiment. For the neat sulfuric acid systems (1–3, Table 1), a larger degree of scattering at low Q is present in the experimental data than is captured within the EPSR model which may reflect either incomplete subtraction of the inelastic hydrogen background from the data, or additional long range order. Similar profiles are also apparent for the fully deuteriated PILs (samples 6 and 13) suggesting that some hydrogen is present, generating inelastic scattering from the sample in this region.

Fig. 2 Total structure factors F(Q) (top), and the corresponding Fourier transform to real space G(r) radial distribution functions (bottom) showing experimental data (red symbols) and EPSR modelled (blue solid line) for left: sulfuric acid (H₂SO₄ : H₂O 1 : 0.2); middle: Brønsted acidic PIL (H₂SO₄ : py : H₂O 2 : 1 : 0.4) and right: hydrated PIL (H₂SO₄ : py : H₂O 1 : 1 : 2.2). Labels represent the experimental compositions shown in Table 1 and the curves have been offset for clarity.

Centre of mass radial distribution functions

Centre of mass (COM) radial distribution functions (RDFs) were calculated using the SHARM routines within EPSR, for each of the components in the three systems (Fig. 3). The RDFs reveal a remarkable persistence of structure, similar between the three systems: H₂SO₄, [Hpy][HSO₄]·H₂SO₄ and [Hpy][HSO₄]·2H₂O.

Fig. 3 COM RDFs between [H-Py]⁺ and {SO₄} (top) and between H₂O and [H-Py]⁺ or {SO₄} units (bottom) in: concentrated sulfuric acid (dotted lines), Brønsted acidic PIL (solid lines) and hydrated PIL (dashed lines), from the EPSR simulations.

In concentrated sulfuric acid, the {SO₄}–{SO₄} RDF shows a first shell correlation with a maximum at ca. 4.6 Å, with a broad second shell correlation between 6.6–11.5 Å (Fig. 3, top, blue dotted line). The corresponding water–{SO₄} first shell correlation (Fig. 3, bottom, blue dotted line) is centred around 4 Å (minimum 5.5 Å), and the water–water RDF correlation (Fig. 3, bottom, dotted green) at 3.2 Å. This is significantly longer than water–water distances in bulk water (2.6 Å), confirming that water molecules are confined within sulfuric acid as hydrates. Further supporting this conclusion, the water–water RDF lacks a second shell peak between 4–6 Å, that would have been indicative of ‘free’ water.

In both PIL systems, the cation–{SO₄} RDFs are characteristic of strong cation–anion association, typical of ionic liquids.⁶⁹ The cation–anion RDFs (Fig. 3, top, green curves) exhibit a first correlation peak at 5.0–5.2 Å with a shoulder at 4.2 Å, and a second broader correlation peak, indicative of the second shell, at ca. 9 Å. The shoulder at 4.2 Å reflects the oblate topology of the pyridinium cations, allowing two distinct routes to approach its centre of mass. The cation–cation first correlations (Fig. 3, top, red curves) are present at larger separations (maxima at ∼6 Å), followed by a second shell at 9–10 Å, overlapping with the second shell of cation–anion correlations. Again, a small shoulder at ca. 4 Å in the cation–cation RDFs may be due to a small number of face-to-face correlations, typical of the π–π interactions observed in liquid pyridine at distances below 5 Å.⁷⁰ Similar features are observed in aprotic ILs containing N-alkylpyridinium cations, arising from anions associating equatorially around pyridinium cations.^71–73

In contrast to typical ionic liquid structure, there is very close anion–anion interaction in both PILs. The corresponding {SO₄}–{SO₄} associations (Fig. 3, top, blue dashed and solid curves) closely resemble sulfate associations in ‘neat’ sulfuric acid (first shell at 4.6 Å, second one at 6.6–11 Å). In PILs, the first correlation lengthens slightly (4.8 Å), which can be attributed to the decreasing number of acidic hydrogens in the H₂SO₄/[HSO₄]⁻ components, therefore reducing the number of available S–O–H⋯O=S hydrogen bonding motifs: from 2 per {SO₄} unit in H₂SO₄, through 1.5 per {SO₄} unit in [Hpy][HSO₄]·H₂SO₄, to 1 per {SO₄} unit in [Hpy][HSO₄]·2H₂O (assuming this is terminal and not bifurcated).

This close anion–anion interaction in both PILs results in the unusual presence of both cations and anions in the first coordination shell of {SO₄}. Their liquid structure combines characteristics of ionic liquid (close cation–anion correlations) and of the parent sulfuric acid (sulfate–sulfate organisation).

The water⋯{SO₄} and water⋯[H-Py]⁺ RDFs (Fig. 3, bottom, blue and red lines, respectively) have their corresponding first peak correlations of 4.0 and 4.8 Å. There is no significant difference in the water association with either {SO₄} or [H-Py]⁺ on changing the water content of the PILs.

In contrast, water–water RDFs show a marked difference. In H₂SO₄ and in [Hpy][HSO₄]·H₂SO₄, that is with low water content, H₂O⋯H₂O correlation is found at 3.2 Å, slightly more intense in [Hpy][HSO₄]·H₂SO₄. In [Hpy][HSO₄]·2H₂O, this distance decreases to 2.7 Å, showing both greater self-association of water molecules and a larger number of correlations, as indicated by the increase in intensity. This distance is close to H₂O⋯H₂O correlation in bulk water (2.6 Å). However, lack of significant second shell correlation (4–6 Å) indicates that there are no large-size water clusters and [Hpy][HSO₄]·2H₂O retains water-in-IL rather than IL-in-water characteristics.

The similarity of RDF correlation profiles (Fig. 3), aside from the water-water correlation, suggests essentially similar liquid structure and character of both PILs, and that the presence of the water (up to 2 moles, ca. 17 wt%) does not perturb the ion-ion structure significantly. Moreover, the hydrogen-bonding network of sulfuric acid appears to be retained as a core structural motif in the PILs, in addition to the typical Coulombic charge screening structure usually observed in ionic liquids.

In the context of applications of Brønsted acidic PILs in esterification, it was initially assumed that phase-separation of the organic phase, that is much more efficient in Brønsted acidic PILs than in concentrated sulfuric acid, may be related to marked differences between the structures of the two liquids: H₂SO₄vs. [Hpy][HSO₄]·H₂SO₄. However, the results here suggest that there are greater similarities between the structure-defining associations within these liquids rather than significant differences that would explain the distinctly different phase behaviours of H₂SO₄ and PILs in esterification reactions.

In contrast, the water-in-salt structure of the hydrated PIL, [Hpy][HSO₄]·2H₂O, with negatively-charged hydrogen-bonded network of hydrogen sulfate and water (with or without H₂SO₄ present) can be expected to have distinctly different properties when compared to anhydrous [Hpy][HSO₄], as described in the literature.^11,74,75 Furthermore, in esterification reactions, where water and ester are generated, the Brønsted acidic PIL can be envisaged to gradually bind water to form a similar hydrogen sulfate – sulfuric acid – water anionic network, in which water is bound as a hydrate and less likely to hydrolyse the ester product.

Detailed, comparative structural analysis of the three liquid systems studied in this work are provided below.

Correlation and association around {SO₄} groups

Detailed site–site analysis of contributions to the scattering were made. The positions of first peaks within the partial RDFs of selected site–site correlations and corresponding coordination numbers, calculated to the first minima after the peak, are included within the ESI.†

Fig. 4 shows oxygen⋯oxygen correlations between {SO₄} groups, originating both from [HSO₄]⁻ and H₂SO₄, were determined from the first peak in the site–site pRDFs. In all three systems, the ‘hetero’ S–OH⋯O=S mode of correlation is dominant, appearing as a strongly defined peak in the RDF at 2.6–2.7 Å (Fig. 4, green line). In contrast, first contact correlations of S–OH⋯HO–S and S=O⋯O=S only occur around 3.0 Å, with a peak at ca. 5 Å, corresponding to the separation in the COM RDF. It is therefore evident that the primary mode of association between {SO₄} groups is S–OH⋯O=S hydrogen bonding, retained from sulfuric acid in both PILs.

Fig. 4 O⋯O correlations; S=O⋯O=S (red), S–OH⋯HO–S (blue) and S=O⋯HO–S (green) in conc. H₂SO₄ (1 : 0 : 0.2), ‘anhydrous’ acid PIL (2 : 1 : 0.4), and ‘hydrated’ PIL (1 : 1 : 2.2) systems showing the strong hydrogen-bonding correlation with a sharp first peak at 2.6 Å between S–OH and O=S oxygen centres and broader less defined correlations at longer distances of 3.0 Å and 3.3 Å for correlations between S–OH oxygens and S=O contact-pairs.

Correlation distances for concentrated H₂SO₄ are broadly consistent with the literature.^37,46,59 Andreani et al. first reported data derived from direct Fourier transform of experimental X-ray and neutron scattering data,³⁷ with S⋯S and O⋯O separation distances of 5.3 Å and 2.42 Å. However, the S⋯S separation, extrapolated from summation of intermolecular S–O and intramolecular O–O distances, appears to be over-estimated. Kameda et al.⁴⁶ subsequently reported a shorter S⋯S correlation of 4.8 Å which is more consistent with simulation between contact pairs in concentrated H₂SO₄/H₂O (4.6 ± 0.1 Å),⁷⁶ and small clusters of bulk H₂SO₄ (4.8 Å)⁶² where an O⋯O distance of 3.1 Å was also reported. Here, the first shell S⋯S separation distance was determined as 4.6 Å, with O⋯O correlations between OA1 and OA2 sites (S–OH⋯O=S) at 2.6 Å, and minima after this first correlation peak at 3 Å. The {SO₄}⋯{SO₄} coordination number (N_coord = 11 ± 1) between neighbouring moieties is also in agreement with the literature (N_coord = 12),^37,59 and confirms the formation of an extended, tetrahedral hydrogen bonded network linked through S–OH⋯O=S interactions.⁷⁷

In both PILs, interatomic distances for the first shell O⋯O correlations, as well as corresponding N_coord values, are very close to sulfuric acid, suggesting hydrogen bonding of similar strength across the three samples. However, the {SO₄}⋯{SO₄} first shell coordination environment (determined from S⋯S correlations) decreases: from 11 in H₂SO₄, to 7.5 in [Hpy][HSO₄]·H₂SO₄, and to 4.8 in [Hpy][HSO₄]·2H₂O, commensurate with the reduction in the number of available S–OH groups to act as hydrogen-bond donors.

Site–site RDFs between water (Ow/Hw) and sulfate units are shown in Fig. 5. For the concentrated acid and anhydrous acidic PIL, the presence of ca. 0.2 mole fraction of water leads to a broad peak in the Ow⋯O1/O2 RDFs between ∼2.6–3.0 Å (Fig. 5, dashed lines). The Hw⋯O=S correlation at 1.8 Å (Fig. 5, solid blue lines) indicates directional hydrogen-bonding retained between the acid and PILs.

Fig. 5 Site–site pRDFs between water Hw (solid line) and Ow (dashed line) and sulfate S=O (blue) and S–OH (red) oxygens in the three systems showing hydrogen-bond donation from the water Hw to the S=O2 oxygen (1.8 Å) and hydrogen-bond acceptance at Ow from S–OH 2.8 Å).

In the hydrated PIL, [Hpy][HSO₄]·2H₂O, the magnitude of these correlations increases, as there are more water molecules available, and less S–OH sites. Associated Ow⋯O=S correlation at 2.8 Å (Fig. 5, dashed blue line) also becomes sharper. Interestingly, the corresponding Ow⋯O(H)–S correlation at 2.8 Å (Fig. 5, dashed red line) is dramatically decreased. This indicates that the remaining available S–OH sites hydrogen bond preferentially to O=S, rather than water. In short, water in [Hpy][HSO₄]·2H₂O (absence of strong Brønsted acid) binds preferentially as Hw⋯O=S, not as Ow⋯HO–S, acting as hydrogen bond donor, rather than hydrogen bond acceptor.

Water–water association

In the low-water samples, H₂SO₄ and [Hpy][HSO₄]·H₂SO₄, the Ow⋯Ow distance is longer than in ‘bulk’ water, and the corresponding coordination number is low (N_coord≈ 0.5), which is indicative of isolated water molecules, strongly associated with the sulfate structure. In contrast, the Ow⋯Ow correlation in [Hpy][HSO₄]·2H₂O (Fig. 6, green line) has a first peak at 2.8 Å, comparable to that in pure water, and the coordination number (N_coord = 4.1 ± 2) slightly lower than that of bulk water (N_coord = 4.7).⁷⁸ However, the O_w⋯O_w RDF does not have the distinctive second peak around 4.5 Å, which would have been indicative of a long-range tetrahedral order seen in bulk water, or its larger clusters.

Fig. 6 Site–site pRDFs between Hw and Ow for water molecules in [Hpy][HSO₄]·2H₂O.

The combination of water-like first shell and unlike-water second shell has been reported for ‘bound’ water in inorganic molten salt hydrates,⁷⁹ and is consistent with the [Hpy][HSO₄]·2H₂O PIL having a water-in-ionic liquid structure,¹⁴ but approaching the transition to a concentrated salt solution.

Correlation and association around [H-Py]⁺

RDFs between [H-Py]⁺ and {SO₄}, and between [H-Py]⁺ and water Ow, are shown in Fig. 7. In both PILs, the hydrogen-bond donating N–H site of [H-Py]⁺ has equally close contact with hydrogen bond-accepting sites in {SO₄} and in water. The N1⋯O2 and N1⋯Ow correlations occur at 2.7 Å in [Hpy][HSO₄]·H₂SO₄ (Fig. 7, black solid lines) and at 2.8 Å in [Hpy][HSO₄]·2H₂O (Fig. 7, black dashed lines). Carbon atoms of pyridine are separated by 3.4–3.6 Å from both O=S and Ow sites; these are consistent with weak contacts at the van der Waals separation distances.

Fig. 7 Site–site RDFs from pyridinium N (black) and C1 (red), C2 (blue) and C3 (green) sites to O2 oxygen atoms of the {SO₄} units to hydrogensulfate (top) and Ow sites in water (bottom) for [Hpy][HSO₄]·H₂SO₄ (solid lines) and [Hpy][HSO₄]·2H₂O (dashed). Each set of correlations is displaced by 0.5 in the y-axis for clarity.

Hydrogen bond donation from S–OH sites (O1/OA1) to the pyridinium cation is not observed. Consequently, we can see water molecules acting as hydrogen-bond donors to [HSO₄]⁻ anions through Hw⋯O=S interaction, and as hydrogen-bond acceptors from [H-Py]⁺ cations through, Ow⋯H-Py interaction. The presence and directionality of water molecules within the first shells of both {SO₄} and [H-Py]⁺ species demonstrates the structure-forming nature of water molecules, which contribute to the overall hydrogen bond network, reinforcing the sulfate/sulfuric acid network and bridging cations and anions.^14,80

Spatial association

There is a remarkable retention of the correlation pattern across the three systems examined, as shown in the pRDFs, and it is interesting to explore whether this translates to the retention of the network structure present in sulfuric acid to PILs, despite the reduced number of acidic S–OH sites and the introduction of [H-Py]⁺ cations.

Spatial distribution functions (SDFs) in Fig. 8 are plotting the top 15% probability for correlations within the first coordination shell.

Fig. 8 Spatial distribution functions (SDFs) showing the first shell environments around H₂SO₄ (a), [Hpy][HSO₄]·H₂SO₄ (b) and (c), and [Hpy][HSO₄]·2H₂O (d) and (e), presenting the {SO₄} (a), (b), (d) and [H-Py]⁺ (c), (e) environments, with the nitrogen-site of [H-Py]⁺ pointing up. All SDFs are plotted to show the top 15% probability for correlation within the first shell, determined from the first minimum in the corresponding COM RDFs (Fig. 3). The [HSO₄]⁻/H₂SO₄ moieties are shown in yellow, H₂O in green and [H-Py]⁺ in blue.

For sulfuric acid, {SO₄}⋯{SO₄} correlations (Fig. 8(a), yellow surface) show a pronounced tetrahedral symmetry with four high probability nodes, each sitting over a triangular face of the {SO₄} tetrahedron, bridged by six bands bisecting O–S–O edges. The SDF map shows holes around each oxygen atom, presumably occupied by hydrogen atoms participating in S–OH⋯O=S bonding from adjacent acids in the first coordination shell. The weakly correlated association of water molecules with sulfuric acid, shown in Fig. 5 RDFs, is also evident in the SDF, (Fig. 8(a), green surface), lacking a distinct spatial ordering. Plotting water–sulfuric acid SDF at 50% probability (ESI†) shows a non-defined spherical distribution.

Structure refinement for [Hpy][HSO₄]·H₂SO₄ was made with two different {SO₄} moieties: [HSO₄]⁻ and [H₂SO₄]. Comparable distributions of both species with a central reference [HSO₄]⁻ were found, and are plotted as merged functions, forming the same sulfuric acid-like tetrahedral distribution (Fig. 8(b), yellow surface). The equivalent SDFs around H₂SO₄ are included in the ESI.† Compared to H₂SO₄, the symmetry of the distribution of {SO₄}⋯{SO₄} association was somewhat reduced, with the S–OH site in [HSO₄]⁻ showing a greater probability density than the corresponding S–O oxygens. This is a consequence of the change in relative numbers of S–OH and O=S oxygens in the system, from 1 : 1 to 3 : 4, reducing the relative proportion of hydrogen-bond donor to acceptor sites. In contrast, distribution of H₂O molecules around [HSO₄]⁻ (Fig. 8(b), green surface) was more structured in [Hpy][HSO₄]·H₂SO₄ than it was in H₂SO₄, tracking to the positions of {SO₄} moieties in the first shell.

Likewise, [H-Py]⁺ cations (Fig. 8(b), green surface) show correlations in these positions, in an approximately tetrahedral distribution with maxima associated with each triangular face of {SO₄} reflecting the association through hydrogen-bond donation from [H-Py]⁺ cations to O=S sites (see Fig. 7). Both the water and [H-Py]⁺ SDFs around [HSO₄]⁻ are truncated over the acidic S–OH group, as a result of the predominance of this site as a hydrogen-bond donor to other {SO₄} units, rather than a hydrogen-bond acceptor.

In the hydrated PIL, [Hpy][HSO₄]·2H₂O, the S–OH to O=S ratio is reduced to 1 : 3, which results in closer {SO₄}⋯{SO₄} association through the remaining S–OH site in [HSO₄]⁻ (Fig. 8(d), yellow surface). The reduced number of the S–OH hydrogen bond donors leads to increased correlation of water with the O=S sites (Fig. 8(d), green surface), consistent with the increased magnitude and definition of the Hw⋯O2 pRDF (Fig. 5).

Solvation environments around [H-Py]⁺ in both PILs are characterised by very similar spatial distributions of {SO₄}, in a band above/below the pyridinium ring, straddling the N–H site (Fig. 8(c) and (e), yellow surface). Water occupies similar positions, and also arranges more broadly within the equatorial plane of the [H-Py]⁺ ring, especially in the hydrated PIL (Fig. 8(c) and (e), yellow surface). It is in alignment with water acting as a hydrogen bond acceptor via Ow⋯H–N and to a lesser extent Ow⋯H–C hydrogens of the pyridine ring (Fig. 7).

Finally, the [H-Py]⁺⋯[H-Py]⁺ SDFs (Fig. 8(c) and (e), blue surface) show a broad correlation around the C2/C3 positions of pyridinium rings, that even plotting the top 15% probability is highly diffuse and non-specific.

Overall, from H₂SO₄, through the Brønsted acidic PIL, and to the hydrated PIL, the first shell environment of the {SO₄} moiety shows a transition from a highly symmetric tetrahedral distribution of acid {SO₄} groups towards an increased probability density for {SO₄}⋯{SO₄} association at the S–OH position, as a function of the increase in anionic O=S oxygens relative to S–OH acid groups. This is evident in [Hpy][HSO₄]·H₂SO₄ through the larger node at the S–OH site, with water–{SO₄} and [H-Py]⁺⋯{SO₄} correlations to sites associated with the O=S oxygens. For [Hpy][HSO₄]·2H₂O, the highest probability SDF correlations between [HSO₄]⁻ anions are with the S–OH site, with hydrogen-bonding between water and O=S sites becoming more dominant, substituting for S–OH⋯O=S interactions in the first shell. However these changes in the first shell correlations around {SO₄}, induced by the changes in availability of different hydrogen-bond donors, have remarkably little effect on the longer range order in the liquids. The second shell {SO₄}⋯{SO₄} correlations between {SO₄} units in the three systems are shown in Fig. 9, plotting the top 15% probability surfaces for the first shell (3–6.5 Å) and second shell (6.5–11 Å). Remarkably, across all three systems a strong tetrahedral structure is retained, irrespective of the changes in relative {SO₄} and water distributions in the first correlation shell. All systems show the same tetrahedral pattern, despite differences in the first shell. This gives strong evidence that water (and to a lesser extent pyridinium cations) act as surrogates for S–OH hydrogen-bond donors retaining the structure of the parent acid within the PILs.

Fig. 9 First and second shell correlations around {SO₄} central groups in H₂SO₄ (a); [Hpy][HSO₄]·H₂SO₄ (b), and [Hpy][HSO₄]·2H₂O (c). The first shell {SO₄}⋯{SO₄} is in red, the first shell {SO₄}⋯water is in green and the second shell {SO₄}⋯{SO₄} association (6.5–11 Å) is in yellow.

Conclusions

The RDFs indicate that anion–cation correlations between protonated [H-py]⁺ cations and [HSO₄]⁻ anions typical of ionic liquids (and molten salts)⁶⁹ are formed in both the ‘anhydrous’ acidic PIL and ‘hydrated' PIL with charge screening between alternate oppositely charged ions. However, in addition to the formation of this typical cation–anion ionic liquid structure, the overall tetrahedral network structure, directed by hydrogen-bonding around the {SO₄} groups in ‘neat’ sulfuric acid is persistent and retained in the PILs. This is complemented by interactions with the [H-Py]⁺ cations (as can be seen in the presence of correlation nodes between [H-Py⁺] and O=S sites in 2 : 1 : 0.4 ‘anhydrous’ acidic PIL) and increasingly, by replacement of acidic S–OH hydrogen bond donors by water molecules in the 1 : 1 : 2.2 ‘hydrated’ PIL to retain the supramolecular {SO₄}-network present in the parent sulfuric acid.

As such, it is clear that the ‘anhydrous’ acidic 2 : 1 : 0.2 PIL retains many features of concentrated sulfuric acid in terms of both acidity¹⁰ and network structure, while simultaneously adopting the anticipated anion–cation correlation pattern characteristic of ionic liquids. Consequently, difference in phase behaviour between sulfuric acid and PILs, which result, for example, in different performances as solvents for biomass fractionation or esterification reactions, cannot be attributed directly to differences in the liquid structures as the ‘anhydrous’ acidic PIL strongly resembles ‘neat’ sulfuric acid. The addition of 2 moles of water (ca. 17 wt%) provides additional hydrogen bond donation capacity to complement and replace the diminished number of S–OH hydrogen-bond donors present in the parent acid. This results in a change in the nature of the first shell hydrogen-bond donors around [HSO₄]⁻ anions, but not in the overall pattern of hydrogen bonding. This ‘hydrated’ sulfuric acid : pyridine : water (1 : 1 : 2.2) system has an equivalent water content to that of the aqueous alkylammonium PILs reported by Hallett et al.^{4,11,12,57,81–86} as media for delignification for cellulosic biomass, with ca. 15 wt% water in the IL. It is clear that the water molecules here are present as ‘bound’ water participating in the ionic liquid solvation structure and not as ‘free’ water. That is, the system can be viewed as one with water-in-IL rather than as a concentrated IL-in-water environment.

This finding allows for certain speculations in terms of phase behaviour. In esterification reactions, where water and ester are generated, the ionic liquid gradually binds water incorporated in the hydrogen sulfate network, without the formation of ‘bulk’ water that can contribute to the reverse reaction of ester hydrolysis. The resulting hydrated PIL is more hydrophilic, which contributes to a lower affinity to the ester products and, in consequence, enhanced phase separation. Likewise, it appears that the “composite” anionic structure of water-doped PIL has a higher propensity to dissolve lignin, its structure being different from that of anhydrous IL, but unlikely to contain “bulk” water at the optimised ratios of 10–40% (1 : 1 : 2 composition amounts to ca. 20% water by weight).

These conclusions are aligned with the available experimental evidence, but nevertheless remain speculative. Further evidence can be provided by the study of solvation of model compounds in wet and dry PILs by neutron scattering, more advanced computational approaches, or thermodynamic studies of the energy of solvation.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

DfE (EB) and EPSRC (AMcG) are kindly acknowledged for PhD studentship funding and the Science and Technology Facilities Research Council thanked for use of SANDALS spectrometer during beam time (RB2010681).10.5286/ISIS.E.RB2010681.

References

1. F. J. V. Gschwend, L. M. Hennequin, A. Brandt-Talbot, F. Bedoya-lora, G. H. Kelsall, K. Polizzi, P. S. Fennell and J. P. Hallett, Green Chem., 2020, 22, 5032.
2. H. Baaqel, I. Díaz, V. Tulus, B. Chachuat, G. Guillén-gosálbez and J. P. Hallett, Green Chem., 2020, 22, 3132.
3. L. Chen, M. Sharifzadeh, N. Mac Dowell, T. Welton, N. Shah and J. P. Hallett, Green Chem., 2014, 16, 3098.
4. A. George, A. Brandt, K. Tran, S. M. S. N. S. Zahari, D. Klein-Marcuschamer, N. Sun, N. Sathitsuksanoh, J. Shi, V. Stavila, R. Parthasarathi, S. Singh, B. M. Holmes, T. Welton, B. A. Simmons and J. P. Hallett, Green Chem., 2015, 17, 1728.
5. (a) A. Brzęczek-Szafran, J. Więcławik, N. Barteczko, A. Szelwicka, E. Byrne, A. Kolanowska, M. Swadźba Kwaśny and A. Chrobok, Green Chem., 2021, 23, 4421; (b) A. Brzęczek-Szafran, K. Erfurt, M. Swadźba-Kwaśny, T. Piotrowski and A. Chrobok, ACS Sustainable Chem. Eng., 2022, 10, 13568.
6. A. A. Quintana, A. M. Sztapka, V. de C. Santos Ebinuma and C. Agatemor, Angew. Chem., Int. Ed., 2022, 37, 61.
7. M. P. Atkins, M. J. Earle, K. R. Seddon, M. Swadźba-Kwaśny and L. Vanoye, Chem. Commun., 2010, 46, 1745.
8. M. Przypis, K. Matuszek, A. Chrobok, M. Swadźba-Kwaśny and D. Gillner, J. Mol. Liq., 2020, 308, 113166.
9. K. Matuszek, A. Brzecek-Szafran, D. Kobus, D. R. MacFarlane, M. Swadźba-Kwaśny and A. Chrobok, Aust. J. Chem., 2019, 72, 130.
10. K. Matuszek, A. Chrobok, F. Coleman, K. R. Seddon and M. Swadźba-Kwaśny, Green Chem., 2014, 16, 3463.
11. A. Brandt-Talbot, F. J. V. Gschwend, P. S. Fennell, T. M. Lammens, B. Tan, J. Weale and J. P. Hallett, Green Chem., 2017, 19, 3078.
12. P. Verdía, A. Brandt, J. P. Hallett, M. J. Ray and T. Welton, Green Chem., 2014, 16, 1617.
13. A. Brandt, M. J. Ray, T. Q. To, D. J. Leak, R. J. Murphy and T. Welton, Green Chem., 2011, 13, 2489.
14. D. R. MacFarlane, A. L. Chong, M. Forsyth, M. Kar, R. Vijayaraghavan, A. Somers and J. M. Pringle, Faraday Discuss., 2018, 206, 9.
15. D. F. Evans, S. H. Chen, G. W. Schriver and E. M. Arnett, J. Am. Chem. Soc., 1981, 103, 481.
16. K. Fumino, A. Wulf and R. Ludwig, Angew. Chem., Int. Ed., 2009, 48, 3184.
17. R. Atkin and G. G. Warr, J. Phys. Chem. B, 2008, 112, 4164.
18. R. Hayes, S. Imberti, G. G. Warr and R. Atkin, Phys. Chem. Chem. Phys., 2011, 13, 3237.
19. R. Hayes, G. G. Warr and R. Atkin, Chem. Rev., 2015, 115, 6357.
20. R. Hayes, S. Imberti, G. G. Warr and R. Atkin, Angew. Chem., Int. Ed., 2013, 125, 4721.
21. Y. Umebayashi, W. Chung, T. Mitsugi, S. Fukuda, M. Takeuchi, K. Fujii, T. Takamuku, R. Kanzaki and S. Ishiguro, J. Comput. Chem., Jpn., 2008, 7, 125.
22. R. Hayes, S. Imberti, G. G. Warr and R. Atkin, Angew. Chem., Int. Ed., 2013, 52, 4623.
23. J. A. Mccune, A. H. Turner, F. Coleman, C. M. White, S. K. Callear, T. G. A. Youngs, M. Swadźba-Kwaśny and J. D. Holbrey, Phys. Chem. Chem. Phys., 2015, 17, 6767.
24. R. Hagiwara, K. Matsumoto, Y. Nakamori, T. Tsuda, Y. Ito, H. Matsumoto and K. Momota, J. Electrochem. Soc., 2003, 150, D195.
25. R. Hagiwara and Y. Ito, J. Fluorine Chem., 2000, 105, 221.
26. K. Matsumoto and R. Hagiwara, J. Fluorine Chem., 2007, 128, 317.
27. R. Hagiwara, Y. Nakamori, K. Matsumoto and Y. Ito, J. Phys. Chem. B, 2005, 109, 5445.
28. R. Hagiwara, T. Hirashige, T. Tsuda and Y. Ito, J. Fluorine Chem., 1999, 99, 1.
29. Y. Saito, K. Hirai, K. Matsumoto, R. Hagiwara and Y. Minamizaki, J. Phys. Chem. B, 2005, 109, 2942.
30. J. W. Shuppert and C. A. Angell, J. Chem. Phys., 1977, 67, 3050.
31. G. Driver and K. E. Johnson, Green Chem., 2003, 5, 163.
32. K. M. Johansson, E. I. Izgorodina, M. Forsyth, D. R. MacFarlane and K. R. Seddon, Phys. Chem. Chem. Phys., 2008, 10, 2972.
33. G. A. Olah, T. Mathew, A. Goeppert, B. Török, I. Bucsi, X.-Y. Li, Q. Wang, E. R. Marinez, P. Batamack, R. Aniszfeld and G. K. Surya Prakash, J. Am. Chem. Soc., 2005, 127, 5964.
34. M. Yoshizawa, W. Xu and C. A. Angell, J. Am. Chem. Soc., 2003, 125, 15411.
35. R. Hayes, S. Imberti, G. G. Warr and R. Atkin, Angew. Chem., Int. Ed., 2012, 51, 7468.
36. T. L. Greaves and C. J. Drummond, Chem. Rev., 2015, 115, 11379.
37. C. Andreani, C. Petrillo and F. Sacchetti, Mol. Phys., 1986, 58, 299.
38. A. R. Moodenbaugh, J. E. Hartt, J. J. Hurst, W. Youngblood, D. E. Cox and B. C. Frazer, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 28, 3501.
39. P. C. Pascard-Billy, Acta Crystallogr., 1965, 18, 827.
40. A. D. Fortes, I. G. Wood and K. S. Knight, J. Chem. Phys., 2006, 125, 1.
41. H. E. Maynard-Casely, H. E. A. Brand and K. S. Wallwork, J. Appl. Crystallogr., 2012, 45, 1198.
42. T. K. Hirsch and L. Ojamae, Acta Crystallogr., 2004, B60, 179.
43. D. Mootz and A. Merschenz-Quack, Z. Naturforsch., B: J. Chem. Sci., 1987, 42, 1231.
44. A. D. Fortes, I. G. Wood, L. Vočadlo, L. Chapon, K. S. Knight and R. I. Smith, J. Chem. Phys., 2008, 5, 128.
45. A. K. Soper and M. G. Phillips, Chem. Phys., 1986, 107, 47.
46. Y. Kameda, K. Hosoya, S. Sakamoto, H. Suzuki, T. Usuki and O. Uemura, Stud. Phys. Theor. Chem., 1995, 83, 305.
47. J. Curtius, K. D. Froyd and E. R. Lovejoy, J. Phys. Chem. A, 2001, 105, 10867.
48. E. R. Lovejoy and J. Curtius, J. Phys. Chem. A, 2001, 105, 10874.
49. G.-L. Hou, W. Lin, S. H. M. Deng, J. Zhang, W.-J. Zheng, F. Paesani and X.-B. Wang, J. Phys. Chem. Lett., 2013, 4, 779.
50. T. I. Yacovitch, N. Heine, C. Brieger, T. Wende, C. Hock, D. M. Neumark and K. R. Asmis, J. Phys. Chem. A, 2013, 117, 7081.
51. A. K. Soper, GudrunN and GudrunX: Programs for correcting raw neutron and X-ray diffraction data to differential scattering cross section, 2011.
52. J. A. Mccune, A. H. Turner, F. Coleman, C. M. White, S. K. Callear, T. G. A. Youngs, M. Swadźba-Kwaśny and J. D. Holbrey, Phys. Chem. Chem. Phys., 2015, 17, 6767.
53. A. K. Soper, C. Phys., 1996, 202, 295.
54. A. K. Soper, M. Phys., 2001, 99, 1503.
55. T. G. A. Youngs, J. D. Holbrey, C. L. Mullan, S. E. Norman, M. C. Lagunas, C. D’Agostino, M. D. Mantle, L. F. Gladden, D. T. Bowron and C. Hardacre, Chem. Sci., 2011, 2, 1594.
56. D. Bedrov, J.-P. Piquemal, O. Borodin, A. D. Mackerell Jr., B. Roux and C. Schröder, Chem. Rev., 2019, 119, 7940.
57. W. C. Tu, L. Weigand, M. Hummel, H. Sixta, A. Brandt-Talbot and J. P. Hallett, Cellulose, 2020, 27, 4745.
58. S. Imberti and D. T. Bowron, J. Phys.: Consens. Matter., 2010, 22, 404212.
59. M. Canales and E. Guàrdia, J. Mol. Liq., 2016, 224, 1064.
60. L. Saiz, J. A. Padro and E. Guardia, Mol. Phys., 1999, 97, 897.
61. T. F. Headen, C. A. Howard, N. T. Skipper, M. A. Wilkinson, D. T. Bowron and A. K. Soper, J. Am. Chem. Soc., 2010, 132, 5735.
62. J. J. Towey, A. K. Soper and L. Dougan, Faraday Discuss., 2013, 167, 159.
63. B. D. T. Bowron, J. L. Finney and A. K. Soper, Mol. Phys., 1998, 93, 531.
64. M. Falkowska, D. T. Bowron, H. G. Manyar, C. Hardacre and T. G. A. Youngs, ChemPhysChem, 2016, 17, 2043.
65. O. S. Hammond, D. T. Bowron and K. J. Edler, Green Chem., 2016, 18, 2736.
66. O. S. Hammond, K. J. Edler, D. T. Bowron and L. Torrente-murciano, Nat. Commun., 2017, 8, 14150.
67. I. Tankov, R. Yankova, S. Genieva, M. Mitkova and D. Stratiev, J. Mol. Struct., 2017, 1139, 400.
68. R. D. Rogers and C. B. Bauer, J. Chem. Crystallogr., 1994, 24, 285.
69. C. Hardacre, J. D. Holbrey, M. Nieuwenhuyzen and T. G. A. Youngs, Acc. Chem. Res., 2007, 40, 1146.
70. T. F. Headen, P. L. Cullen, R. Patel, A. Taylor and N. T. Skipper, Phys. Chem. Chem. Phys., 2018, 20, 2704.
71. A. H. Turner, S. Imberti, M. Swadźba-Kwaśny and J. D. Holbrey, Faraday Discuss., 2018, 206, 247.
72. A. H. Turner, E. L. Byrne, T. Pereira and J. D. Holbrey, Phys. Chem. Chem. Phys., 2020, 22, 10219.
73. A. H. Turner and J. D. Holbrey, J. Solution Chem., 2015, 44, 621.
74. M. M. Seitkalieva, A. v Vavina, A. v Posvyatenko, K. S. Egorova, A. S. Kashin, E. G. Gordeev, E. N. Strukova, L. v Romashov and V. P. Ananikov, ACS Sustainable Chem. Eng., 2021, 9, 3552.
75. A. R. Abouelela, A. Al Ghatta, P. Verdía, M. Shan Koo, J. Lemus and J. P. Hallett, ACS Sustainable Chem. Eng., 2021, 9, 10524.
76. C.-G. Ding, T. Taskila, K. Laasonen and A. Laaksonen, Chem. Phys., 2003, 287, 7.
77. G. F. King and M. Mobli, in Comprehensive Natural Products II, ed. H.-W. Liu and L. Mander, 2010, p.314.
78. A. K. Soper, ISRN Phys. Chem., 2013, 1.
79. S. Lenton, N. H. Rhys, J. J. Towey, A. K. Soper and L. Dougan, Nat. Commun., 2017, 8, 919.
80. H. K. Stassen, R. Ludwig, A. Wulf and J. Dupont, Chem. – Eur. J., 2015, 21, 1.
81. F. J. V. Gschwend, F. Malaret, S. Shinde, A. Brandt-Talbot and J. P. Hallett, Green Chem., 2018, 20, 3486.
82. F. Malaret, F. J. V. Gschwend, J. M. Lopes, W. C. Tu and J. P. Hallett, RSC Adv., 2020, 10, 16050.
83. C. L. Chambon, P. Verdía, P. S. Fennell and J. P. Hallett, Sci. Rep., 2021, 11, 15383.
84. C. L. Chambon, T. Y. Mkhize, P. Reddy, A. Brandt-Talbot, N. Deenadayalu, P. S. Fennell and J. P. Hallett, Biotechnol. Biofuels, 2018, 11, 1.
85. R. Muazzam, A. M. Asim, M. Uroos, N. Muhammad and J. P. Hallett, RSC Adv., 2021, 11, 19095.
86. A. R. Abouelela and J. P. Hallett, ACS Sustainable Chem. Eng., 2021, 9, 704.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp04292d

---