On the microscopic origin of Soret coefficient minima in liquid mixtures

Abstract

Temperature gradients induce mass separation in mixtures in a process called thermodiffusion and quantified by the Soret coefficient. The existence of minima in the Soret coefficient of aqueous solutions at specific salt concentrations was controversial until fairly recently, where a combination of experiments and simulations provided evidence for the existence of this physical phenomenon. However, the physical origin of the minima and more importantly its generality, e.g. in non-aqueous liquid mixtures, is still an outstanding question. Here, we report the existence of a minimum in liquid mixtures of non-polar liquids modelled as Lennard-Jones mixtures, demonstrating the generality of minima in the Soret coefficient. The minimum originates from a coincident minimum in the thermodynamic factor, and hence denotes a maximization of non-ideality mixing conditions. We rationalize the microscopic origin of this effect in terms of the atomic coordination structure of the mixtures.

---

Introduction

Thermal gradients induce the transport of colloids in suspension (thermophoresis) and concentration gradients in liquid mixtures and solutions (thermodiffusion). The Soret coefficient, S_T, measures the mass separation of mixtures in thermal fields and is becoming a central property to characterise the non-equilibrium response of soft matter and fluids.^1–8

Experimental and computational studies have advanced significantly in recent years, but several outstanding questions remain. One such question is the microscopic origin of the forces driving the phenomenology observed in thermodiffusion measurements. Aqueous solutions feature a particularly rich phenomenology.^9–11 Gaeta et al.¹⁰ reported minima in the Soret coefficients of NaCl_(aq) and KCl_(aq) as a function of concentration. These experiments were performed with thermogravitational columns, and the minima could not be reproduced using state-of-the-art thermal diffusion forced Rayleigh scattering techniques, which circumvent convection effects.¹¹ Hence the S_T minimum remained controversial for many years. However, this situation changed with recent experiments and computer simulations of LiCl_(aq), which support the existence of a minimum in the Soret coefficient.^12,13 Very recently, minima at high concentrations (∼2 M) were observed for thiocyanate (NaSCN_(aq) and KSCN_(aq)) and acetate (CH₃COOK_(aq)) salt solutions,^14,15 giving further impetus to the investigation of the physical origin of the S_T minima.

In addition to aqueous electrolyte solutions, minima in S_T with composition were observed in mixtures of polar fluids: ethanol/water,^5,16,17 dimethyl-sulfoxide/water¹⁸ and acetone/water.^18,19 In all these systems (electrolyte solutions and polar fluid mixtures), one of the components is water. This observation might suggest that the S_T minima are interlinked with water as a solvent and, therefore, its specific thermal transport properties. Indeed, molecular simulations of atomistic (non-polar) Lennard-Jones (LJ) binary mixtures at supercritical conditions do not offer evidence for the existence of minima in S_T with composition.²⁰ However, some experiments of non-polar or weakly polar liquid mixtures reported maxima/minima in S_T (e.g. cyclohexane/cis-decaline) and in some cases, accounting for an extrapolation to infinite dilution, a weak extrema can be inferred (e.g. toluene/1,3-dichlorobenzene).²¹ That work made no attempt to explain the microscopic origin of the extrema in S_T, but crucially highlights the importance of the thermodynamic factor, Γ, a key quantity determining the heat of transport.^13,22

To investigate the existence of Soret coefficient minima in non-polar mixtures, and to probe the microscopic origin of such minima, we have performed computer simulations of the simplest liquid binary mixture, modelled with the Lennard-Jones model, which accounts for dispersion interactions. We show for the first time that a minimum in the Soret coefficient at a specific composition, and constant temperature T and pressure P, can be observed in simple non-polar liquid mixtures, hence showing that the minimum is a completely general physical phenomenon.

Methods

We consider binary LJ mixtures at constant T and P, and different mole fractions x₁. Inter-particle interactions were modelled using the LJTS potential, which is the LJ potential |[scr V, script letter V]^LJ_ij(r) = 4ε_ij[(σ_ij/r)¹² − (σ_ij/r)⁶] truncated and shifted at a cutoff radius of r_c = 2.5σ, |[scr V, script letter V]^LJTS_ij(r) = ([scr V, script letter V]^LJ_ij(r) − [scr V, script letter V]^LJ_ij(r_c))θ(r_c − r) with θ being the Heaviside step function. All the particles have the same diameter and mass, but the interactions between of particles of type “1” or “2” are different. The parameters ε = ε₂₂ and σ = σ₁₁ = σ₂₂ together with the mass of each particle m₁ = m₂ = m define the usual LJ units. The energy scale was defined in terms of the high-boiling component, with ε₁₁/ε₂₂ = 0.6. The Lorentz–Berthelot combining rules were used for and σ₁₂ = (σ₁₁ + σ₂₂)/2 = σ. Experiments of liquid–liquid mixtures have reported extrema in S_T, therefore we target subcritical conditions for the LJ mixtures. Mixtures were modelled at T = 0.62εk_B⁻¹ (k_B is the Boltzmann constant) and P = 0.46 εσ⁻³, below the critical point²³ for both species. The entire 0 ≤ x₁ ≤ 1 composition domain is therefore expected to be subcritical. We note that along this isobar-isotherm, the thermodynamically stable phase for x₁ = 0 is a solid and we estimate the liquids to be at x₁ ≈ 0.2 (see the ESI†). Simulations below this mole fraction correspond to a metastable liquid–liquid mixture. Nevertheless, as we will show below, the observed S_T minimum is safely within the liquid–liquid mixture portion of the phase diagram.

We performed a variety of equilibrium molecular simulations (EMS), molecular dynamics (MD) and Monte Carlo methods, as well as non-equilibrium molecular dynamics (NEMD) simulations to calculate S_T and related quantities. From NEMD, S_T was evaluated at the stationary state characterised by zero net mass flux as S_T = − (w₁w₂)⁻¹(∇w₁/∇T) = −(x₁x₂)⁻¹(∇x₁/∇T) where x_i and w_i are the mole and mass fractions of species i. EMS methods calculate S_T ≡ D_T/D₁₂ from²⁴ the mutual diffusion coefficient D₁₂ = L₁₁(∂μ_s,1/∂w₁)_P,T/(ρw₂T) and thermal diffusion coefficient . Onsager's phenomenological coefficients L_αβ were calculated using the Green–Kubo (GK) integral formulas and taking into account the enthalpy terms for . The chemical potential μ₁, and subsequently the specific chemical potential μ_s,1 = μ₁/m₁, was calculated using a free energy perturbation (FEP) method at constant T and P. (∂μ₁/∂x₁)_P,T was then calculated from the numerical derivative of μ₁. (∂μ₁/∂x₁)_P,T was also obtained from Kirkwood–Buff solution theory via two different methods of evaluating the Kirkwood–Buff integrals (KBIs): (1) from particle number fluctuations in grand canonical Monte Carlo (GCMC) simulations and (2) from the extrapolation to infinite system size of finite-volume KBIs,²⁵ which were in turn calculated using radial distribution functions (RDFs) from MD simulations in the NVT ensemble. Thus, three EMS methods were used to calculate (∂μ₁/∂x₁)_P,T and subsequently the thermodynamic factor: FEP, KBI(RDF) and KBI(GCMC). Combining these with the GK calculations for L₁₁ and give three corresponding “equilibrium” routes to S_T: GK + FEP, GK + KBI(RDF) and GK + KBI(GCMC). Other thermophysical properties were also calculated from MD simulations. Details about all these simulations and calculations are given in the ESI.† All simulations were performed using LAMMPS²⁶ (v. 3 March 2020).

Results & discussion

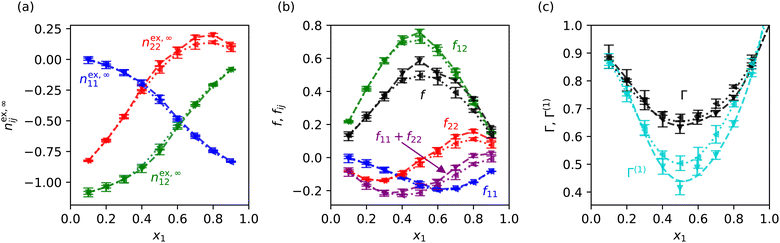
Fig. 1(a) contains the main result of this communication: S_T features a minimum as a function of composition at . Fitting cubic functions to the data give for all four methods: NEMD, GK + FEP, GK + KBI(RDF) and GK + KBI(GCMC). The thermodiffusion response at the minimum is significantly enhanced with respect to diluted mixtures, by ∼30–40% relative to x₁ = 0.1, 0.9, and by ∼60–80% when compared to the extrapolated value of S_T at x₁ = 1. For all compositions, S_T < 0 which indicates that species 1 (the low-boiling component) is thermophilic and preferentially collects in the hot region. The S_T values calculated from NEMD and all three EMS methods are in excellent agreement.

Fig. 1 The Soret coefficient S_T and related properties as a function mole fraction x₁. (a) S_T; the solid lines show cubic functions fit to the S_T(x₁) data. (b) The mutual diffusion coefficient D₁₂ (left axis) and thermal diffusion coefficient D_T (right axis). (c) The thermodynamic factor Γ; the solid lines show polynomial functions fit to Γ(x₁) with the infinite-dilution constraint Γ(1) = 1. (d) The ratio of phenomenological coefficients ; the solid line shows the weighted arithmetic mean.

S _T ≡ D_T/D₁₂ is determined by D₁₂ and D_T, which monotonically increase and decrease with x₁, respectively (Fig. 1(b)). Thus, the S_T minimum arises from a balance of D_T and D₁₂, as opposed to being carried through only by one of the transport coefficients.

The Soret coefficient S_T can be written in terms of the phenomenological coefficients and the thermodynamic factor Γ, as²⁴

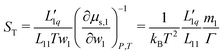where m₁ = m₂ ⇔ x₁ = w₁. The analysis of the different contributions to the RHS of eqn (1) offers microscopic insight into the mechanisms determining the minimum in S_T. We find that the ratio is essentially constant for all compositions (Fig. 1(d)). This suggests that the minimum arises from the w₁(∂μ₁/∂w₁)_P,T term. As shown in Fig. 1(c), Γ features a distinctive minimum at x^min(Γ)₁ ∼ 0.5, with all three EMS methods predicting values in good agreement with each other. The minimum in S_Tis connected to the minimum in the thermodynamic factor, and therefore the minimum signals the composition at which the mixture features the largest non-ideality, max|1 − Γ|.

We note that in our work, the minimum in Γ leads to a minimum in S_T since (L₁₁ ≥ 0,²⁴ and a stable single-phase binary mixture requires Γ > 0). For , the minimum in Γ leads to a maximum in S_T. Indeed, since S_T and D_T change sign under the permutation of components in a binary mixture (S_T,1 = −S_T,2 and D_T,1 = −D_T,2), the Γ minimum leads to a maximum in the Soret coefficient of species 2.

The results presented above indicate that the non-ideal contribution dominates at conditions near the minimum. This can be visualised by splitting Γ into its ideal (id) and excess (ex) parts (see ESI,† Section S1.2), showing as expected that Γ^ex, is responsible for the minimum in Γ. To gain insight into the microscopic origins of the minimum in Γ and S_T, we turn to Kirkwood–Buff theory, which connects Γ to the structural properties of the binary mixture,

where ρ_N is the total number density of the mixture. The Kirkwood–Buff integral (KBI) G_ij is defined as the spatial integral over g^μVT_ij(r) − 1, and quantifies the excess (or deficiency) of species j around i. g^μVT_ij(r) is the pair correlation function in the grand canonical ensemble. The KBIs can be expressed in terms of the excess coordination numbers n^ex_ij(r′) = n_ij(r′) − n^id_ij(r′) where n_ij is the total coordination number, obtained from an integral over the pair correlation function, and is the ideal coordination number. ρ_N,j is the number density of species j. Hence, the KBIs are given by , and the thermodynamic factor by Γ = (1 + f)⁻¹ where f = (1 − x₁)n^ex,∞₁₁ + x₁n^ex,∞₂₂ − 2x₁n^ex,∞₁₂ = f₁₁ + f₂₂ + f₁₂.

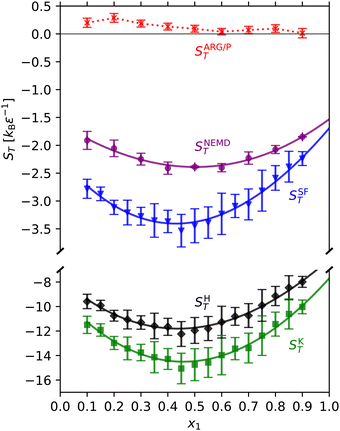
In order to disentangle the contributions from n^ex,∞₁₁, n^ex,∞₂₂ and n^ex,∞₁₂ we take the first-order approximation to the thermodynamic factor, Γ⁽¹⁾ = 1 − f. As shown in Fig. 2(c), Γ⁽¹⁾ results in underestimations of 1–35% across the range of compositions, with larger errors for more non-ideal mixtures, but nevertheless provides insight into the relative importance of the f_ij terms. f₁₂ features a maximum at x₁ ∼ 0.5 (Fig. 2(b)), indicating that the cross-species contribution is responsible for the minimum in Γ⁽¹⁾ and Γ. |(f₁₁ + f₂₂)/f₁₂| = 0–0.41 making the cross-species contribution much more significant, and ∼3–4 times larger in the region of the Γ⁽¹⁾ and Γ minima. Consequently, the phenomenology of Γ⁽¹⁾ and Γ are primarily determined by f₁₂. Thus, the composition dependence of n^ex,∞₁₂ (Fig. 2(a)), which represents a net depletion of species 2 around 1 relative to the ideal state, and increases monotonically with x₁, is the primary microscopic origin of the minimum in Γ and therefore S_T.

Fig. 2 Analysis of the thermodynamic factor Γ as a function of mole fraction x₁ using Kirkwood–Buff theory. (a) Excess coordination numbers n^ex,∞_ij and (b) related functions f and f_ij. (c) Γ and its first-order approximation Γ⁽¹⁾. Symbols: sideways triangles and dotted lines (··◁··) denote the KBI(RDF) data; downwards triangles (--▽--) and dashed lines denote the KBI(GCMC) data. In (c), dotted and dashed lines show polynomial functions fit to the KBI(RDF) and KBI(GCMC) data respectively. Fits to Γ(x₁) were performed with the infinite-dilution constraint Γ(1) = 1.

Now we examine the accuracy of theoretical approaches to predict the S_T minimum reported above. We note that existing theoretical models do not accurately predict S_T in general.^27–33 In some cases, even the sign of S_T is not predicted correctly.^28–33 Especially in earlier works, the discrepancies can, at least in part, be attributed to inaccuracies in experimentally determined properties. For example the Haase^30,34 and Kempers³⁰ models are very sensitive to partial molar properties, and therefore the equation of state used.^30,31 In computer simulations all the required quantities can be accurately calculated, and as shown here using an exact model, all the theories examined herein feature noticeable deviations from the S_T values obtained by direct simulation. Previous simulations have shown that the theories are accurate only in a very limited number of cases, even for simple LJ mixtures and hard-sphere mixtures.^20,32,33 We have tested the standard theoretical models against our simulation data. We calculate the Soret coefficient according to the models of Haase^30,34 (S^H_T), Kempers³⁰ (S^K_T), Shukla and Firoozabadi²⁹ (S^SF_T), and Artola, Rousseau and Galliéro³²/Prigogine^35,36 (S^ARG/P_T). Further details are given in the ESI.†

We show in Fig. 3 the Soret coefficients predicted by these models, alongside the NEMD values for reference. Out of the four models, S^SF_T is the most accurate: it overestimates |S_T| by ∼20–50%. S^K_T and S^H_T overestimate |S_T| by ∼400–500% and ∼300–400%, respectively. S^ARG/P_T underestimates |S_T| by ∼100–110%, predicting values ∼10⁻¹k_Bε⁻¹. Furthermore, the model predicts the wrong sign: S^ARG/P_T > 0 or straddles 0 when accounting for the associated uncertainties.

Fig. 3 Soret coefficient S_T as a function of x₁ as predicted by various models, as defined in the main text. The NEMD values S^NEMD_T are shown for reference. The solid lines show cubic functions fit to the S_T(x₁) data.

S ^H_T, S^K_T and S^SF_T all possess a minimum because they contain x₁(∂μ₁/∂x₁)_P,T = k_BTΓ in the denominator (see the ESI†). The x₁(∂μ₁/∂x₁)_P,T term in S^SF_T originates directly from the phenomenological equations for thermodiffusion from linear non-equilibrium thermodynamics, which the model uses as a starting point for its derivation. For S^K_T, the x₁(∂μ₁/∂x₁)_P,T term arises naturally from the statistical thermodynamics approach employed by Kempers. Originally an educated guess, S^H_T can be derived more rigorously within the framework of Kempers.³⁰ In contrast, S^ARG/P_T does not predict a minimum: it features a weak concentration dependence, and generally decreases with increasing x₁. S^ARG/P_T contains k_BT (as opposed to k_BTΓ) in the denominator, which is only valid for ideal mixtures. Indeed the ARG/P model does not explicitly consider a concentration gradient along the reaction coordinate; doing so would result in a similar “non-ideality” term in the denominator.³⁷

Closing remarks

We close this communication with a discussion of our results in the context of recent literature. LJ mixtures are representative of mixtures of approximately spherical non-polar molecules, in which intermolecular interactions are dominated by van der Waals forces. Comparing to mixtures of non-polar organic solvents, at 25 °C cyclohexane/cis-decalin possesses a S_T maximum at x₁ ≈ 0.2 but Γ ≈ 1.0 for the entire 0 ≤ x₁ ≤ 1 range (there is a very shallow Γ minimum at x₁ ≈ 0.8), indicative of a different origin compared to the LJ mixture. Also in contrast with the LJ mixture, cyclohexane/benzene features a monotonic increase of S_T with x₁ at 25 °C, but does have a strong minimum in Γ at x₁ ≈ 0.5.²¹

S _T minima have been observed in mixtures of polar organic solvents with water. Ethanol/water and acetone/water mixtures have minima at x₁ ∼ 0.6 and x₁ ∼ 0.5, respectively, roughly coincident with minima in D₁₂ and Γ for both mixtures.^{5,16–19,38,39} Comparing to aqueous solutions, while the S_T minimum examined in this work originates from a coincident minimum in Γ, for LiCl_(aq), Γ increases monotonically in the concentration range of the S_T minimum.¹³ Furthermore, simulations have highlighted the importance of ion solvation structure on the existence of the minimum in LiCl_(aq).⁴⁰ In contrast, local structural changes in the LJ mixture are minor (see ESI,† Section S1.4). We note that many simple salts are thought to have a D₁₂ minimum at low concentrations (∼10⁻¹ mol dm⁻³) often attributed to ion-pair formation and solute–solvent association.^14,41–43 Recent experiments observed S_T minima in NaSCN_(aq), KSCN_(aq), K₂CO_3(aq) and CH₃COOK_(aq) that are carried through D_T.^14,15 Hence, the physical origin of the minima in aqueous solutions and mixtures might be quite different to the one reported here for non-polar liquids, since the LJ mixtures do not feature extrema in D₁₂ or D_T.

It is evident that the physical origins of S_T minima/maxima must be considered on a case-by-case basis for different mixtures, even those belonging to the same class (aqueous solution, non-polar organic solvent mixtures, etc.). We provide here a proof of principle and demonstrate that S_T minima can exist in even the simplest of mixtures, as exemplified by a binary LJ mixture in which the components differ by only the interaction parameter ε. The concentration dependence of the S_T is, at least for simple mixtures, typically attributed to the cross-interactions between unlike particles²⁰ – a notion sustained in recent reviews.^7,44,45 For dense supercritical LJ mixtures with cross-interactions given by 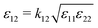it was found that S_T(x₁) ≈ bx₁ + c, with the slope b controlled by k₁₂.²⁰ Greater |1 − k₁₂| values resulted in greater |b| values. In this work, we identify a mixture with k₁₂ = 1 that nevertheless features a strong composition dependence and more complex phenomenology (the S_T minimum). Extrapolating our results, we expect that the observation of Soret coefficient minima/maxima in LJ mixtures is strongly correlated with their degree of non-ideality; sufficiently non-ideal mixtures might be more difficult to achieve at e.g. supercritical conditions. Clearly, further work is required to explain the composition dependence of S_T in liquid mixtures and different thermodynamic conditions.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank the Leverhulme Trust for Grant No. RPG-2018-384. We gratefully acknowledge a PhD studentship (Project Reference 2135626) for O. R. G. sponsored by ICL's Chemistry Doctoral Scholarship Award, funded by the EPSRC Doctoral Training Partnership Account (EP/N509486/1). We acknowledge the ICL RCS High Performance Computing facility and the UK Materials and Molecular Modelling Hub for computational resources, partially funded by the EPSRC (Grant No. EP/P020194/1 and EP/T022213/1).

Notes and references

1. S. Duhr and D. Braun, Phys. Rev. Lett., 2006, 96, 168301.
2. S. Duhr and D. Braun, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 19678–19682.
3. S. N. Rasuli and R. Golestanian, Phys. Rev. Lett., 2008, 101, 108301.
4. A. Würger, Phys. Rev. Lett., 2008, 101, 108302.
5. S. Wiegand, J. Phys.: Condens. Matter, 2004, 16, R357–R379.
6. R. Piazza, Soft Matter, 2008, 4, 1740–1744.
7. W. Köhler and K. I. Morozov, J. Non-Equilib. Thermodyn., 2016, 41, 151–197.
8. C. J. Wienken, P. Baaske, U. Rothbauer, D. Braun and S. Duhr, Nat. Commun., 2010, 1, 100.
9. K. Alexander, Z. Phys. Chem., 1954, 203, 213–227.
10. F. S. Gaeta, G. Perna, G. Scala and F. Bellucci, J. Phys. Chem., 1982, 86, 2967–2974.
11. F. Römer, Z. Wang, S. Wiegand and F. Bresme, J. Phys. Chem. B, 2013, 117, 8209–8222.
12. J. Colombani, J. Bert and J. Dupuy-Philon, J. Chem. Phys., 1999, 110, 8622–8627.
13. S. Di Lecce, T. Albrecht and F. Bresme, Sci. Rep., 2017, 7, 44833.
14. S. Mohanakumar, J. Luettmer-Strathmann and S. Wiegand, J. Chem. Phys., 2021, 154, 084506.
15. S. Mohanakumar and S. Wiegand, Eur. Phys. J. E: Soft Matter Biol. Phys., 2022, 45, 10.
16. A. Königer, B. Meier and W. Köhler, Philos. Mag., 2009, 89, 907–923.
17. L. Zhang, Q. Wang, Y.-C. Liu and L.-Z. Zhang, J. Chem. Phys., 2006, 125, 104502.
18. H. Ning and S. Wiegand, J. Chem. Phys., 2006, 125, 221102.
19. H. Cabrera, L. Martí-López, E. Sira, K. Rahn and M. García-Sucre, J. Chem. Phys., 2009, 131, 031106.
20. P.-A. Artola and B. Rousseau, Phys. Rev. Lett., 2007, 98, 125901.
21. S. Hartmann, G. Wittko, F. Schock, W. Groß, F. Lindner, W. Köhler and K. I. Morozov, J. Chem. Phys., 2014, 141, 134503.
22. J. N. Agar, C. Y. Mou and J. L. Lin, J. Phys. Chem., 1989, 93, 2079–2082.
23. M. Thol, G. Rutkai, R. Span, J. Vrabec and R. Lustig, Int. J. Thermophys., 2015, 36, 25–43.
24. S. R. de Groot and P. Mazur, Non-Equilibrium Thermodynamics, Dover, 1984.
25. P. Krüger, S. K. Schnell, D. Bedeaux, S. Kjelstrup, T. J. H. Vlugt and J.-M. Simon, J. Phys. Chem. Lett., 2013, 4, 235–238.
26. A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in’t Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171.
27. M. Eslamian and M. Z. Saghir, J. Non-Equilib. Thermodyn., 2009, 34, 97–131.
28. L. J. T. M. Kempers, J. Chem. Phys., 1989, 90, 6541–6548.
29. K. Shukla and A. Firoozabadi, Ind. Eng. Chem. Res., 1998, 37, 3331–3342.
30. L. J. T. M. Kempers, J. Chem. Phys., 2001, 115, 6330–6341.
31. M. G. Gonzalez-Bagnoli, A. A. Shapiro and E. H. Stenby, Philos. Mag., 2003, 83, 2171–2183.
32. P.-A. Artola, B. Rousseau and G. Galliéro, J. Am. Chem. Soc., 2008, 130, 10963–10969.
33. H. Hoang and G. Galliero, Eur. Phys. J. E: Soft Matter Biol. Phys., 2022, 45, 42.
34. R. Haase, Z. Phys., 1949, 127, 1–10.
35. I. Prigogine, L. De Brouckere and R. Amand, Physica, 1950, 16, 577–598.
36. I. Prigogine, L. De Brouckere and M. R. Amand, Physica, 1950, 16, 851–860.
37. W. M. Rutherford and H. G. Drickamer, J. Chem. Phys., 1954, 22, 1157–1165.
38. M. T. Tyn and W. F. Calus, J. Chem. Eng. Data, 1975, 20, 310–316.
39. R. Taylor and H. A. Kooijman, Chem. Eng. Commun., 1991, 102, 87–106.
40. S. Di Lecce, T. Albrecht and F. Bresme, Phys. Chem. Chem. Phys., 2017, 19, 9575–9583.
41. G.-H. Gao, H.-B. Shi and Y.-X. Yu, Fluid Phase Equilib., 2007, 256, 105–111.
42. J. P. Mitchell, J. B. Butler and J. G. Albright, J. Solution Chem., 1992, 21, 1115–1129.
43. A. Katz and S. Ben-Yaakov, Mar. Chem., 1980, 8, 263–280.
44. P.-A. Artola and B. Rousseau, Mol. Phys., 2013, 111, 3394–3403.
45. K. Harstad, Ind. Eng. Chem. Res., 2009, 48, 6907–6915.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp04256h

---