DOI:
10.1039/D2CP04155C
(Perspective)
Phys. Chem. Chem. Phys., 2023,
25, 1546-1555
Machine learning in computational chemistry: interplay between (non)linearity, basis sets, and dimensionality
Received
7th September 2022
, Accepted 6th December 2022
First published on 7th December 2022
Abstract
Machine learning (ML) based methods and tools have now firmly established themselves in physical chemistry and in particular in theoretical and computational chemistry and in materials chemistry. The generality of popular ML techniques such as neural networks or kernel methods (Gaussian process and kernel ridge regression and their flavors) permitted their application to diverse problems from prediction of properties of functional materials (catalysts, solid state ionic conductors, etc.) from descriptors to the building of interatomic potentials (where ML is currently routinely used in applications) and electron density functionals. These ML techniques are assumed to have superior expressive power of nonlinear methods, and are often used “as is”, with concepts such as “non-parametric” or “deep learning“ used without a clear justification for their need or advantage over simpler and more robust alternatives. In this Perspective, we highlight some interrelations between popular ML techniques and traditional linear regressions and basis expansions and demonstrate that in certain regimes (such as a very high dimensionality) these approximations might collapse. We also discuss ways to recover the expressive power of a nonlinear approach and to help select hyperparameters with the help of high-dimensional model representation and to obtain elements of insight while preserving the generality of the method.
1. Introduction
Constructing an input–output mapping is an often-encountered problem in physical chemistry. Rational design of materials is facilitated by understanding the dependence of performance characteristics (such as the catalytic activity of surfaces or nanoparticles used in heterogeneous catalysis, the ionic conductance of solids used in solid oxide fuel cells and metal ion batteries, the band gap of organic and inorganic materials used in optoelectronic application, etc) on a set of descriptors.1–8 This dependence is in general multi-dimensional, with descriptions typically including multiple atomistic composition descriptors, electronic structure related descriptors, and others.9–12
Machine learning (ML) methods are more and more often used for this purpose as they allow one to build structure–property/performance mappings in a black-box way, with limited need for a domain-specific method or software choice. ML is also more and more used in method development for computational and theoretical chemistry. Machine-learned interatomic potentials are now routine,13–18 and there is good potential for machine-learned functionals for DFT (density functional theory), including exchange correlation and kinetic energy functionals, to be available in end-user codes in the near future.19–25
Two classes of ML methods stand out as the most widely used in the above applications: neural networks (NNs)26 and kernel-based regression methods such as Gaussian process regression27 or kernel ridge regression.28 Even though a single-hidden layer NN is a universal approximator, multilayer NNs are often used, from traditional multilayer feed-forward NNs to more complex architectures such as convolutional NNs, making use of the concept of “deep learning”. The kernel methods are used for their “non-parametric” nature and have been argued to possess a higher learning power than NNs.29,30
It is the generality of these ML techniques that permits their application to such diverse problems. It also allows easy use by non-experts including students. This generality comes at a price of a lack of insight provided by physically motivated models. ML techniques (and black-box methods in general) are also notoriously bad at extrapolation. This means that despite their generality, domain knowledge should be used to define descriptors in such a way that the ML method is not called in the extrapolation regime. ML approaches such as NN and other non-linear methods also require more data than physically motivated models and simple linear regressions. This can be an issue in high-dimensional spaces, as data acquisition may be costly (for example, CPU-costly ab initio calculations), and the low-density of data may not allow for quality ML. We note that data density is bound to be low in high-dimensional spaces, and this issue cannot be resolved by simply adding more data by virtue of the curse of dimensionality.31
ML methods are often used “as is”, with concepts such as “non-parametric” or “deep learning“ used without a clear justification for their need or advantage over simpler and more robust alternatives such as plain linear regressions or single hidden layer NNs. ML techniques are assumed to have the superior expressive power of nonlinear methods. In this Perspective, we highlight some interrelations between popular ML techniques and traditional linear regressions and basis expansions and demonstrate that in certain regimes (such as a very high dimensionality of the feature space) these approximations might collapse. We also discuss ways to recover the expressive power of a nonlinear approach with the help of high-dimensional model representation (HDMR)32–35 which also allows introducing elements of insight while preserving the general nature of the method.
2. Popular machine learning methods and some connections
The key promise of ML techniques is that they help avoid the exponential scaling of the number of terms in a representation and in the number of data needed to determine the terms of the representation. The exponential scaling, the so-called curse of dimensionality,31 holds for the direct product type of representations (such as the Fourier expansion). The ML techniques briefly recapitulated below are effectively representations making use of non-direct product types of basis expansions, which are also flexibilized by parameterization.
2.1. Neural networks as basis expansion with a non-direct product basis
We do not aim here to give an introduction to neural networks, the reader is referred for that to the abundant literature,15,26 but to highlight their certain properties. We are interested in regression types of feed torward NN. A simple single-hidden layer NN meant to represent a function f(x), x ∈ RD can be described by the equation| | 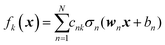 | (2.1.1) |
where we introduced the subscript k (dropped in the following) to indicate that an NN may have multiple outputs (e.g. a potential energy and its gradient or multiple wavefunctions of the same potential). Eqn (2.1.1) assumes a linear output neuron without the loss of generality, as a nonlinear monotonic output neuron, as well as any output bias, can be subsumed into the left hand side of the equation. We also introduced a subscript n to account for the possibility of using different activation functions σn for different neurons, although this is not common in applications. With any smooth nonlinear σn and even with σn(x) = σ(x) (i.e. all neurons having the same functional form), this is a universal approximator36–39 in the sense that 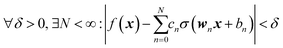 .
.
Eqn (2.1.1) is an expansion over a flexible, tunable to the problem basis set {σn}. Here we use the subscript n to indicate that even when the functional form is the same for all neurons, the basis functions are different due to the effect of wn, bn. This view also holds for the multilayer NN
| | 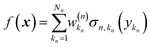 | (2.1.2) |
where
| | 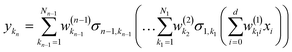 | (2.1.3) |
and where the basis is {
σn,kn}. This also highlights the fact that a nonlinear regression can be viewed as a linear regression over a set of generally redundant descriptors
y ∈ R
Nn which nonlinearly depend on the vector of original descriptors
x. Note that in
eqn (2.1.2) and (2.1.3) we subsumed biases into weights (which can be done by introducing dummy variables
x0 set to 1) without loss of generality.
2.2. Kernel methods on the example of Gaussian process regression – a fancy name for a linear regression
In Gaussian process regression (GPR)27 one postulates a covariance function between training set data points x(i) and x(j): k(x,x′). It is typically assumed to be one of Matern type of functions| | 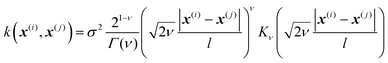 | (2.2.1) |
where σ2 is a prefactor which is often set to the variance of the target, and v and l are hyperparameters. Γ(v) is the Gamma function and Kv is the modified Bessel function. v is typically preset to one of ∞, 1/2, 3/2, 5/2, giving rise, respectively, to the square exponential (Gaussian-like), simple exponential, Matern3/2 and Matern5/2 kernels.40 The length parameter l as well as the prefactor may be optimized with methods such as MLE (maximum likelihood estimator)41 or other.42–46 The value of the target function at an arbitrary point x is then estimated aswhere f is a vector of all known f(x(n)) values, K is the covariance matrix| | 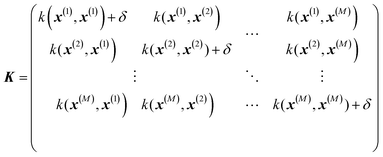 | (2.2.3) |
and| | | K* = (k(x, x(1)), k(x, x(2)), …, k(x, x(M)), K** = k(x,x) | (2.2.4) |
where M is the size of the training set. A “noise” hyperparameter δ is added to improve the generalization.
GPR is none other than a regularized linear regression, with a Tikhonov regularization parameter δ, over the basis bn(x) = k(x, x(n)):28
| | 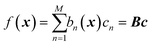 | (2.2.5) |
with coefficients
c =
K−1f. It is a linear regression where the number of basis functions is equal to the number of data points (matrix
B is square). This means there are no degrees of freedom left to appropriately optimize the basis parameters. The meaning of “Gaussian process” derives from the use of a covariance function for basis functions. Then
eqn (2.2.2) can be viewed as an estimate of the mean of a Gaussian distribution of values of
f(
x), and the variance of that distribution can be computed as
| | | Δf(x) = K** − K* K−1K*T | (2.2.6) |
Eqn (2.2.6) should not be used to compute error bars: the estimate of the mean can be quite accurate even when the fitting error is high. This happens in particular with additive models.
47–49 Note also that
eqn (2.2.6) as written (and as it usually appears in the literature) holds when the target is normalized or when the kernel has a prefactor equal to
σ2, as in
eqn (2.2.1); otherwise it should be scaled by the variance.
3. NN vs GPR: expressive power of a genuinely nonlinear method vs. robustness of a linear regression
3.1. Expressive power and the number of parameters
Both NN and GPR are expansions over a non-direct product basis. The basis functions of an NN, the neurons, are explicitly parameterized (with different parameters of each neuron) which gives rise to a large number of nonlinear parameters and associated dangers of overfitting. We note, however, that recent research indicates50 that overfitting need not happen even when the number of NN parameters is larger than the number of training data. In GPR, the basis parameters are forced to have the same value in all basis functions and are called hyperparameters. The number of neurons of a NN is typically much smaller than the number of training data points. In standard GPR, the number of basis functions is equal to the number of training data. A single hidden layer NN with N neurons-basis functions has (D + 1) × N nonlinear parameters and (if it has a linear output neuron) N linear parameters (eqn (2.2.1)). The GPR has M (number of training data) basis functions, correspondingly M linear parameters and the number of nonlinear (hyper)parameters is small, often ranging from one to D (length parameters of isotropic or anisotropic Matern kernels). Granted, the fitting of a multitude of nonlinear parameters is relatively CPU-costly, but as far as expressive power is concerned, NN is still a competitive proposition. In ref. 30 it was argued that GPR is equivalent to an infinite NN, and in ref. 29 it was demonstrated that GPR was “better” than NN in that it obtained a lower (test set) error with the same number of training data or alternatively that fewer data were needed to achieve the same error. In the example of ref. 29 when fitting 625 samples of the six-dimensional potential energy surface (PES) of the H2CO molecule, the GPR obtained a test error of 5.98 cm−1 with, respectively, 625 linear parameters and 625 basis functions. The NN required 1250 data and 100 neurons – basis functions to obtain a similar test set error of 5.74 cm−1, i.e. 700 nonlinear and 100 linear parameters. With 2500 training data, GPR obtained a test set error of 1.08 cm−1 with, respectively, 2500 linear parameters and 2500 basis functions. NN obtained a similar test set error of 1.12 cm−1 with 250 neurons – basis functions, i.e. 1750 nonlinear and 250 linear parameters. In light of the above, that result can be read as showcasing the more robust nature of a fixed-basis linear regression that is GPR when data are few rather than a higher expressive power. The expressive power of an NN is higher due to the more flexible (tuneable to each problem and independently for each basis function) basis set it uses. An NN requires fewer basis functions and sometimes fewer parameters overall than GPR. Good results have also been demonstrated in the literature with NNs which do not fit the nonlinear parameters at all – effectively using random basis functions.51 Radial basis function neural networks (RBFF), which are also universal approximators,52,53 feature more flexible basis functions of a similar type as GPR.
3.2. Sum of products property
Both NNs and GPR allow easy building of representations in the sum-of-products (SOP) form important for quantum dynamics54 and for any application where integration in multidimensional spaces is important, as then the integrals factor, i.e.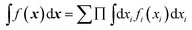 . With an NN, this is achieved by using a simple exponential neuron (σ(x) = ex) in a single hidden layer network:55
. With an NN, this is achieved by using a simple exponential neuron (σ(x) = ex) in a single hidden layer network:55| | 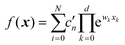 | (3.2.1) |
Multiplicative NNs were also introduced for this purpose but are somewhat more involved:56,57| | 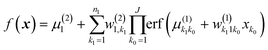 | (3.2.2) |
With GPR, a classic square exponential kernel being a product of corresponding univariate kernels, the GPR representation is a SOP. SOP NNs have been successfully used in MCTDH calculations58–60 and the SOP nature of GPR deserves to be explored more in quantum dynamics.
3.3. On hyperparameter tuning
We stressed above that, contrary to NNs, the Gaussian process linear regression uses as many basis functions as there are training data. This inhibits the ability to automatically tune basis parameters. Hyperparameters such as the length parameter still need to be carefully selected. We have documented failures of MLE when automatically optimizing hyperparameters when data are sparse.49,61 Automatic hyperparameter optimizers necessarily rely on information contained in available samples. What should be done, however, is the choice of hyperparameters to maximise the completeness of the basis bn(x) = k(x, x(n)) in relevant parts of the space of descriptors. In our experience, this required setting the length parameters to larger values than those recommended by automatic optimizers.
We proposed two ways to improve hyperparameter optimization. One is the rectangularization of GPR, using fewer basis functions than training data.61 This is related so some of the sparse GPR methods.62 Instead of the square matrix of eqn (2.2.5), one can use a rectangular matrix of size M × N with elements Bmn = k(x(n), x(m)), where N is the number of basis functions and M the number of training data. When M > N, i.e. with a rectangular version of eqn (2.2.5), it in general cannot be solved exactly, and the residual of a least-squared solution can be used to guide hyperparameter optimization to improve basis completeness,63–65
| | 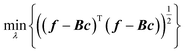 | (3.3.1) |
where
c =
B+f,
B+ is a Moore–Penrose pseudoinverse
66 of
B, and
λ subsumes all optimized hyperparameters. One can select (
e.g. randomly)
N from the available
M datapoints as basis centres. As one solves a rectangular problem in the least-squares sense, the parameter
δ (which could be introduced
via a singular value decomposition of
B) is not needed. We found that the rectangular approach gives as good a test set error without
δ as traditional GPR with optimized
δ,
49,61 and allows finding optimal hyperparameters with
eqn (3.3.1).
Another approach is using an additive model48,67,68 based on high-dimensional model representation (HDMR).33 We will introduce HDMR in more detail in Section 5; here it suffices to introduce a simple additive model
| | 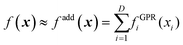 | (3.3.2) |
The component functions fGPRi(xi) can be built with high confidence from few data (if they are built with GPR, eqn (2.2.6) they will return very low variance precisely because the one-dimensional fGPRi(xi) are well-defined and will generally grossly understate the fitting error f(x) − fadd(x) which is due to the additive approximation). fadd(x) can then be used to sample from it a large pool of data that can be used to optimize the hyperparameters of the high-dimensional GPR model of f(x). We have shown, on the example of fitting a 15-dimensional PES of UF6, that “good enough” (albeit not perfect, due to the difference between f(x) and fadd(x)) hyperparameters can be identified in this way.49
4. When is “deep learning” needed?
We stressed above that a single hidden layer NN is a universal approximator. The universal approximator theorems37 concerned themselves with the power of representation and did not take into account the data aspect of machine learning. In other words, there is in them an implicit condition “provided that as many samples of the target function are available as needed, in all relevant parts of the space”. When they are available, in principle, one should never need a multi-layer NN. In our experience with NNs fitting of potential energy surfaces of small molecules,15,16 as well as in other settings, we did not find it advantageous to use multilayer NNs. The data distribution in the case of PES fitting is smooth. When a low density of data in some parts of the configuration space led to overfitting, tandem NNs, where first a smaller NN is fitted without the danger of overfitting, and the error of that model is refitted with a larger NN and capped by using e.g. a sigmoid output neuron, was found to be useful.69
The data, however, may not be available on demand. The cost of their computation may be high (examples are ab initio data for systems beyond small molecules) and/or because of the nature of the problem, the data may be very unevenly distributed. An example of this kind of application is machine learning of Kohn-Sham kinetic energy density (KED) τ or its positive-definite version τ+ from the electron density for the construction of kinetic energy functionals (KEF) for orbital-free DFT:70
| | 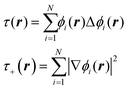 | (4.1) |
where
ϕi® are Kohn–Sham orbitals and the sum is over occupied orbitals (spin and partial occupancies are ignored without the loss of generality). The distributions of the KED and of the density-dependent machine learning features (such as those considered in Section 6) are extremely uneven. Examples of the distribution of
τ+ for crystalline aluminum and magnesium are shown in
Fig. 1.
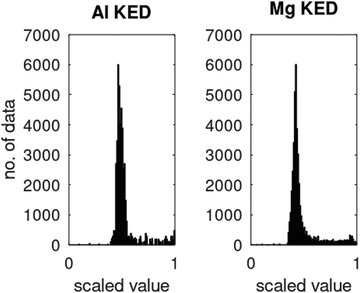 |
| | Fig. 1 Distributions of kinetic energy densities τ+ of crystalline aluminium and magnesium computed as described in ref. 19. The values are scaled to [0, 1]. | |
Distributions of some density-dependent features (such as those in eqn (6.1) below) are even more extreme (see ref. 19). We found that in this case, multi-layer NNs are useful. While we were able to obtain good fits to Kohn–Sham KED of individual materials with single hidden layer NNs, it was not possible when machine learning KED from several materials simultaneously – which is needed to achieve the portability of the KEF. A multilayer NN was able to achieve an accurate fitting of the data from several materials simultaneously (Li, Mg, and Al in the occurrence, see ref. 20 for details).
5. Interplay of (non)linearity and dimensionality
5.1. Collapse of the Matern kernel-based regression in very high dimensional feature spaces
While the SOP form of the square exponential kernel,| | 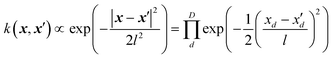 | (5.1.1) |
is very useful for quantum dynamics or other applications requiring integration, it may lead to a collapse of the GPR approximation when the dimensionality is very high. The univariate factors of eqn (5.1.1) are all smaller than 1, and the product tends toward zero as D → ∞ unless also l → ∞. This effect is also expected with the other Matern kernels because of their qualitatively similar shape even though they are not formally in the product form. The optimal length parameter tends to increase with dimensionality. For example, when fitting the six-dimensional PES of formaldehyde (in normalized bond coordinates), the optimal length parameter was on the order of 5, while for the 15-dimensional PES of UF6 it was on the order of 30 (also with normalized descriptors).49,61,67 As l increases, there is a loss of resolution of the kernel in any one direction, and the GPR approximation loses its advantage over a simple linear regression. Moreover, when the distribution of the data on which the model is used after it is trained is any different (which it practically always is) from the distribution of the training data, the GPR approximation necessarily collapses when D → ∞. This was observed in the GPR of forecasted electricity demand d(t) of a “smart building” from about 1000 features x(t) in ref. 71. Here, we show the same effect on an example from quantitative finance. We forecast the value of Nikkei 225 index one week into the future as a function of the present-day (closing) values of major stock indices (Nikkei 225, S&P500, DAX, S&P/TSX and other, for a total of 27 indices), their components, major commodities (oil, gold, silver and other, for a total of 31 commodities) and currencies (USD, JPY, EUR, CNY and other, for a total of 23 currencies). The total dimensionality of the dataset is D = 2346. The data from January 2002 to December 2011 are used for training and later time periods were used to check the predictive ability of the model. The descriptors were scaled to [0, 1]. The problem of forecasting in time is cast as a time-independent ML problem as| | | d(t + Δt) = f(x(t)) | (5.1.2) |
This way the problem of extrapolation in time is cast as an interpolation problem in the space of descriptors. In Fig. 2, top panel, we show the results of forecasting of the value of Nikkei 225 with GPR using squared exponential kernels with different length parameters. The training period data (those to the left of the vertical dashed line) were used to draw both train and test points (which were in proportion 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3). Both train and test data from that period were reasonably well fitted using kernels with width parameters as small as 10 (the features were scaled). Both train and test data were randomly drawn from the same time period and are therefore distributed in the same way. The predicted value in the prediction period, however, collapses unless l is made much higher (the optimum value was about 500). This is related to necessarily, albeit slightly, different distributions of the data in the training and prediction periods, which leads to k(x, x′) → 0 as D → ∞.
3). Both train and test data from that period were reasonably well fitted using kernels with width parameters as small as 10 (the features were scaled). Both train and test data were randomly drawn from the same time period and are therefore distributed in the same way. The predicted value in the prediction period, however, collapses unless l is made much higher (the optimum value was about 500). This is related to necessarily, albeit slightly, different distributions of the data in the training and prediction periods, which leads to k(x, x′) → 0 as D → ∞.
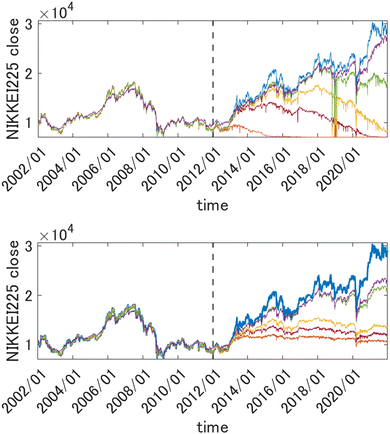 |
| | Fig. 2 Top panel: Forecasting the value of Nikkei225 one week into the future with GPR from 2346 descriptors (scaled to [0, 1]) with different length parameters l of a square exponential kernel. Orange: l = 10, brown: l = 30, yellow: l = 50, green: l = 100, purple: l = 500. The true value is shown in blue. Bottom panel: the same when using a 1st order HDMR-GPR. Orange: l = 0.1, brown: l = 0.5, yellow: l = 1, green: l = 5, purple: l = 10. The data to the left of the vertical dashed line were used for training, and the data to the right of it are the prediction period. | |
The example above is not from physical chemistry and is chosen to illustrate the effect of an extremely large D. As ML makes further inroads into physical and computational chemistry, it is important to keep these effects in mind. Examples of situations where extremely high-dimensional spaces that might arise are optimizations directly of grid points or basis coefficients.25 A way to deal with this issue is naturally to avoid using products of too many rapidly decaying functions. This can be achieved by using the high-dimensional model representation (HDMR).
5.2. High-dimensional model representation (HDMR) which is a representation with low-dimensional terms
High-dimensional model representation (HDMR) is an expansion over orders of coupling that has been formalized in a series of papers by Rabitz and co-workers.32–35 It is constructed as a sum of terms depending on subsets of original coordinates/features (xi1, xi2,…,xid),d ≤ D.| | 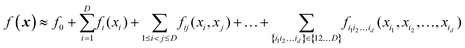 | (5.2.1) |
Taken to d = D, this expansion is exact; when d < D, it is an approximation. Eqn (3.3.2) is a particular case of eqn (5.2.1) for d = 1. In most real-life applications, the importance of orders of coupling, i.e. of the magnitude of the component functions fi1i2…id(xi1, xi2,…,xid), drops rapidly with d.32 We specifically consider RS (random sampling) HDMR32,33 which allows constructing all fi1i2…id(xi1, xi2,…,xid) from one and the same set of samples of f(x) however distributed in the D-dimensional space (the term “random sampling” should be understood in the sense of allowing any distribution rather than randomness, but we will follow the terminology used in the original HDMR literature32–35). This is not to be confused with the N-mode representation72 which has the same form of eqn (5.2.1) and where the component functions are sampled on sub-dimensional hyperplanes passing through an expansion centre and therefore requiring a separate dataset for each term (the N-mode approach is a particular case of HDMR called cut-HDMR33).
The advantage of an HDMR form with d < D is that lower-dimensional terms are easier to construct and are easier to use in applications (e.g. when integration is required). A major advantage of HDMR is that lower-dimensional terms can be reliably recovered from fewer data.32,47,49,68 As sampling in multidimensional spaces is bound to be sparse, this is attractive for multi-dimensional problems. The original formulation of RS-HDMR required computing fi1i2…id(xi1, xi2,…,xid) as (D–d)-dimensional integrals, which may be very costly.32,33 Some of us previously introduced combinations of HDMR with neural networks (RS-HDMR-NN)73–75 and, recently, with Gaussian process regressions (RS-HDMR-GPR)47,68 which allow dispensing with integrals and also allow combining terms of any dimensionality, e.g. one may lump terms with d′ < d into d-dimensional terms, in which case the approximation becomes
| | 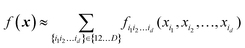 | (5.2.2) |
Specifically, when using GPR in multi-dimensional spaces, HMDR allows using lower-dimensional kernels and avoiding some of the problems associated with Matern-type kernels with very high D. To achieve the approximation eqn (5.2.2) with GPR, one can define a custom kernel which is itself in an HDMR form:48,67
| | 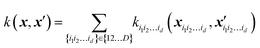 | (5.2.3) |
where
xi1i2…id = (
xi1,
xi2,…,
xid) and
ki1i2…id can be chosen as one of Matern kernels in
d dimensions. Individual component functions are then computable as
| | 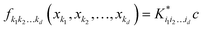 | (5.2.4) |
where
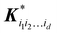
is a row vector with elements
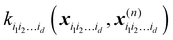
. In particular, the values of the component functions at the training set are
fi1i2…id =
Ki1i2…idc, where
c =
K−1f, and can be used to evaluate the relative importance of different component functions by computing the variance of
Ki1i2…idc, where the (
m,n) elements of the matrix
Ki1i2…id are
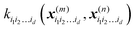
.
5.3. Recovering the expressive power of a nonlinear method with HDMR
For the problems of electricity demand prediction in a very high dimensional feature space in ref. 71 and financial data time series prediction illustrated above, with the HDMR-GPR, we were able to get good predictive power with much lower length parameters. As can be seen in Fig. 2, bottom panel, with the first order HDMR model, a good predictive power of the model is preserved for more than a year with l values as low as 0.1, and the model does not collapse even at much later times (even as its predictive power progressively deteriorates when the model is used further and further into the future without retraining).
Small values of l allow preserving the higher expressive power of a nonlinear method, as can be seen in Fig. 3, where we show an example of a component function fi(xi) of a 1st order HDMR-GPR model (eqn (3.2.2)) achieved with different values of the length parameter of the square exponential kernel. When l is large, the component functions are practically linear, and the model becomes equivalent to a plain linear regression f(x) = cx. Smaller values of l, enabled by the HDMR structure's avoiding a product of many functions with values smaller than 1, allow the HDMR-GPR model to construct the most suitable, non-linear, basis functions that are the component functions fi(xi).
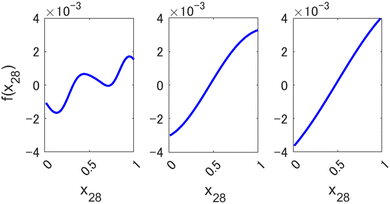 |
| | Fig. 3 Examples of a component function of a 1st order HDMR-GPR model for forecasting the value of Nikkei 225 from 2346 descriptors (scaled to [0, 1]) with different length parameters l of a square exponential kernel. Left to right: l = 0.1, 0.5, 1. | |
6. Elements of insight with a general method
Already the bare GPR allows obtaining some insight, specifically that into relative importance of descriptors. In the automated relevance determination (ARD) approach,27 one uses an anisotropic squared exponential kernel with optimized (e.g. using MLE41) length parameters li for each feature xi. A large li would correspond to less important and small li to more important variables.
The combination of HDMR with GPR allows assessing the relative importance of different combinations of variables by comparing the length parameters of the kernels of different component functions. For example, in ref. 67 and 68 kinetic energy densities τ of Al, Mg, and Si were fitted with HDMR-GPR as a function(al) of the terms of the 4th order gradient expansion76 and the product of electron density ρ(r) and the Kohn–Sham effective potential Veff(r):
| | 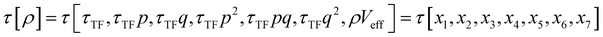 | (6.1) |
where
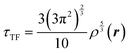
is the Thomas-Fermi KED, and
p and
q are the scaled
77 gradient and Laplacian of the electron density, respectively,
| | 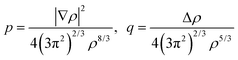 | (6.2) |
Table 1 lists the results, for example, for component function length parameters and variances when fitting a 2nd order HDMR-GPR to 5000 training data.
68
Table 1 The length parameter l and the variance var of the 2nd order HDMR-GPR component functions fi,j(xi,xj) when fitting kinetic energy densities of Al, Mg, and Si to 5000 data. The maximum allowed value of l was 105. The target and features were scaled to [0, 1] before fitting. See eqn (6.1) for the definition of the features
| Features |
Var{fi1,i2} |
l
|
|
x
1, x2 |
3.36 × 10−2 |
4.94 × 10−1 |
|
x
1, x3 |
4.51 × 10−4 |
3.33 × 102 |
|
x
1, x4 |
3.69 × 10−9 |
105 |
|
x
1, x5 |
3.70 × 10−9 |
105 |
|
x
1, x6 |
3.68 × 10−9 |
105 |
|
x
1, x7 |
3.94 × 10−9 |
105 |
|
x
2, x3 |
5.09 × 10−3 |
2.16 × 101 |
|
x
2, x4 |
3.11 × 10−10 |
105 |
|
x
2, x5 |
2.81 × 10−10 |
105 |
|
x
2, x6 |
1.65 × 10−10 |
105 |
|
x
2, x7 |
6.03 × 10−3 |
3.12 × 101 |
|
x
3, x4 |
9.87 × 10−10 |
105 |
|
x
3, x5 |
9.95 × 10−10 |
105 |
|
x
3, x6 |
1.03 × 10−9 |
105 |
|
x
3, x7 |
3.53 × 10−2 |
9.51 × 10-2 |
|
x
4, x5 |
6.70 × 10−10 |
105 |
|
x
4, x6 |
4.76 × 10−10 |
105 |
|
x
4, x7 |
5.08 × 10−10 |
105 |
|
x
5, x6 |
1.38 × 10−10 |
105 |
|
x
7, x7 |
1.78 × 10−10 |
105 |
|
x
6, x7 |
1.52 × 10−2 |
2.48 × 10-1 |
Some component functions have a very high l and a very low variance – these can effectively be excluded as a result of this analysis, alleviating thereby the issue of the combinatorial scaling of the number of HDMR terms. It was also shown that the importance of terms depends on the amount of available training data, highlighting the issue that the density of sampling determines the number of coupling terms that can be recovered.73 In that work, isotropic kernels were used for each component function; using anisotropic kernels would provide even more detail about the relative importance of variables within different subsets. The information obtained about the relative importance of subsets of features with HDMR-GPR can be used independently for building approximations relying on the most important subsets with any method (not necessarily ML-based).
7. ML-based expansion over orders of coupling can facilitate VSCF and VCI calculations
Another connection we would like to make is the use of ML in accurate (i.e., anharmonic) computational vibrational spectroscopy. Calculations of vibrational spectra including anharmonicity and coupling are still problematic for a range of practically important systems, including big molecules, molecules on surfaces, and solid state.78 In these systems, even though the effects of anharmonicity can be more significant than in free small molecules, accurate calculations of spectra are inhibited by the absence of potential energy surfaces (PES) as well as by the computational complexity of solving the vibrational Schrödinger equation. The latter is alleviated using VSCF (vibrational self-consistent field)79,80 and VCI (vibrational configuration interaction)81–83 methods, which use the PES in the form of an expansion over orders of coupling which has the same form as HDMR. Often, this expansion is built with the N-mode approach72 (corresponding to cut-HDMR33) whereby each component function 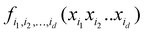 is sampled separately while keeping other coordinates at the equilibrium values. This leads to a combinatorically scaling number of datasets with both D and d. By using RS-HDMR,33 one can compute all terms of the HDMR representation from one and the same set of full-dimensional (i.e. not confined to sub-dimensional hyperplanes passing through the equilibrium geometry) samples. As mentioned above, in the original RS-HDMR formulation, d-dimensional terms were computed as (D–d)-dimensional integrals which can be debilitating,32,33,35 but the use of ML trivially dispenses with this issue – all terms are fitted simultaneously or in self-consistency cycles.47,67,68,74,75 We have demonstrated RS-HDMR with NN73,74 and GPR component functions (HDMR-NN, HDMR-GPR),47,67,68 and we have shown that RS-HDMR PESs built from one full-dimensional dataset result in accurate vibrational spectra.47 The potential of HDMR-ML combination to facilitate VSCF and VCI calculations is therefore significant and should be explored. This includes the capability of HDMR-GPR to prune the number of coupling terms as described above. HDMR-ML combination is useful not only for PESs suited for VSCF and VCI calculations but also for other applications in cases where the low-density of data does not allow recovering higher orders of coupling.47,73
is sampled separately while keeping other coordinates at the equilibrium values. This leads to a combinatorically scaling number of datasets with both D and d. By using RS-HDMR,33 one can compute all terms of the HDMR representation from one and the same set of full-dimensional (i.e. not confined to sub-dimensional hyperplanes passing through the equilibrium geometry) samples. As mentioned above, in the original RS-HDMR formulation, d-dimensional terms were computed as (D–d)-dimensional integrals which can be debilitating,32,33,35 but the use of ML trivially dispenses with this issue – all terms are fitted simultaneously or in self-consistency cycles.47,67,68,74,75 We have demonstrated RS-HDMR with NN73,74 and GPR component functions (HDMR-NN, HDMR-GPR),47,67,68 and we have shown that RS-HDMR PESs built from one full-dimensional dataset result in accurate vibrational spectra.47 The potential of HDMR-ML combination to facilitate VSCF and VCI calculations is therefore significant and should be explored. This includes the capability of HDMR-GPR to prune the number of coupling terms as described above. HDMR-ML combination is useful not only for PESs suited for VSCF and VCI calculations but also for other applications in cases where the low-density of data does not allow recovering higher orders of coupling.47,73
8. Conclusions
Machine learning has already been widely used in different areas of chemical physics, physical chemistry, including computational and theoretical chemistry, and beyond. The areas of penetration continue to increase. ML-based interatomic potentials are already routine, including spectroscopically accurate potentials.84 ML-based exchange correlation and kinetic energy functionals are expected to enter publicly accessible codes for use in applications in the near future. ML-predicted or designed with ML assistance catalysts, chromophores, metallic alloys, and ionic conductors are beginning to practically impact the field of functional materials. Off-the-shelf machine learning methods are often used, precisely for their off-the-shelf, black-box nature allowing their easy application to diverse problems and operation by non-experts.
In this Perspective, we tried to bring attention to some interconnections as well as tricky parts of commonly used methods, specifically focusing on neural networks and kernel-based regression methods which found the widest use to date in the above-mentioned applications. Despite the popularity of multilayer NNs (“deep learning”), in our experience with ML of interatomic potentials, kinetic energy densities, as well as in other applications, single hidden NNs are sufficient and more efficient unless the data distribution is very uneven. Both NNs and kernel-type regressions (considered here on the example of GPR) can be viewed as expansions over parameterized, non-direct product bases. Both allow achieving a sum-of-product representation which is very useful when computing integrals (in quantum dynamics applications and elsewhere). The basis set of GPR is much less flexible than that formed by NN neurons, and typically many more basis functions (as many as there are training data) are needed compared with the number of NN neurons for the same quality of regression. The perceived ability of GPR to achieve a similar test set error (as a NN) with fewer data reported before has to do with the robustness of a linear regression that is GPR. GPR is not necessarily advantageous with respect to the total number of parameters (linear and nonlinear) although it is advantageous over NNs in terms of an only small number of nonlinear (hyper)parameters typically used. The square nature of the linear problem in the standard GPR is not well-suited for hyperparameter optimization; rectangularization of GPR equations facilitates hyperparameter optimization.
When the dimensionality of the feature space is very large, GPR with common Matern kernels may fail when the distribution of the test data is any different from that of the training data. In this case, using representations with lower-dimensional terms, based in particular on HDMR, is useful. It is also useful because with a low density of training data (which is always the case in high-dimensional spaces and cannot be fixed by simply adding however many more data, because of the curse of dimensionality), only lower-order coupling terms can be recovered. Representations with lower-dimensional terms built with ML methods are relatively easy to construct (e.g. by defining a GPR kernel in an HDMR form). They can also facilitate hyperparameter optimization. They also allow obtaining elements of insight (the sore point of black-box methods) while preserving the generality of the method, in particular, informing on the relative importance of difference combinations of features. Random sampling HDMR, which allows constructing all coupling terms from one and the same dataset, should be explored for applications with VSCF and VCI as it has the potential to significantly simplify PES construction in the form needed by those methods. Overall, there is an advantage in going beyond off-the-shelf methods; one can achieve more powerful approaches when using these methods as a base for more involved approaches such as HDMR-NN or HDMR-GPR combinations.
Author contributions
Sergei Manzhos: conceptualization, methodology, writing- original draft preparation, project administration, and supervision. Shunsaku Tsuda: calculations and data analysis. Manabu Ihara: writing - reviewing and editing, resources, project administration, and supervision.
Conflicts of interest
There are no conflicts to declare.
References
- Q. Tong, P. Gao, H. Liu, Y. Xie, J. Lv, Y. Wang and J. Zhao, J. Phys. Chem. Lett., 2020, 11, 8710–8720 CrossRef CAS PubMed.
- W. P. Walters and R. Barzilay, Acc. Chem. Res., 2021, 54, 263–270 CrossRef CAS PubMed.
- R. Ramprasad, R. Batra, G. Pilania, A. Mannodi-Kanakkithodi and C. Kim, npj Comput. Mater., 2017, 3, 1–13 CrossRef.
- A. Y.-T. Wang, R. J. Murdock, S. K. Kauwe, A. O. Oliynyk, A. Gurlo, J. Brgoch, K. A. Persson and T. D. Sparks, Chem. Mater., 2020, 32, 4954–4965 CrossRef CAS.
- K. T. Butler, D. W. Davies, H. Cartwright, O. Isayev and A. Walsh, Nature, 2018, 559, 547–555 CrossRef CAS PubMed.
- S. M. Moosavi, K. M. Jablonka and B. Smit, J. Am. Chem. Soc., 2020, 142, 20273–20287 CrossRef CAS PubMed.
- M. del Cueto and A. Troisi, Phys. Chem. Chem. Phys., 2021, 23, 14156–14163 RSC.
- S. Manzhos and M. Ihara, PhysChemComm, 2022, 2, 72–95 CrossRef.
- S. R. Kalidindi, J. Appl. Phys., 2020, 128, 041103 CrossRef.
- S. Li, Y. Liu, D. Chen, Y. Jiang, Z. Nie and F. Pan, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1558 CAS.
- P. Schlexer Lamoureux, K. T. Winther, J. A. Garrido Torres, V. Streibel, M. Zhao, M. Bajdich, F. Abild-Pedersen and T. Bligaard, ChemCatChem, 2019, 11, 3581–3601 CrossRef CAS.
- S. Palkovits, ChemCatChem, 2020, 12, 3995–4008 CrossRef CAS.
- J. Behler, J. Chem. Phys., 2016, 145, 170901 CrossRef PubMed.
- J. Behler, Int. J. Quantum Chem., 2015, 115, 1032–1050 CrossRef CAS.
- S. Manzhos and T. Carrington, Chem. Rev., 2021, 121, 10187–10217 CrossRef CAS PubMed.
- S. Manzhos, R. Dawes and T. Carrington, Int. J. Quantum Chem., 2015, 115, 1012–1020 CrossRef CAS.
- I. Poltavsky and A. Tkatchenko, J. Phys. Chem. Lett., 2021, 12, 6551–6564 CrossRef CAS PubMed.
- O. T. Unke, S. Chmiela, H. E. Sauceda, M. Gastegger, I. Poltavsky, K. T. Schütt, A. Tkatchenko and K.-R. Müller, Chem. Rev., 2021, 121, 10142–10186 CrossRef CAS PubMed.
- S. Manzhos and P. Golub, J. Chem. Phys., 2020, 153, 074104 CrossRef CAS PubMed.
- P. Golub and S. Manzhos, Phys. Chem. Chem. Phys., 2018, 21, 378–395 RSC.
- M. Fujinami, R. Kageyama, J. Seino, Y. Ikabata and H. Nakai, Chem. Phys. Lett., 2020, 748, 137358 CrossRef CAS.
- J. Seino, R. Kageyama, M. Fujinami, Y. Ikabata and H. Nakai, Chem. Phys. Lett., 2019, 734, 136732 CrossRef CAS.
- J. C. Snyder, M. Rupp, K. Hansen, L. Blooston, K.-R. Müller and K. Burke, J. Chem. Phys., 2013, 139, 224104 CrossRef PubMed.
- K. Yao and J. Parkhill, J. Chem. Theory Comput., 2016, 12, 1139–1147 CrossRef CAS PubMed.
- S. Manzhos, Mach. Learn.: Sci. Technol., 2020, 1, 013002 Search PubMed.
-
G. Montavon, G. B. Orr and K.-R. Mueller, Neural Networks: Tricks of the Trade, Springer, Berlin Heidelberg, 2nd edn, 2012 Search PubMed.
-
C. E. Rasmussen and C. K. I. Williams, Gaussian Processes for Machine Learning, MIT Press, Cambridge MA, USA, 2006 Search PubMed.
-
C. M. Bishop, Pattern Recognition and Machine Learning, Springer, Singapore, 2006 Search PubMed.
- A. Kamath, R. A. Vargas-Hernández, R. V. Krems, T. Carrington and S. Manzhos, J. Chem. Phys., 2018, 148, 241702 CrossRef PubMed.
-
R. M. Neal, PhD Thesis, University of Toronto, 1995.
-
D. L. Donoho, AMS Conference on Math Challenges of the 21st Century, AMS, 2000.
- G. Li, J. Hu, S.-W. Wang, P. G. Georgopoulos, J. Schoendorf and H. Rabitz, J. Phys. Chem. A, 2006, 110, 2474–2485 CrossRef CAS PubMed.
- H. Rabitz and Ö. F. Aliş, J. Math. Chem., 1999, 25, 197–233 CrossRef CAS.
- Ö. F. Alış and H. Rabitz, J. Math. Chem., 2001, 29, 127–142 CrossRef.
- G. Li, S.-W. Wang and H. Rabitz, J. Phys. Chem. A, 2002, 106, 8721–8733 CrossRef CAS.
- A. N. Gorban, Appl. Math. Lett., 1998, 11, 45–49 CrossRef.
- K. Hornik, Neural Networks, 1991, 4, 251–257 CrossRef.
- K. Hornik, M. Stinchcombe and H. White, Neural Networks, 1990, 3, 551–560 CrossRef.
- V. Kůrková, Neural Networks, 1992, 5, 501–506 CrossRef.
- M. G. Genton, J. Mach. Learn. Res., 2001, 2, 299–312 Search PubMed.
- I. J. Myung, J. Math. Psychol., 2003, 47, 90–100 CrossRef.
- J. Bergstra and Y. Bengio, J. Mach. Learn. Res., 2012, 13, 281–305 Search PubMed.
-
E. Brochu, V. M. Cora and N. de Freitas, arXiv, 2010, preprint, arXiv:1012.2599 [cs] DOI:10.48550/arXiv.1012.2599.
-
J. Snoek, H. Larochelle and R. P. Adams, Advances in Neural Information Processing Systems, ed. F. Pereira, C. J. C. Burges, L. Bottou and K. Q. Weinberger, Curran Associates, Inc., vol. 25, 2012 Search PubMed.
-
M. Fischetti and M. Stringher, arXiv, 2019, preprint, arXiv.1906.01504 [cs, math, stat] DOI:10.48550/arXiv.1906.01504.
-
H. Alibrahim and S. A. Ludwig, in 2021 IEEE Congress on Evolutionary Computation (CEC), 2021, pp. 1551–1559.
- M. A. Boussaidi, O. Ren, D. Voytsekhovsky and S. Manzhos, J. Phys. Chem. A, 2020, 124, 7598–7607 CrossRef CAS PubMed.
-
D. Duvenaud, H. Nickisch and C. E. Rasmussen, Advances in Neural Information Processing Systems, 2011, pp. 226–234 Search PubMed.
- S. Manzhos and M. Ihara, J. Math. Chem., 2022 DOI:10.1007/s10910-022-01407-x.
-
S. Bubeck and M. Sellke, Advances in Neural Information Processing Systems, Curran Associates, Inc., 2021, vol. 34, pp. 28811–28822 Search PubMed.
- G.-B. Huang, Q.-Y. Zhu and C.-K. Siew, Neurocomputing, 2006, 70, 489–501 CrossRef.
- Y. Liao, S.-C. Fang and H. L. W. Nuttle, Neural Networks, 2003, 16, 1019–1028 CrossRef PubMed.
- W. Wu, D. Nan, J. Long and Y. Ma, Neural Networks, 2008, 21, 1464–1465 CrossRef PubMed.
- M. H. Beck, A. Jäckle, G. A. Worth and H.-D. Meyer, Phys. Rep., 2000, 324, 1–105 CrossRef CAS.
- S. Manzhos and T. Carrington, J. Chem. Phys., 2006, 125, 194105 CrossRef PubMed.
- M. Schmitt, Neural Comput., 2002, 14, 241–301 CrossRef PubMed.
- W. Koch and D. H. Zhang, J. Chem. Phys., 2014, 141, 021101 CrossRef PubMed.
- A. Brown and E. Pradhan, J. Theor. Comput. Chem., 2017, 16, 1730001 CrossRef CAS.
- E. Pradhan and A. Brown, J. Chem. Phys., 2016, 144, 174305 CrossRef PubMed.
- E. Pradhan and A. Brown, J. Mol. Spectrosc., 2016, 330, 158–164 CrossRef CAS.
-
S. Manzhos and M. Ihara, arXiv, 2022, preprint, arXiv.2112.02467 [cs, math] DOI:10.48550/arXiv.2112.02467.
- V. L. Deringer, A. P. Bartók, N. Bernstein, D. M. Wilkins, M. Ceriotti and G. Csányi, Chem. Rev., 2021, 121, 10073–10141 CrossRef CAS PubMed.
- S. Manzhos, K. Yamashita and T. Carrington, Chem. Phys. Lett., 2011, 511, 434–439 CrossRef CAS.
- M. Chan, S. Manzhos, T. Carrington and K. Yamashita, J. Chem. Theory Comput., 2012, 8, 2053–2061 CrossRef CAS PubMed.
- S. Manzhos, T. J. Carrington and K. Yamashita, J. Phys. Chem. Lett., 2011, 2, 2193–2199 CrossRef CAS.
- R. Penrose, Math. Proc. Cambridge Philos. Soc., 1955, 51, 406–413 CrossRef.
- S. Manzhos, E. Sasaki and M. Ihara, Mach. Learn.: Sci. Technol., 2022, 3, 01LT02 Search PubMed.
- O. Ren, M. A. Boussaidi, D. Voytsekhovsky, M. Ihara and S. Manzhos, Comput. Phys. Commun., 2021, 108220 Search PubMed.
- S. Manzhos, X. Wang, R. Dawes and T. Carrington, J. Phys. Chem. A, 2006, 110, 5295–5304 CrossRef CAS PubMed.
- W. C. Witt, B. G. del Rio, J. M. Dieterich and E. A. Carter, J. Mater. Res., 2018, 33, 777–795 CrossRef CAS.
-
E. Sasaki, M.Eng. thesis, Tokyo Institute of Techology, 2022.
- S. Carter, S. J. Culik and J. M. Bowman, J. Chem. Phys., 1997, 107, 10458–10469 CrossRef CAS.
- S. Manzhos and T. Carrington, J. Chem. Phys., 2006, 125, 084109 CrossRef PubMed.
- S. Manzhos, K. Yamashita and T. Carrington, Comput. Phys. Commun., 2009, 180, 2002–2012 CrossRef CAS.
-
S. Manzhos, K. Yamashita and T. Carrington, in Coping with Complexity: Model Reduction and Data Analysis, ed. A. N. Gorban and D. Roose, Springer, Berlin, Heidelberg, 2011, pp. 133–149 Search PubMed.
- C. H. Hodges, Can. J. Phys., 1973, 51, 1428–1437 CrossRef.
- R. J. Bartlett and D. S. Ranasinghe, Chem. Phys. Lett., 2017, 669, 54–70 CrossRef CAS.
- S. Manzhos and M. Ihara, Phys. Chem. Chem. Phys., 2022, 24, 15158–15172 RSC.
- T. K. Roy and R. B. Gerber, Phys. Chem. Chem. Phys., 2013, 15, 9468–9492 RSC.
- D. Shemesh, J. Mullin, M. S. Gordon and R. B. Gerber, Chem. Phys., 2008, 347, 218–228 CrossRef CAS.
- P. Carbonnière, A. Dargelos and C. Pouchan, Theor. Chem. Acc., 2010, 125, 543–554 Search PubMed.
- A. Erba, J. Maul, M. Ferrabone, P. Carbonnière, M. Rérat and R. Dovesi, J. Chem. Theory Comput., 2019, 15, 3755–3765 CrossRef CAS PubMed.
- A. Erba, J. Maul, M. Ferrabone, R. Dovesi, M. Rérat and P. Carbonnière, J. Chem. Theory Comput., 2019, 15, 3766–3777 CrossRef CAS PubMed.
- H. Kulik, T. Hammerschmidt, J. Schmidt, S. Botti, M. A. L. Marques, M. Boley, M. Scheffler, M. Todorović, P. Rinke, C. Oses, A. Smolyanyuk, S. Curtarolo, A. Tkatchenko, A. Bartok, S. Manzhos, M. Ihara, T. Carrington, J. Behler, O. Isayev, M. Veit, A. Grisafi, J. Nigam, M. Ceriotti, K. T. Schütt, J. Westermayr, M. Gastegger, R. Maurer, B. Kalita, K. Burke, R. Nagai, R. Akashi, O. Sugino, J. Hermann, F. Noé, S. Pilati, C. Draxl, M. Kuban, S. Rigamonti, M. Scheidgen, M. Esters, D. Hicks, C. Toher, P. Balachandran, I. Tamblyn, S. Whitelam, C. Bellinger and L. M. Ghiringhelli, Electron. Struct., 2022, 4, 0230004 Search PubMed.
|
| This journal is © the Owner Societies 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  *,
Shunsaku
Tsuda
and
Manabu
Ihara
*,
Shunsaku
Tsuda
and
Manabu
Ihara
 *
*
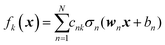
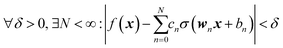 .
.
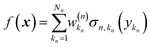
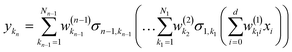
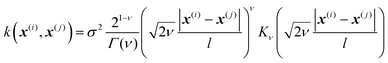
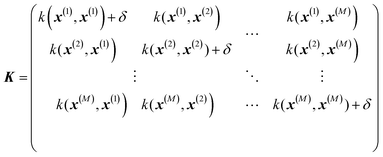
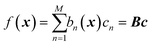
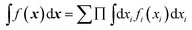 . With an NN, this is achieved by using a simple exponential neuron (σ(x) = ex) in a single hidden layer network:55
. With an NN, this is achieved by using a simple exponential neuron (σ(x) = ex) in a single hidden layer network:55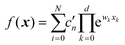
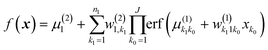
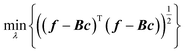
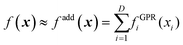
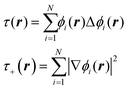

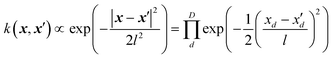
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3). Both train and test data from that period were reasonably well fitted using kernels with width parameters as small as 10 (the features were scaled). Both train and test data were randomly drawn from the same time period and are therefore distributed in the same way. The predicted value in the prediction period, however, collapses unless l is made much higher (the optimum value was about 500). This is related to necessarily, albeit slightly, different distributions of the data in the training and prediction periods, which leads to k(x, x′) → 0 as D → ∞.
3). Both train and test data from that period were reasonably well fitted using kernels with width parameters as small as 10 (the features were scaled). Both train and test data were randomly drawn from the same time period and are therefore distributed in the same way. The predicted value in the prediction period, however, collapses unless l is made much higher (the optimum value was about 500). This is related to necessarily, albeit slightly, different distributions of the data in the training and prediction periods, which leads to k(x, x′) → 0 as D → ∞.
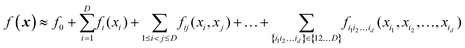
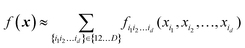
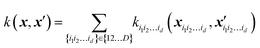
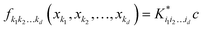
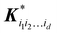 is a row vector with elements
is a row vector with elements 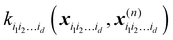 . In particular, the values of the component functions at the training set are fi1i2…id = Ki1i2…idc, where c = K−1f, and can be used to evaluate the relative importance of different component functions by computing the variance of Ki1i2…idc, where the (m,n) elements of the matrix Ki1i2…id are
. In particular, the values of the component functions at the training set are fi1i2…id = Ki1i2…idc, where c = K−1f, and can be used to evaluate the relative importance of different component functions by computing the variance of Ki1i2…idc, where the (m,n) elements of the matrix Ki1i2…id are 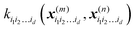 .
.
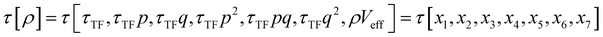
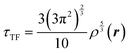 is the Thomas-Fermi KED, and p and q are the scaled77 gradient and Laplacian of the electron density, respectively,
is the Thomas-Fermi KED, and p and q are the scaled77 gradient and Laplacian of the electron density, respectively,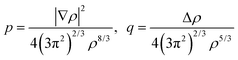
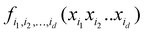 is sampled separately while keeping other coordinates at the equilibrium values. This leads to a combinatorically scaling number of datasets with both D and d. By using RS-HDMR,33 one can compute all terms of the HDMR representation from one and the same set of full-dimensional (i.e. not confined to sub-dimensional hyperplanes passing through the equilibrium geometry) samples. As mentioned above, in the original RS-HDMR formulation, d-dimensional terms were computed as (D–d)-dimensional integrals which can be debilitating,32,33,35 but the use of ML trivially dispenses with this issue – all terms are fitted simultaneously or in self-consistency cycles.47,67,68,74,75 We have demonstrated RS-HDMR with NN73,74 and GPR component functions (HDMR-NN, HDMR-GPR),47,67,68 and we have shown that RS-HDMR PESs built from one full-dimensional dataset result in accurate vibrational spectra.47 The potential of HDMR-ML combination to facilitate VSCF and VCI calculations is therefore significant and should be explored. This includes the capability of HDMR-GPR to prune the number of coupling terms as described above. HDMR-ML combination is useful not only for PESs suited for VSCF and VCI calculations but also for other applications in cases where the low-density of data does not allow recovering higher orders of coupling.47,73
is sampled separately while keeping other coordinates at the equilibrium values. This leads to a combinatorically scaling number of datasets with both D and d. By using RS-HDMR,33 one can compute all terms of the HDMR representation from one and the same set of full-dimensional (i.e. not confined to sub-dimensional hyperplanes passing through the equilibrium geometry) samples. As mentioned above, in the original RS-HDMR formulation, d-dimensional terms were computed as (D–d)-dimensional integrals which can be debilitating,32,33,35 but the use of ML trivially dispenses with this issue – all terms are fitted simultaneously or in self-consistency cycles.47,67,68,74,75 We have demonstrated RS-HDMR with NN73,74 and GPR component functions (HDMR-NN, HDMR-GPR),47,67,68 and we have shown that RS-HDMR PESs built from one full-dimensional dataset result in accurate vibrational spectra.47 The potential of HDMR-ML combination to facilitate VSCF and VCI calculations is therefore significant and should be explored. This includes the capability of HDMR-GPR to prune the number of coupling terms as described above. HDMR-ML combination is useful not only for PESs suited for VSCF and VCI calculations but also for other applications in cases where the low-density of data does not allow recovering higher orders of coupling.47,73


