Open Access Article
Open Access ArticleMagnetic field effects on radical pair reactions: estimation of B1/2 for flavin-tryptophan radical pairs in cryptochromes†
Siu Ying
Wong‡
 a,
Philip
Benjamin‡
b and
P. J.
Hore
a,
Philip
Benjamin‡
b and
P. J.
Hore
 *b
*b
aInstitut für Physik, Carl-von-Ossietzky Universität Oldenburg, Oldenburg 26111, Germany. E-mail: peter.hore@chem.ox.ac.uk
bDepartment of Chemistry, University of Oxford, Oxford, OX1 3QZ, UK
First published on 7th December 2022
Abstract
Magnetic field effects on the yields of radical pair reactions are often characterised by the “half-field” parameter, B1/2, which encodes useful information on spin relaxation, radical recombination kinetics and electron-electron couplings as well as electron–nuclear hyperfine interactions. Here we use a variety of spin dynamics simulation methods to estimate the hyperfine-only values of B1/2 for the flavin-tryptophan radical pair, [FAD˙− TrpH˙+], thought to be the detector in the magnetic compass sense of migratory songbirds. The main findings are: (a) in the absence of fast recombination and spin relaxation, [FAD˙− TrpH˙+] radical pairs in solution and in the putative magnetoreceptor protein, cryptochrome, have B1/2 ≈ 1.89 mT and 2.46 mT, respectively. (b) The widely used expression for B1/2 due to Weller et al. (Chem. Phys. Lett, 1983, 96, 24–27) is only applicable to small, short-lived (∼5 ns), rapidly tumbling radical pairs in solution, and is quantitatively unreliable in the context of magnetoreception. (c) In the absence of molecular tumbling, the low-field effect for [FAD˙− TrpH˙+] is predicted to be abolished by the anisotropic components of the hyperfine interactions. Armed with the 2.46 mT “base value” for cryptochrome, measurements of B1/2 can be used to understand the impact of spin relaxation on its performance as a magnetic compass sensor.
Introduction
Radical pairs are short-lived reaction intermediates with the unusual property that their chemistry can be influenced by magnetic interactions orders of magnitude smaller than the thermal energy, kBT (Boltzmann's constant times temperature).1–4 A combination of spin-selective reactivity, relatively slow spin relaxation, and electron–nuclear hyperfine interactions leads to the coherent interconversion of the electronic singlet and triplet states of the pair which can be affected by applied magnetic fields as weak as ∼50 μT.5,6 As a result, the yields of the reaction products, Φ(B), are frequently found to depend sigmoidally on the strength of the applied magnetic field, B.7–10 This behaviour is often characterised by a parameter, B1/2, defined as the magnetic field at which Φ(B) is mid-way between the reaction yield at zero field and the “saturation” value at high field (Fig. 1a): | (1) |
 | ||
| Fig. 1 (a) Schematic magnetic field effect on the fractional yield, ΦT(B), of the product formed from the triplet state of a singlet-born radical pair. The applied magnetic field is assumed to be weak enough that effects arising from the Δg mechanism1 are negligible. (b) Simplified photocycle of avian Cry4a.11 The red and blue curly arrows represent the coherent singlet–triplet interconversion of the magnetically sensitive [FAD˙− TrpH˙+] radical pair. FADH˙ is the protonated form of FAD˙−. Trp˙ is the deprotonated form of TrpH˙+. 1FAD* is the excited singlet state of FAD. | ||
In some cases this “half-field” parameter is dominated by the hyperfine interactions in the radicals but there can also be contributions from fast recombination reactions,9,10 spin relaxation processes,12–14 paramagnetic–diamagnetic exchange,15,16 and electron exchange and dipolar interactions.17,18 It is therefore important to be able to estimate the hyperfine contribution to B1/2 so that information on these other factors, about which less is usually known, can be extracted from experimental data. An equation due to Weller et al. has been widely used for this purpose.7 For a pair of radicals, A and B:
 | (2) |
 | (3) |
 and
and 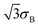 , with weights equal to σA/
, with weights equal to σA/![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) and σB/
and σB/![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) , respectively, where
, respectively, where  . Note that the definitions of σK and B1/2 in ref. 7 did not use the factors of
. Note that the definitions of σK and B1/2 in ref. 7 did not use the factors of  in eqn (2) and (3).
in eqn (2) and (3).
Not only does eqn (2) have little basis in theory, it is also not the only empirical expression consistent with the B1/2 measurements reported by Weller et al.7 For example, the simpler expression,
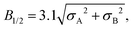 | (4) |
We are aware of only one attempt to test the accuracy of eqn (2). Rodgers et al.19 used a quantum mechanical Monte-Carlo approach (QMMC) to calculate Φ(B) and hence B1/2 for more than 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 radical pairs containing three spin-1/2 nuclei in each radical. The hyperfine couplings were chosen randomly such that σK for each radical was uniformly distributed between 0 and 0.75 mT. The study concluded that eqn (2) is best regarded as a useful, but not very accurate, rule of thumb for radical pairs with lifetimes in the range 10 to 100 ns. The discrepancies between eqn (2) and the QMMC results were more pronounced for both shorter and longer lived pairs.
000 radical pairs containing three spin-1/2 nuclei in each radical. The hyperfine couplings were chosen randomly such that σK for each radical was uniformly distributed between 0 and 0.75 mT. The study concluded that eqn (2) is best regarded as a useful, but not very accurate, rule of thumb for radical pairs with lifetimes in the range 10 to 100 ns. The discrepancies between eqn (2) and the QMMC results were more pronounced for both shorter and longer lived pairs.
Our purpose here is to assess in greater detail the accuracy of eqn (2) with a particular focus on the radical pair, [FAD˙− TrpH˙+], thought to be the sensor in the light-dependent magnetic compass of migratory songbirds.4,11,20–24 The radicals are formed within Cry4a, one of the six known avian cryptochrome proteins,11,25–32via photo-excitation of the flavin adenine dinucleotide (FAD) cofactor followed by sequential electron transfers along a chain of four tryptophan (TrpH) residues. Competition between singlet radical pair recombination and TrpH˙+ deprotonation results in magnetic field effects on the quantum yield of a relatively long-lived form of the protein which could act as a signalling state (Fig. 1b).11 The FAD˙− and TrpH˙+ radicals in Cry4a are separated by ∼2 nm and have dipolar and exchange interactions: |D| ≈ 300–500 μT and |J| ≤ 2 μT, respectively.11
In the following, we use spin dynamics simulations to estimate the contribution of isotropic hyperfine interactions to B1/2 for the [FAD˙− TrpH˙+] radical pair in cryptochrome for different radical pair lifetimes. We also treat the case of static, randomly oriented cryptochrome molecules for which anisotropic hyperfine and dipolar interactions cannot be ignored. A variety of approximate simulation methods have been deployed because of the computational challenges posed by an exact quantum mechanical treatment of a system of ∼30 coupled spins comprising ∼1010 spin states. The main aims are: (a) to assess the reliability of eqn (2) as a predictor of B1/2, and (b) to determine the true contribution of hyperfine interactions to B1/2 for [FAD˙− TrpH˙+] as a basis for future studies of the effects of spin relaxation on its performance as a magnetic compass sensor.
Results
Weller equation
To evaluate eqn (2) for [FAD˙− TrpH˙+] we used a complete set of isotropic hyperfine coupling constants, previously calculated using density functional theory.33 A total of 27 nuclei were included (ESI,† Section S2): four 14N and eleven 1H in FAD˙− and two 14N and ten 1H in TrpH˙+. Using eqn (3), the effective hyperfine interactions in the two radicals are σFAD = 0.70 mT and σTrp = 0.97 mT and hence BW1/2 = 2.97 mT. Note that this estimate includes no contribution from spin relaxation, fast recombination reactions, electron–electron couplings or anisotropic hyperfine interactions.Schulten–Wolynes method
Schulten and Wolynes (SW) have proposed an approximate treatment of the spin dynamics of radical pairs in which the electron spins were considered to precess around the vector sum of the applied magnetic field and a time-independent magnetic field arising from the hyperfine interactions.34 In the implementation used here (ESI,† Section S3), the latter was modelled by Monte-Carlo averaging over isotropic Gaussian distributions of hyperfine fields for each radical (mean zero, standard deviation σK).35 Singlet and triplet pairs were considered to react with the same first-order rate constant, k, to give distinct products (the “exponential model”36). The magnetic field effect was quantified by calculating the quantum yield, ΦT(B), of the product formed from the triplet state of a singlet-born radical pair. B1/2 was obtained by interpolating ΦT(B) (ESI,† Sections S4 and S5). Exchange and dipolar interactions between the radicals and spin relaxation were not included. Applied to a radical pair comprising pyrene and N,N-dimethylaniline radicals, the SW approach was originally shown to give excellent agreement with exact quantum simulations.34 It has subsequently been found to be less reliable at predicting the spin dynamics of long-lived radical pairs.37,38
Fig. 2 shows how B1/2 calculated using the SW method varies with (a) σAB = (σA2 + σB2)1/2, (b) σA/σB, and (c) k. Under the conditions of these calculations, detailed in the figure caption, a number of deviations from BW1/2 are immediately apparent. Both estimates of B1/2 are proportional to σAB (Fig. 2a), but with different gradients: 2.11 for SW and  for Weller. B1/2 obtained using the SW method is approximately independent of the ratio σA/σB (Fig. 2b) while BW1/2 decreases markedly as σA/σB is increased towards 1.0. Versions of Fig. 2a and b, calculated for different values of k can be found in the ESI† (Section S5) together with representative plots of the field-dependence of ΦT(B).
for Weller. B1/2 obtained using the SW method is approximately independent of the ratio σA/σB (Fig. 2b) while BW1/2 decreases markedly as σA/σB is increased towards 1.0. Versions of Fig. 2a and b, calculated for different values of k can be found in the ESI† (Section S5) together with representative plots of the field-dependence of ΦT(B).
 | ||
Fig. 2
B
1/2 calculated using the Schulten–Wolynes (SW) semiclassical method (blue) compared to BW1/2 obtained from eqn (2) (red). 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Monte-Carlo samples of the hyperfine field distributions were used for the former. (a) B1/2 as a function of σAB for σA = σB and k = 106 s−1. The blue line is the best linear fit to the calculated values of B1/2 (gradient 2.11, intercept ≈ −0.11 mT). (b) B1/2 as a function of σA/σB for σAB = 1 mT and k = 106 s−1. (c) B1/2 as a function of log10 000 Monte-Carlo samples of the hyperfine field distributions were used for the former. (a) B1/2 as a function of σAB for σA = σB and k = 106 s−1. The blue line is the best linear fit to the calculated values of B1/2 (gradient 2.11, intercept ≈ −0.11 mT). (b) B1/2 as a function of σA/σB for σAB = 1 mT and k = 106 s−1. (c) B1/2 as a function of log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k for σAB = 1 mT and σA = σB. k for σAB = 1 mT and σA = σB. | ||
Finally, SW predicts that B1/2 is approximately independent of k up to ∼5 × 107 s−1, and then increases sharply for faster recombination rates (Fig. 2c). BW1/2, by contrast, is independent of k. Under the conditions of Fig. 2c, the two approaches agree when k ≈ 1.6 × 108 s−1, i.e. when the radical pairs have a lifetime of ∼6 ns.
For the cryptochrome-based radical pair, [FAD˙− TrpH˙+], using the values of σFAD and σTrp quoted above, and k = 106 s−1, we find B1/2 = 2.51 mT, approximately 15% smaller than BW1/2. Further discussion of this and other estimates of B1/2 (collected together in Table 1) is deferred to the Discussion section.
| Method | Wellerb | SWb | QMMCbc | QDd | SCe |
|---|---|---|---|---|---|
| a HFI: hyperfine interaction; D: dipolar interaction. k = 106 s−1. b σ FAD = 0.70 mT and σTrp = 0.97 mT. c Extrapolated from 3–7 nuclei per radical. d n nuc = 15. e n nuc = 27. f σ FAD = 1.03 mT, σTrp = 1.11 mT. g Average over nnuc = 13–16. | |||||
| Isotropic HFIaD = 0 | 2.97 | 2.51 | 2.04 | 1.98 | 1.89 |
Quantum mechanical Monte-Carlo method
We have extended the previous QMMC test of Weller's equation19 by including up to seven spin-1/2 nuclei per radical. ΦT(B) was calculated exactly, as described in ref. 19, and interpolated to obtain B1/2 (ESI,† Sections S4 and S6). The hyperfine coupling constants for each radical were randomly chosen to be uniformly distributed between −1 mT and +1 mT and then scaled to obtain σFAD = 0.70 mT and σTrp = 0.97 mT. In all other respects, the calculations were performed under the same conditions as the SW simulations (isotropic hyperfine couplings, no exchange or dipolar interactions, equal singlet and triplet reaction rate constants, no spin relaxation).Distributions of B1/2 values for 1500 radical pairs containing 3, 4, 5, 6, or 7 nuclear spins per radical and k = 106 s−1 are shown in Fig. 3. As the number of nuclear spins was increased, both the mean and standard deviation decreased, with the mean tending towards ∼2.0 mT, i.e. 33% smaller than BW1/2. The B1/2 distributions for k = 107 s−1, 108 s−1, and 109 s−1 displayed similar behaviour with extrapolated means of 2.1, 2.5, and 6.6 mT, respectively (ESI,† Section S6).
 | ||
| Fig. 3 B 1/2 distributions calculated using the QMMC method for model [FAD˙− TrpH˙+] radical pairs containing 3, 4, 5, 6, or 7 hyperfine interactions per radical, as indicated. | ||
Quantum dynamics method
The QMMC approach described above used random hyperfine coupling constants to achieve the appropriate values of σFAD and σTrp. A more direct approach would be to simulate the quantum dynamics (QD) in exactly the same way but using the actual hyperfine coupling constants of FAD˙− and TrpH˙+. The challenge is that the dimensions of the matrices involved in the calculation scale exponentially with the number of spins in each radical, such that the calculations become impracticable for radical pairs with more than about nnuc = 15 nuclei. We therefore performed a series of calculations in which the nuclear spins in FAD˙− and TrpH˙+ were introduced one by one in approximate order of decreasing hyperfine coupling (ESI,† Section S2) in the hope that B1/2 would cease to depend on nnuc before the calculations became inconveniently slow or impossible (ESI,† Section S7).The results are shown in Fig. 4a for several values of the recombination rate constant k and up to 15 nuclear spins. Although B1/2 for the two smallest rate constants (106 and 107 s−1) appears to level out by the time nnuc = 15, the same cannot be said for the four larger values of k. It appears that the shorter the lifetime of the radical pair, the more sensitive B1/2 is to small hyperfine interactions.
The value of B1/2 for k = 106 s−1 and nnuc = 15 (∼1.98 mT) is similar to the QMMC result (above) and 33% smaller than predicted by the Weller equation.
Improved semiclassical dynamics method
To include a larger number of nuclear spins than is feasible in the QD approach, we used an improved version of the SW method, denoted SC.37 Rather than assuming that the sum of the nuclear spin vectors, weighted by the hyperfine couplings, is fixed in space, the SC method allows each nuclear spin in a radical to precess around the electron spin. In both cases, the electron spin simultaneously precesses around the total nuclear spin vector. Valid for radical pairs with no exchange or dipolar interactions, and equal singlet and triplet reaction rate constants, the computational effort increases only linearly with the number of nuclear spins, rather than exponentially as in an exact quantum mechanical calculation and approaches quantitative agreement with quantum mechanics as the number of nuclear spins increases.37 Further details of the method are given in the ESI† (Section S3).The SC results for 6 ≤ nnuc ≤ 27 are compared with the QD calculations in Fig. 4a. The improved semiclassical values of B1/2 become independent of the number of nuclei for nnuc ≥ 20 but are larger than the exact values (by, at most, 0.12 mT for nnuc = 15). This discrepancy reflects the approximate nature of the SC approach, the reliability of which should improve as nnuc is increased. In agreement with this, we find that the QD values, when extrapolated exponentially to nnuc = ∞, are a good match to the SC results for nnuc = 27 (ESI,† Section S8).
As we found using the SW approach (Fig. 2c), B1/2 is almost independent of k when k ≤ 107 s−1 and then increases when the recombination is faster. Fig. 4b shows the SC values of B1/2 for nnuc = 27 as a function of k, together with the best linear fit: B1/2/mT ≈ 2.02 + k/(2.15 × 108 s−1). The origin of this behaviour appears to be analogous to the lifetime-broadening seen in magnetic resonance spectra.39 Under conditions of “slow exchange”, the additional linewidth in an electron paramagnetic resonance spectrum arising from a chemical reaction with rate constant k is k/π (in Hz) or k/2γe (in mT) where γe = 1.76 × 108 mT−1 s−1 is the electron magnetogyric ratio. Consistent with this, the reciprocal of the gradient in Fig. 4b (2.15 × 108 mT−1 s−1) is not far off 2γe (3.52 × 108 mT−1 s−1).
Anisotropic interactions
All of the calculations reported above have been performed with isotropic hyperfine interactions and no radical–radical interactions. This is a good approximation when the radicals tumble rapidly in solution, such that the effects of anisotropic interactions average out, and when the radicals are far enough apart that, on average, their exchange and dipolar interactions are small. However, the FAD˙− and TrpH˙+ radicals of interest here are embedded in cryptochrome, a large slowly tumbling protein, and are separated by a distance (∼2 nm) at which the electron dipolar interaction cannot be neglected.40 Hyperfine anisotropy and dipolar coupling must therefore be considered.The effect of including the complete hyperfine tensors instead of their isotropic components can be estimated using a modified form of eqn (3) (ref. 41):
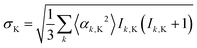 | (5) |
The simulation methods used above are either valid only when there are no exchange or dipolar interactions or take advantage of the absence of electron coupling to avoid using matrices with the dimension of the full spin space. To determine B1/2 with anisotropic hyperfine and dipolar interactions included, we have used a method proposed by Fay et al. to model spin relaxation in radical pairs.42 The initial singlet state of the radical pair was propagated in 1 ns time-steps to 5 μs and then integrated (using k = 106 s−1) to obtain ΦT(B). The initial nuclear spin space was trace-sampled using a single SU(Z) coherent state42 with averaging over 16 randomly distributed directions of the magnetic field. The relative orientation of the two radicals and the dipolar coupling parameter (D = −0.511 mT) were appropriate for FAD and Trp318 in the crystal structure of pigeon cryptochrome 4a.32 We refer to this method here as SU(Z) (instead of stochastic Schrödinger equation, SSE42) because we do not use it to model spin relaxation.
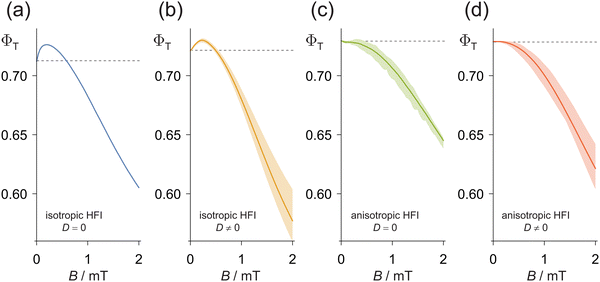
Fig. 5 shows values of B1/2 calculated using the SU(Z) method for nnuc = 7–16, introducing the nuclei one at a time in the same order as before (ESI,† Sections S2 and S9). As in Fig. 4a, B1/2 for isotropic hyperfine interactions and no dipolar interaction is a little less than 2.0 mT for nnuc = 14–16. When the anisotropic hyperfine components and the dipolar interaction were included, B1/2 increased to ∼2.46 mT. This is substantially smaller than the estimate using eqn (2) and (5), BW1/2 = 3.71 mT.
The individual effects of the two anisotropic interactions are also shown in Fig. 5. Inclusion of just the dipolar coupling causes a small reduction in B1/2 which is more than outweighed by the increase arising from the hyperfine anisotropy.
Discussion
We have explored the validity of eqn (2) as a predictor of B1/2, using a range of simulation methods, concentrating on the [FAD˙− TrpH˙+] radical pair in cryptochrome because of its potential role as the magnetic compass sensor in migratory songbirds.4Table 1 collects together our estimates of B1/2 for this radical pair when it recombines with a rate constant of 106 s−1. A 1 μs lifetime is probably about optimal for magnetoreception: any shorter and there would be insufficient time for the Earth's magnetic field (∼50 μT) to influence the spin dynamics and any longer would risk attenuating the magnetic sensitivity through spin relaxation.4,43–45 However, since B1/2 is hardly affected by the recombination kinetics when k < 107 s−1 (Fig. 4), the precise value of k is not important for our assessment of the reliability of the Weller equation in the context of magnetoreception.Weller equation
Compared to quantum and semiclassical spin dynamics simulations, the Weller equation is seen to be unreliable, both qualitatively (Fig. 2b and c) and quantitatively (Table 1). To some extent, this is expected. Eqn (2) was originally proposed to rationalise the effects of magnetic fields on the chemistry of small, freely diffusing, rapidly tumbling radicals in non-viscous solutions. It is therefore not surprising that eqn (2) cannot account for the effects of anisotropic hyperfine interactions or radical–radical interactions. However, even with these limitations, eqn (2) is still found wanting. As judged by the calculations presented here, it consistently overestimates B1/2. (Table 1) under conditions of slow (k < 107 s−1) recombination.The only circumstances under which eqn (2) agrees with our simulations is for a narrow range of much shorter lifetimes. For a radical pair with σAB = 1 mT, the SW approach (Fig. 2c) agrees with eqn (2) when k ≈ 1.6 × 108 s−1 while the SC method (Fig. 4b) only gives Weller's value of B1/2 for [FAD˙− TrpH˙+] when k ≈ 2.0 × 108 s−1. This suggests that eqn (2) may only be applicable to radical pairs comprising small radicals in solution with lifetimes of the order of 5 ns.
This conclusion seems to be supported by a study of one of the radical pairs for which Weller's equation was originally proposed. Rodgers et al. measured magnetic field effects on the photochemical reactions of N,N-dimethylaniline with pyrene in which neither, one or both of the reactants had been perdeuterated.19 By exploiting the different hyperfine interactions of the four isotopologues, it was possible to estimate the radical encounter times that were most effective for the generation of magnetic field effects. Encounters within 2 ns of radical pair formation contributed little because there was insufficient time for the applied magnetic field to affect the spin dynamics. Encounters at times longer than 10 ns were also ineffectual because of their low probability. The conclusion of Rodgers et al.19 that only encounters on a 2–10 ns timescale are important for the magnetic sensitivity of the pyrene + N,N-dimethylaniline reaction agrees well with the finding here that eqn (2) works best when k−1 ≈ 5 ns.
Comparison of simulation methods
We have simulated magnetic field effects on [FAD˙− TrpH˙+] for two extreme cases: (A) fast rotational tumbling (such that anisotropic interactions are averaged to zero) with extensive translational diffusion (such that radical–radical interactions can be neglected), and (B) static, randomly oriented radical pairs with non-zero anisotropic (hyperfine and dipolar) interactions.
Table 1 presents the estimated values of B1/2, in order of increasing sophistication of the method used to simulate the magnetic field effects. The SW semiclassical approach is known to be of limited reliability for the long-lived (∼1 μs) radical pairs of interest here.37,38 QMMC and QD treat the quantum spin dynamics exactly but are restricted in the number of nuclear spins that can be included and so require extrapolation to estimate B1/2 for the intact 29-spin system of [FAD˙− TrpH˙+]. Introducing the dipolar coupling would restrict the number of nuclear spins even further. The computational effort required for the improved semiclassical method, SC, increases linearly with the number of nuclear spins, allowing all 27 isotropic hyperfine interactions to be modelled reasonably accurately. However, this approach is only applicable when there is no electron-electron coupling. Finally, the SU(Z) method, for which the computational effort scales as D![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) D (with D = 4Z being the size of the full electron–nuclear Hilbert space), is compatible with a reasonably large number of nuclei with dipolar coupling included.
D (with D = 4Z being the size of the full electron–nuclear Hilbert space), is compatible with a reasonably large number of nuclei with dipolar coupling included.
Cryptochrome B1/2
The best estimates of B1/2 for [FAD˙− TrpH˙+] are (Table 1): 1.89 mT for case (A) (isotropic hyperfine interactions, no dipolar coupling, SC method) and 2.46 mT for case (B) (anisotropic hyperfine interactions, non-zero dipolar coupling, no rotational motion, SU(Z) method). The majority of the difference between the two arises from the anisotropic components of the hyperfine interactions which outweigh a small reduction in B1/2 caused by the dipolar interaction of FAD˙− and TrpH˙+.Case (B) above is more appropriate than case (A) for cryptochrome, a molecule with molecular mass ∼64 kDa. Under the conditions of the experiments used to measure B1/2 for this protein (typically 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80 glycerol
80 glycerol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water mixtures at 5 °C11), the rotational correlation time τc of an avian Cry4a is estimated to be ∼80 ns (ESI,† Section S10). With this value, γeΔBτc = 1 when ΔB = 0.1 mT implying that only anisotropic interactions (ΔB) smaller than ∼0.1 mT would be efficiently averaged by such slow tumbling. Both the anisotropic hyperfine interactions and the dipolar coupling in [FAD˙− TrpH˙+] are considerably larger than 0.1 mT and would therefore not be much affected by rotational motion of the protein in solution.
water mixtures at 5 °C11), the rotational correlation time τc of an avian Cry4a is estimated to be ∼80 ns (ESI,† Section S10). With this value, γeΔBτc = 1 when ΔB = 0.1 mT implying that only anisotropic interactions (ΔB) smaller than ∼0.1 mT would be efficiently averaged by such slow tumbling. Both the anisotropic hyperfine interactions and the dipolar coupling in [FAD˙− TrpH˙+] are considerably larger than 0.1 mT and would therefore not be much affected by rotational motion of the protein in solution.
The “baseline” value of B1/2 for [FAD˙− TrpH˙+] in Cry4a, resulting from anisotropic hyperfine and dipolar interactions alone, should therefore be taken as 2.46 mT.
Low-field effects
Finally, we consider the related issue of why “low-field effects” are not more commonly observed for cryptochrome-based radical pairs. The low-field effect is a characteristic of radical pairs that have long-lived spin coherence and manifests as a biphasic field-dependence of the reaction yield.36 Typically, for a singlet-born radical pair, ΦT(B) rises as B is increased from zero and then falls once B is comparable to or larger than σAB. The existence of a low-field effect has been interpreted as an indication that a radical pair could be suitable for detection of magnetic fields as weak as the Earth's (∼50 μT), for which spin-coherence times of at least ∼1 μs are required.12,46Fig. 6a shows ΦT(B) in the range 0 ≤ B ≤ 2 mT for [FAD˙− TrpH˙+], calculated using the SU(Z) approach for case (A) (isotropic hyperfine interactions and no dipolar interaction) with nnuc = 14, k = 106 s−1. A weak but distinct low-field effect is clearly visible below ∼0.5 mT. The fairly steep gradient of ΦT(B) at B = 0, implies a reasonably large sensitivity to Earth-strength magnetic fields. However, the corresponding calculation for case (B) (anisotropic hyperfine and non-zero dipolar interactions, no rotational motion) in Fig. 6d has no suggestion of a low-field effect. Fig. 6b (isotropic hyperfine and non-zero dipolar interactions) and Fig. 6c (anisotropic hyperfine and no dipolar interactions) show that it is the hyperfine anisotropy rather than the dipolar coupling that abolishes the low-field effect in these simulations.
The correspondence between this prediction and experimental measurements of magnetic field effects on cryptochromes is unclear. Small low field effects have been reported for a plant cryptochrome (Arabidopsis thaliana cryptochrome 1, AtCry1) and the structurally related DNA photolyase from E. coli (EcPL).12 If other magnetically sensitive members of the cryptochrome-photolyase family have low field effects, they have so far been too small to detect. These proteins include both wild-type and W369F mutant versions of European robin (Erithacus rubecula) cryptochrome 4a (ErCry4a)11 and the cryptochrome from the fruit fly Drosophila melanogaster (DmCry).47 The measurements for AtCry1 and EcPL were made at 260 or 270 K in 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 or 60
50 or 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 glycerol
40 glycerol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water mixtures. Those for ErCry4a and DmCry were done at 278 K in 20
water mixtures. Those for ErCry4a and DmCry were done at 278 K in 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80 glycerol
80 glycerol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water solutions. Given the lower viscosity of the ErCry4a and DmCry samples, one might have expected a larger low field effect as a result of the more efficient averaging of anisotropic components of the hyperfine interactions. Nor can the absence of a low field effect in ErCry4a and DmCry be attributed to the additional tryptophan in the electron transfer chains of these proteins because the W369F mutant of ErCry4a, which lacks the terminal tryptophan residue of the Trp-tetrad, shows no discernible low field effect. Further experiments will be required to resolve the apparent discrepancy with the simulations in Fig. 6.
water solutions. Given the lower viscosity of the ErCry4a and DmCry samples, one might have expected a larger low field effect as a result of the more efficient averaging of anisotropic components of the hyperfine interactions. Nor can the absence of a low field effect in ErCry4a and DmCry be attributed to the additional tryptophan in the electron transfer chains of these proteins because the W369F mutant of ErCry4a, which lacks the terminal tryptophan residue of the Trp-tetrad, shows no discernible low field effect. Further experiments will be required to resolve the apparent discrepancy with the simulations in Fig. 6.
Conclusions
A number of conclusions emerge from this study. First, it appears that Weller's expression for B1/2 is only applicable to small, short-lived (∼5 ns), rapidly tumbling radical pairs in solution. It is unreliable for both longer and shorter lifetimes and/or in situations where anisotropic hyperfine and/or exchange/dipolar interactions affect the spin dynamics. Second, the hyperfine-only value of B1/2 for the [FAD˙− TrpH˙+] radical pair in cryptochrome in solution is ∼2.46 mT. The observation of B1/2 values larger than this should be taken as a strong indication that additional factors, such as electron spin relaxation, are at play. Third, for reactions of free flavin and tryptophan radicals in non-viscous solution, the corresponding value of B1/2 is ∼1.89 mT. Fourth, the low-field effect for [FAD˙− TrpH˙+] pairs in cryptochromes in solution is predicted to be abolished by the anisotropic components of the hyperfine interactions. These insights will be valuable in future studies of the effects of spin relaxation on the performance of [FAD˙− TrpH˙+] as a magnetic compass sensor.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are grateful to the following for financial support: the European Research Council (under the European Union's Horizon 2020 research and innovation programme, grant agreement no. 810002, Synergy Grant, QuantumBirds), the Office of Naval Research Global (award no. N62909-19-1-2045), and the Deutsche Forschungsgemeinschaft, project no. 395940726 (SFB 1372, Magnetoreception and Navigation in Vertebrates).References
- U. E. Steiner and T. Ulrich, Chem. Rev., 1989, 89, 51–147 CrossRef CAS.
- C. T. Rodgers, Pure Appl. Chem., 2009, 81, 19–43 CrossRef CAS.
- A. R. Jones, Molec. Phys., 2016, 114, 1691–1702 CrossRef CAS.
- P. J. Hore and H. Mouritsen, Annu. Rev. Biophys., 2016, 45, 299–344 CrossRef CAS PubMed.
- K. Maeda, K. B. Henbest, F. Cintolesi, I. Kuprov, C. T. Rodgers, P. A. Liddell, D. Gust, C. R. Timmel and P. J. Hore, Nature, 2008, 453, 387–390 CrossRef CAS PubMed.
- C. Kerpal, S. Richert, J. G. Storey, S. Pillai, P. A. Liddell, D. Gust, S. R. Mackenzie, P. J. Hore and C. R. Timmel, Nat. Commun., 2019, 10, 3707 CrossRef PubMed.
- A. Weller, F. Nolting and H. Staerk, Chem. Phys. Lett., 1983, 96, 24–27 CrossRef CAS.
- M. E. Michel-Beyerle, R. Haberkorn, W. Bube, E. Steffens, H. Schröder, H. J. Neusser, E. W. Schlag and H. Seidlitz, Chem. Phys., 1976, 17, 139–145 CrossRef CAS.
- M. E. Michel-Beyerle, H. W. Krüger, R. Haberkorn and H. Seidlitz, Chem. Phys., 1979, 42, 441–447 CrossRef CAS.
- H. J. Werner, K. Schulten and A. Weller, Biochim. Biophys. Acta, 1978, 502, 255–268 CrossRef CAS PubMed.
- J. Xu, L. E. Jarocha, T. Zollitsch, M. Konowalczyk, K. B. Henbest, S. Richert, M. J. Golesworthy, J. Schmidt, V. Déjean, D. J. C. Sowood, M. Bassetto, J. Luo, J. R. Walton, J. Fleming, Y. Wei, T. L. Pitcher, G. Moise, M. Herrmann, H. Yin, H. Wu, R. Bartölke, S. J. Käsehagen, S. Horst, G. Dautaj, P. D. F. Murton, A. S. Gehrckens, Y. Chelliah, J. S. Takahashi, K.-W. Koch, S. Weber, I. A. Solov’yov, C. Xie, S. R. Mackenzie, C. R. Timmel, H. Mouritsen and P. J. Hore, Nature, 2021, 594, 535–540 CrossRef CAS PubMed.
- K. Maeda, A. J. Robinson, K. B. Henbest, H. J. Hogben, T. Biskup, M. Ahmad, E. Schleicher, S. Weber, C. R. Timmel and P. J. Hore, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 4774–4779 CrossRef CAS PubMed.
- U. E. Steiner and J. Q. Wu, Chem. Phys., 1992, 162, 53–67 CrossRef CAS.
- E. A. Weiss, M. A. Ratner and M. R. Wasielewski, J. Phys. Chem. A, 2003, 107, 3639–3647 CrossRef CAS.
- M. Justinek, G. Grampp, S. Landgraf, P. J. Hore and N. N. Lukzen, J. Am. Chem. Soc., 2004, 126, 5635–5646 CrossRef CAS PubMed.
- K. Schulten, J. Chem. Phys., 1985, 82, 1312–1316 CrossRef CAS.
- R. Haberkorn, M. E. Michel-Beyerle and R. A. Marcus, Proc. Natl. Acad. Sci. U. S. A., 1979, 76, 4185–4188 CrossRef CAS PubMed.
- A. Ogrodnik, H. W. Kruger, H. Orthuber, R. Haberkorn, M. E. Michelbeyerle and H. Scheer, Biophys. J., 1982, 39, 91–99 CrossRef CAS PubMed.
- C. T. Rodgers, S. A. Norman, K. B. Henbest, C. R. Timmel and P. J. Hore, J. Amer. Chem. Soc., 2007, 129, 6746–6755 CrossRef CAS PubMed.
- S. Y. Wong, Y. Wei, H. Mouritsen, I. A. Solov’yov and P. J. Hore, J. R. Soc., Interface, 2021, 18, 20210601 CrossRef CAS PubMed.
- S. Y. Wong, A. Frederiksen, M. Hanic, F. Schuhmann, G. Grüning, P. J. Hore and I. A. Solov’yov, Neuroforum, 2021, 27, 141–150 CrossRef.
- N. Karki, S. Vergish and B. D. Zoltowski, Protein Sci., 2021, 30, 1521–1534 CrossRef CAS PubMed.
- R. Kavet and J. Brain, Physiology, 2021, 36, 183–194 CrossRef CAS PubMed.
- T. Ritz, S. Adem and K. Schulten, Biophys. J., 2000, 78, 707–718 CrossRef CAS PubMed.
- T. Hochstoeger, T. Al Said, D. Maestre, F. Walter, A. Vilceanu, M. Pedron, T. D. Cushion, W. Snider, S. Nimpf, G. C. Nordmann, L. Landler, N. Edelman, L. Kruppa, G. Durnberger, K. Mechtler, S. Schuechner, E. Ogris, E. P. Malkemper, S. Weber, E. Schleicher and D. A. Keays, Sci. Adv., 2020, 6, eabb9110 CrossRef CAS PubMed.
- N. Ozturk, C. P. Selby, S. H. Song, R. Ye, C. Tan, Y. T. Kao, D. P. Zhong and A. Sancar, Biochemistry, 2009, 48, 8585–8593 CrossRef CAS PubMed.
- A. Günther, A. Einwich, E. Sjulstok, R. Feederle, P. Bolte, K.-W. Koch, I. A. Solov’yov and H. Mouritsen, Curr. Biol., 2018, 28, 211–223.e214 CrossRef PubMed.
- H. Wu, A. Scholten, A. Einwich, H. Mouritsen and K.-W. Koch, Sci. Rep., 2020, 10, 7364 CrossRef CAS PubMed.
- A. Einwich, K. Dedek, P. K. Seth, S. Laubinger and H. Mouritsen, Sci. Rep., 2020, 10, 15794 CrossRef CAS PubMed.
- H. Mitsui, T. Maeda, C. Yamaguchi, Y. Tsuji, R. Watari, Y. Kubo, K. Okano and T. Okano, Biochemistry, 2015, 54, 1908–1917 CrossRef CAS PubMed.
- X. Wang, C. Jing, C. P. Selby, Y.-Y. Chiou, Y. Yang, W. J. Wu, A. Sancar and J. Wang, Cell. Molec. Life Sci., 2018, 75, 4629–4641 CrossRef CAS PubMed.
- B. D. Zoltowski, Y. Chelliah, A. Wickramaratne, L. Jarocha, N. Karki, W. Xu, H. Mouritsen, P. J. Hore, R. E. Hibbs, C. B. Green and J. S. Takahashi, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 19449–19457 CrossRef CAS PubMed.
- A. A. Lee, J. C. S. Lau, H. J. Hogben, T. Biskup, D. R. Kattnig and P. J. Hore, J. R. Soc., Interface, 2014, 11, 20131063 CrossRef PubMed.
- K. Schulten and P. G. Wolynes, J. Chem. Phys., 1978, 68, 3292–3297 CrossRef CAS.
- K. Maeda, T. Miura and T. Arai, Mol. Phys., 2006, 104, 1779–1788 CrossRef CAS.
- C. R. Timmel, U. Till, B. Brocklehurst, K. A. McLauchlan and P. J. Hore, Mol. Phys., 1998, 95, 71–89 CrossRef CAS.
- D. E. Manolopoulos and P. J. Hore, J. Chem. Phys., 2013, 139, 124106 CrossRef CAS PubMed.
- T. P. Fay, L. P. Lindoy, D. E. Manolopoulos and P. J. Hore, Faraday Discuss., 2020, 221, 77–91 RSC.
- P. J. Hore, Nuclear magnetic resonance, Oxford University Press, Oxford, 2015 Search PubMed.
- N. S. Babcock and D. R. Kattnig, J. Phys. Chem. Lett., 2020, 11, 2414–2421 CrossRef CAS PubMed.
- V. I. Borovkov, V. A. Bagryansky, G. A. Letyagin, I. V. Beregovaya, L. N. Shchegoleva and Y. N. Molin, Chem. Phys. Lett., 2018, 712, 208–213 CrossRef CAS.
- T. P. Fay, L. P. Lindoy and D. E. Manolopoulos, J. Chem. Phys., 2021, 154, 084121 CrossRef CAS PubMed.
- D. R. Kattnig, I. A. Solov'yov and P. J. Hore, Phys. Chem. Chem. Phys., 2016, 18, 12443–12456 RSC.
- S. Worster, D. R. Kattnig and P. J. Hore, J. Chem. Phys., 2016, 145, 035104 CrossRef PubMed.
- D. R. Kattnig, J. K. Sowa, I. A. Solov'yov and P. J. Hore, New J. Phys., 2016, 18, 063007 CrossRef.
- F. Cintolesi, T. Ritz, C. W. M. Kay, C. R. Timmel and P. J. Hore, Chem. Phys., 2003, 294, 385–399 CrossRef CAS.
- D. M. W. Sheppard, J. Li, K. B. Henbest, S. R. T. Neil, K. Maeda, J. Storey, E. Schleicher, T. Biskup, R. Rodriguez, S. Weber, P. J. Hore, C. R. Timmel and S. R. Mackenzie, Sci. Rep., 2017, 7, 42228 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp03793a |
| ‡ These authors contributed equally. |
| This journal is © the Owner Societies 2023 |