Periodic aggregation patterns of oxide particles on corroding metals: chemical waves due to solution feedback processes

Abstract

Chemical waves that produce periodic patterns are common occurrences in nature. The underlying processes involved have been studied in many disciplines of science, but rarely reported in the chemistry of corrosion. In this study of carbon steel corrosion, iron oxide crystals are observed to deposit in concentric wave patterns or in discrete bands, known as Liesegang patterns. We demonstrate that oxide growth in these patterns is preceded by the formation of a hydrogel network, which consists of a semi-stationary phase of loosely connected metal-hydroxide colloids and a mobile phase of solution saturated with metal cations. Once the hydrogel network covers the metal surface, a metal cation produced by corrosion reactions at the metal surface must diffuse through the layer into the bulk solution. While diffusing through the porous network, the metal cation undergoes adsorption–precipitation as metal-hydroxide colloids which later can dissolve back into the solution. When the kinetics of precipitation and dissolution of the metal cation can be effectively coupled with the transport flux of the dissolved metal cation, the precipitation–dissolution–diffusion cycles can be sustained over time which can lead to periodic aggregation patterns of metal-hydroxide colloids at a specific time. We also establish that for transition metal cations the precipitation–dissolution–diffusion process can couple with reversible redox reactions between the soluble and less soluble metal cations, which can affect the overall transport of banded aggregates of metal-hydroxide colloids and the growth and transformation of metal-hydroxides into crystalline oxides. If systemic feedback between different elementary processes is sustained over long durations, iron-oxide crystals of different chemical compositions and shapes aggregate in Liesegang patterns. This work demonstrates unequivocally that non-uniform deposition of metal oxides during corrosion can occur via strongly coupled solution reactions and transport processes, and not simply as a result of metallurgical non-uniformity and/or localized solution environments.

---

Introduction

Chemical waves in space and time domains are a well-known phenomenon. Some familiar examples are oscillating reactions (e.g., chemical clock reactions) and Turing pattern formation.^1–3 In the presence of transport processes such as diffusion and convective flow, chemical systems that undergo temporal oscillations can also exhibit a spatial periodicity.^4,5 The Belousov–Zhabotinsky (B–Z) reaction is a famous chemical oscillation reaction that results in a non-homogeneous spatial distribution of products in solution.^1,6 In such systems, the products diffuse and become uniformly distributed; once the feedback cycles shut down, the periodic patterns eventually dissipate. However, these wave patterns can manifest in a semi-permanent form if adsorption on solid surfaces or precipitation of solid species is involved in the reaction–diffusion system. The periodic formation and/or aggregation of adsorbed or precipitate products is known as the Liesegang phenomenon, and it typically occurs when dissolved species diffuse through a slow-transport medium such as a gel or a porous material, causing solid products to periodically precipitate and re-dissolve (and/or adsorb or desorb).^7–10

In nature, periodic patterns are observed over vast ranges of size and duration, from fungal colonies to banded rock formations.^11–13 Here, we show clear examples of chemical waves induced by systemic feedback during the corrosion of carbon steel (CS). The chemical wave phenomenon described here involves concentric circular bands or discrete layers of aggregated iron hydroxide and oxide particles. We compare the oxide waves formed on corroding metals with those formed by the reaction of Fe²⁺ at near saturation with OH⁻ in gelatin when the two aqueous solutions containing Fe²⁺ and OH⁻ diffuse into each other.

Oxide formation in concentric ring patterns on corroded surfaces has been previously observed but never fully explained or erroneously interpreted as a localized corrosion phenomenon arising from spatial variations in redox activity across metal surfaces.^14–16 In this work, we establish for the first time that the oxide formation in periodic patterns is a Liesegang phenomenon that arises from the sustained cyclic feedback between the chemical reactions and transport processes of metal cations in solution. While systemic feedback involving the formation of a membrane-like metal hydroxide or a salt layer over the metal surface has been suggested for spatiotemporal phenomena observed in various electrochemical studies of corrosion,^17,18 this study is the first to demonstrate unequivocally that the formation of a metal-hydroxide hydrogel network is the key condition for systemic feedback. The hydrogel network consisting of a semi-stationary phase made of loosely connected metal hydroxide colloidal particles provides a slow transport medium that allows the kinetics of diffusion and precipitation of metal cations dissolved in solution to be strongly coupled, resulting in metal cations oscillating between different quasi-stable states, dissolved ionic and solid colloidal states. We also propose a mechanism based on the reaction–diffusion kinetics of ferrous and ferric ions coupled with the kinetics of a newly identified process which we refer to as “redox-assisted Ostwald ripening”, for oxide formation and growth in Liesegang patterns during corrosion.

The mechanism proposed here for oxide growth during corrosion is a significant departure from the current understanding of corrosion behavior. The findings of this work challenge the existing methodologies and practices for corrosion testing and modelling but also have wider implications for other processes involving metal/solution interfaces, such as nanoparticle growth,^19,20 solid electrolyte degradation²¹ and remediation of metal-contaminated wastewater.^22,23

Experimental

The oxide-wave patterns on corroded CS surfaces presented in this paper are a compilation of those formed during corrosion under several different exposure conditions.²⁴ In this section, the conditions and procedures of the corrosion tests are presented. The specifics of other supporting tests such as the diffusion of OH⁻ in gelatin prepared using solution containing FeSO₄, and hydrogel formation and the development of oxide bands in solutions are given when the results are presented.

Materials and solutions

Carbon steel (CS) used in corrosion studies was SA-106 Gr. C. A rod of this material was cut into circular discs of 1 cm in diameter and 3 mm in height (referred to as “coupons”). Prior to each test, the coupons flat circular surfaces were abraded using a series of fine SiC papers up to 2500 grit, then polished using a 1 μm diamond suspension, washed with Type 1 water, and dried under flowing argon gas. Each disc was sealed with Teflon or Parafilm and only one circular face with a surface area of 0.785 cm² was exposed to the test solution.

All solutions were prepared with Type 1 water purified using a NANOpure Diamond UV ultra-pure water system (Barnstead International) to give a resistivity of 18.2 MΩ cm. The hydrogen peroxide solutions used in some of the corrosion tests were prepared by diluting a 3 wt%, stock H₂O₂ solution (Fisher Chemical) with Type 1 water to desired concentrations.

The saturated FeSO₄ solution was prepared from reagent grade FeSO₄·7H₂O (Sigma-Aldrich). The gelatin used for generating hydroxide waves was prepared by dissolving 1.5 wt% of Type B gelatin (EMD Chemicals Inc.) in Type 1 water at 40 °C. To this mixture, FeSO₄ was added to give a Fe²⁺ concentration of 0.03 M. The solution was then poured onto a Petri dish and allowed to set for 24 h at room temperature. The 2 M sodium hydroxide solution was prepared from reagent grade NaOH (Fisher Chemical) and Type 1 water.

Coupon exposure test procedure

The freshly polished and argon-dried CS coupons were placed in individual vials and exposed to the test solution (pure water or H₂O₂ solution) for the desired time. The solutions were naturally aerated, prepared under air, with no other aerating gases used. Thus, there was no convective flow of solution (solutions were stagnant). At the end of each experiment, the coupons were carefully removed from the test solution and dried under vacuum.

Irradiation

Some corrosion tests were performed using a ⁶⁰Co gamma cell irradiator (220 Excel, MDS Nordion), which provided an absorbed radiation dose rate of 2.5 kGy h⁻¹ at the time of the tests (where 1 Gy = 1 J absorbed per kg of water). The individual vials containing the CS coupons were placed in a circular sample holder to ensure that all samples received a uniform dose. We use γ-radiation to generate redox active species (e.g., ˙OH, H₂O₂) at low but steady state concentrations without affecting the solvation properties of water.

Post-test analyses

Following each corrosion test in a specific solution and radiation environment, the corrosion products, both dissolved in the solution and present on the metal surface, were analyzed. Although the solution analysis results are not reported here, the dissolved iron content was determined by first digesting the solution using TraceMetal™ grade nitric acid (Fisher Chemical) followed by analyzing the metal content using a PerkinElmer Avio 200 Inductively Coupled Plasma Optical Emissions Spectrometer (ICP-OES). The concentration of H₂O₂ was determined using the Ghormley tri-iodide method.²⁵

The oxide composition was analyzed using a Raman spectrometer (Renishaw model 2000) with a laser excitation wavelength of 633 nm and a spatial resolution of ∼1 μm. The morphology of the oxide particles was examined using optical microscopy (Leica DVM 6A digital microscope) and scanning electron microscopy (SEM: LEO (Zeiss) 1540XB) equipped with a focused ion beam.

Computational simulations

Numerical simulations were performed using the transport of diluted species and chemistry modules in COMSOL Multiphysics® v5.0.²⁶ The time-dependent diffusion of a droplet of 2 M NaOH into a gel consisting of 0.03 M FeSO₄ was simulated using Fick's second law of diffusion as implemented in COMSOL Multiphysics®.

Results and discussion

Oxide wave patterns observed on corroded surfaces

We have observed the aggregation of metal-oxide crystals of different chemical compositions and shapes in wave patterns during the corrosion of carbon steel in different solution environments. The corrosion environmental parameters studied include the solution volume to surface area ratio, the presence or absence of γ-radiation, stagnant or with continuous gas purging (Ar or air), varying concentrations of hydrogen peroxide, and the corrosion duration.²⁴ Examples of oxide-wave patterns observed from these studies are shown in Fig. 1, with further examples presented throughout this paper.

Fig. 1 Optical micrographs of the surfaces of CS coupons (1 cm in diameter) corroded for different durations in naturally aerated solutions, showing circular wave patterns (a–h). The key corrosion parameters (duration, solution volume, H₂O₂ concentration, and γ-radiation (RAD)) are noted at the top of the optical images. For each corroded surface, two optical images are shown, lower magnification images in the upper rows and higher magnification images in the lower rows. The areas marked with squares in the low-magnification images indicate where the higher magnification images were taken.

The oxide-wave patterns were investigated primarily by optical microscopy. Transition metal oxides/hydroxides have characteristic colours, depending on the oxidation state of the metal cation and the oxide crystal structure.²⁷ For iron species, ferrous hydroxide is green, ferric hydroxide is brownish yellow, mixed Fe^II/Fe^III oxide/hydroxide, magnetite (Fe₃O₄) and maghemite (γ-Fe₂O₃) are black, lepidocrocite (γ-FeOOH) is yellow to orange, and hematite (α-Fe₂O₃) is red.²⁷ Although the formation of a pure single-phase oxide during CS corrosion is not likely, the oxide colour still provides qualitative information on the main oxidation state of iron and the extent of hydration and hydroxylation (i.e., hydroxide, oxyhydroxide, or oxide).

The Raman spectra of areas with different colours confirmed that compounds identified by their characteristic colours observed under an optical microscope are the accurate characterstics of the oxide chemical compositions and phase structures. One example of the Raman analysis of oxide bands is presented in Fig. 2. A comparison with the Raman spectra of standard iron-oxide powder samples shows that the black bands consist mostly of magnetite (Fe₃O₄) crystals and the yellow bands consist mostly of lepidocrocite (γ-FeOOH).

Fig. 2 Optical and SEM micrographs of various magnifications of the oxide bands present on CS (1 cm in diameter) corroded for 5 h in 500 mL of stagnant solution initially containing 0.1 mM H₂O₂ solution. The Raman spectra of the black and yellow bands are compared with those of the standard magnetite and lepidocrocite powder samples.

The SEM images of the oxides of different-coloured bands are shown in Fig. 2. The SEM images show that the bands of distinct colours in the optical images represent areas where oxide crystals have aggregated, not only of the same chemical composition and oxide phase, but also of the same crystal shape and size. The black band is the area where magnetite crystals in the octahedral shape of similar sizes have aggregated, whereas the yellow band is the area where mainly lepidocrocite crystals in the needle-like shape of similar sizes have aggregated. These are characteristic morphologies for these crystalline compounds,²⁷ and further confirm their characterization. The boundary region between the black and yellow bands consists of approximately equal numbers of magnetite and lepidocrocite crystals, but the average sizes of individual crystals are smaller than those in the black or yellow bands.

The results presented in Fig. 2 clearly show that the oxide wave is a result of the aggregation of Fe₃O₄ crystals and γ-FeOOH crystals at alternating distances from the centre (i.e., an initiation point) of the wave. This aggregation of Fe₃O₄ and γ-FeOOH crystals occurs through dissolution/precipitation, coupled with oxidation/reduction of ferrous and ferric species, see discussion later.

As shown in Fig. 1, the oxide wave pattern diameter and the type and size of individual oxide crystals in the individual bands of each wave vary with not only corrosion conditions but also duration. The wave patterns contained discrete bands of 2–3 different but repeating colours. The colour combination also varied with corrosion conditions and duration. In the early stages of corrosion (Fig. 1(a, f, and h)), the repeating band colours were green, black and pale yellow, representing ferrous hydroxide (containing ferric species at an impurity level), mixed Fe^II/Fe^III oxide/hydroxide, and ferric hydroxide. In the later stages of corrosion (Fig. 1(c, d, e and g)), the band colours were mostly black, orange and red, consisting of the aggregated crystalline particles of Fe₃O₄/γ-Fe₂O₃ (magnetite/maghemite), γ-FeOOH (lepidocrocite) and α-Fe₂O₃ (hematite), respectively.

As the conversion of ferrous and ferric hydroxides to more crystalline oxides and oxyhydroxides occurs with time, the oxide rings, which initially propagated as perfect concentric circles, became less discrete and more disordered, with some oxide waves intersecting and creating interference patterns over longer durations. At longer times, some of the circles were as large as hundreds of microns in diameter.

The aggregation of solid metal oxide particles in periodic discrete bands is a Liesegang phenomenon, which is a common occurrence in rock formations, such as banded agates.^10–12,28 Although the mechanism by which Liesegang bands develop in rocks is not completely understood, it is generally accepted that bands of repeating colours are formed when there is a lack of convection (slow transport) of water carrying dissolved metal cations (e.g., ferrous or cupric ion), and by a process involving the diffusion of the metal cations in solution coupled with the adsorption–desorption and/or precipitation–dissolution of the metal cation.^8,29

We propose here a similar mechanism for the development of metal oxide wave patterns during corrosion, but with some key differences. These differences arise primarily from the nature of corrosion. Aqueous corrosion is an electrochemical process; the metal oxidation half-reaction is coupled with oxidant reduction half-reaction(s) via exchange of electrons through an electron conducting medium, the metal. For example,

Ox half-reaction:

2Fe⁰_(m) ⇄ 2Fe²⁺_(sol’n) + 4e⁻ (1a)

Red half-reaction:

O₂ + 2H₂O + 4e⁻ ⇄ 4OH⁻ (1b)

Overall reaction:

2Fe⁰_(m) + O₂ + 2H₂O ⇄ 2Fe²⁺_(sol’n) + 4OH⁻ (1c)

In corrosion, metal cations are continuously injected into the solution phase at the metal–solution interface, and then diffuse from the interface to the bulk solution. Without the removal of the metal cation from the interfacial solution into the bulk solution, the net metal oxidation cannot continue because the metal cation can as easily reduce back, reaching metal/metal cation redox equilibrium.

In the initial kinetic stage of corrosion, the main cation removal process is diffusion along its concentration gradient. What complicates the corrosion dynamics of transition metals or alloys is that the oxidant reduction half-reaction (eqn (1b)) can alter the pH of the solution, affecting the solubility of the metal cation and inducing the precipitation of the metal cation (with OH⁻) as metal hydroxide/oxide particles.^24,30–33 Precipitation of colloids and/or crystalline particles can have a significant effect on the diffusion rate of the initial corrosion product, dissolved metal cations. That is, a cyclic feedback loop can be established between different chemical processes (reactions, precipitation/dissolution and solution transport). Hence, we propose that when such cyclic feedback is sustained for an extended period, solid particles can aggregate in a Liesegang pattern.

The oxides formed at later stages of corrosion are crystalline, with clearly defined facets and distinctive shapes. In addition, the shape and size of the oxide crystals vary with corrosion time. The fact that the shape and size of individual crystals change over time suggests that the oxides grow via diffusion–precipitation–dissolution–diffusion cycles, a process known as Ostwald-ripening.³⁴ In our studies on corrosion of various metals and alloys,^{24,31–33,35,36} we have also observed that oxide crystals continually undergo transformation with time in their chemical composition (the Fe^II to Fe^III ratio, and the OH⁻ to O²⁻ ratio) and oxide-particle phase (e.g., from colloids of Fe^II to mixed Fe^II/Fe^III hydroxides to crystalline magnetite and/or lepidocrocite).

The Liesegang banding, combined with the Ostwald-ripening of metal hydroxide/oxide particles, requires a slow diffusion medium for the dissolved crystal constituent ions, metal cations and OH⁻. The diffusion of Fe²⁺ and OH⁻ from the metal–solution interface, where they are produced, into the bulk solution through aqueous solution would be too fast for these ions to precipitate and grow into solid oxide and oxyhydroxide crystals and to aggregate in Liesegang patterns. Hence, we propose that:

• A slow transport medium is formed by the reaction of the initial corrosion products, Fe²⁺ and OH⁻, in the interfacial volume between the metal and the bulk solution, while they are diffusing from the interface to the bulk solution.

• This slow transport medium is a hydrogel network^37–39 consisting of a semi-stationary phase made of loosely connected (aggregated) metal hydroxide colloidal particles and a mobile phase of solution containing metal cations at their saturation level.

We performed two sets of experiments to confirm these hypotheses:

1. Iron-oxide ring pattern formation in gelatin to confirm that the initiation of oxide wave patterns observed on corroded metal requires a slow transport medium for Fe²⁺ and OH⁻.

2. Formation of a metal hydroxide hydrogel layer that serves as a slow transport medium by adding aqueous OH⁻ solution to the solution containing Fe²⁺ at near saturation level.

Oxide wave initiation

Initiation of iron hydroxide waves in gelatin. The oxide wave patterns formed in the gelatin and on the surfaces of CS corroded for short durations are compared in Fig. 3. The gelatin used in this study was prepared using an air-saturated solution containing Fe²⁺. Gelatin has a structure consisting of a biopolymeric (polypeptide) stationary phase and a solution mobile phase.^40,41 In the gelatin used in this study, Fe²⁺, OH⁻ and O₂ are initially distributed homogeneously throughout the gel medium.

Fig. 3 (a) Comparison of Liesegang rings formed on carbon steel corroded in 2 mL of 0.5 mM H₂O₂ for 30 minutes (where 1, 2 and 3 are the high magnification images of the boxed areas on the image shown on the far left-hand side) and (b) Liesegang rings simulated by placing drops of 2 M NaOH solution on the gelatin prepared using 0.03 M FeSO₄ solution (where t = 0 min refers to the time of addition of the two 10 μL drops, 5 min after the 20 μL drop).

A chemical wave was initiated by placing a droplet of solution containing OH⁻ on a thin layer of the gelatin in a Petri dish. In this test, the total amount of OH⁻ available was limited by the droplet size. In comparison, corrosion involves the oxidation of one Fe⁰_(m) to one Fe²⁺ coupled with oxidant reduction to two OH⁻ (independent of type or the concentration of oxidant on CS) at the metal–solution interface (eqn (1)). That is, on the corroding surface, Fe²⁺ and 2OH⁻ are produced simultaneously at the metal–solution interface, and then diffuse out in a 3-D hemispherical direction into the bulk solution.

The oxide wave patterns formed in the two different reaction media have common characteristic features. In both systems, the individual oxide waves have propagated in perfect circular patterns which consist of concentric rings of green ferrous hydroxide and orange to brown ferric hydroxide.

The Liesegang rings and bands that are more commonly observed and discussed in the literature are monochromatic; rings or bands consisting of one type of solid (and/or adsorbed) species are separated by areas void of these species, in a repeating pattern. What we observed in the gelatin experiments is that each ring consists of distinct bands of two different colloidal species, ferrous hydroxide and ferric hydroxide, even at the very early stages of wave development. Due to the one-time addition of a small amount of OH⁻, each wave formed within 20 minutes contained only three concentric rings with two alternating colours, green, brownish orange, and green, from the centre outwards. While the widths of each of these rings increased with time, the colours and their intensities of the individual rings also changed; the initially green bands became reddish orange while the initially brownish orange bands became orange-black. These colour changes indicate that ferrous and ferric hydroxides are changing to ferric oxyhydroxide and mixed ferrous and ferric oxide.

In the case of CS corrosion, the oxide ring patterns formed in the early stages also have repeating bands of green ferrous hydroxide and yellowish-orange ferric hydroxide, but the colours are not as intense as those formed in the gelatin. The SEM images of the differently colored rings of one of the waves shown in Fig. 3a are presented in Fig. 4. The metal hydroxides formed in early stages of corrosion are nano-sized, non-crystalline particles. The green colored ring consisting of mostly Fe(OH)₂ shows that the small particles are connected via a semi-stationary network, whereas the yellowish orange colored ring consisting of mostly Fe(OH)₃ shows the aggregation of small spherical particles, and the boundary region shows a smoother surface with less grainy particles.

Fig. 4 SEM micrographs of the areas of differently colored rings in the optical image shown in Fig. 3.

The larger ring patterns, which had grown over longer corrosion durations, no longer contained green rings, but contained black and yellowish to reddish orange rings; and the black bands of mixed Fe^II/Fe^III hydroxide/oxide were clearly separated from the orange bands of Fe^III oxyhydroxide/oxide. These observations indicate that hydroxide nucleates formed in the early stages of corrosion continue to go through dissolution precipitation cycles, growing in size while slowly transforming into crystalline oxides as shown in Fig. 2.

Liesegang phenomena are often described as involving the propagation of an adsorption–diffusion and/or a reaction–diffusion front.⁸ The chemical waves observed in the early stages of CS corrosion under conditions that promote metal hydroxide precipitation involve two reactions–greenish ferrous-hydroxide production and orange ferric-hydroxide production. In the discussion that follows, we propose a mechanism for the initiation and early stages of the wave propagation of the two iron hydroxides.

Mechanism of the initiation and early stages of iron-hydroxide wave propagation. The diffusion of two dissolved species into each other through a slow transport medium such as gelatin is much slower than that through an aqueous solution. Upon placing a droplet of OH⁻ solution on the gelatin containing Fe²⁺, the OH⁻ solution began to diffuse through the mobile phase of the gelatin creating concentration gradients. In the thin gelatin, the diffusion of OH⁻ can be considered to occur radially on the horizontal plane of the gelatin layer. Consequently, the concentrations of Fe²⁺ and OH⁻ dissolved in the mobile-phase solution change with the radius r from the centre of the OH⁻ droplet and time t:

Solution transport:

where OH⁻(r,t) and Fe²⁺(r,t) represent OH⁻ and Fe²⁺ dissolved in the mixed solution at radius r and at time t and r₀ and t₀ are the radius of the initial OH⁻ droplet and the time of the droplet addition. The overall transport of Fe²⁺ is much slower than that of OH⁻, as Fe²⁺ was initially distributed uniformly in the gelatin, whereas OH⁻ experiences a steep concentration gradient, as its concentration in the gelatin is initially very low. As discussed in more detail later, in corrosion, the transport of the supersaturation front of Fe²⁺ (with OH⁻) at early stages can be adequately described by the radial diffusion on the horizontal plane next to the metal surface.

The increase in [OH⁻] promotes the hydrolysis reactions of Fe²⁺:

Hydrolysis:

Fe²⁺ + 3 OH⁻ ⇌ Fe(OH)⁺ + 2OH⁻ ⇌ Fe(OH)₂ + OH⁻ ⇌ Fe(OH)₃⁻ (3)

where all the species in this chemical equation are dissolved or solvated species, including the neutral molecule Fe(OH)₂. Being acid–base reactions, the forward and reverse hydrolysis reactions are much faster than the transport of the dissolved species through the porous medium. That is, Fe²⁺ and OH⁻ in the mixed solution at radius r and time t can be considered to be always in hydrolysis equilibrium, even though the concentrations of Fe²⁺ and OH⁻ at a given r may change slowly with time t due to the diffusion of Fe²⁺ and OH⁻. That is, the ferrous ions dissolved in solution, represented by Fe²⁺_(sol’n), actually comprise all the different chemical forms listed in eqn (3):

[Fe²⁺_(sol’n)] ≡ [Fe²⁺] + [Fe(OH)⁺] + [Fe(OH)₂] + [Fe(OH)₃⁻] (4)

The relative fractions of the different dissolved ferrous species depend on the concentrations of Fe²⁺_(sol’n) and OH⁻ in the solution, and the pK_a values of the hydrolysis reactions are shown in eqn (3).²⁹

When the total concentration of Fe²⁺_(sol’n) in the solution at radius r and time t ([Fe²⁺_(sol’n)]_r,t) remains below the solubility limit of Fe(OH)₂ no precipitation of Fe(OH)₂ occurs. The solubility of a transition metal cation varies significantly depending on the pH and the oxidation state of the metal cation.²⁹ The gelatin was prepared using a solution containing 0.03 M Fe²⁺_(sol’n) at pH ∼ 6.0, which is more than two orders of magnitude lower than at the initial pH. However, as OH⁻ diffuses into the mobile-phase of the gelatin containing Fe²⁺, the pH of the mixed solution at radius r changes with time t. Accordingly, the value at radius r and time t decreases from its initial value, and the mobile-phase becomes supersaturated with Fe²⁺_(sol’n) while the supersaturation level varies with r and t.

As [Fe²⁺_(sol’n)]_r,t exceeds the dissolved neutral species Fe(OH)₂, which is in hydrolysis equilibrium with other dissolved ferrous ions (eqn (3)), begins to precipitate as solid Fe(OH)₂ on the surface of the stationary-phase of the gelatin. Fe(OH)₂ precipitates initially as nano-sized colloidal particles, Fe(OH)_2(colloid). The colloid particles adsorbed on the surfaces of the stationary phase also easily desorb and dissolve back into the solution phase as Fe²⁺_(sol’n) and OH⁻:

Liquid–solid phase partitioning:

Fe(OH)₂ ⇌ Fe(OH)_2(colloid) (5)

where Fe(OH)₂ represents the solvated ferrous hydroxide molecule, which is in hydrolysis equilibrium with other dissolved ferrous species as shown in eqn (3). Note that colloidal particles carry surface charges (i.e., Fe²⁺_(sol’n) and OH⁻ adsorbed on their surfaces while maintaining overall charge neutrality)⁴² and easily disperse in non-porous aqueous solution.

The liquid–solid phase-partitioning of a ferrous ion (Fe^II) is a reversible process. However, the forward process (precipitation) and the reverse process (dissolution) are slower than homogeneous solution reactions. Hence, unlike the reversible hydrolysis reaction (eqn (3)), the phase-partitioning is not at equilibrium. Instead, it oscillates from net precipitation to net dissolution. Thus, when OH⁻ is added into the gelatin medium and begins to flow downstream, the mobile-phase solution becomes supersaturated. As the supersaturation front moves along the 2-D radial diffusion path of OH⁻, Fe(OH)₂ that is in hydrolysis equilibrium with Fe²⁺_(sol’n) and OH⁻ precipitates as Fe(OH)_2(colloid) on the surface of the stationary phase at radius r and time t. As a result, the solution in contact with the surface at that position and at that time is temporarily depleted of Fe²⁺_(sol’n) and OH⁻ (below 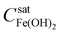). As the OH⁻ solution continues to flow downstream, the supersaturation front moves from r to r + Δr over duration Δt, while the previously precipitated Fe(OH)_2(colloid) at r dissolves back into the mobile phase as Fe²⁺_(sol’n) and OH⁻ at that position but at time t + Δt. The dissolution, in turn, results in the stationary phase temporarily depleted of Fe(OH)_2(colloid) while the solution temporarily supersaturated again at radius r and time t + Δt.

The cycles of the diffusion–precipitation–dissolution–diffusion of Fe²⁺_(sol’n) and OH⁻ continue, resulting in the aggregation of Fe(OH)_2(colloid) in a repeating band pattern. That is, rather than reaching the phase partitioning (quasi-) equilibrium at all r and t, Fe^II in the gelatin network at a specific distance r oscillates with time t between the two chemical phases (dissolved Fe²⁺_(sol’n) and solid Fe(OH)_2(colloid)), while the oscillation with time results in the Fe(OH)_2(colloid) aggregated in a periodic pattern along r at a specific time t. The chemical oscillation and periodic pattern formation as a function of distance r and time t are schematically illustrated in Fig. 5(a).

Fig. 5 Schematics of chemical oscillation and periodic pattern formation by (a) diffusion–precipitation–dissolution–diffusion cycles of ferrous species and (b) diffusion–precipitation–oxidation–reduction–dissolution–diffusion cycles of ferrous and ferric species. Fe(OH)₂ and Fe(OH)₃ are represented by the green- and orange-coloured dots, respectively. is the saturation limit of Fe²⁺_(sol’n). The blue lines show the fluctuation of [Fe²⁺_(sol’n)] relative to .

Thus, when the elementary steps, from eqn (2)–(5), occur at rates that promote strong coupling between these steps, the cycles of diffusion–precipitation–dissolution–diffusion of Fe^II can be sustained over long-time and wide-space domains. If no other elementary steps are involved, the overall consequence of the sustained cycles following the initiation of OH⁻ diffusion in the 2-D radial direction in the Fe²⁺-containing gelatin would be that

• The aggregates of Fe(OH)_2(colloid) are transported as a discrete band along the diffusion path of OH⁻.

• The bands of Fe(OH)_2(colloid) aggregates would be separated by gaps depleted of the colloids in a periodic pattern.

That is, if no other elementary steps are involved, the corrosion product deposits would have formed a monochromatic periodic pattern; rings of greenish Fe(OH)_2(colloids) separated by bands void of the colloidal species in a repeating pattern. What we observed in the gelatin experiments is that each wave consists of distinct bands of two different colloidal species, ferrous hydroxide and ferric hydroxide, even at the very early stages (<20 min). We attribute this to coupling of redox reactions between ferrous and ferric ions with the diffusion–precipitation–dissolution–diffusion of ferrous ions.

The oxidation of Fe²⁺_(sol’n) to Fe³⁺_(sol’n) by dissolved O₂ in the homogeneous solution phase is known to be very slow; it requires a much stronger oxidant such as ˙OH.^43,44 However, the oxidation of ferrous to ferric species occurs more readily on surfaces such as those of the stationary phase of the gelatin and/or solid colloidal particles. Thus, the precipitation of Fe(OH)_2(colloid) along the OH⁻ diffusion path through the gelatin medium promotes its oxidation to Fe(OH)_3(colloid). As the ferric species accumulate, they can also reduce back to Fe(OH)_2(colloid). That is, the redox process between Fe(OH)_2(colloid) and Fe(OH)_3(colloid) is also a reversible process.

Redox reactions of Fe^II and Fe^III:

Oxidation of Fe(OH)₂:

2Fe(OH)_2(colloid) + 2H₂O + O₂ → 2Fe(OH)_3(colloid) + H₂O₂ (6a)

2Fe(OH)_2(colloid) + H₂O₂ → 2Fe(OH)_3(colloid) (6b)

Reduction of Fe(OH)₃:

2Fe(OH)_3(colloid) + H₂O₂ → 2Fe(OH)_2(colloid) + 2H₂O + O₂ (6c)

The oxidation product, Fe(OH)_3(colloid), undergoes its own precipitation–dissolution cycles, similar to those of Fe(OH)_2(colloid) (eqn (5)), and the dissolved ferric ion (Fe³⁺_(sol’n)) undergoes its own hydrolysis equilibrium reactions, similar to those of Fe²⁺_(sol’n) (eqn (3)). However, Fe(OH)_3(colloid) has the stronger Fe–OH bonding and a significantly lower solubility in solution than Fe(OH)_2(colloid).³⁰ Hence, although ferric species may undergo the diffusion–precipitation–dissolution–diffusion cycles, the overall transport of Fe³⁺_(sol’n) is much slower than that of Fe²⁺_(sol’n) and hence, it will have a negligible influence on the overall rate of oxide wave propagation. (That is, the main carrier for the metal cation transport through the solution phase is Fe²⁺_(sol’n).)

Under certain solution redox conditions, such as in aerated and/or gamma-irradiated solutions, the Fe^II–Fe^III redox reactions occur at rates such that they can couple strongly with the diffusion–precipitation–dissolution–diffusion of Fe^II. The overall transport of Fe²⁺_(sol’n) and OH⁻ (eqn (2)) through the gelatin now consists of cycles of the diffusion–precipitation of Fe^II–oxidation of Fe^II to Fe^III, followed by the reduction of Fe^III to Fe^II and the dissolution–diffusion of Fe^II. If the formation of the ferric-hydroxide colloids had a negligible effect on the overall transport of Fe^II through the gelatin, the Fe speciation in the gelatin network at a specific radius r oscillates with time t between Fe²⁺_(sol’n), Fe(OH)_2(colloid) and Fe(OH)_3(colloid). However, because the transport through the gelatin network is primarily carried out by Fe²⁺_(sol’n), once Fe(OH)_3(colloid) particles aggregate into a band, the overall transport of Fe^II through the band is very slow. Hence, the phase-partitioning of Fe^II species (eqn (5)) is at (quasi-) equilibrium, and chemical oscillation occurs primarily due to the cyclic feedback between the net oxidation of Fe(OH)_2(colloid) to Fe(OH)_3(colloid) and the net reduction of Fe(OH)_3(colloid) back to Fe(OH)_2(colloid) (eqn (6)).

The overall consequence is the aggregation of Fe(OH)_2(colloid)–Fe(OH)_3(colloid)–Fe(OH)_2(colloid) in alternating bands (without the gaps void of colloids), while the supersaturation front of Fe²⁺_(sol’n) is moving ahead of the alternating bands of two solid products, as schematically illustrated in Fig. 5(b). (Note that when the net oxidation of Fe(OH)_2(colloid) to Fe(OH)_3(colloid) is faster than the net precipitation of Fe²⁺_(sol’n) and OH⁻ to Fe(OH)_2(colloid), the oxide-wave propagation would resemble that of monochromatic Liesegang banding shown in Fig. 5(a) but with bands of Fe(OH)_3(colloid) aggregates, see further discussion later).

Thus, under the right combinations of solution redox and mass transport conditions, the Fe^II–Fe^III redox reaction steps (eqn (6)) can couple strongly with the steps involving Fe^II species (eqn (2)–(5)), and the cycles of the diffusion–precipitation–oxidation–reduction–dissolution–diffusion of Fe^II can be sustained over some time. The overall consequence of the sustained cycles following the initiation of OH⁻ diffusion in the 2-D radial direction in the Fe²⁺-containing gelatin would be that

• The aggregates of Fe(OH)_3(colloid) are transported as a group (band) along with the overall transport of the band of Fe(OH)_2(colloid) aggregates.

• The band of Fe(OH)_3(colloid) aggregates is transported at a slightly lower rate than that of Fe(OH)_2(colloid), resulting in more clear separation of the two hydroxide colloidal bands over time.

In the gelatin experiments, due to the limited amount of OH⁻, the propagation of oxide waves was limited to the formation of only 2–3 bands; from the centre outwards, a band depleted of Fe(OH)_2(colloid), to a band of mixed Fe^II/Fe^III hydroxide colloids, to a band of mostly Fe(OH)_2(colloid) at early times (<20 min). As these bands broadened with time, hydroxides in these bands slowly underwent phase transformation to oxide or oxyhydroxide particles, ranging from anhydrous Fe(OH)₃, mixed Fe^II/Fe^III oxide (Fe₃O₄), and ferric oxy-hydroxide (γ-FeOOH), respectively.

The hydroxide-wave patterns on CS surfaces corroded over short durations contained more than 2–3 bands (Fig. 3). During corrosion, Fe²⁺ and OH⁻ are continuously produced at the metal–solution interface, which then diffuse out of the interfacial solution to the bulk solution. Hence, the steady state concentration of Fe²⁺_(sol’n) in the interfacial solution depends on both the rate of metal oxidation at the interface that injects Fe²⁺_(sol’n) into the interfacial solution and the rate of diffusion that removes Fe²⁺_(sol’n) from the interfacial solution. Fe²⁺ and OH⁻ injected into the interfacial solution diffuse hemi-spherically from the injection point into the bulk solution. However, the diffusion spheres of Fe²⁺_(sol’n) and/or OH⁻ overlap quickly near the interface. Their interference patterns result in a 1-D or planar diffusion of Fe²⁺_(sol’n) and OH⁻ in the direction perpendicular to the metal surface (z-direction). Hence, for corrosion over a large surface area (or planar electrode), the diffusion of the metal cation into the bulk solution is often considered to occur perpendicular to the metal surface plane. However, the 1-D diffusion does not mean that the Fe²⁺_(sol’n) concentration is the same across the horizontal plane at distance z.

Depending on the redox, pH and transport conditions of the solution, the average [Fe²⁺_(sol’n)] in the interfacial solution can quickly reach its solubility limit. If and when this occurs, the overall metal oxidation (or corrosion) can occur only at the rate of movement of the saturation front. The movement of the saturation front can be also considered as a 1-D mass transport problem. However, because many elementary chemical steps are involved leading to the saturation condition, the Fe²⁺_(sol’n) concentration across the interfacial solution plane varies about the saturation level. That is, pockets of supersaturated solution begin to appear, randomly distributed across the interfacial solution. The number density of the pockets of supersaturated solutions is initially small, and they are far apart from each other, as schematically shown in Fig. 6. While the saturation (or the supersaturation) front continues to move in the direction, perpendicular to the metal surface, Fe²⁺_(sol’n) and OH⁻ also diffuse radially from the supersaturated region to the near-saturated region within the interfacial solution. As a result, the pockets of supersaturated solution act as the initiation points for the diffusion–precipitation–oxidation–reduction–dissolution–diffusion cycles of ferrous and ferric species, as shown in Fig. 5b. The cyclic feedback thus propagates radially on the horizontal plane of the interfacial solution that contains Fe²⁺_(sol’n) near the saturation level, resulting in alternating aggregation of Fe(OH)₂ and Fe(OH)₃ colloids in the concentric ring patterns.

Fig. 6 Schematic representation of the supersaturated pockets of solution appearing far apart from each other, at early time frames, acting as initiation points for the diffusion–precipitation–oxidation–reduction–dissolution–diffusion cycles of ferrous and ferric species. From the top view, a Liesegang ring, aligning with t₂, is shown in Fig. 5b.

As Fe²⁺ and OH⁻ are continuously produced at the metal–solution interface, they continue to transport, through the interfacial solution into the bulk solution. However, the diffusion in the direction, perpendicular to the metal surface, will not induce the systemic feedback cycles when the Fe²⁺_(sol’n) concentration in the bulk solution is far below the saturation level.

The propagation of the hydroxide wave initiated from a pocket of supersaturated solution will stop and the wave will dissolve and disappear, while new pockets of saturated solution appear at different times as corrosion progresses. However, at later stages of corrosion, the concentration of Fe²⁺ in the bulk solution can approach its saturation level. If and when this condition arises, the diffusion of Fe²⁺ and/or OH⁻ in the direction, perpendicular to the metal surface, can induce the diffusion–precipitation–oxidation–reduction–dissolution–diffusion cycles of ferrous and ferric species in the z-direction. In this case, the overall transport of ferrous and ferric species can be treated as a one-dimensional mass transport problem, see discussion later.

With time the hydroxide wave propagates, i.e., the number of alternating bands of Fe(OH)_2(colloid), mixed Fe^II/Fe^III hydroxide, and Fe(OH)_3(colloid) aggregates increases while the individual band widths also increase. While the hydroxide wave propagates, hydroxide colloids will slowly convert to bands of more stable crystalline oxyhydroxides and/or oxides with time. The oxide wave propagation at later times is discussed in detail later, following the discussion on the computational simulation of oxide wave propagation in the gelatin over a short duration.

Computational simulation of early stages of oxide wave propagation in the gelatin. The mechanism of metal hydroxide wave propagation involving more than one reaction–diffusion front was explored by computational simulation using COMSOL Multiphysics®.²⁶ A one-dimensional, axisymmetric geometry was employed to simulate spherical symmetry in the gel experiment. The droplet was drawn as an interval extending from a radius of 0 to 2.5 mm. The total geometry was 50 mm long in radius. Radial symmetry was implemented at radius 0, while a no flux boundary was enforced at the edge of the simulation length (Fig. 7).

Fig. 7 Schematic descriptions of (a) the simulation geometry and physics (not to scale) and (b) the net transport direction of the reacting species and chemical reactions.

The diffusion and reaction rate equations and the values of the rate constants used for the simulations are provided in the ESI,A.† As the experiments were performed in the gelatin, apparent diffusion coefficients were implemented in the model. When considering the systemic feedback, the diffusion coefficients of OH⁻ and Fe²⁺ were replaced with apparent diffusion coefficients that were further reduced, based on the permeability (ε([Fe_x(OH)_y])) of gelatinous ferrous and ferric hydroxides.^45,46

The simulation results for oxide wave propagation in the gelatin over a short duration (<20 min) are presented in Fig. 8. For short-term propagation, the processes considered in the model are the diffusion of Fe²⁺_(sol’n) and OH⁻ (eqn (2)), their reaction to produce Fe(OH)_2(colloid) (eqn (5)) and oxidation of Fe(OH)_2(colloid) to Fe(OH)_3(colloid) (eqn (6)). Because of the fast establishment of hydrolysis equilibria, the hydrolysis (eqn (3)) and the phase-partitioning process (eqn (5)) were treated as one rate-determining step.

Fig. 8 COMSOL Multiphysics® simulation showing the (a) changing concentrations of OH⁻, Fe²⁺, Fe(OH)₂ and Fe(OH)₃, (b) concentrations of Fe(OH)₂ and Fe(OH)₃ as a function of radius after 10 and 20 min and the simulated concentration surface map (the dotted vertical lines indicate the initial interface between OH⁻ and Fe²⁺) and (c) radius of the circular diffusion fronts of Fe(OH)₂ with and without the feedback effect (“With FB”/“No FB”) compared to the experimental results.

In the model, the diffusion coefficients of Fe²⁺_(sol’n) and OH⁻ through the gelatin were formulated as a function of the concentrations of Fe(OH)_2(colloid) and Fe(OH)_3(colloid) to account for the systemic feedback between the elementary steps leading to the diffusion–precipitation–oxidation–reduction–dissolution–diffusion cycles of Fe²⁺_(sol’n). The computational simulation of the same system with constant diffusion coefficients of Fe²⁺_(sol’n) and OH⁻ resulted in the diffusion fronts of Fe²⁺_(sol’n) and OH⁻ propagating at much faster rates without developing the clear separation of the Fe(OH)_2(colloid) and Fe(OH)_3(colloid) bands, further confirming that the oxide waves would not be formed without the systemic feedback (i.e., constant diffusion coefficients).

The simulation results demonstrate that the Fe(OH)_2(colloid) precipitation front propagates radially from the center into the Fe²⁺-containing volume as OH⁻ diffuses out and reacts with Fe²⁺. Fe²⁺ diffusion in the opposite direction also occurs but at a much slower rate. As the OH⁻ diffusion front continues to propagate radially (followed by the Fe(OH)_2(colloid) precipitation front lagging behind), the oxidation of Fe(OH)₂ to Fe(OH)₃ also takes place. That is, the secondary reaction front, that of Fe(OH)_3(colloid) production, follows the Fe(OH)_2(colloid) production front with an even greater lag. The net result is oxide wave propagation by two different reaction fronts moving at different rates: the outer ring consisting of mainly Fe(OH)₂ colloids (green) and the inner ring consisting of mainly Fe(OH)₃ colloids (brownish orange).

The two hydroxide rings are not clearly separated at very early reaction times. However, as the Fe(OH)_2(colloid) concentration increases, the ferrous species oxidizes to the less soluble Fe(OH)_3(colloid). This slows down the overall diffusion of OH⁻ and Fe²⁺_(sol’n) into each other to progressively slower rates, which further slows down the propagation of the Fe(OH)_2(colloid) and Fe(OH)_3(colloid) production fronts. The Fe(OH)_3(colloid) production front slows down faster than the Fe(OH)_2(colloid) production front, resulting in clearer separation between the two oxide rings with time. The progression of the oxide-band separation can be seen from the simulated concentration profiles of Fe(OH)₂ and Fe(OH)₃ as a function of time presented in Fig. 8.

The numerically simulated surface map showing the concentrations of Fe^II and Fe^III species at 20 min is compared with a snapshot of the pattern observed in the gelatin test as shown in Fig. 9. The two patterns show very similar progressions of the differently coloured reaction fronts – the faster green Fe(OH)₂ propagation front, followed by the brownish orange Fe(OH)₃ formation fronts. These patterns are consistent with the mechanistic description of band separation due to different diffusion–dissolution–precipitation–dissolution cycles of ferrous and ferric ions schematically shown in Fig. 5(b).

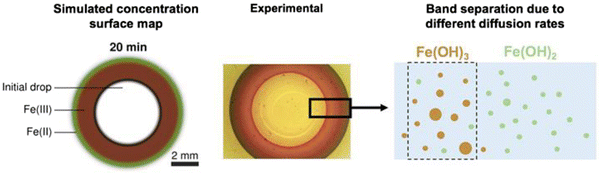Fig. 9 Comparison of the COMSOL Multiphysics® simulated surface map with the oxide wave pattern observed in the gelatin experiment. Also, the schematic of the separation of Fe(OH)₂ and Fe(OH)₃ bands is shown in Fig. 5b.

The computational simulation of the diffusion of Fe(OH)_2(colloid) and Fe(OH)_3(colloid) species clearly indicates that a slow transport medium is critical for the formation of Liesegang bands in corrosion systems, and describes how the Fe²⁺ and Fe³⁺ reaction fronts propagate differently through the gel medium, resulting in distinct bands of corrosion products. While this simulation of metal cation diffusion demonstrates the need for a slow transport medium, it is not intended to model the complex corrosion processes and elementary steps that occur before the accumulation of the corrosion products at the electrode–solution interface.

The empirical simulation of iron-oxide waves in gelatin (Fig. 3) and the computational simulation of the separation of the Fe(OH)_2(colloid) bands from the Fe(OH)_3(colloid) bands with time (Fig. 5) confirm that the development of oxide waves requires a slow transport medium for Fe²⁺_(sol’n) and OH⁻ so that the cyclic feedback between the diffusion of Fe²⁺_(sol’n) and OH⁻ (eqn (2)), hydrolysis (eqn (3)), precipitation–dissolution (eqn (5)) and redox reactions of Fe(OH)_2(colloid) and Fe(OH)_3(colloid) (eqn (6)), can be sustained over a long duration. In the gelatin, the overall transport of OH⁻ into Fe²⁺_(sol’n) occurs at slow enough rates to sustain the cyclic feedback. The next question is then what acts as the slow transport medium in corrosion.

Hydrogel formation

Hydrogel formation on corroding metals. In aqueous corrosion, Fe²⁺_(sol’n) and OH⁻ are produced by the electrochemical redox reaction listed in eqn (1) at the metal–solution interface, and then diffuse to the bulk solution. As described earlier, the average [Fe²⁺_(sol’n)] in the interfacial solution can quickly reach its solubility limit depending on the redox, pH and transport conditions of the solution. If and when the concentration of Fe²⁺_(sol’n) reaches its solubility limit (or above), Fe(OH)₂ begins to precipitate, initially as colloidal particles. If the interfacial solution remains as aqueous solution, the colloids will quickly disperse into the bulk solution, resulting in a negligible effect on the subsequent production of Fe²⁺_(sol’n) and OH⁻ at the interface and their transport into the bulk solution. The overall transport of ferrous species would be too fast to produce Fe(OH)_2(colloid) at sufficiently high concentrations to aggregate in distinctly separated bands or rings, as shown in Fig. 1. Thus, we propose that a slow transport medium is formed as a result of the reaction of the initial corrosion products, which spreads uniformly across the CS surface (or at least over the areas covering the emerging waves) before the oxide waves are initiated and propagate. We propose that this slow transport medium is a hydrogel network of loosely connected metal-hydroxide colloidal particles.

Under certain combinations of solution redox and transport conditions, the interfacial solution becomes quickly saturated with Fe²⁺_(sol’n), triggering the precipitation of Fe(OH)_2(colloid) due to the hydrolysis and phase-partitioning reactions (eqn (3) and (5)). Because the precipitation of Fe(OH)_2(colloid) removes Fe²⁺_(sol’n) from the solution phase, the metal oxidation coupled with the oxidant reduction (eqn (1)) can continue to produce Fe²⁺_(sol’n) and OH⁻. The colloids can also disperse into the bulk solution but at a much slower rate than dissolved Fe²⁺_(sol’n). Due to the continuous production of Fe²⁺_(sol’n) and OH⁻, coupled with the slower transport rate of colloids, once Fe(OH)_2(colloid) begins to precipitate the Fe(OH)_2(colloid) production accelerates. The colloidal concentration in the interfacial solution increases very rapidly, which triggers the aggregation of the Fe(OH)_2(colloid) particles. The aggregates become loosely connected via weak chemical bonding, such as hydrogen bonding, to grow a semi-rigid chemical network, known as a hydrogel:^37–39

Hydrogel

Thus, the metal-hydroxide hydrogel network can be described as a macroscopic gel-like structure consisting of a semi-stationary phase of the metal-hydroxide colloidal framework, and a mobile phase of solution containing metal cations near their saturation limit, as schematically shown in Fig. 10.

Fig. 10 Schematic representation of the metal-hydroxide hydrogel network, and the overall transport of ferrous species through the network.

When Fe²⁺_(sol’n) and OH⁻ are continuously injected into the solution, as in corrosion, the metal-hydroxide hydrogel is not a stationary structure. The concentration (the number density) of Fe(OH)_2(colloid) particles increases at an accelerated rate with time, the band of the Fe(OH)_2(colloid) aggregates widens with time, and the oxidation of Fe(OH)_2(colloid) to Fe(OH)_3(colloid) (eqn (6a) and (6b)) begins to occur which further helps the aggregation of the colloids.

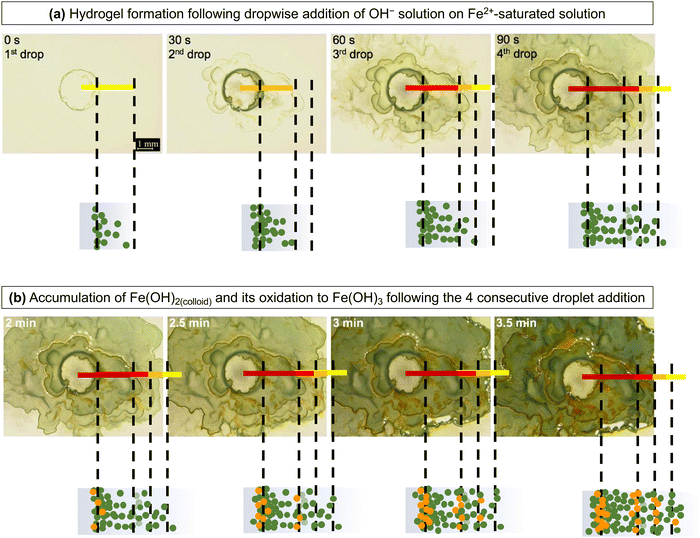
The near-stepwise formation and the rapid change of the hydrogel network during aqueous corrosion is nearly impossible to detect using in situ techniques, although various post-corrosion test analyses can show what remains of the hydrogel layers after preparing the samples for analysis.²⁴ Thus, the hydrogel formation in the solution that becomes supersaturated with Fe²⁺_(sol’n) was studied by mixing two aqueous solutions, one saturated with Fe²⁺_(sol’n) and the other containing OH⁻, and observing the formation of hydrogel at the interface of the two solutions.

Hydrogel formation from 2-D diffusion of OH⁻ droplets into Fe²⁺-saturated solutions. The rate of precipitation as colloids, followed by the aggregation of the colloids, increases with the increase in the degree of supersaturation. Hence, hydrogel formation is expected to be rapid (on a mass transport time scale) when mixing two solutions, one saturated with Fe²⁺_(sol’n) and the other containing OH⁻ at a higher concentration. This hypothesis was tested, and the results are shown in Fig. 11. In this test, a droplet of 2 M NaOH solution was added every 30 seconds onto a 2 mm thick layer of water saturated with FeSO₄, with four droplets in total added. The development of the greenish gel-like layer was monitored by taking an optical image at 5 s after each droplet addition. After the addition of the final droplet, the change in the gel-like layer was continuously monitored by taking optical images every 30 s for another 2 min. The green color indicates that the layer consists primarily of Fe(OH)_2(colloid). Due to the turbulence generated during the addition of the OH⁻ droplets, the green bands did not spread in perfect concentric circles. Nevertheless, the figure shows that discrete Fe(OH)_2(colloid) production fronts develop from the successive additions of OH⁻. The colloid production fronts spread along the OH⁻ diffusion path in the 2-D radial direction with time. The green colour of the individual circles becomes more intense with time and a brownish colour begins to appear near the outer edges of individual circles.

Fig. 11 Optical images of hydrogel formation by the dropwise addition of 2 M NaOH solution on a thin layer of saturated FeSO₄ solution showing (a) transport of the Fe²⁺_(sol’n) saturation front and Fe(OH)₂ colloid formation and (b) continuous accumulation and oxidation of Fe(OH)_2(colloid) to Fe(OH)₃.

The results indicate that Fe(OH)_2(colloid) is formed very quickly when the OH⁻ solution diffuses into a solution containing Fe²⁺_(sol’n) at or near the saturation level, and Fe(OH)_3(colloid) is formed from the precipitated Fe(OH)_2(colloid). The precipitation rate of Fe(OH)_2(colloid) increases with the degree of supersaturation and hence, it will depend on [Fe²⁺_(sol’n)] and [OH⁻]. Accordingly, after the first droplet was added, the concentration (the number density) of Fe(OH)_2(colloid) particles was highest at the interface of the two solutions where the supersaturation level was highest, but its concentration at any given distance z would decrease with time as Fe²⁺_(sol’n) and OH⁻ continue to diffuse out, and the successive addition of the OH⁻ solution at 30 s interval would induce another wave of the Fe²⁺_(sol’n) saturation front, followed by the Fe(OH)_2(colloid) production front. However, if the colloidal particles had not aggregated to form a semi-rigid hydrogel network, the colloidal concentration would be expected to decrease gradually with distance from the centre (more of a smooth gradient, as in an aqueous reaction).

What we observed, however, was that although the number of green (quasi-) rings increased with each addition of OH⁻, the boundaries of the rings that had formed prior to the subsequent addition were not disturbed, but only their intensities were increased (Fig. 11(a)). When Fe²⁺_(sol’n) and OH⁻ are continually injected and diffuse out, the hydrogel network structure continues to change; the colloidal concentration changes with distance z and time t and so the rigidity of the hydrogel network. The increase in the colloidal concentration effectively decreases the pore size and the volume of the mobile phase, further impeding the diffusion of Fe²⁺_(sol’n) while promoting Fe(OH)_2(colloid) production. Hence, the colloid production from the supersaturated solution continues even long after OH⁻ addition was terminated as Fe²⁺_(sol’n) and OH⁻ diffuse through the hydrogel network at progressively slower rates (Fig. 11(b)).

These observations clearly demonstrate that when OH⁻ and Fe²⁺_(sol’n) at or near the saturation level diffuse into each other, they can quickly precipitate as metal hydroxide colloids, which then aggregate into a semi-rigid hydrogel network.

The in situ monitoring of gel-layer formation and growth during corrosion was not possible. However, translucent wafer-like layers (thickness typically less than 1 μm) were often present on corroded CS. The optical and SEM images of one of these layers presented in Fig. 12 show that cracks expose extensive formation of granular oxides, separated by a void volume from the thin layer. The underside of the layer is also covered with granular oxides. Although the wafer-like layers are no longer viscous by the time we examine them under SEM, this morphology requires a viscous liquid precursor.

Fig. 12 Translucent wafer-like layers present on a CS coupon corroded for 3 days in pure water in the presence of γ-radiation. The two images on the left are optical images and the two on the right are SEM micrographs.

Hydrogel formation from the 1-D diffusion of Fe²⁺ and OH⁻ solutions into each other. The formation and growth of the hydrogel network, and its effect on oxide wave propagation over long durations were further investigated by allowing an OH⁻ solution to diffuse into a saturated Fe²⁺ solution in an upright glass tube, i.e., in a 1-D diffusion geometry. The results are shown in Fig. 13. The hydrogel network formation within 15 min is discussed first. The oxide-phase transformation at longer times is discussed in the later section.

Fig. 13 (a) Hydrogel formed by mixing 2 M NaOH solution and saturated FeSO₄ solution and the evolution of oxide bands, and (b) comparison of the simulated oxide bands and the oxide bands formed on corroded carbon steel surfaces. Different oxide bands form in the upper and the lower solutions due to different production ratios of Fe(OH)_2(colloid) to Fe(OH)_3(colloid). In the upper solution, the concentration gradient of Fe(OH)_2(colloid) changes drastically with distance from the interface, resulting in the formation of distinct bands of Fe(OH)_3(colloid) and Fe(OH)_2(colloid), represented by orange and green dots, respectively, and mixed Fe^II/Fe^III oxide bands, represented by black dots, between the orange and green bands. In the lower solution, the hydrogel consists mainly of Fe(OH)_3(colloid), resulting in the formation of monochromatic orange bands separated by a clear and colourless gap as described by the schematics on the right as shown in (a).

As observed in the 2-D diffusion test (Fig. 11), a mass transport barrier was formed almost immediately at the interface of the two solutions, preventing the two solutions from mixing homogeneously. Nevertheless, the colours of the upper and lower solutions at early times (≤15 min) were different, indicating that the hydrogel networks in the two solutions consist of different colloidal compositions. In the upper solution, a network of a mostly green substance with a slight tint of brown spreads from the interface to the bulk of the upper solution nearly immediately (∼0 min), indicating that the formation of Fe(OH)_2(colloid) is very fast and quickly spread into the entire volume of the upper solution. Fe(OH)_2(colloid) begins to aggregate and grow a hydrogel network primarily made of Fe(OH)_2(colloid) with a very low Fe^III content.

On the other hand, the colour of the lower solution, which was initially a very pale greenish-brown, changed to yellow by 15 min. Precipitation of colloids or ionic-salt particles depends on supersaturation levels of constituent ions.⁴⁷ The concentration of OH⁻ is significantly lower in the lower solution than that in the upper solution. Hence, the solubility limit of Fe(OH)_2(colloid) is significantly higher. Accordingly, the supersaturation level (not the absolute concentration) of Fe²⁺_(sol’n) is significantly lower in the lower solution, leading to slower precipitation of Fe(OH)_2(colloid). As Fe(OH)_2(colloid) precipitates and aggregates, it oxidizes to Fe(OH)_3(colloid). The net production of Fe(OH)_2(colloid) is the difference between the rates of the precipitation and the oxidation of Fe(OH)_2(colloid). Hence, the overall consequence of the slower precipitation of Fe(OH)_2(colloid) is that the concentration of Fe(OH)_2(colloid) is lower, while the Fe^III content is higher, in the hydrogel network formed in the lower solution.

In this 1-D mixing experiment, OH⁻ and Fe²⁺_(sol’n) diffuse into each other (eqn (2)) continuously over extended duration, albeit at progressively slower rates, through the hydrogel network that has been formed and propagated ahead. While diffusing through the hydrogel network, Fe²⁺_(sol’n) and OH⁻ continue to undergo diffusion–precipitation–oxidation–reduction–dissolution–diffusion cycles (eqn (2)–(6)). This, in turn, changes the colloidal composition and rigidity of the previously formed hydrogel network. The different evolutions of the colloidal composition in the upper and lower solutions are due to the different evolutions in the concentration ratio of OH⁻ to Fe²⁺_(sol’n) in the two solutions.

Oxide-phase transformation and crystalline oxide growth

Propagation and transformation of hydroxide colloidal aggregates in the 1-D diffusion test. The results presented in Fig. 13 further show that the ferrous and ferric hydroxides in the hydrogel network are also gradually transforming into more stable crystalline oxide particles with time. As the Fe²⁺_(sol’n) and OH⁻ solutions continue to diffuse into each other through the hydrogel networks, the concentration of Fe(OH)_2(colloid) and the Fe^III content in the colloidal networks continually change. As more hydroxide colloids precipitate, the colloidal aggregates also transform into more stable crystalline oxide particles.

In both the upper and lower solutions, as Fe²⁺_(sol’n) and OH⁻ continue to diffuse into each other through the mobile phase of the hydrogel network formed ahead, Fe(OH)_2(colloid) is continually produced. As Fe(OH)_2(colloid) continually precipitates, it oxidizes to Fe(OH)_3(colloid). The development of different oxide bands in the upper solution versus the lower solution is due to difference in the production ratio of Fe(OH)_2(colloid) to Fe(OH)_3(colloid).

In the lower solution, as OH⁻ continues to diffuse through the hydrogel network formed ahead, Fe²⁺_(sol’n) and OH⁻ continue to precipitate as Fe(OH)_2(colloid). As Fe(OH)_2(colloid) precipitates, it quickly oxidizes to Fe(OH)_3(colloid), and the Fe^II/Fe^III redox equilibrium (eqn (6)) is established. The Fe²⁺_(sol’n) supersaturation level is lower due to the lower OH⁻ concentration in the lower solution than that in the upper solution, as described above. Hence, although Fe(OH)_2(colloid) and Fe(OH)_3(colloid) are continually produced, the ratio of the production rate of Fe(OH)_3(colloid) to Fe(OH)_2(colloid) in the hydrogel network is significantly higher in the lower solution than that in the upper solution. As the hydrogel network in the lower solution consists of mainly Fe(OH)_3(colloid) particles, the colloidal aggregates slowly transform, via the Ostwald ripening process, to thermodynamically more stable ferric oxyhydroxides, α-FeOOH and γ-FeOOH.

Oxide phase transformation of Fe(OH)_3(colloid) into FeOOH:

Fe(OH)_3(colloid) →→ α- or γ-FeOOH_(crystal) + H₂O (8)

The sequential arrow in eqn (8) refers to the multiple intermediate elementary steps that occur to form the product. In the upper solution, the Fe²⁺_(sol’n) supersaturation level is higher, leading to the faster precipitation of Fe(OH)_2(colloid). The Fe(OH)_2(colloid) concentration in the hydrogel network also changes more rapidly with distance from the interface at a specific time. However, the relative ratio of Fe^III to Fe^II also changes along the Fe(OH)_2(colloid) concentration gradient (i.e., along the Fe²⁺_(sol’n) diffusion path), being the lowest at the solution interface and gradually increasing with distance from the interface. Thus, at a specific time (within the studied duration), Fe(OH)_2(colloid) remains the dominant species, resulting in the green colored band, in the region closest to the interface (Fig. 13). The Fe^III content increases with the distance from the interface. Hence, slightly further away from the interface where both ferrous and ferric hydroxides are present at comparable levels, the Fe(OH)_2(colloid) and Fe(OH)_3(colloid) aggregates gradually transform into black mixed Fe^II/Fe^III oxide (magnetite) crystals:

Oxide phase transformation of mixed Fe^II/Fe^III hydroxide to Magnetite:

Fe(OH)_2(colloid) + 2Fe(OH)_3(colloid) →→ Fe₃O_4(crystal) + 4H₂O (9)

In the region furthest away from the interface where the Fe^III content is highest, the Fe(OH)_3(colloid) aggregates gradually transform into ferric oxides, the same process as the bands of ferric oxides formed in the lower solution (eqn (8)). The production rate of Fe(OH)_3(colloid) in the hydrogel network also influences the phase of the FeOOH crystal (α-FeOOH versus γ-FeOOH) that Fe(OH)_3(colloid) can transform to.⁴⁸

The transformation of hydroxide colloids to different crystalline oxides (eqn (8) and (9)) further affects the evolution of the composition and concentration of colloids in the hydrogel network. That is, the growth of individual oxide particles (by the Ostwald ripening) and the aggregation of these crystals (Liesegang banding) are strongly coupled with the diffusion–precipitation–oxidation–reduction–dissolution–diffusion cycles of Fe²⁺_(sol’n). The overall consequence of this systemic feedback over a longer test duration is the aggregation of solid oxide crystals in periodic patterns. In the upper solution, the bands of bluish-green hydroxide, black magnetite and yellow goethite (α-FeOOH) become more clearly separated with time. In the lower solution, magnetite formation is negligible. Instead, distinct yellowish orange bands develop, separated by clear solution bands. The clear gaps between these ferric hydroxide bands widen with time. This pattern, orange bands separated by clear bands, is a classic monochromatic Liesegang pattern, described earlier (see Fig. 5(a)).

Comparison of the oxide bands formed during 1-D solution mixing versus corrosion. Development of different oxide wave patterns depending on solution redox and transport conditions and duration is also observed during CS corrosion. Two examples of oxide waves observed on corroded CS are compared with those observed in the lower and the upper solutions in the 1-D diffusion test as shown in Fig. 13(b). The example on the left-hand side shows distinct solid oxide layers with uniform thicknesses separated by void volumes in the vertical direction from the metal surface corroded for one day in 0.5 mM H₂O₂, air-saturated solution at room temperature (solution volume to metal surface area = 2 mL/0.785 cm²). The thin wafer-like layers were typically observed under a collapsed or cracked surface layer that had covered a much wider area, where the cracks occurred along the boundaries of the pearlite phase (having a lamellar structure of alternating cementite and ferrite) and the α-Fe phase. We could not unequivocally determine whether the cracks occurred during corrosion or during drying for the surface analysis preparation. The layered structure, consisting of thin wafer-like solid layers with voids in-between, is similar to that of the repeating ferric-oxide bands observed in the lower solution of the 1-D diffusion of the Fe²⁺_(sol’n) and OH⁻ solutions (Fig. 13(a)).

Also, compared to Fig. 13(b), the oxide rings on corroded CS are shown in Fig. 2 and the oxide bands are formed in the upper solution of the 1-D diffusion test. In both cases, black magnetite crystals and orange lepidocrocite crystals are aggregated in discrete bands in a repeating pattern. However, in the 1-D diffusion test, the reaction–diffusion fronts are traveling in one direction, whereas in the corrosion case, the reaction–diffusion fronts are traveling in a 2-D radial direction.

As discussed earlier, the diffusion–precipitation–oxidation–reduction–dissolution–diffusion cycles of ferrous and ferric species can propagate in either 1-D direction, perpendicular to the metal surface, or in a 2-D radial direction along the horizontal plane of the interfacial solution (Fig. 6). The 2-D radial propagation occurs if and when the pockets of supersaturated solutions can form in the interfacial layer containing the Fe²⁺_(sol’n) near saturation level, while the Fe²⁺_(sol’n) concentration in the bulk solution is far below the saturation level. This will result in alternating aggregation of Fe(OH)₂ and Fe(OH)₃ colloids in the concentric ring patterns at early times. Depending on the solution environment, the cyclic feedback loop within the saturated interfacial solution can be sustained over a long duration, long enough for the systemic feedback to expand to include the conversion of hydroxide particles to crystalline oxyhydroxide or oxide particles as discussed below.

The 1-D propagation occurs if and when the concentration of Fe²⁺ in the bulk solution approaches its saturation level. The diffusion of Fe²⁺ and/or OH⁻ from the supersaturated interfacial region to the near saturated bulk solution will induce the diffusion–precipitation–oxidation–reduction–dissolution–diffusion cycles of ferrous and ferric species in the direction, perpendicular to the metal surface, resulting in solid oxides in the layered structure at longer times.

The comparisons indicate that in corrosion solid oxide particles can be formed and grown in periodic patterns when the hydrogel network can be formed and spread uniformly (in a macroscopic scale) across the metal surface. Fe²⁺_(sol’n) and OH⁻ produced subsequently at the metal–solution interface and then must diffuse though the already uniformly spread hydrogel network. The oxide aggregation and growth in different patterns, concentric rings versus wafer-like layers, can be attributed to different rates of progression of cyclic feedback processes.

The redox activity of metal atoms may vary across the surface of CS, the Fe in the cementite phase is very stable while the Fe in the α-Fe phase can easily oxidize to Fe²⁺_(sol’n) and dissolve in the interfacial solution. In the solution, the metal cation then diffuses in the 3-D hemi-spherical direction. Mass diffusion in the solution is a much faster process than the net interfacial transfer of mass (Fe atoms) by the electrochemical process. Hence, the metal surface activity may vary across the surface but the concentrations of Fe²⁺_(sol’n) and OH⁻ in the interfacial solution are quickly distributed uniformly across the metal surface. Hence, once the interfacial solution becomes saturated and Fe(OH)_2(colloid) begins to precipitate, the hydrogel network can spread near instantly in a 2-D radial direction, covering a very wide area of the corroding surface. That is, the coverage of the hydrogel network is not sensitive to variation in surface activity. Hence, the fluid-like hydrogel layer spreads over the pearlite structure as well as the pure α-Fe phase.

Different surface activities can lead to different metal dissolution fronts, which can create pits, inducing further spatial variation in the metal cation diffusion rate. For example, as the Fe⁰_(m) from α-Fe phase continues to oxidize to Fe²⁺_(sol’n) and diffuse into the bulk solution, the metal–solution interface (the metal dissolution front) moves deeper into the metal substrate from the position of the original metal surface, whereas the metal atoms in Fe₃C (cementite) do not dissolve and the cementite–solution interface does not change. Over an extended period, the different rates of the movement of the metal dissolution front result in stagnant water pools between cementite layers, which can further accelerate the progression of corrosion to the production of solid crystalline particulates. On the other hand, the diffusion of Fe²⁺_(sol’n) from the pure α-Fe phase having wider surface areas is less affected, and the overall corrosion process to solid oxide particle formation is slower, growing a larger (in 2-D) oxide structure. (Slower oxide growth conditions produce larger crystals.)

The concentric ring patterns are typically observed at the early stages of corrosion, and the initiation points of the oxide waves are randomly distributed across the metal surface. At the early stages of hydrogel network growth, the concentration of mixed hydroxide colloids and the Fe^III content in the hydrogel are low. The oxidation of Fe⁰_(m) to Fe²⁺_(sol’n) at the interface, followed by the diffusion of Fe²⁺_(sol’n) from the interface, through the hydrogel layer, to the bulk solution still occurs at a relatively fast rate. While diffusing through the hydrogel, Fe²⁺_(sol’n) will undergo hydrolysis and continuously precipitate as Fe(OH)_2(colloid), which is then oxidized to Fe(OH)_3(colloid). The ratio of and the overall production rates of Fe(OH)_2(colloid) to Fe(OH)_3(colloid) is highest at the initiation points of the oxide waves but the ratio decreases along the Fe²⁺_(sol’n) diffusion path. This corrosion situation mimics the upper layer of the 1-D addition experiment (Fig. 13(b)). Accordingly, what we observed on the corroded surface is clearly separated black magnetite and γ-FeOOH rings in a periodic pattern, similar to the discrete bands of magnetite and α-FeOOH observed in the upper solution in the 1-D solution addition test. Note that the diffusion rates of Fe²⁺_(sol’n) and OH⁻ during corrosion are different from those in the 1-D test (giving rise to a different FeOOH phase) and the oxide wave pattern has propagated for longer times (and hence, there are more repeating bands) on the corroded surface.

The colloidal concentration and the Fe^III content in the hydrogel network increase with time. The overall transport of Fe²⁺_(sol’n) from the metal (α-Fe)–solution interface, through the hydrogel layer, to the bulk solution progressively slows down. On the other hand, the overall transport of OH⁻ is less affected. (Note that [OH⁻] is determined by not only the oxidant reduction and hydrolysis, but also various acid–base equilibria.) Hence, once a hydrogel network fully covers the surface of the pure α-Fe phase and the metal–solution boundary moves further into the metal substrate from the hydrogel layer creating a pit, the relative concentrations of Fe²⁺_(sol’n) and OH⁻ in the pit at longer times become more closely resemble the solution environment in the lower solution in the 1-D mixing experiment (Fig. 13(b)). The same Liesegang banding coupled with the Ostwald ripening results in the aggregation of discrete oxide bands separated by the solution void of solid oxide particles.

The transformation of hydroxide colloids and oxide particles observed over extended periods, both in the solution mixing experiment and on corroded surfaces, indicates that the individual oxide crystals grow and aggregate also by the continuous cycle of the diffusion–precipitation–oxidation–reduction–dissolution–diffusion of Fe^II. It is well established that the growth of ionic-salt crystals in solution occurs via the similar cycles of the diffusion–precipitation–dissolution–diffusion of ions between different crystals, the process known as Ostwald ripening.³⁴ In corrosion, the crystal growth by the Ostwald-ripening is coupled with the precipitation–dissolution and redox cycles of ferrous and ferric species as Fe²⁺_(sol’n) is continuously injected into the solution and diffuses into the bulk solution, through the hydrogel network that has already formed. The sustained cyclic feedback results in the aggregation of oxide crystals in Liesegang bands.

Multi-reaction–diffusion front propagation via redox-assisted Ostwald ripening

Ostwald ripening is a crystal growth phenomenon in which larger crystals grow larger at the expense of smaller crystals.^34,47 The driving force for this process is the minimization of the interfacial energy of the particles. Small particles have a larger surface area to volume ratio than large particles and hence have higher interfacial energy.^49,50

In a closed chemical system, the total mass of the particles in the crystal growth medium would be maintained during Ostwald ripening. The cycles of the diffusion–adsorption/precipitation–desorption/dissolution–diffusion of crystal constituent ions occur at the crystal–solution interfaces. However, the desorption/dissolution is slightly faster than the adsorption/precipitation on the smaller crystals, while it is the opposite on the larger crystals. The overall result is the continuous transfer of the salt crystal ions from the smaller to larger crystals, as schematically shown in Fig. 14(a).

Fig. 14 Schematic representations of (a) typical Ostwald ripening in a closed system and (b) redox-assisted Ostwald ripening in an open (corroding) system.

Typically, Ostwald ripening is used to describe the growth of crystals of same compositions. In this work, we observed the aggregation of oxide crystals of different chemical compositions and/or different shapes and sizes in alternating bands. This observation indicates that the oxide crystals that are transformed from nano-sized hydroxide colloidal particles (eqn (5)) continue to grow by the Ostwald-ripening coupled with the redox cycles between soluble Fe^II and insoluble Fe^III, which we term “the redox-assisted Ostwald ripening”. The redox-assisted Ostwald-ripening process is schematically compared with the typical Ostwald-ripening in Fig. 14.

In an open system, as in the case of the interfacial solution volume during metal corrosion described here, the crystal constituent ions are continuously injected into the crystal growth medium (aqueous solution). Small colloidal particles are continually formed and precipitated which then slowly undergo oxide-phase transformation, while the hydroxide/oxide particles formed earlier continue to undergo Ostwald ripening. That is, the redox-assisted Ostwald ripening occurs in the presence of the concentration gradient of colloidal particles. The overall consequence of the redox-assisted Ostwald ripening coupled with the transport of metal cations (and OH⁻) in the colloidal concentration gradient is that the aggregation of oxide crystals of different compositions and/or sizes in Liesegang patterns.

Implications of the oxide wave formation and propagation to the corrosion mechanism

Corrosion continuously transfers metal atoms from the solid metal to the solution phase, making the solution phase or the metal oxide growth medium an open system. In corrosion, Mⁿ⁺_(sol’n) and OH⁻ are continuously produced at the metal–solution interface (eqn (1)), and then transported from the interface to the bulk solution (eqn (2)). Many existing corrosion rate analysis methods and/or corrosion models of active metals consider an electrochemical kinetic stage, either when the metal oxidation produces mainly the soluble metal cation dissolving into the solution,^51–54 or mainly the insoluble metal cation transporting through a solid metal-oxide layer.^55,56

Spatiotemporal pattern formation during the corrosion of iron under potentiostatic conditions,⁵⁷ current oscillation at the limiting current region during iron electrodissolution,^58–60 oscillations in corrosion product concentrations at a zinc/polymer interface,⁶¹ and temporal potential patterning of passive iron oxide in the presence of chloride^62,63 have been previously reported. These studies have proposed the existence of a feedback loop between electrochemical/chemical reactions, diffusion, convection and electrical coupling between active areas and salt layer covered area on the electrode surface to explain the nonlinear spatiotemporal phenomena. We have also previously reported the oscillatory behaviours of corrosion potential and corrosion current during carbon steel corrosion in aerated solutions at near neutral pH.⁶⁴ This study builds on the existing work and provides unequivocal evidence for the systemic feedback in corrosion. This work is the first to clearly show that the non-uniform deposition of metal oxides during corrosion can occur via strongly coupled solution reactions and transport processes, and not simply as a result of metallurgical non-uniformity or localized solution environments.

The results from this study clearly demonstrate that if and when the [Mⁿ⁺_(sol’n)] in the interfacial solution reaches its saturation limit, it will begin to precipitate as metal hydroxide colloids, which then aggregate and begins to form a hydrogel network. The precipitation of colloids facilitates the oxidation (e.g., from Fe²⁺ to Fe³⁺) or reduction (e.g., from Cu²⁺ to Cu⁺) of the soluble to the nearly insoluble metal cation, which further accelerates the precipitation and aggregation of mixed hydroxide colloids. However, as the insoluble metal cation concentration increases, it can reduce (or oxidize for Cu case) to the soluble metal cation. This induces the cycles of diffusion–precipitation–oxidation–reduction (or reduction–oxidation)–dissolution–diffusion. Under certain combinations of solution redox and transport conditions, these cycles can continue for an extended period. However, while these cycles continue, the hydroxide particles slowly transform to thermodynamically more stable oxyhydroxide or oxide crystalline particles.

This study has shown that the formation of a hydrogel network is critical in changing the corrosion path from primarily dissolution to primarily oxide deposition. Accordingly, the overall corrosion (metal loss) rate also changes. The amount of oxide deposits on the surface does not necessarily correlate to the metal loss rate when dissolution is the dominant corrosion path. Nor the changes in the oxide morphology and chemical composition at the later stages of corrosion necessarily indicate that metal oxidation still occurs at a substantial rate at these late stages. At these stages, the oxide growth and transformation occurs via solution processes.

Hydrogel formation strongly depends on [Fe²⁺] and [OH⁻]. In corrosion, Fe²⁺ and OH⁻ are simultaneously produced at the metal surface and diffuse to the bulk solution. Their concentrations in the solution adjacent to the metal surface are determined by the rate of interfacial charge transfer at the metal surface (eqn (1)), and transport of Fe²⁺ and OH⁻ from the metal surface into the bulk solution (eqn (2)). The diffusion rates of Fe²⁺ and OH⁻ depend on their concentration gradients and mass transport coefficients. In addition, the concentration of Fe²⁺ cannot exceed its saturation capacity. Hence, hydrogel formation strongly depends on the oxidizing and transport conditions of the solution. Once the hydrogel has formed, net metal oxidation, metal dissolution, and oxide growth and conversion are all strongly coupled.

Hence, small changes in the oxidizing and transport conditions can lead to the long-term production of oxides that differ greatly in composition, thickness, and uniformity. Slight differences in the surface morphology and topography that can affect solution diffusion can then be amplified via prolonged redox-assisted Ostwald ripening to create striking patterns, as shown in Fig. 15. This spatial variation in the oxide thickness is often misinterpreted as a localized phenomenon caused by differences in the redox reactivity of the metal surface resulting from microstructural variations.^65–67 This study demonstrates that the phase composition and morphology of oxides change with time in a given solution environment and that their evolution depends on solution parameters, rather than metallographic structures.

Fig. 15 Elevation profiles of Liesegang bands formed on CS corroded (a) submerged in 2 mL of pure water for one day in the presence of γ-radiation at 2.5 kGy h⁻¹ (upper images) and (b) hanging upside-down in 500 mL of pure water for two days (lower images).

Conclusion

The aggregation of iron oxide crystals of different chemical compositions and shapes in concentric wave patterns or in discrete bands during corrosion of carbon steel was presented. We have demonstrated that these patterns are a Liesegang phenomenon, arising from the sustained cyclic feedback between strongly coupled reaction–transport kinetics of the initial corrosion product, soluble Fe²⁺ cations. For chemical waves to propagate, the chemical system requires a slow transport medium. We have shown that the formation of metal-oxide Liesegang bands during CS corrosion is preceded by the formation and growth of a hydrogel network. We describe this hydrogel network as a biphasic structure similar to that of organic- or bio-polymeric gels: a semi-stationary phase composed of loosely connected or aggregated metal hydroxide colloidal particles, and a mobile phase of solution containing dissolved metal cations (Fe²⁺_(sol’n)).

Corrosion continually injects metal cations into the metal–solution interface. As the corrosion progresses, the interfacial solution becomes saturated with metal cations, which precipitate as metal hydroxide, initially as colloidal particles. As their concentration increases, the colloidal particles aggregate, forming a hydrogel network. Once a hydrogel layer has spread across the metal surface, it serves as the slow transport medium. With the continuous injection of metal cations into the hydrogel layer, the diffusion kinetics of metal cations can effectively couple with the precipitation–dissolution and oxidation–reduction kinetics between Fe^II and Fe^III species. This results in an increasing colloidal concentration in the hydrogel layer and an increasing ferric content in the mixed hydrogel.

As metal oxidation continues, diffusion coupled with the precipitation–oxidation–reduction–dissolution of metal cations slowly transforms the hydroxide colloids into crystalline oxides via an Ostwald-ripening process. While the oxide crystals grow by Ostwald-ripening, the main diffusing metal cation is the more soluble ferrous ion. Hence, diffusion and the precipitation–dissolution cycles of ferrous ions are coupled with the redox cycle between Fe^II and Fe^III on the crystal surfaces during the growth of solid oxyhydroxide or oxide crystals. We refer to this novel phenomenon as “redox-assisted Ostwald ripening”. The aggregation of oxide crystals of different compositions and phases in alternating or periodic Liesegang patterns is the result of oxide growth by this redox-assisted Ostwald-ripening as the soluble metal cation diffuses along its concentration gradient (diffusion path) through the hydrogel network.

In conclusion, we have presented experimental evidence of systemic feedback in corrosion, which results from the accumulation and subsequent reactions of the initial corrosion products in the solution phase near the metal surface. This work demonstrates that strong coupling between the solution reactions and transport processes can result in non-uniform deposition of metal oxides and are not simply a result of localized surface or solution phenomena. The findings of this work challenge the existing methodologies and practices for corrosion testing and modelling, but also have wider implications for other processes involving metal/solution interfaces, such as nanoparticle growth, solid electrolyte degradation and remediation of metal-contaminated wastewater.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

We thank Dr Peter Keech and Dr Mehran Behazin at Nuclear Waste Management Organization (NWMO) for their encouragement and discussion. This work was funded by the Natural Sciences and Engineering Research Council of Canada (NSERC) under the Industrial Research Chair agreement in Radiation-Induced Chemical and Materials Science (IRCPJ-2014-326245) and by the NSERC Discovery grant in Radiation-Induced Materials Performance (RGPIN-2018-04459).

References

1. J. L. Hudson and J. C. Mankin, Chaos in the Belousov-Zhabotinskii reaction, J. Chem. Phys., 1981, 74, 6171–6177.
2. L. Gyorgyi, T. Turanyi and R. J. Field, Mechanistic details of the oscillatory Belousov-Zhabotinskii reaction, J. Phys. Chem., 1990, 94, 7162–7170.
3. A. M. Turing, The chemical basis of morphogenesis, Proc. R. Soc. London, Ser. B, 1952, 237, 37–72.
4. J. B. Keller, Proceedings of the Advanced Seminar on Dynamics and Modeling of Reactive Systems, Elsevier, 1980, pp. 211–224.
5. A. A. Pogodaev, T. T. Lap and W. T. S. Huck, The Dynamics of an Oscillating Enzymatic Reaction Network is Crucially Determined by Side Reactions, ChemSystemsChem, 2021, 3, e2000033.
6. I. R. Epstein and J. A. Pojman, An Introduction to Nonlinear Chemical Dynamics: Oscillations, Waves, Patterns, and Chaos, Oxford University Press, 1998.
7. R. E. Liesegang, Ueber einige Eigenschaften von Gallerten, Naturwiss. Wochenschr., 1896, 11, 353–363.
8. K. H. Stern, The Liesegang Phenomenon, Chem. Rev., 1954, 54, 79–99.
9. H. K. Henisch, Liesegang ring formation in gels, J. Crystallogr. Growth, 1986, 76, 279–289.
10. H. K. Henisch, In Vitro Veritas: Crystals in Gels and Liesegang Rings, Cambridge University Press, 1988.
11. P. Ortoleva, E. Merino and P. Strickholm, Kinetics of metamorphic layering in anisotropically stressed rocks, Am. J. Sci., 1982, 282, 617–643.
12. Y. Wang and E. Merino, Self-organizational origin of agates: Banding, fiber twisting, composition, and dynamic crystallization model, Geochim. Cosmochim. Acta, 1990, 54, 1627–1638.
13. E. Merino, Chem. Instab., Springer Netherlands, Dordrecht, 1984, pp. 305–328.
14. T. Chu, Y. Nuli, H. Cui and F. Lu, Pitting behaviour of welded joint and the role of carbon ring in improving corrosion resistance, Mater. Des., 2019, 183, 108120.
15. C. H. Chen and J. Li, A ring area formed around the erosion pit on 1Cr18Ni9Ti stainless steel surface in incipient cavitation erosion, Wear, 2009, 266, 884–887.
16. S. A. Karrab, M. A. Doheim, M. S. Mohammed and S. M. Ahmed, Investigation of the ring area formed around cavitation erosion pits on the surface of carbon steel, Tribol. Lett., 2012, 45, 437–444.
17. D. Iqbal, A. Sarfraz, M. Stratmann and A. Erbe, Solvent-starved conditions in confinement cause chemical oscillations excited by passage of a cathodic delamination front, Chem. Commun., 2015, 51, 16041–16044.
18. J. Jorne, Oscillations and concentration patterns in electrochemical systems, Electrochim. Acta, 1983, 28, 1713–1717.
19. J. Quinson and K. M. Ø. Jensen, From platinum atoms in molecules to colloidal nanoparticles: A review on reduction, nucleation and growth mechanisms, Adv. Colloid Interface Sci., 2020, 286, 102300.
20. J. Polte, Fundamental growth principles of colloidal metal nanoparticles – a new perspective, CrystEngComm, 2015, 17, 6809–6830.
21. P. Verma, P. Maire and P. Novák, A review of the features and analyses of the solid electrolyte interphase in Li-ion batteries, Electrochim. Acta, 2010, 55, 6332–6341.
22. F. Fu and Q. Wang, Removal of heavy metal ions from wastewaters: A review, J. Environ. Manage., 2011, 92, 407–418.
23. W. Liu, S. Tian, X. Zhao, W. Xie, Y. Gong and D. Zhao, Application of Stabilized Nanoparticles for In Situ Remediation of Metal-Contaminated Soil and Groundwater: a Critical Review, Curr Pollution Rep, 2015, 1, 280–291.
24. Y. G. Shin, Nonlinear Dynamics of Carbon Steel Corrosion under Gamma Radiation, PhD thesis, Western University, 2020.
25. C. Hochanadel, Effect of cobalt gamma-radiation on water and aqueous solutions, J. Phys. Chem., 1952, 56, 587.
26. COMSOL Multiphysics® v.5.0. http://www.comsol.com, COMSOL AB, Stockholm, Sweden.
27. R. M. Cornell and U. Schwertmann, The Iron Oxides: Structure, Properties, Reactions, Occurrences and Uses, Wiley, Weinheim, 2003.
28. I. L’Heureux, Self-organized rhythmic patterns in geochemical systems, Proc. R. Soc. London, Ser. A, 2013, 371, 20120356.
29. H. Nabika, M. Itatani and I. Lagzi, Pattern Formation in Precipitation Reactions: The Liesegang Phenomenon, Langmuir, 2020, 36, 481–497.
30. C. F. Baes Jr. and R. E. Mesmer, The Hydrolysis of Cations, Krieger Publishing Company, 1976.
31. D. Guo, Corrosion Dynamics of Carbon Steel in Used Fuel Container Environments, PhD thesis, Western University, 2018.
32. W. Xu, K. Daub, X. Zhang, J. J. Noel, D. W. Shoesmith and J. C. Wren, Oxide formation and conversion on carbon steel in mildly basic solutions, Electrochim. Acta, 2009, 54, 5727–5738.
33. K. Daub, X. Zhang, J. J. Noël and J. C. Wren, Effects of γ-radiation versus H₂O₂ on carbon steel corrosion, Electrochim. Acta, 2010, 55, 2767–2776.
34. W. Ostwald, Über die vermeintliche isomere des roten und gelben quecksilberoxid und die oberflächenspannung fester körper, Zeitschrift fur Phys. Chemie, Stochiometrie und Verwandschaftslehre, 1900, 34, 495–503.
35. M. Behazin, M. C. Biesinger, J. J. Noël and J. C. Wren, Comparative study of film formation on high-purity Co and Stellite-6: Probing the roles of a chromium oxide layer and gamma-radiation, Corros. Sci., 2012, 63, 40–50.
36. M. Momeni and J. C. Wren, A mechanistic model for oxide growth and dissolution during corrosion of Cr-containing alloys, Faraday Discuss., 2015, 180, 113–135.
37. H. Tamura, The role of rusts in corrosion and corrosion protection of iron and steel, Corros. Sci., 2008, 50, 1872–1883.
38. T. Sugimoto and E. Matijević, Formation of uniform spherical magnetite particles by crystallization from ferrous hydroxide gels, J. Colloid Interface Sci., 1980, 74, 227–243.
39. T. Sugimoto and K. Sakata, Preparation of monodisperse pseudocubic α-Fe₂O₃ particles from condensed ferric hydroxide gel, J. Colloid Interface Sci., 1992, 152, 587–590.
40. P. V. Kozlov and G. I. Burdygina, The structure and properties of solid gelatin and the principles of their modification, Polymer, 1983, 24, 651–666.
41. S. Van Vlierberghe, P. Dubruel and E. Schacht, Biopolymer-Based Hydrogels as Scaffolds for Tissue Engineering Applications: A Review, Biomacromolecules, 2011, 12, 1387–1408.
42. P. Atkins and J. De Paula, Physical Chemistry, W.H. Freeman and Company, New York, 2010.
43. P. A. Yakabuskie, J. M. Joseph, P. Keech, G. A. Botton, D. Guzonas and J. C. Wren, Iron oxyhydroxide colloid formation by gamma-radiolysis, Phys. Chem. Chem. Phys., 2011, 13, 7198–7206.
44. T. I. Sutherland, C. J. Sparks, J. M. Joseph, Z. Wang, G. Whitaker, T. K. Sham and J. C. Wren, Effect of ferrous ion concentration on the kinetics of radiation-induced iron-oxide nanoparticle formation and growth, Phys. Chem. Chem. Phys., 2017, 19, 695–708.
45. S. I. Pechenyuk, Y. V. Ivanov and Y. P. Semushina, Porosity of some iron(III), chromium(III), and zirconium(IV) hydroxide oxide xerogels, Russ. J. Inorg. Chem., 2006, 51, 189–193.
46. D. A. G. Bruggeman, Berechnung verschiedener physikalischer Konstanten von heterogenen Substanzen. I. Dielektrizitätskonstanten und Leitfähigkeiten der Mischkörper aus isotropen Substanzen, Ann. Phys., 1935, 416, 636–664.
47. I. Markov, Crystal Growth for Beginners: Fundamentals of Nucleation, Crystal Growth and Epitaxy, World Scientific Publishing Co., Singapore, Third Edn, 2017.
48. D. Fu, P. G. Keech, X. Sun and J. C. Wren, Iron oxyhydroxide nanoparticles formed by forced hydrolysis: dependence of phase composition on solution concentration, Phys. Chem. Chem. Phys., 2011, 13, 18523.
49. W. Thomson (Lord Kelvin), Proc. R. Soc. Edinburgh, 1871, 7, 63.
50. L. Skinner and J. Sambles, The Kelvin equation – A review, J. Aerosol Sci., 1972, 3, 199–210.
51. N. F. Mott, A theory of the formation of protective oxide films on metals, Trans. Faraday Soc., 1939, 35, 1175–1177.
52. N. F. Mott, The theory of the formation of protective oxide films on metals, II, Trans. Faraday Soc., 1940, 35, 472–483.
53. N. F. Mott, The theory of the formation of protective oxide films on metals. III, Trans. Faraday Soc., 1947, 43, 429–434.
54. N. Cabrera and N. F. Mott, Theory of the oxidation of metals, Reports Prog. Phys, 1949, 12, 163–184.
55. A. Seyeux, V. Maurice and P. Marcus, Oxide Film Growth Kinetics on Metals and Alloys, J. Electrochem. Soc., 2013, 160, C189–C196.
56. K. Leistner, C. Toulemonde, B. Diawara, A. Seyeux and P. Marcus, Oxide Film Growth Kinetics on Metals and Alloys, J. Electrochem. Soc., 2013, 160, C197C205.
57. J. C. Sayer and J. L. Hudson, Spatiotemporal Patterns on a Ring Electrode, Ind. Eng. Chem. Res., 1995, 34, 3246–3251.
58. D. Sazou and M. Pagitsas, Non-linear dynamics of the passivity breakdown of iron in acidic solutions, Chaos Solit., 2003, 17, 505–522.
59. D. Sazou and M. Pagitsas, On the onset of current oscillations at the limiting current region emerged during iron electrodissolution in sulfuric acid solutions, Electrochim. Acta, 2006, 51, 6281–6296.
60. A. B. Geraldo, O. E. Barcia, O. R. Mattos, F. Huet and B. Tribollet, New results concerning the oscillations observed for the system iron–sulphuric acid, Electrochim. Acta, 1998, 44, 455–465.
61. D. Iqbal, A. Sarfraz, M. Stratmann and A. Erbe, Solvent-starved conditions in confinement cause chemical oscillations excited by passage of a cathodic delamination front, Chem. Commun., 2015, 51, 16041–16044.
62. D. Sazou, M. Pavlidou and M. Pagitsas, Temporal patterning of the potential induced by localized corrosion of iron passivity in acid media. Growth and breakdown of the oxide film described in terms of a point defect model, Phys. Chem. Chem. Phys., 2009, 11, 8841.
63. N. Sato, Interfacial ion-selective diffusion layer and passivation of metal anodes, Electrochim. Acta, 1996, 41, 1525–1532.
64. D. Guo, M. Li, J. M. Joseph and J. C. Wren, A New Method for Corrosion Current Measurement: the Dual-Electrochemical Cell (DEC), J. Electrochem. Soc., 2020, 167, 111505.
65. E. McCafferty, Introduction to Corrosion Science, Springer New York, New York, NY, 2010.
66. D. A. Jones, Principles and Prevention of Corrosion, Prentice Hall, Upper Saddle River, NJ, 1996.
67. D. Landolt, Corrosion and Surface Chemistry of Metals, EPFL Press, 2007.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp03470k

---