Open Access Article
Open Access ArticleThe influence of anisotropy on the microstructure and magnetic properties of dipolar nanoplatelet suspensions
Margaret
Rosenberg
 *a and
Sofia
Kantorovich
*a and
Sofia
Kantorovich
 ab
ab
aFaculty of Physics, University of Vienna, Bolzmanngasse 5, Vienna 1090, Austria. E-mail: margaret.rosenberg@univie.ac.at
bResearch Platform MMM Mathematics-Magnetism-Materials, Vienna, Austria
First published on 14th September 2022
Abstract
In recent years, there has been an increasing interest in magnetic nanoparticles with non-spherical shapes. This is largely due to their broad span of tuneable properties, which allow for tailoring of the colloidal properties by altering the magnetic anisometry or shape anisotropy of the nanoparticle. Although extensive research has gone into novel synthesis methods, the theoretical and analytical treatment of magnetic colloidal suspensions still predominantly focuses on spherical particles. This paper explores the microstructure and initial static magnetic susceptibility of systems of anisometric dipolar magnetic nanoplatelets in order to understand the applicability of dipolar sphere-based theories and models for such systems. We find that the microstructure as characterized by the particle distribution and magnetic clustering of platelets diverges significantly from that of spheres both quantitatively and qualitatively. We find lower initial static magnetic susceptibilities in nanoplatelet systems than in comparable suspensions of dipolar spheres. At lower values of the magnetic coupling constant, this can be accounted for by applying corrections to the volume fraction. However, this approach is less accurate for systems with stronger magnetic interactions. By providing predictions of and explanations for the observed effects, we aim to facilitate the use of magnetic nanoplatelet suspensions in the broad range of applications.
1 Introduction
Following multiple experimental breakthroughs in the early 2000s, anisotropic and anisometric magnetic nanoparticles have become a veritable subfield of magnetic soft matter.1–6 It has been shown that even small alterations in particle shape strongly affect the overall microscopic properties of such suspensions,7 which is what makes them appealing candidates for applications with tailored requirements,8 in addition to the already broad range of applications for ferrofluids without any modifications.9 Before discussing the specifics of anisotropic systems, it is important to note that dipolar spheres already have a rich phase diagram which has been studied in some detail10–16 and is not without its share of controversy in low-temperature and low-density regimes.17,18 This diagram ranges from isotropic distributions to the formation of chains, rings, branched and/or fully networked structure in dependence on parameters such as the nanoparticle concentration, temperature and magnetic moments. Similarly, the phase diagram of hard platelets is well-known and, depending on the aspect ratio and volume fraction, exhibits liquid-crystalline phases.19,20 There have also been some early computational21 and experimental22 investigations of discotic systems, which focus primarily on the orientations and isotropic-to-nematic phase transition of the suspensions.This paper targets a different region of the phase diagram: keeping both the concentration and aspect ratio of the colloids well below the threshold for a liquid-crystalline phase transition, we simulate systems of discs with varying aspect ratios to examine if their structural properties deviate from the those of dipolar spheres. Our goal is to understand whether or not there are shape effects aside from the mesogenic properties, and if so, how they impact the magnetic properties of the system. To maintain a broad range of applicability, we will condense the influence of the factors listed above into three key parameters: the aspect ratio, given in disc thickness to diameter (e.g. 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3), the volume fraction ϕ and the magnetic coupling constant λ, which is used to characterize the relative strength of magnetic interactions relative to the thermal energy scale of the system. For dipolar spheres, it is defined as
3), the volume fraction ϕ and the magnetic coupling constant λ, which is used to characterize the relative strength of magnetic interactions relative to the thermal energy scale of the system. For dipolar spheres, it is defined as
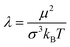 | (1) |
2 Results and discussion
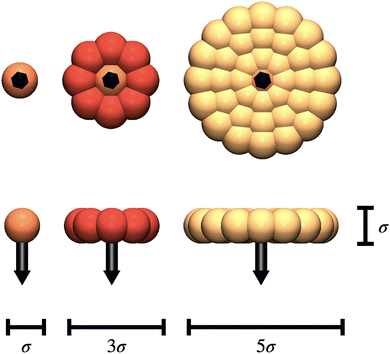
In order to lend a visual aid to the different system properties discussed in this section, we show the three different particle aspect ratios examined in this work in Fig. 1. From left to right, we see a sphere (aspect ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), a platelet with moderate anisotropy (aspect ratio 1
1), a platelet with moderate anisotropy (aspect ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3) and a platelet with strong anisotropy (aspect ratio 1
3) and a platelet with strong anisotropy (aspect ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5). These aspect ratios were chosen to sample the region of aspect ratios where the anisotropy is both pronounced enough to influence the microstructure, and low enough that the isotropic to nematic phase transition does not occur at the densities studied.
5). These aspect ratios were chosen to sample the region of aspect ratios where the anisotropy is both pronounced enough to influence the microstructure, and low enough that the isotropic to nematic phase transition does not occur at the densities studied.
Although a quick count shows that the rightmost platelet contains 7 spheres across one diameter, due to their overlap, the resulting aspect ratio is only 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5. Further discussions of the model and technical challenges can be found in Section 4.
5. Further discussions of the model and technical challenges can be found in Section 4.
2.1 Phase microstructure
As a general note, due to the large number of parameter sets explored, each plot will only show one representative curve per type of structure or behavior observed. Unless otherwise specified, this means that if for a given λ, only a very low and very high ϕ are shown, the curves for all other densities can safely be assumed to lie between the two.Examining the radial distribution of dipolar spheres in Fig. 2 as a reference, we see a gaseous state regardless of density for λ = 1 (green curves). Increasing λ to three (blue curves) already results in the formation of an early nearest-neighbor peak. This peak flattens out with increasing density. At λ = 5 (purple), the radial distribution function indicates that the system has some clusters with regular spacing (suggesting chains or rings), as well as particles at intermediate distances. This persists despite the flattening of the curve at higher densities. At λ = 7 (orange) and λ = 10 (red), the distribution function shows a shifted and even more strongly structured version of the curves corresponding to the smaller λ values. This effect arises due to the dipole moment being strong enough to overcome part of the steric particle repulsion, shifting the nearest-neighbor peak from the Weeks-Chandler-Anderson minimum23 of 21/6 (≈1.12) to 0.9. Although the two highest λ values would appear a featureless dense network in simulation snapshots, the radial distributions show that they are assembled with clear spacing.
For systems of platelets with aspect ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, we see in Fig. 3 that the λ = 1 and λ = 3 systems (blue and green curves) are in a gaseous state. At λ = 5 (purple), the shape of g(r) begins to change as some close-range pairs form, although even at the highest density the system remains dispersed and spatially isotropic overall. The actual self-assembly into pairs begins at λ = 7 (red), with a peak for the nearest neighbors that increases with higher density. At the next increase of magnetic moment, λ = 10 (orange), we see that the system is already assembled into regularly spaced structures. Comparison with simulation snapshots shows that this corresponds to the regime where long chains are formed. This results in a clear pattern of g(r) However, it needs to be noted that in this regime the chain lengths have become comparable to the box length, which means the last curves must be interpreted qualitatively. Aside from the fundamental differences that dipolar spheres' radial distribution functions evolves with λ to show an initially gaseous phase moving to a fluid with increasing levels of regular structure, as opposed to the gaseous, then suddenly highly periodic radial distribution of aspect ratio 1
3, we see in Fig. 3 that the λ = 1 and λ = 3 systems (blue and green curves) are in a gaseous state. At λ = 5 (purple), the shape of g(r) begins to change as some close-range pairs form, although even at the highest density the system remains dispersed and spatially isotropic overall. The actual self-assembly into pairs begins at λ = 7 (red), with a peak for the nearest neighbors that increases with higher density. At the next increase of magnetic moment, λ = 10 (orange), we see that the system is already assembled into regularly spaced structures. Comparison with simulation snapshots shows that this corresponds to the regime where long chains are formed. This results in a clear pattern of g(r) However, it needs to be noted that in this regime the chain lengths have become comparable to the box length, which means the last curves must be interpreted qualitatively. Aside from the fundamental differences that dipolar spheres' radial distribution functions evolves with λ to show an initially gaseous phase moving to a fluid with increasing levels of regular structure, as opposed to the gaseous, then suddenly highly periodic radial distribution of aspect ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 platelets, it should also be noted that the process of this evolution is quite different between the two suspensions. In systems of spheres, there is a gradual increase of peak height with λ and dependence on ϕ, with little qualitative change between systems adjacent in parameter-space. For platelets, there is a rather abrupt transition from λ = 7 on, with no overlap between different values of λ.
3 platelets, it should also be noted that the process of this evolution is quite different between the two suspensions. In systems of spheres, there is a gradual increase of peak height with λ and dependence on ϕ, with little qualitative change between systems adjacent in parameter-space. For platelets, there is a rather abrupt transition from λ = 7 on, with no overlap between different values of λ.
At the highest aspect ratio investigated, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5, shown in Fig. 4 we observe a similar progression as with aspect ratio 1
5, shown in Fig. 4 we observe a similar progression as with aspect ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3. As this system faces the same issue of chains approaching box length for λ = 10, we omit those curves and focus on tracking the transition from the gaseous state to the beginnings of the assembly process. The lower values of λ = 3 and λ = 5 (light blue, light purple) are clearly still gaseous in the case of aspect ratio 1
3. As this system faces the same issue of chains approaching box length for λ = 10, we omit those curves and focus on tracking the transition from the gaseous state to the beginnings of the assembly process. The lower values of λ = 3 and λ = 5 (light blue, light purple) are clearly still gaseous in the case of aspect ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 platelets, with the same hint of a nearest-neighbor peak at the higher densities just over the distance of one diameter (5-less visible in logscale). The shape of the curve is slightly flatter due to the larger spread of interparticle distances due to the shape (with the closest contact distance between 1 and 5 depending on the mutual orientation). Interestingly, we see that while λ = 7 does start to form a peak at the assembled distance for the highest density (pink polygons), it is still below 1 despite the next increase of λ leading to a full chained regime. This indicates that the transition from an isotropic to a self-assembled state is either shifted to higher λ, or takes place in a narrower region of the phase space. All the peaks found for aspect ratio 1
5 platelets, with the same hint of a nearest-neighbor peak at the higher densities just over the distance of one diameter (5-less visible in logscale). The shape of the curve is slightly flatter due to the larger spread of interparticle distances due to the shape (with the closest contact distance between 1 and 5 depending on the mutual orientation). Interestingly, we see that while λ = 7 does start to form a peak at the assembled distance for the highest density (pink polygons), it is still below 1 despite the next increase of λ leading to a full chained regime. This indicates that the transition from an isotropic to a self-assembled state is either shifted to higher λ, or takes place in a narrower region of the phase space. All the peaks found for aspect ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 platelets' system monotonically increase with density.
5 platelets' system monotonically increase with density.
We can see this behavior reflected in the center-to-center structure factors S(q) as well, shown in Fig. 5. In the leftmost graph, the structure factor of dipolar spheres at a higher density (ϕ = 0.15) shows an increase in isothermal compressibility even at the lower λ = 3 (before significant self-assembly) which only increases for high λ = 7. At high λ, we also see the nearest neighbor peak increase in height and shift to higher q, as well as the increase low-q values, suggesting the formation of a percolating network. As these effects have already been studied in detail (see e.g. ref. 24), we will focus our attention on the plot at the center, which shows the same λ and ϕ values in a system of aspect ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 platelets. For λ = 3, this platelet ferrofluid is in a simple liquid phase. Increasing λ does show a clear effect, with the formation of a second peak (corresponding to the onset of self-assembly) and a shift of the first peak. However, this structuring is much less pronounced than that of even λ = 3 dipolar spheres, despite both having low self-assembly. Finally, in the rightmost graph, we see that the structure factors for aspect ratio 1
3 platelets. For λ = 3, this platelet ferrofluid is in a simple liquid phase. Increasing λ does show a clear effect, with the formation of a second peak (corresponding to the onset of self-assembly) and a shift of the first peak. However, this structuring is much less pronounced than that of even λ = 3 dipolar spheres, despite both having low self-assembly. Finally, in the rightmost graph, we see that the structure factors for aspect ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 platelets the structure factors are essentially identical within the statistical precision reached and correspond to a homogeneous liquid.
5 platelets the structure factors are essentially identical within the statistical precision reached and correspond to a homogeneous liquid.
Having discussed the onset of clustering and the progression of phases of the system, we now turn to investigating the clusters themselves by quantitatively characterizing the development of the clustering with increasing λ and ϕ. As before, we begin by showing a reference system of dipolar spheres in Fig. 6. For λ = 1 (green), we see that the particles are mostly dispersed, with a clear progression towards small clusters at very high densities. This same effect takes place on a shifted scale for λ = 3. It is important to note that the clustering criterion cutoff used here was adapted slightly from that used in (similar studies7), which is discussed in greater detail in the Section 4. This ensures greater comparability between dipolar sphere and platelet system, but causes a slight deviation from the literature in terms of the onset of clustering for low λ. At λ = 5 (purple), clusters dominate from the outset and large clusters begin to form. Finally, both λ = 7 and λ = 10 show networks encompassing almost all particles as the dominant structure, except for the lowest densities, where distinct intermediately sized clusters can still coexist. Comparing across all systems, we can roughly parse 3 regimes. The first regime, at the lower ends of the lambda and density regimes, dipolar interactions do not play a significant role in the overall system structure. While particles can self-assemble, these clusters remain small. Regime 2 is the clustered region of the phase diagram, where different sizes and based on literature, types of clusters coexist. Based on studies of similar systems,25 we expect the system to form rings (closed-flux structures) that are inherently limited in size, so this range of cluster size deserves its own mention as a distinct region of the phase behavior as opposed to an intermediate state. Ultimately, for the highest λ and density, the system collapses into a (fully) networked state. At the high λ and ϕ limit, it is difficult to give confident quantitative statements as the exact density at which the system transitions to a fully networked state can be influenced by the box-size. For the purposes of this paper, we restrict ourselves to pointing out that qualitatively, the limiting case of the system behavior for dipolar spheres is as described.
Slightly deforming the aspect ratio from 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 1
1 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, we already expect a decrease in cluster formation based on the radial distribution functions. One naive conjecture based on the clustering shown for spheres is that platelets do show the same qualitative and quantitative behavior, simply shifted by density-while a unit sphere has a volume of
3, we already expect a decrease in cluster formation based on the radial distribution functions. One naive conjecture based on the clustering shown for spheres is that platelets do show the same qualitative and quantitative behavior, simply shifted by density-while a unit sphere has a volume of  a 1
a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 platelet has the volume
3 platelet has the volume  which corresponds to a ratio of 1
which corresponds to a ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 13.5. Examining Fig. 7 shows significantly less clustering: none for any of the densities for λ < 7 (save a minuscule percentage at λ = 5, ϕ = 0.2) show any assembly. The shift to small clusters observed in λ = 7 could be argued to resemble the behavior of λ = 3 for spheres; however, this breaks down at λ = 10 when assembly does occur, but clearly peaks in an intermediate regime not favored by dipolar spheres.
13.5. Examining Fig. 7 shows significantly less clustering: none for any of the densities for λ < 7 (save a minuscule percentage at λ = 5, ϕ = 0.2) show any assembly. The shift to small clusters observed in λ = 7 could be argued to resemble the behavior of λ = 3 for spheres; however, this breaks down at λ = 10 when assembly does occur, but clearly peaks in an intermediate regime not favored by dipolar spheres.
The aspect ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 platelets do not exhibit this intermediate peak, going from majority isolated to majority clustered in assemblies of 20 < n < 100 particles. The largest clusters sizes shown to be the limiting cases to not appear at all. It could be argued that by increasing λ sufficiently, larger clusters might be attained. For this argument, it is instructive to question what sort of structures platelets can be expected to form: it is not clear if platelets can form the networks of branched structures necessarily to achieve such large clusters considering the interplay between the steric repulsion and the weakened dipolar interactions due to the greater distances. We expect platelets to form stacks (the equivalent of chains in spheres), which should grow in length for increasing λ: due to the steric repulsion, we would not expect rings or strongly curved structures to form.
3 platelets do not exhibit this intermediate peak, going from majority isolated to majority clustered in assemblies of 20 < n < 100 particles. The largest clusters sizes shown to be the limiting cases to not appear at all. It could be argued that by increasing λ sufficiently, larger clusters might be attained. For this argument, it is instructive to question what sort of structures platelets can be expected to form: it is not clear if platelets can form the networks of branched structures necessarily to achieve such large clusters considering the interplay between the steric repulsion and the weakened dipolar interactions due to the greater distances. We expect platelets to form stacks (the equivalent of chains in spheres), which should grow in length for increasing λ: due to the steric repulsion, we would not expect rings or strongly curved structures to form.
The clustering of platelets with aspect ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 was integrated into Fig. 7 as its meaningful quantification is quite succinct: there is no clustering for λ < 7 (pastel blue and purple), a very small fraction for the highest density at λ = 7 (pink) and a jump to long chains for λ = 10. The latter could not be evaluated quantitatively due to issues with equilibration, as the chains spanned the box length. These discrepancies in clustering are not purely a question of volumetric differences. While the different density surely places a role, it is clear from Fig. 7 that shifting ϕ would not be sufficient to transform the platelet distribution into those formed by spheres.
5 was integrated into Fig. 7 as its meaningful quantification is quite succinct: there is no clustering for λ < 7 (pastel blue and purple), a very small fraction for the highest density at λ = 7 (pink) and a jump to long chains for λ = 10. The latter could not be evaluated quantitatively due to issues with equilibration, as the chains spanned the box length. These discrepancies in clustering are not purely a question of volumetric differences. While the different density surely places a role, it is clear from Fig. 7 that shifting ϕ would not be sufficient to transform the platelet distribution into those formed by spheres.
This is explored further in Fig. 8, which shows a more detailed cluster size distribution for spheres and aspect ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 platelets at fixed densities. Based on previous work by Sciortino et al.,26–28 we expect that the size distribution of clusters of dipolar spheres should follow a power law as given by Wertheim theory. If we examine the curves marked with spherical points, we find excellent agreement with studies of defect clusters28 for clusters with 3–100 particles, which show a clear linear trend. For the platelet clustering (stars), the limited clustering for λ = 5 is still linear. The next highest value, λ = 7 is arguably still similar to trends for lower-λ spheres: however, λ = 10 (orange curve) does not follow any form of power law.
3 platelets at fixed densities. Based on previous work by Sciortino et al.,26–28 we expect that the size distribution of clusters of dipolar spheres should follow a power law as given by Wertheim theory. If we examine the curves marked with spherical points, we find excellent agreement with studies of defect clusters28 for clusters with 3–100 particles, which show a clear linear trend. For the platelet clustering (stars), the limited clustering for λ = 5 is still linear. The next highest value, λ = 7 is arguably still similar to trends for lower-λ spheres: however, λ = 10 (orange curve) does not follow any form of power law.
Another explanation could be that differences in structures formed plays a role in the quantity of clustering. As the platelets are rigid, they are not able to self-assemble into certain compact structures – such as rings – due to steric exclusion. Perhaps the lower clustering only reflects the difference in configuration space due to the shape?
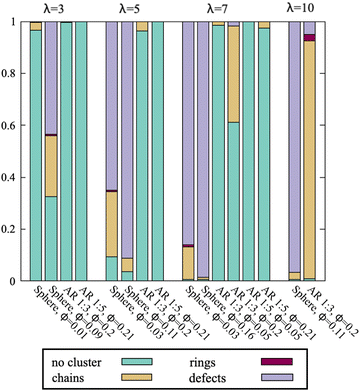
In order to explore this hypothesis, we study which microstructure motifs are formed and the relative frequency of their occurrence. Fig. 9 shows the percentage of particles in either not in clusters (singlets and pairs, fewer than 3 particles), defect-free chains and rings and branched or “defect” structures, i.e. self-assembled structures that contain at least one defect. As the defects structures for dipolar spheres have already been studied in-depth for comparable systems,28 we do not engage in further discussions of the different defect types and relative frequencies. For spheres, defect structures rapidly begin to dominate over all other structures, with some chains and, at specific densities, rings. The lack of the latter is due to the higher densities studied. The proportion of defects to chains does not change significantly once λ is sufficiently high. For aspect ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 platelets, we see an entirely different progression-there is very limited assembly into chains even for high λ, until for very high λ = 10 chains come to dominate the assembled structures. While there is a small fraction of rings at the highest densities, these were revealed to largely stem from the technical issue that sufficiently large chains at very high λ and ϕ reach the length of the simulation box and self-interact across the periodic boundary conditions. Very few defects were found. As expected, aspect ratio 1
3 platelets, we see an entirely different progression-there is very limited assembly into chains even for high λ, until for very high λ = 10 chains come to dominate the assembled structures. While there is a small fraction of rings at the highest densities, these were revealed to largely stem from the technical issue that sufficiently large chains at very high λ and ϕ reach the length of the simulation box and self-interact across the periodic boundary conditions. Very few defects were found. As expected, aspect ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 did not yield any structures for the densities studied, except some chains at high λ. While the difference in rings can be explained away by steric exclusion, it is interesting to note the stark discrepancy in terms of defect structures which are – in principle – available in configuration space. This suggests that the secondary energy minimum of the dipole–dipole interaction is too shallow for both aspect ratio 1
5 did not yield any structures for the densities studied, except some chains at high λ. While the difference in rings can be explained away by steric exclusion, it is interesting to note the stark discrepancy in terms of defect structures which are – in principle – available in configuration space. This suggests that the secondary energy minimum of the dipole–dipole interaction is too shallow for both aspect ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and aspect ratio 1
3 and aspect ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 platelets to form branched structures, barring a small fraction at very specific densities.
5 platelets to form branched structures, barring a small fraction at very specific densities.
To summarize, the lack of available configurations strongly reduces the types and the quantity of clusters formed in the system. This is illustrated in Fig. 10, where we compared a system of aspect ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 at the λ and ϕ values with the highest percentage of defect formation to an equivalently dense system of dipolar spheres, which consists of a network of branched structures. It is interesting to note that although both systems are initially quite similar in the isotropic low λ, low ϕ regime, the high λ and high ϕ limiting cases of the particles are a fully connected network with no overall orientational order, and, in case of platelets, stacks which cannot curve significantly due to their rigidity and therefore have greater local orientational order. We will explore the orientational-related attributes of the system microstructure in the following section.
3 at the λ and ϕ values with the highest percentage of defect formation to an equivalently dense system of dipolar spheres, which consists of a network of branched structures. It is interesting to note that although both systems are initially quite similar in the isotropic low λ, low ϕ regime, the high λ and high ϕ limiting cases of the particles are a fully connected network with no overall orientational order, and, in case of platelets, stacks which cannot curve significantly due to their rigidity and therefore have greater local orientational order. We will explore the orientational-related attributes of the system microstructure in the following section.
Examining the orientational correlations in the sphere system, shown in Fig. 11, we find that g2(r) is almost identically 0 for λ = 1 (green) regardless of density, only slightly going above the x-axis for r ≈ 1 where some pairs may have formed. This grows more pronounced for λ = 3 (dark blue), matching the expected start of pair formation. For λ = 5 (purple), we see periodic structure of peaks starting at the lowest density. At close ranges and multiples of slightly higher values than the diameter, there is a significant correlation which drops off in between. This pattern, which even shows a hint of negative correlation after the first peak, is most present for the lowest density ϕ = 0.01. As the density increases, the correlation of close particles remains and the secondary remaining peaks flatten, with the curve at the highest density being reduced to two peaks at the nearest and second-nearest distances. Both the same pattern and trend are found in the λ = 7 curves, although there are two important differences. Firstly, the curve retains multiple three peaks even at higher densities. Secondly, these peaks are significantly higher-while the exact threshold for is debatable, overall correlation values of >0.3 are generally considered to be the criterion for significant ordering. Finally λ = 10 (orange) completes this pattern to a seemingly almost periodic ordering. As opposed to the clustering, the orientational correlations show a clear progression from disorder to order that increases with λ.
The orientational correlations for platelets in Fig. 12 show a very clear shape at close range: if we presume a particle at distance roughly the order of the platelet diameter, it must be highly aligned with the platelet in order to not violate the steric exclusion. This is enforced even for otherwise low-density systems: it should be noted that in this measure, as opposed to the previously shown radial distribution functions, the frequency of particles at a given distance is irrelevant. As opposed to the more diffuse peaks shown for spheres, platelets have a very clear pattern of alignment. For λ < 7 (green, blue, violet) this explains the gentle decorrelation we see: at close range, the particle shape enforces an ordering, while at greater distances the correlation drops to 0. This remains at low-density λ = 7, while for higher densities we see the formation of periodic correlations corresponding to the chain formation, which appears fairly pronounced considering the few chains in the system at this stage. Finally, for λ = 10, there is a clear periodicity to the correlations which seems to span the entire box, corresponding to the result that the particles are aligned (in long chains).
For aspect ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 (Fig. 13), we see the same shape for all densities and λ values as in the previous figure, albeit shifted and stretched to account for the greater aspect ratio of the platelets. This lends credence to the idea that these close-range orientational correlations are an effect strongly driven by shape. The figure also shows that there is no pre-nematic ordering affecting the platelets. In summary, the orientational correlations in the system seem to fall into two distinct categories: short-range correlations driven primarily by the shape for low λ, and periodically occurring correlations at larger distances in assembled chain structures driven by magnetic self-assembly.
5 (Fig. 13), we see the same shape for all densities and λ values as in the previous figure, albeit shifted and stretched to account for the greater aspect ratio of the platelets. This lends credence to the idea that these close-range orientational correlations are an effect strongly driven by shape. The figure also shows that there is no pre-nematic ordering affecting the platelets. In summary, the orientational correlations in the system seem to fall into two distinct categories: short-range correlations driven primarily by the shape for low λ, and periodically occurring correlations at larger distances in assembled chain structures driven by magnetic self-assembly.
Another possibility for characterizing the ordered structures formed in such systems are the Steinhardt order parameters.29 These can shed light on the structure of the system as a whole, provided it shows a sufficiently high first peak of the radial distribution function from which to define nearest neighbors. We therefore only investigate systems with a clear first peak of the radial distribution function.
For spheres (Fig. 14), the bond order parameters are relatively low and have the consistent trend of even-valued Q being higher than odd-valued Q, presumably due to the chain formation. The order parameters also decrease for higher values of the density, and the gap between even and odd parameters decreases. For λ ≤ 5, high densities flatten all bond order parameters into essentially 0; for higher λ, some difference between even and odd values is preserved regardless of density.
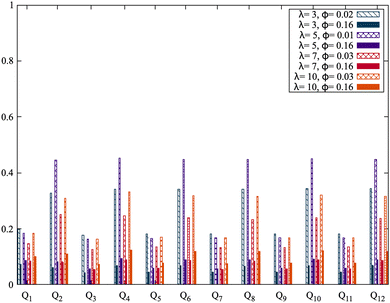 | ||
| Fig. 14 Steinhardt Bond order parameters for spheres, Q1 through Q12. We see that the even Q values are significantly higher than the odds, especially for higher λ. | ||
In terms of bond order parameters, platelets (Fig. 15) show noticeably higher values for the even bond order parameters, but qualitatively follow the same trends as the higher λ spheres for lower values of λ or higher densities. At low densities and high values of λ, shown by the patterned orange and red bars, the values of the even bond order exceed those of spheres by far. In particular, the system of aspect ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 platelets with λ = 10 has a peak at Q2, although this should be considered critically since the system as at the boundary of what could be equilibrated due to the long chain formation. The only aspect ratio 1
3 platelets with λ = 10 has a peak at Q2, although this should be considered critically since the system as at the boundary of what could be equilibrated due to the long chain formation. The only aspect ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 platelet system for which bond order parameters could be defined, λ = 7 and ϕ = 20, behaves similarly to the low-density variant of the λ = 7, aspect ratio 1
5 platelet system for which bond order parameters could be defined, λ = 7 and ϕ = 20, behaves similarly to the low-density variant of the λ = 7, aspect ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 system. The conclusion of this section is that while predominance of chains in platelet systems does lend itself to some structuring, due to the homogeneity of the order parameters there is no overall lattice-type structure formed. Despite the different microstrucutres in terms of clustering, and the lower orientational correlation, spheres and platelets show surprising qualitative similarities where bond order parameters apply, presumably because the treatment of orientations in the definition of bond order parameters collapses the differences between chains which are bent (including network-like structures) and rigid, inflexible chains.
3 system. The conclusion of this section is that while predominance of chains in platelet systems does lend itself to some structuring, due to the homogeneity of the order parameters there is no overall lattice-type structure formed. Despite the different microstrucutres in terms of clustering, and the lower orientational correlation, spheres and platelets show surprising qualitative similarities where bond order parameters apply, presumably because the treatment of orientations in the definition of bond order parameters collapses the differences between chains which are bent (including network-like structures) and rigid, inflexible chains.
2.2 Initial magnetic susceptibility
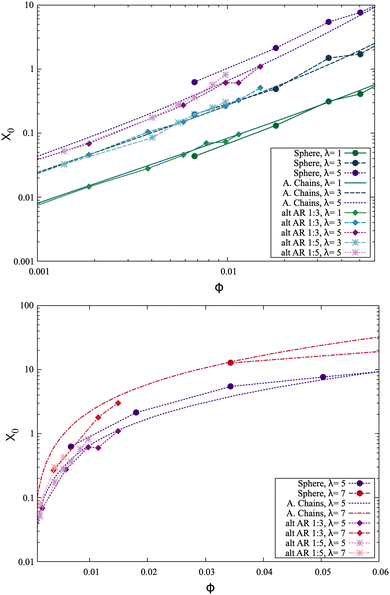
What consequences do the differences in microstructure explored in the previous sections of this paper have for the magnetic susceptibilities? Fig. 16 shows the analytical expression for dipolar spheres for different values of λ as dashed lines, calculated using the chain approximation by Ivanov et al.30 and the static initial magnetic susceptibilities calculated as in similar works7 as solid lines with point represented by small spheres. Comparing these two sets of curves, we see good agreement as expected. In contrast, the curves and values for platelets of various aspect ratios, shown with squares and stars, do not match the analytical approach. Two opposing conjectures to explain this behavior spring to mind. Firstly, while the platelets do behave very differently than spheres as evidenced above, neither system shows a significant fraction of closed-flux structures (rings) which would decrease the susceptibility. It could be that the differences in microstructure are largely irrelevant, and that the qualitative shape of the curve that comes from mechanisms could still be the same, albeit shifted due to the difference in volume. Perhaps these initial susceptibilities for platelets are qualitatively equivalent to spheres at a lower volume fraction. If there is a constant shift factor for each platelet aspect ratio, this would indicate that there is no significant impact of the shape on the static initial magnetic susceptibilities. Alternatively, the platelets might exhibit qualitatively different susceptibilities that will not fit to the equivalent curves for spheres.To approach this distinction systematically, we begin by recalling that the Langevin susceptibility of non-interacting dipolar spheres is given by χ0 = 8λϕ. Does the shape of the particles already affect their initial magnetic susceptibility even without interparticle interactions? Considering that at higher densities, platelets can form nematic and columnar phases, it is possible that there exists some orientational ordering of the platelets which in turn would result in an alignment of the dipole moments, departing from the Langevin curve. As this is a simulation work, we can simply remove magnetic interparticle interactions and check if the initial magnetic susceptibility of platelets still follows the Langevin law, i.e. if there are yet no nematic- or pre-nematic correlations affecting the susceptibility of platelets. Fig. 17 tests this hypothesis by showing initial magnetic susceptibilities of systems without interparticle dipole–dipole interactions, rescaled by volume to correspond to the spherical case. We see that the magnetic susceptibilities fall exactly onto the Langevin curve. This suggests that there are no purely steric shape effects on the initial magnetic susceptibilities in the studied range of parameters, aside from the difference in density.
It also suggests that, although denser systems are more difficult to equilibrate, the rescaling shown in this plot, specifically calculating the volume fraction based on the central magnetic sphere as opposed to the entire platelet, is a reasonable approach for low enough densities. We therefore select some of the susceptibilities shown in Fig. 16 and rescale the densities in this manner, the result of which is depicted in Fig. 18. In the top plot of the Figure, we see that for low values of λ = 1 and λ = 3, both aspect ratios of platelets fit the theoretical curves very well and essentially agree with the results for spheres, considering simulation accuracy. However, for λ = 5 at aspect ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5, and λ = 7 at aspect ratio 1
5, and λ = 7 at aspect ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 in the lower plot, the slope of the initial magnetic susceptibility appears steeper than that of spheres. The challenge in this context is that, as the density of the platelets needs to be so dramatically rescaled to be fitted to the curves, it is difficult to leave the region where dipolar spheres are still completely isotropic. Therefore, the difference in microstructure is not as apparent as might be expected. While Fig. 18 is difficult to interpret consistently across the scales, comparing to previous works on cubes7 suggests that spheres agree very well with the analytical expression for magnetic susceptibilities at low ϕ, which for rescaled platelets hold for λ = 1 and λ = 3 but grows progressively worse for higher λ. This suggests that rescaling is an effective solution for low-density systems (which still exhibit a qualitatively microstructure to spheres) but becomes increasingly inaccurate once the platelets and spheres microstructures diverge.
3 in the lower plot, the slope of the initial magnetic susceptibility appears steeper than that of spheres. The challenge in this context is that, as the density of the platelets needs to be so dramatically rescaled to be fitted to the curves, it is difficult to leave the region where dipolar spheres are still completely isotropic. Therefore, the difference in microstructure is not as apparent as might be expected. While Fig. 18 is difficult to interpret consistently across the scales, comparing to previous works on cubes7 suggests that spheres agree very well with the analytical expression for magnetic susceptibilities at low ϕ, which for rescaled platelets hold for λ = 1 and λ = 3 but grows progressively worse for higher λ. This suggests that rescaling is an effective solution for low-density systems (which still exhibit a qualitatively microstructure to spheres) but becomes increasingly inaccurate once the platelets and spheres microstructures diverge.
3 Conclusions
Although dipolar spheres and platelets might not be expected to differ strongly, we find significant differences in the microstructure of these systems, especially where self-assembly is concerned. Using a standard definition of the magnetic coupling constant poorly serves to predict magnetic platelet behavior, as a significantly higher value of the magnetic moment is required to elicit structure formation. For fixed values of λ and density ϕ, platelets self-assemble into fewer structures both quantitatively and qualitatively. When assembled, platelets favor chain structures with no rings and few defects. The cluster size distribution of platelets does not follow Wertheim exponential law. Despite the platelet aspect ratios being significantly below the threshold for nematic or pre-nematic ordering, once self-assembly begins, the platelet systems shows much higher short-range orientational correlations due to the particle shape. The resulting structures, especially for high λ, shows higher even-valued Steinhardt bond order parameters. The initial susceptibilities for platelets are significantly lower than those of spheres. Introducing volume corrections can solve this issue for lower λ, but higher λ values still do not agree with the rescaled spherical case. These discrepancies do not appear to be related to any pre-nematic ordering, as platelets without interparticle magnetic interactions follow the Langevin laws perfectly. Overall, systems of magnetic dipolar platelets show large discrepancies in microstructure to the reference case of dipolar spheres, which also affects their magnetic susceptibilities and therefore must be taken into consideration.4 Methods
4.1 Simulation procedure and particle model
All of the simulation data in this work was obtained by carrying out Molecular Dynamics simulations using the software package ESPResSo 4.1.4,31 with a coarse-grained approach towards modelling the system. The underlying thermodynamic ensemble was chosen to be NVT, where N = 1024 particles in a cubic simulation box of volume V are propagated according to the Langevin equations, with a Langevin thermostat ensuring constant temperature T. Instead of hydrodynamics, an implicit solvent is considered by way of the stochastic and friction terms included in the translational and rotational equations of motion. We restrict ourselves to studying equilibrium properties, in full 3D, with periodic boundary conditions used to mimic a larger suspension.The simulation protocol was straightforward: given the fixed number of total particles N = 1024 and particle volume v determined by the choice of aspect ratio, the box length a was calculated to give a target volume fraction  . Generally speaking, simulations were run for aspect ratios 1
. Generally speaking, simulations were run for aspect ratios 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and 1
3 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5, with ϕ ranging from 0.01 to 0.2 (with additional high density runs for Fig. 18) and λ varying between 1 and 10. At the start of the simulations, the particles were placed randomly in the box, then separated to avoid steric overlaps. The time step was taken to be δt = 0.01. Simulations were warmed up for 1000δt, then run for 10
5, with ϕ ranging from 0.01 to 0.2 (with additional high density runs for Fig. 18) and λ varying between 1 and 10. At the start of the simulations, the particles were placed randomly in the box, then separated to avoid steric overlaps. The time step was taken to be δt = 0.01. Simulations were warmed up for 1000δt, then run for 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000·100δt. During the simulation run, checkpoints were taken every 10
000·100δt. During the simulation run, checkpoints were taken every 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000δt. Before the begin of statistical evaluation, the energy of the system was carefully checked in order to determine if thermodynamic equilibrium was reached. For simplicity's sake, the threshold of 10
000δt. Before the begin of statistical evaluation, the energy of the system was carefully checked in order to determine if thermodynamic equilibrium was reached. For simplicity's sake, the threshold of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000δt was chosen as threshold after which checkpoints were considered equilibrated, since all low λ and almost all high λ were equilibrated. The λ = 10, aspect ratio 1
000δt was chosen as threshold after which checkpoints were considered equilibrated, since all low λ and almost all high λ were equilibrated. The λ = 10, aspect ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 systems required higher, custom thresholds based on the energy. At high densities and magnetic moments, some planned systems could not be properly equilibrated (e.g. aspect ratio 1
3 systems required higher, custom thresholds based on the energy. At high densities and magnetic moments, some planned systems could not be properly equilibrated (e.g. aspect ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5, λ = 10): therefore, they are mentioned qualitatively and not included in any statistics.
5, λ = 10): therefore, they are mentioned qualitatively and not included in any statistics.
In order to ensure comparability with a broad range of experiments, dimensionless parameters are used. The length scale, σ, is chosen to be one platelet diameter (as seen in Fig. 1). This leaves the energy scale, kBT, which was also set to 1 in order to ensure a straightforward comparison between the thermal fluctuation and the strength of the dipole–dipole interaction, which was characterized by λ as defined in eqn (1). The time scale was implicitly constrained by adding a fictitious simulation mass: this is necessary in order to properly set the rotational inertia of platelets.
The particles were modelled as rigid assemblies of multiple interaction sites (raspberry model) with a repulsive Weeks Chandler Anderson potential to prevent steric overlap, as shown in Fig. 1. This potential is given by
 | (2) |
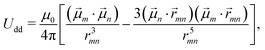 | (3) |
4.2 Analysis
Since defects in DHS systems have already been studied intensively, we simplify the categorization used in ref. 25 and only consider the number of “bonds” each particle has, collapsing defects into a single category due to their rarity in platelet systems. This leads us to the following cases and definitions (for clusters with n ≥ 2 particles):
1. A cluster containing at least one particle with more than 2 bonds is a defect cluster (“branched structure”)
2. A cluster where each particle has exactly two bonds is a ring
3. Any remaining cluster is a chain
Some high-λ systems of platelets appear to form rings. Closer investigation showed that these appear to be simulation artefacts, either resulting from the definition listed below which allows 3-particle “clusters” to count as rings despite the fact that in the platelet case, the magnetic flux is typically not closed, or resulting from a technical problem with chains that span the length of the box being counted as rings due to the periodic boundary conditions. Since the former is argueably still a valid ring, these structures were retained as such. Most of the simulation runs that showed the latter type of ring were cut from the quantitative results due to equilibration concerns.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
M. R. thanks the Austrian Academy of Sciences for funding via the DOC-Fellowship program. Simulations were performed on the Vienna Scientific Cluster (VSC4). S. S. K. also acknowledges partial support of RSF 19-12-00209.References
- M. Meyer, A. Bée, D. Talbot, V. Cabuil, J. Boyer, B. Répetti and R. Garrigos, J. Colloid Interface Sci., 2004, 277, 309–315 CrossRef CAS.
- C. J. Murphy, T. K. Sau, A. M. Gole, C. J. Orendorff, J. Gao, L. Gou, S. E. Hunyadi and T. Li, J. Phys. Chem. B, 2005, 109, 13857–13870 CrossRef CAS PubMed.
- D. Lisjak and A. Mertelj, Prog. Mater. Sci., 2018, 95, 286–328 CrossRef CAS.
- R. G. D. Andrade, S. R. S. Veloso and E. M. S. Castanheira, Int. J. Mol. Sci., 2020, 21, 2455 CrossRef CAS PubMed.
- S. Sacanna and D. J. Pine, Curr. Opin. Colloid Interface Sci., 2011, 16, 96–105 CrossRef CAS.
- L. Rossi, S. Sacanna, W. T. M. Irvine, P. M. Chaikin, D. J. Pine and A. P. Philipse, Soft Matter, 2011, 7, 4139–4142 RSC.
- J. G. Donaldson, E. S. Pyanzina and S. S. Kantorovich, ACS Nano, 2017, 11, 8153–8166 CrossRef CAS PubMed.
- P. Tierno, Phys. Chem. Chem. Phys., 2014, 16, 23515–23528 RSC.
- M. Kole and S. Khandekar, J. Magn. Magn. Mater., 2021, 537, 168222 CrossRef CAS.
- J. J. Weis and D. Levesque, Phys. Rev. Lett., 1993, 71, 2729–2732 CrossRef CAS.
- M. E. van Leeuwen and B. Smit, Phys. Rev. Lett., 1993, 71, 3991–3994 CrossRef CAS PubMed.
- Y. V. Kalyuzhnyi, I. A. Protsykevytch and P. T. Cummings, EPL, 2007, 80, 56002 CrossRef.
- D. Levesque and J.-J. Weis, Mol. Phys., 2011, 109, 2747–2756 CrossRef CAS.
- D. Levesque and J. J. Weis, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1994, 49, 5131–5140 CrossRef CAS PubMed.
- J. J. Weis and D. Levesque, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1993, 48, 3728–3740 CrossRef CAS.
- A.-P. Hynninen and M. Dijkstra, Phys. Rev. Lett., 2005, 94, 138303 CrossRef.
- R. P. Sear, Phys. Rev. Lett., 1996, 76, 2310–2313 CrossRef CAS PubMed.
- L. Rovigatti, J. Russo and F. Sciortino, Phys. Rev. Lett., 2011, 107, 237801 CrossRef PubMed.
- R. Eppenga and D. Frenkel, Mol. Phys., 1984, 52, 1303–1334 CrossRef CAS.
- J. A. C. Veerman and D. Frenkel, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 45, 5632–5648 CrossRef.
- R. Berardi, S. Orlandi and C. Zannoni, J. Chem. Soc., Faraday Trans., 1997, 93, 1493–1496 RSC.
- P. Hribar Boštjančič, Ž. Gregorin, N. Sebastián, N. Osterman, D. Lisjak and A. Mertelj, J. Mol. Liq., 2022, 348, 118038 CrossRef.
- E. S. Pyanzina, S. S. Kantorovich and C. De Michele, Eur. Phys. J. E: Soft Matter Biol. Phys., 2015, 38, 81 CrossRef PubMed.
- E. S. Minina, E. S. Pyanzina, E. V. Novak and S. S. Kantorovich, Eur. Phys. J. E: Soft Matter Biol. Phys., 2018, 41, 67 CrossRef.
- A. Ivanov, S. Kantorovich, L. Rovigatti, J. Tavares and F. Sciortino, J. Magn. Magn. Mater., 2015, 383, 272–276 CrossRef CAS.
- J. Russo, J. M. Tavares, P. I. C. Teixeira, M. M. Telo da Gama and F. Sciortino, Phys. Rev. Lett., 2011, 106, 085703 CrossRef CAS.
- L. Rovigatti, J. M. Tavares and F. Sciortino, Phys. Rev. Lett., 2013, 111, 168302 CrossRef.
- L. Rovigatti, S. Kantorovich, A. O. Ivanov, J. M. Tavares and F. Sciortino, J. Chem. Phys., 2013, 139, 134901 CrossRef.
- W. Lechner and C. Dellago, J. Chem. Phys., 2008, 129, 114707 CrossRef PubMed.
- V. S. Mendelev and A. O. Ivanov, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 051502 CrossRef.
- F. Weik, R. Weeber, K. Szuttor, K. Breitsprecher, J. de Graaf, M. Kuron, J. Landsgesell, H. Menke, D. Sean and C. Holm, Eur. Phys. J.: Spec. Top., 2019, 227, 1789–1816 Search PubMed.
- J. J. Cerdà, V. Ballenegger, O. Lenz and C. Holm, J. Chem. Phys., 2008, 129, 234104 CrossRef PubMed.
| This journal is © the Owner Societies 2023 |