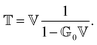Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Perspectives on weak interactions in complex materials at different length scales
J.
Fiedler
 *a,
K.
Berland
*a,
K.
Berland
 b,
J. W.
Borchert
c,
R. W.
Corkery
d,
A.
Eisfeld
e,
D.
Gelbwaser-Klimovsky
f,
M. M.
Greve
a,
B.
Holst
b,
J. W.
Borchert
c,
R. W.
Corkery
d,
A.
Eisfeld
e,
D.
Gelbwaser-Klimovsky
f,
M. M.
Greve
a,
B.
Holst
 a,
K.
Jacobs
gh,
M.
Krüger
i,
D. F.
Parsons
a,
K.
Jacobs
gh,
M.
Krüger
i,
D. F.
Parsons
 j,
C.
Persson
j,
C.
Persson
 kl,
M.
Presselt
kl,
M.
Presselt
 m,
T.
Reisinger
m,
T.
Reisinger
 n,
S.
Scheel
n,
S.
Scheel
 o,
F.
Stienkemeier
o,
F.
Stienkemeier
 p,
M.
Tømterud
p,
M.
Tømterud
 a,
M.
Walter
a,
M.
Walter
 p,
R. T.
Weitz
p,
R. T.
Weitz
 c and
J.
Zalieckas
a
c and
J.
Zalieckas
a
aDepartment of Physics and Technology, University of Bergen, Allégaten 55, 5007 Bergen, Norway. E-mail: johannes.fiedler@uib.no
bDepartment of Mechanical Engineering and Technology Management, Norwegian University of Life Sciences, Campus Ås Universitetstunet 3, 1430 Ås, Norway
c1st Institute of Physics, Georg-August-University, Göttingen, Germany
dSurface and Corrosion Science, Department of Chemistry, KTH Royal Institute of Technology, SE 100 44 Stockholm, Sweden
eMax-Planck-Institut für Physik komplexer Systeme, Nöthnitzer Strasse 38, 01187 Dresden, Germany
fSchulich Faculty of Chemistry and Helen Diller Quantum Center, Technion-Israel Institute of Technology, Haifa 3200003, Israel
gExperimental Physics, Saarland University, Center for Biophysics, 66123 Saarbrücken, Germany
hMax Planck School Matter to Life, 69120 Heidelberg, Germany
iInstitute for Theoretical Physics, Georg-August-Universität Göttingen, 37073 Göttingen, Germany
jDepartment of Chemical and Geological Sciences, University of Cagliari, Cittadella Universitaria, 09042 Monserrato, CA, Italy
kCentre for Materials Science and Nanotechnology, University of Oslo, P. O. Box 1048 Blindern, 0316 Oslo, Norway
lDepartment of Materials Science and Engineering, KTH Royal Institute of Technology, 100 44 Stockholm, Sweden
mLeibniz Institute of Photonic Technology (IPHT), Albert-Einstein-Str. 9, 07745 Jena, Germany
nInstitute for Quantum Materials and Technologies, Karlsruhe Institute of Technology, 76344 Eggenstein-Leopoldshafen, Germany
oInstitute of Physics, University of Rostock, Albert-Einstein-Str. 23-24, 18059 Rostock, Germany
pInstitute of Physics, University of Freiburg, Hermann-Herder-Str. 3, 79104 Freiburg, Germany
First published on 15th November 2022
Abstract
Nanocomposite materials consist of nanometer-sized quantum objects such as atoms, molecules, voids or nanoparticles embedded in a host material. These quantum objects can be exploited as a super-structure, which can be designed to create material properties targeted for specific applications. For electromagnetism, such targeted properties include field enhancements around the bandgap of a semiconductor used for solar cells, directional decay in topological insulators, high kinetic inductance in superconducting circuits, and many more. Despite very different application areas, all of these properties are united by the common aim of exploiting collective interaction effects between quantum objects. The literature on the topic spreads over very many different disciplines and scientific communities. In this review, we present a cross-disciplinary overview of different approaches for the creation, analysis and theoretical description of nanocomposites with applications related to electromagnetic properties.
1 Introduction
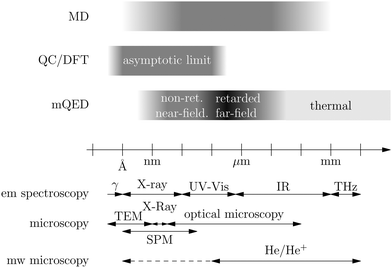
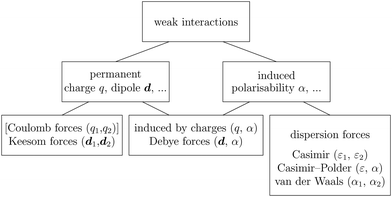
Recent investigations on novel materials such as solar cells,1 especially on the photoexcitation-driven processes in such systems,2,3 aim to increase the efficiency of organic solar cells,4,5 for instance, by exploiting concepts such as singlet fission, the decay from a singlet excitation into two triplet excitations of lower energy. Further applications in organic photovoltaics,6 optoelectronic devices,7,8 quantum circuits,9,10 and quantum computers11 are related to the study of interactions that are weaker than covalent bonding, ranging from non-covalent bonding in supermolecular complexes12–14 to long-range electrostatic and Casimir forces governing the formation of colloids.15 While such “weak” interactions (not to be confused with the weak fundamental force governing lepton decay) are often studied in separate fields of science. These investigations often demand an interdisciplinary approach where methods and approaches of different fields must be combined. However, in using a method beyond the domain it was developed for, one needs to be acutely aware of the various often implicit approximations involved. Moreover, bridging methods developed for different length scales without double counting require an understanding of which physical mechanisms are captured at different length scales. Thus to make progress, a birds-eye view of the different methods employed to describe long-range interactions in a complex matter is acutely needed. The task of these investigations can be summarised by finding the relationship between the microscopic properties of systems and the resulting macroscopic effect. In other words, the microscopic properties are propagated to larger macroscopic scales. Different theoretical techniques, given in Fig. 1, have been developed to address this issue. While methods that are fully quantum (such as quantum chemistry or density functional theory) are restricted to small systems with a limited number of electrons, classical force field-based molecular dynamics (MD) simulations can treat systems consisting of a large number of molecules. An alternative to MD simulations is the quantum optical methods, in particular macroscopic quantum electrodynamics (mQED). This method considers the coupling of quantised objects via quantised fields. For this reason, it provides a higher accuracy but it does not predict single-particle responses. These properties are input parameters of this theory which provides their propagation to larger systems. Described as propagating electromagnetic waves, the relevant length scales provide different regimes: the non-retarded regime at small separations, where the finite speed of light does not matter; the retarded regime at larger lengths scales, where retardation effects of the propagating electromagnetic waves play the major role, and the thermal limit, where the interaction is driven by the thermal radiation at the specific system's temperature.The wide range of applications also reflects the broad range of researchers investigating these systems, from physicists to physicians and chemists to biochemists. This variety causes several issues in the communication between the different researchers due to the differently used nomenclatures and notations. One problematic phrase is “weak interactions”, which cannot be defined by giving a particular energy threshold under which the interactions are weak and above which they are strong. In Fig. 2, a systematic scheme is presented covering the range of weak interactions based on the type of the interacting constituents in line with the traditional chemical view16 apart from the further distinction of induced forces concerning macroscopic (bulk) responses, such as the dielectric function ε. Traditionally, one restricts the dispersion forces to be induced by microscopic polarisable objects leading to the van der Waals (vdW) force. For this reason, one often denominates this class by vdW forces and includes the interactions with dielectric bodies. Nowadays, several researchers denote the entire field of weak interactions by vdW interaction, especially in chemistry and colloidal science. From the quantum-optical point of view, this makes sense by applying the electrostatic limit to the dispersive interactions.17 In contrast, in soft-matter physics, the traditional distinction is strictly considered, and the asymptotic transitions from induced to static interactions are neglected. An overview of the denominations within the different communities is presented in Table 2. In quantum chemistry, the binding between two particles is typically considered, which leads to the phrase “non-covalent” for weak interactions. Concerning non-covalent bonding, ionic and hydrogen bonds belong to the weak interactions, see Fig. 2, as well, but will not be considered explicitly within this review.
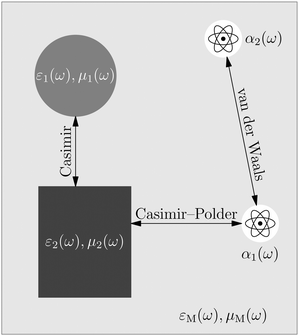
The phrase “dispersion forces” traces back to the application of the dispersion relation 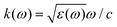 to take into account the finite speed of light c within a macroscopic medium. In contrast to the traditionally applied chemical distinction with the restriction to polarisable objects, the consideration of dispersion forces in the quantum-optical framework yields the distinction between the size of the considered objects which can be microscopic polarisable objects or macroscopic dielectric bodies. The resulting distinction between the different interactions is summarised in Table 1, which denotes the Casimir force interacting between two dielectric objects; the Casimir–Polder force between a dielectric body and a polarisable object; and the vdW force between two polarisable objects. These three forces built a hierarchical system: by considering two solid objects the Casimir force between both can be obtained; by applying the dilute limit to one of them, one reaches the Casimir–Polder force; by applying the dilute limit to both objects, the vdW force will remain. This transition is not reversible, in general. By increasing the density of particles, further interactions will play a role which can not be mapped by a simple up-scaling. For weak responding materials, the Clausius–Mossotti relation
to take into account the finite speed of light c within a macroscopic medium. In contrast to the traditionally applied chemical distinction with the restriction to polarisable objects, the consideration of dispersion forces in the quantum-optical framework yields the distinction between the size of the considered objects which can be microscopic polarisable objects or macroscopic dielectric bodies. The resulting distinction between the different interactions is summarised in Table 1, which denotes the Casimir force interacting between two dielectric objects; the Casimir–Polder force between a dielectric body and a polarisable object; and the vdW force between two polarisable objects. These three forces built a hierarchical system: by considering two solid objects the Casimir force between both can be obtained; by applying the dilute limit to one of them, one reaches the Casimir–Polder force; by applying the dilute limit to both objects, the vdW force will remain. This transition is not reversible, in general. By increasing the density of particles, further interactions will play a role which can not be mapped by a simple up-scaling. For weak responding materials, the Clausius–Mossotti relation
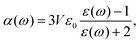 | (1) |
![[B with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0042_0302.gif) , respectively, and the quantised charge density
, respectively, and the quantised charge density ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) and current ĵ; the Casimir–Polder interaction as second-order perturbation (index 2 on the expectation value: 〈…〉2) of the dipole interaction with the particle's dipole operator
and current ĵ; the Casimir–Polder interaction as second-order perturbation (index 2 on the expectation value: 〈…〉2) of the dipole interaction with the particle's dipole operator ![[d with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0064_0302.gif) and the dressed electromagnetic field Ê at the position of the particle; and the van der Waals interaction as fourth-order perturbation (index 4 on the expectation value: 〈…〉4) of the dipole interaction. Details are described in Section 4.4.1
and the dressed electromagnetic field Ê at the position of the particle; and the van der Waals interaction as fourth-order perturbation (index 4 on the expectation value: 〈…〉4) of the dipole interaction. Details are described in Section 4.4.1
| Dispersion interaction | Origin |
|---|---|
| Casimir force | 〈![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) Ê + ĵ × Ê + ĵ × ![[B with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0042_0302.gif) 〉 〉 |
| Casimir–Polder force | 〈![[d with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0064_0302.gif) ·Ê〉2 ·Ê〉2 |
| van der Waals force | 〈![[d with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0064_0302.gif) 1·Ê(r1) + 1·Ê(r1) + ![[d with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0064_0302.gif) 2·Ê(r2)〉4 2·Ê(r2)〉4 |
| Particle 1 | Particle 2 | Quantum optics | Traditional chemistry | Soft-matter | Statistics | Modern chemistry |
|---|---|---|---|---|---|---|
| Charge q1 | Charge q2 | Coulomb interaction | ||||
| Dipole d1 | Dipole d2 | Keesom interaction | ||||
| Dipole d | Polarisability α | Debye interaction | van der Waals interaction | |||
| Neutral | Neutral | Dispersion interaction | van der Waals interaction | |||
| Polarisability α1 | Polarisability α2 | |||||
| Non-retarded | van der Waals interaction | van der Waals interaction | ||||
| Retarded | Casimir–Polder–van-der-Waals | |||||
| Polarisability α | Permittivity ε | |||||
| Non-retarded | Casimir–Polder | Molecular Lifshitz | ||||
| Retarded | Casimir–Polder–Lifshitz | |||||
| Permittivity ε1 | Permittivity ε2 | |||||
| Non-retarded | Casimir | Casimir–Lifshitz | ||||
| Retarded | Casimir–Polder–Lifshitz | |||||
| Perfect conductors | Casimir | |||||
As discussed in the beginning, weak interactions are covered by a wide range of research and give rise to several devices and functional materials. In the following, we want to introduce recent investigations related to weak interaction studies, covering the application side with the topics of materials and devices; an introduction to relevant characterisation techniques; and an introduction to the most-important theoretical methods describing these materials and effects. We concentrate on ground-state interactions and illustrate partly the treatment of excitations. This review does not provide a comprehensive overview which would quickly fill several books. Instead, we concentrate on the most-relevant effects, experiments and current theoretical methods.
2 Devices and materials
As introduced above, materials and devices in the context of weak interactions can generally be described as a many-particle effect due to weak interactions, such as atomic clouds, an ensemble of molecules or small clusters, either in a vacuum or in the presence of dielectric solid or liquid surfaces, or the presence of external electromagnetic fields. The most-relevant effects in such systems are the self-organisation near surfaces, leading to vdW heterostructures (Section 2.2), the excitation dynamics, such as superradiance and singlet fission (Section 2.1) and the Rabi oscillations in the strong coupling regime (Section 2.6). The latter occurs by confining the optical mode density for the weak interactions leading to substantial field enhancements. Furthermore, several practical devices result from these interactions, namely solar cells (Section 2.4), especially organic photovoltaics and top and bottom layers, enhancing the efficiency, electrochemical transistors (Section 2.3), nano- and micro-electro-mechanical systems (Section 2.5). Further related topics are due to quantum dots, especially in the context of quantum sensing23 and quantum computing.242.1 Interactions and organisation on surfaces
In order to isolate weak interactions, ideally one would like to establish experimental conditions without perturbations from a strongly-interacting environment. Furthermore, having weak interactions and corresponding shallow binding potentials, the competition with thermal energies often requires low-temperature conditions in order to reach state specificity and selective probing. Rare-gas clusters, travelling as isolated cluster beams in a vacuum, have been demonstrated to serve as versatile laboratories for the study of weakly-interacting molecular systems.3,25,26 Technically such clusters having nanometre-sized dimension are condensed in a supersonic expansion from high pressure and mostly cold (down to 3 K) reservoirs. Evaporative cooling of the weakly bound rare gases leads to cluster temperatures ranging from several tens of Kelvin for e.g. argon or neon,27 down to 400 mK/150 mK in the case of helium-4/helium-3 isotopes.28,29The clusters can be doped with atoms or molecules of interest by the so-called pickup technique, whereupon sticky collision dopants are attached to the clusters. The number of dopants can be controlled by the pressure in designated vapour cells. Putting such doping units in series along the cluster beam path allows in a well-controlled order an assembly of dopants on the clusters. Whereas helium clusters are liquid, allowing an agglomeration of dopants inside the clusters, all other larger rare-gas clusters are in a solid state. Aromatic molecules, as discussed in the following, are pinned to the surface of these clusters and do even on electronic excitation not migrate to interact with other dopants.26 By varying the dopant density at statistical low coverage, one can probe weak interactions as a function of the mean intermolecular distance. Here, we want to discuss a prime example of interacting acene molecules. Acenes are of applied interest as absorbers in organic photovoltaics and, in particular, exploiting collective effects by means of singlet fission (SF) has been identified as an alternative route for an increased efficiency converting absorbed photons into separated charges,30,31 applied in solar cells, see Section 2.4.
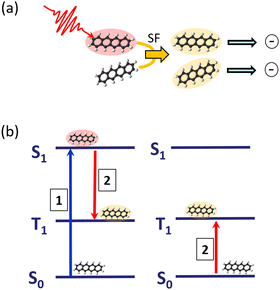
The process of SF is illustrated in Fig. 3: an absorbed photon leading to an electronically-excited singlet state, which would undergo fluorescence emission in an isolated molecule, can, communicated by the interaction with a neighbouring molecule, transfer the excitation energy into two triplet states, localised on two molecules. Having now two excited molecules can in turn with an appropriate charge separation mechanism lead to the generation of two charges, having only one photon absorbed in the first place. In this way, one is in principle even able to overcome the Shockley–Queisser efficiency limit,32 acting as the ultimate upper bound for efficient energy conversion.
Tetracene and pentacene molecules are typical examples of having a suitable energy structure of singlet and triplet states enabling SF. By attaching these molecules to the surface of rare-gas clusters, it was demonstrated that SF is even active at dilute conditions with very weak intermolecular interaction.2,33
In Fig. 4(a), the measured lifetime of tetracene molecules attached to neon clusters is plotted as a function of the mean intermolecular distance. Whereas at larger distances there is only a slight reduction due to Dicke superradiance, below approximately 30 Å one observes a steep decrease due to SF, reducing the lifetime down to only a few nanoseconds. The assignment to SF and superradiance, respectively, as evidenced by pump–probe schemes and power dependencies and accompanying theoretical simulations.2 Intriguingly the interaction is so weak that it can not be identified in the spectroscopy of the excited system [perturbation of the spectra, cf.Fig. 4(b)].
 | ||
| Fig. 4 (a) Lifetime of excited tetracene molecules attached to the surface of neon clusters as a function of the mean internuclear distance given by the surface coverage. At low coverage, only superradiance leads to a reduction of a lifetime; the prominent reduction at increased coverage is due to singlet fission. (b) Laser-induced fluorescence excitation spectra of the 000 excitation, and the first prominent vibrational mode at low and high coverage, respectively. nTc denotes the mean number of tetracene molecules attached to the cluster. Within the cluster-induced broadening, no perturbation from the interaction of the molecules can be identified, based on data from ref. 33. | ||
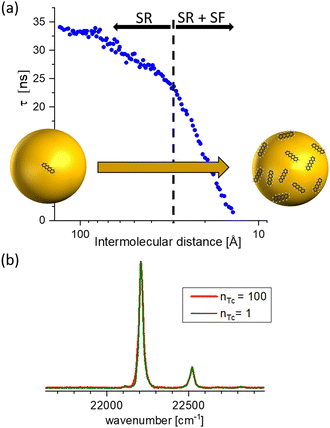
Furthermore, the interaction with the surface can be studied in these experiments. In comparison with DFT, described in Section 4.3, calculations for pentacene molecules attached to neon clusters, vibrationally resolved spectra clearly identify active low-frequency butterfly vibrations from the interactions with the rare-gas surface.34 Moreover, the weak interaction can even induce perturbations in the organic structure of the molecules leading to suppressed or completely altered decay mechanisms. Such effects are, for instances, capable via mQED (Section 4.4) or modelling aggregate structures (Section 4.6). As an example in Fig. 5 anthracene molecules are probed as a function of the mean inter-molecular distance on neon and argon clusters, respectively. Since in the case of neon a significantly decreased lifetime at smaller inter-molecular distances has been observed, for argon, the lifetime of the excited state is increasing.35
 | ||
| Fig. 5 Comparison of the coverage-dependent lifetime reduction of the first excited singlet state of anthracene molecules attached to Ne and Ar clusters, respectively. The weak perturbation from the interaction with the rare gas leads for Ne to a reduction at high coverage, whereas for Ar the lifetime is increased. Based on data from ref. 35. | ||
Besides rare gas clusters also other dielectric surfaces only weakly perturb the optical properties of molecules deposited on the surface,36,37 see Section 4.4.1. Such molecule surface structures can for example be produced by epitaxial growth in an ultra-high vacuum. Typically one can vary the surface density of the molecules over orders of magnitude from very low coverage to full monolayers. It is often possible to use the surface as a template to induce a specific regular arrangement of the molecules,36,38,39 which can be probed by atomic force microscopy (AFM) or scanning tunnelling microscopy (STM), see Section 3.1. Similar to the situation of rage gas clusters one can perform optical far-field spectroscopy. In addition, one can also use various near-field techniques to gain information on these samples.40–44 It is also possible to change the temperature of the sample from a few Kelvin up to room temperature and above. This allows one, for example, to study the temperature dependence of superradiance.45
Another example, where dispersion forces play a major role, is the interaction between nanodiamonds (NDs). Typically, 4–5 nm NDs tend to self-assemble into larger aggregates either in the liquid phase or during drying. In the latter case, agglomeration during drying makes ND functionalisation difficult since it often requires a dry starting ND material.46 In the liquid phase, DFT computations in conjunction with Monte Carlo molecular simulations show that assembly interactions between ND particles are dominated by vdW forces rather than electrostatic forces.47 Therefore, dispersion forces between ND particles or ND and surfaces should be considered carefully in experimental or theoretical investigations. For example, it has been demonstrated that fluorescent NDs tethered by double-stranded DNA to a surface can be used as an ultrasensitive label for in vitro diagnostics.48 Consideration of weak interactions for such systems is expected to improve experiment settings and yield better sensitivities.
2.2 van der Waals heterostructures
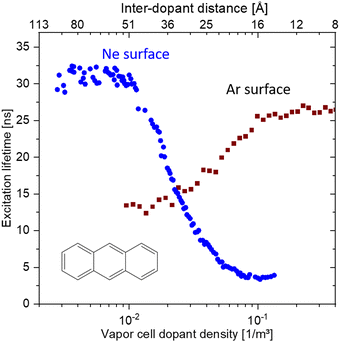
It has been long known that the weak short-range vdW interaction holds together layered materials like graphite and MoS2. The vdW force is weak enough to allow easy sliding of the individual layers against each other such that graphite and MoS2 have been long established as dry lubricants. The weak interaction between graphene layers has also been the reason why graphite (in the form of highly oriented pyrolytic graphite, HOPG) has been used as a substrate for scanning probe microscopy: simply by mechanical cleavage by scotch tape, a HOPG crystal fresh surface could be prepared.49 More recently, it has been realised, that this mechanical cleavage can be used to prepare monolayers of such vdW materials, with graphene being the first one subsequently jump-starting the field of novel 2D materials.50,51While initially mainly monolayers of graphene and other 2D materials had been isolated, it soon was realised that also disjunct materials can be stacked on top of one another. A breakthrough study in this regard had been the work by Dean et al.52 where for the first time, graphene was placed onto h-BN (which is a large-bandgap insulator synthesised in highest quality, e.g., by the group of T. Taniguchi and K. Watanabe53) to form a vdW heterostructure. The cleanliness of graphene was significantly improved in this heterostructure (as can be for example quantified by a threefold increase of the charge carrier mobility) due to the atomic flatness and absence of defects of h-BN (see Fig. 6).54 Recently, h-BN has been also used as an inert substrate for other materials, e.g., organic semiconductors.55
 | ||
| Fig. 6 Supporting graphene on hexagonal boron nitride (BN) substrates. (a) Schematic showing how the graphene is transferred onto multilayer BN, which is supported on a SiO2 substrate, with a stamping technique. (b) A single piece of graphene (red) is supported by a SiO2 substrate (left) and a flat BN multilayer (right). The corrugations, dangling bonds (inside a dashed circle) and charge inhomogeneities that are inherent to SiO2 surfaces shift and broaden the resistivity peak of graphene (black line in plot) relative to that of graphene on BN (blue line). Figure taken from ref. 54. | ||
This first h-BN-graphene heterostructure already makes the distinction to multilayers of materials grown by conventional vapour deposition methods (e.g. molecular beam epitaxy, MBE) clear, in which layers of disjunct materials are connected by covalent bonds and where interfacial lattice matching and defects have to be carefully managed. Consequently, the growth of such materials is done in an ultrahigh vacuum.56 The weak vdW interaction, however, has a consequence of the resulting layer arrangements not being as stable as e.g. MBE grown heterostructures. For example, it was shown that strain can lead to a transformation of the rhombohedral to Bernal stacking in graphene multilayers.57,58 Nevertheless, the assembly of the wide range of 2D materials (more than 1000 unique 2D materials have been predicted to exist59) can be in principle performed under ambient conditions using stamping methods, by which the to-be-assembled materials are picked up sequentially using piezo-controlled stamps and placed on top of one another.60 Like these heterostructures of arbitrary (that is independent of lattice matching conditions required e.g. required for epitaxy) vdW materials can be realised. The resulting interfaces turn out to be very clean due to the so-called “self-cleaning” properties of the materials since often the vdW forces between the to-be-assembled materials turn out to be larger than between that of individual vdW materials and contaminants (typically hydrocarbons).60,61 This cleaning process can also artificially be initiated with an AFM tip and the self-cleaning imaged in real-time (termed hydrophobic collapse here).62
The vdW assembly method offers the exciting possibility to design complex materials on demand by coupling disjunct materials that interact via a Moiré potential creating a superlattice,63 tunnelling,64 spin–orbit interaction65 just to name a few. The coupling can have an impact on the spin degree of freedom, resulting in bandstructure, weakened exchange66,67 and magnetic properties. One exciting advancement recently known is that if materials of the same type (e.g. two layers of graphene) are twisted by an angle of 1.1° with respect to one another, due to interlayer coupling the bandstructure of the individual graphene layers is modified due to the Moirè potential formed. This leads to a flattening of the band structure and the formation of minibands at the Dirac point with the subsequent observation of correlated phases and unconventional superconductivity.68,69
When assembling individual quantum objects into monolayers or their stacks, the material properties are determined by the interactions of the quantum objects with each other70 (see Section 4.6 for predicting such interactions) within the individual layers as well as with the surface, possibly the matrix,71,72 and possibly the cavity73,74 surrounding the quantum objects. In order to tailor the material properties, various experimental techniques have been developed that allow the arrangement of quantum objects, for example, DNA origami75–77 or the Langmuir–Blodgett (LB) and related techniques.78–81
Using DNA origami, quantum objects can be arranged with sub-nanometre precision, for which they are covalently bonded to the DNA scaffold.75–77 Since the resulting arrangements do not interact via vdW forces alone, but initial work has been initiated to develop current small arrangements towards (vdW) heterostructure materials, they are briefly mentioned in this chapter.82 Both DNA origami objects, but especially quantum dots and dyes, have been processed by Langmuir–Blodgett and related techniques into thin films or layered structures that interact within and between layers via vdW forces. To do this, for example, typically water-insoluble dyes in solution are applied in small concentrations to a water surface, and the surface concentration is increased by decreasing the available water surface area until a close-packed monolayer is formed, which is tracked via interfacial pressure. Recently, it was demonstrated how the LB technique can also be used to process water-soluble dyes.
In the case of dyes, their arrangement in the monolayer determines the interactions between the transition dipole moments (TDMs, see Section 3.4) of the dyes and thus the optical and electronic properties of the resulting films.70 The arrangement is determined by the position of the dyes at the water–air interface and the intermolecular interactions, which are studied by molecular dynamics, and force-field-based, and density functional theory methods (see Section 4.3). In addition, the intermolecular interactions can be affected by embedding the dyes in Langmuir matrices.71,72 Variation in optical properties with differences in supramolecular structure ranges from spectral shifts due to interactions between TDMs,83–91 to optical anisotropy,92 variation in oscillator strengths due to symmetry breaking,71,93–96 and the expression of vibronic fine structures84,88,97–99 in the optical spectra. At intermediate distances 2D materials also offer interesting phenomena related to Casimir interactions,100 as discussed in Section 4.1.
2.3 Electrochemical transistors
While the role of the Casimir–Polder force in the interaction between ions has been described (see Section 4.2.2), a field in which weak interactions have not been considered widely in the field of electrolyte gating in (organic) field-effect transistors. While focusing here on organic polymer semiconductors, the difference between electrostatic and electrolyte gating is, that while in electrostatic gating a purely electrostatic field leads to the accumulation of charges in the semiconductor, in the case of electrolyte gating a liquid electrolyte is placed on the semiconductor and upon application of a voltage difference between the electrolyte and the semiconductor, ions move toward the semiconductor.101 Then, depending on the materials used the ions can either form a double layer at the liquid/semiconductor interface (called electrostatic gating then as well), or penetrate into the semiconductor (called electrochemical doping).102 With this method, thin organic semiconducting films but also semiconducting polymers between contacts separated only a few nm can be gated and thus operated as transistors with ultrahigh performance ratios103 or be used as neuromorphic devices.104,105 The current flow in such organic electrochemical transistors has also been recently modelled by introducing the movement of the ions in the polymer by the steady-state Nernst–Planck equation and solved numerically.106 However, the role of the Casimir–Polder interaction has not been included and might be an interesting extension of further work.2.4 Solar cells
An important field for possible applications is photovoltaic energy generation. A multitude of recent solar cell concepts compete with each other: the prevalent crystalline silicon cells, single-junction GaAs or multi-junction cells, thin-film technologies such as CdTe and CIGS, and other emerging photovoltaic concepts such as organic solar cells or ones based on perovskite structured materials.5 Their common denominator is the use of irradiance from the solar spectrum to generate electric current. To this end, most solar cells rely on an active layer which has the function of photon absorption and subsequent generation of excitons (usually bound electron–hole pairs). The main challenge is to maximise efficiency, utilising the largest possible part of the solar spectrum, while keeping the fabrication costs as low as possible, which remains the ultimate challenge despite significant advances in the last decade. Multi-junction solar cells have the absolute highest efficiencies with the current record of 39.2% under one sun conditions.107 However, to achieve this, a six-junction cell was designed and fabricated – exemplifying the complexity and consequently the cost of such cells. Therefore, there is a prevailing interest in single-junction cells and methods for enhancing their efficiency. Commonly, the maximum efficiency of any single junction cell is estimated using the infamous Schockley–Queisser limit, which as a first approach is an adequate description. For an ideal band-gap (1.3 eV) cell the upper limit efficiency is around 32%.108 The limit is met by three loss mechanisms: (1) non-absorbed photons (limitation in photon absorption (intrinsic), reflection losses (extrinsic), (2) thermalisation of excited charge carriers (photon/band-gap miss match), and (3) electronic losses through recombination and ohmic losses.109 The main energy losses are found in the first two categories above. For the first point, traditional and effective methods, use randomised texturing of the sample surface and simple single-layer anti-reflective coatings for maximising the light entering the cell. Using a Lambertian scatterer model for light trapping schemes, the upper light absorption enhancement limit is 4n2 compared to single pass absorption, where n is the refractive index of the material.110Using an electromagnetic approach, however, which is necessary to describe sub-wavelength, nano-photonic systems, it has been shown by several research groups that it is possible to increase the light trapping significantly beyond the 4n2 limit,111–113 and also demonstrated experimentally.114
With the goal of pushing the efficiency further, light trapping using sub-wavelength structures has been pursued by many research groups, and a wide range of promising nano-structured elements have been investigated such as nano-wires, nano-pillars, upright and inverted nano-pyramids, photonic-crystal-based structures,110,115–117 and organic molecules, as described in Section 2.1 Common for all these nano-structure examples is that typically several nano-lithography steps are needed for the fabrication, a process which significantly complicates the fabrication and consequently limits widespread application. Therefore, another promising nano-structure for solar cell applications is metal nanoparticles (MNPs).118 The main interest for using MNP in solar applications lies in the strong and tunable light scattering and absorption properties through the localised surface plasmon resonance (LSPR), describable for instance via mQED, see Section 4.4. However, the fabrication of MNP is also widely established for a large selection of materials including methods for direct deposition without complex lithography steps, which speaks for scalability.119
For solar applications MNPs are typically proposed: (1) placed on the front surface for increased light scattering and consequently light in-coupling into the active layer; (2) embedded in the active layer for increased optical density through light scattering and near-field effects; (3) on the back surface of the active layer for coupling light not absorbed in the single pass of the active layer to surface plasmon polaritons.120,121
The addition of MNPs to the front of solar cells is perhaps the simplest configuration and has been investigated by several research groups.122–124 In particular, metals such as Au and Ag have been investigated due to their strong plasmonic activity in the visible spectrum. Larger nanoparticles (>30 nm) are typically employed as these have a strong light-scattering component. Promising results for improvements in light incoupling and consequently photocurrent have been demonstrated, but improvements have typically been limited to the longer wavelength ranges. At shorter wavelengths, negative contributions have been reported due to parasitic light absorption of the MNPs. Parasitic light absorption has been a challenge for obtaining excellent broad-band results. It is caused by MNPs used in general exhibiting an increased light absorption at shorter wavelengths, but also electron inter-band transitions in the metals.125–127 These parasitic losses can potentially be omitted by exploring other materials, and recently Al nanoparticles have gained attention. With the plasmon resonance in the UV range, the light absorption losses are minimised, and mainly scattering effects are found in the visible range making them a promising candidate for wide range and efficient light incoupling.128–130
For MNPs with a diameter below 30 nm, far-field scattering will be reduced, and the plasmon interaction will be dominated by near-field effects.130 Small particles embedded in the active layer have been investigated for enhancing light absorption for both organic solar cells and inorganic solar cells (a-Si).131,132 Increased light absorption can allow for decreased active layer thicknesses, which in turn would raise the theoretical efficiency limit and yield higher solar cell efficiencies as the charge carrier recombination would be lowered.133 Theoretical predictions have shown that by using small Ag nanoparticles, a conversion efficiency of 18% with only a 15 nm active layer (a-Si) is possible.131
The final approach is to increase the optical path length of light not absorbed in a single pass of the active layer, reaching the back surface plane of the active layer to surface plasmon polaritons (SPPs). SPPs are charge density waves propagating parallel to the back metal/semiconductor interface and are strongly confined once excited and can propagate several micrometres with a minimal loss.134 Due to the momentum mismatch between incident light and the in-plane SPPs methods for efficient coupling need to be employed. Using a periodic grating structure allows an efficient way for coupling incident radiation to SPP modes.135 Theoretical studies have demonstrated significantly enhanced absorption enhancement by coupling light to SPP.134 Furthermore, several nanograting structures such as nano-dents, nano-voids, nano-wires and nano-cones have been realised experimentally and noticeable improvement has been reported, and the overall trend is that efficiency on average is improved 1–2%.136–139 The complicated nano-structuring has so far limited these studies to a-Si solar cells.
2.5 MEMS and NEMS
MEMS and NEMS (micro and nano electromechanical systems), sometimes referred to as micromachines or microsystem technology (MST), are defined as devices which include one or more micro/nano scale parts enhancing functionality.They are often silicon based, but can also be made of other materials such as quartz, silicon carbide, sapphire and aluminium nitride, as well as polymers140 (particularly relevant for microfluidic-related applications). Recently, there has been a focus on the application of vdW heterostructure materials for NEMS applications,141,142 see also Section 2.2. NEMS can also include components such as nanotubes, nanodots and nanowires. MEMS/NEMS are of significant industrial importance, with an annual market of around 100 million dollars for NEMS alone according to various market reports.
MEMS/NEMS devices can be divided into sensors, actuators and what may be termed passive structures. Sensors include gyroscopes, accelerometers and pressure sensors (extensively used in the automotive industry) and various medical and biochemical diagnostic devices. Actuators include data storage, drug-delivery devices, drug synthesis, fluid regulators, ink-jet printing devices, micro fuel cells, micro-mirror devices, microphones, optoelectric devices, radio-frequency devices and surgical devices and finally passive structures such as atomisers, fluid spray systems, fuel injection, and medical inhalers.143
As the dimensions of a system reduce so that the surface-to-volume ratio increases, dispersion forces start to play a role and so it is no surprise that they are crucial in determining the behaviour of in particular a range of NEMS devices. In fact around a decade ago, Casimir forces were seen as a potential obstacle to useful NEMS devices. For example, it was pointed out that at a separation of 10 nm the Casimir force can produce the equivalent of one-atmosphere pressure,144 see also ref. 145. It has been shown both experimentally and theoretically that Casimir and vdW forces have a huge effect on the instability of nano-cantilevers, leading to the so-called snap-down (pull-in) behaviour initiated by electrostatic actuation or mechanical shock.146 The pull-in behaviour occurs when the electrostatic force exceeds the elastic resistance of the beam, which “pulls in” and suddenly adheres to the ground.147 In general, stiction (adhesion) is a big challenge for NEMS devices. The situation is complicated by the fact that for small distances (in the 100 nm range) the surface roughness starts to play a role.148 Theoretical models via mQED, see Section 4.4 quantise the forces and help in improving such systems.149
It has been reported on numerous occasions that 2D materials tend to roll up and form stable scrolls. This is an undesired effect in device fabrication, but it can be used also for nanowires and/or mechanical structures. The roll-up process is governed by a competition between vdW forces and elastic forces.150
With the expansion in the technological possibilities for device fabrication, the focus in NEMS development is shifting towards exploiting the dispersion forces actively as an integrated part of the NEMS devices.151 It should be pointed out, however, that this is not a completely new idea, for example, the Casimir-induced sensitivity to small changes in distances was exploited in actuators already two decades ago.152
2.6 Strong coupling
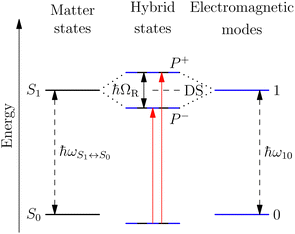
A striking phenomenon occurs when bringing a material in close proximity to an optical microresonator with electromagnetic modes of similar energies to the material's energetic (e.g. vibrational, electronic) transitions governed by weak (e.g. dipole–dipole) interactions. When the system is properly tuned (depicted schematically in Fig. 7), the resulting interaction between weak resonant dipole modes with the electromagnetic modes can become strong enough to generate a population of pairs of more strongly-interacting hybrid light-matter states within the material, which are then occupied with quasiparticles called ‘polaritons’. This relatively simple concept forms the basis of the rapidly-growing body of experimental work in the field of polaritonics encompassing both fundamental and practical studies in chemistry, physics, and materials science.153–155A detailed theoretical treatment of the quantum electrodynamics of strongly coupled systems is discussed in more detail in Section 4.5. In brief, to facilitate discussions of the experimental work within this section, the polaritonic-state formation can be described as a first approximation by a coupled oscillator model, wherein the strength of the light–matter interaction is indicated by the energy separating the upper and lower hybrid states (P+ and P−, respectively) with a characteristic Rabi-splitting frequency
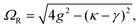 | (2) |
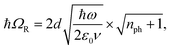 | (3) |
What has started out as a model quantum optics system where intraatomic transitions have been coupled to cavities156 has been expanded to the diverse fields of solid-state physics, chemistry and materials science.155 A multitude of various device physics and potential applications have now been investigated (Fig. 8a–c), including organic polariton transistors,157 enhanced light-emitting transistors using exciton–polaritons in carbon nanotubes158 and semiconducting polymers,159 inversion of singlet and triplet excited states in organic chromophores to enhance quantum efficiency in organic light-emitting diodes,160 enhancement of ferromagnetism in high-temperature superconductors,161 modifications of the integer quantum Hall effect,162 graphene polaritonics,163,164 and increased charge-carrier transport in e.g. organic semiconductors165,166 and transition metal dichalchogenides.167 This latter effect, in particular, introduces both an interesting platform for fundamental studies in charge transport and potentially opens a route towards transistors based on diverse materials that are more efficient. Transport enhancement has been attributed so far to the promotion of greater delocalisation of charge carriers by virtue of the opening of additional bands in a coupled two-level system.168 However, development of a comprehensive understanding of the parameters that determine whether or not enhanced transport is realised in a given system is ongoing and will need to account for e.g. the role of disorder on carrier and polariton delocalisation under strong coupling conditions169,170 and dark states.171 Another promising approach may be to bestow charge on the highly delocalised polaritons by coupling not to charge-neutral excitons, but rather to polarons172 or trions.173 In general, the realisation of strongly-coupled systems relies on the availability of sufficient knowledge of the optical and electrical properties of the materials used in the system. Thus characterisation methods to determine e.g. the transition dipole moment of the encapsulated material (see Section 3.4) are especially useful.
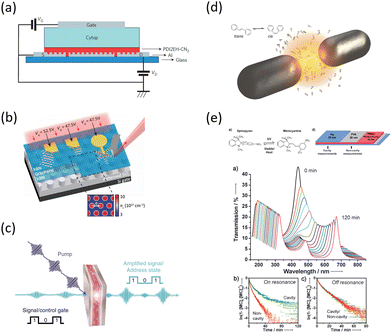 | ||
| Fig. 8 Examples of recent experiments involving strong coupling. (a) An organic field-effect transistor coupled to the plasmon resonance from a periodic array in an aluminium layer, taken from ref. 174. (b) A gated device for manipulating Bloch polaritons generated in graphene encapsulated in hexagonal boron nitride using a plasmonic array in SiO2, taken from ref. 164 according to the Creative Commons license.175 (c) An organic polariton transistor, taken from ref. 157. (d) Suppression of photoisomerization by coupling to plasmonic modes between metallic nanoparticles, taken from ref. 176 according to the Creative Commons license.175 (e) Modification of photoisomerization rate of spiropyran-myocyanine by encapsulation in a Fabry–Pérot cavity, taken from ref. 177. | ||
The interest in strongly-coupled systems also stems from the potentially powerful capability of polaritonic states to influence chemical reactions by enhancing the normally weak interactions between the reactants (Fig. 8d and e).178 It has been reported that the strong coupling to light in a cavity may influence chemical reaction dynamics, which led to the development of the field of polaritonic chemistry or quantum electrodynamics (QED) chemistry.177,179–181 The strong coupling to the cavity field is envisioned as a control for chemical reaction rates177 or energy-transfer rates between molecules,182 and a method for the engineering of novel quantum materials.183 Some recent studies in practical implementations include the promotion of site selectivity in chemical reactions,184 enhancement of intermolecular vibrational energy transfer in liquid phase donor–acceptor solutions,185 and suppression of unwanted photoisomerisation in light-sensitive organic molecules.176 While the volume of experimental evidence in support of strong-coupling effects on photochemistry continues to grow, the precise mechanisms and limitations with respect to vacuum vibrational strong coupling (i.e. without pumping in additional photons) are the subjects of active debate in the theoretical community, especially in regards to the role of dark states in ground state reactions.186
Looking ahead, while the above mentioned experimental studies all involve the use of an optical resonator to achieve strong coupling, such as a plasmonic array or Fabry–Pérot cavity, recent studies have shown that the use of a resonator may not strictly be necessary to achieve and take advantage of the strong coupling effects in some cases. Polaritonic states can, in fact, be realised by tuning the intrinsic properties and nanostructures of the materials of interest and their dielectric environment in order to promote ‘self’ or ‘cavity-less’ coupling.187,188 Indeed, it has been suggested that exciton–polaritons can be the primary source of photoexcitation in a variety of organic molecular nanostructures.189 Harnessing this aspect may be a key route to the development of simpler implementations of polaritonic devices.
3 Characterisation techniques
Beyond the applications of weak interactions in devices and materials, there are several experimental characterisation techniques analysing nano-structured materials or explicitly using effects occurring from these interactions. In the following, we introduce small sections illustrating the broad range starting with the most commonly used technique of surface force apparatus and atomic force microscopes, Section 3.1, via matter-wave scattering experiments probing surface phonons, Section 3.2, and dispersion forces, Section 3.3, and finalising this section with the characterisation of spatially orientated aggregates in thin films and on surfaces, Section 3.4.3.1 Insights into intermolecular interactions by surface forces apparatus and atomic force microscopy
The surface force apparatus (SFA) is one of the earliest techniques that allows quantifying the interactions between two surfaces. Introduced in the late 1960s by Tabor and Winterton,190 it has been used until today to measure forces in the Piconewton range.191 Prominent results were e.g. gained for ionic liquids, where long-range electrostatic forces were recorded192 or for bringing evidence of liquid layering due to a balance of van der Waals attraction and steric and osmotic repulsive forces.193Weak vdW forces also play a significant role in nanoscopic imaging of surfaces using the so-called atomic force microscopy (AFM)194 which was first introduced in 1986 by Binning, Quate and Gerber.195,196 Here, a tip (ideally atomically sharp) is attached to a mechanical resonator (e.g., a cantilever195 or one arm of a tuning fork197) and is approached to a surface or an object. This way, force–distance curves like by an SFA can be recorded. To obtain images, the tip is raster-scanned across the surface or the object using piezo scanners that allow for sub-nm control of tip (or sample) movement. Thereby, various modes of operation can be chosen, ranging from a mechanical (and tribological) contact between the tip and the substrate over “intermittent” to “truly non-contact” AFM modes, depending on the chosen feedback parameters.198 As between all objects, the forces between tip, medium (e.g. air, vacuum or a liquid) and sample feature long- and short-range contributions. Long-range contributions include van der Waals, electrostatic and magnetic interactions, if one uses the “traditional terms” of interactions, see Section 1 and Table 2.
Short-range contributions mostly stem from quantum-mechanical Born repulsion (also steric repulsion) and, in case fluids are involved, hydration forces or hydrophobic interactions can also lead to short-range contributions.16 Typically, AFM is used to study distances between contact (0 nm) and a few 100 nm, so both short- and long-range forces are important. Since the tip is usually not atomically sharp, a number of atoms interact with another number of the (flat or curved) surface, across a medium, which needs to be taken into account for modelling the interactions.16 Moreover, even in an ultrahigh vacuum, water molecules are present, adsorbing in wedges, especially if the AFM tip contacts the surface. Therefore, capillary forces also contribute to the sum of interactions and many experiments are conducted in water or aqueous solution to avoid uncontrolled capillary forces. Performing AFM measurements inside a (slightly) conductive fluid can help avoid static charges that can otherwise affect a sensitive force measurement in an uncontrolled manner.
By AFM, it is not possible to record the entire interaction potential between tip and object, since the cantilever imposes an external force that makes the system “jump to contact” at a certain distance above the surface.199 However, the AFM can nevertheless help to identify the different forces, if individual parameters (e.g., salt concentration or wettability) can be varied separately.200 Indirectly, by recording the topography of a thin polymer film, AFM helped to reveal the effective interface potential of the system air/thin polymer film/silicon wafer, which can be described by a Lennard–Jones-type potential in the appropriate geometry (two flat semi-infinite interfaces interact):201,202 at temperatures above the glass transition temperature (here T > 480 K), the thin polystyrene film can dewet spinodally under certain conditions off a Si wafer. The spinodal wavelength λS depends on the prepared film thickness h and relates to the second derivative of the effective interface potential ϕ′′(h) via
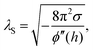 | (4) |
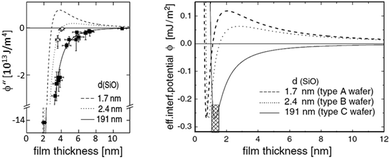 | ||
| Fig. 9 Example of a reconstruction of the effective interface potential between a thin polystyrene film of the displayed film thickness and a Si wafer with variable SiO2-thickness d. Left: the second derivative of the effective interface potential as a function of film thickness. Data points display the observed spinodal wavelength λ of the dewetting polystyrene film. ϕ′′(h) and λ are connected viaeqn (4), Right: fitted effective interface potential ϕ(h) for the three Si dioxide thicknesses, taken from ref. 202. | ||
Here, the interaction between the film and the surface can be described by
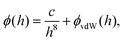 | (5) |
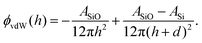 | (6) |
At very short tip–sample distances, about below 1 nm, the repulsive term that stems from quantum-mechanical Born repulsion dominates. Using careful control of the distance, the force between tip and sample can be measured, and using a feedback mechanism that operates the tip e.g. at a constant force high-resolution images can be obtained, even with sub-molecular resolution, see for instance ref. 204.
The AFM can be operated in various imaging modes (e.g., tapping, contact, etc.) and in various positions of the Lennard–Jones potential (on the attractive or the repulsive part, see Fig. 9). Furthermore, the long-range part of the vdW force (along with electrostatic interactions) adds a large background (typically attractive) force between the tip and the sample that can be 10 nN larger than the short-range part of the vdW forces (typically <0.1 nN).194 This long-range part of the vdW force (also termed Casimir or Casimir–Lifshitz force, see Table 2) can be made small by imaging in a liquid medium, as mentioned before205,206 or even turned into negative.207,208 Since the initial demonstration of atomic force microscopy imaging in 1986, AFMs have become a standard tool in university and industry laboratories.
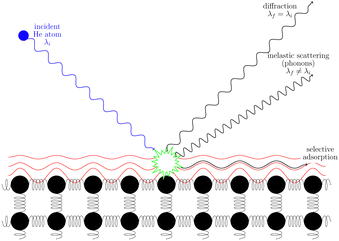
3.2 Helium scattering
Helium atom scattering (HAS) is a surface-sensitive characterisation technique; ideal for use when probing fragile and insulating materials, surfaces, and 2D materials. This is due to a combination of low incident energies, usually in the 10–100 meV range, with wavelengths comparable to interparticle separation. Helium atoms are electrically neutral, chemically inert, and are scattered by the tail of the electron distribution that seeps out of the probed surface, see Section 4.3. HAS is therefore a non-penetrating technique that leaves the sample undamaged. An overview of the technique is presented in Fig. 10.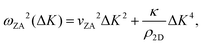 | (7) |
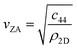 , the shear force constant of the material c44, the 2D mass density ρ2D, and the bending rigidity κ. In an inelastic time-of-flight (TOF) experiment, the ZA-mode will show up as phonon excitation peaks in the recorded spectrum. By varying the incident angle, it is possible to vary the parallel wave vector transfer ΔK. Recording the resulting ZA-excitations allows for mapping out the dispersion relation of the ZA-mode and to extract a value for κ by making a fit of eqn (7).
, the shear force constant of the material c44, the 2D mass density ρ2D, and the bending rigidity κ. In an inelastic time-of-flight (TOF) experiment, the ZA-mode will show up as phonon excitation peaks in the recorded spectrum. By varying the incident angle, it is possible to vary the parallel wave vector transfer ΔK. Recording the resulting ZA-excitations allows for mapping out the dispersion relation of the ZA-mode and to extract a value for κ by making a fit of eqn (7).
It is also worth noting that for substrate-supported membranes, the dispersion relation (7) is modified by the inclusion of the binding energy, ω0, between the substrate and the membrane.212 In this case, the dispersion relation reads
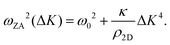 | (8) |
The quadratic acoustic term in eqn (7) is in principle presented in eqn (8) as well, but it is at long wavelengths (short ΔK) completely dominated by the constant binding energy, and therefore negligible.
This technique was first applied by Al Taleb et al. to measure the bending rigidity of graphene grown on copper foil,213 more recently to measure the bending rigidity of bilayer silica on ruthenium,214,215 as well as the temperature dependence of the bending rigidity of AB-stacked bilayer graphene.216
Thermal attenuation of the elastic peak in a (helium) atom surface scattering experiment is given by
I(T) = I0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−2W(ki, kf, T)], (9) exp[−2W(ki, kf, T)], (9) | (9) |
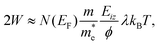 | (10) |
3.3 Matter-wave diffraction and Poisson's spot
The most convenient and direct method for sensing the minute dispersive interaction between a polarisable, but neutral atom or molecule and a surface is matter-wave diffraction.224–226 Here, the usually attractive interaction leads to a phase shift imposed on the de Broglie wavefunction of atoms and molecules that coherently pass by a surface, often in the form of a diffraction grating. The phase shift modifies the observed diffraction pattern, and the strength of the interaction can be extracted by means of careful modelling.Matter-wave diffraction has been used, among others, to measure C3 constants for the interaction between silicon nitride gratings and inert gas atoms227 or sodium atoms.228 In a more recent example, researchers demonstrated the significantly reduced van der Waals interaction between various ultra-thin carbon-based nanostructured gratings and massive phthalocyanine molecules.229
In these experiments, the probed surfaces are restricted to materials that are sufficiently tough so that they can be patterned into freely suspended grating structures on the nanoscale. An alternative near-field diffraction method exists that makes use of the simpler geometry of a sphere as a diffraction obstacle.230,231 Due to the availability of simple chemical methods to grow spherically shaped sub-micron particles in a bottom-up approach, this has the potential to open matter-wave diffraction to a wide variety of surface materials.
This alternative method is based on the observation of Poisson's spot, which is the bright interference spot in the wave shadow cast by a circular or spherical object.232–235 Its intensity relative to the undisturbed wavefront, with wavelength λ, for a spatially incoherent source of width ws, and without any van der Waals induced phase shifts is given by the expression236
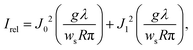 | (11) |
Due to the spherical symmetry, the interaction potential can be expressed in a particularly neat expression.230 Its effect on the Poisson spot can be well described in the Wentzel–Kramers–Brillouin (WKB) approximation by an additional phase shift Δφ(a) in the Fresnel–Kirchhoff integral228,234,237 as a function of distance a from the sphere's surface.
In experiments, the assumption of a large sphere and neglecting retardation are applicable. In this case, the shift can be approximated by
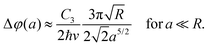 | (12) |
We expect that sensing dispersion forces using matter-wave diffraction will contribute to their understanding under realistic conditions such as rough surfaces and finite temperature among others. While results are directly relevant in for example NEMS applications, they may help to advance new concepts for matter-wave interferometry238 or improve diffractive optics for imaging with neutral atoms.239,240
3.4 Determination of transition dipole orientations
Knowledge of, and in many cases a degree of control over, the transition dipole moment (TDM) for a given electronic transition is often of key interest for understanding and utilising complex materials.92,242 As a prime example, the organometallic molecules implemented in the emissive layers of organic light-emitting diodes (OLEDs) emit light perpendicular to their TDM, thus control over the molecular/TMD orientation has been a critical step for increasing external quantum efficiencies (EQE).243,244 The TDMs of quantum nanostructures are also an important aspect for the development of quantum photonics applications.241Besides classical angle- and polarisation-resolved spectroscopy92,242,245,246 and sophisticated time-resolved techniques,247 especially back focal plane (BFP) imaging is an elegant and powerful method to determine TMD orientations,241,248 see Fig. 11. Here, the sample is observed through an oil immersion or high-NA objective to maximise the angular resolution. Emitted light from the photo-excited sample is then collected, and the angular dispersion is resolved via a Bertrand lens focusing onto the BFP of the objective and projected onto a spectrometer CCD. Dipoles p in the sample emit with different angles θ according to the orientation within the sample. This results in an intensity profile for the different k-vectors which are mapped onto the BFP.
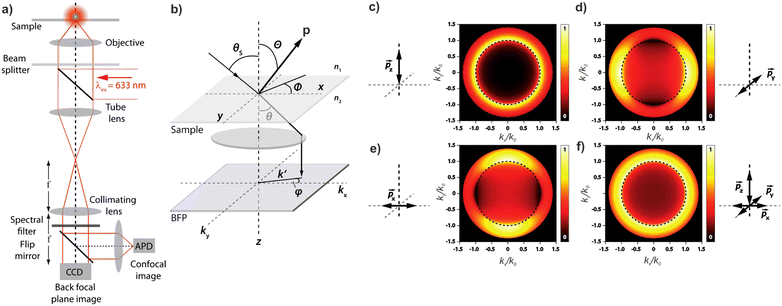 | ||
| Fig. 11 (a) Example of a setup for back focal plane (BFP) imaging and spectroscopy. (b) Schematic diagram illustrating the mapping of dipoles from a sample onto the BFP. (c–f) Numerical calculations of the BFP intensity patterns for differently oriented dipoles. Figure unchanged taken from ref. 241 according to the Creative Commons license.175 | ||
4 Theoretical methods
After introducing various systems where weak interactions play an essential role, we will illustrate the typical theoretical framework describing them. We will focus on the quantum mechanical description of matter's states (Section 4.3) and demonstrate the statistical (Section 4.1), electrodynamical (Section 4.2), and quantum electrodynamical approaches (Section 4.4) to characterise mesoscopic or macroscopic many-particle systems, such as molecular aggregates (Section 4.6). Finally, we will continue with systems under extreme conditions leading to strong coupling (Section 4.5) and Rydberg physics (Section 4.7).4.1 Forces on mesoscopic scales
How can Casimir or dispersion forces be treated on mesoscopic scales? We start by treating the involved objects classically, i.e., using their classical scattering operator![[Doublestruck T]](https://www.rsc.org/images/entities/char_e177.gif) = Tij(r,r′), depending on two spacial arguments r and r′, and being a 3 × 3 matrix in the space of an electric field vector. It is related to the dielectric and magnetic properties via (
= Tij(r,r′), depending on two spacial arguments r and r′, and being a 3 × 3 matrix in the space of an electric field vector. It is related to the dielectric and magnetic properties via (![[Doublestruck G]](https://www.rsc.org/images/entities/char_e16a.gif) 0 is the vacuum Green's function)
0 is the vacuum Green's function)The potential ![[Doublestruck V]](https://www.rsc.org/images/entities/char_e179.gif) encodes the dielectric (via ε) and magnetic (via μ) responses
encodes the dielectric (via ε) and magnetic (via μ) responses
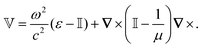 | (13) |
Note that ε and μ are in general 3 × 3 matrices, thus potentially encoding anisotropic material properties. They depend on space, thereby characterising the material distributions of the objects, and may also depend on two spacial arguments in case of non-local properties. The Green's function in the presence of an object with operator ![[Doublestruck T]](https://www.rsc.org/images/entities/char_e177.gif) reads
reads
![[Doublestruck G]](https://www.rsc.org/images/entities/char_e16a.gif) = = ![[Doublestruck G]](https://www.rsc.org/images/entities/char_e16a.gif) 0 + 0 + ![[Doublestruck G]](https://www.rsc.org/images/entities/char_e16a.gif) 0 0![[Doublestruck T]](https://www.rsc.org/images/entities/char_e177.gif) ![[Doublestruck G]](https://www.rsc.org/images/entities/char_e16a.gif) 0. 0. |
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) , i.e., the potential corresponding to the Casimir force for two objects with operators
, i.e., the potential corresponding to the Casimir force for two objects with operators ![[Doublestruck T]](https://www.rsc.org/images/entities/char_e177.gif) 1 and
1 and ![[Doublestruck T]](https://www.rsc.org/images/entities/char_e177.gif) 2 is then found to be249–251
2 is then found to be249–251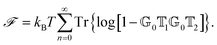 | (14) |
![[Doublestruck G]](https://www.rsc.org/images/entities/char_e16a.gif) 0 and
0 and ![[Doublestruck T]](https://www.rsc.org/images/entities/char_e177.gif) 2 are evaluated at imaginary frequencies.249
2 are evaluated at imaginary frequencies.249
Notably, the forces resulting from eqn (14) are indeed identical to the average of Lorentz forces acting on the fluctuating charges in the objects as described in Table 1,252 see Section 4.4.1.
The form of eqn (14) allows a number of remarkable general statements for non-magnetic objects (μ = 1) to be provided. For example, two objects that are each other's mirror images always attract.253 More general, for any shape of objects, a statement equivalent to Earshaw's theorem for electrostatics is possible:254 the Laplacian of the free energy with respect to the positions of the objects is non-positive so that the free energy does not have minima as a function of particle positions; in other words, mechanically stable configurations are ruled out.
The above statements hold true for reciprocal objects, i.e., if ![[Doublestruck T]](https://www.rsc.org/images/entities/char_e177.gif) =
= ![[Doublestruck T]](https://www.rsc.org/images/entities/char_e177.gif) T [with transpose
T [with transpose ![[Doublestruck T]](https://www.rsc.org/images/entities/char_e177.gif) T, i.e., [Tij(r,r′)]T = Tji(r′,r)], a property following from micro-reversibility.255 In contrast, recent discoveries have highlighted the relevance of the so-called non-reciprocal materials, for which
T, i.e., [Tij(r,r′)]T = Tji(r′,r)], a property following from micro-reversibility.255 In contrast, recent discoveries have highlighted the relevance of the so-called non-reciprocal materials, for which ![[Doublestruck T]](https://www.rsc.org/images/entities/char_e177.gif) ≠
≠ ![[Doublestruck T]](https://www.rsc.org/images/entities/char_e177.gif) T. This breakage of micro-reversibility is, for example, possible in the presence of magnetic fields,256 and such non-reciprocal objects find a variety of new phenomena regarding fluctuating electromagnetic fields, including near field energy transfer.257
T. This breakage of micro-reversibility is, for example, possible in the presence of magnetic fields,256 and such non-reciprocal objects find a variety of new phenomena regarding fluctuating electromagnetic fields, including near field energy transfer.257
To better understand and prove these properties and to connect to Section 4.4.1, we expand the log in eqn (14), keeping only the leading term. This approximation becomes exact when the separation of the objects is much larger than the sizes of the objects, e.g., in the Casimir–Polder or vdW limits. It yields the following simpler expression
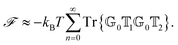 | (15) |
Tr{![[Doublestruck G]](https://www.rsc.org/images/entities/char_e16a.gif) 0 0![[Doublestruck T]](https://www.rsc.org/images/entities/char_e177.gif) 1 1![[Doublestruck G]](https://www.rsc.org/images/entities/char_e16a.gif) 0 0![[Doublestruck T]](https://www.rsc.org/images/entities/char_e177.gif) 2} ≥ 0 → 2} ≥ 0 → ![[scr F, script letter F]](https://www.rsc.org/images/entities/i_char_e141.gif) < 0. < 0. | (16) |
As mentioned, these proofs rely on the symmetry of the scattering operator, which thus is not given for non-symmetric operators like those related to non-reciprocal objects.
By splitting the scattering operator into a symmetric and an antisymmetric contribution, it is possible to show that the antisymmetric part gives rise to a positive part of the free energy, which typically produces a repulsive force.258 The latter could dominate for a large antisymmetric part. As an explicit example, we regard two non-reciprocal particles located along the z axis with the following polarisability tensor,
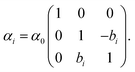 | (17) |
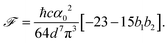 | (18) |
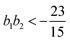 , the free energy is positive, and the resulting force is repulsive.
, the free energy is positive, and the resulting force is repulsive.
Fig. 12 shows a numerical evaluation of the free energy as a function of the position of the second particle in the xy-plane, with the first particle at the origin. The mentioned properties are seen, i.e., the free energy can be positive or negative, and the force can be attractive or repulsive. Notably, the Laplacian of the free energy (not shown) can be positive or negative, in violation of the corresponding findings for reciprocal cases.254 This would, in principle, allow for mechanically stable configurations, which are, however, not present for this simple toy model. The free energy in this toy model shows saddle points but not minima.
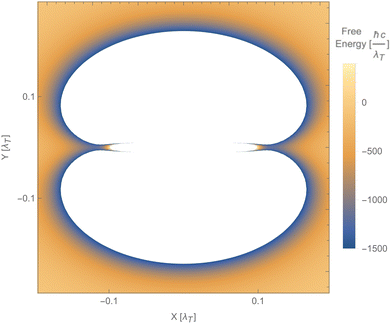 | ||
| Fig. 12 Free energy of particle 2 as a function of its position relative to particle 1, using the polarisability tensor of eqn (17), b1b2 = 2 and T = 300 K. The blue areas along the x-axis indicate saddle points (minima along the radial direction but maxima along both angular directions). The white areas represent values of the free energy beyond the ones indicated on the vertical bar. | ||
Despite all these fundamental differences between reciprocal and non-reciprocal objects, in both cases, the Casimir forces are gradients of free energy, and therefore the forces are conservative. This forbids the creation of propulsion forces or cyclic work extraction, which requires the objects to be at different temperatures.259
Besides the differences found for equilibrium situations, non-reciprocal objects have other features absent in their reciprocal counterpart such as novel lateral forces,259–261 nontrivial optical torques,262,263 recoil forces,264 lateral thermal-fluctuations-induced forces265,266 and repulsive forces.267,268
Future work can investigate the connection of the presented framework to microscopic approaches as in Section 4.4, or including charges as in Section 4.2. Also, the connection of these energies to electronic states in van der Waals Heterostructures, Section 2.2, is an exciting topic.
4.2 Regulation of nanoparticle interactions through a balance of charge and ionic Casimir–Polder interactions
In the study of interactions at surfaces and between microscopic bodies, attention is often drawn first to the charge state of the surface, giving rise to electrostatic forces. The negative surface charge typically arises from the dissociation of acidic oxide sites, hydroxyl groups in the case of mineral oxide materials, and carboxylate groups in the case of protein molecules. The likewise positive charge typically arises through chemisorption of H+ ions at previously uncharged oxide sites or binding to amine groups. Alternatively, in electrochemical systems, the surface charge can arise due to redox half-reactions or through coupling to an external electrical circuit. An adsorption layer of electrolyte ions can form through physisorption driven by electrostatic interactions with the surface charge.The conventional theory of surface forces employed to interpret interactions of bodies in electrolyte (salt) solutions is known as DLVO theory, after Derjaguin and Landau,269 Verwey and Overbeek.270 The net force in DLVO theory balances electrostatic forces, the entropy of adsorbed ions, and macroscopic dispersion forces. An initial theory of dispersion forces was developed by Hamaker through summation of the individual London dispersion forces between individual molecules comprising the interacting bodies.271 Dzyaloshinskii later improved the theory of dispersion interaction, Lifshitz and Pitaevskii21 using macroscopic quantum electrodynamics. This description of dispersion energy is in common use today, often known in short form as Lifshitz theory, see Section 4.1 above. The strength, but also the limitation, of Lifshitz theory, is that it presents material properties simply through the permittivity ε(iω) over imaginary frequencies iω. This makes Lifshitz theory relatively simple to implement, when the dielectric response is known on the imaginary frequency axis ε = ε(iω), see Sections 4.1 and 4.4. But by treating the materials, including the medium, with a spatially homogeneous dielectric function ε(iω), spatially resolved effects are neglected. In particular, the standard formulation does not account for the dielectric impact of the ionic adsorption layer itself on macroscopic dispersion interaction.
As for the formation of the ion adsorption layer, it is commonly described using a Boltzmann profile ci(x) = ci0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−qiψ(x)/kBT) determined by the electrostatic potential ψ(x), ci0 being the bulk concentration of the ion. The electrostatic potential, in turn, is determined by the Poisson equation,
exp(−qiψ(x)/kBT) determined by the electrostatic potential ψ(x), ci0 being the bulk concentration of the ion. The electrostatic potential, in turn, is determined by the Poisson equation,
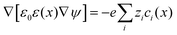 | (19) |
There are two core deficiencies in the Poisson–Boltzmann model that limit its usefulness in applications, particularly in the development of new applications that aim to achieve a paradigm shift of what is possible beyond the general trends of conventional DLVO theory. Both deficiencies arise from the use of a point-charge model to describe electrolyte ions, which effectively limits the validity of the model to concentrations below 0.1 mol L−1 and surface potentials less than 100 mV.
The first deficiency in the point-charge model is that ions are distinguished solely by valency. There is no means of distinguishing Cl− from ClO4−, or Li+ from K+. But specific ion effects have been observed experimentally since 1886 when Franz Hofmeister examined the effect of different salts on egg-white protein precipitation.272 And the differences matter. Na+ is the dominant cation in normal physiological saline. Li+ is used as a treatment for bipolar disorder.273 K+ is used in lethal injections.274
The second deficiency of the point-charge model is that, tautologically, it does not account for the finite size of ions. Its consequence for the Poisson–Boltzmann model is that calculated ion concentrations reach unbounded physically unrealistic levels of 106 mol L−1 or more with consequent unbounded surface forces or electrode capacitances.
Some techniques are already known for dealing with these deficiencies. But the methods currently available leave a set of questions unanswered with respect to the ramifications for dispersion forces used in DLVO analysis. Further development of the underlying Casimir–Lifshitz theory is required to address these questions.
In general, the Boltzmann component of the Poisson–Boltzmann model can be constructed in terms of an excess chemical potential μi(x) of an ion i describing the ion's interactions at position x relative to its chemical potential in bulk solution. The ion concentration at position x is then ci(x) = ci0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−μi(x)/kBT). In the conventional point-charge model, the excess chemical potential is simply the electrostatic energy of the point-like ion with charge qi in an electrostatic potential ψ(x), μi(x) = qiψ(x).
exp(−μi(x)/kBT). In the conventional point-charge model, the excess chemical potential is simply the electrostatic energy of the point-like ion with charge qi in an electrostatic potential ψ(x), μi(x) = qiψ(x).
Within the framework of the mean-field Poisson–Boltzmann model, the point-charge deficiencies can be addressed by incorporating various additional interactions μexi(x) to the chemical potential, resulting in a modified Poisson–Boltzmann model with ion concentrations given by280
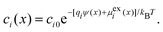 | (20) |
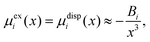 | (21) |
The Casimir–Polder interaction enables an interpretation of Hofmeister effects due to the non-electrostatic physisorption of ions at an interface. The expression as written here is problematic for a model of surface adsorption because of the divergence of the interaction at x = 0. Mahanty and Ninham provided a methodology281,282 to address the problem by introducing a finite size to the ion. In their model, the polarisability αi of the ion is smeared over the volume of the ion, represented as a Gaussian sphere exp(−r2/ai2) with Gaussian radius ai, r being the radial distance from the centre of the ion. Conceptually this picture represents the finite volume of the electron cloud of the ion, which is intrinsically ion-specific. However, using a Gaussian sphere is made for mathematical convenience and, strictly speaking, describes a 3D quantum harmonic oscillator. With the Gaussian-sphere representation of the Casimir–Polder interaction, the ion dispersion interaction at an interface becomes
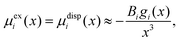 | (22) |
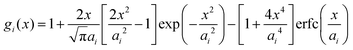 | (23) |
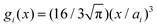 such that the Casimir–Polder interaction energy becomes finite at contact,
such that the Casimir–Polder interaction energy becomes finite at contact, 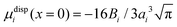 .
.
It should be noted that although the Mahanty–Ninham model incorporates ions of finite size, it embeds the ion in a dielectric medium such that the dielectric response of the medium smears into the volume of the ion. This model neglects additional effects that arise due to the reflection of virtual photons of the interface of an ion cavity cut out of the medium.283 Nevertheless the model has successfully described the buffer specific effects observed in experimental measurements of protein zeta potentials284 as well as the surface charge of protein285 and silica particles,286 and charge reversal effects.284,287 Once ion cavity effects are included,288 theory of weak interactions is able to reproduce a wide range of bulk experimental properties, including ion solvation energies,288 partial molar volumes and entropies,289 activity coefficients,290 and surface tensions.291,292 Further work is needed to assess the impact of the cavity local field effect on the Casimir–Polder interactions of ions near solid interfaces.
4.3 Non-covalent interactions between molecules and surfaces from electronic structure theory
A microscopic approach to describing non-covalent interactions is to solve the many-electron Schrödinger equation, which accounts for all non-retarded dispersion interactions. Direct diagonalisation is all but impossible for the simplest systems, but perturbation theory approaches have been hugely successful and form the foundations of quantum chemistry. Expressing the wavefunction in antisymmetric Fock-basis in terms of single-particle orbitals between two separate electronic fragments, London-dispersion forces arise naturally to second-order perturbation theory, i.e. in the Møller–Plesset perturbation theory (MP2). While MP2 found some usage in the 2000s for studying bonding between molecules293 the accuracy is low.294 Higher-order perturbation theory coupled-cluster (CC) methods especially at the CCSD(T) level is generally too expensive for addressing broad systems of interest,295,296 but play an invaluable role in providing reference data, for more approximate methods.297,298 The same role is also played by diffusion Monte–Carlo calculations.299 A computationally effective method to overcome the computational challenges in particular of CC is symmetry-adapted perturbation theory300 explicitly defined for accurate exploration of non-covalent interactions. These highly accurate but computationally costly methods might find increased usage in combination with machine-learning approaches301 as they provide highly accurate training data.While the theory of DFT is more general,308 the acronym DFT refers generally to the Kohn–Sham (KS) realisation,309 in which the systems are described as consisting of effectively independent electrons ψi(r), obeying Pauli repulsion so that 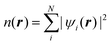 . Formally, KS-DFT is an exact theory for the ground state energy of an electronic system, thus the method has the potential to include non-covalent interactions. In practice, its performance and ability to describe such interactions hinge on approximations made. Overall, however, DFT is a highly versatile method due to its ability to predict the energy; it can also describe forces acting on atoms of a given atomic configuration and it generally has an excellent trade-off between accuracy and computational cost.
. Formally, KS-DFT is an exact theory for the ground state energy of an electronic system, thus the method has the potential to include non-covalent interactions. In practice, its performance and ability to describe such interactions hinge on approximations made. Overall, however, DFT is a highly versatile method due to its ability to predict the energy; it can also describe forces acting on atoms of a given atomic configuration and it generally has an excellent trade-off between accuracy and computational cost.
The KS equation has the form of an independent-particle Schrödinger equation,
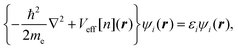 | (24) |
| Veff[n](r) = Vext(r) + VH[n](r) + VXC[n](r). | (25) |
In addition to dispersion forces, longer-ranged electrostatic interactions can also raise the sum of 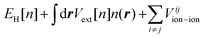 , which includes monopole and static dipole–dipole interactions. Monopole interactions are, of course, the biggest contribution to “strong” ionic bonding, such as halides and oxides. Dipole–dipole interactions are the biggest contribution to hydrogen and halogen bonding. The term also includes Keesom forces, which arise once the KS equation is solved self-consistently, where the existence of dipoles causes a shift in the charge density n(r) that sets up permanent dipole–dipole interactions.
, which includes monopole and static dipole–dipole interactions. Monopole interactions are, of course, the biggest contribution to “strong” ionic bonding, such as halides and oxides. Dipole–dipole interactions are the biggest contribution to hydrogen and halogen bonding. The term also includes Keesom forces, which arise once the KS equation is solved self-consistently, where the existence of dipoles causes a shift in the charge density n(r) that sets up permanent dipole–dipole interactions.
In sparse materials,307 hydrogen bonding is crucial for the structure of materials.310 However, at longer ranges, dipoles tend to cancel out in complex materials, thus the London dispersion forces tend to be the dominant forces between electrically neutral objects at larger separations. While textbooks often describe “hydrogen bonding” as a purely electrostatic force, the total binding energy also contributes significantly from short-range London dispersion forces311 and including dispersion forces is important for an accurate description of liquid water.312
Proper inclusion of London dispersion forces in DFT, or more broadly Casimir forces, hinges on the approximations used to describe the exchange–correlation functional EXC[n]. Many of the most widely used and successful exchange–correlation functional approximations for describing chemistry and covalent and ionic-bonded materials completely lack long-range dispersion forces. The generalised-gradient approximation (GGA), for instance, is based on information on the local density n(r) and the reduced gradient s(r) ∝ |∇n(r)|/n(r)4/3 to construct EXC[n]. It is a generalisation of the local density approximation (LDA), which is a weighting of the numerically exact exchange and correlation energy density of the homogeneous electron at different densities n, i.e.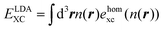 . Integrating only over local functions of n(r) and s(r), GGAs lack information on long-range interactions. Thus while GGAs can show good accuracy for covalently bound systems, they are very inaccurate for systems where dispersion forces are important. In the approach developed by Grimme,313 explicit long-range contribution to the GGA-xc energy are added to the DFT energy, i.e.
. Integrating only over local functions of n(r) and s(r), GGAs lack information on long-range interactions. Thus while GGAs can show good accuracy for covalently bound systems, they are very inaccurate for systems where dispersion forces are important. In the approach developed by Grimme,313 explicit long-range contribution to the GGA-xc energy are added to the DFT energy, i.e.
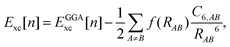 | (26) |
Dispersion forces can also be obtained from the many-body theory for electron gases. In particular, the adiabatic-connection fluctuation–dissipation theory (ACFD) provides an exact expression for the exchange–correlation energy,317,318 as follows:
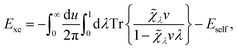 | (27) |
![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) λv is the local field response function for given coupling constant strength, λ. In this expression, the electron self-energy Eself must be subtracted. In the coupling-constant integration, the external potential is adjusted to keep density nλ(r) = n(r) fixed during the integration. In the so-called ACFD-RPA method, the response function of independent Kohn–Sham orbitals χλ → λKS is used. The ACDF-RPA method is a rather expensive but quite accurate method for some material classes, including layered materials.319–321
λv is the local field response function for given coupling constant strength, λ. In this expression, the electron self-energy Eself must be subtracted. In the coupling-constant integration, the external potential is adjusted to keep density nλ(r) = n(r) fixed during the integration. In the so-called ACFD-RPA method, the response function of independent Kohn–Sham orbitals χλ → λKS is used. The ACDF-RPA method is a rather expensive but quite accurate method for some material classes, including layered materials.319–321
The vdW-DF322–324 framework instead assumes ACDF-mean-value evaluation325–327 of eqn (27), which results in ref. 326 and 328
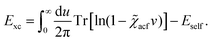 | (28) |
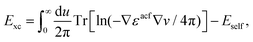 | (29) |
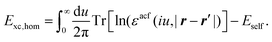 | (30) |
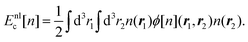 | (31) |
The non-locality of the total energy in eqn (31) still gives a local exchange-potential operator in eqn (31), and with clever computational approximations, the computational cost of DFT with vdW-DF is comparable to that of GGAs.329 Hartree–Fock theory uses full Slater determinant to describe the many-particle wavefunction and hybrid DFTs, which can be viewed as a mixture of Hatree–Fock theory and standard KS-DFT; however, this results in non-local exchange potentials, which are costly to compute, especially so for plane-wave DFT. However, such non-local exchange does not cross voids and only becomes long-ranged for systems with extended wavefunctions. The use of hybrid functionals, however, provides more accurate electronic densities and exchange energies and, including dispersion interactions with hybrid DFT provides highly accurate (albeit somewhat costly) functionals for chemical interactions and hydrogen bonds330–332 including proton transfer.333
4.4 Divide and conquer
In the sense of this article, complex materials are many-particle systems composed of (quantum) nano-objects that scale up to micron-sized systems. Their theoretical description is rather complicated due to the many degrees of freedom. Most fundamentally, such systems are described by the many-particle Hamiltonian for a set of charges![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) 334
334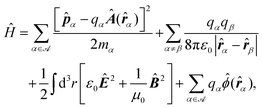 | (32) |
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) α and
α and ![[P with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0050_0302.gif) α, the electric and magnetic field operators Ê and
α, the electric and magnetic field operators Ê and ![[B with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0042_0302.gif) and the corresponding scalar and vector potentials
and the corresponding scalar and vector potentials ![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) and Â. The electromagnetic fields in eqn (32) also describe the quantum vacuum in the absence of absorbing (realistic) materials. For classical electromagnetic fields, the effect of dielectric materials is included via the macroscopic displacement field D = ε0E + P, with the polarisation P describing the response of the dielectric object, and the magnetic field strength
and Â. The electromagnetic fields in eqn (32) also describe the quantum vacuum in the absence of absorbing (realistic) materials. For classical electromagnetic fields, the effect of dielectric materials is included via the macroscopic displacement field D = ε0E + P, with the polarisation P describing the response of the dielectric object, and the magnetic field strength  with the magnetisation M including the magnetic response of the media.335 This method can be adapted to the quantised fields and yields the diagonalised field Hamiltonian336
with the magnetisation M including the magnetic response of the media.335 This method can be adapted to the quantised fields and yields the diagonalised field Hamiltonian336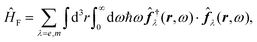 | (33) |
![[f with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0066_0302.gif) λ are related to the electric and magnetic fields via the dyadic Green function
λ are related to the electric and magnetic fields via the dyadic Green function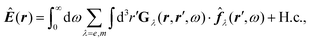 | (34) |
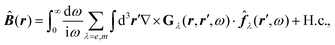 | (35) |
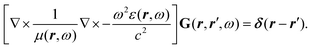 | (36) |
One possibility to handle this complexity is the separation of the set of charges ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) into disjointed subsets of neutral particles
into disjointed subsets of neutral particles ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) i with “non”-overlapping wavefunctions. For instance, particles with wavefunctions ψi,j (from subset
i with “non”-overlapping wavefunctions. For instance, particles with wavefunctions ψi,j (from subset ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) i,j with i ≠ j) fulfilling
i,j with i ≠ j) fulfilling
| 〈ψi|ψj〉 ↦→ 0. | (37) |
This separation is formally equivalent to the series expansion of the Coulomb interaction in eqn (32). According to this separation, the resulting subsets either describe quantum objects, such as atoms, molecules, and small clusters, or macroscopic objects, such as solid surfaces. Concerning the illustrated method, the macroscopic objects will be considered as boundary conditions of the vector Helmholtz eqn (36), whereas microscopic objects will be treated as quantised particles in eigenstates334
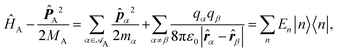 | (38) |
![[P with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0050_0302.gif) A and the total mass of the particle
A and the total mass of the particle 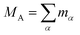 . Thus, a particle is completely described by the set of eigen-energies and eigenstates (En,|n〉). However, typical particles are characterised by by optical data, such as transition energies337
. Thus, a particle is completely described by the set of eigen-energies and eigenstates (En,|n〉). However, typical particles are characterised by by optical data, such as transition energies337| Emn = ħωmn = ħ[En − Em], | (39) |
dnm = 〈m|![[d with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0064_0302.gif) |n〉 = e〈m| |n〉 = e〈m|![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) |n〉, |n〉, | (40) |
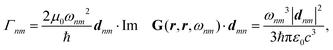 | (41) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G(0)(r,r,ω) = ω
G(0)(r,r,ω) = ω![[Doublestruck I]](https://www.rsc.org/images/entities/char_e16c.gif) /(6πc) to obtain Fermi's Golden rule.339 These quantities are usually combined with the polarisability of the quantised particle338
/(6πc) to obtain Fermi's Golden rule.339 These quantities are usually combined with the polarisability of the quantised particle338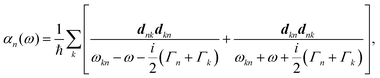 | (42) |
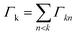 . The advantage of this technique is that it dramatically reduces the number of considered particles. Furthermore, non-relevant quantised objects at the positions ri can directly be treated via their induced fields
. The advantage of this technique is that it dramatically reduces the number of considered particles. Furthermore, non-relevant quantised objects at the positions ri can directly be treated via their induced fields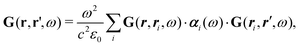 | (43) |
Within the macroscopic quantum electrodynamics, the electromagnetic fields are considered as a (macroscopically dressed) response to the vacuum field excitations (33) and the quantised particle in eigenbasis (38). The remaining part of the total Hamiltonian (32) is the interaction between the fields and the particles
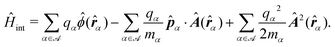 | (44) |
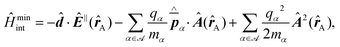 | (45) |
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) A and the relative momentum
A and the relative momentum 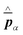 . An alternative approach to the minimal coupling regime is the multipolar coupling,342 that yields a series of interacting multipoles via a Power–Zienau–Woolley transform.343,344 In the following, we restrict ourselves to consider the dominant dipole interaction Ĥint = −
. An alternative approach to the minimal coupling regime is the multipolar coupling,342 that yields a series of interacting multipoles via a Power–Zienau–Woolley transform.343,344 In the following, we restrict ourselves to consider the dominant dipole interaction Ĥint = −![[d with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0064_0302.gif) ·Ê‖(
·Ê‖(![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) A).
A).
Casimir force. One possibility to introduce the Casimir force is the volume averaged ground-state expectation value of the quantum Lorentz force342
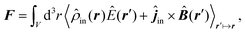 | (46) |
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (r) and ĵ(r), respectively. Together with the continuity equation
(r) and ĵ(r), respectively. Together with the continuity equation ![[small rho, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a6.gif) in + ∇·jin = 0, and the decomposition into noises (index N) and induced charges and currents, ρin = ρN − ε0∇·[χE] and jin = jN − iε0ωχE, the internal densities in the quantum Lorentz eqn (46) can be rewritten in terms of the field operators
in + ∇·jin = 0, and the decomposition into noises (index N) and induced charges and currents, ρin = ρN − ε0∇·[χE] and jin = jN − iε0ωχE, the internal densities in the quantum Lorentz eqn (46) can be rewritten in terms of the field operators ![[f with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0066_0302.gif) (quantisation via the noise current density jN → ĵN →
(quantisation via the noise current density jN → ĵN → ![[f with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0066_0302.gif) ) and the ground-state expectation value can be obtained leading the Casimir force342
) and the ground-state expectation value can be obtained leading the Casimir force342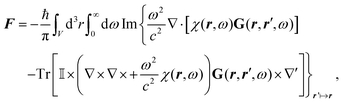 | (47) |
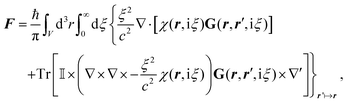 | (48) |
Casimir–Polder force. This appears between a polarisable object, which can be described viaeqn (38), and a dielectric surface entering the theory via the induced electromagnetic fields, eqn (33). Both systems are described via the Fock state |I〉 = |k〉|{n}〉, as the product state of the particles and field states |k〉 and |{n}〉, respectively. Both systems are typically coupled perturbatively with the leading second-order
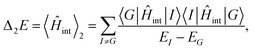 | (49) |
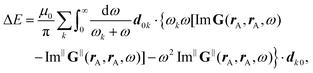 | (50) |
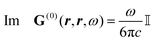 yields the Lamb-shift345
yields the Lamb-shift345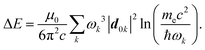 | (51) |
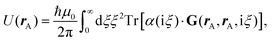 | (52) |
van der Waals force
This arises between two neutral quantised objects which classically do not interact. Due to the selection rules of the dipole operator, which couples only different states, the perturbative approach (as followed for the Casimir–Polder interaction) yields the fourth order with a non-vanishing contribution. Details about this approach can be found in ref. 342. However for an intuitive understanding, a simpler approach starts from the Casimir–Polder interaction (52) and applying the dilute limit of the interacting dielectric surface. In this case, the corresponding Green function is given by eqn (43) leading the vdW potential334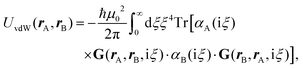 | (53) |
Dispersion forces, in general, have been widely studied in theory16,282,336,346–348 and experiments.227,231,349–351 Hence, we do not want to overstress their further discussions. However, to end this section, we will discuss finite-size effects for microscopic particles and the transition between different dispersion forces. Most relevant systems described in this review deal with bounded particles or at least in very close separation. Thus, the typical relevant length scales are of the same order as the extension of the particles leading to a breakdown of the point-particle assumption. In classical electrodynamics, there are different ways to account for finite system sizes represented by a collection of charges, namely the multipole expansion335
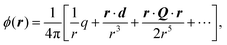 | (54) |
 | (55) |
![[d with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0064_0302.gif) ·Ê(rA),
·Ê(rA),| Ĥ = ĤA + ĤF + ĤAF. | (56) |
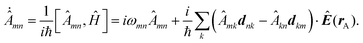 | (57) |
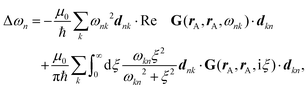 | (58) |
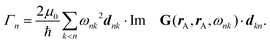 | (59) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G(rA,rA,ωnk + δωnk) gets relevant.
G(rA,rA,ωnk + δωnk) gets relevant.
The resulting changes of the resonances frequencies (58) and transition rates (59) can be interpreted as an environmental induced state mixing. Inb particular, the energy change is equivalent to the Casimir–Polder force of excited particles.356
 | (60) |
For ionic materials, there is a contribution to the dielectric response from the dipole-active phonon modes. The vibrations associated with the longitudinal optical phonons build up an electric field that screens the carries. In the long-wavelength limit the phonon dispersion is approximated to be constant for both the longitudinal optical (LO) and the transverse optical (TO) modes. The contribution to the imaginary part of the dielectric function can be modelled as Lorentz oscillators
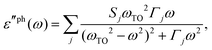 | (61) |
For metals, the Drude theory with the plasma frequency ωpl describes the intraband screening from the nearly free carriers in the partially occupied band
 | (62) |
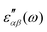 , is the summation of the three contributions. The corresponding response function for imaginary frequencies is obtained from the Kramers–Kronig relation
, is the summation of the three contributions. The corresponding response function for imaginary frequencies is obtained from the Kramers–Kronig relation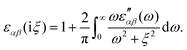 | (63) |
The summation over the k-mesh in eqn (60) is a computational challenge. For bulk-like materials, the summation can be replaced by an integration over the first Brillouin zone; however, the issue to compute the eigenstates for sufficiently many k-points remains. The reasons are, first, energy band crossing yields incorrect integration for each band. This could be avoided by analysing the symmetry of the eigenfunctions362 and reordering the energy states. Second, a compact k-mesh is required for metals in order to accurately determine the Fermi level, especially when several bands are partially filled.363 Third, since the energy bands have quadratic dispersion around band extrema, i.e., εj,k ∝ k2, the density-of-states should there be proportional to the square root of the energy. The linear tetrahedron integration is a standard algorithm; however, assuming a linear dispersion εj,k ∝ |k| implies that the density-of-states is direct proportional to the square of the energy. A dense k-mesh is therefore required to account for details in the energy dispersion.364 Furthermore, for a nano-sized material, assuming Bloch functions and neglecting surface effects, the summation over the k-points is still demanding unless the material comprises only a moderate number of unit cells.
To compute the energy states for a dense k-mesh is time consuming with hybrid functionals, GW approaches, or other beyond-DFT methods. There are different approaches to address this issue, for instance, polynomial fitting,365 smoothed Fourier interpolation,366 construction of optimal basis,367 or Wannier-like functions.368 A straightforward method is the full-band k·p calculation.363,369 The scheme is to perform a DFT calculation for a sparsely sampled k-mesh, whereupon the energy states for the dense k-mesh are determined by describing those states as linear combinations of the DFT eigenfunctions. The method generates exact results if an infinite number of bands is used, but already for a rather modest number of bands the k·p calculations yield accurate results, describing also band crossing.
An environmental solvent has, in general, two effects on a dissolved ensemble: (i) restraining of the electronic wave functions and the electron density, and (ii) screening of the long-range interactions through the medium.374
While dispersive contributions between solute and solvent are important to obtain accurate solvation energies, dispersive interactions between different solutes have so far received less attention. The PCM influences electric fields,375 where e.g. the Coulomb energy of point charges embedded within a continuous ε at distance R is screened by 1/ε largely stabilising local charges. This continuum assumption opens the field of access polarisability models283 considering local-field effects at the particles. These models describe effectively the impact of the surrounding media on the interactions via an effective dielectric response of the particle. The established model is Onsager's real cavity model376 assuming a point-like particle embedded in a vacuum bubble of finite radius. This assumption is questionable due to finite particle size leading to more complex models283 and concerning the hard wall.377,378 Similar to point charges screening occurs also for dispersive interactions, where one expects screening by 1/ε(ωopt)2 with the frequency ωopt in the optical range for usual molecular systems.374,379 Water has ε(ωopt) ≈ 1.7, such that the screening is much less than for pure Coulomb fields. A comprehensive experimental and theoretical study concerning correct assumptions for such models is still required.
4.5 Cavity QED
The interaction of atoms or molecules with the electromagnetic field is, to lowest order in the perturbative expansion of the light-matter coupling, determined by the electric–dipole interaction Ĥint = −![[d with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0064_0302.gif) ·Ê(rA), with the electric field taken at the position rA of the atom. In view of second-order perturbation theory with this interaction Hamiltonian, it is clear that the interaction strength crucially depends on the local density of states (LDOS) of the electromagnetic field (see also the discussion on dispersion forces, Section 4.4.1). In a situation in which the light field is confined in a resonator-like structure, the density of field modes can be very sharply peaked around one or more discretely spaced frequencies. If that cavity mode is resonant with a particular atomic transition, the light–matter interaction can be treated in a two-level approximation for the atom, and a single-mode approximation for the field.
·Ê(rA), with the electric field taken at the position rA of the atom. In view of second-order perturbation theory with this interaction Hamiltonian, it is clear that the interaction strength crucially depends on the local density of states (LDOS) of the electromagnetic field (see also the discussion on dispersion forces, Section 4.4.1). In a situation in which the light field is confined in a resonator-like structure, the density of field modes can be very sharply peaked around one or more discretely spaced frequencies. If that cavity mode is resonant with a particular atomic transition, the light–matter interaction can be treated in a two-level approximation for the atom, and a single-mode approximation for the field.
Within the framework of macroscopic quantum electrodynamics, one can define position-dependent ladder operators for photon-like excitations as380
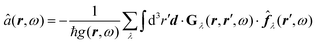 | (64) |
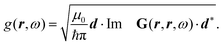 | (65) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G(r,r,ω). The ladder operators define single-quantum field excitations |r,ω〉 = â†(r,ω)|{0}〉. In the limit of a sharply peaked LDOS with a Lorentzian profile around a centre frequency ωc with width γ,
G(r,r,ω). The ladder operators define single-quantum field excitations |r,ω〉 = â†(r,ω)|{0}〉. In the limit of a sharply peaked LDOS with a Lorentzian profile around a centre frequency ωc with width γ,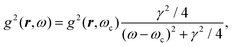 | (66) |
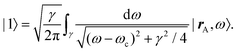 | (67) |
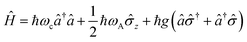 | (68) |
![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) † = |e〉〈g|, and σz = |e〉〈e| − |g〉〈g| denotes the atomic inversion operator. The coupling strength g (
† = |e〉〈g|, and σz = |e〉〈e| − |g〉〈g| denotes the atomic inversion operator. The coupling strength g (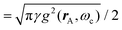 in the framework of macroscopic QED380) is given by the overlap of the atomic transition dipole moment and the cavity electric field. As we have assumed near resonance between atomic transition and the cavity mode, we have employed the rotating-wave approximation and dropped the off-resonant, counter-rotating terms that would ordinarily be present in the electric–dipole Hamiltonian (for ultra-strong coupling, this assumption is no longer valid and has to be relaxed, leading to the Tavis–Cummings model383).
in the framework of macroscopic QED380) is given by the overlap of the atomic transition dipole moment and the cavity electric field. As we have assumed near resonance between atomic transition and the cavity mode, we have employed the rotating-wave approximation and dropped the off-resonant, counter-rotating terms that would ordinarily be present in the electric–dipole Hamiltonian (for ultra-strong coupling, this assumption is no longer valid and has to be relaxed, leading to the Tavis–Cummings model383).
The Jaynes–Cummings model is a rare example of an exactly solvable model of interacting quantum systems. The Hamiltonian (68) is block-diagonal in the basis of atom-field states {|n,e〉,|n + 1,g〉} containing either n photons and with the atom in its excited state, or the field containing n + 1 photons on the expense of the atom residing in its ground state,
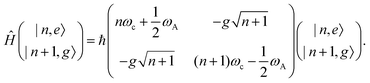 | (69) |
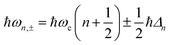 | (70) |
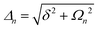 that depends on the detuning δ = ωA − ωc of the atomic transition from the cavity resonance, and the n-photon Rabi frequency
that depends on the detuning δ = ωA − ωc of the atomic transition from the cavity resonance, and the n-photon Rabi frequency 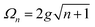 . Its eigenstates are linear combinations of the unperturbed states
. Its eigenstates are linear combinations of the unperturbed states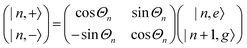 | (71) |
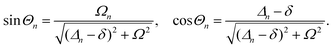 | (72) |
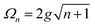 . It is worth noting that even in the absence of a photon, n = 0, the eigenstates |0,±〉 are split by the vacuum Rabi splitting Ω0 = 2g. At exact resonance, the exact eigenstates (or dressed states) are (anti-)symmetric combinations of the unperturbed states
. It is worth noting that even in the absence of a photon, n = 0, the eigenstates |0,±〉 are split by the vacuum Rabi splitting Ω0 = 2g. At exact resonance, the exact eigenstates (or dressed states) are (anti-)symmetric combinations of the unperturbed states  .
.
Because the Jaynes–Cummings model is exactly solvable, the resulting unitary evolution is also known exactly.334 Its experimental verification384 using superconducting microwave cavities and circular Rydberg atoms has been remarkably successful, and included the generation of maximally entangled pairs of atoms385 as well as of Schrödinger cat-like states between an atom and the radiation field,386 the development of a single-atom single-photon quantum interface387 or the observation of photon blockade388 in a cavity.
More recently, it has been realised that the strong coupling to light in a cavity also influences the dynamics of chemical reactions177,180,181 which led to the development of the field of polaritonic chemistry or QED chemistry.179 The strong coupling to the cavity field can be used to control chemical reaction rates177 or energy-transfer rates between molecules.182 These developments opened up a new field in which even the engineering of novel quantum materials becomes feasible.183 What has started out as a model system in quantum optics, strong coupling to light fields has turned into an important tool in fields ranging from quantum information processing and quantum engineering to QED-enhanced chemistry.
4.6 Prediction of molecular aggregate structures
A fascinating field of experimental applications is to use the ability of weakly interacting molecules to self-organise on interfaces and surfaces (see, e.g., Sections 2.1, 2.2, 2.4, 2.3).39,93 The resulting structures are often stable at elevated temperatures and can therefore be produced at air–water interfaces78,79 or within liquid environments.389–391 The latter allows for electrochemical control that gives an additional handle on a variety of structures that can be achieved.392 Theoretical descriptions of such aggregates are mostly based on modelling experimentally observed patterns, but efforts for ab initio theoretical predictions of molecular aggregate structures are less frequent. Such a possibility would be an essential prerequisite to develop molecular target structures that will exhibit tailored photonic and electronic properties as materials (see Section 2.4 on solar cells). Usually, geometries of small aggregates are created manually, extracted from experimental crystal structures, or are identified by searching for minima on the energy hypersurface. Due to the obvious drawbacks of the first two ways, namely limitation by chemical intuition and availability of crystal structures, an overview of currently available methods for theoretical determination of aggregate structures is given here.An established method to determine energetically favourable, hence frequently appearing, aggregate structures is molecular dynamics (MD) simulations,393 but it is often very time-consuming and does not accurately describe the dispersion interactions. Faster coarse-grained simulations does not always allow a simple back-mapping of the coarse structure to the underlying atomistic structure.394–396 Alternatively, the energy hypersurface of dimers might be explicitly sampled, what can be very demanding also. Therefore, fitting approaches that necessitate only a few quantum chemical calculations of possible dimer structures and approaches where multiple dimer structures are created randomly or systematically have been developed.397,398
In one of such systematic approaches, all possible dimers of a pre-defined spatial (e.g., 100 × 100 × 100 points) and rotational grid (e.g., yielding 106 × 10 × 10 × 10 total grid points) are energetically evaluated with force fields methods as implemented in the OpenBabel program. The program EnergyScan,399 which utilises OpenBabel libraries, efficiently identifies energetically favourable and geometrically distinct dimer structures. For the case of urea, identical dimers have been identified through extensive MD runs,393 but π-stacks are not properly recognised as energetically favourable due to the disadvantages of the force fields.399 For example in porphin, approximately 6400, 3260, and 1900 energy evaluations can be performed per second and thread on a desktop computer (year 2018) for a dimer, a trimer, and a quadrumer of porphin, respectively. To properly identify all relevant aggregate structures, i.e., those bound by dispersion forces, supplementary searches based on DFT (see Section 4.3) or other methods (see Section 4.4.1) are necessary (Fig. 14).
 | ||
| Fig. 14 Local energy minimum geometries and associated binding energies of urea dimers as found by EnergyScan with subsequent quantum chemical optimisation. The first four types are urea–urea pair-conformations known from the literature, the first three of which have been identified in the literature through extensive MD simulations. Dot-dashed lines indicate hydrogen bonds. Reprinted with permission from Sachse et al.,399 Copyright (2018) John Wiley and Sons. | ||
Upon increasing the concentration of organic dyes in solution, the individual dye molecules can self-assemble in supra-molecular structures (e.g., cylinders) consisting of thousands of molecules.400 The resulting structure depends on an intricate interplay between the morphology of the dye molecules, entropic effects, and electrostatic and dispersive interactions. Direct imaging of these fragile structures is a difficult task and therefore, typically a combination of optical spectroscopy techniques is used to obtain information about possible structures.400–404 A promising future direction is the application of machine-learning methods to extract the arrangement of the molecules of the aggregate from optical spectra and theoretical calculations, ref. 405. In recent years, these spectroscopic approaches have been amended by Cryo-STM images406,407 and also first steps have been made to investigate the stability of the predicted structures using molecular dynamics simulations.408–413
4.7 Ensembles of highly excited atoms
In nearly all of the examples discussed in this review, the dispersion forces are mostly relevant at small distances in the nanometer range. Highly excited atoms (the so called Rydberg atoms) are paradigmatic systems to precisely study dispersion interactions, which manifest themselves even at interatomic distances in the order of several micrometers. This is because of the huge polarisability of such Rydberg atoms, which scales roughly as n7, where n is the principal quantum number of the Rydberg electron.This long-range interaction leads for example to the formation of macrodimers414,415 and it is important for the implementation of quantum gates.416–419 Ensembles of Rydberg atoms can for example be excited in ultra-cold gases or Bose–Einstein condensates. Here, the long range interactions play a crucial role in forming correlated distributions of the excited atoms. In recent years it became also possible to create arrangements of Rydberg atoms in nearly arbitrary arrangements using optical lattices or tweezer arrays.420,421
To get a feeling about the most relevant aspects of the long-range interactions between Rydberg atoms, we will discuss the example of alkali atoms (such as lithium or rubidium), which are commonly used in experiments. Alkali atoms are hydrogen-like, with their single valence electron moving in a modified Coulomb potential because of the polarisability of the core electrons.422 The size of their wavefunction scales with n2. As it is common to work in experiments with principal quantum numbers in the range from n = 20 up to n = 200, their classical Bohr radius of roughly 1 μm for n = 200 makes them mesoscopic quantum objects.
In the following we consider two atoms, denoted by A and B. Their quantum evolution is governed by the Hamiltonian H = HA + HB + Vint, where HA and HB are the Hamiltonians of the individual atoms [eqn (38)] and Vint is the interaction between the two atoms. We consider the case in which the distance between the atoms located at RA and RB is so large that there is negligible overlap of their wavefunctions,423i.e. we assume R = |R| = |RA − RB| > 2(〈rA2〉1/2 + 〈rB2〉1/2), where the coordinates of the valence electron of each atom with respect to the position of the atom core are denoted by rA and rB, respectively. On the other hand, we restrict ourselves to distances where the retardation effects of the interaction between the two atoms can be neglected. This distance can be estimated424 by Rret ≈ (n − δl)3/(8πRy) with Ry the Rydberg constant of the respective atom and δl the quantum defect, which depends on the angular momentum state l. For distances |RA − RB| < Rret, the interaction between the atoms is approximated as the sum of the Coulomb interactions between the positively charged cores and the Rydberg electrons which is conveniently expressed in terms of interactions between the multipoles of the individual atoms. For not too small separations between the atoms, the dominant term is the dipole–dipole interaction 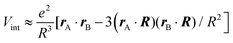 . At these distances, one can perform second-order perturbation theory425 with respect to the eigenstates of the individual atoms |nA,lA,jA,mA〉|nB,lB,jB,mB〉, where n, l, j and m denote the principal quantum number, the orbital angular momentum, the total angular momentum and the corresponding magnetic quantum number of the individual atoms, respectively. The energy of such a state is EnA,lA,jA + EnB,lB,jB and is independent of the magnetic quantum numbers mA and mB. Let us first consider the case when both atoms have the same quantum numbers n, l, and j, i.e., they have the same energy En,l,j and the unperturbed energy of the pair state is 2En,l,j, which is (2j + 1)2 fold degenerate. Consider for example the case when both atoms are in a state with principal quantum number n state and angular momentum l = 0. Ignoring the fine structure splitting and the magnetic quantum numbers, the second-order expression for the energy correction becomes425–427
. At these distances, one can perform second-order perturbation theory425 with respect to the eigenstates of the individual atoms |nA,lA,jA,mA〉|nB,lB,jB,mB〉, where n, l, j and m denote the principal quantum number, the orbital angular momentum, the total angular momentum and the corresponding magnetic quantum number of the individual atoms, respectively. The energy of such a state is EnA,lA,jA + EnB,lB,jB and is independent of the magnetic quantum numbers mA and mB. Let us first consider the case when both atoms have the same quantum numbers n, l, and j, i.e., they have the same energy En,l,j and the unperturbed energy of the pair state is 2En,l,j, which is (2j + 1)2 fold degenerate. Consider for example the case when both atoms are in a state with principal quantum number n state and angular momentum l = 0. Ignoring the fine structure splitting and the magnetic quantum numbers, the second-order expression for the energy correction becomes425–427
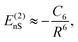 | (73) |
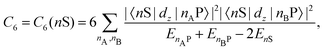 | (74) |
So far, we discussed the dispersion interaction for the case when both atoms are in the same Rydberg state. If the atoms are in angular momentum states that differ by one, then one of the pair states is degenerate and one has first to diagonalise the respective subspaces, which results in a 1/R3 distance scaling.
Many recent experiments are performed at rather small distances and with such a precision that perturbative calculations as well as restrictions to the leading dipole–dipole interaction term are no longer sufficient. Then, diagonalisation within a suitable two-particle basis is the method of choice. In ref. 424, 428 and 429, relevant aspects of such calculation for Rydberg energy potential surfaces are reviewed. One finds that overall the eigenenergies and eigenstates as function of distance show a rich behaviour with strong state mixing at small distances, and even at larger distances different power laws can appear. This picture is even more complicated when the Rydberg atoms are close to a surface430 or when more than two Rydberg atoms are involved.
Experimentally, there is a long tradition to investigate the van der Waals interaction between Rydberg atoms and surfaces.431,432 Recently, it has also become possible to investigate the interaction between two individual Rydberg atoms.433,434 Good agreements between experiment and numerical results based on the full diagonalisation in a large basis have been found.
5 Conclusions
This review aims to give an overview of weak (non-covalent) interactions, demonstrating the role they have played in recent research projects. Due to the huge variety in different applications, such as nano-structured materials for solar cells (Section 2.4); vdW heterostructures (Section 2.2); micro- and nano-electro-mechanical systems (Section 2.5); and electrochemical transistors (Section 2.3) (to name some applications discussed in this article); resulting applications from interactions on surfaces (Section 2.1); self-organisation (Section 4.6) and many besides, weak interactions are studied from different perspectives that we want to bring closer together. We introduced the research topic with a summary of the terminologies used in various scientific communities, Section 1. We illuminated their investigations by discussing the effects, such as Rabi splitting, Section 2.6, or superradiance, Section 2.1, and characterisation methods such as microscopy, Section 3.1, helium scattering, Sections 3.2 and 3.3, and back-focal plane imagining, Section 2.3. Finally, we summarised different theories describing these materials and their dielectric properties. Here, we focused on microscopic modelling via density functional theory, Section 4.3, and their propagation to larger scales in the mean-field approximation, Section 4.6, and via statistical methods, Section 4.1, and macroscopic quantum electrodynamics, Section 4.4. These models work best in a vacuum, whereas most experiments occur in a solution or are strongly influenced by a surrounding medium. To this end, we illustrated extensions to continuum models, Section 4.4.4, and included an entire chapter on interactions between colloids, Section 4.2, and finalised the manuscript with an outlook on field enhancements via cavities leading to strong coupling, Section 4.5, and effects caused by highly excited (Rydberg) atoms, Section 4.7. Finally, weak interactions in complex materials are a vast topic and studied by many different scientists. This article cannot reflect the entire research, but we are confident that it supports the exchange between the involved researchers.Author contributions
In the following, we summarise the authors being mainly responsible for the separate Sections: J. F.: Sections 4.4, 4.4.1, 4.4.2, and 4.4.5; K. B.: Sections 2.1 and 4.3; J. W. B.: Sections 2.6 and 3.4; R. W. C.: Section 3.1; A. E.: Sections 2.1 and 4.7; D. G.-K.: Section 4.1; M. M. G.: Section 2.4; B. H.: Sections 2.5 and 3.2; K. J.: Section 3.1; M. K.: Section 4.1; D. F. P.: Sections 4.2 and 4.4.4; C. P.: Sections 4.3.1 and 4.4.3; M. P.: Sections 2.2, 3.4, and 4.6; T. R.: Sections 2.4 and 3.3; S. S.: Sections 4.5 and 4.7; F. S.: Section 2.1; M. T.: Section 3.2; M. W.: Sections 2.1, 4.3.1, 4.4.4, and 4.6; R. T. W.: Sections 2.2, 2.3, 2.6, 3.1, and 3.4; and J. Z.: Section 2.1. All authors contributed equally to the Sections 1 and 5.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge support from the Research Council of Norway (NFR; project: 332447). C. P. acknowledges European Union's Horizon 2020 research and innovation programme, grant no. 869815. F. S. acknowledges funding by the Deutsche Forschungsgemeinschaft (DFG; project STI 125/25-1 and DFG; project RTG 2717 DYNCAM). D. G.-K. acknowledges funding by the Israel Science Foundation (grant No. 2247/22) and the Council for Higher Education Support Program for Hiring Outstanding Faculty Members in Quantum Science and Technology in Research Universities. J. F. gratefully acknowledges support from the European Union (H2020-MSCA-IF-2020, grant number: 101031712). M. W. and J. F. acknowledge funding by the Deutsche Forschungsgemeinschaft (DFG; project WA 1687/10-1 and DFG; project BU 1803/6-1). T. R. acknowledges support by the Ministry of Science, Research and Art of Baden-Württemberg via a Research Seed Capital (RISC) grant, as well as the Helmholtz Association.Notes and references
- E. Klampaftis, D. Ross, K. R. McIntosh and B. S. Richards, Sol. Energy Mater. Sol. Cells, 2009, 93, 1182–1194 CrossRef CAS.
- S. Izadnia, D. W. Schönleber, A. Eisfeld, A. Ruf, A. C. LaForge and F. Stienkemeier, J. Phys. Chem. Lett., 2017, 8, 2068–2073 CrossRef CAS PubMed.
- F. Stienkemeier and K. K. Lehmann, J. Phys. B: At., Mol. Opt. Phys., 2006, 39, R127 CrossRef CAS.
- P. Moraitis, R. Schropp and W. van Sark, Opt. Mat., 2018, 84, 636–645 CrossRef CAS.
- P. K. Nayak, S. Mahesh, H. J. Snaith and D. Cahen, Nat. Rev. Mat., 2019, 4, 269–285 CrossRef CAS.
- A. Zatirostami, J. Alloys Compd., 2020, 844, 156151 CrossRef CAS.
- W. Cai, H. Li, M. Li, M. Wang, H. Wang, J. Chen and Z. Zang, J. Phys. D: Appl. Phys., 2021, 54, 293002 CrossRef CAS.
- A. Christou, F. Liu and R. Dahiya, Microsyst. Nanoeng., 2021, 7, 82 CrossRef CAS PubMed.
- J. Nemirovsky and Y. Sagi, Phys. Rev. Res., 2021, 3, 013113 CrossRef CAS.
- N. Gack, G. Iankevich, C. Benel, R. Kruk, D. Wang, H. Hahn and T. Reisinger, Nanomaterials, 2020, 10, 2192 CrossRef CAS PubMed.
- C. Outeiral, M. Strahm, J. Shi, G. M. Morris, S. C. Benjamin and C. M. Deane, WIREs Comput. Mol. Sci., 2021, 11, e1481 CAS.
- F. Biedermann and H.-J. Schneider, Chem. Rev., 2016, 116, 5216–5300 CrossRef CAS PubMed.
- F. Zheng, X. Gao and A. Eisfeld, Phys. Rev. Lett., 2019, 123, 163202 CrossRef CAS PubMed.
- T. Nesse, I. Simonsen and B. Holst, Phys. Rev. Appl., 2019, 11, 024009 CrossRef CAS.
- M. Boström, V. Esteso, J. Fiedler, I. Brevik, S. Y. Buhmann, C. Persson, S. Carretero-Palacios, D. F. Parsons and R. W. Corkery, Astron. Astrophys., 2021, 650, A54 CrossRef.
- Intermolecular and Surface Forces, ed. J. N. Israelachvili, Academic Press, San Diego, 3rd edn, 2011 Search PubMed.
- P. Barcellona, R. Bennett and S. Y. Buhmann, J. Phys. Commun., 2018, 2, 035027 CrossRef.
- B. Guillot, J. Mol. Liq., 2002, 101, 219–260 CrossRef CAS.
- H. B. G. Casimir, K. Ned. Akad. Wet., 1948, 51, 793 Search PubMed.
- H. B. G. Casimir and D. Polder, Phys. Rev., 1948, 73, 360–372 CrossRef CAS.
- I. E. Dzyaloshinskii, E. M. Lifshitz and L. P. Pitaevskii, Adv. Phys., 1961, 10, 165–209 CrossRef.
- V. Esteso, S. Carretero-Palacios, L. G. MacDowell, J. Fiedler, D. F. Parsons, F. Spallek, H. Míguez, C. Persson, S. Y. Buhmann, I. Brevik and M. Boström, Phys. Chem. Chem. Phys., 2020, 22, 11362–11373 RSC.
- M. Chern, J. C. Kays, S. Bhuckory and A. M. Dennis, Methods Appl. Fluoresc., 2019, 7, 012005 CrossRef CAS PubMed.
- H. Watzinger, J. Kukučka, L. Vukuši, F. Gao, T. Wang, F. Schäffler, J.-J. Zhang and G. Katsaros, Nat. Commun., 2018, 9, 3902 CrossRef PubMed.
- J. P. Toennies and A. F. Vilesov, Angew. Chem., Int. Ed., 2004, 43, 2622–2648 CrossRef CAS PubMed.
- M. Dvorak, M. Müller, T. Knoblauch, O. Bünermann, A. Rydlo, S. Minniberger, W. Harbich and F. Stienkemeier, J. Chem. Phys., 2012, 137, 164301 CrossRef PubMed.
- J. Farges, M. de Feraudy, B. Raoult and G. Torchet, Surf. Sci., 1981, 106, 95–100 CrossRef CAS.
- M. Hartmann, R. E. Miller, J. P. Toennies and A. Vilesov, Phys. Rev. Lett., 1995, 75, 1566–1569 CrossRef CAS PubMed.
- J. Harms, M. Hartmann, J. P. Toennies, A. F. Vilesov and B. Sartakov, J. Mol. Spectrosc., 1997, 185, 204–206 CrossRef CAS PubMed.
- G. B. Piland and C. J. Bardeen, J. Phys. Chem. Lett., 2015, 6, 1841–1846 CrossRef CAS PubMed.
- E. Garoni, J. Zirzlmeier, B. S. Basel, C. Hetzer, K. Kamada, D. M. Guldi and R. R. Tykwinski, J. Am. Chem. Soc., 2017, 139, 14017–14020 CrossRef CAS PubMed.
- A. Rao and R. H. Friend, Nat. Rev. Mat., 2017, 2, 17063 CrossRef CAS.
- M. Müller, S. Izadnia, S. M. Vlaming, A. Eisfeld, A. LaForge and F. Stienkemeier, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 121408 CrossRef.
- O. Stauffert, S. Izadnia, F. Stienkemeier and M. Walter, J. Chem. Phys., 2019, 150, 244703 CrossRef PubMed.
- M. Bohlen, R. Michiels, M. Michelbach, S. Ferchane, M. Walter, A. Eisfeld and F. Stienkemeier, J. Chem. Phys., 2022, 156, 034305 CrossRef CAS PubMed.
- E. Le Moal, M. Müller, O. Bauer and M. Sokolowski, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 045301 CrossRef.
- M. Müller, A. Paulheim, A. Eisfeld and M. Sokolowski, J. Chem. Phys., 2013, 139, 044302 CrossRef PubMed.
- R. Hoffmann-Vogel, Rep. Prog. Phys., 2017, 81, 016501 CrossRef PubMed.
- D. P. Goronzy, M. Ebrahimi, F. Rosei, A. Arramel, Y. Fang, S. De Feyter, S. L. Tait, C. Wang, P. H. Beton, A. T. S. Wee, P. S. Weiss and D. F. Perepichka, ACS Nano, 2018, 12, 7445 CrossRef CAS PubMed.
- Y. Zhang, Y. Luo, Y. Zhang, Y.-J. Yu, Y.-M. Kuang, L. Zhang, Q.-S. Meng, Y. Luo, J.-L. Yang, Z.-C. Dong and J. G. Hou, Nature, 2016, 531, 623 CrossRef CAS PubMed.
- B. Yang, G. Chen, A. Ghafoor, Y. Zhang, Y. Zhang, Y. Zhang, Y. Luo, J. Yang, V. Sandoghdar, J. Aizpurua, Z. Dong and J. G. Hou, Nat. Phot., 2020, 14, 693 CrossRef CAS.
- X. Gao and A. Eisfeld, J. Phys. Chem. Lett., 2018, 9, 6003–6010 CrossRef CAS PubMed.
- Y. Luo, G. Chen, Y. Zhang, L. Zhang, Y. Yu, F. Kong, X. Tian, Y. Zhang, C. Shan, Y. Luo, J. Yang, V. Sandoghdar, Z. Dong and J. G. Hou, Phys. Rev. Lett., 2019, 122, 233901 CrossRef CAS PubMed.
- J. Doležal, S. Canola, P. Hapala, R. C. de Campos Ferreira, P. Merino and M. Švec, ACS Nano, 2022, 16, 1082–1088 CrossRef PubMed.
- A. Eisfeld, C. Marquardt, A. Paulheim and M. Sokolowski, Phys. Rev. Lett., 2017, 119, 097402 CrossRef PubMed.
- Diamond-Based Materials for Biomedical Applications, ed. R. Narayan, Woodhead Publishing, 2013 Search PubMed.
- Q. Xu and X. Zhao, J. Mater. Chem., 2012, 22, 16416–16421 RSC.
- B. S. Miller, L. Bezinge, H. D. Gliddon, D. Huang, G. Dold, E. R. Gray, J. Heaney, P. J. Dobson, E. Nastouli, J. J. L. Morton and R. A. McKendry, Nature, 2020, 587, 588–593 CrossRef CAS PubMed.
- D. P. Bottaro, J. S. Rubin, D. L. Faletto, A. M.-L. Chan, T. E. Kmiecik, G. F. V. Woude and S. A. Aaronson, Science, 1991, 251, 802–804 CrossRef CAS PubMed.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, M. I. Katsnelson, I. V. Grigorieva, S. V. Dubonos and A. A. Firsov, Nature, 2005, 438, 197–200 CrossRef CAS PubMed.
- Y. Zhang, Y.-W. Tan, H. L. Stormer and P. Kim, Nature, 2005, 438, 201–204 CrossRef CAS PubMed.
- C. R. Dean, A. F. Young, I. Meric, C. Lee, L. Wang, S. Sorgenfrei, K. Watanabe, T. Taniguchi, P. Kim, K. L. Shepard and J. Hone, Nat. Nanotechnol., 2010, 5, 722–726 CrossRef CAS PubMed.
- T. Taniguchi and K. Watanabe, J. Cryst. Growth, 2007, 303, 525–529 CrossRef CAS.
- R. T. Weitz and A. Yacoby, Nat. Nanotechnol., 2010, 5, 699–700 CrossRef CAS PubMed.
- L. Renn, L. S. Walter, K. Watanabe, T. Taniguchi and R. T. Weitz, Adv. Mater. Interfaces, 2022, 9, 2101701 CrossRef CAS.
- Y. J. Chung, K. A. Villegas Rosales, K. W. Baldwin, P. T. Madathil, K. W. West, M. Shayegan and L. N. Pfeiffer, Nat. Mater., 2021, 20, 632–637 CrossRef CAS PubMed.
- F. R. Geisenhof, F. Winterer, S. Wakolbinger, T. D. Gokus, Y. C. Durmaz, D. Priesack, J. Lenz, F. Keilmann, K. Watanabe, T. Taniguchi, R. Guerrero-Avilés, M. Pelc, A. Ayuela and R. T. Weitz, ACS Appl. Nano Mater., 2019, 2, 6067–6075 CrossRef CAS.
- R. Guerrero-Avilés, M. Pelc, F. Geisenhof, T. Weitz and A. Ayuela, Relative Stability of Bernal and Rhombohedral Stackings in Trilayer Graphene under Distortions, 2021, https://arxiv.org/abs/2110.06590.
- N. Mounet, M. Gibertini, P. Schwaller, D. Campi, A. Merkys, A. Marrazzo, T. Sohier, I. E. Castelli, A. Cepellotti, G. Pizzi and N. Marzari, Nat. Nanotechnol., 2018, 13, 246–252 CrossRef CAS PubMed.
- D. G. Purdie, N. M. Pugno, T. Taniguchi, K. Watanabe, A. C. Ferrari and A. Lombardo, Nat. Commun., 2018, 9, 5387 CrossRef CAS PubMed.
- K. S. Novoselov, A. Mishchenko, A. Carvalho and A. H. C. Neto, Science, 2016, 353, aac9439 CrossRef CAS PubMed.
- S. Wakolbinger, F. R. Geisenhof, F. Winterer, S. Palmer, J. G. Crimmann, K. Watanabe, T. Taniguchi, F. Trixler and R. T. Weitz, 2D Mater., 2020, 7, 035002 CrossRef CAS.
- C. R. Dean, L. Wang, P. Maher, C. Forsythe, F. Ghahari, Y. Gao, J. Katoch, M. Ishigami, P. Moon, M. Koshino, T. Taniguchi, K. Watanabe, K. L. Shepard, J. Hone and P. Kim, Nature, 2013, 497, 598–602 CrossRef CAS PubMed.
- J. I. A. Li, T. Taniguchi, K. Watanabe, J. Hone and C. R. Dean, Nat. Phys., 2017, 13, 751–755 Search PubMed.
- J. O. Island, X. Cui, C. Lewandowski, J. Y. Khoo, E. M. Spanton, H. Zhou, D. Rhodes, J. C. Hone, T. Taniguchi, K. Watanabe, L. S. Levitov, M. P. Zaletel and A. F. Young, Nature, 2019, 571, 85–89 CrossRef CAS PubMed.
- A. M. Seiler, F. R. Geisenhof, F. Winterer, K. Watanabe, T. Taniguchi, T. Xu, F. Zhang and R. T. Weitz, Quantum cascade of new correlated phases in trigonally warped bilayer graphene, 2021, https://arxiv.org/abs/2111.06413.
- F. R. Geisenhof, F. Winterer, A. M. Seiler, J. Lenz, T. Xu, F. Zhang and R. T. Weitz, Nature, 2021, 598, 53–58 CrossRef CAS PubMed.
- Y. Cao, V. Fatemi, A. Demir, S. Fang, S. L. Tomarken, J. Y. Luo, J. D. Sanchez-Yamagishi, K. Watanabe, T. Taniguchi, E. Kaxiras, R. C. Ashoori and P. Jarillo-Herrero, Nature, 2018, 556, 80–84 CrossRef CAS PubMed.
- Y. Cao, V. Fatemi, S. Fang, K. Watanabe, T. Taniguchi, E. Kaxiras and P. Jarillo-Herrero, Nature, 2018, 556, 43–50 CrossRef CAS PubMed.
- M. Kasha, Radiat. Res., 1963, 20, 55–70 CrossRef CAS PubMed.
- S. Das, F. Herrmann-Westendorf, F. H. Schacher, E. Tauscher, U. Ritter, B. Dietzek and M. Presselt, ACS Appl. Mater. Interfaces, 2016, 8, 21512–21521 CrossRef CAS PubMed.
- M. L. Hupfer, D. Blaschke, H. Schmidt and M. Presselt, Langmuir, 2021, 37, 13255–13264 CrossRef CAS PubMed.
- J. Bellessa, C. Symonds, K. Vynck, A. Lemaitre, A. Brioude, L. Beaur, J. C. Plenet, P. Viste, D. Felbacq, E. Cambril and P. Valvin, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 033303 CrossRef.
- J. George, T. Chervy, A. Shalabney, E. Devaux, H. Hiura, C. Genet and T. W. Ebbesen, Phys. Rev. Lett., 2016, 117, 153601 CrossRef PubMed.
- S. Dey, C. Fan, K. V. Gothelf, J. Li, C. Lin, L. Liu, N. Liu, M. A. D. Nijenhuis, B. Saccà, F. C. Simmel, H. Yan and P. Zhan, Nat. Rev. Methods Primers, 2021, 1, 13 CrossRef CAS.
- F. Hong, F. Zhang, Y. Liu and H. Yan, Chem. Rev., 2017, 117, 12584–12640 CrossRef CAS PubMed.
- W. Liu, H. Duan, D. Zhang, X. Zhang, Q. Luo, T. Xie, H. Yan, L. Peng, Y. Hu, L. Liang, G. Zhao, Z. Xie and J. Hu, Appl. Bionics. Biomech., 2021, 2021, 9112407 Search PubMed.
- K. Ariga, Langmuir, 2020, 36, 7158–7180 CrossRef CAS PubMed.
- K. Ariga, Y. Yamauchi, T. Mori and J. P. Hill, Adv. Mater., 2013, 25, 6477–6512 CrossRef CAS PubMed.
- I. Langmuir, J. Am. Chem. Soc., 1917, 39, 1848–1906 CrossRef CAS.
- I. Langmuir and K. B. Blodgett, Kolloid-Z., 1935, 73, 257–263 CrossRef.
- Y. Yonamine, K. Cervantes-Salguero, K. Minami, I. Kawamata, W. Nakanishi, J. P. Hill, S. Murata and K. Ariga, Phys. Chem. Chem. Phys., 2016, 18, 12576–12581 RSC.
- D. Bialas, C. W. Zhong, F. Wurthner and F. C. Spano, J. Phys. Chem. C, 2019, 123, 18654–18664 CrossRef CAS.
- N. J. Hestand and F. C. Spano, Chem. Rev., 2018, 118, 7069–7163 CrossRef CAS PubMed.
- B. Heyne, Photochem. Photobiol. Sci., 2016, 15, 1103–1114 CrossRef CAS PubMed.
- E. E. Jelley, Nature, 1937, 139, 631 CrossRef CAS.
- G. Scheibe, Angew. Chem., 1937, 50, 212–219 CrossRef CAS.
- F. C. Spano, Acc. Chem. Res., 2010, 43, 429–439 CrossRef CAS PubMed.
- F. Würthner, Acc. Chem. Res., 2016, 49, 868–876 CrossRef PubMed.
- F. Würthner, S. Yao, T. Debaerdemaeker and R. Wortmann, J. Am. Chem. Soc., 2002, 124, 9431–9447 CrossRef PubMed.
- C. W. Zhong, D. Bialas and F. C. Spano, J. Phys. Chem. C, 2020, 124, 2146–2159 CrossRef CAS.
- M. L. Hupfer, S. Ghosh, Y. Wang, T. Opsomer, W. Dehaen and M. Presselt, Adv. Mater. Interfaces, 2021, 9, 2101490 CrossRef.
- S. Das and M. Presselt, J. Mater. Chem. C, 2019, 7, 6194–6216 RSC.
- G. Herzberg and E. Teller, Z. Phys. Chem. (Frankfurt am Main), 1933, B21, 410 CrossRef CAS.
- F. Negri, G. Orlandi and F. Zerbetto, J. Chem. Phys., 1992, 97, 6496–6503 CrossRef CAS.
- G. Orlandi and W. Siebrand, J. Chem. Phys., 1973, 58, 4513–4523 CrossRef CAS.
- N. J. Hestand, H. Yamagata, B. L. Xu, D. Z. Sun, Y. Zhong, A. R. Harutyunyan, G. G. Chen, H. L. Dai, Y. Rao and F. C. Spano, J. Phys. Chem. C, 2015, 119, 22137–22147 CrossRef CAS.
- O. Ostroverkhova, S. Shcherbyna, D. G. Cooke, R. F. Egerton, F. A. Hegmann, R. R. Tykwinski, S. R. Parkin and J. E. Anthony, J. Appl. Phys., 2005, 98, 033701 CrossRef.
- J. A. Reinspach, Y. Diao, G. Giri, T. Sachse, K. England, Y. Zhou, C. Tassone, B. J. Worfolk, M. Presselt, M. F. Toney, S. Mannsfeld and Z. Bao, ACS Appl. Mater. Interfaces, 2016, 8, 1742–1751 CrossRef CAS PubMed.
- B. Munkhbat, A. Canales, B. Küçüköz, D. G. Baranov and T. O. Shegai, Nature, 2021, 597, 214–219 CrossRef CAS PubMed.
- S. H. Kim, K. Hong, W. Xie, K. H. Lee, S. Zhang, T. P. Lodge and C. D. Frisbie, Adv. Mater., 2013, 25, 1822–1846 CrossRef CAS PubMed.
- M. Kettner, I. Vladimirov, A. J. Strudwick, M. G. Schwab and R. T. Weitz, J. Appl. Phys., 2015, 118, 025501 CrossRef.
- J. Lenz, A. M. Seiler, F. R. Geisenhof, F. Winterer, K. Watanabe, T. Taniguchi and R. T. Weitz, Nano Lett., 2021, 21, 4430–4436 CrossRef CAS PubMed.
- Y. van de Burgt, E. Lubberman, E. J. Fuller, S. T. Keene, G. C. Faria, S. Agarwal, M. J. Marinella, A. Alec Talin and A. Salleo, Nat. Mater., 2017, 16, 414–418 CrossRef CAS PubMed.
- C. Eckel, J. Lenz, A. Melianas, A. Salleo and R. T. Weitz, Nano Lett., 2022, 22, 973–978 CrossRef CAS PubMed.
- A. Shirinskaya, G. Horowitz, J. Rivnay, G. G. Malliaras and Y. Bonnassieux, Biosensors, 2018, 8, 103 CrossRef CAS PubMed.
- J. F. Geisz, R. M. France, K. L. Schulte, M. A. Steiner, A. G. Norman, H. L. Guthrey, M. R. Young, T. Song and T. Moriarty, Nat. Energy, 2020, 5, 326–335 CrossRef CAS.
- C. A. Nelson, N. R. Monahan and X.-Y. Zhu, Energy Environ. Sci., 2013, 6, 3508–3519 RSC.
- J.-F. Guillemoles, T. Kirchartz, D. Cahen and U. Rau, Nat. Photonics, 2019, 13, 501–505 CrossRef CAS.
- A. Deinega and S. John, J. Appl. Phys., 2012, 112, 074327 CrossRef.
- D. M. Callahan, J. N. Munday and H. A. Atwater, Nano Lett., 2012, 12, 214–218 CrossRef CAS PubMed.
- Z. Yu, A. Raman and S. Fan, Proc. Nat. Acad. Sci. U. S. A., 2010, 107, 17491–17496 CrossRef CAS PubMed.
- S. Buddhiraju and S. Fan, Phys. Rev. B, 2017, 96, 035304 CrossRef.
- J. Wallentin, N. Anttu, D. Asoli, M. Huffman, I. Åberg, M. H. Magnusson, G. Siefer, P. Fuss-Kailuweit, F. Dimroth, B. Witzigmann, H. Q. Xu, L. Samuelson, K. Deppert and M. T. Borgström, Science, 2013, 339, 1057–1060 CrossRef CAS PubMed.
- R. Kapadia, Z. Fan, K. Takei and A. Javey, Nano Energy, 2012, 1, 132–144 CrossRef CAS.
- S.-F. Leung, M. Yu, Q. Lin, K. Kwon, K.-L. Ching, L. Gu, K. Yu and Z. Fan, Nano Lett., 2012, 12, 3682–3689 CrossRef CAS PubMed.
- A. Peter Amalathas and M. M. Alkaisi, Mater. Sci. Semicond. Process., 2017, 57, 54–58 CrossRef.
- M. A. Green and S. Pillai, Nat. Photonics, 2012, 6, 130–132 CrossRef CAS.
- P. G. Jamkhande, N. W. Ghule, A. H. Bamer and M. G. Kalaskar, J. Drug Delivery Sci. Technol., 2019, 53, 101174 CrossRef CAS.
- H. A. Atwater and A. Polman, Nat. Mater., 2010, 9, 205–213 CrossRef CAS PubMed.
- V. Giannini, Y. Zhang, M. Forcales and J. G. Rivas, Opt. Express, 2008, 16, 19674–19685 CrossRef CAS PubMed.
- D. Derkacs, S. H. Lim, P. Matheu, W. Mar and E. T. Yu, Appl. Phys. Lett., 2006, 89, 093103 CrossRef.
- H. R. Stuart and D. G. Hall, Appl. Phys. Lett., 1996, 69, 2327–2329 CrossRef CAS.
- S. Pillai, K. R. Catchpole, T. Trupke and M. A. Green, J. Appl. Phys., 2007, 101, 093105 CrossRef.
- C. E. R. Disney, S. Pillai and M. A. Green, Sci. Rep., 2017, 7, 12826 CrossRef PubMed.
- S. H. Lim, W. Mar, P. Matheu, D. Derkacs and E. T. Yu, J. Appl. Phys., 2007, 101, 104309 CrossRef.
- F. J. Beck, A. Polman and K. R. Catchpole, J. Appl. Phys., 2009, 105, 114310 CrossRef.
- N. P. Hylton, X. F. Li, V. Giannini, K.-H. Lee, N. J. Ekins-Daukes, J. Loo, D. Vercruysse, P. Van Dorpe, H. Sodabanlu, M. Sugiyama and S. A. Maier, Sci. Rep., 2013, 3, 1–6 Search PubMed.
- Y. Zhang, B. Cai and B. Jia, Nanomaterials, 2016, 6, 1–10 CAS.
- C. Bohren and D. R. Huffman, Absorption and Scattering of Light by Small Particles, John Wiley & Sons, Ltd, 1998 Search PubMed.
- C. Hägglund and S. P. Apell, J. Phys. Chem. Lett., 2012, 3, 1275–1285 CrossRef PubMed.
- H. Shen, P. Bienstman and B. Maes, J. App. Phys., 2009, 106, 073109 CrossRef.
- A. Augusto, E. Looney, C. del Cañizo, S. G. Bowden and T. Buonassisi, Energy Procedia, 2017, 124, 706–711 CrossRef CAS.
- V. E. Ferry, L. A. Sweatlock, D. Pacifici and H. A. Atwater, Nano Lett., 2008, 8, 4391–4397 CrossRef CAS PubMed.
- I. R. Hooper and J. R. Sambles, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 165432 CrossRef.
- H. Huang, L. Lu, J. Wang, J. Yang, S.-F. Leung, Y. Wang, D. Chen, X. Chen, G. Shen, D. Li and Z. Fan, Energy Environ. Sci., 2013, 6, 2965–2971 RSC.
- T. A. Kelf, Y. Sugawara, R. M. Cole, J. J. Baumberg, M. E. Abdelsalam, S. Cintra, S. Mahajan, A. E. Russell and P. N. Bartlett, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 245415 CrossRef.
- J. Zhu, Z. Yu, G. F. Burkhard, C.-M. Hsu, S. T. Connor, Y. Xu, Q. Wang, M. McGehee, S. Fan and Y. Cui, Nano Lett., 2009, 9, 279–282 CrossRef CAS PubMed.
- C.-M. Hsu, C. Battaglia, C. Pahud, Z. Ruan, F.-J. Haug, S. Fan, C. Ballif and Y. Cui, Adv. Energy Mater., 2012, 2, 628–633 CrossRef CAS.
- R. Bogue, Sens. Rev., 2016, 36, 225–230 CrossRef.
- C. Li, P. Zhou and D. W. Zhang, J. Semicond., 2017, 38, 031005 CrossRef.
- R. Liu and L. Wang, J. Appl. Phys., 2020, 128, 145105 CrossRef CAS.
- W. C. Crone, in A Brief Introduction to MEMS and NEMS, ed. W. N. Sharpe, Springer US, Boston, MA, 2008, pp. 203–228 Search PubMed.
- Sens. Rev., 2011, 35 DOI:10.1108/sr.2011.08731aab.004.
- R. Bogue, Sens. Rev., 2016, 36, 1–6 CrossRef.
- A. Hajarian, M. M. Zand and N. Zolfaghari, Int. J. Appl. Mech., 2019, 11, 1950085 CrossRef.
- Y. T. Beni, I. Karimipöur and M. Abadyan, J. Mech. Sci. Technol., 2014, 28, 3749–3757 CrossRef.
- V. B. Svetovoy and G. Palasantzas, Mod. Phys. Lett. A, 2020, 35, 2040014 CrossRef CAS.
- S. Akhundzada, X. Yang, J. Fiedler, E. Käkel, B. Al-Qargholi, S. Buhmann, A. Ehresmann and H. Hillmer, Microsyst. Technol., 2022, 28, 2139–2148 CrossRef CAS.
- M. Trushin and A. H. Castro Neto, Phys. Rev. Lett., 2021, 127, 156101 CrossRef CAS PubMed.
- T. Gong, M. R. Corrado, A. R. Mahbub, C. Shelden and J. N. Munday, Nanophotonics, 2021, 10, 523–536 CAS.
- H. B. Chan, V. A. Aksyuk, R. N. Kleiman, D. J. Bishop and F. Capasso, Science, 2001, 291, 1941–1944 CrossRef CAS PubMed.
- D. S. Dovzhenko, S. V. Ryabchuk, Y. P. Rakovich and I. R. Nabiev, Nanoscale, 2018, 10, 3589–3605 RSC.
- M. Hertzog, M. Wang, J. Mony and K. Börjesson, Chem. Soc. Rev., 2019, 48, 937–961 RSC.
- F. J. Garcia-Vidal, C. Ciuti and T. W. Ebbesen, Science, 2021, 373, eabd0336 CrossRef CAS PubMed.
- Y. Yamamoto and A. Imamoglu, Mesoscoptic Quantum Optics, Wiley-Interscience, Hoboken, NJ, USA, 1999 Search PubMed.
- A. V. Zasedatelev, A. V. Baranikov, D. Urbonas, F. Scafirimuto, U. Scherf, T. Stöferle, R. F. Mahrt and P. G. Lagoudakis, Nat. Photonics, 2019, 13, 378–383 CrossRef CAS.
- A. Graf, M. Held, Y. Zakharko, L. Tropf, M. C. Gather and J. Zaumseil, Nat. Mater., 2017, 16, 911–917 CrossRef CAS PubMed.
- M. Held, A. Graf, Y. Zakharko, P. Chao, L. Tropf, M. C. Gather and J. Zaumseil, Adv. Opt. Mater., 2018, 6, 1700962 CrossRef.
- Y. Yu, S. Mallick, M. Wang and K. Börjesson, Nat. Commun., 2021, 12, 3255 CrossRef CAS PubMed.
- A. Thomas, E. Devaux, K. Nagarajan, G. Rogez, M. Seidel, F. Richard, C. Genet, M. Drillon and T. W. Ebbesen, Nano Lett., 2021, 21, 4365–4370 CrossRef CAS PubMed.
- F. Appugliese, J. Enkner, G. L. Paravicini-Bagliani, M. Beck, C. Reichl, W. Wegscheider, G. Scalari, C. Ciuti and J. Faist, Science, 2022, 375, 1030–1034 CrossRef CAS PubMed.
- S. Xiao, X. Zhu, B.-H. Li and N. A. Mortensen, Front. Phys., 2016, 11, 117801 CrossRef.
- L. Xiong, Y. Li, M. Jung, C. Forsythe, S. Zhang, A. S. McLeod, Y. Dong, S. Liu, F. L. Ruta, C. Li, K. Watanabe, T. Taniguchi, M. M. Fogler, J. H. Edgar, G. Shvets, C. R. Dean and D. N. Basov, Sci. Adv., 2021, 7, eabe8087 CrossRef CAS PubMed.
- E. Orgiu, J. George, J. A. Hutchison, E. Devaux, J. F. Dayen, B. Doudin, F. Stellacci, C. Genet, J. Schachenmayer, C. Genes, G. Pupillo, P. Samorì and T. W. Ebbesen, Nat. Mater., 2015, 14, 1123–1129 CrossRef CAS PubMed.
- K. Nagarajan, J. George, A. Thomas, E. Devaux, T. Chervy, S. Azzini, K. Joseph, A. Jouaiti, M. W. Hosseini, A. Kumar, C. Genet, N. Bartolo, C. Ciuti and T. W. Ebbesen, ACS Nano, 2020, 14, 10219–10225 CrossRef CAS PubMed.
- P. Bhatt, K. Kaur and J. George, ACS Nano, 2021, 15, 13616–13622 CrossRef CAS PubMed.
- D. Hagenmüller, J. Schachenmayer, S. Schütz, C. Genes and G. Pupillo, Phys. Rev. Lett., 2017, 119, 223601 CrossRef PubMed.
- R. Pandya, A. Ashoka, K. Georgiou, J. Sung, R. Jayaprakash, S. Renken, L. Gai, Z. Shen, A. Rao and A. J. Musser, Adv. Sci., 2022, 2105569 CrossRef CAS PubMed.
- J. D. B. Van Schenck, W. T. Goldthwaite, R. Puro, J. E. Anthony and O. Ostroverkhova, J. Phys. Chem. C, 2021, 125, 27381–27393 CrossRef CAS.
- C. Gonzalez-Ballestero, J. Feist, E. Gonzalo Badía, E. Moreno and F. J. Garcia-Vidal, Phys. Rev. Lett., 2016, 117, 156402 CrossRef PubMed.
- C.-Y. Cheng, R. Dhanker, C. L. Gray, S. Mukhopadhyay, E. R. Kennehan, J. B. Asbury, A. Sokolov and N. C. Giebink, Phys. Rev. Lett., 2018, 120, 017402 CrossRef CAS PubMed.
- C. Möhl, A. Graf, F. J. Berger, J. Lüttgens, Y. Zakharko, V. Lumsargis, M. C. Gather and J. Zaumseil, ACS Photonics, 2018, 5, 2074–2080 CrossRef PubMed.
- E. Orgiu, J. George, J. A. Hutchison, E. Devaux, J. F. Dayen, B. Doudin, F. Stellacci, C. Genet, J. Schachenmayer, C. Genes, G. Pupillo, P. Samorì and T. W. Ebbesen, Nat. Mater., 2015, 14, 1123–1129 CrossRef CAS PubMed.
- https://creativecommons.org/licenses/by/4.0/ .
- J. Galego, F. J. Garcia-Vidal and J. Feist, Nat. Commun., 2016, 7, 13841 CrossRef CAS PubMed.
- J. A. Hutchison, T. Schwartz, C. Genet, E. Devaux and T. W. Ebbesen, Angew. Chem., Int. Ed., 2012, 51, 1592–1596 CrossRef CAS PubMed.
- K. Nagarajan, A. Thomas and T. W. Ebbesen, J. Am. Chem. Soc., 2021, 143, 16877–16889 CrossRef CAS PubMed.
- J. Flick, M. Ruggenthaler, H. Appel and A. Rubio, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 3026–3034 CrossRef CAS PubMed.
- D. Sidler, M. Ruggenthaler, H. Appel and A. Rubio, J. Phys. Chem. Lett., 2020, 11, 7525–7530 CrossRef CAS PubMed.
- T. S. Haugland, C. Schäfer, E. Ronca, A. Rubio and H. Koch, J. Chem. Phys., 2021, 154, 094113 CrossRef CAS PubMed.
- D. M. Coles, N. Somaschi, P. Michetti, C. Clark, P. G. Lagoudakis, P. G. Savvidis and D. G. Lidzey, Nat. Mater., 2014, 13, 712–719 CrossRef CAS PubMed.
- H. Hübener, U. De Giovannini, C. Schäfer, J. Andberger, M. Ruggenthaler, J. Faist and A. Rubio, Nat. Mater., 2021, 20, 438–442 CrossRef PubMed.
- A. Thomas, L. Lethuillier-Karl, K. Nagarajan, R. M. A. Vergauwe, J. George, T. Chervy, A. Shalabney, E. Devaux, C. Genet, J. Moran and T. W. Ebbesen, Science, 2019, 363, 615–619 CrossRef CAS PubMed.
- B. Xiang, R. F. Ribeiro, M. Du, L. Chen, Z. Yang, J. Wang, J. Yuen-Zhou and W. Xiong, Science, 2020, 368, 665–667 CrossRef CAS PubMed.
- B. S. Simpkins, A. D. Dunkelberger and J. C. Owrutsky, J. Phys. Chem. C, 2021, 125, 19081–19087 CrossRef.
- Y.-C. Chen, B. Song, A. J. Leggett, P. Ao and X. Zhu, Phys. Rev. Lett., 2019, 122, 257402 CrossRef CAS PubMed.
- A. Canales, D. G. Baranov, T. J. Antosiewicz and T. Shegai, J. Chem. Phys., 2021, 154, 024701 CrossRef CAS PubMed.
- R. Pandya, R. Y. S. Chen, Q. Gu, J. Sung, C. Schnedermann, O. S. Ojambati, R. Chikkaraddy, J. Gorman, G. Jacucci, O. D. Onelli, T. Willhammar, D. N. Johnstone, S. M. Collins, P. A. Midgley, F. Auras, T. Baikie, R. Jayaprakash, F. Mathevet, R. Soucek, M. Du, A. M. Alvertis, A. Ashoka, S. Vignolini, D. G. Lidzey, J. J. Baumberg, R. H. Friend, T. Barisien, L. Legrand, A. W. Chin, J. Yuen-Zhou, S. K. Saikin, P. Kukura, A. J. Musser and A. Rao, Nat. Commun., 2021, 12, 6519 CrossRef PubMed.
- D. Tabor and R. H. S. Winterton, Proc. R. Soc. A: Math. Phys. Eng. Sci., 1969, 312, 435–450 CAS.
- G. D. Degen, P. Delparastan, B. D. B. Tiu and P. B. Messersmith, ACS Appl. Mater. Interfaces, 2022, 14, 6212–6220 CrossRef CAS PubMed.
- M. A. Gebbie, A. M. Smith, H. A. Dobbs, A. A. Lee, G. G. Warr, X. Banquy, M. Valtiner, M. W. Rutland, J. N. Israelachvili, S. Perkin and R. Atkin, Chem. Commun., 2017, 53, 1214–1224 RSC.
- S. Perkin, L. Chai, N. Kampf, U. Raviv, W. Briscoe, I. Dunlop, S. Titmuss, M. Seo, E. Kumacheva and J. Klein, Langmuir, 2006, 22, 6142–6152 CrossRef CAS PubMed.
- F. J. Giessibl, Rev. Mod. Phys., 2003, 75, 949–983 CrossRef CAS.
- G. Binnig, C. F. Quate and C. Gerber, Phys. Rev. Lett., 1986, 56, 930–933 CrossRef PubMed.
- F. J. Giessibl, Rev. Mod. Phys., 2003, 75, 949–983 CrossRef CAS.
- H. Edwards, L. Taylor, W. Duncan and A. J. Melmed, J. Appl. Phys., 1997, 82, 980–984 CrossRef CAS.
- E. Meyer, H. Hug and R. Bennewitz, Scanning Probe Microscopy: The Lab on a Tip, Springer Berlin Heidelberg, 2003 Search PubMed.
- N. Ishida and V. S. J. Craig, KONA Powder Part. J., 2019, 36, 187–200 CrossRef.
- P. Loskill, J. Puthoff, M. Wilkinson, K. Mecke, K. Jacobs and K. Autumn, J. R. Soc., Interface, 2013, 10, 20120587 CrossRef PubMed.
- R. Seemann, S. Herminghaus and K. Jacobs, Phys. Rev. Lett., 2001, 86, 5534–5537 CrossRef CAS PubMed.
- R. Seemann, S. Herminghaus and K. Jacobs, J. Phys.: Condens. Matter, 2001, 13, 4925–4938 CrossRef CAS.
- A. Vrij, Discuss. Faraday Soc., 1966, 42, 23–33 RSC.
- L. Gross, F. Mohn, N. Moll, P. Liljeroth and G. Meyer, Science, 2009, 325, 1110–1114 CrossRef CAS PubMed.
- J. L. Hutter and J. Bechhoefer, J. Appl. Phys., 1993, 73, 4123–4129 CrossRef CAS.
- F. Ohnesorge and G. Binnig, Science, 1993, 260, 1451–1456 CrossRef CAS PubMed.
- J. N. Munday, F. Capasso and V. A. Parsegian, Nature, 2009, 457, 170–173 CrossRef CAS PubMed.
- F. A. Burger, R. W. Corkery, S. Y. Buhmann and J. Fiedler, J. Phys. Chem. C, 2020, 124, 24179–24186 CrossRef CAS.
- L. D. Landau and I. M. Lifshitz, Theory of Elasticity, Elsevier, Amsterdam, 1986 Search PubMed.
- T. Nihira and T. Iwata, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 134305 CrossRef.
- D. L. Nika and A. A. Balandin, Rep. Prog. Phys., 2017, 80, 036502 CrossRef PubMed.
- B. Amorim and F. Guinea, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 115418 CrossRef.
- A. Al Taleb, H. K. Yu, G. Anemone, D. Farías and A. M. Wodtke, Carbon, 2015, 95, 731–737 CrossRef CAS.
- C. Büchner, S. D. Eder, T. Nesse, D. Kuhness, P. Schlexer, G. Pacchioni, J. R. Manson, M. Heyde, B. Holst and H.-J. Freund, Phys. Rev. Lett., 2018, 120, 226101 CrossRef PubMed.
- M. Tømterud, S. D. Eder, C. Büchner, M. Heyde, H.-J. Freund, J. R. Manson and B. Holst, Phys. Chem. Chem. Phys., 2022, 24, 17941–17945, 10.1039/D2CP01960D.
- S. D. Eder, S. K. Hellner, S. Forti, J. M. Nordbotten, J. R. Manson, C. Coletti and B. Holst, Phys. Rev. Lett., 2021, 127, 266102 CrossRef CAS PubMed.
- I. Y. Sklyadneva, G. Benedek, E. V. Chulkov, P. M. Echenique, R. Heid, K.-P. Bohnen and J. P. Toennies, Phys. Rev. Lett., 2011, 107, 095502 CrossRef PubMed.
- G. Benedek, M. Bernasconi, K.-P. Bohnen, D. Campi, E. V. Chulkov, P. M. Echenique, R. Heid, I. Y. Sklyadneva and J. P. Toennies, Phys. Chem. Chem. Phys., 2014, 16, 7159 RSC.
- J. R. Manson, G. Benedek and S. Miret-Artés, J. Phys. Chem. Lett., 2016, 7, 1016–1021 CrossRef CAS PubMed.
- G. Benedek, S. Miret-Artés, J. P. Toennies and J. R. Manson, J. Phys. Chem. Lett., 2017, 9, 76–83 CrossRef PubMed.
- G. Benedek, J. R. Manson and S. Miret-Artés, Phys. Chem. Chem. Phys., 2021, 23, 7575–7585 RSC.
- A. Tamtögl, P. Kraus, N. Avidor, M. Bremholm, E. M. J. Hedegaard, B. B. Iversen, M. Bianchi, P. Hofmann, J. Ellis, W. Allison, G. Benedek and W. E. Ernst, Phys. Rev. B, 2017, 95, 195401 CrossRef.
- G. Benedek, S. Miret-Artés, J. R. Manson, A. Ruckhofer, W. E. Ernst and A. Tamtögl, J. Phys. Chem. Lett., 2020, 11, 1927–1933 CrossRef CAS PubMed.
- A. D. Cronin, J. Schmiedmayer and D. E. Pritchard, Rev. Mod. Phys., 2009, 81, 1051–1129 CrossRef CAS.
- K. Hornberger, S. Gerlich, P. Haslinger, S. Nimmrichter and M. Arndt, Rev. Mod. Phys., 2012, 84, 157–173 CrossRef CAS.
- J. H. Lee, L. Y. Kim, Y.-T. Kim, C. Y. Lee, W. Schöllkopf and B. S. Zhao, Phys. Rev. Lett., 2019, 122, 040401 CrossRef CAS PubMed.
- R. E. Grisenti, W. Schöllkopf, J. P. Toennies, G. C. Hegerfeldt and T. Köhler, Phys. Rev. Lett., 1999, 83, 1755 CrossRef CAS.
- J. D. Perreault and A. D. Cronin, Phys. Rev. Lett., 2005, 95, 133201 CrossRef PubMed.
- C. Brand, M. Sclafani, C. Knobloch, Y. Lilach, T. Juffmann, J. Kotakoski, C. Mangler, A. Winter, A. Turchanin, J. Meyer, O. Cheshnovsky and M. Arndt, Nat. Nanotechnol., 2015, 10, 845–848 CrossRef CAS PubMed.
- J. L. Hemmerich, R. Bennett, T. Reisinger, S. Nimmrichter, J. Fiedler, H. Hahn, H. Gleiter and S. Y. Buhmann, Phys. Rev. A, 2016, 94, 023621 CrossRef.
- N. Gack, C. Reitz, J. L. Hemmerich, M. Könne, R. Bennett, J. Fiedler, H. Gleiter, S. Y. Buhmann, H. Hahn and T. Reisinger, Phys. Rev. Lett., 2020, 125, 050401 CrossRef CAS PubMed.
- S. Nowak, N. Stuhler, T. Pfau and J. Mlynek, Phys. Rev. Lett., 1998, 81, 5792–5795 CrossRef CAS.
- T. Reisinger, A. A. Patel, H. Reingruber, K. Fladischer, W. E. Ernst, G. Bracco, H. I. Smith and B. Holst, Phys. Rev. A: At., Mol., Opt. Phys., 2009, 79, 053823 CrossRef.
- T. Juffmann, S. Nimmrichter, M. Arndt, H. Gleiter and K. Hornberger, Found. Phys., 2012, 42, 98–110 CrossRef.
- M. Könne, R. Bennett, T. Reisinger and S. Y. Buhmann, Phys. Rev. A, 2017, 96, 013626 CrossRef.
- T. Reisinger, P. M. Leufke, H. Gleiter and H. Hahn, N. J. Phys., 2017, 19, 033022 CrossRef.
- T. Reisinger, G. Bracco and B. Holst, N. J. Phys., 2011, 13, 065016 CrossRef.
- C. Brand, M. Debiossac, T. Susi, F. Aguillon, J. Kotakoski, P. Roncin and M. Arndt, N. J. Phys., 2019, 21, 033004 CrossRef CAS.
- M. Koch, S. Rehbein, G. Schmahl, T. Reisinger, G. Bracco, W. E. Ernst and B. Holst, J. Microsc., 2008, 229, 1 CrossRef CAS PubMed.
- T. Reisinger, S. Eder, M. M. Greve, H. I. Smith and B. Holst, Microelectron. Eng., 2010, 87, 1011–1014 CrossRef CAS.
- N. F. Hartmann, M. Otten, I. Fedin, D. Talapin, M. Cygorek, P. Hawrylak, M. Korkusinski, S. Gray, A. Hartschuh and X. Ma, Nat. Commun., 2019, 10, 3253 CrossRef PubMed.
- M. L. Hupfer, M. Kaufmann, F. Herrmann-Westendorf, T. Sachse, L. Roussille, K. H. Feller, D. Weiss, V. Deckert, R. Beckert, B. Dietzek and M. Presselt, ACS Appl. Mater. Interfaces, 2017, 9, 44181–44191 CrossRef CAS PubMed.
- M. J. Jurow, C. Mayr, T. D. Schmidt, T. Lampe, P. I. Djurovich, W. Brütting and M. E. Thompson, Nat. Mater., 2016, 15, 85–91 CrossRef CAS PubMed.
- S. Y. Byeon, J. Kim, D. R. Lee, S. H. Han, S. R. Forrest and J. Y. Lee, Adv. Optical Mater., 2018, 6, 1701340 CrossRef.
- M. Orrit, D. Möbius, U. Lehmann and H. Meyer, J. Chem. Phys., 1986, 85, 4966–4979 CrossRef CAS.
- M. Yoneyama, M. Sugi, M. Saito, K. Ikegami, S. Kuroda and S. Iizima, Jpn. J. Appl. Phys., Part 1, 1986, 25, 961–965 CrossRef CAS.
- H. Yong, N. Zotev, B. Stankus, J. M. Ruddock, D. Bellshaw, S. Boutet, T. J. Lane, M. Liang, S. Carbajo, J. S. Robinson, W. Du, N. Goff, Y. Chang, J. E. Koglin, M. D. J. Waters, T. I. Sølling, M. P. Minitti, A. Kirrander and P. M. Weber, J. Phys. Chem. Lett., 2018, 9, 6556–6562 CrossRef CAS PubMed.
- M. A. Lieb, J. M. Zavislan and L. Novotny, J. Opt. Soc. Am. B, 2004, 21, 1210–1215 CrossRef CAS.
- E. Lifshitz, JETP Lett., 1956, 2, 73 Search PubMed.
- P. A. Maia Neto, A. Lambrecht and S. Reynaud, Phys. Rev. A: At., Mol., Opt. Phys., 2008, 78, 012115 CrossRef.
- S. J. Rahi, T. Emig, N. Graham, R. L. Jaffe and M. Kardar, Phys. Rev. D: Part., Fields, Gravitation, Cosmol., 2009, 80, 085021 CrossRef.
- M. Krüger, G. Bimonte, T. Emig and M. Kardar, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 115423 CrossRef.
- O. Kenneth and I. Klich, Phys. Rev. Lett., 2006, 97, 160401 CrossRef PubMed.
- S. J. Rahi, M. Kardar and T. Emig, Phys. Rev. Lett., 2010, 105, 070404 CrossRef PubMed.
- W. Eckhardt, Phys. Rev. A: At., Mol., Opt. Phys., 1984, 29, 1991 CrossRef.
- V. S. Asadchy, M. S. Mirmoosa, A. Daz-Rubio, S. Fan and S. A. Tretyakov, Proc. IEEE, 2020, 108, 1684–1727 CAS.
- S.-A. Biehs, R. Messina, P. S. Venkataram, A. W. Rodriguez, J. C. Cuevas and P. Ben-Abdallah, Rev. Mod. Phys., 2021, 93, 025009 CrossRef CAS.
- D. Gelbwaser-Klimovsky, N. Graham, M. Kardar and M. Krüger, Phys. Rev. B, 2002, 106, 115106 CrossRef.
- D. Gelbwaser-Klimovsky, N. Graham, M. Kardar and M. Krüger, Phys. Rev. Lett., 2021, 126, 170401 CrossRef CAS PubMed.
- M. G. Silveirinha, S. A. H. Gangaraj, G. W. Hanson and M. Antezza, Phys. Rev. A, 2018, 97, 022509 CrossRef CAS.
- J. A. Girón-Sedas, J. J. Kingsley-Smith and F. J. Rodrguez-Fortuño, Phys. Rev. B, 2019, 100, 075419 CrossRef.
- S. A. H. Gangaraj, M. G. Silveirinha, G. W. Hanson, M. Antezza and F. Monticone, Phys. Rev. B, 2018, 98, 125146 CrossRef CAS.
- F. Lindel, G. W. Hanson, M. Antezza and S. Y. Buhmann, Phys. Rev. B, 2018, 98, 144101 CrossRef CAS.
- S. A. Hassani Gangaraj, G. W. Hanson, M. Antezza and M. G. Silveirinha, Phys. Rev. B, 2018, 97, 201108 CrossRef CAS.
- C. Khandekar, S. Buddhiraju, P. R. Wilkinson, J. K. Gimzewski, A. W. Rodriguez, C. Chase and S. Fan, Phys. Rev. B, 2021, 104, 245433 CrossRef CAS.
- Y. Tsurimaki, X. Qian, S. Pajovic, S. Boriskina and G. Chen, Casimir force among spheres made of Weyl semimetals breaking Lorentz reciprocity, arXiv, 2021, preprint, arXiv:2109.03809 DOI:10.48550/arXiv:2109.03809.
- M. B. Farias, A. A. Zyuzin and T. L. Schmidt, Phys. Rev. B, 2020, 101, 235446 CrossRef CAS.
- Q.-D. Jiang and F. Wilczek, Phys. Rev. B, 2019, 99, 125403 CrossRef CAS.
- B. V. Derjaguin and L. D. Landau, Acta Physicochim. URSS, 1941, 14, 633–662 Search PubMed.
- E. J. W. Verwey and J. T. G. Overbeek, Theory of the Stability of Lyophobic Colloids, Elsevier, 1948, p. 205 Search PubMed.
- H. C. Hamaker, Physica, 1937, 4, 1058–1072 CrossRef CAS.
- F. Hofmeister, Arch. Exp. Pathol. Pharmakol., 1888, 24, 247–260 CrossRef.
- S. S. A. Burgess, J. Geddes, K. K. E. Hawton, M. J. Taylor, E. Townsend, K. Jamison and G. Goodwin, Cochrane Database Syst. Rev., 2001, 1–49 Search PubMed.
- T. A. Zimmers, J. Sheldon, D. A. Lubarsky, F. López-Muñoz, L. Waterman, R. Weisman and L. G. Koniaris, PLoS Med., 2007, 4, e156 CrossRef PubMed.
- R. Kjellander, J. Phys.: Condens. Matter, 2009, 21, 424101 CrossRef PubMed.
- R. Kjellander, J. Chem. Phys., 2018, 148, 193701 CrossRef PubMed.
- J. P. De Souza, K. Pivnic, M. Z. Bazant, M. Urbakh and A. A. Kornyshev, J. Phys. Chem. B, 2021, 2022, 1242–1253 Search PubMed.
- D. J. Bonthuis and R. R. Netz, J. Phys. Chem. B, 2013, 117, 11397–11413 CrossRef CAS PubMed.
- M. Galib, T. T. Duignan, Y. Misteli, M. D. Baer, G. K. Schenter, J. Hutter and C. J. Mundy, J. Chem. Phys., 2017, 146, 244501 CrossRef PubMed.
- B. W. Ninham and V. Yaminsky, Langmuir, 1997, 13, 2097–2108 CrossRef CAS.
- J. Mahanty and B. W. Ninham, J. Chem. Phys., 1973, 59, 6157–6162 CrossRef CAS.
- J. Mahanty and B. W. Ninham, Dispersion Forces, Academic Press, London, 1976 Search PubMed.
- J. Fiedler, P. Thiyam, A. Kurumbail, F. A. Burger, M. Walter, C. Persson, I. Brevik, D. F. Parsons, M. Boström and S. Y. Buhmann, J. Phys. Chem. A, 2017, 121, 9742–9751 CrossRef CAS PubMed.
- D. F. Parsons, C. Carucci and A. Salis, Phys. Chem. Chem. Phys., 2022, 24, 6544–6551 RSC.
- M. Boström, D. F. Parsons, A. Salis, B. W. Ninham and M. Monduzzi, Langmuir, 2011, 27, 9504–9511 CrossRef PubMed.
- A. Salis, D. F. Parsons, M. Boström, L. Medda, B. Barse, B. W. Ninham and M. Monduzzi, Langmuir, 2010, 26, 2484–2490 CrossRef CAS PubMed.
- D. F. Parsons and B. W. Ninham, Langmuir, 2010, 26, 6430–6436 CrossRef CAS PubMed.
- T. T. Duignan, D. F. Parsons and B. W. Ninham, J. Phys. Chem. B, 2013, 117, 9412–9420 CrossRef CAS PubMed.
- T. T. Duignan, D. F. Parsons and B. W. Ninham, J. Phys. Chem. B, 2014, 118, 3122–3132 CrossRef CAS PubMed.
- T. T. Duignan, D. F. Parsons and B. W. Ninham, Phys. Chem. Chem. Phys., 2014, 16, 22014–22027 RSC.
- T. T. Duignan, D. F. Parsons and B. W. Ninham, J. Phys. Chem. B, 2014, 118, 8700–8710 CrossRef CAS PubMed.
- T. T. Duignan, D. F. Parsons and B. W. Ninham, Chem. Phys. Lett., 2015, 635, 1–12 CrossRef CAS.
- A. Reyes, M. A. Tlenkopatchev, L. Fomina, P. Guadarrama and S. Fomine, J. Phys. Chem. A, 2003, 107, 7027–7031 CrossRef CAS.
- P. Jurečka, J. Šponer and P. Hobza, J. Phys. Chem. B, 2004, 108, 5466–5471 CrossRef.
- P. Jurečka, J. Šponer, J. Černý and P. Hobza, Phys. Chem. Chem. Phys., 2006, 8, 1985–1993 RSC.
- J. Řezáč, K. E. Riley and P. Hobza, J. Chem. Theory Comput., 2011, 7, 2427–2438 CrossRef PubMed.
- S. Grimme, C. Diedrich and M. Korth, Angew. Chem., Int. Ed., 2006, 45, 625–629 CrossRef CAS PubMed.
- Y. S. Al-Hamdani, P. R. Nagy, A. Zen, D. Barton, M. Kállay, J. G. Brandenburg and A. Tkatchenko, Nat. Commun., 2021, 12, 3927 CrossRef CAS PubMed.
- F. Zahariev and M. S. Gordon, Phys. Chem. Chem. Phys., 2021, 23, 14308–14314 RSC.
- K. Patkowski, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10, e1452 CAS.
- S. Chmiela, H. E. Sauceda, K.-R. Müller and A. Tkatchenko, Nat. Commun., 2018, 9, 3887 CrossRef PubMed.
- R. O. Jones, Rev. Mod. Phys., 2015, 87, 897–923 CrossRef.
- A. Pribram-Jones, D. A. Gross and K. Burke, Annu. Rev. Phys. Chem., 2015, 66, 283–304 CrossRef CAS PubMed.
- D. S. Sholl and J. A. Steckel, Density Functional Theory, John Wiley & Sons, Inc., Hoboken, NJ, USA, 2009 Search PubMed.
- P. Makkar and N. N. Ghosh, RSC Adv., 2021, 11, 27897–27924 RSC.
- J. Hafner, C. Wolverton and G. Ceder, MRS Bull., 2006, 31, 659–668 CrossRef.
- D. C. Langreth, B. I. Lundqvist, S. D. Chakarova-Käck, V. R. Cooper, M. Dion, P. Hyldgaard, A. Kelkkanen, J. Kleis, L. Kong, S. Li, P. G. Moses, E. Murray, A. Puzder, H. Rydberg, E. Schröder and T. Thonhauser, J. Phys.: Condens. Matter, 2009, 21, 084203 CrossRef CAS PubMed.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- A. Nangia, J. Chem. Sci., 2010, 122, 295–310 CrossRef CAS.
- J. S. Arey, P. C. Aeberhard, I.-C. Lin and U. Rothlisberger, J. Phys. Chem. B, 2009, 113, 4726–4732 CrossRef CAS PubMed.
- J. Wang, G. Román-Pérez, J. M. Soler, E. Artacho and M.-V. Fernández-Serra, J. Chem. Phys., 2011, 134, 024516 CrossRef PubMed.
- S. Grimme, J. Comput. Chem., 2004, 25, 1463–1473 CrossRef CAS PubMed.
- A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005 CrossRef PubMed.
- A. Tkatchenko, R. A. DiStasio, R. Car and M. Scheffler, Phys. Rev. Lett., 2012, 108, 236402 CrossRef PubMed.
- J. F. Dobson, Int. J. Quantum Chem., 2014, 114, 1157–1161 CrossRef CAS.
- D. Langreth and J. Perdew, Solid State Commun., 1975, 17, 1425–1429 CrossRef.
- G. Giuliani and G. Vignale, Quantum Theory of the Electron Liquid, Cambridge University Press, 2005 Search PubMed.
- J. Harl and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 045136 CrossRef.
- J. Harl, L. Schimka and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 115126 CrossRef.
- T. Björkman, A. Gulans, A. V. Krasheninnikov and R. M. Nieminen, J. Phys.: Condens. Matter, 2012, 24, 424218 CrossRef PubMed.
- M. Dion, H. Rydberg, E. Schröder, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 2004, 92, 246401 CrossRef CAS PubMed.
- K. Lee, É. D. Murray, L. Kong, B. I. Lundqvist and D. C. Langreth, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 081101 CrossRef.
- D. Chakraborty, K. Berland and T. Thonhauser, J. Chem. Theory Comput., 2020, 16, 5893–5911 CrossRef CAS PubMed.
- P. Hyldgaard, K. Berland and E. Schröder, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 075148 CrossRef CAS.
- K. Berland, V. R. Cooper, K. Lee, E. Schröder, T. Thonhauser, P. Hyldgaard and B. I. Lundqvist, Rep. Prog. Phys., 2015, 78, 066501 CrossRef PubMed.
- K. Berland, C. A. Arter, V. R. Cooper, K. Lee, B. I. Lundqvist, E. Schröder, T. Thonhauser and P. Hyldgaard, J. Chem. Phys., 2014, 140, 18A539 CrossRef PubMed.
- K. Berland, PhD thesis, Department of Microtechnology and Nanoscience – MC2, Chalmers University of Technology, Göteborg, Sweden, 2012 Search PubMed.
- G. Román-Pérez and J. M. Soler, Phys. Rev. Lett., 2009, 103, 096102 CrossRef PubMed.
- E. Torres and G. A. DiLabio, J. Phys. Chem. Lett., 2012, 3, 1738–1744 CrossRef CAS PubMed.
- K. Berland, Y. Jiao, J.-H. Lee, T. Rangel, J. B. Neaton and P. Hyldgaard, J. Chem. Phys., 2017, 146, 234106 CrossRef PubMed.
- V. Shukla, Y. Jiao, J.-H. Lee, E. Schröder, J. B. Neaton and P. Hyldgaard, Phys. Rev. X, 2022, 12, 041003 Search PubMed.
- S. Seyedraoufi and K. Berland, J. Chem. Phys., 2022, 156, 244106 CrossRef CAS PubMed.
- S. Scheel and S. Y. Buhmann, Acta Phys. Slovaca, 2008, 58, 675–809 CAS.
- L. D. Landau and E. M. Lifshitz, The Classical Theory of Fields, Pergamon Press, Oxford, 4th edn, 1975, vol. 2 Search PubMed.
- L. Knöll, S. Scheel and D.-G. Welsch, Coherence and Statistics of Photons and Atoms, New York, 2001 Search PubMed.
- A. Messiah, Quantum Mechanics, Dover Publications, Mineola, New York, 2014 Search PubMed.
- S. Y. Buhmann, Dispersion Forces II: Many-Body Effects, Excited Atoms, Finite Temperature and Quantum Friction, Springer, Heidelberg, 2012 Search PubMed.
- H. T. Dung, S. Y. Buhmann, L. Knöll, D.-G. Welsch, S. Scheel and J. Kästel, Phys. Rev. A: At., Mol., Opt. Phys., 2003, 68, 043816 CrossRef.
- J. Klatt, M. B. Farías, D. A. R. Dalvit and S. Y. Buhmann, Phys. Rev. A, 2017, 95, 052510 CrossRef.
- S. Ribeiro, S. Y. Buhmann, T. Stielow and S. Scheel, Europhys. Lett., 2015, 110, 51003 CrossRef.
- S. Y. Buhmann, Dispersion Forces I: Macroscopic quantum electrodynamics and ground-state Casimir, Casimir-Polder and van der Waals forces, Springer, Heidelberg, 2012 Search PubMed.
- E. A. Power and S. Zienau, Philos. Trans. R. Soc., A, 1959, 251, 427–454 CrossRef.
- R. G. Woolley and C. A. Coulson, Proc. R. Soc. A: Math. Phys. Eng. Sci., 1971, 321, 557–572 Search PubMed.
- W. E. Lamb and R. C. Retherford, Phys. Rev., 1947, 72, 241–243 CrossRef CAS.
- B. W. Ninham and P. Lo Nostro, Molecular Forces and Self Assembly in Colloid, Nano Sciences and Biology, Cambridge University Press, Cambridge, 2010 Search PubMed.
- T. Gruner and D.-G. Welsch, Phys. Rev. A: At., Mol., Opt. Phys., 1996, 53, 1818 CrossRef CAS PubMed.
- W. M. R. Simpson and U. Leonhardt, Forces of the Quantum Vacuum, World Scientific, 2015 Search PubMed.
- H. Bender, C. Stehle, C. Zimmermann, S. Slama, J. Fiedler, S. Scheel, S. Y. Buhmann and V. N. Marachevsky, Phys. Rev. X, 2014, 4, 011029 CAS.
- M. Arndt, O. Nairz, J. Vos-Andreae,. Keller, G. van der Zouw and A. Zeilinger, Nature, 1999, 401, 680 CrossRef CAS PubMed.
- C. Brand, J. Fiedler, T. Juffmann, M. Sclafani, C. Knobloch, S. Scheel, Y. Lilach, O. Cheshnovsky and M. Arndt, Ann. Phys., 2015, 527, 580 CrossRef CAS.
- A. Salam, Molecular Quantum Electrodynamics: Long-Range Intermolecular Interactions, Wiley, 2009 Search PubMed.
- D. F. Parsons and B. W. Ninham, J. Phys. Chem. A, 2009, 113, 1141–1150 CrossRef CAS PubMed.
- J. Fiedler and S. Scheel, Ann. Phys., 2015, 527, 570–579 CrossRef CAS.
- J. Fiedler, C. Persson, M. Boström and S. Y. Buhmann, J. Phys. Chem. A, 2018, 122, 4663–4669 CrossRef CAS PubMed.
- S. Das, J. Fiedler, O. Stauffert, M. Walter, S. Y. Buhmann and M. Presselt, Phys. Chem. Chem. Phys., 2020, 22, 23295–23306 RSC.
- S. Fuchs and S. Y. Buhmann, Europhys. Lett., 2018, 124, 34003 CrossRef.
- E. M. Purcell, H. C. Torrey and R. V. Pound, Phys. Rev., 1946, 69, 37 CrossRef CAS.
- R. H. Dicke, Phys. Rev., 1954, 93, 99 CrossRef CAS.
- M. Gross and S. Haroche, Phys. Rep., 1982, 93, 301 CrossRef CAS.
- M. Gajdoš, K. Hummer, G. Kresse, J. Furthmüller and F. Bechstedt, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 045112 CrossRef.
- J. Gao, Q. Wu, C. Persson and Z. Wang, Comp. Phys. Commun., 2021, 261, 107760 CrossRef CAS.
- C. Persson and C. Ambrosch-Draxl, Comp. Phys. Commun., 2007, 177, 280–287 CrossRef CAS.
- A. Crovetto, R. Chen, R. B. Ettlinger, A. C. Cazzaniga, J. Schou, C. Persson and O. Hansen, Sol. Energy Mater. Sol. Cells, 2016, 154, 121–129 CrossRef CAS.
- J. F. Cooke and R. F. Wood, Phys. Rev. B: Solid State, 1972, 5, 1276–1283 CrossRef.
- D. G. Shankland, Int. J. Quantum Chem., 1971, 5, 497–500 CrossRef.
- E. L. Shirley, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 16464–16469 CrossRef CAS PubMed.
- I. Souza, N. Marzari and D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 65, 035109 CrossRef.
- K. Berland and C. Persson, J. Appl. Phys., 2018, 123, 205703 CrossRef.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed.
- A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC.
- A. Klamt, V. Jonas, T. Bürger and J. C. Lohrenz, J. Phys. Chem. A, 1998, 102, 5074–5085 CrossRef CAS.
- R. Ghassemizadeh, B. Moore, T. Momose and M. Walter, J. Phys. Chem. B, 2019, 123, 4392–4399 CrossRef CAS PubMed.
- J. Fiedler, M. Walter and S. Y. Buhmann, J. Chem. Phys., 2021, 154, 104102 CrossRef CAS PubMed.
- S. Pipolo, S. Corni and R. Cammi, J. Chem. Phys., 2014, 140, 164114 CrossRef PubMed.
- L. Onsager, J. Am. Chem. Soc., 1936, 58, 1486–1493 CrossRef CAS.
- A. Held and M. Walter, J. Chem. Phys., 2014, 141, 174108 CrossRef PubMed.
- J. Fiedler, F. Spallek, P. Thiyam, C. Persson, M. Boström, M. Walter and S. Y. Buhmann, Phys. Rev. A, 2019, 99, 062512 CrossRef CAS.
- B. Hartl, S. Sharma, O. Brügner, S. F. L. Mertens, M. Walter and G. Kahl, J. Chem. Theory Comput., 2020, 16, 5227–5243 CrossRef CAS PubMed.
- S. Y. Buhmann and D.-G. Welsch, Phys. Rev. A: At., Mol., Opt. Phys., 2007, 77, 012110 CrossRef.
- E. T. Jaynes and F. W. Cummings, Proc. IEEE, 1963, 51, 89 Search PubMed.
- B. W. Shore and P. L. Knight, J. Mod. Opt., 1993, 40, 1195–1238 CrossRef CAS.
- M. Tavis and F. W. Cummings, Phys. Rev., 1968, 170, 379–384 CrossRef.
- H. Walther, B. T. H. Varcoe, B.-G. Englert and T. Becker, Rep. Prog. Phys., 2006, 69, 1325 CrossRef.
- E. Hagley, X. Maître, G. Nogues, C. Wunderlich, M. Brune, J. M. Raimond and S. Haroche, Phys. Rev. Lett., 1997, 79, 1–4 CrossRef CAS.
- M. Brune, E. Hagley, J. Dreyer, X. Maître, A. Maali, C. Wunderlich, J. M. Raimond and S. Haroche, Phys. Rev. Lett., 1996, 77, 4887–4890 CrossRef CAS PubMed.
- T. Wilk, S. C. Webster, A. Kuhn and G. Rempe, Science, 2007, 317, 488–490 CrossRef CAS PubMed.
- C. Hamsen, K. N. Tolazzi, T. Wilk and G. Rempe, Phys. Rev. Lett., 2017, 118, 133604 CrossRef PubMed.
- K. Cui, K. S. Mali, D. Wu, X. Feng, K. Müllen, M. Walter, S. De Feyter and S. F. L. Mertens, Small, 2017, 13, 1702379 CrossRef PubMed.
- P. Bairi, K. Minami, J. P. Hill, W. Nakanishi, L. K. Shrestha, C. Liu, K. Harano, E. Nakamura and K. Ariga, ACS Nano, 2016, 10, 8796–8802 CrossRef CAS PubMed.
- S. Das, J. Preiß, J. Plentz, U. Brückner, M. von der Lühe, O. Eckardt, A. Dathe, F. H. Schacher, E. Täuscher, U. Ritter, A. Csáki, G. Andrä, B. Dietzek and M. Presselt, Adv. Energy Mater., 2018, 8, 1801737 CrossRef.
- K. Cui, K. S. Mali, O. Ivasenko, D. Wu, X. Feng, M. Walter, K. Müllen, S. De Feyter and S. F. L. Mertens, Angew. Chem., Int. Ed., 2014, 53, 12951–12954 CrossRef CAS PubMed.
- M. C. Stumpe and H. Grubmüller, J. Phys. Chem. B, 2007, 111, 6220–6228 CrossRef CAS PubMed.
- C. Peter and K. Kremer, Soft Matter, 2009, 5, 4357–4366 RSC.
- O. Bezkorovaynaya, A. Lukyanov, K. Kremer and C. Peter, J. Comput. Chem., 2012, 33, 937–949 CrossRef CAS PubMed.
- M. R. Machado and S. Pantano, Bioinform., 2016, 32, 1568–1570 CrossRef CAS PubMed.
- L. A. Montero, J. Molina and J. Fabian, Int. J. Quantum Chem., 2000, 79, 8–16 CrossRef CAS.
- M. P. Metz, K. Piszczatowski and K. Szalewicz, J. Chem. Theory Comput., 2016, 12, 5895–5919 CrossRef CAS PubMed.
- T. Sachse, T. J. Martinez, B. Dietzek and M. Presselt, J. Comput. Chem., 2018, 39, 763–772 CrossRef CAS PubMed.
- J-Aggregates, ed. T. Kobayashi, World Scientific, 1996 Search PubMed.
- B. Kopainsky, J. K. Hallermeier and W. Kaiser, Chem. Phys. Lett., 1981, 83, 498–502 CrossRef CAS.
- A. Eisfeld, R. Kniprath and J. Briggs, J. Chem. Phys., 2007, 126, 104904 CrossRef CAS PubMed.
- C. Didraga, A. Pugžlys, P. R. Hania, H. von Berlepsch, K. Duppen and J. Knoester, J. Phys. Chem. B, 2004, 108, 14976–14985 CrossRef CAS.
- F. Milota, V. I. Prokhorenko, T. Mancal, H. von Berlepsch, O. Bixner, H. F. Kauffmann and J. Hauer, J. Phys. Chem. A, 2013, 117, 6007–6014 CrossRef CAS PubMed.
- F. Taher-Ghahramani, F. Zheng and A. Eisfeld, Spectrochim. Acta, Part A, 2022, 275, 121091 CrossRef CAS PubMed.
- H. von Berlepsch and C. Böttcher, J. Phys. Chem. B, 2002, 106, 3146–3150 CrossRef CAS.
- H. von Berlepsch, K. Ludwig and C. Böttcher, Phys. Chem. Chem. Phys., 2014, 16, 10659–10668 RSC.
- F. Haverkort, A. Stradomska, A. H. de Vries and J. Knoester, J. Phys. Chem. B, 2013, 117, 5857–5867 CrossRef CAS PubMed.
- J. Megow, T. Körzdörfer, T. Renger, M. Sparenberg, S. Blumstengel, F. Henneberger and V. May, J. Phys. Chem. C, 2015, 5747–5751 CrossRef CAS PubMed.
- C. Friedl, T. Renger, H. V. Berlepsch, K. Ludwig, M. Schmidt Am Busch and J. Megow, J. Phys. Chem. C, 2016, 120, 19416–19433 CrossRef CAS PubMed.
- G. Zajac, E. Machalska, A. Kaczor, J. Kessler, P. Bouř and M. Baranska, Phys. Chem. Chem. Phys., 2018, 20, 18038–18046 RSC.
- P. W. J. M. Frederix, I. Patmanidis and S. J. Marrink, Chem. Soc. Rev., 2018, 47, 3470–3489 RSC.
- A. S. Bondarenko, I. Patmanidis, R. Alessandri, P. C. T. Souza, T. L. C. Jansen, A. H. D. Vries, S. J. Marrink and J. Knoester, Chem. Sci., 2020, 11, 11514–11524 RSC.
- C. Boisseau, I. Simbotin and R. Côté, Phys. Rev. Lett., 2002, 88, 133004 CrossRef PubMed.
- K. R. Overstreet, A. Schwettmann, J. Tallant, D. Booth and J. P. Shaffer, Nat. Phys., 2009, 5, 581–585 Search PubMed.
- D. Jaksch, J. I. Cirac, P. Zoller, S. L. Rolston, R. Côté and M. D. Lukin, Phys. Rev. Lett., 2000, 85, 2208–2211 CrossRef CAS PubMed.
- M. Saffman, T. G. Walker and K. Mølmer, Rev. Mod. Phys., 2010, 82, 2313–2363 CrossRef CAS.
- M. Saffman, J. Phys. B: At., Mol. Opt. Phys., 2016, 49, 202001 CrossRef.
- I. S. Madjarov, J. P. Covey, A. L. Shaw, J. Choi, A. Kale, A. Cooper, H. Pichler, V. Schkolnik, J. R. Williams and M. Endres, Nat. Phys., 2020, 16, 857–861 Search PubMed.
- A. Browaeys and T. Lahaye, Nat. Phys., 2020, 16, 132–142 Search PubMed.
- M. Schlosser, D. O. de Mello, D. Schäffner, T. Preuschoff, L. Kohfahl and G. Birkl, J. Phys. B: At., Mol. Opt. Phys., 2020, 53, 144001 CrossRef CAS.
- T. Gallagher, Rydberg Atoms, Cambridge University Press, Cambridge, 2005 Search PubMed.
- R. J. LeRoy, Can. J. Phys., 1974, 52, 246–256 CrossRef CAS.
- J. Deiglmayr, Phys. Scr., 2016, 91, 104007 CrossRef.
- T. G. Walker and M. Saffman, Phys. Rev. A: At., Mol., Opt. Phys., 2008, 77, 032723 CrossRef.
- K. Singer, J. Stanojevic, M. Weidemüller and R. Côté, J. Phys. B: At., Mol. Opt. Phys., 2005, 38, 295–307 CrossRef.
- A. A. Kamenski, N. L. Manakov, S. N. Mokhnenko and V. D. Ovsiannikov, Phys. Rev. A, 2017, 96, 032716 CrossRef.
- S. Weber, C. Tresp, H. Menke, A. Urvoy, O. Firstenberg, H. P. Büchler and S. Hofferberth, J. Phys. B: At., Mol. Opt. Phys., 2017, 50, 133001 CrossRef.
- N. Šibalić, J. D. Pritchard, C. S. Adams and K. J. Weatherill, Comput. Phys. Commun., 2017, 220, 319–331 CrossRef.
- J. Block and S. Scheel, Phys. Rev. A, 2017, 96, 062509 CrossRef.
- A. Anderson, S. Haroche, E. A. Hinds, W. Jhe and D. Meschede, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 37, 3594–3597 CrossRef CAS PubMed.
- V. Sandoghdar, C. I. Sukenik, E. A. Hinds and S. Haroche, Phys. Rev. Lett., 1992, 68, 3432–3435 CrossRef CAS PubMed.
- L. Béguin, A. Vernier, R. Chicireanu, T. Lahaye and A. Browaeys, Phys. Rev. Lett., 2013, 110, 263201 CrossRef PubMed.
- S. Hollerith, J. Zeiher, J. Rui, A. Rubio-Abadal, V. Walther, T. Pohl, D. M. Stamper-Kurn, I. Bloch and C. Gross, Science, 2019, 364, 664–667 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2023 |