Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Recalibrating the calcium trap in amino acid carboxyl groups via classical molecular dynamics simulations†
Janou A.
Koskamp
 a,
Sergio E.
Ruiz Hernandez
a,
Nora H.
de Leeuw
a,
Sergio E.
Ruiz Hernandez
a,
Nora H.
de Leeuw
 ab and
Mariette
Wolthers
ab and
Mariette
Wolthers
 *a
*a
aDepartment of Earth Sciences, Utrecht University, 3584 CB Utrecht, The Netherlands. E-mail: j.a.koskamp@uu.nl; s.e.ruizhernandez@uu.nl; n.h.deleeuw@uu.nl; m.wolthers@uu.nl; Tel: +31302535042
bSchool of Chemistry, University of Leeds, Leeds LS2 9JT, UK. E-mail: n.h.deleeuw@leeds.ac.uk
First published on 5th December 2022
Abstract
In order to use classical molecular dynamics to complement experiments accurately, it is important to use robust descriptions of the system. The interactions between biomolecules, like aspartic and glutamic acid, and dissolved ions are often studied using standard biomolecular force-fields, where the interactions between biomolecules and cations are often not parameterized explicitly. In this study, we have employed metadynamics simulations to investigate different interactions of Ca with aspartic and glutamic acid and constructed the free energy profiles of Ca2+–carboxylate association. Starting from a generally accepted, AMBER-based force field, the association was substantially over and under-estimated, depending on the choice of water model (TIP3P and SPC/fw, respectively). To rectify this discrepancy, we have replaced the default calcium parameters. Additionally, we modified the σij value in the hetero-atomic Lennard-Jones interaction by 0.5% to further improve the interaction between Ca and carboxylate, based on comparison with the experimentally determined association constant for Ca with the carboxylate group of L-aspartic acid. The corrected description retrieved the structural properties of the ion pair in agreement with the original biomolecule – Ca2+ interaction in AMBER, whilst also producing an association constant comparable to experimental observations. This refined force field was then used to investigate the interactions between amino acids, calcium and carbonate ions during biogenic and biomimetic calcium carbonate mineralisation.
Introduction
Calcium is an important ion in many biological processes, for example interacting with biomolecules to regulate enzyme activity.1 It is also an important building block in biominerals, e.g. in the bone mineral apatite and in CaCO3 minerals to create for example the shells of molluscs, eggs and corals (e.g. ref. 2,3). The conditions under which such biominerals are formed are complex and some of the biomineralization mechanisms remain unresolved. Atomistic computational approaches can be employed to provide detailed insight into the structure and dynamics between calcium ions and complex biomolecules that are considered to play an important role in biomineralization (e.g. ref. 4–8).Biomolecules are complex, usually flexible, systems containing many atoms. The treatment of such many-electrons systems using pure ab initio or density functional theory (DFT) methods is highly compute-intensive and, in some cases, simply unachievable. Therefore, computationally less demanding classical atomistic simulation techniques are widely used to simulate proteins and large peptides and their interactions with other systems. Multiple force fields and software packages have been developed to accurately describe a range of biomolecules. For example, AMBER,9 CHARMM10 and GROMOS11 are software packages with their own set of biomolecular force fields and all are widely used to perform molecular dynamics simulations (MD). Over the years, the force fields have been improved and updated alongside developments in experimental techniques and insights gained from ab initio calculations.12–17
Generally, biomineralization is thought to be guided by proteins that are rich in glutamic and aspartic acid that trap calcium.18–20 However, in classical MD this calcium-trapping is not observed for these amino acids, nor in small aspartic acid–based biomolecules.4,21 This observation is in contrast with conclusions from experiments, where biomolecules bind Ca,22–25 and ab initio (DFT) calculations with implicit water, which have reported a shorter distance between oxygen of the carboxyl group in the amino acid and Ca than between carboxyl and carbonate.22 To obtain meaningful insights into the calcium trapping behaviour of these specific amino acids and their impact on CaCO3 formation, it is important to address why classical computational outcomes differ from experimental work.
In atomistic simulations, it is crucial to achieve an accurate description of the free energy surface (FES) of the system.26 Although ab initio calculations commonly provide the most reliable results, the high computational costs make them less suitable to calculate the FES for large biosystems.26 In these large systems the convergence requires very prolonged simulations, necessary to generate accurate data. It is worth noting that recently an ab initio investigation verified results obtained with classical MD, despite inherent features of the latter such as fixed-charge force-fields and a lack of accounting polarizability and nuclear quantum effects.27
By using a force field, as in MD approaches, the FES is mimicked and thereby physical insights are acquired. The derivation of such force fields can be achieved through a number of approaches, resulting in multiple ways to describe the same system. In commonly used force fields, the non-bonding interactions are obtained using one of the Lorentz–Berthelot mixing rules and in many cases the parameters for the non-biological interactions in the systems (i.e. between ions, water, etc.) are transferred from other published parameters, which in some cases may lead to an unphysical or incorrect description of the FES.28
In this work, we have used well-tempered metadynamics simulations to investigate the interaction of Ca with the carboxylate oxygen (Ocarboxylate or OD) in glutamic and aspartic acid dissolved in water. We have compared the binding energies of our AMBER-based force field with experimental data. Using different Ca descriptions, our results show that the standard AMBER parameters combined with a Ca description reported previously29 either under- or over-estimate the Ca–Ocarboxylate binding energy. We therefore propose a refinement of the Ca–Ocarboxylate Lennard-Jones (LJ) parameters from the SPC/fw water model and a Ca description based on previously reported parameters29 used in combination with AMBER-based biomolecules with carboxyl groups. Using this refinement, MD simulations show the impact of aspartic acid on growing amorphous calcium carbonate clusters, with the most striking result the inhibition of dehydration of the formed ACC.
Methods
For the calculations of the free energies, and the refinement of the interatomic potential parameters for dissolved calcium and the carboxylate-oxygen interaction in specific biomolecules, we have created two different simulation cells, both containing 2163 water molecules and one Ca2+. The first cell contains an L-aspartic acid (L-Asp) molecule, and the second cell contains a glutamic acid molecule. The representation of the biomolecules corresponds to a pH condition ∼10. Using the refined force field parameters, we studied the impact of aspartic acid on the spinodal decomposition of a CaCO3 rich solution. We placed one enantiomers (L or D) of aspartic acid in a box with 15831 water molecules, and 255 Ca2+ and 255 CO32− ions randomly distributed. The systems contained either one L-Asp, one D-Asp or nothing (pure). In the systems with biomolecules, two Na2+ were added as background electrolytes to charge balance the 2e-overall charge of the biomolecule. We created four different starting configurations, to enhance the statistics of the results, and a similarity analysis between the initial configurations was conducted to quantify the differences in ion distributions using the Tanimoto distance.30–32 For the Tanimoto distance, the vectors (configuration A and B, eqn (1)) were ordered according to the distance to the center of mass (COM) of the biomolecule, whereas the pure systems were created by removing L-Asp from the starting configurations. The vectors contain, first, the distance between the atom closest to the COM of the biomolecule and the other atoms in the CaCO3 cluster, followed by the distances between the atom closest to this first atom and the other atoms and so on. The Tanimoto distance was calculated and only random ion-configurations with a Tanimoto distance of less than 0.7 were used to guarantee that the starting configurations were different.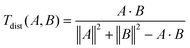 | (1) |
The description of the biomolecules was taken from the AMBER force field using the leap program to generate all the structures and extract the topology and interaction parameters.36 The amino acids were C-terminated and capped with a proton on the nitrogen to produce the final structure (Fig. S1, ESI†). The Ca2+ and CO32− ions were simulated using the parameters from ref. 37 and the parameters for the water are those of the SPC/fw force field,38 which we have chosen given the validated CaCO3 interactions29,39 and because the TIP3P model (incorporated in AMBER) has a diffusion coefficient which is twice the experimental value.40
We used the Lorentz–Berthelot rules (for consistency with AMBER, where the same rules have been applied36) to create the Lennard-Jones potentials between the Ca and the atoms in the biomolecule.41,42 Several parameter sets (εii and σii) for the description of Ca using Lennard-Jones potentials can be found in the literature, Table 1. Out of the several sets, we tested three different sets of parameters for Ca in combination with the biomolecules and labelled them Set_1, Set_2 and Set_3 (Table 1 and in the (ESI†) Table S1 until Table S3). For completeness, the Ca parameters of Set_19 were tested using both the SPC/fw and AMBER's original TIP3P water models (ESI,† Table S1). The Set_2 Ca parameters were based on a previously reported force field,29 which we extracted from the Owater–Owater and Owater–Ca interaction parameters (ESI,† Table S2). Set_3 was created by modifying Set_2 to refine the interactions for Ca–amino acid and the corresponding energy profile (ESI,† Table S3). This was done by changing both ε and σ parameters;28,43,44 in this case σCa_Set3 and εCa_Set3 were taken as the average of Set_2 and the parameters of Ocarboxylate. In the LJ-interaction, σ alters the distance of the well and thus the equilibrium distance between the ion pair, which may also change the depth of the well. We increased the σ LJ-parameter for Ca2+–Ocarboxylate stepwise up to +2.0% (see Table 3) to decrease the well depth to match experimental observations, in a similar approach to the method described in. ref. 28
| Ca2+ | Acronym | ε ii (eV) | σ ii (Å) | A ii | B ii | A ii /Bii |
|---|---|---|---|---|---|---|
| Hornak, 20069 | Set_1 | 0.019937830 | 3.426200 | 208685 | 129 | 1618 |
| Mamatkulov, 201350 AMBER | 0.019899403 | 3.050000 | 51582 | 64 | 805 | |
| Aqvist, 199051 | 0.019692117 | 2.410000 | 3024 | 15 | 196 | |
| Wang, 200852 | 0.011457217 | 2.789015 | 10152 | 22 | 471 | |
| Mamatkulov, 201350 | 0.009742416 | 2.410000 | 1496 | 8 | 196 | |
| Martinek, 201753,54 | 0.005256800 | 2.819600 | 5309 | 11 | 502 | |
| Beglov, 199455 CHARMM | 0.005182136 | 2.430000 | 879 | 4 | 206 | |
| Dang, 199556 | 0.004336300 | 2.895000 | 6011 | 10 | 589 | |
| Shen57 | 0.003316575 | 2.450000 | 621 | 3 | 216 | |
| Babu and Lim, 200658 | 0.001243713 | 3.250000 | 6908 | 6 | 1178 | |
| This work (based on ref. 39) | Set_2 | 0.000133902 | 3.534508 | 2036 | 1 | 1950 |
| Adjusted Set_2 | Set_3 | 0.001104240 | 3.247210 | 6071 | 5 | 1172 |
The free energy profiles were constructed using well-tempered metadynamics simulations for every modified set of interactions. The PLUMED 2.5.345 plug-in for LAMMPS was used to perform all free energy calculations. The collective variable (CV) was defined as the distance between Ca and the central carbon of the carboxylate group of the biomolecule. Gaussian hills were deposited every 10 ps with a hill height of 1.0 kJ mol−1 and a width of 0.02 nm. The bias factor was set at 10. Since Ca is considered fully dissolved at approximately 1 nm, we explored the CV up to 1.6 nm distance, and we placed an upper wall at 1.6 nm with a force constant (κ) of 2000. The total simulation time was 100 ns per metadynamics simulation to achieve convergence. The obtained free energy profiles were normalized by setting the asymptotic region to zero. The average energy of the CV distance from 1 to 1.4 nm was set to zero and the correction value was subtracted from the energy profile.
The comparison of the free energy profiles from the metadynamics simulations with the experimentally obtained association constant (Ka) was achieved through predicting the Ka from the profiles. Ka is a stability constant, in the literature also referred to as the formation or binding constant, and in terms of activities, Ka is defined as:
 | (2) |
 | (3) |
 | (4) |
dGassociation = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) ln(Ka) ln(Ka) | (5) |
To investigate the impact of our modified Ca–ligand interaction from the AMBER-based force field, we analysed the formation of an amorphous calcium carbonate (ACC) cluster in the presence of L- or D-aspartic acid. An in-house python script was used to calculate the number of clusters and their sizes in terms of ions over the course of the simulation. An ion was considered part of a cluster if the distance to another ion in the cluster was less than the distance of the first coordination shell of the two species. For example, the maximum distance between Ca2+ and Oc was set to 0.34 nm (based on the first minimum in the Ca–Oc RDF). We averaged the cluster size distributions of the duplicates to follow the evolution in time. To study the possibility of the presence of water in and around the clusters, the solvent accessible surface area (SASA) was computed over the full trajectory to follow the change with time, using the Mdtraj48 module in the Anaconda Python distribution. The method consisted of running the Shrake and Rupley49 algorithm to explore the area around all Ca2+ and CO32− ions with a probe of the size of a water molecule (radius = 0.14 nm). The local density of ACC (Ca2+ and CO32−) was calculated from the integral of the radial distribution function until 0.9 nm divided by the volume corresponding to that radius. Several radial distribution functions were calculated between the different ions and functional groups, where the RDFs were calculated from the final 10 ns of each simulation.
Results and discussion
Calcium description
The description of Ca2+ in interatomic Lennard-Jones potentials for MD varies over different studies (Table 1). As can be seen from Table 1, ε varies by more than one order of magnitude while the maximum difference in σ is approximately 0.1 nm. The intrinsic Pauli repulsion is described by the A parameter (A = 4πεσ12), while the attraction between two Ca ions is described by the B parameter (B = 4πεσ6). For the highest and the lowest value of ε, the A parameter of Set_19 is 2.0 orders of magnitude larger than the Ca repulsion of Set_2. The attraction that compensates this repulsion, was also a 2.1 order of magnitude larger, which resulted in a similar balance between repulsion and attraction as seen in the A/B values. In the continuing sections, we have compared the two most extreme descriptions for Ca, i.e., Set_1 and Set_2, and the proposed alternative description, Set_3.Free energy of association
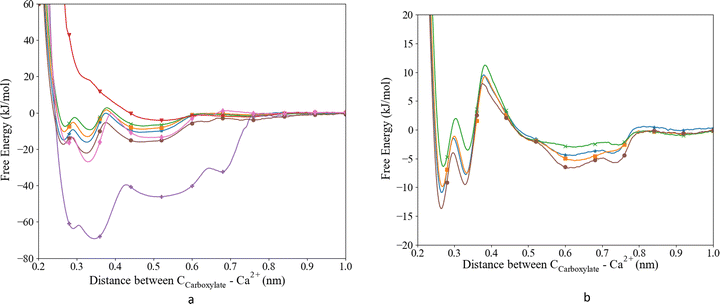
The potential parameters of Ca were combined with the parameters of the biomolecule to describe the interaction with the aspartic acid and glutamic acid as used in our MD. To evaluate and improve the Ca2+–Ocarboxylate interaction, the MD results were reviewed considering the experimental Ka and the coordination distance obtained from ab initio MD. As a starting point we constructed the free energy profiles using the unmodified Set_1, Set_2 and Set_3 interactions, Fig. 1a. We combined the parameters from Set_1 with TIP3P and SPC/fw water. The combination with TIP3P resulted in the deepest well in the energy profile compared to all other parameters published here. The well ends at 0.78 nm and has four local minima at 0.290, 0.346, 0.513 and 0.677 nm. The minima correspond to different Ca–ligand–water structures, i.e., the first and second minima correspond to a CIP that was split in a bidentate and a monodentate configuration. In the bidentate (biCIP) configuration, Ca was coordinated to both oxygens in the carboxylate group, while in the monodentate (monoCIP) configuration, Ca was only coordinated to one of the oxygens. The third and the fourth minima resemble SIP and SSIP, respectively.From the free energy profile, we extracted the largest ΔGa (−62.3 kJ mol−1) and Ka (7.07 × 1010) compared to the other parameter sets and literature values (Table 2). The coordination distance between Ca and Ocarboxylate was slightly longer than observed experimentally. The TIP3P water model was then replaced by the SPC/fw water model in combination with Set_1, since this water model has been found to behave in a more realistic manner.40 However, the corresponding free energy profile of this system did not show clear minima Fig. 1a. The global minimum was at 0.546 nm which indicated a long Ca–Ocarboxylate distance of 0.466 nm. The shallow minimum in the energy profile led to the lowest observed Ka (Table 2). Neither water models in combination with the parameters from Set_1 were able to reproduce the most recent experimentally observed Ka (11.3 kJ mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 59) and distance between the Ca and the ligand (0.241–0.254 nm;60Table 2), although the distance for Ca–Ocarboxylate with Set_1 and SPC/fw compared favourably with previously published distances obtained from MD (0.459 nm21).
59) and distance between the Ca and the ligand (0.241–0.254 nm;60Table 2), although the distance for Ca–Ocarboxylate with Set_1 and SPC/fw compared favourably with previously published distances obtained from MD (0.459 nm21).
| Ca | Water model | Acronym | Asp | Glu | ||||
|---|---|---|---|---|---|---|---|---|
| r Ca-OD (nm) | −ΔGa | K a | r Ca-OD (nm) | −ΔGa | K a | |||
| a No experimental reference. | ||||||||
| 9 | TIP3P | Set_1TIP3P | 0.274 | 62.3 | 7.07 × 1010 | n.a. | n.a. | n.a. |
| SPC/fw | Set_1SPC/fw | 0.466 | 4.9 | 7.07 | n.a. | n.a. | n.a. | |
| Based on ref. 39 | SPC/fw | Set_2 | 2.224 | 18.70 | 1802.71 | n.a. | n.a. | n.a. |
| Adjusted Set_2 | SPC/fw | Set_3unmodified | 0.238 | 15.7 | 548.22 | 0.242 | 7.7 | 22.06 |
| SPC/fw | Set_3σ+0.5%σ | 0.242 | 10.4 | 65.46 | 0.242 | 6.0 | 10.98 | |
| SPC/fw | Set_3σ+1.0%σ | 0.242 | 8.1 | 25.87 | 0.245 | 6.3 | 12.43 | |
| SPC/fw | Set_3σ+2.0%σ | 0.245 | 6.5 | 13.58 | 0.248 | 5.0 | 7.40 | |
| Experiments | ||||||||
| 200959 | 11.3 | 91.20 | 7.4 | 19.05 | ||||
| 199062 | 11.4 | 97.50 | ||||||
| 198763 | 6.5 | 13.64 | ||||||
| 2012a61 | 0.243–0.261 | |||||||
| 199860 | 0.241–0.254 | |||||||
| Simulations | ||||||||
| DFT22 | 0.245 | 0.243 | ||||||
| 2012 MD-CHARMM61 | 0.244–0.260 | 12.2 | 133.10 | |||||
| 2017 MD-AMBER-Buck21 | 0.459 | 4.5 | 6.07 | |||||
| Modified CHARMM28 | 6.1 | 11.54 | ||||||
To improve the energy of association we replaced the Ca parameters with the parameters used in the CaCO3 force field (Set_2); we obtained a ΔGa of −18.70 kJ mol−1, which is in better agreement with experimental values than those from Set_1 (Table 2), although it still overestimates the free energy of association by approximately 7.4 kJ mol−1.22,59–61 In the free energy profile of Set_2, we observed three distinct minima: around 0.28, 0.33 and 0.50 nm (Fig. 1a), corresponding to biCIP, monoCIP, and SIP, respectively, and in agreement with ref. 28 A less distinguishable minimum was observed around 0.8 nm that correlates with SSIP. The deepest minimum of the energy profile was found at the second well at 0.33 nm. The coordination distance (0.224 nm) is smaller than previously published distances (based on DFT or experimental studies). The free energy of association obtained from the Set_3 simulation was calculated to be −15.7 kJ mol−1 and the locations of the different ion pair geometries remained unaltered compared to Set_2. The coordination distance was closer to the distances reported in the literature than those produced by Set_1TIP3P, Set_1SPC/fw and Set_2 interactions (Table 2) but slightly shorter than reported by ref. 22, 60 and 61. Thus, the simulations that used the parameters from Set_3 improved the coordination distance and association energy.59,61
Subsequently, we optimized the Ca–Ocarboxylate interaction through modifying the σCa-OD values in the LJ potential by increasing it by 0.5, 1.0 or 2.0% (see Table 3 for the absolute values), i.e. comparable to other studies using the same method for glutamic acid, γ-carboxyglutamic acid (CHARMM).28 The energy profile and corresponding ΔGa and Ka (Fig. 1a and Table 2) revealed that a modified σ of +0.5% yielded the best match with the latest experimental data.59 Moreover, the equilibrium coordination distance was almost the same as published using ab initio calculations.22,61 Higher increases to σ resulted in a lower ΔGa, although still within the range of experimentally observed values. Increasing σ by 2.0% resulted in a distance exactly matching previously reported values,22 but the association free energy became slightly lower than the lowest experimental value.63 For all modifications, three distinct minima were observed, corresponding to the different ion pair configurations biCIP, monoCIP and SIP. However, increasing σ changed the difference between biCIP and monoCIP, especially at σ + 0.5%, which reduced this difference the most, from 4.8 kJ mol−1 in the unmodified profile to 1.2 kJ mol−1. As for Set_3unmodified, the modified interactions generated the lowest minimum for monoCIP.
| Ca-OD | σ (Å) |
|---|---|
| Set_3unmodified | 3.10356595082234 |
| Set_3σ+0.5%σ | 3.11908378057645 |
| Set_3σ+1.0%σ | 3.13460161033056 |
| Set_3σ+2.0%σ | 3.16563726983879 |
As to glutamic acid, a similar approach yielded the energy profiles shown in Fig. 1b. We observed four minima around 0.26, 0.33, 0.61 and 0.74 nm. The first minimum is found to be the deepest and corresponded to the biCIP. Following the same modification method as for aspartic acid, upon increasing σ the CIP well became shallower and the separation of SIP and SSIP became less clear. For glutamic acid, the association energies were lower compared to aspartic acid. When comparing to previous studies, the unmodified interaction slightly overestimated the association energy,59 while the association energy calculated for σ + 0.5% was lower than experimental and computational values.28,59 The value of σ + 1.0% appeared to achieve a value between the experimental and previous computational association energies. However, since σ + 0.5% was closer to the unmodified value and comparable to the more recent MD, we proceed to evaluate the effect on the water structure only for the Set_3unmodified and + 0.5% modification.
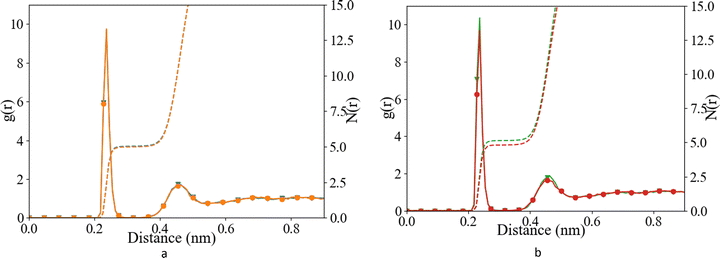
Water structure
We have investigated the details of the solvent structuring around the ion pair in the CIP coordination mode. We calculated the radial distribution function (RDF) between the carboxylate-oxygen atom and the water oxygen atom and compared our findings for both the Set_3unmodified and our σ + 0.5% modification, as shown in Fig. 2. Two peaks in the RDF were apparent, the first solvation shell at an Ocarboxylate–Owater separation of ∼0.29 nm, and a second solvation shell at ∼0.46 nm. The RDF was taken between the Ocarboxylate and Owater with the Ca bonded to the carboxylate. This caused the coordination number to drop and affected the water structuring around the Ocarboxylate, resulting in a sharper second peak similar to previously published RDFs for Ocarboxylate and Owater.28 The data showed that our modification did not induce a significant difference in these RDFs, for either Asp or Glu. The angular distribution function (ADF) in Fig. 3 confirms that the hydrogen-bond angle between the coordinated water and Ocarboxylate also remained unaltered upon our modification, when Ca–Ocarboxulate were in the CIP geometry. To complete our analysis, we studied the RDF between Ca and water when Ca was paired with the biomolecule. Fig. 4 shows that the RDF and coordination of water around calcium also remained the same and in both cases a coordination number of 5 was found. However, note the slight increase in number of water molecules around Ca in CIP with glutamic acid, as the CN increases by 0.33 for Set_3σ+0.5%σ compared to the unmodified force field.Overall, the Set_3unmodified interaction in combination with the AMBER description of the amino acid appears to be more realistic than the Set_1 Ca description. However, it still over-estimates the binding of Ca to the carboxylate group as compared with experiment (Table 2). Modifying this single interaction individually to Set_3σ+0.5%σ helped to improve further the description of the binding energy of the ligand–Ca pair in water (Table 2), without affecting the surrounding water structure (Fig. 2–4).
Association mechanism
Insights into the association and dissociation mechanism of Ca2+ with the carboxyl group of Asp and Glu were provided by free energy calculations plotted as a function of 2 CV's, in this case the Ca–Ocarboxylate coordination number and the coordination number of Ca2+ to Owater. The left graph of Fig. 5 shows that in Ca fully dissolved in water the CNwater was between ∼6 and ∼9, with three wells indicating three main configurations with CN's around ∼8.3, ∼7.4, and ∼6.6. When Ca was coordinated to one, two or three Ocarboxylate, the CNwater ranged from 5 to 8, 4 to 7 and 4 to 6, respectively. The same pattern was observed for Glu, the right-hand side graph of Fig. 5, with the addition of the Ca coordinated to four Ocarboxylate's. When this latter case was observed the CNwater was narrowed to 4. | ||
| Fig. 5 Free energy as a function of distance Ca2+ and Ocarboxylate and coordination number of Ca2+ and Owater. | ||
ACC formation in the presence of L/D-aspartic acid
Further implications of our proposed modification of the interatomic potential between Ca2+ and Ocarboxylate (Set_3σ+0.5%σ) were investigated in a more complex system. We studied the interaction of freely dissolved Ca2+ and CO32− with D-aspartic acid or L-aspartic acid in a system that was highly supersaturated with respect to ACC. We compared cluster structure, cluster density, cluster composition and cluster size. To reproduce the results, we simulated four different starting configurations with a similarity coefficient of less than 70%. Unless stated otherwise, the data shown are therefore the average of the four simulations.ACC cluster structure
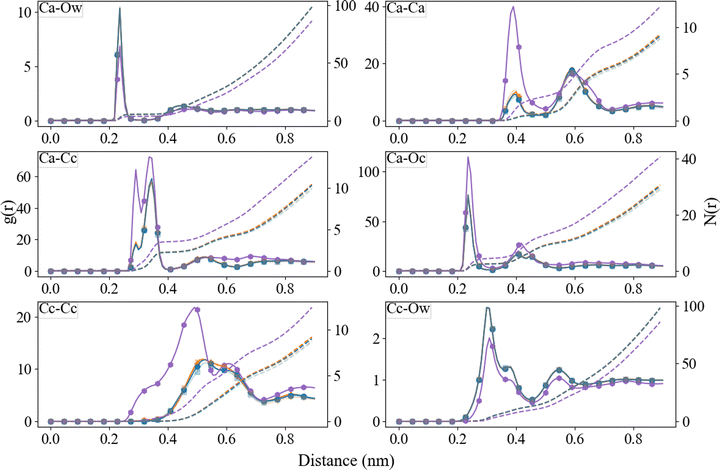
The radial distribution functions between different species, obtained from the final 10 ns of the simulations, are reported in Fig. 6 and 7. For comparison, we have also included the RDFs of a single simulation using Set_1SPC/fw. As observed in the ACC RDFs, the distances remained unaltered upon the refinement of the force field. The RDFs between the different parts of Asp, as shown in Fig. 7, reveal a clear difference between the force fields in the distance between the carboxyl oxygen (OD) and the coordinated Ca, which decreased from 0.46 nm to 0.24 nm. In addition, a clear separation between biCIP and monoCIP was observed at 0.28 and 0.35 nm, respectively. The intensities of the biCIP and monoCIP for D-Asp were inverted compared to L-Asp. The refined Ocarboxylate–Ca potential parameters also resulted in more structure between the amine group and Ca, as reflected by the more pronounced minima in the N–Ca and especially the N–Cc RDFs. Data from the other tested σ values (single simulations) can be found in the ESI,† Fig. S2 until Fig. S5).ACC cluster density
We calculated the density of CaCO3 around different groups in the biomolecule, as well as the average density of the ACC clusters, by calculating the density around every Ca2+ in the system (Table 4). The density is calculated around all ions, independent of the cluster they belong to. Fully solvated ions will therefore contribute to the density by lowering it. Since it is a dynamic system, the cluster size of the largest cluster varies. And since the largest cluster contains the most ions this cluster will also contribute the most to the density in Table 4. The cluster size distribution taken from the same part of the simulations as the densities, is shown in Fig. 9. The densities in the pure CaCO3 system were consistently ∼0.2 g cm−3 higher than in the biomolecule systems. An increase in density around the functional groups of the biomolecule, due to the new interaction parameters (Set_3σ+0.5%σ), was most noticeable for D-Asp, as well as the average ACC density. In contrast, the measured densities in both L-Asp and the formed ACC were less affected by the modified interaction. The difference between L-Asp and D-Asp was small and, due to the higher variability within the duplicates, and the densities around the functional groups of the two systems, were indistinguishable. The densities around the Ocarboxyl were slightly higher than values reported in the literature, although note that those previously reported values were for amino acid groups within a protein.4 All formed clusters had lower densities compared to hydrated and ACC clusters determined by ref. 21 In the latter, the ACC clusters were generated prior to the simulations, via a melting process of randomly packed molecules with a restricted number of water molecules. Therefore, the clusters reported before formed via a different pathway and the initial cluster formation steps were not part of their simulations.21 This may be an explanation for the difference in density/water content.| Density (g cm−3) | |||
|---|---|---|---|
| System | OCarboxyl group | NAmine | Ca2+ |
| a Hydrated ACC. | |||
| Pure | n.a. | n.a. | 0.73 ± 0.023 |
| Set_3σ+0.5%σ | |||
| L-Asp | 0.81 ± 0.071 | 0.92 ± 0.127 | 0.55 ± 0.030 |
| D-Asp | 0.82 ± 0.172 | 0.78 ± 0.180 | 0.56 ± 0.007 |
| Set_1SPC/fw | |||
| L-Asp | 0.78 | 0.83 | 0.46 |
| D-Asp | 0.58 | 0.58 | 0.47 |
| Literature | |||
| L-Asp21 | ∼1.1a–1.4 | ||
| Aspartate in lysozyme4 | ∼0.71 | ||
ACC cluster size distribution and their solvent accessible surface area
The calcium carbonate ions in the systems with freely dissolved ions, as well as those with one L/D-aspartic acid, aggregated over the course of the simulation. In all simulations, the ions formed clusters, and in all systems with a biomolecule, the biomolecule was found incorporated in the largest cluster (except for one of the D-Asp simulations). The agglomeration was followed via a calculation of the cluster size distribution at every picosecond of simulation time (Fig. 8). Both L-Asp and D-Asp systems revealed a different clustering pattern compared to pure ACC. Whereas the system without the biomolecule showed sharp and constant lines throughout the simulation, the systems with the biomolecule showed a more smeared out pattern, revealing that the clusters varied more in cluster size through constant addition of ions or small clusters. In contrast, the cluster size variation in the pure ACC is most likely due to the aggregation of various clusters.The average cluster size distribution over the final 10 ns, Fig. 9, shows that the largest cluster in the pure system contained ±507 ions, which is somewhat higher than the L-Asp (±456 ions) and D-Asp (±478 ions) systems. The pure ACC system also comprised more intermediate clusters with a constant size and a longer lifetime, whereas similar intermediate cluster sizes of ±191 and ±284 ions were found in the D-Asp system (Fig. 9), although these intermediate cluster sizes were not observed in the L-Asp system (Fig. 9). If we average the data over the final 10 ns, we see the same contrast between the pure and amino acid-containing systems, with wider peaks in the cluster size distributions when the biomolecule is present (Fig. 9); note that this is also an average of four different simulations. Another difference between the pure CaCO3 system and the systems with L- or D-Asp was the time it took to observe the largest aggregates. While for L- and D-Asp the largest aggregate was already detected before 15 ns, in the pure system it took above 20 ns to form the largest aggregate (Fig. 8).
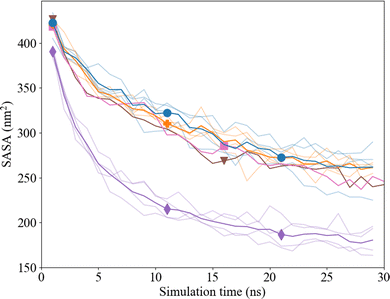
The solvent accessible surface area (SASA) of the Ca2+ and CO32− ions in solution was followed over time to study the effect of clustering on the surface area that was exposed to water with the new proposed interaction parameters. The volume within the cluster was assumed accessible and/or occupied by water molecules when it was equal to or bigger than the volume of one water molecule (with a radius of 0.14 nm). In the presence of Asp, the total SASA decreases by ∼40% within 30 ns, where we observed no difference between the D- and L-Asp systems (Fig. 10). However, a clear difference was seen in comparison with the pure system, where the SASA for the pure systems shrank significantly more over time (∼54%), leaving a much dryer cluster.
Implications
Interaction of calcium with carboxyl groups in aspartic and glutamic acid
In the past years, several studies have emphasised the importance of a re-evaluation of the parametrization of the interactions of charged amino acid side chains with water and ions to achieve a more accurate description of these systems.15,43,44 In previous simulations using AMBER-based force field parameters,21 the conclusion was drawn that it is mainly the amine group that interacts with the CO32− or an ACC surface rather than the carboxyl group, even though, based on experimental evidence, the latter was expected to be the main interacting functional group. The current study into the carboxyl-oxygen–calcium interaction revealed that parameter Set_1 has one of the highest repulsion terms in the Lennard-Jones potential, and although the attraction term is also higher, the overall result is a stronger repulsion in the other force field parameters,50–58 with implications for the simulation of single amino acids and larger biomolecules that are rich in aspartic and/or glutamic acid.64,65 Another description of Ca, derived from a refined CaCO3–waterSPC/fw force field,39 with the lowest repulsion and attraction values, also has a repulsion/attraction ratio of the same order of magnitude as the Ca in Set_1.A common water model used in simulations with biomolecules is the TIP3P water model.66–70 However, the energy profile obtained for the Ca description from Set_1 with TIP3P water overestimates the association constant of Ca with both amino acids by nine orders of magnitude, as seen before in AMBER- and CHARMM-based force fields.28,71 This discrepancy is mainly due to a lack of well-defined, explicit parameterization of the interaction between the amino acid and calcium,28 although this interaction is able to reproduce the different configurations upon association.47 Unfortunately, the TIP3P model has been shown to have a self-diffusion coefficient for water that is twice the experimental value.40 Moreover, other water models are considered to be more suitable for CaCO3 systems in terms of water dynamics and water structuring.40,72,73 For this reason, we have combined the parameters from Set_1 with SPC/fw water. With this force field, we obtained an energy profile that agreed closely with previously published results,21 although these authors used a Buckingham potential rather than the Lennard Jones potential employed in this work, to describe the interaction between Ca and the biomolecule. A Buckingham potential is wider, leading to a less structured solvation shell,74 which therefore contributes to the difference of −0.4 kJ mol−1 between their21 and our results (Table 2). However, unlike the energy profile of Set_1TIP3P, the Set_1SPC/fw force field is unable to capture the structural configurations of the ion pair and shows a global minimum at ∼0.466 nm, indicating that the SIP configuration would be preferred over CIP. Nevertheless, Set_1SPC/fw shows overall improved −ΔGa (Table 2), and in the current work, we therefore refined this force field to capture the carboxyl-Ca configuration known from experiments.
With the refined force field Set_3σ+0.5%σ for aspartic acid, the distance between the carboxyl-oxygen and the calcium corresponds to the monoCIP structure, although the difference between monoCIP and biCIP minima, at 1.22 kJ mol−1 compared to 4.79 kJ for Set_3unmodified is the smallest. In terms of stability, this means that a monoCIP configuration is favoured over a biCIP, which agrees with experimental observations using 13C nuclear magnetic resonance (NMR).75 Moreover, the water structure, in terms of RDF and hydrogen bond-angle around the Ocarboxylate compares well with those previously reported for Ocarboxylate in acetate.44 In short, the refined force field captures known interaction energies and structures for calcium coordinating to the carboxyl group of aspartic acid.
For glutamic acid, the association energy is lower than for aspartic acid: due to the extra CH2 group, the charge density in Glu is lower, and therefore the attraction of Ca2+ is weaker. Although the unmodified interaction gives a ΔGa that compares better to values obtained with an unmodified CHARMM-based force field,28 it is still slightly overestimated compared to experimental observations59 and refined computational results.28 In all cases the biCIP is more stable compared to monoCIP, in contrast with aspartic acid but in agreement with other MD simulations for Ca–Glu interactions.28
In the first step towards association of a dissolved calcium ion with another (dissolved) biomolecule such as Asp or Glu, Ca must lose one of its ∼8.3 water molecules. The first transition state can be characterized by a coordination number of 7.4. The most probable mechanism for this first step is that a water molecule leaves the solvation shell before Ca can approach more closely. Following the energy landscape, one of the Ocarboxylate's coordinates to Ca before another water molecule can leave the coordination shell. A similar mechanism was observed upon increasing the Ocarboxylate CN further. All three exchange mechanisms – associative, dissociative and interchange – as previously described,76 are possible Ca association mechanisms and observed here for Asp and Glu (Fig. 5). However, the lowest energy pathway reveals a preference for an associative mechanism, considering the darkest shaded coordination states in the energy landscape in Fig. 5. This associative mechanism can be traced by following the local minima in the free energy landscape, via ∼7Owater and 1Ocarboxylate, ∼6Owater and 1Ocarboxylate, ∼6Owater and 2Ocarboxylate to ∼5Owater and 2Ocarboxylate. Due to the longer chain length in Glu, the molecule is more flexible making it possible to coordinate all four oxygens to Ca, however this is not the most energetically favoured configuration. Both, Asp and Glu, agree with Ca2+–ligand exchange mechanisms identified with multidimensional vibrational spectroscopy using different ligands.77
Based on the above, we consider that the refined parameters to describe the interaction of calcium with a biomolecule are suitable to be used to study more complex systems.
Implications for ACC cluster formation in the presence and absence of aspartic acids
Due to the extremely high concentration of calcium and carbonate in solution (0.89 M), we could observe rapid cluster formation within MD-accessible timescales. However, this high concentration also means that the starting solution is not stable and will undergo a spontaneous phase separation, via spinodal decomposition.78 Formation of clusters will occur without any free energy barrier to overcome and without a critical nucleus size. This observation is in agreement with experiments using a slightly lower concentration of 0.50 M CaCO379 and even lower concentrations (0.05 M),80,81 and with previous MD (0.53 M),82 and other theoretical results.83,84In our simulations, the rapid formation of the initial ion pairs and small clusters is followed by aggregation of ion pairs and small clusters into larger clusters and – in the presence of biomolecules – almost always the incorporation of the biomolecule into the largest cluster. Further growth of the clusters is substantially slower, because the number of free ions, ion pairs and clusters in solution decreases and, consequently, the agglomeration frequency goes down. Moreover, the lower diffusivity of the larger clusters slows down further growth and makes the agglomeration process and formation of ACC more diffusion-limited.85
The simulation of ACC cluster formation in the presence of D- and L-Asp shows some clear differences compared to the cluster formation in the absence of a biomolecule. Overall, with the refined interactions (Set_3σ+0.5%σ), the aspartic acid enantiomers have the same impact on ACC cluster formation and the cluster stabilization as observed for Set_1SPC/fw and in previous computational86 and experimental work.64 Compared to the pure system, ACC clusters in the presence of Asp formed more rapidly (after 15 ns instead of 20 ns, respectively) and were on average slightly larger. This minimal effect on cluster size is in agreement with findings in experiments, where only marginal effects were reported for the effect of aspartic acid monomers on the particle size.87 Furthermore, the aggregates remained more hydrated, which resulted in a more flexible cluster size (i.e., constant rearrangement of the aggregate including hydration and dehydration processes). The stabilization of the hydrated clusters could explain the inhibition effects of Asp on calcite growth as observed in experiments.88
In terms of cluster size distribution, development in time and hydration levels, both enantiomers behave similarly with more abundant intermediate cluster sizes in the presence of D-Asp. The only clear difference we could identify between the two enantiomers was in terms of ion structuring around the functional groups of the biomolecule. The refined and stronger attraction of Ca with the carboxyl groups resulted in clear changes in RDFs between Ca and the functional groups of the two enantiomers, with a difference in preference for bi- and monoCIP changes between L and D. The biCIP configuration is preferred of over the monoCIP configuration in the case of L-Asp, whereas the monoCIP configuration is preferred in the presence of D-Asp, as it is in the simulations of single calcium ions with L-Asp. This difference could be of importance during other stages of crystal formation, but during the formation of the clusters as part of the spinodal decomposition, the chirality of Asp has an insignificant impact.
In addition to the stabilization of hydrated clusters, other implications of the insights presented in this work for biomineralization can, for example, be related to the role of biomolecules in combination with impurities like magnesium cations. Previous studies have shown that the presence of biomolecules accelerate the growth rate of a calcite surface,89 but where impurity uptake in the crystal is concerned, it has been found that Mg is more strongly affected by the biomolecule compared to Ca.89 Our simulations showed that L- and D-aspartic acid both have a stabilizing effect on the formation of hydrated ACC and could therefore provide a rather fluid-like/malleable reservoir of calcium and carbonate that can facilitate a fast transformation and/or fast ion-attachment and growth of the crystal.
Conclusion
In this study we have employed classical molecular dynamics simulations, using a number of refined force fields, to investigate the interaction of Ca with aspartic and glutamic acid. The results show that the ability to describe the association of the ions and the different structural stages upon ion pairing is crucially affected by the potential parameters, which therefore need to be chosen carefully. Using previously published parameters (Set_19), the force field does not reproduce the correct association energy (when combined with the TIP3P water model), nor the correct structural details (when combined with the SPC/fw model). The refined interaction parameters proposed here adequately enhanced the binding distance and the ΔGassociation without disrupting the solvent structure around the biomolecule and the ion. This new description shows a strong impact in more complex systems, where Ca-binding is now favoured over CO32−, in contrast to previously reported computational results, but supporting experimental findings. Therefore, we would recommend using the Set_3σ+0.5%σ interactions for Ca–Ocarboxylate when conducting MD of systems including Ca2+ and AMBER-based biomolecules with carboxyl functional groups.Subsequently, the impact of aspartic acid on the formation of ACC via spinodal decomposition was studied by performing MD simulations of solutions with dissolved calcium and carbonate ions in the absence and presence of D- or L-Asp. Both enantiomers had a similar effect on the aggregation of the clusters, where the biomolecule was incorporated in the largest cluster and the aggregates retained more water. As a result, the hydrated ACC was more malleable. In our case, an underestimation of the association constant (Set_1SPc/fw) led to similar stabilization of the hydrated ACC. Despite the difference in internal structure of ACC around the functional groups of Asp. In other systems with higher biomolecule concentrations and/or lower mineral concentrations (out of the spinodal decomposition regime), the effect of the Ca-trapping will probably be more significant and more easily compared to experimental observations of calcium trapping mechanisms.23
In general, our study has shown that aspartic acid monomers can be useful tools in biomineralization processes, for example to increase the hydration of amorphous calcium carbonate (ACC), thereby inhibiting dehydration. Potentially, these monomers can also be used to tailor calcium carbonate formation including in the reduction of scale formation.
Author contributions
Conceptualization, J. A. K., S. E. R. H. and M. W.; methodology, J. A. K. and S. E. R. H.; validation, J. A. K., S. E. R. H. and M. W.; formal analysis, J. A. K. and S. E. R. H.; investigation, J. A. K., S. E. R. H. and M. W.; resources, M. W.; data curation, J. A. K.; writing—original draft preparation, J. A. K.; writing—review and editing, S. E. R. H. and M. W.; visualization, J. A. K.; formal analysis and review N. H. L. supervision, M. W.; project administration, M. W.; funding acquisition, M. W. All authors have read and agreed to the published version of the manuscript.Conflicts of interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.Acknowledgements
The research work of J. A. K., S. E. R. H. and M. W. is part of the Industrial Partner- ship Programme i32 Computational Sciences for Energy Research that is carried out under an agreement between Shell and the Netherlands Organisation for Scientific Research (NWO) (grant agreement no. [14CSTT06]). This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement no. [819588]). This work was carried out on the Dutch national e-infrastructure with the support of SURF Cooperative.References
- S. Lee, H. I. Park and Q. X. A. Sang, Calcium regulates tertiary structure and enzymatic activity of human endometase/matrilysin-2 and its role in promoting human breast cancer cell invasion, Biochem. J., 2007, 403, 31–42 CrossRef CAS PubMed.
- M. Robin, S. Von Euw, G. Renaudin, S. Gomes, J. M. Krafft, N. Nassif, T. Azaïs and G. Costentin, Insights into OCP identification and quantification in the context of apatite biomineralization, CrystEngComm, 2020, 22, 2728–2742 RSC.
- F. Marin, G. Luquet, B. Marie and D. Medakovic, Molluscan Shell Proteins: Primary Structure, Origin, and Evolution, Curr. Top. Dev. Biol., 2007, 80, 209–276 CrossRef PubMed.
- R. S. Rani and M. Saharay, Molecular dynamics simulation of protein-mediated biomineralization of amorphous calcium carbonate, RSC Adv., 2019, 9, 1653–1663 RSC.
- L. Hamm, Calcium carbonate biomineralization: A theoretical and experimental investigation of biomolecular controls on nucleation and growth, 2012, pp. 1–130.
- J. Jin, J. D. Miller and L. X. Dang, Molecular dynamics simulation and analysis of interfacial water at selected sulfide mineral surfaces under anaerobic conditions, Int. J. Miner. Process., 2014, 128, 55–67 CrossRef CAS.
- L. B. Gower, Biomimetic model systems for investigating the amorphous precursor pathway and its role in biomineralization, Chem. Rev., 2008, 108, 4551–4627 CrossRef CAS PubMed.
- J. H. E. Cartwright, A. G. Checa, J. D. Gale, D. Gebauer and C. I. Sainz-Díaz, Angew. Chem. Int. Ed., 2012, 51, 11960–11970 CrossRef CAS PubMed.
- V. Hornak, R. Abel, A. Okur, B. Strockbine, A. Roitberg and C. Simmerling, Comparison of multiple Amber force fields and development of improved protein backbone parameters, Proteins: Struct., Funct., Bioinf., 2006, 65, 712–725 CrossRef CAS PubMed.
- A. D. MacKerell, D. Bashford, M. Bellott, R. L. Dunbrack, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiórkiewicz-Kuczera, D. Yin and M. Karplus, All-atom empirical potential for molecular modeling and dynamics studies of proteins, J. Phys. Chem. B, 1998, 102, 3586–3616 CrossRef CAS PubMed.
- J. Hermans, H. J. C. Berendsen, W. F. Van Gunsteren and J. P. M. Postma, A consistent empirical potential for water-protein interactions, Biopolymers, 1984, 23, 1513–1518 CrossRef CAS.
- P. S. Nerenberg and T. Head-Gordon, Curr. Opin. Struct. Biol., 2018, 49, 129–138 CrossRef CAS PubMed.
- J. B. Klauda, R. M. Venable, J. A. Freites, J. W. O’Connor, D. J. Tobias, C. Mondragon-Ramirez, I. Vorobyov, A. D. MacKerell and R. W. Pastor, Update of the CHARMM All-Atom Additive Force Field for Lipids: Validation on Six Lipid Types, J. Phys. Chem. B, 2010, 114, 7830–7843 CrossRef CAS PubMed.
- J. Henriques, C. Cragnell and M. Skepö, Molecular Dynamics Simulations of Intrinsically Disordered Proteins: Force Field Evaluation and Comparison with Experiment, J. Chem. Theory Comput., 2015, 11, 3420–3431 CrossRef CAS PubMed.
- M. M. Reif, P. H. Hünenberger and C. Oostenbrink, New interaction parameters for charged amino acid side chains in the GROMOS force field, J. Chem. Theory Comput., 2012, 8, 3705–3723 CrossRef CAS PubMed.
- D.-W. Li and R. Brüschweiler, NMR-Based Protein Potentials, Angew. Chem., Int. Ed., 2010, 49, 6778–6780 CrossRef CAS PubMed.
- M. J. Robertson, J. Tirado-Rives and W. L. Jorgensen, Improved Peptide and Protein Torsional Energetics with the OPLS-AA Force Field, J. Chem. Theory Comput., 2015, 11, 3499–3509 CrossRef CAS PubMed.
- L. Addadi, S. Raz and S. Weiner, Adv. Mater., 2003, 15, 959–970 CrossRef CAS.
- S. Schulze and H. Vogel, Aspects of the Safe Storage of Acrylic Monomers: Kinetics of the Oxygen Consumption, Chem. Eng. Technol., 1998, 21, 829–837 CrossRef CAS.
- S. Mann, D. D. Archibald, J. M. Didymus, T. Douglas, B. R. Heywood, F. C. Meldrum and N. J. Reeves, Crystallization at Inorganic-organic Interfaces: Biominerals and Biomimetic Synthesis, Science, 1993, 261, 1286–1292 CrossRef CAS PubMed.
- R. Innocenti Malini, A. R. Finney, S. A. Hall, C. L. Freeman and J. H. Harding, The Water–Amorphous Calcium Carbonate Interface and Its Interactions with Amino Acids, Cryst. Growth Des., 2017, 17, 5811–5822 CrossRef CAS.
- N. Tang and L. H. Skibsted, Calcium binding to amino acids and small glycine peptides in aqueous solution: Toward peptide design for better calcium bioavailability, J. Agric. Food Chem., 2016, 64, 4376–4389 CrossRef CAS PubMed.
- J. Su, X. Liang, Q. Zhou, G. Zhang, H. Wang, L. Xie and R. Zhang, Structural characterization of amorphous calcium carbonate-binding protein: An insight into the mechanism of amorphous calcium carbonate formation, Biochem. J., 2013, 453, 179–186 CrossRef CAS PubMed.
- S. P. Colowick and F. C. Womack, Binding of diffusible molecules by macromolecules: rapid measurement by rate of dialysis, J. Biol. Chem., 1969, 244, 774–777 CrossRef CAS PubMed.
- J. F. Maune, C. B. Klee and K. Beckingham, Ca2+ binding and conformational change in two series of point mutations to the individual Ca2 + -binding sites of calmodulin, J. Biol. Chem., 1992, 267, 5286–5295 CrossRef CAS PubMed.
- G. König, P. S. Hudson, S. Boresch and H. L. Woodcock, Multiscale free energy simulations: An efficient method for connecting classical MD simulations to QM or QM/MM free energies using non-Boltzmann Bennett reweighting schemes, J. Chem. Theory Comput., 2014, 10, 1406–1419 CrossRef PubMed.
- G. Cassone, H. Kruse and J. Sponer, Interactions between cyclic nucleotides and common cations: an ab initio molecular dynamics study †, Phys. Chem. Chem. Phys., 2019, 21, 8121 RSC.
- A. T. Church, Z. E. Hughes and T. R. Walsh, Improving the description of interactions between Ca2+ and protein carboxylate groups, including γ-carboxyglutamic acid: revised CHARMM22* parameters, RSC Adv., 2015, 5, 67820–67828 RSC.
- P. Raiteri, J. D. Gale, D. Quigley and P. M. Rodger, Derivation of an Accurate Force-Field for Simulating the Growth of Calcium Carbonate from Aqueous Solution: A New Model for the Calcite−Water Interface, J. Phys. Chem. C, 2010, 114, 5997–6010 CrossRef CAS.
- M. Liu, A. Dalvi, S. Dalapati, N. Prakash, Z. Hu, P. Zhou, K. Jiang, A. Pellicano, I. D. Goldberg and P. Narayan, Targeting Collagen Type III in Proteinuric Kidney Disease: Informing Drug Potential Using the Jaccard–Tanimoto Index, Processes, 2020, 8, 996 CrossRef CAS.
- G. M. Maggiora and V. Shanmugasundaram, Methods in molecular biology, Humana Press, Clifton, N.J., 2004, vol. 275, pp. 1–50 Search PubMed.
- Y. Pérez-Badell and L. A. Montero, Multiple minima hypersurfaces studies of aluminosilicate hydration, Int. J. Quantum Chem., 2010, 110, 586–594 CrossRef.
- S. Plimpton, Fast parallel algorithms for short-range molecular dynamics, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- W. G. Hoover, Canonical dynamics: Equilibrium phase-space distributions, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef PubMed.
- S. Nosé, A unified formulation of the constant temperature molecular dynamics methods, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- V. W. D. C. D. A. Case, K. Belfon, I. Y. Ben-Shalom, S. R. Brozell, D. S. Cerutti, T. E. Cheatham, III, S. A. I. T. A. Darden, R. E. Duke, G. Giambasu, M. K. Gilson, H. Gohlke, A. W. Goetz, R. Harris, S. Izadi, J. L. K. Kasavajhala, A. Kovalenko, R. Krasny, T. Kurtzman, T. S. Lee, S. LeGrand, P. Li, C. Lin, F. T. Luchko, R. Luo, V. Man, K. M. Merz, Y. Miao, O. Mikhailovskii, G. Monard, H. Nguyen, A. Onufriev, N. R. Pan, S. Pantano, R. Qi, D. R. Roe, A. Roitberg, C. Sagui, S. Schott-Verdugo, J. Shen, C. L. Simmerling, Y. X. Skrynnikov, J. Smith, J. Swails, R. C. Walker, J. Wang, L. Wilson, R. M. Wolf, X. Wu, Y. Xiong and S. F. D. M. York and P. A. Kollman, AMBER 2020, University of California, AMBER 2020, J. Chem. Inf. Model., 2020, 53, 1689–1699 Search PubMed.
- R. Demichelis, P. Raiteri, J. D. Gale, D. Quigley and D. Gebauer, Stable prenucleation mineral clusters are liquid-like ionic polymers, Nat. Commun., 2011, 2, 590 CrossRef PubMed.
- Y. Wu, H. L. Tepper and G. A. Voth, Flexible simple point-charge water model with improved liquid-state properties, J. Chem. Phys., 2006, 124 DOI:10.1063/1.2136877.
- P. Raiteri, R. Demichelis and J. D. Gale, Thermodynamically Consistent Force Field for Molecular Dynamics Simulations of Alkaline-Earth Carbonates and Their Aqueous Speciation, J. Phys. Chem. C, 2015, 119, 24447–24458 CrossRef CAS.
- J. A. Koskamp, S. E. Ruiz-Hernandez, D. Di Tommaso, A. M. Elena, N. H. De Leeuw and M. Wolthers, Reconsidering Calcium Dehydration as the Rate-Determining Step in Calcium Mineral Growth, J. Phys. Chem. C, 2019, 123, 26895–26903 CrossRef CAS PubMed.
- H. A. Lorentz, Ueber die Anwendung des Satzes vom Virial in der kinetischen Theorie der Gase, Ann. Phys., 1881, 248, 127–136 CrossRef.
- D. Berthelot, Sur le mélange des gaz, Compt. Rendus, 1898, 126, 1703–1706 Search PubMed.
- E. Project, E. Nachliel and M. Gutman, Parameterization of Ca + 2–protein interactions for molecular dynamics simulations, J. Comput. Chem., 2008, 29, 1163–1169 CrossRef CAS PubMed.
- J. Kahlen, L. Salimi, M. Sulpizi, C. Peter and D. Donadio, Interaction of Charged Amino-Acid Side Chains with Ions: An Optimization Strategy for Classical Force Fields, J. Phys. Chem. B, 2014, 118, 3960–3972 CrossRef CAS PubMed.
- G. A. Tribello, M. Bonomi, D. Branduardi, C. Camilloni and G. Bussi, PLUMED 2: New feathers for an old bird, Comput. Phys. Commun., 2014, 185, 604–613 CrossRef CAS.
- M. Eigen and K. Tamm, Schallabsorption in Elektrolytösungen als Folge chemischer Relaxation. I. Relaxationstheorie der mehrstufigen Dissoziation, Z. Elektrochem., 1962, 66, 93–121 CAS.
- A. A. Chialvo, P. T. Cummings, H. D. Cochran, J. M. Simonson and R. E. Mesmer, Na + -Cl- ion pair association in supercritical water, J. Chem. Phys., 1995, 103, 9379–9387 CrossRef CAS.
- R. T. McGibbon, K. A. Beauchamp, M. P. Harrigan, C. Klein, J. M. Swails, C. X. Hernández, C. R. Schwantes, L. P. Wang, T. J. Lane and V. S. Pande, MDTraj: A Modern Open Library for the Analysis of Molecular Dynamics Trajectories, Biophys. J., 2015, 109, 1528–1532 CrossRef CAS PubMed.
- A. Shrake and J. A. Rupley, Environment and exposure to solvent of protein atoms. Lysozyme and insulin, J. Mol. Biol., 1973, 79, 351–371 CrossRef CAS PubMed.
- S. Mamatkulov, M. Fyta and R. R. Netz, Force fields for divalent cations based on single-ion and ion-pair properties, J. Chem. Phys., 2013, 138, 024505 CrossRef PubMed.
- J. Åqvist, Ion-water interaction potentials derived from free energy perturbation simulations, J. Phys. Chem., 1990, 94, 8021–8024 CrossRef.
- X. Wang, Y. Han, L. Lin, M. Fuji, T. Endo, H. Watanabe and M. Takahashi, A molecular dynamics study on aqueous solutions for preparation of hollow CaCO3 particles, Model. Simul. Mater. Sci. Eng., 2008, 16(3) DOI:10.1088/0965-0393/16/3/035006.
- T. Martinek, E. Duboué-Dijon, Š. Timr, P. E. Mason, K. Baxová, H. E. Fischer, B. Schmidt, E. Pluhařová and P. Jungwirth, Calcium ions in aqueous solutions: Accurate force field description aided by ab initio molecular dynamics and neutron scattering, J. Chem. Phys., 2018, 148, 222813 CrossRef PubMed.
- M. Kohagen, P. E. Mason and P. Jungwirth, Accurate description of calcium solvation in concentrated aqueous solutions, J. Phys. Chem. B, 2014, 118, 7902–7909 CrossRef CAS PubMed.
- D. Beglov and B. Roux, Finite representation of an infinite bulk system: Solvent boundary potential for computer simulations, J. Chem. Phys., 1994, 100, 9050–9063 CrossRef CAS.
- L. X. Dang and D. E. Smith, Comment on ‘“Mean force potential for the calcium–chloride ion pair in water”’ [J. Chem. Phys. 99, 4229 (1993)], J. Chem. Phys., 1995, 102, 3483–3484 CrossRef CAS.
- J. W. Shen, C. Li, N. F. A. Van Der Vegt, C. Peter, N. F. A. Van Der Vegt, C. Peter, N. F. A. Van Der Vegt and C. Peter, Supplementary Information for “ Understanding the Control of Mineralization by Polyelectrolyte Additives: Simulation of Preferential Binding to Calcite Surfaces, J. Phys. Chem. C, 2013, 117, 1–7 Search PubMed.
- C. S. Babu and C. Lim, Empirical force fields for biologically active divalent metal cations in water, J. Phys. Chem. A, 2006, 110, 691–699 CrossRef CAS PubMed.
- A. K. Covington and E. Y. Danish, Measurement of Magnesium Stability Constants of Biologically Relevant Ligands by Simultaneous Use of pH and Ion-Selective Electrodes, J. Solution Chem., 2009, 38, 1449–1462 CrossRef CAS.
- S. Marchand and B. Roux, Molecular dynamics study of calbindin D(9k) in the Apo and singly and doubly calcium-loaded states, Proteins: Struct., Funct., Genet., 1998, 33, 265–284 CrossRef CAS.
- P. Raiteri, R. Demichelis, J. D. Gale, M. Kellermeier, D. Gebauer, D. Quigley, L. B. Wright and T. R. Walsh, Exploring the influence of organic species on pre- and post-nucleation calcium carbonate, Faraday Discuss., 2012, 159, 61 RSC.
- M. Maeda, K. Okada, Y. Tsukamoto, K. Wakabayashi and K. Ito, Complex formation of calcium(II) with amino acids under physiological conditions, J. Chem. Soc. Dalt. Trans., 1990, 2337 RSC.
- C. Blaquiere and G. Berthon, Speciation studies in relation to magnesium bioavailability. Formation of Mg(II) complexes with glutamate, aspartate, glycinate, lactate, pyroglutamate, pyridoxine and citrate, and appraisal of their potential significance towards magnesium gastrointestin, Inorg. Chim. Acta, 1987, 135, 179–189 CrossRef CAS.
- A. Picker, M. Kellermeier, J. Seto, D. Gebauer and H. Cölfen, Zeitschrift fur Kristallographie, De Gruyter, 2012, vol. 227, pp. 744–757 Search PubMed.
- C. L. Freeman, J. H. Harding, D. Quigley and P. M. Rodger, How does an amorphous surface influence molecular binding? – ovocleidin-17 and amorphous calcium carbonate, Phys. Chem. Chem. Phys., 2015, 17, 17494–17500 RSC.
- C. O. Solanke, D. Trapl, Z. Šućur, V. Mareška, I. Tvaroška and V. Spiwok, Atomistic simulation of carbohydrate-protein complex formation: Hevein-32 domain, Sci. Rep., 2019, 9, 18918 CrossRef CAS PubMed.
- M. Mínguez-Toral, B. Cuevas-Zuviría, M. Garrido-Arandia and L. F. Pacios, A computational structural study on the DNA-protecting role of the tardigrade-unique Dsup protein, Sci. Rep., 2020, 10, 1–18 CrossRef PubMed.
- S. Wolf, B. Lickert, S. Bray and G. Stock, Multisecond ligand dissociation dynamics from atomistic simulations, Nat. Commun., 2020, 11, 1–8 CrossRef PubMed.
- H. M. Wahedi, S. Ahmad and S. W. Abbasi, Stilbene-based natural compounds as promising drug candidates against COVID-19, J. Biomol. Struct. Dyn., 2020, 1–10 CrossRef PubMed.
- J. Wang, X. Xu, X. Zhou, P. Chen, H. Liang, X. Li, W. Zhong and P. Hao, Molecular simulation of SARS-CoV- 2 spike protein binding to pangolin ACE2 or human ACE2 natural variants reveals altered susceptibility to infection, J. Gen. Virol., 2020, 101, 921–924 CrossRef CAS PubMed.
- J. Yoo, J. Wilson and A. Aksimentiev, Improved model of hydrated calcium ion for molecular dynamics simulations using classical biomolecular force fields, Biopolymers, 2016, 105, 752–763 CrossRef CAS PubMed.
- M. De La Pierre, P. Raiteri and J. D. Gale, Structure and Dynamics of Water at Step Edges on the Calcite {1014} Surface, Cryst. Growth Des., 2016, 16, 5907–5914 CrossRef CAS.
- P. Fenter, S. Kerisit, P. Raiteri and J. D. Gale, Is the Calcite–Water Interface Understood? Direct Comparisons of Molecular Dynamics Simulations with Specular X-ray Reflectivity Data, J. Phys. Chem. C, 2013, 117, 5028–5042 CrossRef CAS.
- V. Migliorati, A. Serva, F. M. Terenzio and P. D’Angelo, Development of Lennard-Jones and Buckingham Potentials for Lanthanoid Ions in Water, Inorg. Chem., 2017, 56, 6214–6224 CrossRef CAS PubMed.
- A. Kondoh and T. Oi, Interaction of Alkaline Earth Metal Ions with Carboxylic Acids in Aqueous Solutions studied by 13c NMR Spectroscopy, Z. Naturforsch., A: Phys. Sci., 1998, 53, 77–91 CrossRef CAS.
- L. Helm and A. E. Merbach, Water exchange on metal ions: Experiments and simulations, Coord. Chem. Rev., 1999, 187, 151–181 CrossRef CAS.
- Z. Sun, W. Zhang, M. Ji, R. Hartsock and K. J. Gaffney, Aqueous Mg2+ and Ca2+ Ligand Exchange Mechanisms Identified with 2DIR Spectroscopy, J. Phys. Chem. B, 2013, 117(40), 12268–12275 CrossRef CAS PubMed.
- J. W. Cahn and J. E. Hilliard, Free Energy of a Nonuniform System. III. Nucleation in a Two-Component Incompressible Fluid, J. Chem. Phys., 2004, 31, 688 CrossRef.
- P. Bots, L. G. Benning, J.-D. D. Rodriguez-Blanco, T. Roncal-Herrero and S. Shaw, Mechanistic insights into the crystallization of amorphous calcium carbonate (ACC), Cryst. Growth Des., 2012, 12, 3806–3814 CrossRef CAS.
- S. E. Wolf, J. Leiterer, M. Kappl, F. Emmerling and W. Tremel, Early homogenous amorphous precursor stages of calcium carbonate and subsequent crystal growth in levitated droplets, J. Am. Chem. Soc., 2008, 130, 12342–12347 CrossRef CAS PubMed.
- J. Rieger, T. Frechen, G. Cox, W. Heckmann, C. Schmidt and J. Thieme, Precursor structures in the crystallization/precipitation processes of CaCO3 and control of particle formation by polyelectrolytes, Faraday Discuss., 2007, 136, 265–277 RSC.
- G. A. Tribello, F. Bruneval, C. C. Liew and M. Parrinello, A molecular dynamics study of the early stages of calcium carbonate growth, J. Phys. Chem. B, 2009, 113, 11680–11687 CrossRef CAS PubMed.
- D. Di Tommaso and N. H. de Leeuw, The Onset of Calcium Carbonate Nucleation: A Density Functional Theory Molecular Dynamics and Hybrid Microsolvation/Continuum Study, J. Phys. Chem. B, 2008, 112, 6965–6975 CrossRef CAS PubMed.
- D. Di Tommaso and N. H. de Leeuw, Theoretical study of the dimerization of calcium carbonate in aqueous solution under natural water conditions, Geochim. Cosmochim. Acta, 2009, 73, 5394–5405 CrossRef CAS.
- P. Martin, D. Spagnoli, A. Marmier, S. C. Parker, D. C. Sayle and G. Watson, Application of molecular dynamics DL_POLY codes to interfaces of inorganic materials, Mol. Simul., 2006, 32, 1079–1093 CrossRef CAS.
- A. R. Finney and P. M. Rodger, Probing the structure and stability of calcium carbonate pre-nucleation clusters, Faraday Discuss., 2012, 159, 47–60 RSC.
- Z. Zou, I. Polishchuk, L. Bertinetti, B. Pokroy, Y. Politi, P. Fratzl and W. J. E. M. E. M. Habraken, Additives influence the phase behavior of calcium carbonate solution by a cooperative ion-association process, J. Mater. Chem. B, 2018, 6, 449–457 RSC.
- G. Montanari, L. Z. Lakshtanov, D. J. Tobler, K. Dideriksen, K. N. Dalby, N. Bovet and S. L. S. Stipp, Effect of Aspartic Acid and Glycine on Calcite Growth, Cryst. Growth Des., 2016, 16, 4813–4821 CrossRef CAS.
- A. E. Stephenson, J. J. Deyoreo, L. Wu, K. J. Wu, J. Hoyer and P. M. Dove, Peptides enhance magnesium signature in calcite: Insights into origins of vital effects, Science, 2008, 322, 724–727 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp02879d |
| This journal is © the Owner Societies 2023 |