The rich structural phase behaviour of 2,2,2-trifluoroethanol

Abstract

In the fairly modest temperature and pressure regime of 0–2 GPa and 200–295 K, 2,2,2-trifluoroethanol (TFE) exhibits a remarkable degree of polymorphism, with the observation of four ordered phases (forms 1–4) and a cubic plastic phase (form 5). The ordered phases are characterised by hydrogen-bonded chains, with the crystal structures of the three high-pressure forms (forms 2, 3 and 4) based on the same hydrogen-bonded catemeric motif. The structures and relationships between these phases were determined using a combination of high-pressure single-crystal X-ray diffraction, at ambient temperature, and a series of high-pressure neutron powder-diffraction experiments to ∼6 GPa at 295 K, 245 K and 200 K. As well as allowing the determination of the relative compressibilities of the phases, the neutron powder-diffraction studies also provided a preliminary mapping of the surprisingly rich phase diagram of TFE.

---

Introduction

Prototypical monofunctional small-molecule systems offer a range of comparatively simple motifs for the study of intermolecular interactions. They also provide an opportunity to examine how competition between these interactions can influence the molecular packing arrangement in the crystalline state as the interactions are predisposed by the size and shape of the molecules. In the case of mono-alcohols (ROH), the competition between the packing requirements of the relatively bulky R-group and the geometrical constraints that must be met to allow the formation of hydrogen bonds, can have a dramatic effect on the crystal structure formation.^1,2 For the smaller members of the mono-alcohol series, the adopted packing motifs can be considered ‘thin’¹ as the crystal structures are characterised by the formation of catemers, where the molecules assume a coplanar, alternating, sequence about the central chain of hydrogen bonds.^3,4 For mono-alcohol systems with bulkier R-groups, this simple arrangement can be inhibited by steric effects and the catemers may adopt a more helical geometry demonstrated by, for example, phenol⁵ and isopropanol.⁶ In systems where the R-group is particularly bulky, the molecules may no longer yield hydrogen-bonded chains, or catemers, but cyclic trimers,⁷ tetramers,⁸ hexamers⁹ or octamers⁶ may result. Further, in some instances the steric hindrance from the R-group can be sufficiently large, or ‘globular’, to inhibit ordering of the molecules and plastic, or rotor, phases can be formed instead. The hydrogen bond formation may be limited¹⁰ or, as observed in the case of cyclopentanol¹¹ and cyclohexanol,⁸ prevented.

In our studies of low-melting point mono-alcohol systems, we have examined a range of molecular species with differing R-groups and investigated how the application of pressure can alter the crystal packing motifs and hydrogen bonding.^{3–5,8,10–12} Among the first of these studies was the investigation of the structural behaviour of methanol^13,14 and ethanol,^15,16 which are the simplest members of the linear alcohol series, H(CH₂)_nOH. In both systems the high-pressure and low-temperature crystal structures are characterised by the formation of catemers, with varying degrees of strain exhibited within the molecular chains for each phase. More recently, we found that this ‘thin’ molecular behaviour can also be observed for 2,2,2-trifluoroethanol (CF₃CH₂OH).¹⁷ The increased bulk of the methyl group, where the hydrogen atoms have been replaced by fluorine, resulted in low-temperature (form 1) and high-pressure (form 2) structural phases composed of hydrogen-bonded molecular chains, with the structural response broadly reminiscent of the high-pressure and low-temperature behaviour of ethanol.

Although both crystal structures are characterised by the formation of hydrogen-bonded chains, the orientation of the trifluoro groups within the chains in form 2 leads to the exposure of the hydrogen bond and, given the close proximity of the neighbouring chains within the crystal structure, results in bridging interchain O⋯O contacts at a distance of ∼2.89 Å. These are of approximately the same order as the O⋯O distances found for the hydrogen bonds (∼2.72 Å) within each chain. This, rather unusual arrangement, was intriguing as it could reasonably be anticipated that this region of the structure would become unstable under further compression, with the potential to lead to either bond formation or a further phase transition.

Herein, we report a broader study of the high-pressure phases of TFE. A combination of both single-crystal X-ray diffraction and neutron powder-diffraction techniques were used to investigate the crystal structure behaviour at simultaneous high pressure and low temperature so that a provisional phase diagram could be mapped. The studies reveal a surprisingly rich phase behaviour in the relatively small pressure–temperature region investigated. In addition to the two ordered phases observed previously, we have observed two further ordered phases, form 3 and form 4, as well as evidence of a rotor phase, form 5.

Experimental

For all experiments performed in this study, a perdeuterated sample of 2,2,2-trifluoroethanol (CF₃CD₂OD, TFE), with 99.5+ atom% D, was used as received from Sigma-Aldrich. This is a clear colourless liquid with a melting point of 229.7 K and a boiling point of 347.1 K at atmospheric pressure, 0.0001 GPa.

Single-crystal X-ray diffraction

The sample was loaded into a Merrill-Bassett diamond-anvil cell (DAC), equipped with Boehler-Almax cut diamonds and their matched tungsten carbide backing seats.¹⁸ A ruby sphere was added for pressure calibration via the ruby fluorescence method.¹⁹ For the two experiments performed which resulted in the crystallisation of form 4, a 200 μm thick tungsten gasket, that had been pre-indented to a thickness of ∼100 μm, was used with a 200 μm diameter hole drilled through it to act as a pressure chamber. The perdeuterated TFE sample was compressed, at room temperature, until solid and then the temperature was carefully cycled using a heat gun so that the polycrystalline material was partially melted each time with the objective that just a single crystallite would remain¹³ – this method successfully yielded one crystal which grew to fill the gasket hole after the final temperature cycle. Once the DAC had cooled back to room temperature, the pressure was found to be 1.54(5) GPa (form 4_1.54) for the first experiment and 2.09(5) GPa (form 4_2.09) for the second. For the subsequent study of forms 3 and 5, since more careful control of the pressure was required (especially in the regime close to crystallisation of the sample), a softer gasket made from steel, with an initial thickness of 200 μm and gasket hole diameter of 400 μm, was selected. This was filled with perdeuterated TFE and form 5 was produced on the initial application of pressure – the liquid sample crystallised into many relatively large grains with ill-defined facets which, over the period of 48 hours at room temperature, gradually coalesced to form what appeared to be three crystals. At this point, this sample was studied without further intervention and the sample pressure was found to be 0.60(5) GPa. Subsequently, the load applied to the cell was increased to produce form 2 and the temperature cycling method employed to yield just one crystal with the pressure measured having dropped to 0.55(5) GPa. The pressure was increased again and, this time, the remaining fluid surrounding the crystal froze into a dense mass of small, needle-like crystallites at 0.71(5) GPa. Attempts to isolate just one crystal of form 3 in the gasket hole by temperature cycling were unsuccessful as the sample crash-melted, but on collecting the data it was clear that there was only one major crystal present and that the polycrystalline mass did not contribute significantly to the diffraction data as no other reflections were observed and, therefore, it had no detrimental effect on the subsequent analysis. See Fig. S1.1–S1.8 in the ESI† for pictures of the phases in the diamond-anvil cell.

X-ray diffraction data were collected at 295 K in Experiments Hutch 2 (EH2) of Beamline I19, at Diamond Light Source, UK,²⁰ using the Newport κ-geometry 4-circle diffractometer fitted with a Dectris Pilatus 300K pixel-array photon-counting detector. All datasets were collected using a wavelength of λ = 0.4895 Å. Forms 3, 4_2.09 and 5 were collected using a step size and exposure time of 0.2° and 0.2 seconds respectively, but form 4_1.54 was collected with 0.2° images exposed for 0.4 seconds. The data were collected using a series of ω scans with the appropriate φ settings to give the optimal completeness when using a diamond-anvil cell. The data were integrated with the program CrysAlisPro²¹ which incorporates routines that omit regions of the detector shaded by the diamond-anvil cell from integration. The structures were solved by dual-space methods²² and refined by least-squares refinement on all unique measured F² values²³ using the SHELX suite of programs. Molecular graphics were all produced using Mercury.²⁴ The data collection, integration and refinement statistics for all high-pressure data sets are presented in Table 1. For the refinement of form 5, the electron density of the freely-tumbling TFE molecules was mimicked by placing a single carbon atom at the origin and allowing the thermal displacement parameter to vary, along with the scale. The resulting model, despite not fully describing the likely electron density, does provide a reasonable fit to the few reflections that are observed in the diffraction pattern.

Table 1 Crystallographic data for the single-crystal high-pressure phases, forms 3, 4 and 5, of TFE

		Form 3	Form 41.54	Form 42.09	Form 5^a
a Due to the extremely weak data, particularly in the higher resolution shells, the Rint and GoF are poor for the refinement of form 5.
Chemical formula		C2D3F3O	C2D3F3O	C2D3F3O	C2D3F3O
Molecular weight		103.06	103.06	103.06	103.06
Temperature (K)/pressure (GPa)		295(2)/0.71(5)	295(2)/1.54(5)	295(2)/2.09(5)	295(2)/0.60(5)
Crystal system		Monoclinic	Monoclinic	Monoclinic	Cubic
Space group		P21/c	P21/c	P21/c	Im3̄m
Unit cell	a (Å)	4.8630(4)	4.6540(3)	4.6413(3)	5.740(3)
	b (Å)	33.054(7)	16.2590(18)	16.1899(14)	5.740(3)
	c (Å)	8.8694(14)	8.577(4)	8.557(4)	5.740(3)
	α (°)	90	90	90	90
	β (°)	91.519(9)	91.615(13)	91.691(13)	90
	γ (°)	90	90	90	90
	V (Å^3)	1425.2(4)	648.8(3)	642.7(3)	189.1(3)
Z/Z′		16/4	8/2	8/2	2/1
Density (g cm^−3)		1.921	2.110	2.130	1.810
Reflections collected		9835	4006	6244	453
Unique reflections/Rint		2248/0.0520	1036/0.0401	1247/0.0510	22/0.438
R 1 [I > 2σ]		0.0556	0.0781	0.0693	0.0858
wR2 [all data]		0.2279	0.2327	0.2122	0.0630
GoF on F^2		1.027	1.082	1.060	24.168
Largest diff. peak and hole (e A^−3)		0.198/−0.231	0.427/−0.492	0.481/−0.387	0.02/−0.03

---

Neutron powder-diffraction

PEARL

High-pressure time-of-flight neutron powder-diffraction experiments were performed on the PEARL diffractometer at the ISIS Neutron and Muon Source, UK.²⁵ The perdeuterated TFE sample was loaded into an encapsulated gasket machined from null scattering TiZr alloy.²⁶ A small piece of lead, for which the pressure and temperature equation of state has been well characterised,²⁷ was included within the sample chamber, along with powdered glass wool to promote crystallite nucleation and suppress preferred orientation of the sample. The gasket assembly was clamped between a pair of single toroidal profile anvils²⁸ machined from toughened zirconia alumina.²⁵ The gasket and anvil assembly was then mounted in a modified V3 Paris-Edinburgh press²⁹ which permits variation in temperature from 120–480 K by heating against a flow of liquid nitrogen circulating around the outer edge of anvils.²⁵ Powder-diffraction patterns were obtained in the 90° scattering geometry, permitting access to a d-spacing range of 0.5–4.1 Å. Data of sufficient quality were collected at each pressure point to refine the lattice parameters and atomic coordinates. The data were processed and corrected using Mantid.³⁰

GEM

To more closely examine the high-pressure phase behaviour of TFE in the regime below 1 GPa, structural information from a perdeuterated sample was obtained by neutron powder-diffraction on the GEM instrument,³¹ at the ISIS Neutron and Muon Source, UK. The sample was loaded into a TiZr high-pressure cell with the pressure increased by the application of Ar gas, through an intensifier system, to directly compress the sample. Room temperature neutron powder-diffraction data were collected at selected values of applied pressure. Data of sufficient quality were collected at each pressure point to refine the lattice parameters and atomic coordinates. The data were processed and corrected using Mantid.³⁰

The neutron powder-diffraction data from both PEARL and GEM were analysed using GSAS-II,^32,33 with the structures determined from the single-crystal X-ray diffraction results used as starting models in the analysis. For all refinements, as well as including structural models of the relevant phase of TFE (or pair of phases in the case of mixed-phase data) and the Pb pressure marker, additional models were also incorporated for Al₂O₃ and ZrO₂ to account for the peaks in the diffraction pattern from the anvils. The background in each data set was fitted with a Chebyshev polynomial and each of the phases present were refined with a phase fraction and an isotropic microstrain component to model variations in peak width. As free refinement of the atomic coordinates proved to be unstable, the TFE molecules were refined with rigid-body constraints with only the torsion angles for the rotation of the CF₃ (trifluoro) groups around the C–C bond and the rotation of the deuterium around the torsion angle defined by the C–O–D bonds allowed to refine freely. An isotropic thermal displacement parameter was refined for each rigid group. The refined structural models were all found to be physically reasonable and provided convincing fits to all the observed data. There is evidence of sample texture in some of the early data sets in each pressure run, likely due to the formation of relatively large crystallites on initial freezing, but the Rietveld fits improve after a phase transition is observed as these are first order in nature and involve a sudden, pulverising, reduction in volume. The refinements of the GEM data were carried out in an analogous fashion although no pressure marker was required and there were no background diffraction features present from the cell to model. Data from detector bank 2 was used for the refinements, which covers the 2θ range 14–21°. For the form 5 body-centred cubic rotor phase structure, the sphere of scattering distribution from the freely tumbling molecules was mimicked by placing a single carbon atom at the origin and refining an isotropic thermal displacement parameter. Although this model, which is essentially an inflated single-atom scattering density, doesn't capture the full details of the real scattering neutron density it does yield a rather persuasive fit to the data.

Results and discussion

Initially, a high-pressure neutron powder-diffraction study was performed at ambient temperature to establish whether any phase changes could be observed; the powder-diffraction patterns obtained from the experiment are plotted as a series in Fig. 1. The diffraction pattern obtained upon initial compression to 0.44(7) GPa was found to match the known phase of form 2, as determined during the earlier single-crystal X-ray diffraction study. However, on the next pressure increment, to 0.83(5) GPa, the powder-diffraction pattern transformed dramatically indicating a transition to a new phase, form 3. Careful inspection of the series of patterns obtained over the pressure range 1.40(4) to 2.91(9) GPa also indicated another potential transition at about 1.46(3) GPa with the appearance of a peak in the diffraction pattern at a d-spacing of ∼3.06 Å.

Fig. 1 Neutron powder-diffraction patterns of TFE obtained from PEARL, collected at 295 K, shown with increasing pressure. The peak at ∼3.06 Å corresponding to the (112) reflection in form 4 is shown by * (form 2 – blue; form 3 – cyan; form 4 – green; mixed phase of forms 3 and 4 – black).

Since the crystal structures of forms 3 and 4 could not be solved directly from the powder data, attempts were made to prepare these phases using single-crystal X-ray diffraction techniques. Using the same method as that employed in the preparation of form 2, form 4 was prepared quite readily by simply compressing the diamond-anvil cell (DAC) to over ∼1.50 GPa (a higher pressure than used to prepare form 2) and then performing temperature cycling of the DAC until just a single crystal remained. Form 4 of TFE crystallises in the monoclinic space group P2₁/c with 2 independent molecules in the asymmetric unit (Fig. 2b).

Fig. 2 The labelling scheme used for the high-pressure single-crystal X-ray diffraction structures of TFE (a) form 3 [295(2) K; 0.71(5) GPa] and (b) form 4 [295(2) K; 2.09(5) GPa], with thermal ellipsoids drawn at the 50% probability level. The hydrogen-bonded chains formed are shown in (c) form 3 and (d) form 4, where the hydrogen bonds are represented by light-blue dashed lines (C – dark grey, H – light grey, O – red, F – green).

More precise control of the pressure was required to achieve form 3, so a fresh loading, using a different gasket (steel rather than tungsten) with a larger hole (400 μm compared with 200 μm), was employed. The pressure was incremented slowly until a change in appearance of the sample could be observed. A group of very rounded, irregular, crystals were formed which, over the period of approximately 48 hours, at room temperature, gradually coalesced to form what appeared to be three crystals with smooth and unfaceted surfaces. Unlike the other crystalline forms of TFE, however, these crystals exhibited no extinction when viewed through a microscope equipped with crossed polarizers indicating that this is a plastic, or cubic, phase. See Fig. S1.1 and S1.2 in the ESI† for pictures of the phase in the diamond-anvil cell. The pressure was determined to be 0.60(5) GPa and a dataset collected on this sample showed that form 5 crystallises as a plastic phase in the cubic space group Im3̄m (a = 5.740(3) Å) with the molecules organised in a body-centred cubic arrangement (with a volume per molecule of 94.6(3) ų, which is comparable with the other, ordered, phases of TFE). The tumbling of the molecules was modelled, for the single-crystal X-ray diffraction data, by placing a single carbon atom at the unit cell origin and refining only an isotropic thermal parameter. With the paucity of observed data, this elementary model is all that can be justifiably established about the structure. However, the proposed model for the structure has similar characteristics to the phase I face-centred cubic rotor structure of cyclohexanol,⁸ where a simple packing arrangement of freely rotating molecules is also adopted.

Form 3 was prepared, via form 2, using the same DAC loading as that used to determine the structure of form 5. Compression of form 5, and temperature cycling, produced form 2, and a subsequent increase in the pressure from 0.55(5) to 0.71(5) GPa, resulted in the appearance of a mass of needles in the sample chamber of the DAC. Despite several temperature cycling attempts, an isolated single crystal could not be obtained but, nevertheless, a sufficiently large block was present in the surrounding crystallites for the structure of form 3 of TFE to be determined. This was also found to crystallise in the monoclinic space group P2₁/c, but with Z′ = 4 (Fig. 2a).

The crystal structures of both form 3 and form 4 are characterised by the same hydrogen-bonded chains as observed in form 2 (Fig. 2c and d, and Table 2). Unlike the hydrogen bonds exhibited in form 1, it is worth noting that the hydrogen bonds within the chains of forms 2, 3 and 4 all show considerable deviation from linearity, as is commonly observed in the high-pressure structures of the mono-alcohols.^5,6,11 However, there is no significant deviation in the hydrogen bond angles between the three high-pressure forms as they are all based on the same fundamental hydrogen-bonded chain, which is markedly different to that found in the low-temperature form 1 structure. In form 1, the hydrogen bonds are effectively tucked into the chain with the trifluoro groups aligned parallel with the plane of hydrogen bonds whereas, in form 2, the trifluoro groups are approximately orthogonal resulting in the chain of hydrogen bonds being exposed on the outside of the catemer.¹⁷

Table 2 Geometry of intermolecular hydrogen bonds and close O⋯O contacts for forms 1, 2, 3 and 4_2.09 (the better of the two structures) of TFE, for the structures determined by single-crystal X-ray diffraction

D–H⋯A	D–H/Å	H⋯A/Å	D⋯A/Å	D–H⋯A/°
Symmetry codes: i = 3/2 − x, y, z − 1/2; ii = x − 1, y, z; iii = 2 − x, −y − 1, 1 − z; iv = x + 1, y, z; v = 1 − x, 1 − y, 1 − z; vi = −x, 1 − y, 1 − z.
Form 1 (ref. 17)
O1–H1⋯O2	0.77(3)	1.93(3)	2.696(2)	178(3)
O2–H2⋯O1^i	0.94(3)	1.77(3)	2.716(2)	179(3)
Form 2 (ref. 17)
O1–H1⋯O2	0.81(10)	1.99(7)	2.762(7)	158(10)
O2–H2⋯O1^ii	0.92(14)	1.94(7)	2.714(6)	140(12)
O1–O1^iii			2.892(7)
Form 3
O1–D1⋯O2^iv	0.81(7)	2.00(7)	2.746(5)	155(8)
O2–D2⋯O1	0.89(6)	1.90(6)	2.715(5)	152(6)
O3–D3⋯O4^iv	0.82(5)	1.99(5)	2.798(5)	169(6)
O4–D4⋯O3	0.95(7)	1.86(6)	2.757(5)	156(6)
O1–O1^v			2.889(7)
O2–O2^vi			2.997(7)
Form 42.09
O1–D1⋯O2^iv	0.82(6)	1.96(6)	2.724(3)	153(10)
O2–D2⋯O1^ii	0.75(5)	1.98(5)	2.690(3)	159(6)

---

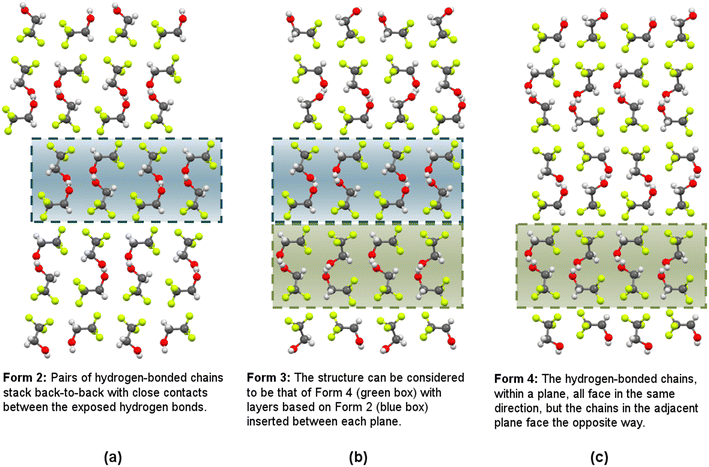
Form 2 crystallises with triclinic P1̄ symmetry and is characterised by the formation of paired hydrogen-bonded molecular chains. These pairs are oriented such that the exposed hydrogen bonds are in close proximity (Fig. 3a), and it could be anticipated that a further pressure increase might make cross-linking hydrogen bonds possible. However, this does not occur and, instead, whilst the hydrogen-bonded chain motif is preserved, the packing arrangement of these catemers is modified as the pressure is increased. In the form 3 structure the chains are organised into two distinct types of pairs which stack in alternating layers along the crystallographic b-axis (Fig. 3b). One of the pairs of molecular chains is essentially identical to that found in form 2, with the hydrogen bonds in each chain placed in close proximity as shown by the sections highlighted in the blue boxes of Fig. 3a and b. In the second catemeric pair, one of the chains is flipped in orientation so that the hydrogen bonds in adjacent chains are essentially equally spaced from one another within each layer. This mode of pairing the hydrogen-bonded chains is also observed in the structure of form 4 (Fig. 3c), and shown in the sections highlighted within the green boxes of Fig. 3b and c, where the molecular layers are again stacked along the b-axis. The form 3 structure can be viewed as an intermediate (chimeric) phase of forms 2 and 4 as it contains the catemer pairing arrangements demonstrated by both of the phases in alternate molecular layers.

Fig. 3 Comparison of the three ordered high-pressure forms of TFE, determined by single-crystal X-ray diffraction, viewed down the a-axis perpendicular to the hydrogen-bonded chains showing (a) form 2 [295(2) K; 0.22(5) GPa], (b) form 3 [295(2) K; 0.71(5) GPa] and (c) form 4 [295(2) K; 2.09(5) GPa]. Planes of hydrogen-bonded chains common to forms 2 and 3 are highlighted in blue boxes whilst planes of hydrogen-bonded chains common to forms 3 and 4 are highlighted in green boxes (C – dark grey, H – light grey, O – red, F – green).

During the analysis of the data collected on form 4 at 1.54 GPa, an additional set of weak reflections was observed with a metrically cubic lattice with cell length 11.79(1) Å. However, it was not possible to determine a structure from these data due to the extremely weak diffraction signal from this minority phase. This may indicate the presence of an unidentified contaminant in the diamond-anvil cell loading used for the determination of form 4_1.54 – although it should be noted that, compellingly, the cell edge is very close to double that of form 5 and, that with a cell volume of 1637.8(17) ų, 20 TFE molecules could be accommodated if the volume per molecule was ∼82 ų. This is comparable with the volumes calculated for the 295 K neutron powder-diffraction structures of form 3 (83.2(5) ų) and form 4 (82.52(9) ų) at 1.46(3) GPa.

Equipped with the single-crystal structures for the new phases of TFE, the data from the neutron powder-diffraction experiment at 295 K was revisited. The observed powder-diffraction patterns were refined against those calculated from the structures determined using the single-crystal data and convincing fits were obtained for all three of the observed high-pressure phases. It was possible to ascertain that form 2 undergoes a phase transition to form 3, between 0.44(7) GPa and 0.83(5) GPa, and then completes a further transition to form 4 at 1.60(6) GPa. The subsequent powder-diffraction patterns matched form 4 up to 6.1(2) GPa, the maximum pressure achieved in the experiment. Although rigid body constraints were required to keep the Rietveld refinements stable and physically reasonable, the cell parameters were allowed to refine freely and Fig. 4a–c show representative fits of forms 2, 3 and 4, respectively. The data also indicated that both form 3 and form 4 coexist between 1.40(4) GPa and 1.46(3) GPa with a mixture of the two phases present in the powder patterns (Fig. 1). Refined unit cell parameters and atomic positions are provided in Tables S2.1 and S2.2, respectively, within the ESI.†

Fig. 4 Selected Rietveld refinements of the neutron powder-diffraction PEARL data collected on TFE at 295 K for (a) form 2 [0.44(7) GPa], (b) form 3 [0.83(5) GPa] and (c) form 4 [1.60(6) GPa]. The refinements are shown for the patterns recorded at the lowest pressure exhibiting a single phase (black circle – observed data; red line – calculated patterns; black tick marks – TFE; green tick marks – Al₂O₃; red tick marks – Pb; blue tick marks – ZrO₂; blue line – difference between observed and calculated data). The comparatively poorer fit for form 2 is likely to be due to the formation of large crystallites on initial freezing, while the samples for form 3 and form 4 have undergone pulverising first-order phase transitions at their formation, leading to better fits due to improved powder-averaging.

To provide a preliminary mapping of the phase diagram of TFE, and to establish the phase stability of the low-temperature form 1 structure, additional high-pressure neutron powder-diffraction studies were carried out on PEARL at temperatures of 245 K (approximately midway between 200 K and the 295 K pressure series, while well above the melting point) and 200 K (∼30 K below the TFE melting point of 229.7 K).

At 245 K (Fig. 5) the sample is initially a liquid, but on compression to 0.003(37) GPa (within the measuring uncertainty of the Pb pressure marker; the fact the sample has crystallised clearly indicates the pressure within the cell is greater than atmospheric) the sample crystallised into the form 1 structure. On increasing the pressure to 0.52(2) GPa, the powder pattern changed to match the form 2 structure, whilst on the next pressure increase, a mixed-phase pattern was observed with both form 2 and form 3 present. Although the applied load on the cell was increased, the sample pressure did not change (within error) indicating a significant decrease in sample volume at the transition. The form 3 structure was found to be stable up to at least 3.09(3) GPa, beyond which significant pressure broadening began to be observed in the powder-diffraction patterns, although the absence of a peak at ∼3.06 Å indicates the sample did not undergo a further transition to form 4 within the pressure range studied at this temperature – Fig. S2.3 in the ESI† shows all diffraction patterns collected on TFE at 245 K. Selected Rietveld refinements for form 1 [0.003(37) GPa], form 2 [0.52(2) GPa] and form 3 [0.72(2) GPa] are shown in Fig. S2.4,† and refined unit cell parameters and atomic positions are provided for the data collected up to 3.09 GPa in Tables S2.3 and S2.4, respectively, within the ESI.†

Fig. 5 Neutron powder-diffraction patterns of TFE obtained from PEARL, collected at 245 K, shown with increasing pressure (liquid – purple; form 1 – red; form 2 – blue; form 3 – cyan; mixed phase of forms 2 and 3 – black).

Data from the first pressure loading of the cell (6 Tonnes) at 200 K indicated that the sample had already crystallised, with the resulting powder pattern corresponding to the orthorhombic (Pca2₁) structure of form 1, the known low-temperature phase established in the previous study – Fig. S2.7 in the ESI† shows all diffraction patterns collected on TFE at 200 K. Further 2 Tonne load increments on the cell indicated no shift in the diffraction peaks, presumably due to the sample shrinking as it froze creating a void space in the sample chamber, and peak shifts only became discernible when a cell loading of 22 Tonnes (corresponding to a pressure of 0.19(3) GPa from the Pb calibrant) had been reached (Fig. 6). Rietveld refinements on the diffraction patterns show that form 1 remains stable to at least 1.59(3) GPa. For the data collected at pressures beyond 1.59(3) GPa, Rietveld refinements were not performed as peak broadening indicated the onset of non-hydrostatic conditions (suggesting the compressibilities would not be meaningful beyond this pressure). There were no other apparent changes to the diffraction patterns in this region that would indicate a change of phase. For the data collected up to 1.59(3) GPa, refined unit cell parameters (Table S2.5†) and atomic positions (Table S2.6†) are provided in the ESI,† along with a representative Rietveld refinement of form 1 at 0.10(3) GPa (Fig. S2.8†), where the relatively poor fit is likely to be due to the formation of coarse crystalline grains on initial freezing.

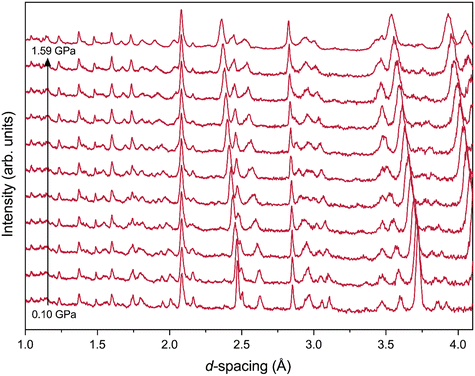Fig. 6 Neutron powder-diffraction patterns of TFE obtained from PEARL, collected at 200 K, shown with increasing pressure (form 1 – red).

In order to better understand the formation of forms 5 and 2, the pressurised gas cell available at GEM was utilised as this offered the capability to perform measurements with precisely defined, and relatively small, pressure increments through the phase boundaries. The pressure was increased in 0.025 GPa increments with data collected for approximately 10 minutes at each pressure point until the sample solidified. The sample remained a liquid to a pressure of 0.5 GPa where a single diffraction peak was observed in the powder pattern, indicating that form 5 had crystallised (Fig. 7a). Data were collected at 0.498 GPa for 12 hours to provide a powder pattern with sufficiently good statistics for Rietveld refinement on this phase but, during this period the sample underwent a phase transition from form 5 to form 2, with only a small fraction of the sample remaining as form 5, which could be identified by its characteristic (110) reflection. The pressure had fallen slightly, from 0.498 GPa to 0.49 GPa, during the data collection and the next data collection, performed at 0.49 GPa provided a “clean” form 2 powder pattern which was retained to 0.53 GPa, the pressure limit of the cell. A further long (12 hour) data collection was performed at 0.53 GPa and the pattern could be fitted with the form 2 structure, as shown in Fig. 7b. Fig. S2.10 in the ESI† shows all diffraction patterns collected on TFE at 290 K, once the sample had crystallised.

Fig. 7 Rietveld refinements of the neutron powder-diffraction GEM data collected on TFE at 290 K for (a) form 5 [0.50 GPa] and (b) form 2 [0.53 GPa] (black circle – observed data; red line – calculated patterns; black tick marks – TFE; blue line – difference between observed and calculated data).

Despite the imposition of rigid body constraints on the structure refinements of the ordered phases of TFE from the neutron powder-diffraction data, it was not possible to analyse trends in the pressure dependence of the crystal structures as the uncertainties in the bond length and bond angle determinations were too large. Nevertheless, it was possible to determine accurate relative compressibilities of the phases. The unit cell volumes (normalised by Z so that a common scale could be adopted) are shown as a function of pressure in Fig. 8 for all three temperature studies. It is clear from the abrupt volume changes that all the observed phase transitions are first order in character and that there is a trend for consecutive phases to become less compressible with pressure. The bulk modulus for forms 1, 3 and 4 are shown in Table 3, along with the associated second order Birch–Murnaghan fit.³⁴ The values are comparable with other, similar, molecular solids and, for comparison, the bulk modulus (B₀) for the parent compound ethanol is 12.9(5) GPa.¹⁵ The compressibility of form 2 was not determined as it appears to be stable in a relatively narrow pressure and temperature regime; while it should also be noted that the determination of the bulk modulus of form 1 at 200 K gave a relatively poor fit and the sample was likely subject to non-hydrostatic conditions.

Fig. 8 The volume per formula unit (f.u.) of TFE, plotted against pressure for each neutron powder-diffraction pressure series collected using PEARL at (a) 200 K, (b) 245 K and (c) 295 K. The determined second order Birch–Murnaghan equations of state are shown as solid lines, whilst the third order determination, at 200 K, is included as a dashed line (form 1 – squares, red line; form 2 – circles; form 3 – triangles, cyan line; form 4 – diamonds, green line).

Table 3 The isothermal compressibilities of the observed phases of TFE derived from the second order Birch–Murnaghan models

Temperature (K)	Form	B 0 (GPa)	V 0 (Å^3)
a This fits the data poorly, but by using a third order equation the following (which is not sensible but fits) is obtained: B0 = 1.8(14) GPa, V0 = 803(13) Å^3 and B′ = 31(22) – see dashed line in Fig. 8a.
200^a	1	7.8(4)	778(3)
245	1	9.6(5)	773(1)
245	3	11.3(3)	1469(4)
295	3	10.5(16)	1493(18)
295	4	15.0(7)	716(4)

---

Combining the observations from the X-ray and neutron studies, a preliminary outline of the phase diagram of TFE can be constructed (Fig. 9). Although the phase diagram is, at best, only approximate it is revealing that the form 2 structure occupies a very restricted region compared to the other observed, ordered, phases. The stability regime of the rotor form 5 phase, though not fully mapped, is likely to define an equally narrow boundary around the liquid state. Clearly, this limited set of measurements leaves much of the phase diagram of TFE largely unexplored. Nevertheless, it is remarkable that, in comparison to other similar hydrogen-bonded molecular systems, for example ethanol where only the low-temperature and high-pressure forms were observed over a comparable pressure and temperature range, such a rich number of structural phases occur in a relatively modest temperature and pressure regime.

Fig. 9 Provisional phase diagram based on the known regions of the high-pressure and low-temperature forms of TFE (liquid [L] – purple region; form 1 – open squares, red region; form 2 – black circles, blue region; form 3 – open triangles, cyan region; form 4 – open diamonds; green region; form 5 – yellow diamonds, dotted circle).

A similar degree of polymorphism is observed in the mono-alcohol cyclohexanol⁸ at low temperature, which has four ordered phases (II, III, III′ and IV) and a plastic, orientationally disordered, phase (phase I) that adopts a face-centred cubic structure. In TFE, all the ordered crystalline forms are composed of chains with the R-groups disposed on either side of the hydrogen bond in an alternating sequence. In cyclohexanol, however, the molecular arrangements within each phase differ significantly with the phase II structure composed of tetrameric rings while the phase III and phase III′ structures consist of infinite hydrogen-bonded chains with the molecules adopting ‘wavelike’ and threefold helical arrangements respectively. The wavelike² catemers have an alternating arrangement found in other primary alcohols such as methanol,¹³ ethanol¹⁵ and, as now demonstrated, all four ordered forms of TFE. However, the tetrameric ring and helical chain are features which more commonly characterise secondary or tertiary alcohols.² This behaviour is observed in the simplest secondary mono-alcohol, isopropanol,⁶ where threefold helical hydrogen-bonded chains were observed in the crystal structure of the low-temperature polymorph while the structure of the high-pressure form was found to be composed of isolated 8-membered rings. Isopropanol, therefore, has low-temperature and high-pressure behaviour more closely associated with secondary and tertiary alcohols. For TFE, however, despite the increased bulk of the methyl due to the substitution of the hydrogen atoms with fluorine, the crystal structures at both low-temperature and high-pressure are characteristic of primary alcohols. Only the form 5 rotor phase indicates some degree of secondary alcohol behaviour and is reminiscent of the face-centred cubic phase I structure of cyclohexanol and the hexagonal low-temperature phase-I and phase-II structures of cyclopentanol.¹¹

Conclusions

2,2,2-Trifluoroethanol has been studied under a range of non-ambient conditions and found to exhibit a remarkable degree of polymorphism in the sub 2.0 GPa regime, with the observation of four ordered hydrogen-bonded forms and a cubic plastic phase. All of the ordered phases are characterised by hydrogen-bonded chains, with the three high-pressure forms all being based on the same hydrogen-bonded motif. This motif is maintained throughout the phase transitions with just the packing arrangement varying across the different forms. Form 3, at the intermediate pressure regime, can be considered as a chimeric combination of the lower-pressure form 2 and the higher-pressure form 4 as it demonstrates alternating layers of both structures. A series of high-pressure neutron powder-diffraction experiments were performed on GEM and at three different temperatures on PEARL to establish the relationships between each of the phases. As well as allowing the determination of the relative compressibilities of the phases, the powder-diffraction studies also provided a preliminary mapping of the TFE phase diagram. With such a surprisingly rich phase diagram, further high-pressure structural studies of TFE, particularly at higher pressures, would almost certainly prove fruitful.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors are grateful to Diamond Light Source Limited for the provision of beamtime on I19 (NT24766) and to ISIS for the award of time on PEARL (10.5286/ISIS.E.RB1820042 and 10.5286/ISIS.E.RB2010588) and GEM (10.5286/ISIS.E.RB1910318). The authors are also grateful for assistance with GSAS-II from Brian Toby and Robert Von Dreele.

Notes and references

1. C. P. Brock and L. L. Duncan, Chem. Mater., 1994, 6, 1307.
2. R. Taylor and C. F. Macrae, Acta Crystallogr., Sect. B: Struct. Sci., 2001, 57, 815.
3. P. A. McGregor, D. R. Allan, S. Parsons and C. R. Pulham, Acta Crystallogr., Sect. B: Struct. Sci., 2005, 61, 449.
4. I. D. H. Oswald, D. R. Allan, G. M. Day, W. D. S. Motherwell and S. Parsons, Cryst. Growth Des., 2005, 5, 1055.
5. D. R. Allan, S. J. Clark, A. Dawson, P. A. McGregor and S. Parsons, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 1018.
6. J. Ridout and M. R. Probert, CrystEngComm, 2014, 16, 7397.
7. R. Karlsson, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1976, 32, 2609.
8. R. M. Ibberson, S. Parsons, D. R. Allan and A. M. T. Bell, Acta Crystallogr., Sect. B: Struct. Sci., 2008, 64, 573.
9. P. A. McGregor, D. R. Allan, S. Parsons and S. J. Clark, Acta Crystallogr., Sect. B: Struct. Sci., 2006, 62, 599.
10. T. M. R. Maria, M. T. S. Rosado, M. F. Oliveira, S. S. Bebiano, R. A. E. Castro, E. Juszyńska-Gałązka, M. Ramos Silva, J. Canotilho and M. E. S. Eusébio, CrystEngComm, 2019, 21, 3395.
11. S. A. Moggach, D. R. Allan, P. Lozano-Casal and S. Parsons, J. Synchrotron Radiat., 2005, 12, 590.
12. I. D. H. Oswald, D. R. Allan, W. D. S. Motherwell and S. Parsons, Acta Crystallogr., Sect. B: Struct. Sci., 2005, 61, 69.
13. D. R. Allan, S. J. Clark, M. J. P. Brugmans, G. J. Ackland and W. L. Vos, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, R11809 , (and references therein).
14. D. R. Allan and S. J. Clark, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 6328.
15. C. L. Bull, S. A. Barnett, D. R. Allan and W. G. Marshall, High Pressure Res., 2019, 39(1), 179.
16. P.-G. Jönsson, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1976, 32, 232.
17. S. A. Barnett and D. R. Allan, CrystEngComm, 2019, 21, 4501.
18. S. A. Moggach, D. R. Allan, S. Parsons and J. E. Warren, J. Appl. Crystallogr., 2008, 41, 249.
19. H.-K. Mao, J. Xu and P. M. Bell, J. Geophys. Res.: Solid Earth, 1986, 91, 4673.
20. H. Nowell, S. A. Barnett, K. E. Christensen, S. J. Teat and D. R. Allan, J. Synchrotron Radiat., 2012, 19, 435.
21. Rigaku Oxford Diffraction, CrysAlisPro, Rigaku Europe, Unit B6, Chaucer Business Park, Watery Lane, Kemsing Sevenoaks, Kent TN15 6QY, United Kingdom, 2017.
22. G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2015, 71, 3.
23. G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3.
24. C. F. Macrae, P. R. Edgington, P. McCabe, E. Pidcock, G. P. Shields, R. Taylor, M. Towler and J. van de Streek, J. Appl. Crystallogr., 2006, 39, 453.
25. C. L. Bull, N. P. Funnell, M. G. Tucker, S. Hull, D. J. Francis and W. G. Marshall, High Pressure Res., 2016, 36, 493.
26. W. G. Marshall and D. J. Francis, J. Appl. Crystallogr., 2002, 35, 122.
27. A. D. Fortes, RAL Technical Reports, 2019, RAL-TR-2019-002, 2019.
28. L. G. Khovstantsev, High Temp. - High Pressures, 1984, 16, 165.
29. J. M. Besson, R. J. Nelmes, G. Hamel, J. S. Loveday, G. Weill and S. Hull, Phys. B, 1992, 180, 907.
30. O. Arnold, J. C. Bilheux, J. M. Borreguero, A. Buts, S. I. Campbell, L. Chapon, M. Doucet, N. Draper, R. Ferraz Leal, M. A. Gigg, V. E. Lynch, A. Markvardsen, D. J. Mikkelson, R. L. Mikkelson, R. Miller, K. Palmen, P. Parker, G. Passos, T. G. Perring, P. F. Peterson, S. Ren, M. A. Reuter, A. T. Savici, J. W. Taylor, R. J. Taylor, R. Tolchenov, W. Zhou and J. Zikovsky, Nucl. Instrum. Methods Phys. Res., Sect. A, 2014, 764, 156.
31. W. G. Williams, R. M. Ibberson, P. Day and J. E. Enderby, Phys. B, 1998, 234.
32. B. H. Toby, J. Appl. Crystallogr., 2001, 34, 210.
33. B. H. Toby and R. B. Von Dreele, J. Appl. Crystallogr., 2013, 46, 544.
34. M. J. Cliffe and A. L. Goodwin, J. Appl. Crystallogr., 2012, 45, 1321.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC deposition numbers: form 3 – 2280133; form 4_1.54 – 2280132; form 4_2.09 – 2280131. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3ce00737e

---