 Open Access Article
Open Access ArticleDotted crystallisation: nucleation accelerated, regulated, and guided by carbon dots
Mayank
Vashistha†
a,
Caoilfhionn
Cliffe†
a,
Emma
Murphy
a,
Parimaladevi
Palanisamy
a,
Andy
Stewart
b,
Srinivas
Gadipelli
 c,
Christopher A.
Howard
c,
Christopher A.
Howard
 d,
Dan J. L.
Brett
d,
Dan J. L.
Brett
 c and
K. Vasanth
Kumar
c and
K. Vasanth
Kumar
 *ae
*ae
aDepartment of Chemical Sciences, Synthesis and Solid State Pharmaceutical Research Centre, Bernal Research Institute, University of Limerick, Ireland. E-mail: v.kannuchamy@surrey.ac.uk
bDepartment of Chemistry, University College London, 20 Gordon St, London, WC1H 0AJ, UK
cElectrochemical Innovation Lab, Department of Chemical Engineering, UCL, London, WC1E 7JE, UK
dDepartment of Physics & Astronomy, University College London, London WC1E 6BT, UK
eSchool of Chemistry and Chemical Engineering, Faculty of Engineering and Physical Sciences, University of Surrey, Guildford, GU2 7XH, UK
First published on 21st July 2023
Abstract
Crystallisation from solution is an important process in pharmaceutical industries and is commonly used to purify active pharmaceutical ingredients. Crystallisation involves phase change and the mechanisms involved are random which makes the process stochastic. This creates a variation in the time required to reach a fixed percentage of yield from batch to batch. It is essential to regulate the batch crystallisation process and make it more predictable for industrial applications for the ease of process chain scheduling of upstream and downstream unit operations. In this work, we propose a new technique called dotted crystallisation, where carbon dots are used to dictate and regulate events associated with nucleation and crystallisation processes. Following the rules of two-step nucleation theory, the carbon dots intentionally added to a supersaturated solution of curcumin anchors the crystallising compound to form prenucleation clusters that evolve into stable nuclei. Using curcumin as a model compound, we showed that the nucleation of this compound in isopropanol can be regulated, and the nucleation rate can be improved via addition of small quantities of carbon dots to the supersaturated solution. Our results confirmed that the nucleation rate of curcumin by dotted crystallisation was roughly four times higher than the nucleation rate by conventional cooling crystallisation and produced smaller sized crystals with a narrow size distribution.
1. Introduction
Crystallisation is one of the most widely used techniques in industry to purify active pharmaceutical ingredients from their crude compounds.1–3 The traditional approach relies on the cooling crystallisation technique, where a crude product containing the target compound and impurities will be dissolved in a suitable solvent at elevated temperatures followed by cooling at a constant rate in order to create supersaturation. Conceptually, in a supersaturated solution, the target molecules will be selectively crystallised via nucleation leaving the impurities in the solution. Nucleation is assumed to proceed via the classical nucleation theory or via the two-step nucleation theory.4,5 The classical nucleation theory assumes that the target molecules in a supersaturated solution arrange themselves into nuclei that form a new crystalline phase with distinct characteristics. If the radii of these newly formed nuclei were to surpass the critical radius or surpass the free energy barrier, then the nuclei will evolve into a stable crystallite; if not, they will dissolve back into the solution.6 Alternatively, a stable crystallite can develop from its solution following a two-step process, where the molecules will assemble into prenucleation clusters.4,7,8 The molecules in the solution assemble into liquid like prenucleation clusters which further reorganise themselves into stable nuclei which evolve into a larger crystal via crystal growth.9,10The scientific hypothesis of nucleation following the rules of the two-step nucleation theory has been accurately proven using advanced microscopy techniques during the growth of NaCl crystals from their disordered structure and during the formation of flufenamic acid in solution.11,12 Sauter et al. used a small-angle-X-ray scattering technique to show the nucleation of a stable crystallite within an intermediate phase.13 In the context of nucleation, irrespective of the mechanisms involved, the larger the size of the molecule, the tougher is the nucleation. According to the classical nucleation theory, the nucleation rate is approximately inversely proportional to the molecular volume raised to the power of three. Additionally, irrespective of the size of the molecule and the mechanistic events that precede the nucleation, the rate of nucleation will be significantly altered by the presence of impurities in the solution.14 Impurity molecules will disturb the building up of prenucleation clusters or re-organisation of the intermediate structure and thus can delay the induction time, which in turn will alter the nucleation rate, and can delay the induction time from a few to several hours depending on the solution concentration, temperature, impurity concentration, molecular size/volume of the target molecule and the type of impurity. Impurities are unavoidable and are frequently encountered in industrial crystallisation processes. In particular, structurally similar impurities appear in common during the synthesis/manufacturing of several active pharmaceutical ingredients (APIs). Impurities will delay the nucleation kinetics and the overall process time. It is essential to find techniques that allow minimising the induction time and speeding up the crystallisation kinetics without significantly altering the solution and the properties of the final product. Additionally, according to the Gibbs theory, the molecules in a supersaturated solution will spontaneously assemble to form a stable volume.6 However, additional work should be done to observe a thermodynamically stable phase in a solution that has a surface area with a definite volume. Moreover, the entire prenucleation event is not solely a chemically controlled process and thus these events are not deterministic. This makes it challenging to regulate the nucleation process which alters the batch production time associated with a crystallisation process.
In this work, we propose a new technique called dotted crystallisation that allows regulating the nucleation process and minimising the overall process time of the API purification process via crystallisation. Dotted crystallisation relies on both classical and two-step nucleation theory. For dotted crystallisation, the molecules will be forced to crystallise from their supersaturated solution in the presence of carbon dots (Fig. 1, where we showed the concept of nucleation via the established two-step nucleation theory and the proposed dotted crystallisation). The size of carbon nanodots typically ranges from a few nanometres to less than 10 nm, much smaller than the size of prenucleation clusters (which are typically several hundreds of nanometres in size15), although they have a stable surface area. These stable nanodots provide surfaces which can anchor monomers of the molecules to form prenucleation clusters of the compound that we intend to crystallise. The carbon dots are intentionally added to accelerate the crystallisation that instantaneously initiates the assembling of monomers on the surface of the carbon dots, which eventually settle into stable crystallites. More importantly, dotted crystallisation starts with some particles that have a stable surface in the solution. This stable surface hosts the crystallising molecules to build prenucleation clusters rapidly around their surface and volume. As the entire process begins with a stable surface that anchors the prenucleation phase as opposed to conventional crystallisation that needs additional force to create the first stable surface in the solution, carbon dots help to control and regulate the nucleation process and can make the nucleation more deterministic.
The purpose of this work is to show that dotted crystallisation can accelerate the nucleation events following the rules of two-step nucleation theory. The prime objective is to show that the proposed dotted crystallisation can minimise the induction time, regulate the nucleation kinetics, alter the overall crystallisation kinetics, and eventually minimise the batch process time. Another main objective is to show that carbon dots can be used as a potential candidate to physically control the clustering process that precedes the nucleation to make the nucleation more predictable. To test our hypothesis, we used crude curcumin (CUR) as a model active pharmaceutical compound, which contains >20 wt% of two structurally similar impurities. We performed both conventional cooling crystallisation and dotted crystallisation experiments to purify crude CUR (Fig. 2). The first experiment was carried out in conventional mode without the addition of carbon dots in the supersaturated solution. The dotted crystallisation experiments were performed in the presence of a low concentration of carbon dots obtained from milk. Finally, we showed the advantages and the limitations of the proposed dotted crystallisation technique for the purification of the model API, curcumin. Additionally, we proposed a crystal breeding growth (CBG) model to explain the macroscopic kinetics of the conventional and dotted crystallisation.
 | ||
| Fig. 2 Plot of mass crystallised versus time. Regions (1) correspond to the lag phase, (2) acceleration phase, (3) exponential phase, (4) deceleration phase and (5) saturation or no-growth phase. | ||
2. Theory
As we will show later, it is possible to observe multiple distinct zones in the experimentally obtained crystallisation kinetics of crude CUR in IPA. These zones include a lag phase, acceleration phase, exponential phase, deceleration phase and saturation zone (Fig. 2). These zones observed in the crystallisation kinetics can be correlated to the actual crystallisation mechanism that we learned through crystallisation theories like the classical nucleation theory, two-step nucleation theory and the Terrace–Step–Kink model. In the lag phase, the molecules tend to recognise each other in the solution environment, assemble to form prenucleation clusters, and orient themselves in a specific order that may evolve into a thermodynamically stable phase at a later stage. In the acceleration phase, we presume that the pre-nucleation clusters evolve into stable nuclei and into a crystal. The appearance of a thermodynamically stable phase in the solution can instantaneously trigger the birth of several nuclei in the acceleration phase. After the acceleration phase, the observed exponential phase is associated with the birth of several nuclei and the growth of stable nuclei. At the end of the exponential phase, most of the supersaturation is consumed and thus in the deceleration phase, we presume that the increase in the concentration of solids in the solution should be associated solely with the growth of the already formed crystals. After the deceleration phase, the kinetics will reach the saturation zone. In the saturation zone, there will not be any nucleation or growth as the solution at this stage contains a solid concentration, Mm (g L−1), approaching the theoretical yield, Mm,ideal, at the studied temperature. Once the solid concentration, M, reaches Mm, the solution concentration will be equal to the solubility concentration at the working temperature and thus the solid concentration will remain constant. Conceptually, the parameter Mm can also be called as the maximum solid concentration that the solution can carry at the working temperature.We can assume that the crystallisation rate follows a first order expression.
 | (1) |
The specific growth rate, μ, is related to the unused theoretical capacity of the solution or the theoretical yield.
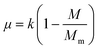 | (2) |
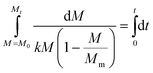 | (3) |
 | (4) |
3. Estimation of the kinetic parameters
As we assumed that there exist multiple zones in the crystallisation kinetics and the crystallisation is limited by the existence of a theoretical carrying capacity of the solution, the model allows us to theoretically predict Mm along with the kinetic constant, k, and a theoretical parameter, Mo, related to the number of molecules required to initiate the crystallisation events happening within the solution. To predict the three parameters involved in the CBG model, we used a non-linear regression technique, where we minimised the error distribution between the experimental data and the predicted kinetics. The error distribution between the experimental data was minimised by minimising the error function, the sum of the errors squared, ∑E2, using the solver add-in with Microsoft's spreadsheet, Microsoft Excel. ∑E2 is given by the expression:| ∑E2 = ∑((Mt)experimental − (Mt)predicted)2 |
Note that it is possible to treat the expression given in eqn (4) as a two-parameter expression by conveniently setting Mm equal to Mm,ideal. However, this is not essential as the Mm value can be predicted theoretically and if the experimental data follow the CBG model and the assumptions made (based on the existence of a carrying capacity of the solution) while deriving this expression, then the predicted Mm should be closer to Mm,ideal.
4. Results and discussion
4.1. Crystallisation kinetics of curcumin: conventional and dotted crystallisation
In Fig. 3a, we showed the plots of the mass crystallised versus time during the crystallisation of crude CUR at 15 °C in the presence (dotted crystallisation) and absence of carbon dots (conventional cooling crystallisation). It can be observed from Fig. 3 that the addition of carbon dots significantly reduced the induction time from 341 min to 81 min. As explained in section 2, the crystallisation kinetics contains several phases, and it is difficult to pick a point that corresponds to the end of the proper lag phase or the beginning of the acceleration phase. To identify the induction time, we rely on a simple graphical technique (see Fig. 3a) to define induction time, tind. We define induction time as the difference between the time at which the solid concentration reaches a specific density that corresponds to the solid concentration at any instant of time within the exponential phase and the ideal time at which the same solid concentration would have been reached had the exponential growth prevailed from the start. This means the nucleation would have started from that specific time called the ‘induction time’ without any lag. The method to identify the induction time is shown in Fig. 3a. The induction time is obtained from the intercept to slope ratio of the linear relationship that correlates the mass crystallised versus time in the exponential region. If we define the static nucleation rate, J = 1/(V × tind), then adding carbon dots increased the nucleation from 29 m−3 min−1 to 118 m−3 min−1. Another noteworthy observation is that the crystallisation rate (mass crystallised per unit time) in the exponential phase region is altered due to the addition of the carbon dots. As a significant amount of the supersaturation is getting consumed during the exponential phase, it is reasonable to assume that the overall crystallisation rate, k, depends on the mass crystallisation rate during the exponential phase and this value can be obtained from the CBG model (explained in section 2). The mass crystallised corresponds to the solid concentration that can be detected by in situ Raman spectroscopy (see section 5.5). In Fig. 3a, we showed the crystallisation kinetics predicted by the CBG model proposed in this work and the determined kinetic constant and the other parameter, γ = 1/Mmax, involved in the CBG model. The proposed crystal breeding growth (CBG) model well predicts the crystallisation kinetics of the conventional and dotted crystallisation of crude CUR in isopropanol. For the case of dotted crystallisation, the calculated crystallisation kinetic constant was found to be equal to 0.059 g L−1 min−1. This value is approximately four times higher than the conventional cooling crystallisation rate of crude CUR (0.0162 g L−1 min−1), suggesting that adding carbon dots increases the overall crystallisation kinetics. | ||
| Fig. 3 (a) Plots of mass crystallised versus time. In the right y-axis, we plotted the first derivative of the mass predicted using the CBG model (see eqn (4)) (blue dots: conventional crystallisation, red dots: dotted crystallisation, red dashed line: dM/dt versus time for the dotted crystallisation, blue dashed line: dM/dt versus time for conventional crystallisation, red dashed-dotted line: t50 for dotted crystallisation, blue dashed-dotted line: t50 for conventional cooling crystallisation). The linear expression that best fits the M versus t in the exponential phase is used to obtain the tind. The t50 is calculated from the plot of dM/dt versus time (t50 is the time at which the value of dM/dt reaches the maximum). (b) Plots of the first derivative of the mass predicted using the CBG model versus time (dashed lines). In the right y-axis, we plotted the second derivative of the mass predicted using the CBG model (solid lines) (red lines correspond to the dotted crystallisation and blue lines correspond to the conventional cooling crystallisation). Note: in Fig. 3a, we showed the method that we used to theoretically obtain the induction time, tind. In Fig. 3b, we showed the method to obtain the induction time and the time at which the exponential phase possibly would have reached the limit and the growth only phase begins (t100) during the crystallisation process. | ||
As the CBG model can predict the crystal growth kinetics, it is possible to use this expression to deduce the parameters that are useful and relevant to the crystallisation process. The CBG model can be used to predict the time required to achieve 50% yield and 100% yield. For demonstration purposes, in Figure 3a and b, we showed the first derivative and the second derivative of the kinetics predicted by the CBG model. Conceptually, in the plot of Mmversus t (Fig. 3a), the first and second inflection points characterise the induction time and the beginning of the saturation phase regions, respectively. The first-order derivative (see the dotted lines in Fig. 3a) is the rate of change of the mass crystallised with respect to time. As shown in Fig. 3a, the first-order derivative, dMt/dt, starts and finishes at zero and it reaches the maximum when the solid concentration is equal to 50% of the theoretical yield (i.e., 50% Mm). The second derivative exhibits three unique features: (1) it passes through zero when the time is equal to the time at which the experimentally observed solid concentration is equal to 50% Mm; (2) a positive band with the maximum at the same time as the first inflection point in the plot of Mm predicted by the CBG model versus t, and (3) a negative band with the minimum at the same time as the second inflection point in the plot of Mm predicted by the CBG model versus t. If we compare these features observed in the first and second derivatives, then it can be realised that it is possible to predict theoretically the time required to achieve 50% yield, t50 (this will be equal to t when the maximum is observed in the first derivative), induction time, tind (this will be equal to t, when the maximum is observed on the positive band of the second derivative), and the time required to achieve 100% yield, t100, when the solid concentration is equal to Mm (this will be equal to t, when the minimum is observed in the negative band of the second derivative). Thus, from Fig. 3a and b, it is possible to estimate theoretically tind, t50 and t100 for both conventional and dotted crystallisation processes. For the case of dotted crystallisation, it can be observed from Fig. 3b that 50% and 100% of the yields are achieved in ∼119 min and 211 min, respectively, compared to ∼465 min and 687 min, in the conventional cooling crystallisation route. Clearly, adding the carbon dots significantly decreased the batch time to achieve 50% yield by 4 times and 100% yield by 3 times. If we assume cleaning, charging (loading) of reactants, and the time to create supersaturation altogether requiring approximately 150 min, then in the presence of carbon dots, it is possible to perform ∼8 crystallisation batch experiments in 48 h to purify crude CUR (we will discuss the product purity later). On the other hand, for the case of conventional crystallisation based on the t100 value, it is possible to run only four crystallisation batches in 48 h. Using the CBG model, we also predicted the tind and the time at which the exponential phase limit and the growth only phase begins (texp,f) during the crystallisation process. The tind and texp,f for the dotted crystallisation obtained from the plot of the second derivative of the mass crystallised predicted using the CBG model versus time were found to be equal to 98 min and 142 min, respectively. The tind obtained theoreitcally was close to tind = 81 min obtained from the trend line that best fits the mass crystallised versus time in the exponential phase. The predicted tind and texp,f for the case of conventional cooling crystallisation from the plot of d2M/dt2versus t were found to be equal to 392 min and 532 min, respectively. The theoretically obtained tind for the case of conventional cooling crystallisation is slightly higher than the value of tind = 341 min obtained from the trend line that best fits the mass crystallised versus time in the exponential phase. The results clearly indicate that the CBG model can be used to successfully predict the crystallisation kinetics of crude CUR and to theoretically estimate the kinetic constant corresponding to the crystallisation process, tind, t50 and t100.
4.2. Crystal size distribution: conventional and dotted crystallisation
To check the effect of addition of carbon dots during crystallisation on the final crystal size distribution, we plotted the particle size distribution of the crystals collected at the end of the conventional and dotted crystallisation (Fig. 4a). To complement the crystal size distribution results, we also plotted the elongation factor and its distribution for the final crystals obtained from the conventional and dotted crystallisation (Fig. 4b). In Fig. 4c and d, we showed representative images of the crystals obtained from the conventional cooling crystallisation and dotted crystallisation. Fig. 4a shows that addition of carbon dots produced smaller crystals with a narrow size distribution. This can be attributed to the earlier discussed higher nucleation rate. Our results confirm that carbon dots can be used to tailor the crystal size distribution and even to obtain crystals with a smaller size when compared to that of the ones obtained using the conventional cooling crystallisation. The elongation factor of the crystals obtained from conventional cooling crystallisation and dotted crystallisation experiments confirms that the addition of carbon dots does not alter the elongation factor of the crystals or in other words the morphology of the final crystals. This agrees with the images shown in Fig. 4c and d, which confirms that adding carbon dots does not alter the crystal habit as both conventional cooling and dotted crystallisation produced crystals with a needle habit, the expected crystal habit of form I (FI) curcumin.4.3. Purity of the final crystals: conventional and dotted crystallisation
To understand the effect of adding carbon dots on the purity of the final crystals, we analysed the purity of the final crystals obtained from the dotted crystallisation using high-performance liquid chromatography (HPLC) and their HPLC chromatogram is shown in Fig. 5a. For comparison purposes, we also showed the HPLC chromatograms of the as-received crude CUR and the CUR crystals obtained from the conventional cooling crystallization experiments. The HPLC chromatogram of the crude CUR shows that the crude product contains a significant amount of structurally similar impurities desmethoxycurcumin (DMC) and bisdemethoxycurcumin (BDMC). The as-received crude CUR contains 78.6 wt% CUR, 17.8 wt% DMC, and 3.6 wt% BDMC. For the convenience of readers, we showed the molecular structures of CUR, DMC and BDMC in Fig. 5b. The HPLC chromatogram clearly indicates that the addition of carbon dots does not show any noticeable effect on the purity of the final crystals when compared to that of the crystals obtained via the cooling crystallisation. The crystals obtained from the conventional cooling crystallisation and the dotted crystallisation contain 92.8 wt% CUR, 7.2 wt% desmethoxycurcumin (DMC) and no bisdemethoxycurcumin (BDMC). This is a significant improvement in the purity of the final crystalline product when compared to that of the crude curcumin that contains 17.8 wt% DMC and 3.6 wt% BDMC. In one of our previous works, we showed that the no transfer of BDMC can be explained based on the driving force available for the transfer of impurities into the crystals and the molecular structure of this compound.2 BDMC is present in low concentration and has to compete with the crystallising molecules and the other impurity DMC during the crystallisation process. If the concentration of BDMC is lower than those of the other two curcuminoids, DMC and CUR, then it is less likely that BDMC can compete over these molecules during the phase transformation process or during the crystal growth process. Additionally, BDMC does not contain any –OCH3 group whereas CUR contains two –OCH3 groups in its molecular structure (see Fig. 5b). Thus, it is less likely that BDMC can replace CUR in the crystal lattice during the crystallisation.2 On the other hand, the second impurity, DMC, contains one –OCH3 group and thus partly resembles the molecular structure of CUR. This means that it is more likely that this molecule can easily replace the molecules in the crystal lattice during the crystallisation process. Additionally, DMC is also present in higher concentration in the crude CUR when compared to BDMC. This means that the driving force is relatively higher when compared to that of BDMC and we believe that this driving force is enough for the transfer of DMC into the crystals during the crystallisation process. Nevertheless, our results are important as they clearly indicate that both conventional cooling and dotted crystallisation produced crystalline products with high purity when compared to that of the starting material. Moreover, in the case of dotted crystallisation, a product of higher purity when compared to that of the starting material is obtained in less time when compared to the product of the conventional cooling crystallisation.4.4. On the stochastic nature of crystallisation: conventional and dotted crystallisation
It is well understood that nucleation is stochastic due to the unknown regulatory mechanism involved during the formation of nuclei and prenucleation stage (i.e., during the lag phase). Due to this experimental fact, nucleation is proven to be a random event and it is more likely that the same compound can crystallise with different nucleation and crystallisation rates. To show the experimental fact that the observed increase in nucleation and crystallisation rates in dotted crystallisation is dictated by carbon dots and is not a randomly observed experimental outcome, we performed multiple runs of dotted and cooling crystallisation experiments and compared their nucleation and overall crystallisation kinetics. In Fig. 6a and b, we showed the plots of mass crystallised versus time obtained from multiple runs of the conventional cooling and dotted crystallisation experiments, respectively. For comparison purposes, we also showed the results obtained from multiple runs of the dotted crystallisation experiments. Fig. 6 clearly shows a noticeable effect on the crystallisation kinetics due to the addition of carbon dots. In general, it is clear from Fig. 6 that the addition of carbon dots significantly decreased the induction time (tind obtained from the intercept to slope ratio of the line that best fits the exponential phase) when compared to that of the conventional crystallisation. The calculated tind of conventional and dotted crystallisation is given in Tables 1 and 2, respectively.| Run 1 | Run 2 | Run 3 | Run 4 | Run 5 | Run 6 | |
|---|---|---|---|---|---|---|
| M o, g per 100 mL | 3.18 × 10−6 | 1.21 × 10−3 | 1.91 × 10−4 | 5.22 × 10−7 | 2.11 × 10−9 | 2.74 × 10−9 |
| k, min−1 | 1.37 × 10−2 | 8.79 × 10−2 | 9.67 × 10−2 | 2.07 × 10−2 | 1.39 × 10−2 | 1.12 × 10−2 |
| γ, 100 mL−1 g | 2.411 | 2.413 | 2.367 | 2.841 | 2.646 | 2.722 |
| M m, g per 100 mL | 0.415 | 0.415 | 0.422 | 0.352 | 0.378 | 0.367 |
| ∑E2 | 1.87 × 10−2 | 1.90 × 10−1 | 1.90 × 10−1 | 2.22 × 10−1 | 2.74 × 10−1 | 2.34 × 10−1 |
| Run 7 | Run 8 | Run 9 | Run 10 | Run 11 | Run 12 | |
| M o, g per 100 mL | 1.42 × 10−3 | 3.14 × 10−9 | 5.78 × 10−5 | 6.00 × 10−12 | 6.25 × 10−7 | 6.24 × 10−5 |
| k, min−1 | 4.43 × 10−3 | 8.24 × 10−3 | 7.10 × 10−3 | 8.90 × 10−3 | 1.35 × 10−2 | 1.89 × 10−2 |
| γ, 100 mL−1 g | 2.870 | 2.697 | 2.734 | 2.589 | 2.696 | 2.661 |
| M m, g per 100 mL | 0.348 | 0.371 | 0.366 | 0.386 | 0.371 | 0.376 |
| ∑E2 | 2.17 × 10−1 | 3.88 × 10−1 | 3.88 × 10−1 | 1.91 × 10−1 | 7.19 × 10−1 | 1.71 × 10−1 |
| Run 1 | Run 2 | Run 3 | Run 4 | Run 5 | Run 6 | Run 7 | Run 8 | Run 9 | |
|---|---|---|---|---|---|---|---|---|---|
| M o, g per 100 mL | 2.55 × 10−3 | 6.29 × 10−4 | 1.80 × 10−4 | 3.70 × 10−4 | 2.32 × 10−4 | 1.21 × 10−4 | 6.01 × 10−4 | 5.09 × 10−5 | 1.46 × 10−3 |
| k, min−1 | 3.94 × 10−2 | 2.85 × 10−2 | 3.26 × 10−2 | 3.09 × 10−2 | 2.73 × 10−2 | 2.61 × 10−2 | 2.40 × 10−2 | 2.85 × 10−2 | 4.46 × 10−2 |
| γ, 100 mL−1 g | 2.783 | 2.717 | 2.748 | 2.610 | 2.668 | 2.707 | 2.705 | 2.788 | 2.801 |
| M m, g per 100 mL | 0.359 | 0.368 | 0.364 | 0.383 | 0.375 | 0.369 | 0.370 | 0.359 | 0.357 |
| ∑E2 | 1.15 × 10−1 | 3.19 × 10−1 | 1.36 × 10−1 | 2.43 × 10−1 | 5.55 × 10−1 | 2.17 × 10−1 | 9.03 × 10−1 | 4.69 × 10−1 | 1.48 × 10−1 |
During dotted and conventional crystallisation, the tind ranges from 41 min to 218 min and 245 min to 2496 min respectively. During the dotted crystallisation of CUR, the variation of induction time is narrower when compared to the observed variations in the induction time during the conventional crystallisation of CUR. To gain insights on the crystallisation process, we calculated the overall crystallisation kinetic constant and the theoretical yield for all the experimental runs (both dotted and conventional cooling crystallisation) using the CBG model and the predicted theoretical kinetics shown in Fig. 6. The CBG kinetic parameters are predicted using nonlinear regression analysis. For nonlinear regression analysis, we minimised the sum of the errors squared, ∑E2, between the experimental data and the predicted kinetics. Fig. 6 clearly indicates that the experimental crystallisation kinetics are well predicted by the CBG model. The calculated overall crystallisation kinetic constant k, the theoretical yield (i.e., Mm = 1/γ) obtained from the CBG model and the corresponding ∑E2 values are given in Table 1 (for conventional cooling crystallisation) and Table 2 (for dotted crystallisation). The ∑E2 in the range of 10−1 to 10−2 for all the crystallisation runs indicates that the kinetics of dotted and conventional cooling crystallisation of CUR follows the CBG model. For all the experimental runs, according to the CBG model, the overall crystallisation kinetic constant, k, of dotted crystallisation was found to be ∼10−2 min−1 and for the case of conventional cooling crystallisation, it ranged from 10−1 to 10−2 min−1. This essentially indicates that theoretically, the kinetics of dotted crystallisation is faster than the kinetics of conventional cooling crystallisation. Another noteworthy observation in Tables 1 and 2 is that the CBG model successfully predicts the theoretical mass that can be crystallised (or the theoretical yield) with a good level of accuracy. In most of the cases, the Mm predicted by the CBG model is closer to the ideal mass that can be crystallised (Mm,ideal = co − c*: 0.378 g per 100 mL; where co is the initial concentration of CUR and c* is the solubility of CUR at the working temperature 20 °C). The results indicate that the CBG model can be successfully used to predict the kinetics of both conventional and dotted crystallisation of CUR in isopropanol.
From the estimated induction time, we calculated the nucleation rate of CUR in conventional cooling crystallisation and in dotted crystallisation using the expression J = 1/(tind × V). The estimated nucleation rates of conventional and dotted crystallisation are shown in Fig. 7. It shows that the nucleation rate of CUR of dotted crystallisation is higher than the nucleation rate of CUR in carbon dot free solution (i.e., the conventional cooling crystallisation). For the case of conventional cooling crystallisation, the nucleation rate ranges from 4 m−3 min−1 to 41 m−3 min−1. In the presence of carbon dots, the nucleation rate of CUR ranges from 41 m−3 min−1 to 218 m−3 min−1. In Fig. 7, we also showed the average of the nucleation rates obtained from multiple experiments for the case of conventional and dotted crystallisation. The average nucleation rate by dotted crystallisation was found to be roughly eight times higher than the nucleation rate of CUR by the conventional cooling crystallisation.
To gain additional insights on the nucleation process, we calculated the probability of nucleation based on the induction time obtained from the multiple experimental runs. In Fig. 8, we showed the plots of the probability of nucleation, P(t), as a function of time which was obtained from the expression:16
| P(t) = N(t)/N | (5) |
 | ||
| Fig. 8 Probability of nucleation during the conventional cooling crystallisation of CUR in isopropanol (open red circles) and during the dotted crystallisation of CUR in isopropanol (open blue circles). Blue and red lines correspond to the P(t) predicted using eqn (7). | ||
There is a noticeable difference in the plots of P(t) versus t between the conventional cooling crystallisation and dotted crystallisation. It can be observed from Fig. 8 that the chance of achieving nucleation in dotted crystallisation is higher when compared to that in conventional crystallisation. For example, the probability P(t) is 50% when t > 524 min via conventional cooling crystallisation. In the case of dotted crystallisation, the estimated P(t) is 50% when t > 162 min. This essentially indicates that addition of carbon dots increases the chance of nucleation. In Fig. 8, we also observed a noticeable difference in the induction time window between the conventional and dotted crystallisation. The induction time window is defined by the expression:
| tindw = tg − t100 | (6) |
To study the influence of the carbon dots on the nucleation rate of CUR, we calculated the nucleation rate, J, using the cumulative exponential-based probability distribution function:16–18
| P(t) = 1 − exp(−JV(t − tg)) | (7) |
The dotted crystallisation proposed here can be taken as a process analogue of heterogeneous nucleation as the crystallisation events are forced to initiate in the presence of an external surface that has a definite volume. However, there exists a difference between the heterogeneous and dotted crystallisation in which the addition of carbon dots initiates the formation of prenucleation clusters around their surface following the nonclassical nucleation pathway that resembles the two-step nucleation theory. As mentioned earlier, the carbon dots can anchor the crystallising molecules to form the first stable nuclei which are essential to initiate the nucleation kinetics.
To gain an insight on the dotted crystallisation process, we captured TEM images of the as-synthesised carbon dots and carbon dots collected from the supersaturated solution (section 5.6) and the images are shown in Fig. 9 and 10, respectively. From Fig. 9 and 10, it can be clearly observed that there is a difference between the size of the as-synthesised carbon dots and the carbon dots collected from the supersaturated solution. The size of the as-synthesised carbon dots roughly ranges from 2.2–5.5 nm with an average size of 3.4 nm (Fig. 11a for the size distribution). The size of the carbon dots collected from the supersaturated solution ranges roughly from 12 to 490 nm (Fig. 11b for the size distribution). In terms of shape, both the as-synthesised carbon dots and the carbon dots collected from the supersaturated solution are essentially spherical. The observed difference in the size of the spherical structures expose the existence of an intermediate structure in the supersaturated solution which should be the prenucleation clusters formed around the carbon dots. It is worthy to mention here that we performed control experiments by performing TEM analysis of the supersaturated solution that does not contain any carbon dots and water (the solvent used to prepare the carbon dot solution – section 5.6 for details) prior to nucleation, which confirmed that there were no existing spherical structures observed in the samples collected from the supersaturated solution containing carbon dots. This confirms the experimental fact that the spherical structures observed in the solution containing carbon dots can be taken as mesostructures or an intermediate phase or stable clusters formed around the carbon dots prior to nucleation. It should be mentioned here that once a stable nucleus is formed via the support of carbon dots in a metastable liquid, then nucleation will occur spontaneously. In that case, the carbon dots in a metastable liquid that helps to build the prenucleation structure that can settle into a stable nucleus can be taken as a crystallisation promoter. Another noteworthy observation is the remarkably spherical shape which is completely different to the needle habit of the form I (FI) CUR crystals. Clearly, the clusters formed around the carbon dots should have reoriented themselves through a chemically controlled process before evolving into a stable nucleus. Although such events cannot be captured with offline microscopy techniques, several theoretical and experimental studies performed using in situ TEM confirmed the formation of a periodic structure from a disordered phase, which agrees with the TEM images shown in Fig. 10. For example, Cookman et al. used liquid phase electron microscopy and captured the evolution of flufenamic acid into a stable crystallite from a densified intermediate phase.11 In our earlier work, we used offline TEM to capture the existence of several featureless intermediate phases during the formation of curcumin spherulites.11 In a recent work, Nakamuro et al. exposed the formation of stable crystallites of an inorganic compound, NaCl, from their disordered phase.12
In our case, the TEM images in Fig. 10 confirm that the carbon dots anchor the crystallising molecules in the supersaturated solution as evidenced by the presence of several spherical structures in the solution containing carbon dots, and these structures exhibited a noticeable effect on the earlier discussed tindw (carbon dots decreased the tindw by 13 times as shown in Fig. 8 when compared to that of the conventional crystallisation). This essentially points to the fact that the added carbon dots not only participate in the prenucleation stages but also control or regulate the entire crystallisation event, making the nucleation process more predictable. This itself is a noteworthy result as addition of carbon dots can not only initiate the nucleation process but also regulate the nucleation by dictating the prenucleation events.
It is worthy to mention here that the TEM images exposed only one type of crystallisation mechanism, where a prenucleation cluster is built around the external surface of carbon dots, which may lead to a stable nucleus followed by spontaneous nucleation (as the presence of a stable nucleus which has a greater size than the size of the critical nucleus in a metastable liquid should create spontaneous nucleation). However, the presence of carbon dots can also promote nucleation via other mechanisms, as discussed in the work of Cacciuto et al.19 in which molecular simulations showed that a foreign particle present in a metastable liquid can host crystallising molecules to form a prenucleation cluster. At some stage, the prenucleation cluster breaks away from the surface of the foreign particle and a stable nucleus is formed in the bulk solution (which is like homogeneous nucleation – this mechanism can be visualised only under a liquid cell TEM and this is beyond the scope of the present work). It was also shown that the foreign particle acts as an ‘assembly line’ for crystal nuclei, as once a nuclei or a precluster is formed they detach from the foreign particle leaving it free to produce the next nuclei. Although such mechanisms are difficult to expose using the TEM images captured in offline mode, we speculate the existence of such a mechanism during the dotted crystallisation process from the calculated nucleation rate. For instance, in this work, we used only trace quantities of carbon dots when compared to the concentration of the crystallising molecules. Nevertheless, at the macroscopic scale, this low concentration of carbon dots improved the nucleation rate when compared to that of the conventional crystallisation. A higher nucleation rate means more nuclei formed in the presence of carbon dots per unit time and we presume that the carbon dots act like crystallising host molecules in the supersaturated solution. The only difference is that the carbon dots should have produced more nuclei in the solution. To be specific, the carbon dots should have assisted in the molecular assembling process to build a cluster whose size should be greater than that of the critical nuclei. The nucleation occurring in the presence of a foreign body like carbon dots can be taken as heterogeneous nucleation. In that case, at a fixed supersaturation, the presence of carbon dots will reduce the energetic barrier and the size of the critical nuclei that should lead to an increased nucleation rate when compared to that of the homogeneous nucleation. In fact, the particle size distribution of crystals obtained from dotted crystallisation confirmed this hypothesis. A higher nucleation rate means more crystals formed at a fixed supersaturation, which means most of the supersaturation will be consumed via nucleation and the remaining supersaturation will be consumed during the crystal growth. If most of the supersaturation is consumed via nucleation, then the crystal growth after nucleation will be minimum due to the lack of supersaturation in the solution. In that case, the PSD of the final crystals (Fig. 4a and the discussions made in section 4.2) can be expected to be smaller when compared to the crystals collected from a process setup with a lower nucleation rate. In essence, the dotted crystallisation can be taken as a useful and effective technique to simultaneously increase the nucleation rate, decrease the process time and narrow down the crystal size.
5. Conclusions
Based on our results, it can be concluded that during crystallisation, addition of carbon dots to a supersaturated solution increased the nucleation rate and overall crystallisation kinetics of curcumin in isopropanol, and more importantly made the nucleation predictable. Dotted crystallisation can be used as a potential technique to decrease the batch production time of active pharmaceutical ingredients when compared to conventional cooling crystallisation. Dotted crystallisation produced crystals with improved purity that matched with the ones obtained from conventional crystallisation and produced crystals with a smaller mean crystal size and a narrow crystal size distribution when compared to those of the conventional crystallisation. The CBG model accurately predicts the kinetics of conventional and dotted crystallisation and the overall kinetic constants. The CBG model also predicts the crystallisation capacity of the solution that matches with the crystal yield obtained using mass balance. The CBG model was also found to be useful to identify the theoretically predict at which different mechanistic phases begins during crystallisation. Results obtained from the offline microscopic technique reveal the fact that carbon dots guide the early stages of the crystallisation events following the rules of the two-step nucleation theory. During the prenucleation stage, the carbon dots anchor the crystallising compound to produce an intermediate phase that should evolve into a stable nucleus. This effect is enough to alter the macroscopic kinetics and significantly decrease the batch production time.6. Experimental
6.1. Materials
Crude CUR was purchased from Merck (CUR >75% nominal purity), containing <5 wt% BDMC and <20 wt% DMC. HPLC-grade IPA (>99.9%) was purchased from Acros Organics Aldrich. The HPLC experiments performed in our lab show that the CUR is 78.6% pure and contains <18 wt% DMC and <4 wt% BDMC. CUR was used as received for the crystallisation experiments. Nestle Carnation evaporated milk was purchased from a local supermarket.6.2. Preparation of carbon dots
Using a glass pipette, 10 mL of evaporated milk was transferred into a 50 mL glass vial. Using a kitchen microwave oven, the milk was irradiated at 800 W for 10 min. To break the froth bubbles formed during the microwave irradiation, we filled the vials with glass beads before irradiation. The irradiation rapidly evaporated the water and carbonised the evaporated milk, yielding a sticky dark brown precipitate at the end. To this precipitate, we added 20 mL of deionised water, followed by sonication to prepare a homogeneous aqueous solution of the carbonised product. Using an ultracentrifuge, the solution was centrifuged for 1 h at 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm to separate the liquid containing fluorescent carbon dots from the brown solid precipitate. The supernatant that contains carbon dots was then filtered using a 0.4 micron nylon filter. The liquid phase was saved as such for further characterisation and use in the crystallisation experiments at 25 °C.
000 rpm to separate the liquid containing fluorescent carbon dots from the brown solid precipitate. The supernatant that contains carbon dots was then filtered using a 0.4 micron nylon filter. The liquid phase was saved as such for further characterisation and use in the crystallisation experiments at 25 °C.
6.3. Characterization of the carbon dots
A LyoQuest Benchtop Freeze Dryer was used to freeze-dry a sample of the aqueous carbon dot solution to quantify the yield of carbon dots. The sample was first held at −40 °C for 24 h and then we kept the sample under vacuum for 24 h. The sample was then heated slowly to 30 °C to allow sublimation to occur. The weight of the sample was recorded before and after freeze-drying to calculate the overall yield and the concentration of carbon dots in the carbon dot solution using the formula given below:| Concentration of carbon dot solution, g L−1 = (Wcdi − Wcdf)/Wsol | (8) |
6.4. Crystallisation experiments
Crystallisation experiments were performed in batch mode using a 100 mL Easymax workstation. We set the reactor volume to 100 mL. The temperature inside the crystalliser was maintained or altered using an external jacket that relies on electrical heating and solid-state cooling technology. The agitation inside the crystalliser in all the experiments was maintained at 250 rpm and the agitation was provided using an overhead stirrer. During the crystallisation experiment, we monitored the suspension density using in situ Raman spectroscopy.Conventional cooling crystallisation experiments were performed by adding 0.588 g of crude curcumin in 0.786 g of isopropanol. All the solids were dissolved by heating the solution to 75 °C at a rapid heating rate. Then, the solution was maintained at 75 °C for 45 min to ensure complete dissolution of CUR. Then, the solution was cooled down to 20 °C at a fixed cooling rate of 8 °C min−1 to generate a supercooled solution, ΔT = T* − Tw (∼50 °C). The term T* refers to the solubility temperature and Tw is the working temperature. This generates a solution with a supersaturation ratio of S = 5.5. The supersaturation was defined in terms of the ratio of the concentration of curcumin in the solution to the solubility concentration at the working temperature, S = c/c*. In all the crystallization experiments, we maintained the solution at the working temperature for ∼24 h to achieve complete saturation after nucleation.
For the dotted crystallisation, we repeated the above experimental procedure and maintained the same experimental conditions. The only difference between the conventional cooling crystallisation and the dotted crystallisation is that we added a known volume of carbon dot solution together with the solid crude curcumin. We added 2.0 mL of the carbon dot solution in isopropanol before dissolving the crude curcumin in isopropanol at elevated temperature. In this work, we performed three dotted crystallisation experiments.
In this work, we performed up to 12 experimental trials for the case of conventional crystallisation and up to 9 experimental trials for the case of dotted crystallisation. All the experimental trials were performed using the same method programmed using Mettler Toledo's iControl software and in the same reactor without disturbing the experimental setup.
6.5. Determination of solid concentration using Raman spectroscopy
As mentioned above, we monitored the increase in suspension density due to crystallisation using in situ Raman spectroscopy. An RX1 Raman spectrometer supplied by Kaiser Optical System, Inc. (Ann Arbor, MI, USA) was used to collect the Raman spectra. A ¼ inch immersion probe which is connected to the spectrometer via a fiber-optic cable was used to collect backscattered radiation from the sample. The probe was positioned roughly 2 cm above the bottom of the base of the crystallizer, with the power at the sample being approximately 150 mW. Using iC Raman software (Mettler Toledo), a measurement region of 150–3425 cm−1 at 786 nm excitation was utilised with a spectral resolution of 4 cm−1 to collect spectra which were averaged over 30 scans using an exposure time of 2 s.We used a calibration free method to correlate the Raman intensity with the supersaturation, ΔC, with the mass crystallised, Mt, at any time t:2
| ΔC = C − C* = (It − Io)/(Io − If) × Mc | (9) |
| Mt = Mc − ΔC | (10) |
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Cring of curcumin to quantify the suspension density in the solution.2 This peak is sensitive to the solid-phase concentration and thus we selected this peak to estimate the solid concentration. Following eqn (9), the ratio of the peak intensity with respect to the peak intensity of the solvent was found to be linearly proportional. The peak intensity of the curcumin here refers to the height of the band from the two-point baseline that connects 1617 cm−1 and 1571 cm−1 in the Raman spectra.2
Cring of curcumin to quantify the suspension density in the solution.2 This peak is sensitive to the solid-phase concentration and thus we selected this peak to estimate the solid concentration. Following eqn (9), the ratio of the peak intensity with respect to the peak intensity of the solvent was found to be linearly proportional. The peak intensity of the curcumin here refers to the height of the band from the two-point baseline that connects 1617 cm−1 and 1571 cm−1 in the Raman spectra.2
6.6. Microscopy analysis
Transmission electron microscopy (TEM) was used to determine the structural details of the sample and degree of nucleation build-up. A Thermo Fisher Titan Themis transmission electron microscope at 300 keV using a Gatan OneView detector was used to obtain the images. 2 mL of curcumin solution and 0.5 mL of carbon dot solution were mixed in an Eppendorf tube and allowed to settle for 10 min. The samples were then transferred to holey carbon TEM grids (200 mesh Cu; Ted Pella, Inc, USA, lot #031117) using a plastic dropper. No nucleation can be visibly observed during the sample preparation. A flash evaporation technique using a holey carbon TEM grid placed on a hot plate at 95 °C was used to evaporate water and IPA and obtain the sample. The supersaturated solution containing carbon dots was dropped via a plastic dropper onto holey carbon TEM grids (natural drying of samples on the TEM grids will result in crystallisation of the API on the TEM grids via slow evaporation).For the analysis of carbon dots, the as-prepared carbon dot solution was diluted with ethanol and the dilute carbon dot solution was then transferred to holey carbon TEM grids (200 mesh Cu; Ted Pella, Inc, USA, lot #031117) and the ethanol was allowed to evaporate naturally at room temperature inside a fume hood.
Note: it should be noted here that in the actual crystal growth experiments, the percentage volume of carbon dot solution is only ∼0.5%. Thus, it will be an extremely difficult task to locate the prenucleation clusters formed around the carbon dots. To capture the mechanism involved, we prepared the TEM samples from a supersaturated solution that contains 50% by volume of carbon dot solution. This way, it is possible to capture the mechanistic events occurring on the surface of carbon dots.
The number-based crystal size distribution of the final crystals was obtained using a Malvern Morphologi G3SE microscopy image analysis instrument. We created a standard operating procedure (SOP) for the sample analysis. Before initiating the SOP, we manually dispersed the samples on a glass plate (180 mm × 110 mm). Diascopic light was passed from the bottom of the glass plate with automatic light calibration intensity using a set value of 80 and an intensity tolerance of 0.20. The particles were analysed using 5× magnification optics (Nikon TU plan ELWD). The length of the particle, defined as the longest projection of two points on the major axis of the particle 2D area and also called the maximum Feret diameter, was used to determine the particle size. We manually stopped the analysis after 45 minutes, which is more than enough to collect images of >25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 crystals. In the SOP, we added a series of procedures to automatically separate aggregated particles, which rely on an automatically estimated image threshold value and watershed segmentation method. The SOP reports the number crystal distribution based on the maximum Feret diameter and the elongation factor (defined as the ratio of length to width) and its distribution.
000 crystals. In the SOP, we added a series of procedures to automatically separate aggregated particles, which rely on an automatically estimated image threshold value and watershed segmentation method. The SOP reports the number crystal distribution based on the maximum Feret diameter and the elongation factor (defined as the ratio of length to width) and its distribution.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the financial support from the Science Foundation Ireland (Grants 12/RC/2275, 12/RI/2345/SOF, and 18/SIRG/5479). P. P. and K. V. K. would like to acknowledge the financial support from Enterprise Ireland and the European Commission through the Marie Curie Career-FIT plus the COFUND fellowship program (Grant MF2020015). M. V. would like to acknowledge the Bernal Institute, Boston Scientific, Department of Chemical Sciences and the University of Limerick Foundation for the funding support through the mULtiply program. K. V. K. would like to dedicate this review to his late dad Dr. V. Kannuchamy.References
- J. Chen, B. Sarma, J. M. B. Evans and A. S. Myerson, Cryst. Growth Des., 2011, 11, 887–895 CrossRef CAS.
- K. V. Kumar, K. A. Ramisetty, K. R. Devi, G. R. Krishna, C. Heffernan, A. A. Stewart, J. Guo, S. Gadipelli, D. J. L. Brett, E. P. Favvas and Å. C. Rasmuson, ACS Omega, 2021, 6(37), 23884–23900 CrossRef CAS PubMed.
- K. H. Hsi, M. Kenny, A. Simi and A. S. Myerson, Cryst. Growth Des., 2013, 13, 1577–1582 CrossRef CAS.
- D. Gebauer, M. Kellermeier, J. D. Gale, L. Bergström and H. Cölfen, Chem. Soc. Rev., 2014, 4(3), 2348–2371 RSC.
- D. Erdemir, A. Y. Lee and A. S. Myerson, Acc. Chem. Res., 2009, 42, 621–629 CrossRef CAS PubMed.
- Crystallization, ed. J. W. Mullin, Butterworth-Heinemann, 4th edn, 2001 Search PubMed.
- P. R. Ten Wolde and D. Frenkel, Science, 1997, 277(5334), 1975 CrossRef CAS PubMed.
- J. Russo and H. Tanaka, MRS Bull., 2016, 41, 369–373 CrossRef CAS.
- E. V. Sturm and H. Cölfen, Chem. Soc. Rev., 2016, 45, 5821–5833 RSC.
- T. Wang, A. H. Cölfen and M. Antonietti, J. Am. Chem. Soc., 2005, 127, 3246–3247 CrossRef CAS PubMed.
- J. Cookman, V. Hamilton, S. R. Hall and U. Bangert, Sci. Rep., 2020, 101(10), 1–10 Search PubMed.
- T. Nakamuro, M. Sakakibara, H. Nada, K. Harano and E. Nakamura, J. Am. Chem. Soc., 2021, 143, 1763–1767 CrossRef CAS PubMed.
- A. Sauter, F. Zhang, N. K. Szekely, V. Pipich, M. Sztucki and F. Schreiber, J. Phys. Chem. B, 2016, 120, 5564–5571 CrossRef CAS PubMed.
- R. M. Ginde and A. S. Myerson, J. Cryst. Growth, 1993, 126, 216–222 CrossRef CAS.
- S. Kakkar, K. R. Devi and Å. C. Rasmuson, Cryst. Growth Des., 2022, 22, 2824–2836 CrossRef CAS.
- C. Brandel and J. H. Ter Horst, Faraday Discuss., 2015, 179, 199–214 RSC.
- J. Hoffmann, J. Flannigan, A. Cashmore, M. L. Briuglia, R. R. E. Steendam, C. J. J. Gerard, M. D. Haw, J. Sefcik and J. H. ter Horst, Faraday Discuss., 2022, 235, 109–131 RSC.
- J. H. ter Horst, C. Schmidt and J. Ulrich, Handb. Cryst. Growth Bulk Cryst. Growth, 2nd edn, 2015, vol. 2, pp. 1317–1349 Search PubMed.
- A. Cacciuto, S. Auer and D. Frenkei, Nature, 2004, 4286981(428), 404–406 CrossRef PubMed.
- D. Wang, L. Zhu, C. McCleese, C. Burda, J. F. Chen and L. Dai, RSC Adv., 2016, 6, 41516–41521 RSC.
- C. Cliffe, A principal attempt to break the stochastic nature of nucleation, BEng Final year research project, University of Limerick, 2021. And Emma Murphy, Crystallisation catalysed accelerated using biomass carbon dots, BSc Final year research project, 2020.
Footnote |
| † Equal contribution. |
| This journal is © The Royal Society of Chemistry 2023 |








