DOI:
10.1039/D3CE00365E
(Communication)
CrystEngComm, 2023,
25, 3588-3597
Ferroelastic phase transition and the role of volume strain in the structural trapping of a metastable quenched low-spin high-symmetry phase in [Ru0.35Fe0.65(ptz)6](BF4)2†
Received
14th April 2023
, Accepted 20th May 2023
First published on 22nd May 2023
Introduction
Entropy-driven molecular bistability, between electronic states separated by an energy barrier of the order of thermal energy, can give rise to crossover phenomena at thermal equilibrium between different electronic states, including charge-transfer or spin states, for example.1 In molecular materials, elastic interactions between sites, for which the change of electronic state is associated with the volume change, can induce cooperative phase transitions associated with thermal hysteresis.2 In many cases, this phenomenon occurs without symmetry change. In solids, symmetry-breaking (SB) phase transitions can also occur, and more and more systems exhibit concerted or sequential changes in electronic state and symmetry.2b,3 This is the case of the spin-crossover (SCO) compound [Fe(ptz)6](BF4)2 iron(II) (ptz = 1-propyltetrazole), which exhibits a spin-transition hysteresis at atmospheric pressure.4 The thermal dependence of the fraction γ of high-spin molecules changes discontinuously through a ≃7 K wide thermal hysteresis. This change of electronic state results from the rearrangement of electrons within metal d-orbitals between the high-spin (HS, S = 2) and low-spin (LS, S = 0) configurations. The high-temperature HS phase is the high symmetry one (HShs), with a rhombohedral R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) space group, while the low-temperature LS phase is low symmetry (LSls) with a triclinic P
space group, while the low-temperature LS phase is low symmetry (LSls) with a triclinic P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) space group.4a,d,g,h,5 There are different contributions to the entropy increase between the LSls and HShs phases. On the one hand, the non-symmetry-breaking SCO includes an electronic entropy change due to the change in spin multiplicity and a vibrational entropy due to the global decrease of the frequency of the modes between LS and HS states.1h,2g,6 On the other hand, there is also a SB contribution due to the order–disorder configurational change and splitting of mode frequencies, and therefore, SCO and SB can occur simultaneously or sequentially depending upon the external parameters.2a,3b Indeed, under pressure, the [Fe(ptz)6](BF4)2 system exhibits sequential conversions on cooling with SB from the HShs phase towards a high-spin low symmetry (HSls) P
space group.4a,d,g,h,5 There are different contributions to the entropy increase between the LSls and HShs phases. On the one hand, the non-symmetry-breaking SCO includes an electronic entropy change due to the change in spin multiplicity and a vibrational entropy due to the global decrease of the frequency of the modes between LS and HS states.1h,2g,6 On the other hand, there is also a SB contribution due to the order–disorder configurational change and splitting of mode frequencies, and therefore, SCO and SB can occur simultaneously or sequentially depending upon the external parameters.2a,3b Indeed, under pressure, the [Fe(ptz)6](BF4)2 system exhibits sequential conversions on cooling with SB from the HShs phase towards a high-spin low symmetry (HSls) P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) phase, followed SCO towards the low-spin low symmetry (LSls) P
phase, followed SCO towards the low-spin low symmetry (LSls) P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) phase.4c,e In addition, upon fast cooling, a metastable low-spin high-symmetry (LShs) R
phase.4c,e In addition, upon fast cooling, a metastable low-spin high-symmetry (LShs) R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phase appears.7
phase appears.7
It was recently shown that the dilution of the [Fe(ptz)6](BF4)2 compound in the isostructural Ru host lattice [Ru(ptz)6](BF4)2, which also undergoes the same R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) → P
→ P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) crystallographic phase transition upon cooling, stabilises the Fe(II) low-spin state.7d In the [Ru0.35Fe0.65(ptz)6](BF4)2 system (1) studied here, the half conversion temperature was found to be of the order of 135 K, i.e., ≃8 K above the one of the neat [Fe(ptz)6](BF4)2 compound. This results from the fact that the Ru(II) host, with lattice dimensions similar to the lattice of the pure LS Fe(II) compound, induces a chemical pressure favouring LS Fe(II) complex of lower volume, shifting SCO towards higher temperatures compared to pure [Fe(ptz)6](BF4)2. In the previous structural characterisation of (1) performed by single-crystal X-ray diffraction, three different phases were identified.7d Above 150 K, the HShs phase is exclusively dominant, displaying the R
crystallographic phase transition upon cooling, stabilises the Fe(II) low-spin state.7d In the [Ru0.35Fe0.65(ptz)6](BF4)2 system (1) studied here, the half conversion temperature was found to be of the order of 135 K, i.e., ≃8 K above the one of the neat [Fe(ptz)6](BF4)2 compound. This results from the fact that the Ru(II) host, with lattice dimensions similar to the lattice of the pure LS Fe(II) compound, induces a chemical pressure favouring LS Fe(II) complex of lower volume, shifting SCO towards higher temperatures compared to pure [Fe(ptz)6](BF4)2. In the previous structural characterisation of (1) performed by single-crystal X-ray diffraction, three different phases were identified.7d Above 150 K, the HShs phase is exclusively dominant, displaying the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) space group. At 150 K, the lattice parameters of the hexagonal lattice are: aH = bH = 10.83 Å, cH = 32.03 Å. Below ≃130 K two possible low-spin phases can be generated, depending on the cooling rate of crystals. On the one hand, a slow cooling (≃0.2 K min−1) induces a LSls phase, which has a triclinic lattice (P
space group. At 150 K, the lattice parameters of the hexagonal lattice are: aH = bH = 10.83 Å, cH = 32.03 Å. Below ≃130 K two possible low-spin phases can be generated, depending on the cooling rate of crystals. On the one hand, a slow cooling (≃0.2 K min−1) induces a LSls phase, which has a triclinic lattice (P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) space group) with aP = 12.33 Å, bP = 10.77 Å, cP = 16.37 Å, α = 90.20°, β = 100.54° and γ = 90.20°. On the other hand, fast quenching at 80 K from the HShs phase induces low-temperature LShs phase, which retains the R
space group) with aP = 12.33 Å, bP = 10.77 Å, cP = 16.37 Å, α = 90.20°, β = 100.54° and γ = 90.20°. On the other hand, fast quenching at 80 K from the HShs phase induces low-temperature LShs phase, which retains the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) space group, with lattice parameters aH = bH = 10.73 Å, cH = 32.01 Å. Therefore, SB and SCO may decouple in the [Ru0.35Fe0.65(ptz)6](BF4)2 solid solution.
space group, with lattice parameters aH = bH = 10.73 Å, cH = 32.01 Å. Therefore, SB and SCO may decouple in the [Ru0.35Fe0.65(ptz)6](BF4)2 solid solution.
In the framework of the Landau theory adapted by Collet for coupled SB and SCO,2a,3a–c the theoretical phase diagram of [Fe(ptz)6](BF4)2 was described through the evolution and coupling of SCO and SB phenomena with temperature and pressure. It provided an excellent qualitative agreement with the experimental data through the evolution of SCO curves or lattice deformations under pressure.2a In the present paper, we study the evolution of SCO and SB during the thermal conversion of (1). First, we present a detailed structural analysis of the HShs-to-LSls phase transition and highlight the associated symmetry-breaking signatures in both real and reciprocal spaces. These show that structural phase transition corresponds to a ferroelastic R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) → P
→ P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) symmetry-breaking phase transition, with a group-subgroup relationship, and not to a reconstructive phase transition. In such a case, the Landau theory approach is relevant to describe the observed phenomena. We also study the metastable low-spin high symmetry (LShs) phase (R
symmetry-breaking phase transition, with a group-subgroup relationship, and not to a reconstructive phase transition. In such a case, the Landau theory approach is relevant to describe the observed phenomena. We also study the metastable low-spin high symmetry (LShs) phase (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) space group) reached upon fast cooling. Within the Landau theory framework of phase transition adapted by Collet, we explain that the metastable nature of the LShs phase is due to the partial volume strain, containing only the contribution of the SCO and not the SB one.
space group) reached upon fast cooling. Within the Landau theory framework of phase transition adapted by Collet, we explain that the metastable nature of the LShs phase is due to the partial volume strain, containing only the contribution of the SCO and not the SB one.
Results and discussion
Materials and methods
Mixed crystals of [Ru0.35Fe0.65(ptz)6](BF4)2 were synthesised from previously synthesised [Ru(ptz)6](BF4)2 and [Fe(ptz)6](BF4)2 crystals, separately redissolved in CH3CN. The two solutions were mixed homogeneously to obtain [Ru0.35Fe0.65(ptz)6](BF4)2 single crystals. Details of the synthesis and characterisation were reported by Chakraborty et al.7d
Single-crystal X-ray diffraction (SCXRD) data of the complex (1) were collected on the same single crystal at 250 K (HShs) and 80 K (LSls) on slow cooling (≃0.2 K min−1) as well as on flash cooling at 80 K (LShs) using an Oxford Diffraction Xcalibur3 X-ray diffractometer with an enhanced source, using Mo Kα (λ = 0.71073 Å) radiation, fitted with a Sapphire3 detector. Changes in unit cell volume, cell parameters, and Bragg peak intensities as a function of temperature were investigated on a new single crystal during cooling from 250 K to 80 K and warming from 80 to 250 K (2–3 K steps with 200 K h−1 cooling/heating rate). Single crystals were mounted on cryo-loops with Parabar 10312 oil. Nitrogen flow 700Plus series cryostat from Oxford Cryosystems was used for the variable-temperature measurements and the complete data collections. The CrysAlisPRO95 software package from Rigaku Oxford Diffraction was used for all data collections and data processing (indexing, integration, and reduction). All structures were solved by dual direct methods with SHELXT8 and refined by full-matrix least-squares on F2 using SHELXL9 in OLEX2.10 All non-hydrogen atoms were refined anisotropically and H-atoms were constrained by geometry. When applicable, DFIX, SIMU and ISOR restraints as well EADP and EXYZ constraints were applied for occupational disorders of selected atoms sites. In case of 80 K data in LSls phase, a domain formation upon transition was detected; only data of a main domain component were taken for final structure determination here. CCDC 2256112 (250 K), CCDC 2256113 (80 K flash cooling), and CCDC 2256114 (80 K) contain the crystal data collection and refinement parameter details for this paper.
Group-subgroup symmetry breaking.
Fig. 1 shows the nodes of the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) rhombohedral lattice and the different unit cells that can be used to describe lattice periodicity: the primitive rhombohedral cell, the hexagonal cell, and the triclinic primitive cell. Any lattice translation vector
rhombohedral lattice and the different unit cells that can be used to describe lattice periodicity: the primitive rhombohedral cell, the hexagonal cell, and the triclinic primitive cell. Any lattice translation vector ![[T with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/b_i_char_0054_20d1.gif) , connecting nodes of the high-temperature lattices can be given in the primitive triclinic P
, connecting nodes of the high-temperature lattices can be given in the primitive triclinic P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) or hexagonal R
or hexagonal R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) lattices:
lattices:| |  | (1) |
where U, V, W, u, v and w are integers. The transformation matrix given in ref. 11 connecting the lattices is:| |  | (2) |
consequently, any vector ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/b_i_char_0051_20d1.gif) of the reciprocal space can be expressed both in the P
of the reciprocal space can be expressed both in the P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) triclinic reciprocal cell or in the R
triclinic reciprocal cell or in the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) hexagonal reciprocal one:
hexagonal reciprocal one:| |  | (3) |
 |
| | Fig. 1 Nodes of the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) rhombohedral lattice (green), showing the relationship with the hexagonal (H subscript purple) and primitive triclinic (P subscript orange) unit cells. rhombohedral lattice (green), showing the relationship with the hexagonal (H subscript purple) and primitive triclinic (P subscript orange) unit cells. | |
Considering the transformation matrix:
| |  | (4) |
we obtain the following developments:
| | 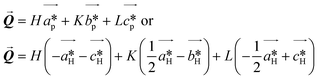 | (5) |
and the relationships between the indexes of the
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif)
and
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
reciprocal lattices:
| |  | (6) |
In the conventional
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif)
hexagonal lattice cell, only (
hkl) peaks with −
h +
k +
l = 3
n are present, while (
HKL) Bragg peaks are allowed for any
H,
K,
L integers in the primitive triclinic cell. Therefore, in the case of a group-subgroup SB phase transition due to a distortion from hexagonal to triclinic lattices, with a pseudo hexagonal reciprocal lattice, the
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif)
→
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
symmetry breaking is characterized by the appearance of Bragg peaks with −
h +
k +
l ≠ 3
n and also with
h =
n + ½.
Fig. 2 shows the diffracted intensity in the reciprocal space using the (pseudo) hexagonal cell. The diffraction patterns were obtained from single crystal diffraction data collected at 250 K for the HShs phase and at 80 K for the LSls and LShs phases. We were cautious about the cooling rate when the low-spin phases were generated: the LShs was reached by fast cooling of the single crystals, directly put under the N2 stream of the cryostat set to 80 K, while the LSls phase was reached on slow cooling (≃0.2 K min−1) from the HShs phase. The diffraction patterns of the HShs and LShs phases are similar (within the thermal contraction): both exhibit hexagonal reciprocal lattices of R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) space group with
space group with 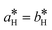 and
and 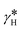 = 60°, and the Bragg peaks present in the (hk0) or (h0l) reciprocal planes obey −h + k + l = 3n. In the LSls phase, the symmetry is broken, as characterized by the appearance of new Bragg peaks on the nodes of the hexagonal lattice and indexed −h + k + l ≠ 3n and additional peaks at h = n + ½, in both (hk0) and (h0l) reciprocal planes. As explained above, the presence of these new diffraction peaks at these specific coordinates of the reciprocal space is a direct proof of the symmetry-breaking relationship between the R
= 60°, and the Bragg peaks present in the (hk0) or (h0l) reciprocal planes obey −h + k + l = 3n. In the LSls phase, the symmetry is broken, as characterized by the appearance of new Bragg peaks on the nodes of the hexagonal lattice and indexed −h + k + l ≠ 3n and additional peaks at h = n + ½, in both (hk0) and (h0l) reciprocal planes. As explained above, the presence of these new diffraction peaks at these specific coordinates of the reciprocal space is a direct proof of the symmetry-breaking relationship between the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) and the P
and the P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) crystalline structures of (1). These results show that the HShs R
crystalline structures of (1). These results show that the HShs R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) → LSls P
→ LSls P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) phase transition is associated with the loss of the 3-fold symmetry axis along
phase transition is associated with the loss of the 3-fold symmetry axis along  , which corresponds therefore to a symmetry-breaking ferroelastic distortion with a group–subgroup relationship.12 Noteworthy, the metastability of the trapped LShs state is characterized by its relaxation towards the LSls ground state. The associated structural reorganization is characterized by the changes in the X-ray diffraction signal due to the R
, which corresponds therefore to a symmetry-breaking ferroelastic distortion with a group–subgroup relationship.12 Noteworthy, the metastability of the trapped LShs state is characterized by its relaxation towards the LSls ground state. The associated structural reorganization is characterized by the changes in the X-ray diffraction signal due to the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) → P
→ P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ferroelastic distortion discussed above. Even after 17 h, we didn't observe any signature of relaxation of the LShs state thermally quenched at 80 K, which is consistent with previous measurements on the [Fe(ptz)6](BF4)2 complex at 90 K.4a
ferroelastic distortion discussed above. Even after 17 h, we didn't observe any signature of relaxation of the LShs state thermally quenched at 80 K, which is consistent with previous measurements on the [Fe(ptz)6](BF4)2 complex at 90 K.4a
 |
| | Fig. 2 Diffracted intensity on the nodes of the hexagonal high symmetry reciprocal lattice, for the HShs (a), LShs (b) and LSls (c) phases, in the (h0l) plane (top) and (hk0) plane (bottom). In the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) HShs and LShs phases, only Bragg peaks fulfilling −h + k + l = 3n rule are present. In the LSls phase, Bragg peaks appear at h = n + 1/2 and −h + k + l ≠ 3n. HShs and LShs phases, only Bragg peaks fulfilling −h + k + l = 3n rule are present. In the LSls phase, Bragg peaks appear at h = n + 1/2 and −h + k + l ≠ 3n. | |
Ferroelastic lattice distortions in the LSls phase.
The thermal evolutions of the lattice parameters of (1), given in the (pseudo) hexagonal cell, were monitored in the 80–250 K range in cooling and warming modes. Fig. 3 show the characteristic R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) → P
→ P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ferroelastic distortions. In the hexagonal cell of the HShs phase, aH = bH, α = β = 90° and γ = 120°. In the slow cooling mode, these relationships remain valid down to 136 K. At lower temperatures, we observe a splitting of the lattice parameters aH and bH, accompanied by a significant deviation of the lattice angles α and β from 90°. Fig. 2c also shows the distortions of the reciprocal lattice in the LSls phase at 80 K (β* ≠ 90°, γ* ≠ 60°). The data in the warming mode show that the R
ferroelastic distortions. In the hexagonal cell of the HShs phase, aH = bH, α = β = 90° and γ = 120°. In the slow cooling mode, these relationships remain valid down to 136 K. At lower temperatures, we observe a splitting of the lattice parameters aH and bH, accompanied by a significant deviation of the lattice angles α and β from 90°. Fig. 2c also shows the distortions of the reciprocal lattice in the LSls phase at 80 K (β* ≠ 90°, γ* ≠ 60°). The data in the warming mode show that the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) HShs state is restored above 144 K. These curves obtained by single-crystal X-ray diffraction reveal ≃8 K wide thermal hysteresis between the HShs phase and the LSls phase reached on slow cooling.
HShs state is restored above 144 K. These curves obtained by single-crystal X-ray diffraction reveal ≃8 K wide thermal hysteresis between the HShs phase and the LSls phase reached on slow cooling.
 |
| | Fig. 3 Thermal dependence of the (pseudo) hexagonal cell volume (a) and lattice parameters aH, bH, α and β (b) between the HShs and LSls phases. The parameters of the LShs phase are shown by the green dots. (c) In the LSls phase, the X-ray diffraction signal is the superposition of the Bragg peaks from the 3 different ferroelastic domains that are 120° apart upon the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) → P → P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) phase transition, which is also characterized by the peak splitting of Bragg peaks such as (0–5 11) shown in the inset. phase transition, which is also characterized by the peak splitting of Bragg peaks such as (0–5 11) shown in the inset. | |
The thermal dependence of the amplitude of the symmetry-breaking order parameter η(T) can be monitored through the evolution of ferroelastic R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) → P
→ P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) distortions, as shown in Fig. 4a through the evolution of the parameter δ defined as:
distortions, as shown in Fig. 4a through the evolution of the parameter δ defined as:
| |  | (7) |
and obtained through a linear fit of the data from
Fig. 3. The symmetry change is also characterised by the thermal dependence of the intensity of the symmetry-breaking (
hkl) Bragg peaks with −
h +
k +
l ≠ 3
n or
h =
n + ½ appearing in the LSls phase (
Fig. 4a). Both the ferroelastic lattice distortion (
δ) and the intensity of the symmetry-breaking Bragg peaks are direct signatures of the
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif)
→
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
ferroelastic phase transition. The curves exhibit thermal hysteresis, and the discontinuous symmetry-breaking corresponds to what is expected for the
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif)
→
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
ferroelastic phase transition.
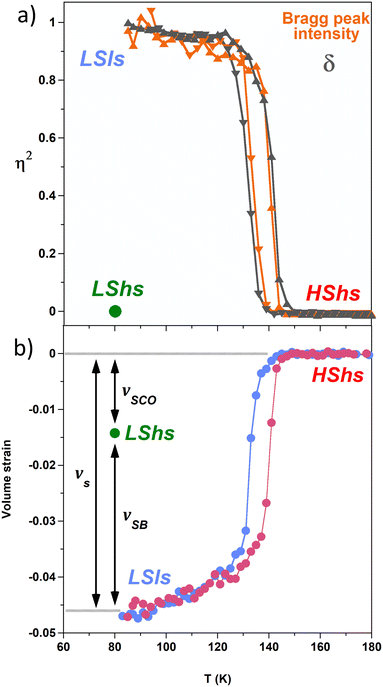 |
| | Fig. 4 (a) Thermal signatures of the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) → P → P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) symmetry breaking monitored through the parameter δ probing the ferroelastic lattice distortions and through the intensity of the symmetry-breaking Bragg peaks. (b) Corresponding volume strain in the LSls and LShs phases. symmetry breaking monitored through the parameter δ probing the ferroelastic lattice distortions and through the intensity of the symmetry-breaking Bragg peaks. (b) Corresponding volume strain in the LSls and LShs phases. | |
Indeed, the symmetry-breaking order parameter η belongs to the bi-dimensional Eg representation of the ![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) point group, which restricts the phase transition to first-order.3c,12d
point group, which restricts the phase transition to first-order.3c,12d
For the ferroelastic R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) → P
→ P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) symmetry breaking, three ferroelastic domains form, due to the loss of the 3-fold axis. This translates into X-ray diffraction data by the superposition of reciprocal lattices of the 3 domains (Fig. 3c), with three equivalent strain axes that are 120° apart. Crystals often break during the phase transition to release the elastic stress associated with the ferroelastic distortion and therefore we could not monitor the deviation of γ lattice angle from 120°.
symmetry breaking, three ferroelastic domains form, due to the loss of the 3-fold axis. This translates into X-ray diffraction data by the superposition of reciprocal lattices of the 3 domains (Fig. 3c), with three equivalent strain axes that are 120° apart. Crystals often break during the phase transition to release the elastic stress associated with the ferroelastic distortion and therefore we could not monitor the deviation of γ lattice angle from 120°.
Fig. 4b shows the large volume strain associated with the phase transition, defined as:
| |  | (8) |
where
VLT(
T) is the low-temperature phase volume at
T and
VHT(
T) the high-temperature one, extrapolated at
T.
vs(
T), normalized to the number of formula unit
Z per unit cell, also exhibits thermal hysteresis curves concomitant with the symmetry-breaking ones. These data confirm that SB and SCO phenomena coincide, which results from their coupling as theoretically explained for [Fe(ptz)
6](BF
4)
2.
2a,3b
Thermal quenching of the LShs phase.
Fig. 3 shows the lattice parameters of the LShs phase, obtained on fast cooling to 80 K, with a R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) lattice (aH = bH, α = β = 90° and γ = 120°). We notice a slight deviation from the thermal contraction of the lattice parameters extrapolated from the HShs phase. This partial volume strain (vSCO = −0.015(1)) is then only due to the SCO of the Fe centres of (1) and is characteristic of the HShs → LShs conversion.7d During the phase transitions, the SB is monitored with the order parameter η, while the SCO is monitored through
lattice (aH = bH, α = β = 90° and γ = 120°). We notice a slight deviation from the thermal contraction of the lattice parameters extrapolated from the HShs phase. This partial volume strain (vSCO = −0.015(1)) is then only due to the SCO of the Fe centres of (1) and is characteristic of the HShs → LShs conversion.7d During the phase transitions, the SB is monitored with the order parameter η, while the SCO is monitored through  (NHS and NLS denote the number of sites in high or low spin states). The Landau analysis3c has shown that both SCO and SB couple, and therefore contribute to vs:
(NHS and NLS denote the number of sites in high or low spin states). The Landau analysis3c has shown that both SCO and SB couple, and therefore contribute to vs:| |  | (9) |
For the [Fe(ptz)6](BF4)2 it was found that vs = −0.058(1), which includes both SCO and SB contributions.
Reorganisation of the molecular structures and packing.
The reversible conversion between the different phases accessible upon the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) → P
→ P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ferroelastic phase transition is accompanied by a significant number of structural rearrangements at the intra- and inter-molecular levels, involving both the cationic complexes and the tetrahedral BF4− counter-anions. The metallic centres of the complex, constituted by a mixture of iron(II) and ruthenium(II) ions in 0.65
ferroelastic phase transition is accompanied by a significant number of structural rearrangements at the intra- and inter-molecular levels, involving both the cationic complexes and the tetrahedral BF4− counter-anions. The metallic centres of the complex, constituted by a mixture of iron(II) and ruthenium(II) ions in 0.65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.35 percentage, are surrounded by six 1-propyl-1H-tetrazole ligands defining a slightly distorted octahedral [MIIN6] coordination environment around the metal M. Table 1 contains the average metal–nitrogen bond lengths and the deviation from the ideal octahedral geometry of the coordination sphere in the different phases, often used to characterise the spin state.13 The average 〈M–N〉 bond length contraction between the HShs phase and the two high and low symmetry LS phases are very similar (0.102 Å and 0.101 Å, respectively). They are in good agreement with a complete spin transition of all the SCO-active Fe sites and clearly show the possibility of decoupling the R
0.35 percentage, are surrounded by six 1-propyl-1H-tetrazole ligands defining a slightly distorted octahedral [MIIN6] coordination environment around the metal M. Table 1 contains the average metal–nitrogen bond lengths and the deviation from the ideal octahedral geometry of the coordination sphere in the different phases, often used to characterise the spin state.13 The average 〈M–N〉 bond length contraction between the HShs phase and the two high and low symmetry LS phases are very similar (0.102 Å and 0.101 Å, respectively). They are in good agreement with a complete spin transition of all the SCO-active Fe sites and clearly show the possibility of decoupling the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) → P
→ P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ferroelastic phase transition from the SCO. The experimental MII–N values reported for the [Ru0.35Fe0.65(ptz)6](BF4)2 in the HShs (2.128 Å) and the LSls phase (2.027 Å) are quite comparable to the expected values considering the values obtained for the pure Fe and Ru complexes:
ferroelastic phase transition from the SCO. The experimental MII–N values reported for the [Ru0.35Fe0.65(ptz)6](BF4)2 in the HShs (2.128 Å) and the LSls phase (2.027 Å) are quite comparable to the expected values considering the values obtained for the pure Fe and Ru complexes:
| d(MII–N)HShs = 〈FeII–N〉HShs × 0.65 + 〈RuII–N〉hs × 0.35 = 2.134 Å and d(MII–N)LSls = 〈FeII–N〉LSls × 0.65 + 〈RuII–N〉ls × 0.35 = 2.021 Å. |
In the same way, for [Fe(ptz)6](BF4)2,2a the volume strain due to the SCO between the HShs phase and the LShs phase, thermally quenched at 84 K is vSCO = −0.028(1), while the volume strain only due to the ferroelastic distortion between LShs phase and the LSls phase is vSB = −0.031(1).2a This is a nice illustration that the total volume strain vs associated with the HShs → LSls transition includes vSB and vSCO components as vs = −0.058 ≃ vSCO + vSB. In the case of [Ru0.35Fe0.65(ptz)6](BF4)2, we find vSCO = −0.015(1) and vSB = −0.032(1). vSB are similar for [Ru0.35Fe0.65(ptz)6](BF4)2 and [Fe(ptz)6](BF4)2 as both crystals exhibit similar ferroelastic distortion. However, vSCO in [Ru0.35Fe0.65(ptz)6](BF4)2 is 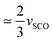 of [Fe(ptz)6](BF4)2, due to the chemical composition including only 2/3 of SCO-active Fe sites. Fig. 5a shows the molecular overlay of the cationic complex in the HShs, LShs, and LSls phases. Small changes are appreciable when the HShs and LShs phases are compared, which involve a subtle reorganisation of the core [MN6] due to the spin state change, as can be seen from the average angular (Σ) and trigonal (Θ) distortion13 in Table 1, and an order–disorder transition of the n-propyl groups.
of [Fe(ptz)6](BF4)2, due to the chemical composition including only 2/3 of SCO-active Fe sites. Fig. 5a shows the molecular overlay of the cationic complex in the HShs, LShs, and LSls phases. Small changes are appreciable when the HShs and LShs phases are compared, which involve a subtle reorganisation of the core [MN6] due to the spin state change, as can be seen from the average angular (Σ) and trigonal (Θ) distortion13 in Table 1, and an order–disorder transition of the n-propyl groups.
Table 1 Average MII–N bond lengths and distortion parameters Σ and Θ of the MIIN6 octahedra in the HShs, LShs and LSls phases, with  and
and  as defined in ref. 13
as defined in ref. 13
|
|
LSls (80 K) |
LShs (80 K) |
HShs (250 K) |
| 〈MII–N〉 (Å) |
2.027 |
2.026 |
2.128 |
|
Σ (°) |
10.3 |
6.9 |
4.1 |
|
Θ (°) |
15.0 |
7.9 |
4.7 |
 |
| | Fig. 5 a) Minimised overlay of the cationic complex in the HShs (pink), LShs (purple) and LSls (green) phases showing the conformational changes of n-propyl groups (C2A–C3A–C4A and C2B–C3B–C4B) in circled areas. Disorder of n-propyl group in the HShs phase is omitted for clarity. b) Symmetry-breaking associated with rearrangement of propyl groups, viewed along the c axis of the (pseudo) rhombohedral lattice. In the HShs and LShs states, the cations are located on ![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) symmetry with equivalent A–B–C–D–E–F n-propyl groups. The cations are related by 3-fold and inversion symmetry. In the LSls phase the 3-fold axis are lost and some symmetry with equivalent A–B–C–D–E–F n-propyl groups. The cations are related by 3-fold and inversion symmetry. In the LSls phase the 3-fold axis are lost and some ![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) symmetry elements are kept in the P symmetry elements are kept in the P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) lattice. lattice. | |
It is important to emphasise that in both phases the 6 n-propyl groups of different monodentate ligands are symmetry-equivalent, by the rotoinversion ![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) symmetry element located on the Fe, keeping therefore same gauche conformation. The dihedral angle changes from 59.76° in the HShs phase to 58.40° in the LShs phase. When the SB phase transition occurs, the n-propyl groups of the different ligands are no more equivalent due to the loss of the
symmetry element located on the Fe, keeping therefore same gauche conformation. The dihedral angle changes from 59.76° in the HShs phase to 58.40° in the LShs phase. When the SB phase transition occurs, the n-propyl groups of the different ligands are no more equivalent due to the loss of the ![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) symmetry. In the LSls phase, four crystallographically independent n-propyl groups retain the same conformational position, showing torsion angles that can vary between 55.97° and 58.60°, similar to those reported for the HShs and LShs phases.
symmetry. In the LSls phase, four crystallographically independent n-propyl groups retain the same conformational position, showing torsion angles that can vary between 55.97° and 58.60°, similar to those reported for the HShs and LShs phases.
A stronger rearrangement of the two-remaining n-propyl groups can be easily seen. From one side, the n-propyl group associated with the C2B–C3B–C4B fragment adopts a new gauche conformation after a rotation of 133.28° of the C4B carbon atom. On the other hand, a more significant change occurs in the fragment C2A–C3A–C4A, where an isomeric transition from gauche- to anti-conformation takes place. Fig. 5b shows the evolution of the supramolecular rearrangements with ![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) and
and ![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) symmetry elements in the HShs phase. In the LSls P
symmetry elements in the HShs phase. In the LSls P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) phase the
phase the ![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) symmetry is lost and some
symmetry is lost and some ![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) symmetry elements are kept in-between some cations complexes. These cation complexes interact with each other through numerous BF4− counter anions as shown in Fig. 6a. The number and strength of these intermolecular contacts depend on the spin state and the symmetry of (1) (Table 2). In the HShs phase, the counter-anions are located on 3-fold axis and display a static disorder between two specific positions (not shown). There are two different types of symmetry-equivalent intermolecular contacts below the Van der Waals radius. When the spin transition is induced without changing the symmetry, generating the LShs phase, the number of symmetry-equivalent intermolecular contacts significantly increases due to the lattice contraction, favouring the formation of a set of particularly very short N⋯F contacts [d(N4⋯F2) = 2.890 Å]. In addition, the static disorder of the BF4− anions disappears, locking the anionic moieties in one of the preferential positions displayed in the HShs phase. The LSls phase also shows a higher number of intermolecular contacts when compared with the HShs phase, but in less extension than the LShs phase does. The R
symmetry elements are kept in-between some cations complexes. These cation complexes interact with each other through numerous BF4− counter anions as shown in Fig. 6a. The number and strength of these intermolecular contacts depend on the spin state and the symmetry of (1) (Table 2). In the HShs phase, the counter-anions are located on 3-fold axis and display a static disorder between two specific positions (not shown). There are two different types of symmetry-equivalent intermolecular contacts below the Van der Waals radius. When the spin transition is induced without changing the symmetry, generating the LShs phase, the number of symmetry-equivalent intermolecular contacts significantly increases due to the lattice contraction, favouring the formation of a set of particularly very short N⋯F contacts [d(N4⋯F2) = 2.890 Å]. In addition, the static disorder of the BF4− anions disappears, locking the anionic moieties in one of the preferential positions displayed in the HShs phase. The LSls phase also shows a higher number of intermolecular contacts when compared with the HShs phase, but in less extension than the LShs phase does. The R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) → P
→ P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ferroelastic phase transition is accompanied by an essential displacement of the BF4− anions in the crystal lattice, significantly impacting the possible supramolecular contacts that can rise between the cationic complex and the counter-anions.
ferroelastic phase transition is accompanied by an essential displacement of the BF4− anions in the crystal lattice, significantly impacting the possible supramolecular contacts that can rise between the cationic complex and the counter-anions.
 |
| | Fig. 6 a) Intermolecular contacts between the cationic complex located on ![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) symmetry and BF4− counter-anions located on 3-fold symmetry axis in the HShs and LShs. In the LSls the inter-molecular contacts are no more symmetry-equivalent. b) Ferroelastic distortion upon the R symmetry and BF4− counter-anions located on 3-fold symmetry axis in the HShs and LShs. In the LSls the inter-molecular contacts are no more symmetry-equivalent. b) Ferroelastic distortion upon the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) → P → P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) transformation of the lattice viewed along the b axis of the pseudo-rhombohedral lattice, with a shear strain shown by the grey arrows. Hydrogen atoms and possible disorder of both n-propyl groups and BF4− counter-anions are omitted for clarity. transformation of the lattice viewed along the b axis of the pseudo-rhombohedral lattice, with a shear strain shown by the grey arrows. Hydrogen atoms and possible disorder of both n-propyl groups and BF4− counter-anions are omitted for clarity. | |
Table 2 Intermolecular contacts for the HShs, LShs and LSls phases
| Inter. contact |
HShs (250 K) |
Inter. contact |
LShs (80 K) |
Inter. contact |
LSls (80 K) |
| C1–F2 |
3.156 Å |
C1–F2 |
3.128 Å |
C1A–F7 |
3.108 Å |
| C3′–F1 |
3.028 Å |
C1–F2 |
3.170 Å |
C1B–F5 |
3.095 Å |
|
|
|
N4–F2 |
2.890 Å |
C1C–F1 |
3.169 Å |
|
|
|
|
|
C1D–F4 |
3.130 Å |
|
|
|
|
|
C1E–F6 |
3.164 Å |
|
|
|
|
|
C1F–F4 |
3.113 Å |
|
|
|
|
|
C1F–F2 |
3.125 Å |
|
|
|
|
|
C2A–F8 |
3.112 Å |
|
|
|
|
|
C2D–F3 |
3.116 Å |
|
|
|
|
|
N4D–F3 |
3.004 Å |
|
|
|
|
|
N4F–F4 |
2.997 Å |
Another characteristic of the symmetry breaking is shown in Fig. 6b. In the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phase, the BF4− tetrahedra are located on 3-fold Wyckoff positions, with one of the F atoms on the 3-fold axis and pointing up or down along the c axis. In the LSls phase, the 3-fold axis is lost, and the tetrahedra can point in any direction. The new disposition of the BF4− plus the special rearrangement of the n-propyl groups are some of the identity signatures of the ferroelastic phase transition. The molecular rearrangement is also associated with a shear strain, shown in Fig. 6b, with opposite motions of the cation layers in the (a, b) plane (grey arrows) responsible for the deviation of the lattice angles α and β from 90°.
phase, the BF4− tetrahedra are located on 3-fold Wyckoff positions, with one of the F atoms on the 3-fold axis and pointing up or down along the c axis. In the LSls phase, the 3-fold axis is lost, and the tetrahedra can point in any direction. The new disposition of the BF4− plus the special rearrangement of the n-propyl groups are some of the identity signatures of the ferroelastic phase transition. The molecular rearrangement is also associated with a shear strain, shown in Fig. 6b, with opposite motions of the cation layers in the (a, b) plane (grey arrows) responsible for the deviation of the lattice angles α and β from 90°.
The neutral layers of complexes are stacked along the c direction in the HShs and LShs phases through very weak intermolecular contacts between the n-propyl groups pointing to the interlayer space. The distance between the layers is 11.007 Å and 10.641 Å for the HShs and LShs phases, respectively. The same stacking can be detected in the LSls phase, showing an interlayer distance slightly smaller than that for the LShs phase (10.224 Å). In addition, the molecular packing clearly shows the shear strain with the deviation of the angle β from 90° in the P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) phase, as it is illustrated in the Fig. 6b.
phase, as it is illustrated in the Fig. 6b.
Origin of the metastable LShs phase.
All these experimental data provide key information on the change of spin state and crystalline structures between the HShs, LShs, and LSls phases. In SCO materials, structural trapping of HShs state at low temperatures was reported in many systems.1e,7d,14 The key feature related to such metastable HS state is the energy barrier between the HS and LS states and the thermally activated relaxation. However, this can't explain the occurrence of a metastable LShs phase observed in [Ru0.35Fe0.65(ptz)6](BF4)2 or in the pure [Fe(ptz)6](BF4)2 materials. To understand the metastable LShs state, we need to discuss in more details Collet's approach of the Landau theory of phase transition applied to SCO materials exhibiting symmetry breaking.2a,3b,c As explained in the case of [Fe(ptz)6](BF4)2, which exhibits similar SCO and SB, the simplest symmetry-adapted Landau potential to describe simultaneously SCO, measured through the order parameter q, and symmetry breaking η, takes the following form:| |  | (10) |
where the η2, η3, η4 terms describe the usual Landau SB potential for R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) → P
→ P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ferroelastic transition, with a = a0(T − TSB) and c > 0 for stability.12d The coefficient a changes sign at the symmetry-breaking temperature TSB, which stabilizes η = 0 above TSB and η ≠ 0 below. Similarly, the q, q2, q4 terms describe the SCO as A changes linearly with T.15 In this model, a key point is to consider the elastic contributions to the potential: the elastic energy
ferroelastic transition, with a = a0(T − TSB) and c > 0 for stability.12d The coefficient a changes sign at the symmetry-breaking temperature TSB, which stabilizes η = 0 above TSB and η ≠ 0 below. Similarly, the q, q2, q4 terms describe the SCO as A changes linearly with T.15 In this model, a key point is to consider the elastic contributions to the potential: the elastic energy  related to elastic constant Cs0, as well as the elastic coupling to vs of i) the ferroelastic distortion (ληvsη2) and ii) the SCO where
related to elastic constant Cs0, as well as the elastic coupling to vs of i) the ferroelastic distortion (ληvsη2) and ii) the SCO where  both taken as reference in HS state (q = 1). Collet et al. have shown that the equilibrium volume strain includes contributions from both SCO and SB2a,3b,c and scales as: vs = vSCO + vSB. Substituting in eqn (10)vs given in eqn (9) results in the renormalized thermodynamic potential:
both taken as reference in HS state (q = 1). Collet et al. have shown that the equilibrium volume strain includes contributions from both SCO and SB2a,3b,c and scales as: vs = vSCO + vSB. Substituting in eqn (10)vs given in eqn (9) results in the renormalized thermodynamic potential:| |  | (11) |
where the SB–SCO coupling term Dqη2 appears, with D > 0 which stabilizes HShs or LSls phases.
The 2D contour plots of G(q, η) in Fig. 7 show how the stability of the HShs (q = 1, η = 0) or LSls phase (q = −1, η ≠ 0) changes with temperature at equilibrium when both SB and SCO degrees of freedom. This is due to the considerable volume strain vS, including vSCO and vSB, which stabilises either the HShs or the LSls phase. Under pressure, [Fe(ptz)6](BF4)2 exhibits sequential SB and SCO with an intermediate HSls phase.4c,e Consequently, the volume strain also evolves sequentially with a first contraction (vSB) at high temperature during the SB phase transition and another one (vSCO) at a lower temperature due to SCO. vSCO and vSB have similar amplitudes and at ambient pressure vs ≃ vSCO + vSB.2a However, on changing temperature from HShs to LSls, the LShs phase does not form at intermediate temperature with this potential. To explain the appearance of the LShs metastable phase, let's consider for simplicity the symmetry-breaking part of the Landau-type expansion of the Gibbs energy describing the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) → P
→ P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ferroelastic phase transition:12b,c,16
ferroelastic phase transition:12b,c,16
| |  | (12) |
The renormalisation of the coefficient
a′ =
a + 2
ληvs includes the elastic coupling of the symmetry breaking to the volume strain (
vs < 0 and
λη > 0). Above
TSB in the HShs phase
a′(HShs) > 0 (since
a > 0 and
vs = 0). Therefore, the potential (11) along
η shows a high symmetry equilibrium phase (
η = 0) corresponding to the
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif)
lattice (red curve in
Fig. 7). The LSls phase (
a < 0)
vs includes SCO and SB components (
vSCO +
vSB =
vs < 0) and
a′(LSls) =
a + 2
ληvs < 0. The

term stabilises the low symmetry
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
lattice with a minimum for
η ≠ 0 (blue curve in
Fig. 7). On fast cooling, SCO occurs, due to rapid equilibration of the spin state degrees of freedom; while slower long-range lattice ordering and propagation of shear strains preclude the emergence of SB. The volume strains on fast cooling (
vFC) towards the LShs state are then reduced to the sole contribution of the SCO:
vFC ≃
vSCO. This situation, which is intermediate between the HShs and LSls cases, can generate a metastable LShs state as the elastic coupling gain of the symmetry-breaking is reduced to
vFC. The

term with reduced amplitude stabilises less the low symmetry
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
lattice (
η ≠ 0) and generates a metastable LShs state (
η = 0), as shown by the green potential curve in
Fig. 7. If the energy barrier is of the order of the thermal energy (
kBT), the system may thermally relax towards the stable LSls phase, which will be even more stabilised by an additional symmetry-breaking component of the volume strain.
 |
| | Fig. 7 2D contour map of the thermodynamic potential G(q, η) in eqn (11) along the spin state (q) and symmetry breaking (η) degrees of freedom. At high temperature (top) the HShs state corresponding to (q ≃ 1, η = 0) is stable. At low temperature (bottom) the LSls state (q ≃ −1, η ≠ 0) is stable. The central panel shows corresponding cuts along the symmetry-breaking axis for the HShs (red) and LSls (blue) phases. In the case of flash cooling, allowing SCO but not SB, the reduced volume strain can generate a metastable LShs state (q ≃ −1, η = 0). | |
Conclusion
The present study shows that for understanding thermal-equilibrium properties and the emergence of metastable phases in the [Ru0.35Fe0.65(ptz)6](BF4)2 material, derivate from the original [Fe(ptz)6](BF4)2 system, it is essential to consider SCO and SB phenomena and their coupling to the volume strain. The critical point is that both SCO and SB contribute to the volume strain, almost equally. At thermal equilibrium on slow cooling, the spin state and symmetry-breaking degrees of freedom have time to equilibrate, which induces a large volume strain that stabilises the low-spin low-symmetry phase. On flash cooling, the SCO occurs, but long-range symmetry breaking doesn't have time to set up. The reduced volume strain, limited to the contribution of the SCO, is responsible for the appearance of a metastable LShs phase. We are therefore convinced that such analysis can be expanded to other SCO compounds, and more generally to other classes of materials exhibiting a coupled change of electronic state and symmetry.
Author contributions
Francisco Javier Valverde-Muñoz: methodology, data curation, formal analysis, writing – original draft; Ricardo Guillermo Torres Ramírez: conceptualization, data curation; Abhilash Ulhe: data curation, formal analysis; Elzbieta Trzop: supervision, methodology, data curation, formal analysis, review & editing; Mousumi Dutta and Chinmoy Das: syntheses and growth of the single crystals [Ru0.35Fe0.65(ptz)6](BF4)2, and manuscript editing; Pradip Chakraborty: resources, review & editing; Eric Collet: funding acquisition, data curation, investigation, conceptualization, supervision, writing – original draft, review & editing. All authors critically reviewed and revised the manuscript draft and approved the final version for submission.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was supported in part by Agence Nationale de la Recherche for financial support under the grant ANR-19-CE30-0004 ELECTROPHONE, ANR-19-CE07-0027 SMAC. EC thanks the University Rennes and the Fondation Rennes 1 for funding. F. J. V.-M. acknowledges the support of the European Social Fund (ESF) and Generalitat Valenciana for his postdoctoral fellowship (APOSTD/2021/359). The authors thank Région Bretagne, Ille-Et-Vilaine Department, French Ministry of Research, Rennes Métropole, CNRS, European Union for financial support (CPER Project Mat&Trans 2021-2027). PC acknowledges financial support from SERB (Grant No. ECR/2018/000923) and Indian Institute of Technology Kharagpur (Grant no. IIT/SRIC/CY/ENE/2018-19/194). MD and CD acknowledge Indian Institute of Technology Kharagpur for research fellowship.
References
-
(a) H. Tokoro and S. Ohkoshi, Bull. Chem. Soc. Jpn., 2015, 88, 227 CrossRef;
(b) Y. S. Meng, O. Sato and T. Liu, Angew. Chem., Int. Ed., 2018, 57, 12216 CrossRef CAS PubMed;
(c) E. Pardo, C. Train, H. Liu, L.-M. Chamoreau, B. Dkhil, K. Boubekeur, F. Lloret, K. Nakatani, H. Tokoro, S. Ohkoshi and M. Verdaguer, Angew. Chem., 2012, 124, 8481 CrossRef;
(d) D. Aguila, Y. Prado, E. S. Koumousi, C. Mathoniere and R. Clerac, Chem. Soc. Rev., 2016, 45, 203 RSC;
(e)
M. A. Halcrow, Spin-crossover materials: properties and applications, John Wiley & Sons, Ltd, Chichester, 2013 CrossRef;
(f) P. Gutlich, A. Hauser and H. Spiering, Angew. Chem., Int. Ed. Engl., 1994, 33, 2024 CrossRef;
(g) A. Bousseksou, G. Molnar, L. Salmon and W. Nicolazzi, Chem. Soc. Rev., 2011, 40, 3313 RSC;
(h) G. Molnár, M. Mikolasek, K. Ridier, A. Fahs, W. Nicolazzi and A. Bousseksou, Ann. Phys., 2019, 531, 1900076 CrossRef;
(i) S. Koshihara, T. Ishikawa, Y. Okimoto, K. Onda, R. Fukaya, M. Hada, Y. Hayashi, S. Ishihara and T. Luty, Phys. Rep., 2022, 942, 1 CrossRef;
(j) T. Ishikawa, S. A. Hayes, S. Keskin, G. Corthey, M. Hada, K. Pichugin, A. Marx, J. Hirscht, K. Shionuma, K. Onda, Y. Okimoto, S.-Y. Koshihara, T. Yamamoto, H. Cui, M. Nomura, Y. Oshima, M. Abdel-Jawad, R. Kato and R. J. D. Miller, Science, 2015, 350, 1501 CrossRef CAS PubMed;
(k) M. Chollet, L. Guerin, N. Uchida, S. Fukaya, H. Shimoda, T. Ishikawa, K. Matsuda, T. Hasegawa, A. Ota, H. Yamochi, G. Saito, R. Tazaki, S.-I. Adachi and S.-Y. Koshihara, Science, 2005, 307, 86 CrossRef CAS PubMed;
(l) L. Guerin, E. Collet, M. H. Lemee-Cailleau, M. Buron-Le Cointe, H. Cailleau, A. Plech, M. Wulff, S. Y. Koshihara and T. Luty, Chem. Phys., 2004, 299, 163 CrossRef CAS.
-
(a) E. Collet, G. Azzolina, J. Jeftić and M.-H. Lemée-Cailleau, Adv. Phys.: X, 2023, 8, 2161936 Search PubMed;
(b) V. B. Jakobsen, E. Trzop, E. Dobbelaar, L. C. Gavin, S. Chikara, X. Ding, M. Lee, K. Esien, H. Müller-Bunz, S. Felton, E. Collet, M. A. Carpenter, V. S. Zapf and G. G. Morgan, J. Am. Chem. Soc., 2022, 144, 195 CrossRef CAS PubMed;
(c) A. Slimani and K. Boukheddaden, J. Appl. Phys., 2021, 129, 173901 CrossRef CAS;
(d) J. Cruddas and B. J. Powell, Inorg. Chem. Front., 2020, 7, 4424 RSC;
(e) G. Félix, M. Mikolasek, H. J. Shepherd, J. Long, J. Larionova, Y. Guari, J.-P. Itié, A. I. Chumakov, W. Nicolazzi, G. Molnár and A. Bousseksou, Eur. J. Inorg. Chem., 2018, 2018, 443 CrossRef;
(f) C. Enachescu and W. Nicolazzi, C. R. Chim., 2018, 21, 1179 CrossRef CAS;
(g) W. Nicolazzi and A. Bousseksou, C. R. Chim., 2018, 21, 1060 CrossRef CAS;
(h) H. Yamochi and S.-Y. Koshihara, Sci. Technol. Adv. Mater., 2009, 10, 024305 CrossRef PubMed.
-
(a) G. Azzolina, R. Bertoni and E. Collet, J. Appl. Phys., 2021, 129, 085106 CrossRef CAS;
(b) E. Collet and G. Azzolina, Phys. Rev. Mater., 2021, 5, 044401 CrossRef CAS;
(c) G. Azzolina, R. Bertoni, C. Ecolivet, H. Tokoro, S. Ohkoshi and E. Collet, Phys. Rev. B, 2020, 102, 134104 CrossRef CAS;
(d) M. Shatruk, H. Phan, B. A. Chrisostomo and A. Suleimenova, Coord. Chem. Rev., 2015, 289–290, 62 CrossRef CAS;
(e) D. Paliwoda, L. Vendier, W. Nicolazzi, G. Molnár and A. Bousseksou, Inorg. Chem., 2022, 15991 CrossRef CAS PubMed;
(f) R. Li, G. Levchenko, F. J. Valverde-Muñoz, A. B. Gaspar, V. V. Ivashko, Q. Li, B. Liu, M. Yuan, H. Fylymonov and J. A. Real, Inorg. Chem., 2021, 60, 16016 CrossRef CAS PubMed;
(g) V. B. Jakobsen, E. Trzop, L. C. Gavin, E. Dobbelaar, S. Chikara, X. Ding, K. Esien, H. Müller-Bunz, S. Felton, V. S. Zapf, E. Collet, M. A. Carpenter and G. G. Morgan, Angew. Chem., Int. Ed., 2020, 59, 13305 CrossRef CAS PubMed;
(h) V. B. Jakobsen, S. Chikara, J.-X. Yu, E. Dobbelaar, C. T. Kelly, X. Ding, F. Weickert, E. Trzop, E. Collet, H.-P. Cheng, G. G. Morgan and V. S. Zapf, Inorg. Chem., 2021, 6167 CrossRef CAS PubMed;
(i) M. Nihei, Y. Okamoto, Y. Sekine, N. Hoshino, T. Shiga, I. P.-C. Liu and H. Oshio, Angew. Chem., Int. Ed., 2012, 51, 6361 CrossRef CAS PubMed.
-
(a) J. Kusz, M. Zubko, R. B. Neder and P. Gutlich, Acta Crystallogr., Sect. B: Struct. Sci., 2012, 68, 40 CrossRef CAS PubMed;
(b) S. Lakhloufi, P. Guionneau, M. H. Lemée-Cailleau, P. Rosa and J. F. Létard, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 132104 CrossRef;
(c) M.-H. Lemée-Cailleau, C. Ecolivet, B. Ouladdiaf, F. Moussa and J.-F. Létard, Phys. B, 2009, 404, 379 CrossRef;
(d) A. Goujon, F. Varret, K. Boukheddaden, C. Chong, J. Jeftić, Y. Garcia, A. D. Naik, J. C. Ameline and E. Collet, Inorg. Chim. Acta, 2008, 361, 4055 CrossRef CAS;
(e) M. H. Lemée-Cailleau, C. Ecolivet, B. Ouladdiaf, F. Moussa, J. Jeftic and J. F. Létard, J. Magn. Magn. Mater., 2007, 310, 1792 CrossRef;
(f) J. Jeftić, H. Romstedt and A. Hauser, J. Phys. Chem. Solids, 1996, 57, 1743 CrossRef;
(g) A. Hauser, Chem. Phys. Lett., 1992, 192, 65 CrossRef CAS;
(h) L. Wiehl, H. Spiering, P. Gutlich and K. Knorr, J. Appl. Crystallogr., 1990, 23, 151 CrossRef CAS;
(i)
P. Gutlich and H. A. Goodwin, Spin Crossover in Transition Metal Compounds I, 2004, vol. 233, p. 1 Search PubMed.
-
(a) L. Wiehl, Acta Crystallogr., Sect. B: Struct. Sci., 1993, 49, 289 CrossRef;
(b) P. Gutlich, Y. Garcia and H. A. Goodwin, Chem. Soc. Rev., 2000, 29, 419 RSC;
(c) A. Marino, P. Chakraborty, M. Servol, M. Lorenc, E. Collet and A. Hauser, Angew. Chem., Int. Ed., 2014, 53, 3863 CrossRef CAS PubMed;
(d) A. Hauser, J. Chem. Phys., 1991, 94, 2741 CrossRef CAS;
(e) J. Jeftić and A. Hauser, J. Phys. Chem. B, 1997, 101, 10262 CrossRef.
- G. Privault, J.-Y. Mevellec, M. Lorenc, B. Humbert, E. Janod, N. Daro, G. Chastanet, A. Subedi and E. Collet, Cryst. Growth Des., 2022, 22, 5100 CrossRef CAS.
-
(a) A. Ozarowski and B. R. McGarvey, Inorg. Chem., 1989, 28, 2262 CrossRef CAS;
(b) J. Jung, F. Bruchhäuser, R. Feile, H. Spiering and P. Gütlich, Z. Phys. B: Condens. Matter, 1996, 100, 517 CrossRef CAS;
(c) J. Jung, G. Schmitt, L. Wiehl, A. Hauser, K. Knorr, H. Spiering and P. Gütlich, Z. Phys. B: Condens. Matter, 1996, 100, 523 CrossRef CAS;
(d) P. Chakraborty, M. Sy, H. Fourati, T. Delgado, M. Dutta, C. Das, C. Besnard, A. Hauser, C. Enachescu and K. Boukheddaden, Phys. Chem. Chem. Phys., 2022, 24, 982 RSC.
- G. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3 CrossRef PubMed.
- G. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3 Search PubMed.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339 CrossRef CAS.
-
H. T. Stokes and D. M. Hatch, Isotropy Subgroups of the 230 Crystallographic Space Groups, 1988 Search PubMed.
-
(a) E. K. H. Salje, Annu. Rev. Mater. Res., 2012, 42, 265 CrossRef CAS;
(b) M. A. Carpenter, E. K. H. Salje and A. Graeme-Barber, Eur. J. Mineral., 1998, 10, 621 CrossRef CAS;
(c) M. A. Carpenter and E. K. Salje, Eur. J. Mineral., 1998, 10, 693 CrossRef CAS;
(d)
E. K. Salje, Phase Transitions in Ferroelastic and Co-elastic Crystals, Cambridge University Press, Cambridge, 1991 CrossRef.
- E. Collet and P. Guionneau, C. R. Chim., 2018, 21, 1133 CrossRef CAS.
-
(a) G. Molnár, S. Rat, L. Salmon, W. Nicolazzi and A. Bousseksou, Adv. Mater., 2018, 30, 1703862 CrossRef PubMed;
(b) A. Hauser, Top. Curr. Chem., 2004, 234, 155 CrossRef CAS;
(c) M. Marchivie, P. Guionneau, J. F. Letard, D. Chasseau and J. A. K. Howard, J. Phys. Chem. Solids, 2004, 65, 17 CrossRef CAS.
- D. Chernyshov, H.-B. Bürgi, M. Hostettler and K. W. Törnroos, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 094116 CrossRef.
- E. K. Salje and M. A. Carpenter, J. Phys.: Condens. Matter, 2011, 23, 462202 CrossRef CAS PubMed.
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Ricardo Guillermo
Torres Ramírez
*a,
Ricardo Guillermo
Torres Ramírez
 a,
Abhilash
Ulhe
a,
Abhilash
Ulhe
 a,
Elzbieta
Trzop
a,
Elzbieta
Trzop
 ab,
Mousumi
Dutta
c,
Chinmoy
Das
c,
Pradip
Chakraborty
*c and
Eric
Collet
ab,
Mousumi
Dutta
c,
Chinmoy
Das
c,
Pradip
Chakraborty
*c and
Eric
Collet
 *abd
*abd
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) space group) and the low-spin low symmetry (LSls) phase (P
space group) and the low-spin low symmetry (LSls) phase (P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) space group). We present a structural analysis of the ferroelastic R
space group). We present a structural analysis of the ferroelastic R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) → P
→ P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) phase transition and highlight the structural SB signatures. We also study the metastable low-spin high symmetry (LShs) phase (R
phase transition and highlight the structural SB signatures. We also study the metastable low-spin high symmetry (LShs) phase (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) space group) reached upon fast cooling. In the framework of the Landau theory of phase transition adapted by Collet, and considering the elastic coupling between SCO and SB, we discuss the structural distortion between the HShs, LShs, and LSls phases and explain the metastable nature of the LShs phase.
space group) reached upon fast cooling. In the framework of the Landau theory of phase transition adapted by Collet, and considering the elastic coupling between SCO and SB, we discuss the structural distortion between the HShs, LShs, and LSls phases and explain the metastable nature of the LShs phase.![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) space group, while the low-temperature LS phase is low symmetry (LSls) with a triclinic P
space group, while the low-temperature LS phase is low symmetry (LSls) with a triclinic P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) space group.4a,d,g,h,5 There are different contributions to the entropy increase between the LSls and HShs phases. On the one hand, the non-symmetry-breaking SCO includes an electronic entropy change due to the change in spin multiplicity and a vibrational entropy due to the global decrease of the frequency of the modes between LS and HS states.1h,2g,6 On the other hand, there is also a SB contribution due to the order–disorder configurational change and splitting of mode frequencies, and therefore, SCO and SB can occur simultaneously or sequentially depending upon the external parameters.2a,3b Indeed, under pressure, the [Fe(ptz)6](BF4)2 system exhibits sequential conversions on cooling with SB from the HShs phase towards a high-spin low symmetry (HSls) P
space group.4a,d,g,h,5 There are different contributions to the entropy increase between the LSls and HShs phases. On the one hand, the non-symmetry-breaking SCO includes an electronic entropy change due to the change in spin multiplicity and a vibrational entropy due to the global decrease of the frequency of the modes between LS and HS states.1h,2g,6 On the other hand, there is also a SB contribution due to the order–disorder configurational change and splitting of mode frequencies, and therefore, SCO and SB can occur simultaneously or sequentially depending upon the external parameters.2a,3b Indeed, under pressure, the [Fe(ptz)6](BF4)2 system exhibits sequential conversions on cooling with SB from the HShs phase towards a high-spin low symmetry (HSls) P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) phase, followed SCO towards the low-spin low symmetry (LSls) P
phase, followed SCO towards the low-spin low symmetry (LSls) P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) phase.4c,e In addition, upon fast cooling, a metastable low-spin high-symmetry (LShs) R
phase.4c,e In addition, upon fast cooling, a metastable low-spin high-symmetry (LShs) R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phase appears.7
phase appears.7
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) → P
→ P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) crystallographic phase transition upon cooling, stabilises the Fe(II) low-spin state.7d In the [Ru0.35Fe0.65(ptz)6](BF4)2 system (1) studied here, the half conversion temperature was found to be of the order of 135 K, i.e., ≃8 K above the one of the neat [Fe(ptz)6](BF4)2 compound. This results from the fact that the Ru(II) host, with lattice dimensions similar to the lattice of the pure LS Fe(II) compound, induces a chemical pressure favouring LS Fe(II) complex of lower volume, shifting SCO towards higher temperatures compared to pure [Fe(ptz)6](BF4)2. In the previous structural characterisation of (1) performed by single-crystal X-ray diffraction, three different phases were identified.7d Above 150 K, the HShs phase is exclusively dominant, displaying the R
crystallographic phase transition upon cooling, stabilises the Fe(II) low-spin state.7d In the [Ru0.35Fe0.65(ptz)6](BF4)2 system (1) studied here, the half conversion temperature was found to be of the order of 135 K, i.e., ≃8 K above the one of the neat [Fe(ptz)6](BF4)2 compound. This results from the fact that the Ru(II) host, with lattice dimensions similar to the lattice of the pure LS Fe(II) compound, induces a chemical pressure favouring LS Fe(II) complex of lower volume, shifting SCO towards higher temperatures compared to pure [Fe(ptz)6](BF4)2. In the previous structural characterisation of (1) performed by single-crystal X-ray diffraction, three different phases were identified.7d Above 150 K, the HShs phase is exclusively dominant, displaying the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) space group. At 150 K, the lattice parameters of the hexagonal lattice are: aH = bH = 10.83 Å, cH = 32.03 Å. Below ≃130 K two possible low-spin phases can be generated, depending on the cooling rate of crystals. On the one hand, a slow cooling (≃0.2 K min−1) induces a LSls phase, which has a triclinic lattice (P
space group. At 150 K, the lattice parameters of the hexagonal lattice are: aH = bH = 10.83 Å, cH = 32.03 Å. Below ≃130 K two possible low-spin phases can be generated, depending on the cooling rate of crystals. On the one hand, a slow cooling (≃0.2 K min−1) induces a LSls phase, which has a triclinic lattice (P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) space group) with aP = 12.33 Å, bP = 10.77 Å, cP = 16.37 Å, α = 90.20°, β = 100.54° and γ = 90.20°. On the other hand, fast quenching at 80 K from the HShs phase induces low-temperature LShs phase, which retains the R
space group) with aP = 12.33 Å, bP = 10.77 Å, cP = 16.37 Å, α = 90.20°, β = 100.54° and γ = 90.20°. On the other hand, fast quenching at 80 K from the HShs phase induces low-temperature LShs phase, which retains the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) space group, with lattice parameters aH = bH = 10.73 Å, cH = 32.01 Å. Therefore, SB and SCO may decouple in the [Ru0.35Fe0.65(ptz)6](BF4)2 solid solution.
space group, with lattice parameters aH = bH = 10.73 Å, cH = 32.01 Å. Therefore, SB and SCO may decouple in the [Ru0.35Fe0.65(ptz)6](BF4)2 solid solution.![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) → P
→ P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) symmetry-breaking phase transition, with a group-subgroup relationship, and not to a reconstructive phase transition. In such a case, the Landau theory approach is relevant to describe the observed phenomena. We also study the metastable low-spin high symmetry (LShs) phase (R
symmetry-breaking phase transition, with a group-subgroup relationship, and not to a reconstructive phase transition. In such a case, the Landau theory approach is relevant to describe the observed phenomena. We also study the metastable low-spin high symmetry (LShs) phase (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) space group) reached upon fast cooling. Within the Landau theory framework of phase transition adapted by Collet, we explain that the metastable nature of the LShs phase is due to the partial volume strain, containing only the contribution of the SCO and not the SB one.
space group) reached upon fast cooling. Within the Landau theory framework of phase transition adapted by Collet, we explain that the metastable nature of the LShs phase is due to the partial volume strain, containing only the contribution of the SCO and not the SB one.![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) rhombohedral lattice and the different unit cells that can be used to describe lattice periodicity: the primitive rhombohedral cell, the hexagonal cell, and the triclinic primitive cell. Any lattice translation vector
rhombohedral lattice and the different unit cells that can be used to describe lattice periodicity: the primitive rhombohedral cell, the hexagonal cell, and the triclinic primitive cell. Any lattice translation vector ![[T with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/b_i_char_0054_20d1.gif) , connecting nodes of the high-temperature lattices can be given in the primitive triclinic P
, connecting nodes of the high-temperature lattices can be given in the primitive triclinic P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) or hexagonal R
or hexagonal R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) lattices:
lattices:

![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/b_i_char_0051_20d1.gif) of the reciprocal space can be expressed both in the P
of the reciprocal space can be expressed both in the P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) triclinic reciprocal cell or in the R
triclinic reciprocal cell or in the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) hexagonal reciprocal one:
hexagonal reciprocal one:

![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) rhombohedral lattice (green), showing the relationship with the hexagonal (H subscript purple) and primitive triclinic (P subscript orange) unit cells.
rhombohedral lattice (green), showing the relationship with the hexagonal (H subscript purple) and primitive triclinic (P subscript orange) unit cells.
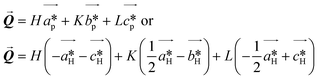
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) and P
and P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) reciprocal lattices:
reciprocal lattices:
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) hexagonal lattice cell, only (hkl) peaks with −h + k + l = 3n are present, while (HKL) Bragg peaks are allowed for any H, K, L integers in the primitive triclinic cell. Therefore, in the case of a group-subgroup SB phase transition due to a distortion from hexagonal to triclinic lattices, with a pseudo hexagonal reciprocal lattice, the R
hexagonal lattice cell, only (hkl) peaks with −h + k + l = 3n are present, while (HKL) Bragg peaks are allowed for any H, K, L integers in the primitive triclinic cell. Therefore, in the case of a group-subgroup SB phase transition due to a distortion from hexagonal to triclinic lattices, with a pseudo hexagonal reciprocal lattice, the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) → P
→ P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) symmetry breaking is characterized by the appearance of Bragg peaks with −h + k + l ≠ 3n and also with h = n + ½.
symmetry breaking is characterized by the appearance of Bragg peaks with −h + k + l ≠ 3n and also with h = n + ½.
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) space group with
space group with 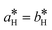 and
and 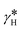 = 60°, and the Bragg peaks present in the (hk0) or (h0l) reciprocal planes obey −h + k + l = 3n. In the LSls phase, the symmetry is broken, as characterized by the appearance of new Bragg peaks on the nodes of the hexagonal lattice and indexed −h + k + l ≠ 3n and additional peaks at h = n + ½, in both (hk0) and (h0l) reciprocal planes. As explained above, the presence of these new diffraction peaks at these specific coordinates of the reciprocal space is a direct proof of the symmetry-breaking relationship between the R
= 60°, and the Bragg peaks present in the (hk0) or (h0l) reciprocal planes obey −h + k + l = 3n. In the LSls phase, the symmetry is broken, as characterized by the appearance of new Bragg peaks on the nodes of the hexagonal lattice and indexed −h + k + l ≠ 3n and additional peaks at h = n + ½, in both (hk0) and (h0l) reciprocal planes. As explained above, the presence of these new diffraction peaks at these specific coordinates of the reciprocal space is a direct proof of the symmetry-breaking relationship between the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) and the P
and the P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) crystalline structures of (1). These results show that the HShs R
crystalline structures of (1). These results show that the HShs R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) → LSls P
→ LSls P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) phase transition is associated with the loss of the 3-fold symmetry axis along
phase transition is associated with the loss of the 3-fold symmetry axis along  , which corresponds therefore to a symmetry-breaking ferroelastic distortion with a group–subgroup relationship.12 Noteworthy, the metastability of the trapped LShs state is characterized by its relaxation towards the LSls ground state. The associated structural reorganization is characterized by the changes in the X-ray diffraction signal due to the R
, which corresponds therefore to a symmetry-breaking ferroelastic distortion with a group–subgroup relationship.12 Noteworthy, the metastability of the trapped LShs state is characterized by its relaxation towards the LSls ground state. The associated structural reorganization is characterized by the changes in the X-ray diffraction signal due to the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) → P
→ P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ferroelastic distortion discussed above. Even after 17 h, we didn't observe any signature of relaxation of the LShs state thermally quenched at 80 K, which is consistent with previous measurements on the [Fe(ptz)6](BF4)2 complex at 90 K.4a
ferroelastic distortion discussed above. Even after 17 h, we didn't observe any signature of relaxation of the LShs state thermally quenched at 80 K, which is consistent with previous measurements on the [Fe(ptz)6](BF4)2 complex at 90 K.4a![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) → P
→ P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ferroelastic distortions. In the hexagonal cell of the HShs phase, aH = bH, α = β = 90° and γ = 120°. In the slow cooling mode, these relationships remain valid down to 136 K. At lower temperatures, we observe a splitting of the lattice parameters aH and bH, accompanied by a significant deviation of the lattice angles α and β from 90°. Fig. 2c also shows the distortions of the reciprocal lattice in the LSls phase at 80 K (β* ≠ 90°, γ* ≠ 60°). The data in the warming mode show that the R
ferroelastic distortions. In the hexagonal cell of the HShs phase, aH = bH, α = β = 90° and γ = 120°. In the slow cooling mode, these relationships remain valid down to 136 K. At lower temperatures, we observe a splitting of the lattice parameters aH and bH, accompanied by a significant deviation of the lattice angles α and β from 90°. Fig. 2c also shows the distortions of the reciprocal lattice in the LSls phase at 80 K (β* ≠ 90°, γ* ≠ 60°). The data in the warming mode show that the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) HShs state is restored above 144 K. These curves obtained by single-crystal X-ray diffraction reveal ≃8 K wide thermal hysteresis between the HShs phase and the LSls phase reached on slow cooling.
HShs state is restored above 144 K. These curves obtained by single-crystal X-ray diffraction reveal ≃8 K wide thermal hysteresis between the HShs phase and the LSls phase reached on slow cooling.
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) → P
→ P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) distortions, as shown in Fig. 4a through the evolution of the parameter δ defined as:
distortions, as shown in Fig. 4a through the evolution of the parameter δ defined as:
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) → P
→ P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ferroelastic phase transition. The curves exhibit thermal hysteresis, and the discontinuous symmetry-breaking corresponds to what is expected for the R
ferroelastic phase transition. The curves exhibit thermal hysteresis, and the discontinuous symmetry-breaking corresponds to what is expected for the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) → P
→ P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ferroelastic phase transition.
ferroelastic phase transition.
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) point group, which restricts the phase transition to first-order.3c,12d
point group, which restricts the phase transition to first-order.3c,12d![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) → P
→ P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) symmetry breaking, three ferroelastic domains form, due to the loss of the 3-fold axis. This translates into X-ray diffraction data by the superposition of reciprocal lattices of the 3 domains (Fig. 3c), with three equivalent strain axes that are 120° apart. Crystals often break during the phase transition to release the elastic stress associated with the ferroelastic distortion and therefore we could not monitor the deviation of γ lattice angle from 120°.
symmetry breaking, three ferroelastic domains form, due to the loss of the 3-fold axis. This translates into X-ray diffraction data by the superposition of reciprocal lattices of the 3 domains (Fig. 3c), with three equivalent strain axes that are 120° apart. Crystals often break during the phase transition to release the elastic stress associated with the ferroelastic distortion and therefore we could not monitor the deviation of γ lattice angle from 120°.
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) lattice (aH = bH, α = β = 90° and γ = 120°). We notice a slight deviation from the thermal contraction of the lattice parameters extrapolated from the HShs phase. This partial volume strain (vSCO = −0.015(1)) is then only due to the SCO of the Fe centres of (1) and is characteristic of the HShs → LShs conversion.7d During the phase transitions, the SB is monitored with the order parameter η, while the SCO is monitored through
lattice (aH = bH, α = β = 90° and γ = 120°). We notice a slight deviation from the thermal contraction of the lattice parameters extrapolated from the HShs phase. This partial volume strain (vSCO = −0.015(1)) is then only due to the SCO of the Fe centres of (1) and is characteristic of the HShs → LShs conversion.7d During the phase transitions, the SB is monitored with the order parameter η, while the SCO is monitored through  (NHS and NLS denote the number of sites in high or low spin states). The Landau analysis3c has shown that both SCO and SB couple, and therefore contribute to vs:
(NHS and NLS denote the number of sites in high or low spin states). The Landau analysis3c has shown that both SCO and SB couple, and therefore contribute to vs:
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) → P
→ P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ferroelastic phase transition is accompanied by a significant number of structural rearrangements at the intra- and inter-molecular levels, involving both the cationic complexes and the tetrahedral BF4− counter-anions. The metallic centres of the complex, constituted by a mixture of iron(II) and ruthenium(II) ions in 0.65
ferroelastic phase transition is accompanied by a significant number of structural rearrangements at the intra- and inter-molecular levels, involving both the cationic complexes and the tetrahedral BF4− counter-anions. The metallic centres of the complex, constituted by a mixture of iron(II) and ruthenium(II) ions in 0.65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.35 percentage, are surrounded by six 1-propyl-1H-tetrazole ligands defining a slightly distorted octahedral [MIIN6] coordination environment around the metal M. Table 1 contains the average metal–nitrogen bond lengths and the deviation from the ideal octahedral geometry of the coordination sphere in the different phases, often used to characterise the spin state.13 The average 〈M–N〉 bond length contraction between the HShs phase and the two high and low symmetry LS phases are very similar (0.102 Å and 0.101 Å, respectively). They are in good agreement with a complete spin transition of all the SCO-active Fe sites and clearly show the possibility of decoupling the R
0.35 percentage, are surrounded by six 1-propyl-1H-tetrazole ligands defining a slightly distorted octahedral [MIIN6] coordination environment around the metal M. Table 1 contains the average metal–nitrogen bond lengths and the deviation from the ideal octahedral geometry of the coordination sphere in the different phases, often used to characterise the spin state.13 The average 〈M–N〉 bond length contraction between the HShs phase and the two high and low symmetry LS phases are very similar (0.102 Å and 0.101 Å, respectively). They are in good agreement with a complete spin transition of all the SCO-active Fe sites and clearly show the possibility of decoupling the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) → P
→ P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ferroelastic phase transition from the SCO. The experimental MII–N values reported for the [Ru0.35Fe0.65(ptz)6](BF4)2 in the HShs (2.128 Å) and the LSls phase (2.027 Å) are quite comparable to the expected values considering the values obtained for the pure Fe and Ru complexes:
ferroelastic phase transition from the SCO. The experimental MII–N values reported for the [Ru0.35Fe0.65(ptz)6](BF4)2 in the HShs (2.128 Å) and the LSls phase (2.027 Å) are quite comparable to the expected values considering the values obtained for the pure Fe and Ru complexes: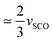 of [Fe(ptz)6](BF4)2, due to the chemical composition including only 2/3 of SCO-active Fe sites. Fig. 5a shows the molecular overlay of the cationic complex in the HShs, LShs, and LSls phases. Small changes are appreciable when the HShs and LShs phases are compared, which involve a subtle reorganisation of the core [MN6] due to the spin state change, as can be seen from the average angular (Σ) and trigonal (Θ) distortion13 in Table 1, and an order–disorder transition of the n-propyl groups.
of [Fe(ptz)6](BF4)2, due to the chemical composition including only 2/3 of SCO-active Fe sites. Fig. 5a shows the molecular overlay of the cationic complex in the HShs, LShs, and LSls phases. Small changes are appreciable when the HShs and LShs phases are compared, which involve a subtle reorganisation of the core [MN6] due to the spin state change, as can be seen from the average angular (Σ) and trigonal (Θ) distortion13 in Table 1, and an order–disorder transition of the n-propyl groups. and
and  as defined in ref. 13
as defined in ref. 13
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) symmetry element located on the Fe, keeping therefore same gauche conformation. The dihedral angle changes from 59.76° in the HShs phase to 58.40° in the LShs phase. When the SB phase transition occurs, the n-propyl groups of the different ligands are no more equivalent due to the loss of the
symmetry element located on the Fe, keeping therefore same gauche conformation. The dihedral angle changes from 59.76° in the HShs phase to 58.40° in the LShs phase. When the SB phase transition occurs, the n-propyl groups of the different ligands are no more equivalent due to the loss of the ![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) symmetry. In the LSls phase, four crystallographically independent n-propyl groups retain the same conformational position, showing torsion angles that can vary between 55.97° and 58.60°, similar to those reported for the HShs and LShs phases.
symmetry. In the LSls phase, four crystallographically independent n-propyl groups retain the same conformational position, showing torsion angles that can vary between 55.97° and 58.60°, similar to those reported for the HShs and LShs phases.![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) and
and ![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) symmetry elements in the HShs phase. In the LSls P
symmetry elements in the HShs phase. In the LSls P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) phase the
phase the ![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) symmetry is lost and some
symmetry is lost and some ![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) symmetry elements are kept in-between some cations complexes. These cation complexes interact with each other through numerous BF4− counter anions as shown in Fig. 6a. The number and strength of these intermolecular contacts depend on the spin state and the symmetry of (1) (Table 2). In the HShs phase, the counter-anions are located on 3-fold axis and display a static disorder between two specific positions (not shown). There are two different types of symmetry-equivalent intermolecular contacts below the Van der Waals radius. When the spin transition is induced without changing the symmetry, generating the LShs phase, the number of symmetry-equivalent intermolecular contacts significantly increases due to the lattice contraction, favouring the formation of a set of particularly very short N⋯F contacts [d(N4⋯F2) = 2.890 Å]. In addition, the static disorder of the BF4− anions disappears, locking the anionic moieties in one of the preferential positions displayed in the HShs phase. The LSls phase also shows a higher number of intermolecular contacts when compared with the HShs phase, but in less extension than the LShs phase does. The R
symmetry elements are kept in-between some cations complexes. These cation complexes interact with each other through numerous BF4− counter anions as shown in Fig. 6a. The number and strength of these intermolecular contacts depend on the spin state and the symmetry of (1) (Table 2). In the HShs phase, the counter-anions are located on 3-fold axis and display a static disorder between two specific positions (not shown). There are two different types of symmetry-equivalent intermolecular contacts below the Van der Waals radius. When the spin transition is induced without changing the symmetry, generating the LShs phase, the number of symmetry-equivalent intermolecular contacts significantly increases due to the lattice contraction, favouring the formation of a set of particularly very short N⋯F contacts [d(N4⋯F2) = 2.890 Å]. In addition, the static disorder of the BF4− anions disappears, locking the anionic moieties in one of the preferential positions displayed in the HShs phase. The LSls phase also shows a higher number of intermolecular contacts when compared with the HShs phase, but in less extension than the LShs phase does. The R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) → P
→ P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ferroelastic phase transition is accompanied by an essential displacement of the BF4− anions in the crystal lattice, significantly impacting the possible supramolecular contacts that can rise between the cationic complex and the counter-anions.
ferroelastic phase transition is accompanied by an essential displacement of the BF4− anions in the crystal lattice, significantly impacting the possible supramolecular contacts that can rise between the cationic complex and the counter-anions.![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phase, the BF4− tetrahedra are located on 3-fold Wyckoff positions, with one of the F atoms on the 3-fold axis and pointing up or down along the c axis. In the LSls phase, the 3-fold axis is lost, and the tetrahedra can point in any direction. The new disposition of the BF4− plus the special rearrangement of the n-propyl groups are some of the identity signatures of the ferroelastic phase transition. The molecular rearrangement is also associated with a shear strain, shown in Fig. 6b, with opposite motions of the cation layers in the (a, b) plane (grey arrows) responsible for the deviation of the lattice angles α and β from 90°.
phase, the BF4− tetrahedra are located on 3-fold Wyckoff positions, with one of the F atoms on the 3-fold axis and pointing up or down along the c axis. In the LSls phase, the 3-fold axis is lost, and the tetrahedra can point in any direction. The new disposition of the BF4− plus the special rearrangement of the n-propyl groups are some of the identity signatures of the ferroelastic phase transition. The molecular rearrangement is also associated with a shear strain, shown in Fig. 6b, with opposite motions of the cation layers in the (a, b) plane (grey arrows) responsible for the deviation of the lattice angles α and β from 90°.![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) phase, as it is illustrated in the Fig. 6b.
phase, as it is illustrated in the Fig. 6b.
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) → P
→ P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ferroelastic transition, with a = a0(T − TSB) and c > 0 for stability.12d The coefficient a changes sign at the symmetry-breaking temperature TSB, which stabilizes η = 0 above TSB and η ≠ 0 below. Similarly, the q, q2, q4 terms describe the SCO as A changes linearly with T.15 In this model, a key point is to consider the elastic contributions to the potential: the elastic energy
ferroelastic transition, with a = a0(T − TSB) and c > 0 for stability.12d The coefficient a changes sign at the symmetry-breaking temperature TSB, which stabilizes η = 0 above TSB and η ≠ 0 below. Similarly, the q, q2, q4 terms describe the SCO as A changes linearly with T.15 In this model, a key point is to consider the elastic contributions to the potential: the elastic energy  related to elastic constant Cs0, as well as the elastic coupling to vs of i) the ferroelastic distortion (ληvsη2) and ii) the SCO where
related to elastic constant Cs0, as well as the elastic coupling to vs of i) the ferroelastic distortion (ληvsη2) and ii) the SCO where  both taken as reference in HS state (q = 1). Collet et al. have shown that the equilibrium volume strain includes contributions from both SCO and SB2a,3b,c and scales as: vs = vSCO + vSB. Substituting in eqn (10)vs given in eqn (9) results in the renormalized thermodynamic potential:
both taken as reference in HS state (q = 1). Collet et al. have shown that the equilibrium volume strain includes contributions from both SCO and SB2a,3b,c and scales as: vs = vSCO + vSB. Substituting in eqn (10)vs given in eqn (9) results in the renormalized thermodynamic potential:
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) → P
→ P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ferroelastic phase transition:12b,c,16
ferroelastic phase transition:12b,c,16
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) lattice (red curve in Fig. 7). The LSls phase (a < 0) vs includes SCO and SB components (vSCO + vSB = vs < 0) and a′(LSls) = a + 2ληvs < 0. The
lattice (red curve in Fig. 7). The LSls phase (a < 0) vs includes SCO and SB components (vSCO + vSB = vs < 0) and a′(LSls) = a + 2ληvs < 0. The  term stabilises the low symmetry P
term stabilises the low symmetry P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) lattice with a minimum for η ≠ 0 (blue curve in Fig. 7). On fast cooling, SCO occurs, due to rapid equilibration of the spin state degrees of freedom; while slower long-range lattice ordering and propagation of shear strains preclude the emergence of SB. The volume strains on fast cooling (vFC) towards the LShs state are then reduced to the sole contribution of the SCO: vFC ≃ vSCO. This situation, which is intermediate between the HShs and LSls cases, can generate a metastable LShs state as the elastic coupling gain of the symmetry-breaking is reduced to vFC. The
lattice with a minimum for η ≠ 0 (blue curve in Fig. 7). On fast cooling, SCO occurs, due to rapid equilibration of the spin state degrees of freedom; while slower long-range lattice ordering and propagation of shear strains preclude the emergence of SB. The volume strains on fast cooling (vFC) towards the LShs state are then reduced to the sole contribution of the SCO: vFC ≃ vSCO. This situation, which is intermediate between the HShs and LSls cases, can generate a metastable LShs state as the elastic coupling gain of the symmetry-breaking is reduced to vFC. The  term with reduced amplitude stabilises less the low symmetry P
term with reduced amplitude stabilises less the low symmetry P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) lattice (η ≠ 0) and generates a metastable LShs state (η = 0), as shown by the green potential curve in Fig. 7. If the energy barrier is of the order of the thermal energy (kBT), the system may thermally relax towards the stable LSls phase, which will be even more stabilised by an additional symmetry-breaking component of the volume strain.
lattice (η ≠ 0) and generates a metastable LShs state (η = 0), as shown by the green potential curve in Fig. 7. If the energy barrier is of the order of the thermal energy (kBT), the system may thermally relax towards the stable LSls phase, which will be even more stabilised by an additional symmetry-breaking component of the volume strain.






