Mesoscale clusters in multicomponent systems: the effect of solution preparation and pre-treatment on primary nucleation of a carbamazepine-saccharin cocrystal

Abstract

In this work, direct investigation of mesoscale clusters in solution using dynamic light scattering is combined with an indirect method based on the study of primary crystal nucleation and its dependence on the conditions of solution preparation and pre-treatment. In a novel approach we have studied how the nucleation induction time of a pharmaceutical cocrystal, a 1 : 1 saccharin–carbamazepine cocrystal, depends on different preparation and pre-treatment conditions, in particular whether solutions are prepared by dissolving the cocrystal solids or the two coformers separately. Nucleation is clearly affected by some pre-treatment conditions, with longer induction times obtained for a high pre-treatment temperature and when solutions are microfiltered after dissolution. The strongest effect was observed when comparing different starting materials, with solutions prepared using cocrystals leading to much shorter induction times than solutions based on the separate coformers. DLS shows that both types of solutions contain mesoscale clusters of the order of 100–300 nm in size, but that there are clear differences in the amount of scattering indicating a higher cluster concentration in the solutions based on cocrystal solids. The results suggest the possibility that mesoscale clusters can have a structural dimension, associated with slow kinetics, which can directly affect nucleation.

---

Introduction

Primary crystal nucleation is the formation of a new solid, long-range ordered phase from a less ordered phase, driven by thermodynamics. It directly affects properties of the product crystals such as structure, size and shape. Despite a long history of extensive research into the phenomenon, the present understanding of the exact mechanisms involved in the phenomenon is limited. Investigating the mechanisms involved in nucleation is a challenging task. Experimentally, direct investigation of nucleation has until recently been limited by the molecular-level scale of the phenomena. Recent advances in detection techniques based on scattering of light, e.g. small- and wide-angle X-ray or neutron scattering (SAXS/SANS/WAXS), dynamic light scattering (DLS), and Brownian microscopy/nanoparticle tracking analysis (NTA), are gradually pushing the frontier towards a point where the aggregation, growth and ordering phenomena involved in nucleation can be studied directly. Meanwhile, nucleation continues to predominantly be investigated indirectly through a thermodynamic/kinetic approach, by measuring quantities such as induction times, crystal properties and crystal size distributions which are correlated to nucleation events.

Nucleation is often treated with the classical theory of nucleation (CNT),^1,2 but growing experimental evidence for the existence and influence of mesoscale molecular aggregates, or clusters,^3–16 has led to the emergence of new, non-classical nucleation theories, emphasizing the role of clusters in the underlying mechanisms.^17,18 Gebauer and Cölfen proposed that nucleation can occur through aggregation of pre-nucleation clusters,¹¹ postulated to be thermodynamically stable entities lacking a defined phase boundary, which could be present in supersaturated as well as undersaturated solutions. The two-step theory proposes that concentration fluctuations in solution produce solute-dense clusters with a disordered, liquid-like structure within which ordered nuclei can arise.^19,20 The literature also contains reports on cases where apparently classical and non-classical pathways can compete under similar conditions.²¹ However, so far, no single theory has been able to completely and comprehensively describe the mechanisms behind nucleation.

It has long been an established fact that the propensity for nucleation is sensitive to the pre-treatment history of the system, for melts²² as well as solutions of inorganic²³ and organic molecules,^24,25 macromolecules,²⁶ covering such esoteric cases as the tendency of sugars to crystallize in raisins,²⁷ and how to increase the working temperature range of energy storage materials.²⁸ A number of studies of the effect of superheating on the metastable zone width^23,29–32 and nucleation induction time^23,33,34 have established qualitatively the effects previously reported; that the propensity to nucleate decreases with increasing time and temperature of superheating during pre-treatment. Nakai³⁵ proposed a kinetic cluster distribution model relating the degree of undersaturation during pre-treatment to the nucleation induction time. More recent work has shown that nucleation of the compound fenoxycarb from isopropanol,³⁶ as well as two polymorphs of the compound m-hydroxybenzoic acid from ethyl acetate,³⁷ exhibits a systematic dependence on the time and temperature of pre-treatment. For the latter, results indicate that these history of solution effects can also have a structural dimension. The timescale of the processes involved in these effects is significant – of the order of hours or days – which facilitates experimental investigation of the phenomenon, but also indicates it can play an important role for the design of robust crystallisation processes. Using a combination of detection techniques (SAXS, DLS and NTA), we recently investigated solute cluster size distributions in solution as a function of time in a range of conditions and proposed a direct link between solute clustering and the dependence of nucleation on pre-treatment.³⁸

In the present work, in a completely novel approach, the impact of solution preparation and pre-treatment conditions on the induction time for primary nucleation has been investigated for a multi-component crystal – the well-studied 1 : 1 cocrystal between carbamazepine and saccharin. The fact that a cocrystal consists of two components, crystallized from a solution which can be prepared either from pure solid phases of the individual components or by dissolution of the cocrystal phase, is here exploited to indirectly probe structuring in the solution. The main hypothesis is that there will be differences between the populations of clusters established as a result of the dissolution of different solid phases, and that this difference could possibly affect the tendency for the cocrystal to nucleate. Moreover, we hypothesize that there will be some response in the clusters, whether in the size distribution, concentration or some inherent structure-related property, to changes in the conditions of the solution between the dissolution and the establishment of supersaturation.

Carbamazepine (CBZ), widely used globally as an antiepileptic drug, is known to exist in at least four polymorphs,³⁹ out of which the monoclinic form III is thermodynamically stable at room temperature.⁴⁰ Saccharin (SAC) is an artificial sweetener used as coformer in cocrystals of several APIs. The molecular structures of CBZ and SAC are shown in Fig. 1a. The 1 : 1 cocrystal itself is known to exist in two monotropically related polymorphs,^41,42 with the triclinic form I being thermodynamically stable. This cocrystal exhibits a higher solubility than its pure coformers in equimolar aqueous solutions, but in methanol the solubility of the cocrystal is lower (congruent dissolution).⁴³ In the form I structure, two neighbouring CBZ molecules form a homosynthon through hydrogen bonding between their carboxamide groups, while neighbouring SAC molecules interact with this dimer through N–H⋯O=C and S=O⋯H–N hydrogen bonds, as shown in Fig. 1b.

Fig. 1 a) The carbamazepine and saccharine molecular structures, and b) the main intermolecular structural motif in the CBZ–SAC cocrystal form I showing hydrogen bonds as dashed lines.

The solubility of the cocrystal in ethanol has been measured as a function of temperature, and primary isothermal nucleation experiments have been conducted following different pre-treatment protocols, and comparing solutions prepared by dissolution of the cocrystal with solutions prepared by dissolution of equimolar amounts of the two cocrystal formers. Acknowledging the stochastic nature of nucleation, for each set of conditions multiple repeat experiments have been performed and the results treated with Poisson statistics. Finally, to complement the nucleation experiments, mesoscale clustering in solutions has been analysed with dynamic light scattering.

Experimental work

Materials and characterisation

Carbamazepine (CBZ, CAS no 298-46-4, >98%) was supplied by Novartis, saccharin (SAC, 81-07-2, >99%) was purchased from Aldrich, methanol (>99.9%) and ethanol (>99.8%) was purchased from VWR. All solvents and chemicals were used as received. Solid samples were characterised by X-ray powder diffraction (XRPD; Siemens D5000, Cu-Kα radiation, λ = 1.54 Å). Solid and solution samples were analysed with attenuated total reflectance Fourier transform infrared spectroscopy (ATR-FTIR; Perkin Elmer Spectrum Two). The commercial CBZ material was verified by XRPD to be form III.³⁹

Cocrystal preparation

Cocrystals were produced by cooling crystallisation from an ethanol:methanol solution. To produce one batch of CBZ–SAC cocrystal, equimolar amounts of CBZ form III (18.8 g) and SAC (14.6 g) were dissolved in a mixture of ethanol and methanol at a volume ratio of 62.5: 37.5 (250 mL) at 343 K for 1 h in an Erlenmeyer flask. The solution was then cooled to room temperature (298 K) in a linear temperature ramp over the course of 9 h and then kept at this temperature overnight. The resulting crystals were recovered by filtration and dried on the filter paper in an oven for 2 days. This recipe was repeated at slightly varying scale during the course of the work. The temperature was controlled using a cryostatic water bath (Julabo) and the solution was stirred by a PTFE-coated magnetic stirrer controlled by a submersible stirring plate (2Mag). The resulting cocrystal material was verified by XRPD to be form I.

Solubility measurement

The solubility of the cocrystal phase in ethanol was determined at different temperatures using a gravimetric method. Cocrystal solids in excess of solubility were mixed with ethanol in Erlenmeyer flasks, and kept agitated using a PTFE-coated magnetic stirrer bar controlled by a submersible stirring plate (2Mag) in a cryostatic bath (Julabo; specified temperature stability ±0.01 K) at different temperatures in the range 278–313 K to equilibrate for 1 h. The short equilibration time was verified at the lowest temperature. Solutions were then allowed to settle briefly before sampling. At each temperature, three samples of the supernatant were collected, and filtered using pre-heated syringes equipped with PTFE filters (0.2 μm) into dry, pre-weighed (m_vial) glass vials. The vials were then immediately weighed again (m_full). The solvent was allowed to evaporate completely in a ventilated fume hood at room temperature and then in an oven at 323 K until complete dryness (verified by repeated weighing). The final dry weight of each vial (m_dry) was measured, and the solution concentration, in units of mass of cocrystal per mass of solvent, calculated as: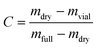All weighing was done using a Mettler AE240 balance, with an accuracy of 0.01 mg. The bath temperature was verified using an external precision thermometer (VWR Traceable, accuracy ±0.05 K). The solid phase present in the suspension at the start as well as after completed solubility measurements was verified by XRPD to be form I of the cocrystal.

Primary nucleation experiments

The propensity for primary nucleation of the cocrystal from ethanol solutions after different, controlled conditions of preparation and pre-treatment was investigated through measurement of the induction time. A set of preliminary experiments were carried out to probe the dependence on nucleation induction time on concentration, in order to establish suitable conditions to obtain induction times of the order of 1 h. Based on these experiments, a base case was established, with a nucleation temperature of 283.15 K and a cocrystal concentration of 27.75 g kg⁻¹ ethanol corresponding approximately to a saturation temperature of 300 K with respect to the cocrystal solubility. At these base conditions, a total of 210 nucleation induction time experiments were then carried out at different conditions with respect to i) the solid phase(s) dissolved to create the solution (the cocrystal or the individual coformers), ii) pre-treatment temperature, iii) agitation conditions during pre-treatment, and iv) microfiltration after dissolution but before the pre-treatment step.

Stock solutions were prepared by dissolving either cocrystal solids or equimolar amounts of the separate coformers in pre-heated ethanol in an Erlenmeyer flask under agitation by a magnetic stirrer bar for exactly 60 min at a pre-treatment temperature of either 305.15 K or 310.15 K. After this, each solution was transferred in 5 mL portions to a batch of 15 to 20 smaller glass vials (70 × 25 mm) using pre-heated plastic syringes (VWR International) with or without a syringe filter (PTFE; 0.2 μm). The vials were capped, and kept at the pre-treatment temperature in water bath connected to a cryostatic water bath (Julabo), with or without continuous agitation at 100 rpm by PTFE-coated magnetic stirrer bars (15 × 5 mm with a pivot ring) controlled by a submersible stirrer plate (2Mag MIXdrive 60). After a controlled pre-treatment time, the vials were moved to a second water bath kept at the nucleation temperature, under agitation at 100 rpm by the magnetic bars. Nucleation was detected using a high-definition camera (Panasonic GX7), at a frame capture rate of 30 seconds. The induction time is taken as the total time from introducing the vials in the bath at the nucleation temperature to the time of the first detection of a change in the solution cloudiness from the captured video. Once nucleation had visibly occurred, the solutions became completely opaque within 1–2 min. A reference vial fitted with an in situ temperature probe (VWR) showed that the solution would reach the nucleation temperature to within 0.5 K in 160 seconds, and to within 0.1 K in 320 seconds. Solids from selected vials of each experiment were filtered, dried and analysed with XRPD to verify that the obtained phase was the cocrystal form I.

Dynamic light scattering

Clustering in ethanol solutions of CBZ + SAC was investigated by dynamic light scattering (DLS). Two solutions of identical, equimolar concentration of CBZ and SAC were compared; one solution was prepared by dissolution of the cocrystal and the other prepared by dissolution of the two individual coformers. Two glass vials equipped with magnetic stirrers were filled with 8.0 g of ethanol, capped and preheated to 305.15 K under agitation at 265 rpm in a cryostatic bath. To one vial, 222 mg cocrystal was added, and to the other, 125 mg CBZ + 97 mg SAC was added, corresponding approx. to the cocrystal solubility at 300 K. The solids were allowed to dissolve completely for exactly 60 min. Each sample was then transferred to a capped glass cuvette and equilibrated at 305.0 K for 5 min before DLS analysis. DLS measurements were carried out using a Zetasizer Pro Red (Malvern Panalytical), using a He Ne laser of wavelength 633 nm. The viscosity of pure ethanol was used to approximate solution viscosities. The solution temperature was controlled at 305.0 K during the analysis runs. Each sample was analysed over 10 repeat runs.

Results

Characterisation of solid phases

Solid samples of starting materials, synthesized cocrystals and solids obtained in crystallisation experiments have been characterised with XRPD and ATR-FTIR. XRPD patterns of the cocrystal prepared by cooling crystallization as well as samples obtained in nucleation experiments all match the pattern of the cocrystal form I.⁴² The IR spectra of the solid materials match published spectra for CBZ form III,⁴⁴ SAC and form I of the cocrystal,⁴² respectively. XRPD pattern comparison and IR spectra of the solid phases are provided in the ESI.†

Solubility of the cocrystal in ethanol

The solubility of the 1 : 1 CBZ–SAC cocrystal in ethanol is given in Table 1 as mass concentrations on pure solvent basis and as mole fraction values on total basis (one mole of cocrystal corresponding to one mole of CBZ and one mole of SAC). The solubility values are obtained as averages over three samples at each temperature, given together with standard errors.

Table 1 Solubility of the cocrystal in ethanol at different temperatures, as g cocrystal per kg solvent and as mole fraction, respectively, given with standard errors

T (K)	C eq (g per kg solvent)	10^3xeq
278.15	13.0 ± 0.10	1.42 ± 0.012
283.15	15.11 ± 0.095	1.66 ± 0.010
288.15	18.03 ± 0.079	1.976 ± 0.009
293.15	21.3 ± 0.14	2.34 ± 0.016
303.15	30.18 ± 0.091	3.30 ± 0.010
313.15	44.09 ± 0.047	4.819 ± 0.005

---

The parameters of an empirical three-parameter equation commonly used for this purpose, eqn (2), was fitted to the experimental solubility data using the software Origin 2022 (v. 9.9, OriginLab, USA) through minimizing the reduced χ² value of the residuals of the mole fraction solubility at the six evaluated temperatures. The resulting coefficients are given in Table 2 together with the goodness of fit values. The fit is very good, with an R² value exceeding 0.999. The experimental data together with the fit of eqn (2) are shown in Fig. 2.

Table 2 Regression parameters of eqn (2) together with goodness of fit values

A	1 596 187
B	−13866.2
C	22.66515
R ^2	0.99988
10^4χ^2red	0.404

---

Fig. 2 Solubility (in units of g per kg solvent) of the cocrystal in ethanol as a function of temperature. Symbols denote experimental data and the line shows the fit of eqn (2).

Primary nucleation of the cocrystal

The thermodynamic driving force for nucleation, expressed as a chemical potential difference, Δμ, is often approximated as:by neglecting the influence of the concentration-dependence of the activity coefficients in solution. In eqn (3), T_N denotes the nucleation temperature (in K), and x/x_eq the ratio of the mole fraction concentration of cocrystal in the solution to the mole fraction solubility at T_N.

A series of preliminary nucleation experiments carried out in the driving force range 1000–2500 J mol⁻¹ at a nucleation temperature of 283.15 K resulted in median induction times in a wide range from 240 s at the highest supersaturation to no nucleation events observed over the course of several hours for the lowest supersaturation. The base case for investigation was chosen to be a cocrystal concentration of 27.75 g per kg ethanol, corresponding to a saturation temperature of 300.7 K and a driving force of 1414 kJ mol⁻¹ for nucleation of the cocrystal at a temperature of 283.15 K.

Nucleation experiments were carried out in batches of 30 or 40 solution vials. In most cases, half the solutions in each batch were created by dissolution of the cocrystal and the other half by dissolution of the separate coformers. In some cases, however, the sets of identical experiments were divided into separate batches for the solutions with different origins. In one case, only solutions based on the separate coformers were used. The experimental conditions are summarised in Table 3. The 210 vials in the nucleation experiments in Table 3 all had a controlled pre-treatment time of exactly 60 min in the vials. In addition, a set of experiments (170 vials in total) with a longer pre-treatment time, approx. 17 h, were carried out. As there were experimental issues with temperature control in some of these unsupervised experiments, they are not discussed in detail in this work, but for the sake of transparency all experiments are tabulated in the ESI.†

Table 3 Summary of nucleation experiments with pre-treatment conditions, number of repeats (N) and median induction time (in min) based on regression by eqn (4) with 95% confidence intervals

No	Solid phase	Pre-treatment conditions			N	Median tind ± 95% CI (min)
		T (K)	Filtration	Stirring
1 a	Separate	310	No	Yes	15	431 ± 44
1 b	Cocrystal	310	No	Yes	15	85 ± 11
2 a	Separate	310	No	No	15	326 ± 40
2 b	Cocrystal	310	No	No	15	92 ± 11
3 a	Separate	310	Yes	Yes	20	640 ± 44
4 a	Separate	310	Yes	No	15	321 ± 49
4 b	Cocrystal	310	Yes	No	15	321 ± 108
5 a	Separate	305	No	Yes	20	91.3 ± 6.3
5 b	Cocrystal	305	No	Yes	40	53.8 ± 2.5
6 a	Separate	305	Yes	Yes	20	240 ± 27
6 b	Cocrystal	305	Yes	Yes	20	84.9 ± 7.9

---

The relationship between nucleation rate and induction time has been treated in depth in the literature.^45–47 If it can be assumed that the important stochastic variable is the time of formation of the first nucleus in the solution volume, the relationship between the nucleation rate (J), the volume (V) and the induction time (t) can be expressed through a Poisson probability distribution:

P(t) = 1 − exp(−A(t − t_g)) (4)

where P(t) is the probability that a supersaturated solution will have nucleated at least one nucleus after time t, A is equal to JV, and t_g is the time until detection of the nucleation event is practically possible. Nucleation rates can be estimated from a plot of the cumulative induction time distribution of a sufficiently large number of identical repeat experiments, typically by assuming either a constant or a zero value of t_g. The underlying assumptions, i.e. that either the first nucleus can be detected or that it will rapidly trigger secondary nucleation leading to sufficient crystal mass to be detected, and that there is no variability in t_g, can however be questioned. Deck and Mazzotti have suggested that this treatment will lead to underestimation of the real nucleation rates.⁴⁶

In the present work, eqn (4) was used primarily as an empirical model to fit to, and compare, nucleation data. Induction time distribution plots are shown for all experiments in Fig. 3 together with fits of eqn (4). For each experiment, median induction times were estimated using the fitted model (i.e. t_P=0.5), with values given in Table 3 together with 95% confidence intervals. Fitted coefficients of eqn (4) are tabulated in ESI.†

Fig. 3 Cumulative distributions of nucleation induction times, grouped according to experiment number in Table 3, shown together with fits of eqn (4) and 95% confidence bands. In each plot, the red circles represent experiments with dissolved separate coformers (set a) and blue squares represent experiments with dissolved cocrystal (set b).

It can be seen in Fig. 3 that, as is commonly observed in similar cases, the induction time distributions are relatively broad, covering a broad dynamic range.^47–50 This is typically handled by a statistical approach, through fitting of a suitable distribution model and comparison of e.g. median values. However, it should be stressed that the objective of the present work is chiefly to make a qualitative comparison of the effect of the different investigated conditions. As such, the fits of eqn (4) are, in most cases, fairly good, with high goodness of fit values and relatively narrow confidence bands. However, in some cases the fits obviously do not well describe the data, with systematic errors in residuals and/or artefacts such as negative t_g values.

Dynamic light scattering

DLS autocorrelation function graphs fitted by distribution analysis to the scattering data show two decays, indicative of a bimodal cluster distribution. This is in agreement with similar published studies,^10,16,38,51 and has been attributed to so-called molecular clusters (possibly solvated solute molecules, dimers or smaller oligomers) and larger mesoscale clusters, respectively. Solvodynamic diameters corresponding to the two peak values were calculated using the standard treatment (using the Stokes–Einstein equation to relate the obtained diffusion coefficients to a spherical diameter). In addition, the derived count rate, in units of counts per second, a function of the flux of scattered photons, was recorded for each measurement. This value can serve as a rough indication of the number concentration of mesoscale clusters. Resulting mean solvodynamic diameters of the two cluster populations are given in Table 4 for two solutions, together with mean derived count rates, for 10 repeat runs of each solution. Overlays of the distribution fits to the autocorrelation data and size distributions for typical cases are shown in Fig. 4.

Table 4 Mean solvodynamic diameters (d_s) of molecular clusters (peak 1) and mesoscale clusters (peak 2) and mean derived count rates, given together with 95% confidence intervals

	Dissolved solid phase
	Cocrystal		Separate coformers
	Peak 1	Peak 2	Peak 1	Peak 2
Mean ds (nm)	0.76 ± 0.03	163 ± 25.0	0.73 ± 0.03	242 ± 69.7
Mean dcr (10^3 cps)	1459 ± 221		544 ± 20

---

Fig. 4 Examples of DLS results showing overlay of correlogram with distribution fit (red; secondary axis) and resulting bimodal size distribution (black; primary axis) for solutions prepared by dissolution of a) cocrystal and b) separate coformers.

The first peak in the DLS distributions correspond to solvodynamic diameters of 0.73 and 0.76 nm, respectively, with no statistically significant difference. This indicates the presence of various homo- and hetero-oligomers, likely dominated by dimers. The fact that the first peak is almost identical in the two solutions suggests that on a molecular level the solutions feature the same type of interactions. The strong presence of the second peak clearly indicates the presence of mesoscale clusters in both solutions, with solvodynamic diameters of the order of 100–300 nm. Unlike the first peak, this second peak differs significantly between the solutions. For the solution prepared by dissolution of the individual coformers, the mean size is larger (242 nm) than for the solution prepared by dissolution of the same molar amount of cocrystal (163 nm). For both solutions, these peaks are associated with fairly large relative uncertainties, with the peak corresponding to the larger size (242 nm) being the broadest. Owing to the lack of knowledge about key properties of these clusters, it is not possible to give a fair estimate of how many solute molecules are involved. However, as a thought experiment, the number of molecules in classical clusters of similar diameters may be estimated, using data on the cell volume of the cocrystal structure. This results in values ranging between 5 × 10⁶ and 15 × 10⁶ supramolecular CBZ + SAC units. Because of the assumptions and uncertainties regarding cluster diameter (solvodynamic diameter instead of ‘real’ diameter), shape (assumed spherical) and composition (assumed pure co-crystal of crystalline structure), the true value is likely order of magnitude smaller, however.

As regards the derived count rate, unlike the estimated cluster diameters it shows a clear difference between the solutions, being almost three times higher in the solution prepared by dissolution of the cocrystal than for the coformer-based solution.

Discussion

In four out of six nucleation experiments the vials prepared by dissolving the cocrystal (‘b’, shown as blue squares in Fig. 3) nucleated earlier or much earlier than the corresponding set prepared by dissolving the separate coformers (‘a’, shown as red circles in Fig. 3). The difference in median induction times between the ‘a’ and ‘b’ sets in these experiments are well clear of statistical uncertainties. In only one experiment (4), the results are inconclusive with respect to the effect of dissolved phase, while in experiment (3) the comparison cannot be made as only the coformers were used. This clearly indicates that nucleation of the cocrystal is affected by the solid phase used to prepare the solution, with a strongly promoting effect observed when the same phase, the cocrystal, is dissolved. The effect remains after the solutions have been pre-treated for 1 h 9.5 K above the saturation temperature (i.e. at 310 K), and under stirring as well as in stagnant state. For solutions that have been microfiltered following dissolution, the results are inconclusive with respect to the effect of the dissolved solid; in experiment 4 no difference between the a and b sets is observed, while in experiment 6 induction times for both sets are increased compared to experiment 5 carried out under otherwise similar conditions, with a marked difference remaining between the a and b sets.

As for the investigated pre-treatment parameters, the effects range from less prominent but clear to inconclusive. A comparison between experiments 1a and 3a, and also between experiments 5 and 6 (for both types of solid) shows that filtration before pre-treatment leads to slightly increased nucleation induction times. All these differences are statistically significant. However, when comparing experiments with stagnant solutions (experiments 2 and 4), this difference was only observed for the cocrystal-based solutions). As for the effect of stirring solutions during pre-treatment compared to leaving them stagnant, the results are inconclusive and the effect minor. A comparison of experiments 1a and 2a shows a small but significant difference, while a comparison of experiments 3a and 4a shows a larger difference, indicating that stirring during pre-treatment leads to longer induction times, but when comparing experiments 1b and 2b, no significant difference is observed. Finally, the influence of pre-treatment temperature is fairly clear and consistent in these results. A lower pre-treatment temperature consistently results in shorter induction times, both for unfiltered (experiments 1 and 5) and filtered solutions (experiments 3 and 6). This difference is statistically significant and observed irrespective of the solid phase used to prepare the solutions.

As mentioned earlier, in addition to the experiments tabulated and discussed here, a set of experiments with a longer pre-treatment time (17 h) under various conditions were also carried out. Although the results of these experiments overall are less conclusive than the experiments in Table 3, the overall trend seems to be that a prolonged pre-treatment time will delay nucleation. These experiments are tabulated in the full set of experiments in the ESI.†

Overall, the results indicate: i) that the tendency of ethanol solutions of CBZ + SAC to nucleate the cocrystal strongly depends on the pre-treatment conditions as well as on the solid phase(s) dissolved to create the solution; ii) that the cocrystal nucleates much more easily when the cocrystal is dissolved compared to when the separate coformers are dissolved; iii) that increasing the pre-treatment temperature and possibly also the duration leads to a reduced tendency to nucleate; and iv) that filtration of solutions tends to decrease their tendency to nucleate. The results of the nucleation experiments can be explained based on the hypothesis previously suggested^36–38 that solutions may contain a population of mesoscale clusters, which at some level are able to carry structural information, and whose interconversion and restructuring are governed by slow kinetics, with time constants at least of the order of hours. The influence of the thermal pre-treatment parameters time and temperature on the tendency of solutions to nucleate has previously been documented for other organic systems,^36,37 as has the inhibiting influence of microfiltration.⁵²

Owing to the small length scales in combination with the localised nature of the phenomenon, where as previously reported^12,15 at any one time only fractions of a percent of the molecules in a solution appear to be involved in clustering at the mesoscale level, direct investigation of the appearance and structure of the clusters is fraught with challenges. The DLS experiments clearly show that both analysed solutions, prepared using different solid phases, contain clusters in the mesoscale size range like previously reported for other systems,^{6,13,15,16,51} including fenoxycarb/propanol³⁸ for which similar solution history effects on nucleation have also been reported.³⁶ Moreover, the results indicate clear differences in the cluster-induced light scattering depending on the method of preparation of solutions that are identical as regards stoichiometry, concentration and temperature. It may be speculated, as an explanation for the observations of both the nucleation and DLS experiments, that the population of mesoscale clusters initially established on dissolution of the cocrystal will differ from that arising after dissolution of the individual coformers. However, DLS alone cannot be used to conclusively show exactly wherein these differences are found. At least for this system, there is no statistically significant difference in the mean solvodynamic diameter (cf.Table 4).

Fig. 5 compares the IR spectra of the solid phases and solutions created by dissolution of the cocrystal and the separate coformers, after 1 h pre-treatment at 310 K under agitation, with and without microfiltration following dissolution, in the region 1500–1800 cm⁻¹. There is no detectable difference between solutions prepared from cocrystal or coformers, respectively. Moreover, no difference can be observed between filtered and unfiltered solutions. However, all solutions show clear shifts to higher wavenumbers in the peak positions corresponding to C=O stretching in the CBZ and SAC molecules (from 1724 to 1743 cm⁻¹ and from 1644 to 1676 cm⁻¹, respectively) compared to the spectrum of the cocrystal solid. Likewise, there is a shift to higher wavenumber in the positions attributable to C=C stretching in the two molecules. This indicates overall weaker interactions of these groups in the CBZ + SAC solutions compared to the solid state. However, the fact that no difference is observed between the four solution spectra confirms that the majority of molecules in solution are not involved in mesoscale clusters, and thus are not affected by dissolved phase or microfiltration.

Fig. 5 Comparison of ATR-IR spectra of solid phases and CBZ + SAC solutions prepared using cocrystal or separate coformers, with and without microfiltration.

The difference in the derived count rate measured by DLS reflects the difference in scattered light reaching the detector. Unlike IR absorption, scattering in the Rayleigh regime is proportional to the diameter of the scattering entity raised to the sixth power, so at least for particles smaller than the laser wavelength the relationship between the intensity of scattered light of two particles with diameters d₁ and d₂ can be written:

If this relationship could be assumed to approximately hold for the entire size range covered by clusters in this work, an average mesoscale cluster would scatter as much light as around 10¹⁴–10¹⁵ molecular clusters. Even allowing for the transition into Mie scattering for the larger clusters, the derived count rate is largely expected be dominated by the scattering from mesoscale clusters. Hence, the statistically significant difference in count rate indicates a considerable difference in the concentration of scattering species in the solutions generated using different starting material, possibly in combination with differences in the structure and density of the clusters promoting scattering. It may be speculated that this difference in the concentration of mesoscale clusters, again possibly in combination with differences in the structural makeup of the clusters, established in solutions on dissolution of the cocrystal phase compared to dissolution of the separate coformers, could explain the marked differences in nucleation induction times observed in this work.

Conclusions

Sets of repeat primary nucleation experiments of the CBZ–SAC cocrystal from ethanol solutions have shown that the tendency to nucleate depends strongly on the preparation and pre-treatment conditions. Average induction times of cocrystal nucleation are significantly shorter in solutions created by dissolution of the cocrystal compared to when the two separate coformers are dissolved. Moreover, nucleation is slower in solutions pre-treated at a higher temperature (310 K) compared to a lower (305 K). Solutions that have been microfiltered after dissolution and before pre-treatment show a tendency to nucleate slower than unfiltered solutions. Using dynamic light scattering it is shown that populations of mesoscale clusters in the approximate size range 100–300 nm exist in solutions after dissolution of cocrystal as well as of the separate coformers, with the former apparently present in significantly higher concentrations, in relative terms. ATR-IR spectroscopy indicates that the absolute number concentration of mesoscale clusters in solution is very low. The connection between the presence and the behaviour of the clusters and the dependence of the nucleation behaviour of solutions on their preparation and pre-treatment is discussed.

Author contributions

J. Crutzen: CRediT conceptualization, formal analysis, investigation. L. Zeng: CRediT conceptualization, methodology, investigation. M. Svärd: CRediT conceptualization, formal analysis, investigation, resources, writing – original draft, supervision, project administration, funding acquisition.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

Funding by the Swedish Research Council (grant number 2019-5059) is gratefully acknowledged.

Notes and references

1. R. Becker and W. Döring, Kinetische Behandlung der Keimbildung in übersättigten Dämpfen, Ann. Phys., 1935, 24, 719.
2. Y. B. Zeldovich, Theory of new phase formation: cavitation, Acta Physicochim. URSS, 1943, 18, 1.
3. M. Svärd, Mesoscale clusters of organic solutes in solution and their role in crystal nucleation, CrystEngComm, 2022, 24, 5182.
4. D. Gebauer, A. Völkel and H. Cölfen, Stable Prenucleation Calcium Carbonate Clusters, Science, 2008, 322, 1819.
5. T. J. Sorensen, Oiling-out and crystallization of vanillin from aqueous solutions, Chem. Eng. Technol., 2014, 37, 1959.
6. T. J. Sorensen, P. C. Sontum, J. Samseth, G. Thorsen and D. Malthe-Sorenssen, Cluster formation in precrystalline solutions, Chem. Eng. Technol., 2003, 26, 307.
7. U. Gasser, E. R. Weeks, A. Schofield, P. N. Pusey and D. A. Weitz, Real-space imaging of nucleation and growth in colloidal crystallization, Science, 2001, 292, 258.
8. S. Chattopadhyay, D. Erdemir, J. M. B. Evans, J. Ilavsky, H. Amenitsch, C. U. Segre and A. S. Myerson, SAXS study of the nucleation of glycine crystals from a supersaturated solution, Cryst. Growth Des., 2005, 5, 523.
9. S. Tanaka, K. Ito, R. Hayakawa and M. Ataka, Size and number density of precrystalline aggregates in lysozyme crystallization process, J. Chem. Phys., 1999, 111, 10330.
10. A. Jawor-Baczynska, J. Sefcik and B. D. Moore, 250 nm Glycine-Rich Nanodroplets Are Formed on Dissolution of Glycine Crystals But Are Too Small To Provide Productive Nucleation Sites, Cryst. Growth Des., 2013, 13, 470.
11. D. Gebauer and H. Cölfen, Prenucleation clusters and non-classical nucleation, Nano Today, 2011, 6, 564.
12. Y. Jiang, M. Kellermeier, D. Gebauer, Z. H. Lu, R. Rosenberg, A. Moise, M. Przybylski and H. Colfen, Growth of organic crystals via attachment and transformation of nanoscopic precursors, Nat. Commun., 2017, 8, 6.
13. S. Zong, J. Wang, X. Huang, T. Wang, Q. Liu, B. Tian, C. Xie and H. Hao, Molecular evolution pathways during nucleation of small organic molecules: solute-rich pre-nucleation species enable control over the nucleation process, Phys. Chem. Chem. Phys., 2020, 22, 18663.
14. J. Cookman, V. Hamilton, S. R. Hall and U. Bangert, Non-classical crystallisation pathway directly observed for a pharmaceutical crystal via liquid phase electron microscopy, Sci. Rep., 2020, 10, 19156.
15. M. Warzecha, M. S. Safari, A. J. Florence and P. G. Vekilov, Mesoscopic Solute-Rich Clusters in Olanzapine Solutions, Cryst. Growth Des., 2017, 17, 6668.
16. G. Zimbitas, A. Jawor-Baczynska, M. J. Vesga, N. Javid, B. D. Moore, J. Parkinson and J. Sefcik, Investigation of molecular and mesoscale clusters in undersaturated glycine aqueous solutions, Colloids Surf., A, 2019, 579, 123633.
17. S. Karthika, T. K. Radhakrishnan and P. Kalaichelvi, A Review of Classical and Nonclassical Nucleation Theories, Cryst. Growth Des., 2016, 16, 6663.
18. B. Jin, Z. Liu and R. Tang, Recent experimental explorations of non-classical nucleation, CrystEngComm, 2020, 22, 4057.
19. W. Pan, A. B. Kolomeisky and P. G. Vekilov, Nucleation of ordered solid phases of proteins via a disordered high-density state: phenomenological approach, J. Chem. Phys., 2005, 122, 174905.
20. P. G. Vekilov, Dense liquid precursor for the nucleation of ordered solid phases from solution, Cryst. Growth Des., 2004, 4, 671.
21. M. H. Nielsen, S. Aloni and J. J. De Yoreo, In situ TEM imaging of CaCO₃ nucleation reveals coexistence of direct and indirect pathways, Science, 2014, 345, 1158.
22. K. Schaum and F. Schoenbeck, Unterkühlung und Krystallisation von Schmelzflüssen polymorpher Stoffe, Ann. Phys., 1902, 313, 652.
23. N. Kubota and Y. Fujisawa, The effects of filtration and thermal history on primary nucleation of potassium bromate from aqueous solution, Process Technol. Proc., 1984, 2, 259.
24. J. Smid, J. Kvapil, J. Mýl and S. Solz, Effect of the supersaturation on the production of parasitic crystals, in Growth of crystals, ed. N. N. Sheftal and A. V. Shubnikov, Consultants bureau, New York, 1962, vol. 3, p. 196.
25. J. Nývlt, Crystallization, IV, Crystal nucleation in solutions, Collect. Czech. Chem. Commun., 1963, 28, 2269.
26. M. W. Burke, R. A. Judge and M. L. Pusey, The effect of solution thermal history on chicken egg white lysozyme nucleation, J. Cryst. Growth, 2001, 232, 301.
27. L. Alvarez, P. Urrutia, A. Olivares, A. Flores, B. Bhandari, T. Truong and S. Almonacid, Impact of thermal pretreatment on crystallization of Thompson raisins, Food Chem., 2020, 317, 126381.
28. J. A. Noël, L. Kreplak, N. N. Getangama, J. R. de Bruyn and M. A. White, Supercooling and Nucleation of Fatty Acids: Influence of Thermal History on the Behavior of the Liquid Phase, J. Phys. Chem. B, 2018, 122, 12386.
29. T. P. Melia and W. P. Moffitt, Crystallization from aqueous solution, J. Colloid Sci., 1964, 19, 433.
30. J. Nývlt, Probable mechanism of the effect of thermal history of solution on the metastable zone width, Collect. Czech. Chem. Commun., 1984, 49, 2045.
31. J. Nývlt, Effect of thermal history of aqueous solutions of potassium chloride on the metastable zone width, Collect. Czech. Chem. Commun., 1984, 49, 559.
32. K. Hussain, G. Thorsen and D. Malthe-Sorenssen, Nucleation and metastability in crystallization of vanillin and ethyl vanillin, Chem. Eng. Sci., 2001, 56, 2295.
33. J. Nývlt and V. Pekárek, Crystallization studies by thermometric methods. III. The effect of thermal history of solutions on nucleation, Z. Phys. Chem., 1980, 122, 199.
34. V. Vacek, V. Pékarek and J. Nývlt, The effect of thermal history of solution on the crystallization process, in Industrial Crystallization '81, North-Holland, 1982, p. 279.
35. T. Nakai, Effects of the thermal history of a solution to nucleation, J. Chin. Inst. Chem. Eng., 1972, 3, 83.
36. M. Kuhs, J. Zeglinski and Å. C. Rasmuson, Influence of History of Solution in Crystal Nucleation of Fenoxycarb: Kinetics and Mechanisms, Cryst. Growth Des., 2014, 14, 905.
37. F. L. Nordström, M. Svärd, B. Malmberg and Å. C. Rasmuson, Influence of Solution Thermal and Structural History on the Nucleation of m-Hydroxybenzoic Acid Polymorphs, Cryst. Growth Des., 2012, 12, 4340.
38. M. Svärd, K. R. Devi, D. Khamar, D. Mealey, D. Cheuk, J. Zeglinski and Å. C. Rasmuson, Solute clustering in undersaturated solutions – systematic dependence on time, temperature and concentration, Phys. Chem. Chem. Phys., 2018, 20, 15550.
39. A. L. Grzesiak, M. Lang, K. Kim and A. J. Matzger, Comparison of the four anhydrous polymorphs of carbamazepine and the crystal structure of form I, J. Pharm. Sci., 2003, 92, 2260.
40. M. A. O'Mahony, A. Maher, D. M. Croker, Å. C. Rasmuson and B. K. Hodnett, Examining Solution and Solid State Composition for the Solution-Mediated Polymorphic Transformation of Carbamazepine and Piracetam, Cryst. Growth Des., 2012, 12, 1925.
41. S. K. Pagire, N. Jadav, V. R. Vangala, B. Whiteside and A. Paradkar, Thermodynamic Investigation of Carbamazepine-Saccharin Co-Crystal Polymorphs, J. Pharm. Sci., 2017, 106, 2009.
42. W. W. Porter III, S. C. Elie and A. J. Matzger, Polymorphism in Carbamazepine Cocrystals, Cryst. Growth Des., 2008, 8, 14.
43. S. Kudo and H. Takiyama, Production method of carbamazepine/saccharin cocrystal particles by using two solution mixing based on the ternary phase diagram, J. Cryst. Growth, 2014, 392, 87.
44. A. L. Grzesiak, M. Lang, K. Kim and A. J. Matzger, Comparison of the Four Anhydrous Polymorphs of Carbamazepine and the Crystal Structure of Form I, J. Pharm. Sci., 2003, 92, 2260.
45. D. Kashchiev, D. Verdoes and G. M. van Rosmalen, Induction time and metastability limit in new phase formation, J. Cryst. Growth, 1991, 110, 373.
46. L.-T. Deck and M. Mazzotti, Conceptual Validation of Stochastic and Deterministic Methods To Estimate Crystal Nucleation Rates, Cryst. Growth Des., 2023, 23, 899.
47. S. Jiang and J. H. ter Horst, Crystal Nucleation Rates from Probability Distributions of Induction Times, Cryst. Growth Des., 2011, 11, 256.
48. D. Mealey, J. Zeglinski, D. Khamar and A. C. Rasmuson, Influence of solvent on crystal nucleation of risperidone, Faraday Discuss., 2015, 179, 309.
49. D. Mealey, D. M. Croker and Å. C. Rasmuson, Crystal nucleation of salicylic acid in organic solvents, CrystEngComm, 2015, 17, 3961.
50. S. Kakkar, K. R. Devi, M. Svärd and Å. Rasmuson, Crystal nucleation of salicylamide and a comparison with salicylic acid, CrystEngComm, 2020, 22, 3329.
51. A. Jawor-Baczynska, B. D. Moore, H. S. Lee, A. V. McCormick and J. Sefcik, Population and size distribution of solute-rich mesospecies within mesostructured aqueous amino acid solutions, Faraday Discuss., 2013, 167, 425.
52. N. Javid, T. Kendall, I. S. Burns and J. Sefcik, Filtration Suppresses Laser-Induced Nucleation of Glycine in Aqueous Solutions, Cryst. Growth Des., 2016, 16, 4196.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ce00324h

‡ These authors contributed equally to the work.

---