Chalcogen bonding and variable charge transfer degree in two polymorphs of 1 : 1 conducting salts with segregated stacks

Abstract

Harnessing a bis(selenomethyl)tetrathiafulvalene (TTF) derivative as a donor, conducting charge transfer (CT) salts are realized thanks to original packing structures supported by chalcogen bonding (ChB) interactions. Specifically, reaction of EDT-TTF(SeMe)₂ (EDT = ethylenedithio) with an acceptor, 2,5-difluoro-7,7,8,8-tetracyanoquinodimethane (F₂TCNQ), afforded two polymorphs of 1 : 1 CT salts, α- and β-[EDT-TTF(SeMe)₂](F₂TCNQ). The donor and the acceptor molecules in both polymorphs organize into segregated and uniform stacks. Based on the structure, the α-salt shows a quasi-complete CT while the β-salt shows a partial CT with ρ ∼±0.8. The oxidation of TTF activates the σ-hole on Se atoms to be engaged in highly linear ChB interactions with the N atoms on F₂TCNQ. The formation of directional ChB interactions resulted in original packing structures of the donor and the acceptor stacks that are distinct between α- and β-salts. In particular, the ChB motif observed in the β-salt allows F₂TCNQ molecules within the stack to be closer than those in the α-salt. Consequently, the α-salt is a semi-conductor, while the β-salt shows metallic behaviour with a two-step metal-to-insulator (MI) transition. Moreover, the observed MI transition temperature in the β-salt (180 K) is substantially higher than that in other known CT salts, likely owing to the 3D coupling of the modulation in different chains brought about by the –SeMe substituents.

---

Introduction

Organic charge transfer (CT) donor–acceptor (D–A) salts constitute an important class of functional materials. The quest for such materials is an active research topic in different research areas covering chemistry and physics, particularly due to the intimate correlation between the structural chemistry, the detailed electronic structure, and conductivity. The most well-known example is TTF–TCNQ (TTF = tetrathiafulvalene; TCNQ = 7,7,8,8-tetracyanoquinodimethane) which is the first organic conductor presenting a metallic behaviour in a wide temperature range.¹ To obtain metallic conductivity in such CT salts, several criteria should be fulfilled. First, the key parameter is the degree of CT (ρ), which depends on the balance between the cost of ionizing a DA pair and the electrostatic (Madelung) energy gain of the ionic lattice.² The partial charge transfer state (0 < ρ < 1) is an essential requirement to create highly conducting mixed-valence salts. In addition to the partial CT, the packing of D and A molecules has also paramount importance. The two main modes of solid-state organizations of CT salts are segregated stacks and mixed alternating stacks of donors and acceptors, where the former is a prerequisite for metallic conductivity. While the redox potential of donors and acceptors can be intuitively modified to preselect an ideal pair of candidates towards the partial CT, the control of its solid-state packing is a challenging task. Indeed, there exists only a handful examples of metallic CT salts developed since the discovery of TTF–TCNQ. This is in stark contrast to the abundant examples of conducting radical salts of TTF derivatives obtained by electrochemical oxidation.³

In order to tentatively control the solid-state structures and ultimately the electronic structures of such DA charge transfer salts, different supramolecular strategies have been investigated (Scheme 1). Examples of purposely introducing hydrogen bonding (HB) within such CT salts are limited to a small set of tetrathiafulvalene (TTF) derivatives comprising the primary amide, thioamide, and imidazole groups.^4–7 In the series of imidazole derivatives, for example, TCNQs and quinones were shown to act simultaneously as electron acceptors and hydrogen acceptors. Here, additional intermolecular interactions activate donor and acceptor molecules toward easier CT despite unfavourable redox differences and allow for uncommon stoichiometries such as the 2 : 1 DAD hydrogen-bonded triad.⁷ In parallel, σ–hole interactions such as halogen bonding (XB) have been also explored in such CT salts with halogenated TTFs.⁸ For example, reaction of EDT-TTF–I₂ (EDT = ethylenedithio) with TCNQ, TCNQF, and F₂TCNQ afforded a series of isostructural 2 : 1 charge transfer salts, where the degree of charge transfer was found to vary with the acceptor ability.⁹ Here, the concept of charge activation upon electron transfer was convincingly illustrated, where stronger I⋯NC XB was found in the charge transfer salt with F₂TCNQ (ρ_F2TCNQ = −1) than in the neutral charge-transfer complex with TCNQ (ρ_TCNQ = 0). The intermediate TCNQF salt exhibits a neutral-ionic transition under temperature and pressure.¹⁰ Despite intriguing structures and electronic properties obtained using the strategies above, none of them showed segregated stacks and metallic conductivity, implying a challenging aspect. Moreover, compared with HB and XB, there is no such example of purposely introducing chalcogen bonding (ChB) interactions in CT salts.

Scheme 1 Supramolecular strategies toward CT salts: examples of introducing hydrogen bonding (HB),⁴ halogen bonding (XB),⁹ and chalcogen bonding (ChB) (this study).

In searching for potential TTF derivatives which can act as ChB donors, we have recently demonstrated strong σ-hole activation of selenium in EDT-TTF(SeMe)₂ (Scheme 1) upon their oxidation.¹¹ Here, the oxidation-induced Se activation in conjunction with geometrically well-disposed –SeMe functional groups led to efficient chalcogen bonding interactions with bromide anions in semiconducting 1 : 1 [EDT-TTF(SeMe)₂]Br salt. Considering the notably proficient ChB-donating ability of EDT-TTF(SeMe)₂, we decided to investigate its incorporation within CT salts and the influence of ChB in their solid-state properties. Herein, we describe the synthesis and solid-state properties of two polymorphs of CT salts, α- and β-[EDT-TTF(SeMe)₂](F₂TCNQ). Both polymorphs indeed feature challenging segregated stacks of donors and acceptors with distinct packing and a slightly different CT degree, leading one of them to show metallic conductivity. More importantly, the organization of stacks in both polymorphs, assisted by ChB interactions, reveals original packing structures compared to those of known metallic conducting CT salts.

Results and discussion

Solution properties

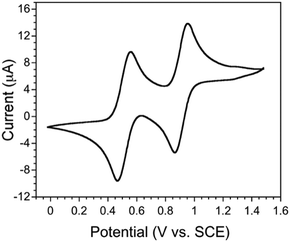
To choose an appropriate electron acceptor that could result in a partial charge transfer with EDT-TTF(SeMe)₂, we first investigated its redox properties using cyclic voltammetry in CH₂Cl₂ solution containing Bu₄NPF₆ as supporting electrolyte. The cyclic voltammogram, shown in Fig. 1, reveals two reversible redox processes, centred at +0.51 and +0.91 V vs. SCE. The value of the first oxidation potential, corresponding to the oxidation of the neutral TTF to its radical cation, is slightly higher than that of BEDT-TTF (E_ox = +0.49 V; BEDT = bisethylenedithio) and lower than that of EDT-TTFI₂ (E_ox = +0.57 V).^9,12 To obtain a partial CT, the reduction potential of acceptor molecules, E_red(A), should be carefully considered. If E_red(A) is larger than E_ox(D), full charge transfer is indeed expected. If Δ(E) = E_red(A) − E_ox(D) is less than approximately −0.35 V, a neutral CT compound is isolated. For intermediate Δ(E) values, a partial charge transfer could be obtained.¹³ Regarding these criteria, TCNQ (E_red = +0.14 V) is too weak to trigger charge transfer from EDT-TTF(SeMe)₂. We have therefore chosen a stronger acceptor, 2,5-difluoro-7,7,8,8-tetracyanoquinodimethane (F₂TCNQ, E_red = +0.30 V).

Fig. 1 Cyclic voltammetry of EDT-TTF(SeMe)₂ in CH₂Cl₂ with 0.2 M Bu₄NPF₆.

Solid-state properties

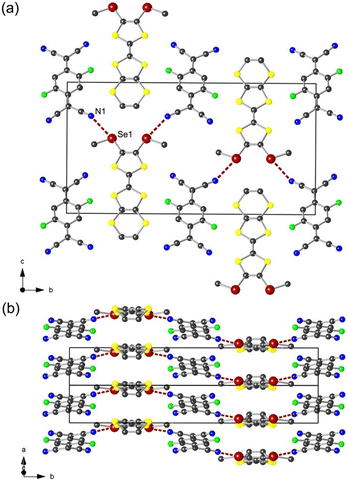
An acetonitrile solution of F₂TCNQ was layered onto a solution of EDT-TTF(SeMe)₂ in 1,1,2-trichloroethane and in CH₂Cl₂ to afford crystals of α- and β-[EDT-TTF(SeMe)₂](F₂TCNQ), respectively. As shown in Fig. 2, the polymorph α crystallizes in the monoclinic system, space group P2₁/m, with the donor molecule located on a mirror plane and the acceptor molecule on an inversion centre, giving the 1 : 1 stoichiometry. In the solid state, the donor and the acceptor molecules each organize into uniform stacks along the a axis (Fig. 2b). Within the stacks, the plane-to-plane distance of donor molecules is 3.565 Å and that of acceptor molecules is 3.355 Å. Both donor and acceptor molecules reveal a bond-over-ring configuration, suggesting favourable orbital overlap. The nearest donor molecules adopt a face-to-face orientation (Fig. 3).

Fig. 2 Structure of α-[EDT-TTF(SeMe)₂](F₂TCNQ) with (a) a projection view along the a axis and (b) a projection view along the [−1 0 1] direction. Se⋯N ChB interactions are shown in dashed lines. Hydrogen atoms have been omitted for clarity.

Fig. 3 Overlap patterns of the donor (a) and the acceptor (b) molecules within α-[EDT-TTF(SeMe)₂](F₂TCNQ).

In the bc plane (Fig. 2a), the donor and the acceptor stacks are alternating along the b axis. A donor stack interacts with two adjacent acceptor stacks through chalcogen bonding interactions between the Se1 atom and the N1 atom of the nitrile substituents in F₂TCNQ with d(Se1⋯N1) = 3.331(5) Å (97% of van der Waals contact distance). More importantly, the interacting σ-hole of the Se atom is in the prolongation of the TTF–Se bond with the ∠C_TTF–Se1⋯N1 = 173°, indicating efficient σ-hole activation.

To estimate the degree of CT, the intramolecular bond distances within the donor and the acceptor molecules were analysed. Based on a formula developed in the literature,¹⁴ the charge of F₂TCNQ is estimated as ρ_A = −1.12. For the donor side, we used the reported structures of EDT-TTF(SeMe)₂ in neutral and radical cation states¹¹ to derive an analogue formula. Regarding the asymmetry of the substituents on TTF, we considered only C=C and C–S bond distances to establish a parameter δ_D = e − d, then made a linear relationship using ρ_D = (δ − δ₀)/(δ₁ − δ₀) as shown in Table 1. The estimated charge is ρ_D = +0.94, which is coherent with the value found for the acceptor. The almost essentially full charge transfer in the polymorph α and hence the fully oxidized radical character of TTF support the observed efficient σ-hole activation of Se and the formation of chalcogen bonding (vide supra).

Table 1 Intramolecular distances within the α-/β-[EDT-TTF(SeMe)₂](F₂TCNQ) salts compared with reference [EDT-TTF(SeMe)₂]^0/1+

	a	b	c	δ A	ρ A
α-Polymorph	1.422	1.411	1.412	0.497	−1.12
β-Polymorph	1.421	1.397	1.428	0.490	−0.70

---

	d	e	δ D	ρ D	Ref.
a–e values are averaged; δA = c/(b + d); δD = e − d; ρ = (δ − δ0)/(δ1 − δ0).
α-Polymorph	1.379(9)	1.724(9)	0.345	+0.94	This work
β-Polymorph	1.372(9)	1.729(9)	0.357	+0.77	This work
[EDT-TTF(SeMe)2]^0	1.348(9)	1.757(6)	0.409	0	10
[EDT-TTF(SeMe)2]^+	1.372(9)	1.729(9)	0.341	+1	10

---

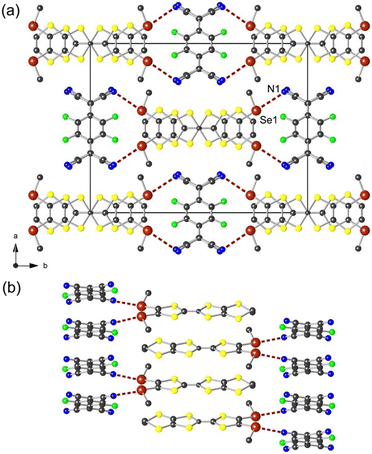
The polymorph β crystallizes in the monoclinic system, space group C2/c, with the donor molecule located on a 2-fold rotation axis and the acceptor molecule on an inversion centre. The donor and the acceptor molecules organize each into segregated uniform stacks along the c axis (Fig. 4). Within the stacks, both TTF and TCNQ molecules adopt the bond-over-ring configuration (Fig. 5). Compared to the polymorph α, the nearest TTF has an alternating head-to-tail overlap mode along the column and a slightly less pronounced longitudinal slip. The plane-to-plane distances for the donor and the acceptor are 3.812 and 3.236 Å, respectively. These values are larger than those observed in (TTF)(TCNQ), 3.451 and 3.188 Å, respectively, which has an impact on the electronic structure (vide infra).

Fig. 4 Structure of β-[EDT-TTF(SeMe)₂](F₂TCNQ) with (a) a projection view along the c axis and (b) a packing view, highlighting Se⋯N ChB interactions in dashed lines. Hydrogen atoms have been omitted for clarity.

Fig. 5 Overlap patterns of the donor (a) and the acceptor (b) molecules within β-[EDT-TTF(SeMe)₂](F₂TCNQ).

In particular, the long axis of the donor molecule is perpendicular to the long axis of the acceptor molecule, rendering an original pattern in the ab plane. As shown in Fig. 4b, this particular arrangement indeed allows for the TTF molecule to pinch the two TCNQ molecules of the same stack through the chalcogen bonding interaction between Se1 and N1 with d(Se1⋯N1) = 3.248(4) Å (94% of van der Waals contact distance). The angle ∠C_TTF–Se1⋯N1 amounts to 178°, again highlighting an efficient σ-hole activation, hence the oxidized character of the donor molecule. Such a ChB motif observed in the β-salt indeed brings F₂TCNQ molecules closer within the stack (3.236 Å) compared to those observed in the α-salt (3.355 Å). Moreover, the degree of charge transfer estimated for the acceptor and the donor correspond to −0.70 and +0.77, respectively, implying probably a partial charge transfer character in the polymorph β and hence a higher conductivity compared to that found for the polymorph α.

The resistivity of the two polymorphs and its temperature dependence reflect the structural observations. As shown in Fig. 6a, the α-salt shows a semiconducting behaviour with ρ_α ≈10 Ω cm (σ ≈ 0.1 S cm⁻¹) at room temperature. Fitting the data with an activation law, ρ = ρ₀ exp(E_a/kT), gives the activation energy E_a = 0.17 eV (2000 K). In contrast, the resistivity of the β-salt at room temperature is more than two orders of magnitude lower than that of the polymorph α: ρ_β ≈ 0.02 Ω cm (σ ≈ 50 S cm⁻¹) (Fig. 6b). Upon lowering the temperature, the resistivity shows a metallic behaviour down to a shallow minimum around 267 K and then a MI transition towards an insulating state at 180 K followed by another step at 160 K. Fitting the data to an activation law in both insulating regimes gives an activation energy E_a of 0.34 eV (4000 K) determined between 180 and 160 K and 0.09 eV (1100 K) determined below 160 K. If we compare the temperatures at which the metal-to-insulator transition occurs amongst organic 1D charge transfer salts, β-EDT-TTF(SeMe)₂[F₂TCNQ] shows a notably higher transition temperature than, for example, (TTF)(TCNQ) and [Me₂(SMe)₂TTF](TCNQ) that show a metal–insulator transition at respectively 59 and 56 K.^1,15 This result is in line with a lower conductivity at room temperature and higher activation energies in β-EDT-TTF(SeMe)₂[F₂TCNQ] compared to these two compounds as all these features are related to the more 2D character of the β-salt.

Fig. 6 Temperature dependence of the resistivity, measured on a single crystal of α- and β-[EDT-TTF(SeMe)₂](F₂TCNQ) (a and b, respectively). The red lines are the fit to the data with an activation law. The dashed black lines indicate the metal-to-insulator transitions in the β-salt. The insets show the same data with a linear vertical scale.

Electronic structure

To gain insights into the correlation between the structural and the electronic properties of the two polymorphs, first-principles DFT calculations were carried out. The degree of the charge transfer was evaluated from the donor and acceptor contributions to the calculated density of states (DOS) in the region of the partially filled bands. The calculated DOS as well as the donor and anion contributions for the hypothetical/real metallic state of the α-/β-[EDT-TTF(SeMe)₂](F₂TCNQ) salts are reported in Fig. 7a and b, respectively. The donor and anion components in both salts have the typical shape for one-dimensional band systems, and integration of these curves up to the Fermi level leads to a charge transfer of ρ = 0.87 e for the α-salt and ρ = 0.82 e for the β-salt. These values are definitely larger than those calculated for the related [Me₂(SMe)₂TTF](TCNQ) (ρ = 0.53 e) or even (TTF)(TCNQ) at room temperature (ρ = 0.57 e [experimental value: 0.59 e]) using the same computational settings,¹⁵ thus reflecting the stronger donor/acceptor character of the two partners in the present salts.

Fig. 7 Calculated densities of states and partial contributions of the donor and acceptor for the α- (a) and β-[EDT-TTF(SeMe)₂](F₂TCNQ) (b) salts, assuming metallic filling of the bands. The DOS values are given in units of states (without considering spin) per eV per unit cell.

Despite the strong donor/acceptor character found for both salts, the charge transfer calculated for the α-salt in its hypothetical metallic state is significantly larger than that found for the β case. The calculated band structures for both salts are shown in Fig. 8. These bands are mostly built from the HOMO of EDT-TTF(SeMe)₂ and the LUMO of F₂TCNQ. The different character of the bands undergoing a real/avoided crossing along the chain direction is indicated in the figures. For the α-salt, the charge transfer is not far from ρ = 1, so that the tendency to adopt a localized electronic distribution should be strong and indeed the dispersion of the energy bands is weak. For instance, the acceptor and donor bands of the α-salt are both narrower than those of TCNQ and TTF in TTF–TCNQ calculated with the same computational settings (26% and 17% for the acceptor LUMO and donor HOMO bands, respectively). Both features attest a strong tendency to localize with a ρ = 1 electron transfer. In contrast, while the donor bands have almost the same dispersion in both the α- and β-salts, the acceptor bands of the β-salt are considerably wider and in fact have exactly the same width as those calculated for TCNQ in metallic TTF–TCNQ.¹⁵ This suggests a stronger tendency to adopt a metallic state, as experimentally found. Taking a full ferromagnetic spin configuration as a simple model for a hypothetical localized state of the two salts with ρ = 1, we found that although with the present computational settings the metallic state is more stable in both cases, the energy difference is 67 meV per formula unit smaller for the α-salt, thus confirming the stronger tendency to localize for the α-salt.

Fig. 8 Calculated band structure for (a) α-[EDT-TTF(SeMe)₂](F₂TCNQ) and (b) β-[EDT-TTF(SeMe)₂](F₂TCNQ). Γ, X, M, Z and Y refer to (0, 0, 0), (a*/2, 0, 0), (a*/2, 0, c*/2), (0, 0, c*/2) and (0, b*/2, 0), respectively.

Since the α-salt contains two sets of symmetry equivalent molecules along the b interchain direction, all bands in Fig. 8a are actually the superposition of two almost identical bands, except around the regions where the bands cross or intend to cross. In the β-salt, there are four symmetry equivalent molecules of each type, two along the interchain diagonal directions, but also two along the chain direction, c. This is the reason why all bands in Fig. 8b are folded along the Γ–Z direction (i.e. the chain direction). The correlation between the crystal and the band structures of the two salts and, consequently, the origin of the different electron transfer, is developed in detail in the ESI.† The key observation is that in the β-salt the total bandwidth of the F₂TCNQ LUMO bands exhibits an increase of 35% with respect to those of the α-salt, whereas that of the EDT-TTF(SeMe)₂ HOMO bands exhibits a decrease of only 10%. Consequently, although the different types of overlap in both the donor and acceptor stacks contribute to the different electron transfer, the change in the acceptor stacks mostly controls the weaker transfer in the β-salt. The shorter interplanar spacing in the acceptor stacks is imposed by the separation between the two –SeMe substituents of the donor because the Se atoms of one donor molecule make short contacts with the N atoms of two acceptor molecules of the same stack because of the head-to-tail overlap mode of the donors. The shorter interplanar spacing induces a larger band dispersion for the acceptor stacks, thus substantially favouring the electronic delocalization. Such delocalization is maximized by decreasing as much as possible the electron transfer so that the system is as far as possible from the half-filled situation (i.e., ρ = 1 e). Ultimately, the electron transfer and the activated or non-activated conductivity of the two [EDT-TTF(SeMe)₂] (F₂TCNQ) salts are a consequence of the face-to-face or head-to-tail molecular overlap of the donors in the stacks. Even if of less importance, the analysis also points out that although weak, the interchain coupling is not nil in any of the two salts but it is indeed stronger in the β-salt. In summary, we conclude that the crystal structure of the β-salt is better prepared to sustain the electronic delocalization of a metallic state than that of the α-salt.

Let us briefly comment on the possible origin of the two transitions observed in the metallic β-salt when lowering the temperature. As for the different members of the TTF–TCNQ and related two-component conducting salts with segregated donor and acceptor stacks, the Fermi surface of β-[EDT-TTF(SeMe)₂](F₂TCNQ) results from the superposition of two very slightly warped planes perpendicular to the stack direction.^16,17 A schematic view of one of the Fermi surface sections is shown in Fig. 9. For all of these salts with segregated donor and acceptor stacks there is a weak hybridization of the planes associated with the donor (shown in blue in Fig. 9) and acceptor (shown in red in Fig. 9) components leading to closed hole and electron pockets. However, such hybridization effects are usually very weak. In general, the system ignores them because thermal effects blur the very small gap openings resulting from the hybridization and the salts behave as real 1D systems (i.e., Peierls distortions occurring in the donor and acceptor chains open bandgaps responsible for the low-temperature activated conduction). In that case, even the small warping of the independent donor and acceptor components of the Fermi surface is blurred by thermal effects and only the component of the nesting vector along the chain direction (q^I in Fig. 9) governs the distortion. The interchain components of the modulation vector are imposed by Coulomb effects between the modulations in different chains.

Fig. 9 Schematic (a*c*)-section of the Fermi surface for β-[EDT-TTF(SeMe)₂](F₂TCNQ) where the possible formation of electron and hole pocket are shown (see text).

If interchain interactions increase, as in the present salt, hybridization effects cannot be ignored. Under such circumstances, two different nesting vectors can be conceived, q^I and q^II (see Fig. 9). q^I would nest donor and acceptor zones of the closed pockets. Since the stacks are spatially separated, the driving force for the distortion will be very weak because of the small value of the matrix elements of the numerator in the real part of the susceptibility.¹⁸ Thus, only q^II can be a good nesting vector if hybridization effects are relevant and one could assume that the two transitions made clear in the resistivity measurements are associated with the two series of pockets.

A close examination of the band structure for the present salt (see X–Γ–Y in Fig. 8b) shows that it is the donor bands that acquire some interchain dispersion and this occurs in both interchain directions (i.e., Γ–X and Γ–Y). Because of the first observation, the closed pockets have a very irregular shape and the nesting vectors relating the hole or electron fragments of the closed pockets are slightly different. Because of the second observation, the pockets are closed along the two interchain directions (i.e. they are not cylinders with elliptical section but real 3D pockets) and thus effective nesting is in fact weak. Both factors would make such a mechanism, where hybridization effects are relevant, quite ineffective. This is not consistent with the high temperature at which the observed transitions take place, suggesting that the energy gain is larger than for any of the systems of the TTF–TCNQ family. We thus dismiss a mechanism where the hybridization effects of the Fermi surface are relevant. Consequently, we believe that a possible origin of the two-step transition of β-[EDT-TTF(SeMe)₂](F₂TCNQ) is the effective 1D mechanism at work for all other salts of the TTF–TCNQ family. However, the better communication between stacks brought about by the –SeMe substituents likely helps the 3D coupling of the modulations in different chains, ultimately leading to a very substantial increase of the transition temperature. It is worth noting at this stage that we cannot fully exclude the occurrence of charge ordering as the origin of the MI transition. To further investigate such a scenario, attempts to obtain low-temperature structures were performed but proved unsuccessful due to the low quality of the crystals, not only above T_MI but also below this abrupt transition. Dielectric measurements are needed to shed some light on these issues.

Conclusions

The foregoing results describe two polymorphs of a 1 : 1 charge transfer salt, α- and β-[EDT-TTF(SeMe)₂](F₂TCNQ). Both salts form segregated stacks of the donor and the acceptor molecules with a uniform inter-plane distance. Based on the structures, the degree of charge transfer was estimated to be ρ ∼±1 and ±0.8, respectively, for the α- and β-polymorphs. The packing of the donor and the acceptor stacks is significantly different between both polymorphs, both of which are uncommon among known conducting CT salts. The observed original packing structures for both polymorphs are in part supported by efficient ChB interactions between the activated Se and N atoms of F₂TCNQ that are highly linear. Owing to the head-to-tail overlap mode of the donor molecules in the β-salt, the ChB interactions between one donor molecule and two acceptor molecules of the same stack resulted in a short plane-to-plane distance. In contrast, the face-to-face overlap mode of the donors in the α-salt allows the formation of ChB between one donor molecule and two acceptor molecules of different stacks. The difference in the CT degree in conjunction with the distinct solid-state organization led to fully different electronic transport in the two polymorphs. A semi-conducting behaviour was observed in the α-polymorph, while a metallic behaviour with a two-step metal-to-insulator transition was observed in the β-polymorph. Furthermore, the 3D coupling of the modulations in different chains brought about by –SeMe substituents likely led to a very substantial increase of the metal-to-insulator transition temperature compared to other known 1D CT salts.

Experimental

General

EDT-TTF(SeMe)₂ was prepared as previously reported¹⁰ and F₂TCNQ is commercially available and was used as received. CVs were carried out on a CH₂Cl₂ solution of complex with 0.2 M Bu₄NPF₆. Potentials were measured versus a saturated calomel electrode (SCE).

α-[EDT-TTF(SeMe)₂](F₂TCNQ). A solution of EDT-TTF(SeMe)₂ (10 mg, 2.1 × 10⁻⁵ mol) in 1,1,2-trichloroethane (0.5 mL) was layered first with a solution of toluene: 1,1,2-trichloroethane = 9 : 1 and then with a solution of F₂TCNQ (4 mg, 1.7 × 10⁻⁵ mol) in CH₃CN (1 mL). Slow diffusion at ambient temperature over two weeks afforded black needle-shaped crystals of the title compound.

β-[EDT-TTF(SeMe)₂](F₂TCNQ). A solution of EDT-TTF(SeMe)₂ (10 mg, 2.1 × 10⁻⁵ mol) in CH₂Cl₂ (0.7 mL) was layered first with a solution of toluene : CH₂Cl₂ = 9 : 1 and then with a solution of F₂TCNQ (4 mg, 1.7 × 10⁻⁵ mol) in CH₃CN (1 mL). Slow diffusion at 4 °C over two weeks afforded black plate-shaped crystals of the title compound.

X-ray crystallography

Single crystals of α-[EDT-TTF(SeMe)₂](F₂TCNQ) and β-[EDT-TTF(SeMe)₂](F₂TCNQ) that were suitable for X-ray analysis were coated with Paratone-N oil and mounted on a MicroMounts™ rod. X-ray diffraction measurements were performed on a Bruker APEX II diffractometer operating with a Mo Kα (λ = 0.71073 Å) X-ray tube with a graphite monochromator. Structures were solved by a dual-space algorithm using SHELXT¹⁹ and then refined with full-matrix least-squares methods based on F² (SHELXL-2014)²⁰ with the aid of the WINGX program.²¹ All non-hydrogen atoms were refined with anisotropic atomic displacement parameters. H atoms were finally included in their calculated positions. The refinement of both structures has been done on the basis of HKLF 5 file, generated with TWINABS. The single reflections that also occur in composites have been omitted. Crystallography data (in cif format) have been deposited with deposition numbers CCDC 2247520 and 2247521. Crystallographic data of the α-salt: C₂₂H₁₂F₂N₄S₆Se₂, M_r = 720.64, monoclinic, a = 4.0174(5), b = 24.7410(18), c = 13.0728(10) Å, β = 95.086(5), V = 1294.2(2) ų, T = 296(2) K, space group P2/m, Z = 2, 3923 reflections measured, 2342 unique (R_int = 0.0553), which were used in all the calculations. The final wR₂(F²) was 0.1047 (all data). Crystallographic data of the β-salt: C₂₂H₁₂F₂N₄S₆Se₂, M_r = 720.64, monoclinic, a = 16.3862(16), b = 20.785(2), c = 7.6276(9) Å, β = 100.272(6), V = 2556.2(5) ų, T = 296(2) K, space group C2/c, Z = 4, 2416 reflections measured, 1929 unique (R_int = 0.0841), which were used in all the calculations. The final wR₂(F²) was 0.1149 (all data).

Transport measurements

The resistivity measurements were performed along the long axis of needle-shaped crystals of α-[EDT-TTF(SeMe)₂](F₂TCNQ) and β-[EDT-TTF(SeMe)₂](F₂TCNQ). Gold wires were glued with silver paste on aligned gold pads previously evaporated on one face of the single crystals to improve the quality of the electrical contacts. For the less conducting α-salt, the temperature dependence of the resistivity was measured either in two points by applying a constant voltage (2 V) and measuring the current with a Keithley 486 picoammeter or in four points by applying a DC current (0.1–1 μA) and measuring the voltage with a Keithley 2400 source meter. We have shown in Fig. 6a the data obtained using the two points method as it allows measuring down to lower temperature. The resistivity value is slightly higher compared to the four points result but the activation energy is the same for both methods. For the more conducting β-salt, resistivity measurements were performed using a low-frequency (<100 Hz) AC current of 1 μA with lock-in amplifier detection. Low temperature was achieved with a homemade cryostat working down to liquid nitrogen temperature.

Theoretical calculations

First-principles calculations were carried out using a numeric atomic orbital density functional theory (DFT) approach^22,23 developed for efficient calculations in large systems and implemented in the SIESTA code.^24–27 We used the generalized gradient approximation (GGA) to DFT and, in particular, the functional of Perdew, Burke, and Ernzerhof.²⁸ All calculations included a Hubbard correction term U_eff = U − J = 6.0 eV for the S 3p states.²⁹ In previous studies¹⁵ we have found that this U term on the chalcogen atoms is needed for appropriately describing the electronic structure of molecular conductors where accurate experimental information on the bandwidth and charge transfer is available. The effect of including an on-site repulsion term U_eff for the Se 4p orbital has also been explored. Only the valence electrons are considered in the calculation, with the core being replaced by norm-conserving scalar relativistic pseudopotentials³⁰ factorized in the Kleinman–Bylander form.³¹ We have used a split-valence double-ζ basis set including polarization orbitals with an energy shift of 10 meV (ref. 32) for all atoms. The energy cutoff of the real space integration mesh was 300 Ry. The Brillouin zone was sampled using grids³³ of (25 × 5 × 5)/(50 × 2 × 2) and (3 × 3 × 10)/(2 × 2 × 40) k-points for generation of the density matrix/DOS of the α- and β-salts, respectively. Room-temperature crystal structures were used for the computations.

Author contributions

I.-R. J. and M. F. formulated the project. M. B. synthesized and crystallized the compounds. O. J. collected and solved X-ray diffraction data. P. A. and E. C. performed the calculations. P. A.-S. and C. P. performed electric measurements. I.-R. J., M. F., and E. C. wrote the paper and all the authors contributed to revising it.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Work in France was supported by the French National Research Agency Grant ANR 17-ERC3-0003 and a PhD grant (to M. Beau) from Région Bretagne. We thank the CDIFX in Rennes for the use of the X-ray diffractometer. Work in Spain was supported by MICIU through Grants PGC2018-096955-B-C44 and PID2021-128217NB-I00, Generalitat de Catalunya (2021SGR01519 and 2021SGR00286). E. C. acknowledges the support of the Spanish MICIU through the Severo Ochoa FUNFUTURE (CEX2019-000917-S) Excellence Centre distinction and P. A. acknowledges the support from the Maria de Maeztu Units of Excellence Program (CEX2021-001202-M).

Notes and references

1. (a) A. J. Heeger and A. F. Garito, AIP Conf. Proc., 1972, 10, 1476; (b) J. H. Perlstein, J. P. Ferraris, V. V. Walatka and D. O. Cowan, AIP Conf. Proc., 1972, 10, 1494; (c) J. P. Ferraris, D. O. Cowan, V. V. Walatka and J. H. Perlstein, J. Am. Chem. Soc., 1973, 95, 948.
2. H. M. McConnell, B. M. Hoffman and R. M. Metzger, Proc. Natl. Acad. Sci. U. S. A., 1965, 53, 46.
3. P. Batail, K. Boubekeur, M. Fourmigué and J.-C. P. Gabriel, Chem. Mater., 1998, 10, 3005.
4. S. A. Baudron, C. Mézière, K. Heuzé, M. Fourmigué, P. Batail, P. Molinié and P. Auban-Senzier, J. Solid State Chem., 2002, 168, 668.
5. G. Ono, H. Terao, S. Higuchi, T. Sugawara, A. Izuoka and T. Mochida, J. Mater. Chem., 2000, 10, 2277.
6. A. J. Moore, M. R. Bryce, A. S. Batsanov, J. N. Heaton, C. W. Lehmann, J. A. K. Howard, N. Robertson, A. E. Underhill and I. F. Perepichka, J. Mater. Chem., 1998, 8, 1541.
7. T. Murata, Y. Morita, Y. Yakiyama, K. Fukui, H. Yamochi, G. Saito and K. Nakasuji, J. Am. Chem. Soc., 2007, 129, 10837.
8. M. Fourmigué and P. Batail, Chem. Rev., 2004, 104, 5379.
9. J. Lieffrig, O. Jeannin, A. Frąckowiak, I. Olejniczak, R. Świetlik, S. Dahaoui, E. Aubert, E. Espinosa, P. Auban-Senzier and M. Fourmigué, Chem. – Eur. J., 2013, 19, 14804.
10. A. Frąckowiak, R. Świetlik, L. Maulana, D. Liu, M. Dressel, O. Jeannin and M. Fourmigué, J. Phys. Chem. C, 2020, 124(10), 5552.
11. M. Beau, O. Jeannin, M. Fourmigué, P. Auban-Senzier, F. Barrière and I.-R. Jeon, CrystEngComm, 2022, 24, 7535.
12. C. Jia, D. Zhang, Y. Xu, W. Xu, H. Hu and D. Zhu, Synth. Met., 2003, 132, 249.
13. G. Saito and J. P. Ferraris, Bull. Chem. Soc. Jpn., 1980, 53, 2141.
14. P. Hu, K. Du, F. Wie, H. Jiang and C. Kloc, Cryst. Growth Des., 2016, 16, 3019.
15. Y. Kiyota, I.-R. Jeon, O. Jeannin, M. Beau, T. Kawamoto, P. Alemany, E. Canadell, T. Mori and M. Fourmigué, Phys. Chem. Chem. Phys., 2019, 21, 22639.
16. J. P. Pouget, in Semiconductors and Semimetals, ed. E. M. Conwell, Academic Press, New York, 1988, 27, p. 87.
17. D. Jérome and H. J. Schulz, Adv. Phys., 1982, 31, 299.
18. H. Ehrenreich and M.-H. Cohen, Phys. Rev., 1959, 115, 786.
19. G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3.
20. G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3.
21. L. J. Farrugia, J. Appl. Crystallogr., 2012, 45, 849.
22. P. Hohenberg and W. Kohn, Phys. Rev. B, 1965, 136, 864.
23. W. Kohn and L. J. Sham, Phys. Rev. A, 1965, 140, 1133.
24. J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745.
25. E. Artacho, E. Anglada, O. Diéguez, J. D. Gale, A. García, J. Junquera, R. D. Martin, P. Ordejón, M. A. Pruneda, D. Sánchez-Portal and J. M. Soler, J. Phys.: Condens. Matter, 2008, 20, 064208.
26. A. García, N. Papior, A. Akhtar, E. Artacho, V. Blum, E. Bosoni, P. Brandimarte, M. Brandbyge, J. I. Cerdá, F. Corsetti, R. Cuadrado, V. Dikan, J. Ferrer, J. D. Gale, P. García-Fernández, V. M. García-Suárez, V. M. García, G. Huhs, S. Illera, R. Korytar, P. Koval, I. Lebedeva, L. Lin, P. López-Tarifa, S. G. Mayo, S. Mohr, P. Ordejón, A. Postnikov, Y. Pouillon, M. A. Pruneda, R. Robles, D. Sánchez-Portal, J. M. Soler, R. Ullah, V. W.-Z. Yu and J. Junquera, J. Chem. Phys., 2020, 152, 204108.
27. For more information on the SIESTA code visit: http://departments.icmab.es/leem/siesta/.
28. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1966, 77, 3865.
29. S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505.
30. N. Troullier and J. L. Martins, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 1993–2006.
31. L. Kleinman and D. M. Bylander, Phys. Rev. Lett., 1982, 48, 1425.
32. E. Artacho, D. Sánchez-Portal, P. Ordejón, A. García and J. M. Soler, Phys. Status Solidi B, 1999, 215, 809–817.
33. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 2247520 and 2247521. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3ce00260h

---