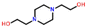Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A to Z of polymorphs related by proton transfer†
Amy
Woods-Ryan
 ab,
Cheryl L.
Doherty
ab,
Cheryl L.
Doherty
 a and
Aurora J.
Cruz-Cabeza
a and
Aurora J.
Cruz-Cabeza
 *b
*b
aMedicine Development and Supply, GlaxoSmithKline, GSK Medicines Research Centre, Gunnels Wood Road, Stevenage, Hertfordshire, UK
bDepartment of Chemistry, Durham University, South Road, Durham, UK. E-mail: aurora.j.cruz-cabeza@durham.ac.uk
First published on 3rd May 2023
Abstract
The occurrence of tautomeric polymorphism in the Cambridge Structural Database (CSD) was established to be very rare in a previous study by A. J. Cruz-Cabeza and C. R. Groom (CrystEngComm, 2011, 13, 93). A decade has now elapsed and the CSD has seen a significant increase in its total number of crystal structures, useful CSD subsets have been introduced and the CSD Python API has been developed to allow for complex data mining. Given this, we wanted to revisit tautomeric polymorphs in the CSD alongside other polymorphs related by proton transfer and compare these results with those from an in-house pharmaceutical database in order to assess their prevalence and significance for pharmaceuticals. From A (amine–imine tautomeric polymorphs) to Z (zwitterionic polymorphs), here we study different types of polymorphs related by proton-transfer in the CSD, the CSD drug subset (DrugCSD), the single component drug subset of the CSD (SDrugCSD), and the GSK small molecule crystal structure database (GSD). First, we assess the potential of compounds to exist as tautomers. Whilst 51% of compounds in the CSD are capable of tautomerism, this number increases to 73% and 70% for the SDrugCSD and the GSD respectively. Tautomerism potential is, thus, more prevalent in pharmaceuticals than in common organic compounds in the CSD. Second, in mining the CSD we identify a total of 95 families of polymorphs related by proton transfer which can then be classified into six different categories depending on the type of proton transfer observed and the ionisation of species involved. The most common of such category is that of tautomeric polymorphs followed by zwitterionic polymorphs. The rarest type of proton transfer polymorphs is that of multi-zwitterionic polymorphs where two different zwitterions of the same compound are found in two different crystal structures. Overall, 3% of polymorphic compositions in the DrugCSD are found to be related by proton transfer which, although not very common, is of relevance to pharmaceuticals and drug development due to the potential impact on physical properties. Specific examples of each of the categories are discussed with calculations of lattice energies presented and consideration of ΔpKa values and likelihood of proton transfer and ionisation.
Introduction
Molecules with labile protons can exist in different chemical states related by the transfer of a proton. The population for each of these states is dictated by chemical equilibrium and thus the environment in which the species exist. The transfer of a proton can occur within a compound or between compounds in the gas-phase, solution or the solid state, and it may or may not be also accompanied by the generation of charge or the re-arrangement of bonds. The most common types of molecular species related by proton transfer are prototropic tautomers and ampholytic compounds able to exist in an overall neutral state without or with separation of charges.Prototropic tautomerism is the interconversion of isomers of a compound via the movement of a proton in combination with the rearrangement of double bonds within the molecule.1 Examples of prototropic tautomerism include functional tautomerism (involving a change in functional groups, i.e. keto–enol and enamine–imine tautomerism) and annular tautomerism2 (involving prototropic tautomerism in heterocyclic ring systems) amongst others. Compounds containing an acidic and a basic group (ampholytes) may be able to exist as a neutral molecule with no separation of charges or as a neutral molecule with localised charges (zwitterion). Zwitterions are also referred to as inner salts.
In solution, tautomers exist in equilibrium and their populations are determined by the relative stability of their molecular structures which can vary as a function of temperature, solvent and pH.3–5 In most cases, these factors lead to an equilibrium which strongly favours a single tautomer. Similarly, ionisable molecules of various types can exist as non-ionised, protonated, deprotonated or even zwitterionic, with their speciation in solution impacted by the same factors and thus their interconversion can be considered a subset of tautomerism with proton transfer but no re-arrangement of bonds. The specific molecular species present in solution impact the physicochemical properties of compounds such as reactivity, pKa, and even biological activity (which has implications for drug development).6–8
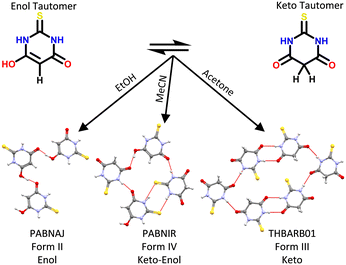
In the solid state, it is generally considered that the tautomeric form present in a crystal is fixed under a specific set of conditions. Unlike in solution, a dynamic equilibrium between molecular species often does not exist in the solid state. Instead, the intermolecular interactions found in the crystal can shift the tautomeric state of the compound for tautomeric states differing by up to 35 kJ mol−1 in tautomeric energy (non-ionised tautomers in this case).9 Different tautomers can be observed within the same crystal (co-crystallised) or within different polymorphic structures.10 A rich example of tautomeric and polymorphic diversity is that of 2-thiobarbituric acid (Fig. 1) which can exist in the solid state in six polymorphs, namely its pure enol form (II), its pure keto form (I, III, V and VI) and its enol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) keto form (IV).11 The specific nomenclature of the various types of these polymorphs can become complex,12 but they all sit under the umbrella of polymorphs related by proton transfer.
keto form (IV).11 The specific nomenclature of the various types of these polymorphs can become complex,12 but they all sit under the umbrella of polymorphs related by proton transfer.
As with other types of polymorphism, polymorphs related by proton transfer can have different solid state properties. From a pharmaceutical perspective, the primary concern with this is the impact of polymorphic form on properties such as solubility, dissolution rate and bioavailability of the drug product. Further to these, the polymorphic form's morphology, bulk density and chemical stability can impact drug product manufacturability.13 Several studies in the literature14–18 have highlighted some difficulties associated with the control and isolation of polymorphs related by proton transfer, with many of them crystallising concomitantly. Consequently, developing solid forms of pharmaceuticals able to tautomerise may be complex since a pure single phase is usually desired to ensure consistent quality and performance of a drug product.
In this context, the main motivation for the present work was to mine available crystallographic data to establish how common tautomerism potential is in general chemical compounds and in pharmaceuticals, and to quantify and report the occurrence of complex polymorphism related by various types of proton transfer. Whilst there has been a previous investigation on tautomerism in the CSD,9 over a decade has elapsed and since the CSD has more than doubled in size to 1 million structures.19 Further to this, here we look at more broad cases of polymorphism related by proton transfer including tautomeric polymorphs, zwitterionic polymorphs and other more complex systems such as salts related by single versus multi-proton transfer.
Overview of tautomerism and the solid state
Techniques for tautomer characterisation
Historically, hydrogen atoms (H-atoms) have been notoriously difficult to locate in crystal structures from direct measurement of conventional X-ray diffraction due to their weak scattering. As a result, H-atom positions are often implied by the geometries of other heavier atoms, provided there is no disorder in the structure. So whilst it is possible to reliably obtain H-atom positions from good X-ray diffraction data, challenges still exist for the study of tautomeric systems and mis-determinations are not uncommon if the quality of diffraction data is not optimal.20Crystal structure determination is usually conducted at sub-ambient temperatures to minimise thermal effects. However, a change in temperature itself can cause proton migration within a crystal and impact the relevance of the structure to the room temperature form. The thermal migration of protons within a crystal structure has been documented in salt–cocrystal pairs and tautomeric molecules.18,21,91 The application of both temperature and pressure has also been shown to cause proton transfer in squaric acid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) bipyridine adducts together also with a change of polymorphic form.22 Additionally, light-induced keto–enol transformations have been observed within the solid state, indicating that exposure to light could be important when handling and collecting structural data on potentially photo-sensitive compounds.23
bipyridine adducts together also with a change of polymorphic form.22 Additionally, light-induced keto–enol transformations have been observed within the solid state, indicating that exposure to light could be important when handling and collecting structural data on potentially photo-sensitive compounds.23
For absolute confidence in crystal structure determination of complex systems, especially for molecules capable of tautomerism or materials for which proton positions are critical, orthogonal techniques such as neutron diffraction, solid state nuclear magnetic resonance (ssNMR) and infrared spectroscopy can be used to re-confirm assignment of proton positions.22,24–27 Emerging techniques such as near-edge X-ray absorption fine structure spectroscopy (NEXAFS), in combination with density functional theory (DFT), have also been used to confirm exact H-atom positions in salt–cocrystal systems.28
DFT can be used to calculate the relative stability of tautomers and to predict the effect of different solvents on their equilibrium. For instance, the computed relative stability of sulfasalazine tautomers in DMF and water has been used to rationalise the preference for specific tautomeric forms observed in these solvents.29 However, modelling can be challenging due to the sensitivity of tautomer energies to model chemistries and basis sets used. Perhaps the most significant errors in the modelling arise from the difficulty of accounting for electron delocalisation30 with DFT. Such errors can be overcome and accuracy improved with the aid of higher order Hartree–Fock methods which comes at a high computational cost.31
Prevalence of tautomerism in chemical databases (prior work)
The potential for tautomerism in various compounds from various databases has been assessed previously. For this, specific definitions of rules for tautomerisation reactions need to be derived and applied, and the types of rules used will undoubtedly impact the resulting statistics. The Chemical Structure Database (of the National Cancer Institute Computer-Aided Drug Design Group) is a collection of 103.5 million synthesised small molecular structures, 68% of which have been reported to have potential for tautomerism.32 Using different tautomerisation rules and different databases, Martin8 reported that 26% of 1791 marketed drugs are tautomeric and Cruz-Cabeza and Groom9 that 10% of molecules in the Cambridge Structural Database (CSD) have the potential for tautomerism. The range of tautomeric potential reported from these various databases, using various tautomerisation rules, spans from just 10% to 68%.Perhaps a more unbiased way of looking at tautomerism prevalence is by direct observation of tautomers in the crystal structures rather than by predicting tautomerism potential based on tautomerisation rules applied on chemical compounds. Even if tautomerism potential is predicted, the energy of the various tautomers will dictate whether they can be observed experimentally. Unsurprisingly, calculated relative stabilities of tautomers mirror the frequency of occurrence of tautomers in the CSD, with high-energy tautomers often not observed in the solid state. Thus, whilst potential for tautomerism may be high, only a small fraction of compounds with tautomerism potential exist in various tautomeric forms in the solid state (0.5%)9 and this is dictated by the tautomer energy as well as the intermolecular interactions in the crystal. Based upon those observations, a general rule was proposed by Cruz-Cabeza and Groom: ‘for different tautomers to be observed in the solid state, their relative energy must not exceed that of a strong hydrogen bond in an organic crystal’.9
From the point of view of ionisation, the prevalence of zwitterionic polymorphs and salt–cocrystal pairs in the CSD has also been investigated in previous works.14,15,33–36 A search of the CSD in 2010 found only four single component molecules (clonixin, norfloxacin, anthranilic acid, torasemide) with both neutral non-ionised and zwitterionic forms.15 The majority of these were molecules of pharmaceutical interest.
Relative stabilities of tautomers
Using computational chemistry, the relative stability of tautomers and ionised species can be estimated and used as a predictor for their experimental observation.For neutral species related by proton transfer, the most commonly observed tautomers are typically also the most stable, except for where the energy difference between them is small (<5 kJ mol−1). In those cases, intermolecular interactions in the solid state can shift the tautomeric outcome.2
There are exceptions, however, which have reported the observation of very high-energy tautomers in the solid state. Such is the case of the enol-tautomer of barbituric acid which, despite being highly metastable (53.7 kJ mol−1), is found in the most stable overall polymorphic form. This stable polymorph of barbituric acid was notoriously difficult to discover and was only produced relatively recently by ball-mill grinding.37,38 The ability of some molecules to tautomerise can be used to our advantage and a specific tautomer targeted and crystallised. For example, Epa et al. used supramolecular cocrystal design to selectively crystallise and isolate the high-energy tautomer of 1-deazapurine.39 This ability to deliberately stabilise a metastable tautomer is important and provides the opportunity to isolate novel solid state forms containing different tautomers and displaying different physical properties.
For neutral vs. charged species related by proton transfer, energy differences between molecular species can be much larger (in the order of hundreds of kJ mol−1 in some cases). Some general trends can be assumed. For example, in the gas-phase, a zwitterion or charged pair of molecules will always have a much higher energy than their non-ionised counterparts, due to the unfavourable separation of charges. This relative stability can often change in solution or the solid state due to the stabilisation of species brought about by coulombic interactions in charged systems. Many of the common amino acids exist as zwitterions in solution and the solid state but as neutral in the gas phase (i.e. glycine40).
Methods
Datasets
Refcode lists (entire CSD, CSD drug subset & CSD single component drug subset) were extracted from the Cambridge Structural Database (CSD) version 5.42 using ConQuest.All datasets were created using the ‘Best Hydrogens List’ subset which removes duplicates and redeterminations. Additionally, the entire CSD dataset was further refined to only allow for compounds containing any combination of a subset of atom types (H, D, C, N, O, F, P, S, Cl, Br, I) and only include organic, non-polymeric structures with 3D co-ordinates determined and no errors. Application of these filters resulted in 293![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 984 entries for the entire CSD (CSD), 7787 entries for the CSD drug subset (DrugCSD) and 729 entries for the CSD single component drug subset (SDrugCSD). Additionally, the GSK structural database (GSD) was assessed with duplicates and redeterminations removed and contained 1820 entries. The GSK database of small-molecule crystal structures contains X-ray crystallography data obtained over the past 40 years by GSK and legacy companies. The structures are not limited to marketed drugs and the GSD contains molecules from all phases of development, including non-API molecules such as intermediates or impurities. Conversely, the DrugCSD consists of small-molecule crystal structures containing only approved drug molecules. The SDrugCSD contains crystal structures of pure neat drug compounds, thus not multi-component systems.
984 entries for the entire CSD (CSD), 7787 entries for the CSD drug subset (DrugCSD) and 729 entries for the CSD single component drug subset (SDrugCSD). Additionally, the GSK structural database (GSD) was assessed with duplicates and redeterminations removed and contained 1820 entries. The GSK database of small-molecule crystal structures contains X-ray crystallography data obtained over the past 40 years by GSK and legacy companies. The structures are not limited to marketed drugs and the GSD contains molecules from all phases of development, including non-API molecules such as intermediates or impurities. Conversely, the DrugCSD consists of small-molecule crystal structures containing only approved drug molecules. The SDrugCSD contains crystal structures of pure neat drug compounds, thus not multi-component systems.
Tautomer generation
The CSD Python API41 was utilised to loop through each crystal entry of each dataset and separate the structure into individual molecular components. The resultant molecules were standardised (bond types assigned and H-atoms positions added if missing). Tautomers for each unique molecule were generated using the ‘Tautomer Enumerator’ function of the RDKit42 module in Python. The tautomer enumeration rules are based upon those described by Sitzmann et al.32 A maximum of 50 tautomers were enumerated for each molecule. Enumeration was conducted twice for each dataset to assess differences in the tautomers generated if bond and sp3 stereochemistry was allowed to be lost or not during enumeration. A molecule was deemed to be potentially tautomeric if more than one tautomer was enumerated during the tautomer generation step.Identification of polymorphs with protonation diversity
A scripted approach comparing canonical SMILES, SMILES, standard InChI and non-standard InChI (FixedH) strings was used to identify ‘same’ molecules where multiple tautomers had been observed in the solid state. The use of these identifiers enabled determination of multiple types of tautomerism including forms where charges are in distinct positions in different structures, multi-component systems that can exist as salts and cocrystals, zwitterionic polymorphs, and tautomeric polymorphs.Processing of polymorphic structures
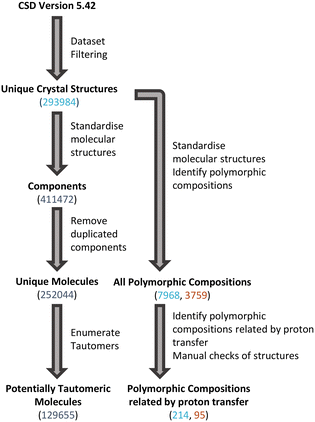
The scripted nature of searches in large databases can result in some incorrectly identified structures beyond the potential for structures with mis-determined H-atom positions. Therefore, additional manual checks were conducted to identify and eliminate any groups of structures which were not real sets of polymorphs related by proton transfer. These checks (performed in Mercury43) included visualisation of structures, Mogul geometry checks, crystal packing similarity and simple metadata checks. The overall process used to identify tautomeric molecules and polymorphic compositions related by proton transfer is shown in Fig. 2.Generation of calculated pKa
Aqueous pKa values were calculated and visualised using JChem for Excel.44 The pKa for the strongest acid and strongest protonated base for relevant molecules in crystal structures of interest were recorded and the ΔpKa was calculated as in eqn (1).| ΔpKa = pKa[protonated base] − pKa[acid] | (1) |
DFT calculations
CSD crystal structures of interest were imported into Materials Studio.46 For each polymorphic pair, structures obtained at the same temperature were chosen where possible. Supercells were prepared when initial unit cell lengths were much less than 10 Å in any dimension. Each crystal structure was geometry optimised using CASTEP47 with the Perdew–Burke–Ernzerhof48 gradient-corrected functional (GGA PBE) with the Tkatchenko and Scheffler (TS)49 scheme for dispersion correction and OTFG ultrasoft pseudopotentials. Geometry optimisations were performed using a plane wave basic cut-off energy of 600 eV. The Brillouin zone was sampled using a k-point spacing of approximately 0.05 Å−1 and a SCF tolerance of 1.0 × 10−6 eV per atom was used. Full cell optimisations were performed.Separately, molecules were geometry optimised in the gas phase using finer settings and starting from molecular geometries taken from the crystal structures. Each molecule was placed in a box with the dimensions ensuring approximately ≥12.5 Å free space surrounding the molecule in all directions. Geometry optimisations were performed using the same procedure as above.
After crystal and gas-phase geometry optimisations, single-point energy calculations were performed on the gas phase molecules and crystal structures with application of the many-body dispersion correction scheme (MBD*)50 and with a plane wave basic cut-off energy of 630 eV. The Brillouin zone was sampled using a k-point spacing of 0.07 Å−1 and a SCF tolerance of 5.0 × 10−7 eV per atom. Geometry optimisation and single-point energy calculation settings were adjusted as required for good convergence.
Lattice energy calculations
Lattice energies (ELatt) were calculated according to the eqn (2) and (3) for single component and multi-component systems, respectively.| ELatt = (Ecell/Z) − Egas | (2) |
| ELatt = (Ecell/Z) − (Egas(A) + Egas(B)) | (3) |
Results and discussion
Tautomerism potential of molecules in the CSD
Based on a broad set of tautomerisation rules (as defined in RDKit), we found that around 52% of molecules in the CSD (129655) have the potential for tautomerisation. Interestingly, this proportion increases slightly for the DrugCSD (53%, 1446 molecules) and significantly for the SDrugCSD (73%, 387 molecules). The SDrugCSD statistics are well in line with the GSD where 70% of compounds were found to have tautomerisation potential (1467 molecules). The statistics are summarised graphically in Fig. 3. Varying the RDKit tautomer enumeration rules (to either keep or lose stereochemistry during enumeration) did not significantly impact the statistics.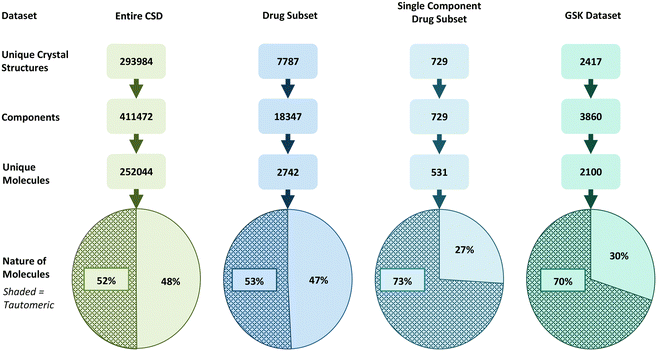 | ||
| Fig. 3 Datasets of crystal structures studied here split into crystal entries, components, and unique molecules able (shaded) and unable (non-shaded) to tautomerise. | ||
The lower incidences of molecules able to tautomerise found in the CSD and DrugCSD datasets may be due to the inclusion of components such as solvents, counter-ions, and co-formers, whereas the SDrugCSD only contains neat drug molecules. Previous analyses of the CSD, DrugCSD and other pharmaceutical databases have shown that drug-like molecules are significantly larger (higher molecular weight) than the organics in the CSD, thus increasing the probability of a drug molecule containing a tautomerisable functional group.51 Also of note is the fact that the GSD has a much larger proportion of ‘free drug’ structures (58.07%) than the DrugCSD (19.53%).52 These results indicate a much higher fraction of molecules in the CSD are capable of tautomerism than initially identified by Cruz-Cabeza and Groom (10%).9 Similarly, these numbers are much higher than those reported in marketed drugs (26%).8 One reason for this discrepancy is likely to be due to the differences in the tautomer enumeration rules. For example, Cruz-Cabeza and Groom did not allow keto–enol tautomerism, which is considered in the transform rules within RDKit.32
Rather than a comparison of absolute numbers across different methods, the value of current analysis lies in the comparison of the different datasets with the same method. This comparison clearly points towards tautomerism potential being significantly more prevalent in drug compounds than in other small molecules in the CSD.
Ampholyte potential of molecules in the CSD
Another important set of species related by proton transfer are ampholytes which may potentially exist as non-ionised and/or zwitterionic. It was found that 32% of the SDrugCSD structures contain a compound identified to have both an acidic and a basic group and therefore a ΔpKselfa could be calculated.45 Only 10% of the CSD and 14% of the DrugCSD molecules (heaviest component) were found to have ampholytic potential. Of those compounds able to be ampholytic, 11%, 32% and 26% are found as zwitterions in the CSD, DrugCSD and SDrugCSD respectively with the remaining existing in the non-ionised state (Fig. 4). These statistics highlight the higher potential for self-proton transfer in drug compounds, with the crystal composition also influencing it.45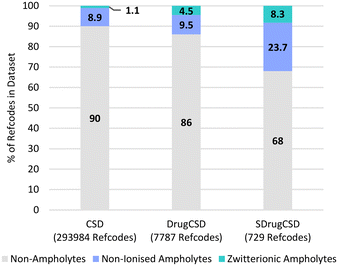 | ||
| Fig. 4 Ionisation behaviour of heaviest component in the various crystal structures within the three CSD subsets studied here. | ||
Classification of polymorphs related by proton transfer
A well accepted definition of crystal polymorphism is that a polymorph is ‘a solid crystalline phase resulting from different arrangements of molecules in the solid state...two polymorphs will be different in crystal structure but identical in the liquid and vapour states’.53 Where interconversion of molecular species is rapid in the liquid, crystals containing different tautomers or charged species of a compound (or compounds) will lead to identical population of species in the liquid and therefore can be classified as polymorphs. Tautomeric polymorphism of this type has been referred to as desmotropy elsewhere.12,16,54–59Polymorphs related by proton transfer may exist with very different or with nearly identical crystal packings (the main difference being the position of a H-atom). If a change in hydrogen position is accompanied with a discontinuity in the heat capacity at some specific conditions of temperature or pressure, the crystal structures shall be considered as polymorphs or phases. This type of high structural similarity polymorphism may indeed be challenging to identify, especially from X-ray data alone.60
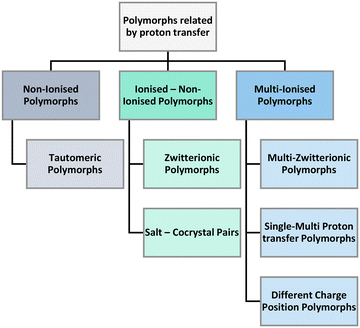
In our search of the CSD we have identified three main umbrellas of polymorphs related by proton transfer branching into six distinct categories (Fig. 5). The three umbrellas relate to the ionisation state of the constituent components. Proton transfer may occur generating sets of polymorphs that are non-ionised or have mixed or multiple ionisations.
Under the first umbrella (no ionisation), we find tautomeric polymorphs where multiple tautomers have been isolated individually (and/or jointly) in different crystal structures. These are observed in single as well as multicomponent systems. Under the second umbrella (non-ionised and ionised pairs), we find zwitterionic polymorphs (where some structures are non-ionised whilst others are zwitterionic) as well as salt–cocrystal pairs (structures exist both with and without proton transfer between the components). Finally, under the third umbrella (multiple ionisation), we find three categories of polymorphs namely multi-zwitterionic polymorphs (where the polymorphs are all zwitterionic but the local charges are distributed in different atoms), multi-component systems with multiple proton transfers (i.e. monovalent and divalent salts) and structures with different protonation positions (i.e. salts where a proton can transfer to/from multiple different functional groups). To aid the understanding of these polymorphs, examples of pairs of each category and their composition are given in Table 1 where the wealth of compositions and ionisation states in these systems can be appreciated.
| Polymorphic type | Composition and speciation of polymorphic pairs |
|---|---|
| Tautomeric polymorphs | [A] , [a] |
[A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a] , [a] a] , [a] |
|
[A] , [A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a] a] |
|
[A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N] , [a N] , [a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N] N] |
|
[A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N] , [a N] , [a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N] N] |
|
[A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N] , [A N] , [A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N] N] |
|
| Zwitterionic polymorphs | [A] , [A±] |
[A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N] , [A± N] , [A±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N] N] |
|
| Salt–cocrystal pairs | [A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B] , [A+ B] , [A+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B−] B−] |
[A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N] , [A+ N] , [A+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B− B−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N] N] |
|
| Multi-zwitterionic polymorphs | [A±] , [a±] |
[A±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N] , [a± N] , [a±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N] N] |
|
| Single–multi proton transfer polymorphs | [A+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B−] , [A2+ B−] , [A2+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B2−] B2−] |
[A+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B− B−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N] , [A2+ N] , [A2+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B2− B2−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N] N] |
|
| Different charge position polymorphs | [A+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B−] , [a+ B−] , [a+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B−] B−] |
[A−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B+] , [a− B+] , [a−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B+] B+] |
|
[A+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B− B−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N] , [a+ N] , [a+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B− B−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N] N] |
|
[A−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B+ B+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N] , [a− N] , [a−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B+ B+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N] N] |
CSD statistics on polymorphs related by proton transfer
In our CSD analysis we identified 3759 polymorphic families, only 2.5% of which correspond to polymorphs related by proton transfer (94 families). The other CSD subsets also show similar incidences of polymorphism related by proton transfer with only 2.9% in the DrugCSD and 2.4% in the SDrugCSD (Table 2). Our analysis, however, did not identify any polymorphs related by proton transfer in the GSK database.All polymorphic structures were analysed manually (to check for errors), and the final 95 families identified were all genuine polymorphs related by proton transfer. We expect, however, that this number is an under-representation of incidences in the CSD since some proton transfer polymorphs may have been eliminated by the redetermination analysis algorithm which is used for the generation of the CSD subsets.61
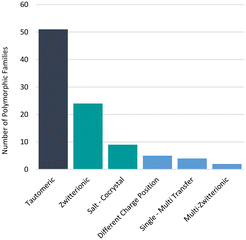
Additionally, in some examples, proton positions have been reliably determined by means other than crystallography (e.g. IR spectroscopy)62 or not determined at all. We note that some of these cases cannot feasibly be accounted for by our comparison algorithms of X-ray data only. For instance, two high profile GSK drugs (albendazole57 and ranitidine hydrochloride63) are known to exhibit tautomeric polymorphism and a GSK development compound GSK25164 exhibits zwitterionic polymorphism, but these were not identified in the GSD for these reasons. Furthermore, we know that not all polymorphs have their structures determined and deposited in the CSD and protons can be difficult to locate, further impacting the confidence in these statistics. Nonetheless, polymorphs related by proton transfer appear to occur frequently enough for them to be considered important. The distribution of polymorphic families across the different types of polymorphs related by proton transfer is given in Fig. 6 where the analysis is given per family. Of the 95 polymorphic systems (214 refcodes), 94 contained only two tautomers whilst one polymorphic family contained three tautomers16 (two observed in our dataset). Tautomeric polymorphs are most common (51) followed by zwitterionic polymorphs (24) and multi-zwitterionic polymorphs (2) are the rarest. Only 9 salt–cocrystal pairs were found. The different polymorphic systems are further discussed in the sections below.
Tautomeric polymorphs
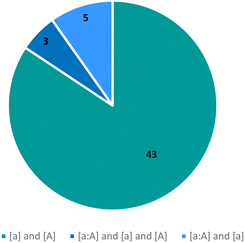
The observed tautomeric compositions of the 51 tautomeric polymorphic systems have been summarised in Fig. 7. The majority (43) are pure systems where two tautomers of a compound (one ‘a’ and the other ‘A’) were crystallised individually in different polymorphs ([a] and [A]), with an additional 3 systems where two tautomers have been isolated individually as well as a mixture ([a], [A] and [a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A]). In 5 systems, two tautomers had been observed with one of them only seen together with the first ([a] and [a
A]). In 5 systems, two tautomers had been observed with one of them only seen together with the first ([a] and [a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A]). Only two of these polymorphic systems are of a hydrate or solvate and none were cocrystals with another molecule.
A]). Only two of these polymorphic systems are of a hydrate or solvate and none were cocrystals with another molecule.
The number of tautomeric polymorphs in the CSD has tripled since 2010 when only 16 such pairs were identified. Additionally, there now exists polymorphic families containing three or more tautomeric forms. For example, 3-methyl-4-(4-methylbenzoyl)-1-phenyl-pyrazo-5-one has now been reported to have three tautomers in the solid state ([a], [a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A] and [α] – where a, A and α are three different tautomers of a compound). Two of these tautomers were found in our CSD analysis within two different refcode families (VIMPAJ65 and ZUMXIQ16).
A] and [α] – where a, A and α are three different tautomers of a compound). Two of these tautomers were found in our CSD analysis within two different refcode families (VIMPAJ65 and ZUMXIQ16).
The crystallisation solvent itself can influence the tautomeric state in a single direction which may partially explain why so few hydrates or solvates form tautomeric polymorphs.66 However, no conclusions shall be drawn on this given that hydrates and solvates are generally less commonly observed in the CSD52,67 and the overall numbers of polymorphs related by proton transfer are small.
Zwitterionic polymorphs
A total of 24 compounds were found to exhibit zwitterionic polymorphism. The majority are neat anhydrate structures (21, [A] and [A±]), none were hydrated and 3 were multi-component systems (cocrystals of piroxicam, [A±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N] and [A
N] and [A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N]).
N]).
For these compounds, the ΔpKselfa is an important parameter to determine the likelihood of a compound to be able to exist as non-ionised and as a zwitterion in the solid state. The equivalence ΔpKselfa point, where molecules containing both acidic and basic pKa have a 50% probability of existing as either the zwitterion or non-ionised molecule, has been reported to be 4.1.45 The ΔpKselfa scale can be classified into domains which describe the likelihood of zwitterion formation. In zone 1 (ΔpKselfa < 0.9), > 99% of molecules crystallise as their non-ionised tautomers, in zone 2 (0.9 ≤ ΔpKa ≤ 7.4) both forms are possible and in zone 3 (ΔpKa > 7.4) > 99% of molecules crystallise as zwitterions. The probability of observing a zwitterion in zone 2 is described by eqn (4).
| Pobs (zwitterion, %) = 15ΔpKselfa − 12 | (4) |
Given the prior knowledge and data, we would in principle expect molecules exhibiting zwitterionic polymorphism to sit in zone 2 of the ΔpKselfa scale. Interestingly, however, the majority of the zwitterionic polymorphs in our dataset had a ΔpKselfa within zone 1 instead. A further analysis of these structures reveals that most of these instances correspond to compounds where the acid and base groups sit very close to each other resulting in an intra-molecular rather than an intermolecular proton transfer (see Fig. 8 and 9). Because these groups interact, the ΔpKselfa prediction may not be as accurate as the actual experimental value, an observation which has been highlighted before.45,68,69 Additionally, different tautomers of a compound will have different pKa values, and therefore the choice of tautomer in pKa calculations may be important.
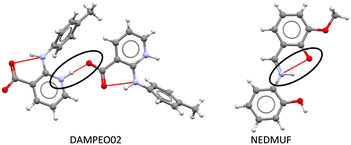 | ||
| Fig. 8 Zwitterion formation via intermolecular proton transfer in DAMPEO02 (left) and via intramolecular proton transfer in NEDMUF (right). | ||
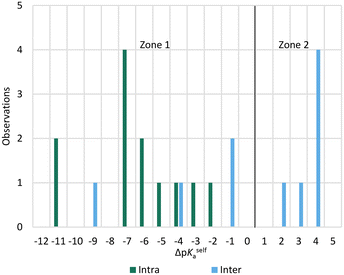 | ||
| Fig. 9 ΔpKa for molecules exhibiting zwitterionic polymorphism, split by the nature of the proton transfer in the crystal (intra or intermolecular). | ||
Our results suggest that when the acid–base proton transfer for zwitterion formation occurs intermolecularly the majority of zwitterionic polymorphs have ΔpKselfa values in zone 2 with a significant proportion also in zone 1. However, when the proton transfer for zwitterion formation occurs intramolecularly, most zwitterionic polymorphs have ΔpKselfa within zone 1. No molecules exhibiting zwitterionic polymorphism had ΔpKselfa > 4, indicating that when there is a large positive ΔpKselfa, zwitterionic polymorphism does not occur, presumably due to the very large driving force to form solids with the zwitterions only. In this zone, normal polymorphism of zwitterionic compounds prevails.
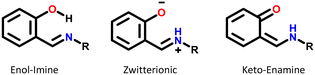
Most of the structures exhibiting zwitterionic polymorphism and intra-molecular proton transfer were Schiff bases with general formula Ar–CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–R (frequently used in co-ordination chemistry). Ortho-Hydroxy derivatives of Schiff bases can exist in enol–imine, keto–enamine or zwitterionic forms depending on the location of the hydrogen in the O⋯H⋯N bond, as shown in Fig. 10.70 These molecules were observed in the enol, zwitterionic and keto forms in our datasets, but the pKa values were calculated for the enol–imine forms rather than the keto–enamine forms. Studies of the tautomerism in Schiff bases have indicated that the presence of peripheral groups enable stabilisation of metastable tautomers in the solid state.55 This appears to be a much bigger factor enabling zwitterionic polymorphism in these compounds rather than the pKa values.
N–R (frequently used in co-ordination chemistry). Ortho-Hydroxy derivatives of Schiff bases can exist in enol–imine, keto–enamine or zwitterionic forms depending on the location of the hydrogen in the O⋯H⋯N bond, as shown in Fig. 10.70 These molecules were observed in the enol, zwitterionic and keto forms in our datasets, but the pKa values were calculated for the enol–imine forms rather than the keto–enamine forms. Studies of the tautomerism in Schiff bases have indicated that the presence of peripheral groups enable stabilisation of metastable tautomers in the solid state.55 This appears to be a much bigger factor enabling zwitterionic polymorphism in these compounds rather than the pKa values.
In summary, whilst there are no reliable trends to draw hard conclusions from these observations, there does appear to be a slight tendency for molecules exhibiting zwitterionic polymorphism to sit within (or close to) zone 2 when proton transfer is intermolecular and zone 1 when it is intramolecular. A ΔpKselfa of ∼4 appears to be an upper limit for observing zwitterionic polymorphism.
Salt–cocrystal polymorphic pairs
Only 9 salt–cocrystal polymorphic pairs were found in the CSD, all of which were anhydrous forms ([A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B] and [A+
B] and [A+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B−]). Cases where the salt and cocrystal have different stoichiometries were not considered to be polymorphs (e.g. TODNIM and WAFCOX, AFICEZ and AFICID) and are thus not included in this number. For the salt–cocrystal polymorphic pairs, the most acidic pKa for the proton donating molecule, and most basic pKa for the proton accepting molecule in each pair was calculated and used to determine the ΔpKa. A recent analysis of the CSD has shown that for non-solvated multicomponent systems, the point of 50% probability for salt versus cocrystal formation occurs where ΔpKa is ∼1.4 whereas for hydrates, this point is at ΔpKa ∼ −0.5.45 The distribution of ΔpKa for these non-solvated salt–cocrystal polymorphic pairs is consistent with that finding, with 7 of the 9 pairs having a ΔpKa within one unit of 1.4 (range 0.43 to 2.21). Thus, the key question when presented with a multicomponent system with a small ΔpKa should therefore not be whether a salt or cocrystal can form, but whether both can form.
B−]). Cases where the salt and cocrystal have different stoichiometries were not considered to be polymorphs (e.g. TODNIM and WAFCOX, AFICEZ and AFICID) and are thus not included in this number. For the salt–cocrystal polymorphic pairs, the most acidic pKa for the proton donating molecule, and most basic pKa for the proton accepting molecule in each pair was calculated and used to determine the ΔpKa. A recent analysis of the CSD has shown that for non-solvated multicomponent systems, the point of 50% probability for salt versus cocrystal formation occurs where ΔpKa is ∼1.4 whereas for hydrates, this point is at ΔpKa ∼ −0.5.45 The distribution of ΔpKa for these non-solvated salt–cocrystal polymorphic pairs is consistent with that finding, with 7 of the 9 pairs having a ΔpKa within one unit of 1.4 (range 0.43 to 2.21). Thus, the key question when presented with a multicomponent system with a small ΔpKa should therefore not be whether a salt or cocrystal can form, but whether both can form.
Multi-zwitterionic polymorphs
Only two compounds exhibiting multi-zwitterionic polymorphism were found ([A±] and [a±]), making this the rarest type of proton transfer polymorphism in our search. These compounds were cinchomeronic acid (often used as a ligand) and N-2-hydroxyethylpiperazine-N-2-ethane sulfonic acid (commonly known as HEPES and used as a buffering agent). Their molecular structures are shown in Fig. 11.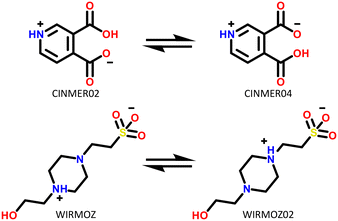 | ||
| Fig. 11 Molecular structures of compounds with multi-zwitterionic polymorphic pairs, and their associated refcodes. | ||
Cinchomeronic acid has 8 crystal structures in its refcode family CINMER71–73 with only two unique polymorphic forms (CINMER02 and CINMER04). All crystal structures of the most stable form I (four structures, which includes CINMER02) show their entries with proton transfer from the 3-substituted carboxylic acid. For form II, however, the proton position has been a matter of debate with two structures showing proton transfer from the 4-substituted carboxylic acid (CINMER04, CINMER05) and two from the 3-substituted carboxylic acid (CINMER01, CINMER03). Orthogonal approaches had to be used to confirm the proton positions for forms I (3-substituted) and II (4-substituted) respectively and established that there is no temperature-induced proton migration for the two forms.73
These disagreements in the literature and the requirement for large amounts of orthogonal data highlight how difficult it can be to accurately describe the protonation states of these molecules in the solid state and how ‘incorrect’ determinations can be hidden in the CSD with seemingly little warning or comment. The calculated pKa for the two carboxylic acid groups are 3.69 for 3-substitued and 5.16 for the 4-substituted. It is intriguing that a zwitterion forms at all due to the weakly basic nature of the pyridine (calculated pKa of the protonated base being 0.95) and the reasonably negative ΔpKa values of between −4.21 and −2.74. The Gibbs free energy for proton transfer in aqueous state at 298 K was calculated according to eqn (5).45
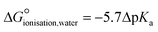 | (5) |
 is positive, indicating that in solution, zwitterion formation will not be spontaneous or favoured. The value is slightly larger for CINMER04, indicating that this zwitterion is the least favourable of the two in water, and corresponds with the lower ΔpKa. In the gas state, the zwitterionic forms are also unfavourable, however in the solid state we only see zwitterionic forms.
is positive, indicating that in solution, zwitterion formation will not be spontaneous or favoured. The value is slightly larger for CINMER04, indicating that this zwitterion is the least favourable of the two in water, and corresponds with the lower ΔpKa. In the gas state, the zwitterionic forms are also unfavourable, however in the solid state we only see zwitterionic forms.
HEPES has 5 crystal structures in its refcode family WIRMOZ20,74,75 with only two unique polymorphic forms. The two piperazine nitrogen atoms have quite different calculated pKa values (1.62 for the N protonated in WIRMOZ, 7.34 for the N protonated in WIRMOZ02). The sulfonic acid is a reasonably strong acid with a calculated pKa of −1.34. Therefore, the ΔpKa is either 2.96 or 8.68 respectively, so a zwitterion might be expected to form in either case (with lower probability for the lower ΔpKa as in WIRMOZ).  is negative for both possible zwitterions of HEPES, meaning this proton transfer is also favourable in aqueous solution. It is lower by 32.6 kJ mol−1 for the zwitterionic molecule corresponding to WIRMOZ04 making this the more stable zwitterion in solution.
is negative for both possible zwitterions of HEPES, meaning this proton transfer is also favourable in aqueous solution. It is lower by 32.6 kJ mol−1 for the zwitterionic molecule corresponding to WIRMOZ04 making this the more stable zwitterion in solution.
Single–multi proton transfer polymorphs
Four systems were found to have single–multi proton transfer polymorphism ([A+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B−] and [A2+
B−] and [A2+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B2−]) all of which consist of a symmetrical di-base with a symmetrical di-acid (Table 3). The first ΔpKIa (the strongest base and strongest acid) and second ΔpKIIa (the second strongest base and second strongest acid) in each pair were calculated for the four pairs of polymorphs identified. In all our systems here, the ΔpKIa is always greater than 1, thus salt formation is predicted as likely for all systems.45 For ΔpKIIa, the equivalence point (50% probability) for making a monovalent versus a di-valent salt is −4.2. All the ΔpKIIa data for our systems lie around that value, indicating the good predictability of the ΔpKa rule for these systems.
B2−]) all of which consist of a symmetrical di-base with a symmetrical di-acid (Table 3). The first ΔpKIa (the strongest base and strongest acid) and second ΔpKIIa (the second strongest base and second strongest acid) in each pair were calculated for the four pairs of polymorphs identified. In all our systems here, the ΔpKIa is always greater than 1, thus salt formation is predicted as likely for all systems.45 For ΔpKIIa, the equivalence point (50% probability) for making a monovalent versus a di-valent salt is −4.2. All the ΔpKIIa data for our systems lie around that value, indicating the good predictability of the ΔpKa rule for these systems.
Finally, the proton positions in the crystal structures for HAZFAP06 (with its HAZFAP01 pair) are not unambiguously determined by X-ray crystallography due to the high temperature of the data collection. Supporting neutron diffraction and modelling data provides evidence that a second proton transfer has occurred in HAZFAP06 compared to HAZFAP01. The second proton transfer and resultant change in form is thermally induced, reversible and also results in a colour change.22 This form change can also been induced by applying an electric field and has been studied using synchrotron X-ray diffraction.76 With increased use of orthogonal techniques such as neutron diffraction or ssNMR, in combination with computational modelling, more polymorphs related by proton transfer may be found where previously proton positions may have been ambiguous.
Polymorphs with charge at different positions
All 5 systems exhibiting polymorphism with charge located on different positions were multicomponent systems (e.g. [A+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B−] and [a+
B−] and [a+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B−]). An example of this polymorphism is found in sodium dihydrogen citrate (NAHCIT77 and NAHCIT0178), where the citric carboxylic acid deprotonation is different in the two polymorphs. A particularly interesting example of this type of polymorphism is lamivudine hydrochloride (LASZAI79 and LASZAI0280) because the protonation at a different location in the lamivudine molecule is also related by tautomerism. Both tautomers of lamivudine (Table 4) are very weakly basic with calculated pKa of 0.21 and −0.05. However, HCl is a reasonably strong acid (experimental pKa = −5.9)81 and thus the ΔpKa is sufficiently large that salt formation is still expected to occur for either tautomer (ΔpKa being 6.1 and 5.9 respectively).
B−]). An example of this polymorphism is found in sodium dihydrogen citrate (NAHCIT77 and NAHCIT0178), where the citric carboxylic acid deprotonation is different in the two polymorphs. A particularly interesting example of this type of polymorphism is lamivudine hydrochloride (LASZAI79 and LASZAI0280) because the protonation at a different location in the lamivudine molecule is also related by tautomerism. Both tautomers of lamivudine (Table 4) are very weakly basic with calculated pKa of 0.21 and −0.05. However, HCl is a reasonably strong acid (experimental pKa = −5.9)81 and thus the ΔpKa is sufficiently large that salt formation is still expected to occur for either tautomer (ΔpKa being 6.1 and 5.9 respectively).
Energy analysis
The lattice energies for several of these proton transfer polymorphs were calculated to assess how differences in lattice energies compare to those of ‘usual’ polymorphs (Table 5). In addition to this, the gas-phase energy difference of the corresponding molecular species were computed. Reassuringly, despite the very large gas-phase energy differences of the molecular species involved in some cases, all polymorphic pairs studied differ in overall lattice energies by somewhere between 1 to 7 kJ mol−1, typical of polymorphs.83,84| Type of polymorphism | Refcode, form | Species | Relative EGas (kJ mol−1) | Relative ELattice (kJ mol−1) |
|---|---|---|---|---|
| a Form names were not found in the literature. b Relative energies for LASZAI gas phase molecules are comparisons of the amine and imine tautomers per specified ionisation state. c DMol3 (ref. 82) with GGA PBE functional and TS DFT-D correction used to calculate gas phase energy of charged species only. | ||||
| Tautomeric | KIJBOX, form I | Imide tautomer | +22.9 | 0.0 |
| QIJZOY03, form II | Amide tautomer | 0.0 | +6.9 | |
| Zwitterionic | AMBNZA02, form IV | Zwitterion | +240.5 | 0.0 |
| AMBNZA, form II | Non-ionised | 0.0 | +5.1 | |
| Multi-zwitterionic | CINMER02, form I | Zwitterion para COO− | 0.0 | 0.0 |
| CINMER04, form II | Zwitterion meta COO− | +4.3 | +4.0 | |
| Multi-zwitterionic | WIRMOZ, form Ia | Zwitterion OH side | +79.1 | 0.0 |
| WIRMOZ04, form IIa | Zwitterion SO3 side | 0.0 | +2.2 | |
| Single–multi proton transfer | MEJYIM, form Ia | Double | +1101.0c | 0.0 |
| UWUJUS, form IIa | Single | 0.0 | +1.1 | |
| Different charge position | LASZAI, form I | Amine tautomer: non-ionised, ionisedb | 0.0, +9.9 | 0.0 |
| LASZAI02, form II | Imine tautomer: non-ionised, ionisedb | +11.9, 0.0 | +5.8 | |
The amide and imide tautomeric polymorphs of sulfasalazine (QIJZOY0385 and KIJBOX,86 respectively) were computed to differ by almost 7 kJ mol−1 in lattice energy. The literature was searched for experimental evidence of the stability ranking these polymorphs, but nothing conclusive was found to have been reported. Commercially available batches of sulfasalazine appear to be consistent with form I which is computed to be the most stable form despite containing the higher-energy tautomer.87 Form II, is computed to be metastable and this agrees with the unusual crystallisation conditions used for its isolation from supercritical CO2.88
The simple compound m-aminobenzoic acid was identified as forming zwitterionic polymorphs with two structures identified in our searches (AMBNZA89 being the non-ionised form II, and AMBNZA0234 being the zwitterionic form IV). There is a large difference in energy in the gas phase for non-ionised versus zwitterionic m-aminobenzoic acid species (240.5 kJ mol−1) as expected since there is no stabilisation of charges in the gas-phase. However, the ΔELatt is 5.1 kJ mol−1, and the relative stability correlates with available experimental data.34,62,90
Four pairs of salt–cocrystal polymorphs have been previously assessed, with differences in formation energy of between ∼8.5 to 11.7 kJ mol−1 reported in the literature.91
Because there were only two examples, the lattice energies of both pairs of multi-zwitterionic polymorphs were assessed. For the CINMER pair, the non-ionised molecule had the lowest energy by ∼100 kJ mol−1, relative to either of the two zwitterionic molecules. The difference in energy between the two zwitterions in the gas phase was just 4.3 kJ mol−1, comparable to the energy difference between many of the non-ionised tautomers assessed. ΔELatt of 4 kJ mol−1 was calculated with CINMER02 being the more stable form. This stability ranking of the two forms correlates with experimental relative stability data in the literature.72 For the WIRMOZ polymorphs, the calculated ΔELatt was 2.2 kJ mol−1.
For single–multi proton transfer polymorphs, the polymorphic pair from the refcodes MEJYIM and UWUJUS were assessed, with the component molecules assumed to be most stable in the non-ionised state in the gas phase. The structure with two proton transfers, MEJYIM, was calculated to be more stable by 1.1 kJ mol−1.
Lamivudine hydrochloride (LASZAI) exhibits charge position polymorphism, seemingly as a consequence of tautomerism. The gas phase energies of the neutral and protonated tautomers were calculated. Interestingly, the amine form is more stable in the gas phase by 11.9 kJ mol−1 for the non-ionised molecule, whereas the imine is more stable by 9.9 kJ mol−1 when the molecule is ionised. In the solid state, the polymorph containing the protonated amine was more stable by 5.8 kJ mol−1.
Conclusions
By assessing the CSD, its drug subsets and the GSD, we have found that tautomerism is not just a serious consideration in the pharmaceutical industry for medicinal chemists, but for solid state scientists alike. Drug-like molecules have an increased tendency to contain functional groups capable of tautomerism, as well as to contain both acidic and basic functional groups, thus enabling zwitterion formation. Evidence suggests that both tautomer equilibrium and speciation in solution may have implications for the solid state outcome and polymorphic control in crystallisations.Polymorphs related by proton transfer represent approximately 3% of polymorphs for drug-like molecules: that is potentially 1 in every 33 drug candidates. Of the 6 categories of these polymorphs found in the CSD, tautomeric polymorphs are by far the most common (54%) followed by zwitterionic polymorphs (25%). Salt–cocrystal pairs make up only 9% of the polymorphs related by proton transfer but a relatively high proportion of cocrystal polymorphs; there were only 145 polymorphic cocrystals identified in a 2015 search of the CSD,83 hence roughly 6% of polymorphic cocrystals may exist as salt–cocrystal pairs. Despite the slower uptake of cocrystals in the industry due to regulatory ambiguity,92 it is significant that these many are salt–cocrystal pairs thus reinforcing the need to intentionally assess whether both can form, especially when the ΔpKa rule indicates a similar probability of forming a salt or cocrystal (ΔpKa is close to 1).
Furthermore, we have noted that some literature examples were not identified in our searches highlighting the limitations of our method. The limitations may be due to inconsistent quality of structures deposited in the CSD (when they exist), restrictions applied to our datasets or the scripted comparison algorithm, which treats individual molecules in a bulk way and may not account for unique scenarios. Importantly, we know that the true number of polymorphs related by proton transfer is likely to be greater than that reported here and when studying individual systems experimentally proton positions should be investigated by multiple orthogonal techniques.
Finally, despite the sometimes large differences in gas-phase energies of different tautomers or ionisation states of a molecule, we have shown the overall lattice energy of these polymorphs is small as expected from ‘typical’ polymorphs. The existence of proton transfer polymorphs demonstrates the power of the crystal lattice to stabilise metastable tautomers or other ionised molecular species and the ability of a molecule to tautomerise or ionise should present opportunities for crystal engineering. Given that these polymorphs could have substantially different properties given the changes in both chemical structure and solid state packing, for a pharmaceutical company with a large portfolio, this type of polymorphism is common enough to be a problem or an opportunity (or both) when designing and developing solid forms.
Author contributions
All authors have contributed to the manuscript. AWR is the primary author and conducted the searches, coding, calculations, and analysis. CLD has contributed to helpful discussions. AJCC has designed the project and contributed to ideas and discussions. AJCC is corresponding author.Conflicts of interest
A. Woods-Ryan and C. L. Doherty are employed by and hold shares in GSK.Acknowledgements
The authors would like to thank Leen Kalash, Nick Henley, Luca Russo, Ian Rosbottom, Jack Ryan and Daniel Woods for their valuable discussions, advice and support and GSK for funding.Notes and references
- P. J. Taylor, G. van der Zwan and L. Antonov, in Tautomerism: Methods and Theories, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2013, pp. 1–24 Search PubMed.
- A. J. Cruz-Cabeza, A. Schreyer and W. R. Pitt, J. Comput.-Aided Mol. Des., 2010, 24, 575–586 CrossRef CAS PubMed.
- J. Powling and H. J. Bernstein, J. Am. Chem. Soc., 1951, 73, 4353–4356 CrossRef CAS.
- R. M. Izatt, J. L. Oscarson, S. E. Gillespie, H. Grimsrud, J. A. R. Renuncio and C. Pando, Biophys. J., 1992, 61, 1394–1401 CrossRef CAS PubMed.
- E. Evangelio, C. Rodriguez-Blanco, Y. Coppel, D. N. Hendrickson, J. P. Sutter, J. Campo and D. Ruiz-Molina, Solid State Sci., 2009, 11, 793–800 CrossRef CAS.
- F. Mesiti, A. Maruca, V. Silva, R. Rocca, C. Fernandes, F. Remião, E. Uriarte, S. Alcaro, A. Gaspar and F. Borges, Eur. J. Med. Chem., 2021, 213, 113183 CrossRef CAS PubMed.
- A. R. Katritzky, C. Dennis Hall, B. E. D. M. El-Gendy and B. Draghici, J. Comput.-Aided Mol. Des., 2010, 24, 475–484 CrossRef CAS PubMed.
- Y. C. Martin, J. Comput.-Aided Mol. Des., 2009, 23, 693–704 CrossRef CAS PubMed.
- A. J. Cruz-Cabeza and C. R. Groom, CrystEngComm, 2011, 13, 93–98 RSC.
- T. L. Threlfall, Analyst, 1995, 120, 2435 RSC.
- M. R. Chierotti, L. Ferrero, N. Garino, R. Gobetto, L. Pellegrino, D. Braga, F. Grepioni and L. Maini, Chem. – Eur. J., 2010, 16, 4347–4358 CrossRef CAS PubMed.
- J. Elguero, Cryst. Growth Des., 2011, 11, 4731–4738 CrossRef CAS.
- Polymorphism in the Pharmaceutical Industry, ed. R. Hilfiker, Wiley-VCH Verlag GmbH & Co. KGaA, 2006 Search PubMed.
- S. S. Kumar and A. Nangia, Cryst. Growth Des., 2014, 14, 1865–1881 CrossRef CAS.
- N. K. Nath, S. S. Kumar and A. Nangia, Cryst. Growth Des., 2011, 11, 4594–4605 CrossRef CAS.
- V. B. Kurteva, B. L. Shivachev, R. P. Nikolova, S. D. Simova, L. M. Antonov, L. A. Lubenov and M. A. Petrova, RSC Adv., 2015, 5, 73859–73867 RSC.
- C. Wales, L. H. Thomas and C. C. Wilson, CrystEngComm, 2012, 14, 7264–7274 RSC.
- G. R. Desiraju, J. Chem. Soc., Perkin Trans. 2, 1983, 1025 RSC.
- CSD Statistics, https://www.ccdc.cam.ac.uk/CCDCStats/Stats, (accessed 17 October 2021).
- M. Woińska, S. Grabowsky, P. M. Dominiak, K. Woźniak and D. Jayatilaka, Sci. Adv., 2016, 2, 1–8 Search PubMed.
- T. Steiner, I. Majerz and C. C. Wilson, Angew. Chem., Int. Ed., 2001, 40, 2651–2654 CrossRef CAS.
- D. M. S. Martins, D. S. Middlemiss, C. R. Pulham, C. C. Wilson, M. T. Weller, P. F. Henry, N. Shankland, K. Shankland, W. G. Marshall, R. M. Ibberson, K. Knight, S. Moggach, M. Brunelli and C. A. Morrison, J. Am. Chem. Soc., 2009, 131, 3884–3893 CrossRef CAS PubMed.
- A. G. Lvov, A. V. Yadykov, K. A. Lyssenko, F. W. Heinemann, V. Z. Shirinian and M. M. Khusniyarov, Org. Lett., 2020, 22, 604–609 CrossRef CAS PubMed.
- J. S. Stevens, S. J. Byard, C. C. Seaton, G. Sadiq, R. J. Davey and S. L. M. Schroeder, Phys. Chem. Chem. Phys., 2014, 16, 1150–1160 RSC.
- J. S. Stevens, S. J. Byard, C. A. Muryn and S. L. M. Schroeder, J. Phys. Chem. B, 2010, 114, 13961–13969 CrossRef CAS PubMed.
- K. Wolnica, G. Szklarz, M. Dulski, M. Wojtyniak, M. Tarnacka, E. Kaminska, R. Wrzalik, K. Kaminski and M. Paluch, Colloids Surf., B, 2019, 182, 110319 CrossRef CAS PubMed.
- P. D. S. Carvalho, L. F. Diniz, G. T. S. T. Da Silva, N. D. Coutinho, P. G. Dos Santos, V. H. Carvalho-Silva, C. Ribeiro and J. Ellena, Cryst. Growth Des., 2021, 21, 1122–1135 CrossRef.
- P. T. Edwards, L. K. Saunders, D. C. Grinter, P. Ferrer, G. Held, E. J. Shotton and S. L. M. Schroeder, J. Phys. Chem. A, 2022, 126, 2889–2898 CrossRef CAS PubMed.
- A. S. Aljaber and A. D. Bani-Yaseen, J. Mol. Graphics Modell., 2019, 86, 160–169 CrossRef CAS PubMed.
- K. R. Bryenton, A. A. Adeleke, S. G. Dale and E. R. Johnson, WIREs Comput. Mol. Sci., 2022, e1631 Search PubMed.
- I. Ciofini, C. Adamo and H. Chermette, Chem. Phys., 2005, 309, 67–76 CrossRef CAS.
- M. Sitzmann, W. D. Ihlenfeldt and M. C. Nicklaus, J. Comput.-Aided Mol. Des., 2010, 24, 521–551 CrossRef CAS PubMed.
- L. Orola, M. V. Veidis, I. Sarcevica, A. Actins, S. Belyakov and A. Platonenko, Int. J. Pharm., 2012, 432, 50–56 CrossRef CAS PubMed.
- P. A. Williams, C. E. Hughes, G. K. Lim, B. M. Kariuki and K. D. M. Harris, Cryst. Growth Des., 2012, 12, 3104–3113 CrossRef CAS.
- E. Simone and Z. K. Nagy, CrystEngComm, 2015, 17, 6538–6547 RSC.
- P. W. Carter and M. D. Ward, J. Am. Chem. Soc., 1994, 116, 769–770 CrossRef CAS.
- M. U. Schmidt, J. Brüning, J. Glinnemann, M. W. Hützler, P. Mörschel, S. N. Ivashevskaya, J. Van De Streek, D. Braga, L. Maini, M. R. Chierotti and R. Gobetto, Angew. Chem., Int. Ed., 2011, 50, 7924–7926 CrossRef CAS PubMed.
- M. R. Chierotti, R. Gobetto, L. Pellegrino, L. Milone and P. Venturello, Cryst. Growth Des., 2008, 8, 1454–1457 CrossRef CAS.
- K. Epa, C. B. Aakeröy, J. Desper, S. Rayat, K. L. Chandra and A. J. Cruz-Cabeza, Chem. Commun., 2013, 49, 7929 RSC.
- Z. Liu, L. Zhong, P. Ying, Z. Feng and C. Li, Biophys. Chem., 2008, 132, 18–22 CrossRef CAS PubMed.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179 CrossRef CAS PubMed.
- G. Landrum, RDKit: Open-source cheminformatics, Version 2021.03.1, https://www.rdkit.org/ Search PubMed.
- C. F. Macrae, I. Sovago, S. J. Cottrell, P. T. A. Galek, P. McCabe, E. Pidcock, M. Platings, G. P. Shields, J. S. Stevens, M. Towler and P. A. Wood, J. Appl. Crystallogr., 2020, 53, 226–235 CrossRef CAS PubMed.
- JChem for Office (Excel) Version 18.22.4.11, ChemAxon, 2018, https://www.chemaxon.com.
- A. J. Cruz-Cabeza, M. Lusi, H. P. Wheatcroft and A. D. Bond, Faraday Discuss., 2022, 235, 446–466 RSC.
- BIOVIA, Dassault Systèmes, Materials Studio, 20.1.0.2728, San Diego: Dassault Systèmes, 2020 Search PubMed.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567–570 CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005 CrossRef PubMed.
- A. Ambrosetti, A. M. Reilly, R. A. Distasio and A. Tkatchenko, J. Chem. Phys., 2014, 140, 18A508 CrossRef PubMed.
- M. J. Bryant, S. N. Black, H. Blade, R. Docherty, A. G. P. Maloney and S. C. Taylor, J. Pharm. Sci., 2019, 108, 1655–1662 CrossRef CAS PubMed.
- L. N. Kalash, J. C. Cole, R. C. B. Copley, C. M. Edge, A. A. Moldovan, G. Sadiq and C. L. Doherty, CrystEngComm, 2021, 23, 5430–5442 RSC.
- J. Haleblian and W. McCrone, J. Pharm. Sci., 1969, 58, 911–929 CrossRef CAS PubMed.
- M. Bauer, R. K. Harris, R. C. Rao, D. C. Apperley and C. A. Rodger, J. Chem. Soc., Perkin Trans. 2, 1998, 475–482 RSC.
- M. Rubčić, K. Užarević, I. Halasz, N. Bregović, M. Mališ, I. Dilović, Z. Kokan, R. S. Stein, R. E. Dinnebier and V. Tomišić, Chem. – Eur. J., 2012, 18, 5620–5631 CrossRef PubMed.
- C. Foces-Foces, A. L. Llamas-Saiz, R. M. Claramunt, C. López and J. Elguero, J. Chem. Soc., Chem. Commun., 1994, 1143–1145 RSC.
- A. Bongioanni, B. S. Araújo, Y. S. de Oliveira, M. R. Longhi, A. Ayala and C. Garnero, AAPS PharmSciTech, 2018, 19, 1468–1476 CrossRef CAS PubMed.
- A. M. Araya-Sibaja, M. Urgellés, F. Vásquez-Castro, F. Vargas-Huertas, J. R. Vega-Baudrit, T. Guillén-Girón, M. Navarro-Hoyos and S. L. Cuffini, RSC Adv., 2019, 9, 5244–5250 RSC.
- A. M. Araya-Sibaja, C. E. Maduro de Campos, C. Fandaruff, J. R. Vega-Baudrit, T. Guillén-Girón, M. Navarro-Hoyos and S. L. Cuffini, J. Pharm. Anal., 2019, 9, 339–346 CrossRef PubMed.
- P. Sacchi, M. Lusi, A. J. Cruz-Cabeza, E. Nauha and J. Bernstein, CrystEngComm, 2020, 22, 7170–7185 RSC.
- A. J. Cruz-Cabeza and J. Bernstein, Chem. Rev., 2014, 114, 2170–2191 CrossRef CAS PubMed.
- L. Gopal, C. I. Jose and A. B. Biswas, Spectrochim. Acta, Part A, 1967, 23, 513–518 CrossRef CAS.
- M. Mirmehrabi, S. Rohani, K. S. K. Murthy and B. Radatus, J. Cryst. Growth, 2004, 260, 517–526 CrossRef CAS.
- K. Down, A. Amour, N. A. Anderson, N. Barton, S. Campos, E. P. Cannons, C. Clissold, M. A. Convery, J. J. Coward, K. Doyle, B. Duempelfeld, C. D. Edwards, M. D. Goldsmith, J. Krause, D. N. Mallett, G. A. McGonagle, V. K. Patel, J. Rowedder, P. Rowland, A. Sharpe, S. Sriskantharajah, D. A. Thomas, D. W. Thomson, S. Uddin, J. N. Hamblin and E. M. Hessel, J. Med. Chem., 2021, 64, 13780–13792 CrossRef CAS PubMed.
- P. N. Remya, C. H. Suresh and M. L. P. Reddy, Polyhedron, 2007, 26, 5016–5022 CrossRef CAS.
- L. Qi, Y. Jin, H. Li, Y. Dong and C. Xie, Trans. Tianjin Univ., 2020, 26, 458–469 CrossRef CAS.
- J. E. Werner and J. A. Swift, CrystEngComm, 2021, 23, 1555–1565 RSC.
- C. Liao and M. C. Nicklaus, J. Chem. Inf. Model., 2009, 49, 2801–2812 CrossRef CAS PubMed.
- A. J. Cruz-Cabeza, CrystEngComm, 2012, 14, 6362 RSC.
- P. M. Dominiak, E. Grech, G. Barr, S. Teat, P. Mallinson and K. Woźniak, Chem. – Eur. J., 2003, 9, 963–970 CrossRef CAS PubMed.
- D. Ang, G. B. Deacon, P. C. Junk and D. R. Turner, Polyhedron, 2007, 26, 385–391 CrossRef CAS.
- D. Braga, L. Maini, C. Fagnano, P. Taddei, M. R. Chierotti and R. Gobetto, Chem. – Eur. J., 2007, 13, 1222–1230 CrossRef CAS PubMed.
- I. R. Evans, J. A. K. Howard, J. S. O. Evans, S. R. Postlethwaite and M. R. Johnson, CrystEngComm, 2008, 10, 1404–1409 RSC.
- F. Gao, C. Yin, P. Yang and G. Xue, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2004, 60, o1328–o1329 CrossRef CAS.
- P. Śledzled, R. Kamiński, M. Chruszcz, M. D. Zimmerman, W. Minor and K. Woniak, Acta Crystallogr., Sect. B: Struct. Sci., 2010, 66, 482–492 CrossRef PubMed.
- L. K. Saunders, H. H.-M. Yeung, M. R. Warren, P. Smith, S. Gurney, S. F. Dodsworth, I. J. Vitorica-Yrezabal, A. Wilcox, P. V. Hathaway, G. Preece, P. Roberts, S. A. Barnett and D. R. Allan, J. Appl. Crystallogr., 2021, 54, 1349–1359 CrossRef CAS PubMed.
- J. P. Glusker, D. Van Der Helm, W. E. Love, M. Dornberg, J. A. Minkin, C. K. Johnson and A. L. Patterson, Acta Crystallogr., 1965, 19, 561–572 CrossRef CAS.
- A. Rammohan and J. A. Kaduk, Acta Crystallogr., Sect. E: Crystallogr. Commun., 2016, 72, 854–857 CrossRef CAS PubMed.
- J. Ellena, N. Paparidis and F. T. Martins, CrystEngComm, 2012, 14, 2373 RSC.
- J. C. Tenorio Clavijo, F. F. Guimarães, J. Ellena and F. T. Martins, CrystEngComm, 2015, 17, 5187–5194 RSC.
- A. Trummal, L. Lipping, I. Kaljurand, I. A. Koppel and I. Leito, J. Phys. Chem. A, 2016, 120, 3663–3669 CrossRef CAS PubMed.
- B. Delley, J. Chem. Phys., 1990, 92, 508–517 CrossRef CAS.
- A. J. Cruz-Cabeza, S. M. Reutzel-Edens and J. Bernstein, Chem. Soc. Rev., 2015, 44, 8619–8635 RSC.
- J. Nyman and G. M. Day, CrystEngComm, 2015, 17, 5154–5165 RSC.
- L. A. Filip, M. R. Caira, S. I. Fǎrcaş and M. T. Bojiţǎ, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2001, 57, 435–436 CrossRef CAS PubMed.
- A. J. Blake, X. Lin, M. Schröder, C. Wilson and R.-X. Yuan, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2004, 60, o226–o228 CrossRef PubMed.
- S. S. Chourasiya, D. R. Patel, C. M. Nagaraja, A. K. Chakraborti and P. V. Bharatam, New J. Chem., 2017, 41, 8118–8129 RSC.
- W. Y. Wu and C. S. Su, J. Cryst. Growth, 2017, 460, 59–66 CrossRef CAS.
- J. Voogd, B. H. M. Verzijl and A. J. M. Duisenberg, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1980, 36, 2805–2806 CrossRef.
- M. Svärd, F. L. Nordström, T. Jasnobulka and Å. C. Rasmuson, Cryst. Growth Des., 2010, 10, 195–204 CrossRef.
- C. L. Jones, J. M. Skelton, S. C. Parker, P. R. Raithby, A. Walsh, C. C. Wilson and L. H. Thomas, CrystEngComm, 2019, 21, 1626–1634 RSC.
- O. N. Kavanagh, D. M. Croker, G. M. Walker and M. J. Zaworotko, Drug Discovery Today, 2019, 24, 796–804 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ce00216k |
| This journal is © The Royal Society of Chemistry 2023 |