Molecular beam epitaxy of InAs quantum wells on InP(001) for high mobility two-dimensional electron gases

Abstract

InAs quantum wells are grown epitaxially as being embedded in (Ga,In)As–(Al,In)As double heterojunctions on InP(001). Despite an extensive gradual composition variation introduced in the buffer layer to overcome the mismatch of the lattices between InAs and InP, the layers relax during the epitaxy, as manifested by a cross-hatch pattern. The mobility of the two-dimensional (2D) electron gases in the quantum wells is nonetheless large, fairly unaffected by the presence of misfit dislocations generated in the lattice relaxation. The strain states in the epitaxial layer is analyzed using the X-ray diffraction. Transmission electron microscopy reveals that the relaxation is localized in the buffer layer, leaving the epitaxial growth in the quantum-well region coherent. The second subband of the 2D state is shown to be occupied when the sheet electron density is relatively low as the higher subbands are confined by the (In,Al)As layers.

---

1 Introduction

Spintronics has attracted significant attention in the last decades for carrying and processing information by means of electron spin.¹ Spin can be manipulated using the spin–orbit interaction.² Materials having a large spin–orbit coupling such as InAs, therefore, play an important role as the medium of the carrier propagation.^3,4 InAs-based quantum wells (QWs) have thus been grown epitaxially for obtaining two-dimensional electron gases (2DEGs) having a strong spin–orbit interaction.^5–11 Here, InAs wafers are conductive. The QW structures for electrical transport need to be grown on other non-conductive substrates, typically of Fe-doped InP.

Besides the above motivation, InAs can be attractive because of the electron accumulation at its surface. We have recently demonstrated energy harvesting from environmental electromagnetic noises.^12–14 A DC voltage was produced from rf noises at temperatures below 90 K by utilizing the magnetic-field-induced transmission asymmetry resulting from the ballistic transport of a 2DEG in circularly-shaped narrow channels fabricated from GaAs–(Al,Ga)As heterostructures.¹⁵ To raise the operation temperature of the rectifier device to room temperature (RT), the channel needs to be made smaller to overcome the reduction of the mean free path l_e due to the scattering by phonons at high temperatures. Here, the side walls of mesa-etched GaAs–(Al,Ga)As channels are depleted over several hundred nanometers.¹⁶ For the circular geometry, the size reduction of the conduction channels is practically impossible in the submicron regime in the presence of such a sidewall depletion. The suppression of the surface depletion for In-containing materials is hence useful for the rectifier device.¹⁷ The surface depletion is negligible for (Ga,In)As–(Al,In)As and (Ga,In)As–InP heterostructures,¹⁸ which have been used widely for optoelectronic devices. The low-temperature electron mobility in these cases is, however, restricted to be relatively low due to the alloy scattering of (Ga,In)As.

In this paper, InAs-based QW structures are grown on InP(001) to achieve a high mobility for the 2DEGs by taking advantage of the absence of the alloy scattering for InAs. The epitaxial layers turn out to relax since the mismatch of the lattices between InAs and InP is too large to be accommodated. Nevertheless, the mobility of the 2DEGs is found to be as large as limited by the scattering from background impurities, which is in agreement with a previous report from Hatke et al.⁶ That is, the presence of misfit dislocations in the heterostructures is not crucial for the mobility. We clarify the origin of the insensitiveness of the mobility to the relaxation. We demonstrate using transmission electron microscopy (TEM) that the relaxation occurs in a manner localized in the buffer layer, leaving the 2DEGs nearly unscattered by the crystalline defects associated with the relaxation. The transport properties of the 2DEGs in the quantum Hall regime are additional presented to identify the electron density threshold for the occupation of the second subband.

2 Epitaxial growth

The heterostructures containing an InAs QW were grown by molecular beam epitaxy (MBE) on (001)-oriented semi-insulating InP substrates doped with Fe. In the epitaxial growth, the fact that InAs has a larger lattice constant than InP needs to be considered. Multiple layers of (Al,In)As and (Ga,In)As were grown as the buffer layer with gradually changing the composition to sustain the strain resulting from the lattice mismatch of 3.2%. We have adopted the buffer layer employed by Hatke et al.,⁶ as illustrated in Fig. 1.

Fig. 1 Layer sequence for InAs quantum well prepared with multiple layers of (Ga,In)As and (Al,In)As on InP(001).

The epitaxy begun with the growth of a 100 nm-thick Al_0.48In_0.52As layer. A superlattice consisting of 5.5 nm-thick Al_0.48In_0.52As and 2.5 nm-thick Ga_0.47In_0.53As layers was then grown with a total thickness of 80 nm. At this point, the substrate temperature was lowered from 480 °C to 360 °C. The buffer layer for the purpose of accommodating the lattice mismatch consisted of two parts. First, the In-content x of Al_1−xIn_xAs was increased linearly in a step-wise manner in 19 steps from x = 0.52 to 0.84, where the thickness of each layer having a uniform composition was 50 nm. Second, in the subsequently grown Al_1−xIn_xAs layer with a thickness of 50 nm, x was decreased continuously from 0.84 to 0.75. The substrate temperature was then raised to 480 °C for the growth of the QW section, which was an InAs layer with the thickness d embedded in an Al_0.25In_0.75As–Ga_0.25In_0.75As–Al_0.25In_0.75As double heterojunction. The electron confinement in the QW was realized by 10.5 nm-thick Ga_0.25In_0.75As layers. The thicknesses of the bottom and top Al_0.25In_0.75As layers were 25 and 120 nm, respectively. For most of the samples, the growth was finished with a Ga_0.25In_0.75As capping layer. Although even undoped heterostructures hosted 2DEGs, Si δ-doping was carried out for some samples in the upper Al_0.25In_0.75As layer with a separation of 3 nm from the heterointerface with the (Ga,In)As layer. The values of these sample-dependent parameters are listed in Table 1.

Table 1 Parameters of epitaxial layers (the thicknesses of InAs QW layer d and Ga_0.25In_0.75As capping layer a and the sheet density of Si δ-doping)

Sample	d (nm)	a (nm)	Doping (10^15 m^−2)
#1	4	0	0
#2	4	2	0
#3	4	2	5
#4	5	2	3
#5	5	2	5
#6	5	2	10
#7	7	0	20

---

3 Results and discussion

3.1 High mobility in relaxed heterostructures

In Fig. 2, we show the Nomarski interference contrast in a surface image of the layer obtained by an optical microscope. Despite the effort to accommodate the lattice mismatch strain in the buffer layer, the epitaxial layer is seen to have relaxed, as manifested by the presence of the cross-hatch pattern.¹⁹ The rectangular geometry of the pattern reflects the orientation of the InP substrate, where the quasi-periodic modulations occur along the [110] and [11̄0] directions in the (001) surface.

Fig. 2 Strain relaxation in epitaxial growth. A cross-hatch pattern is revealed in the Nomarski interference contrast obtained by an optical microscope.

The atomic force microscopy image in Fig. 3(a) shows that the height modulation associated with the cross-hatch pattern is with an amplitude of about 10 nm. The profile along the dotted horizontal line is shown in Fig. 3(b). The anisotropy in the surface morphology results from the kinetics of plastic relaxation.^11,20,21 The nucleation and glide in the relaxation in the [110] and [11̄0] directions are governed by the α and β dislocations, respectively.²⁰ The different core structures of these dislocations give rise to the asymmetric relaxation kinetics.²²

Fig. 3 Surface morphology generated in strain relaxation. The height mapping obtained by an atomic force microscope is shown in (a). The profile of the height along the horizontal dotted line is shown in (b). The autocorrelations C(δ) of the height modulation are shown in (c). The red and green curves were calculated for the horizontal and vertical directions in (a), respectively, which are nearly parallel to the [110] and [11̄0] directions in the surface, respectively.

To evaluate the strain and its relaxation in the heterostructure, we have carried out X-ray diffraction measurements. The Cu Kα radiation was used as the X-ray source with a wavelength of 0.15406 nm. An ω–2θ-scan curve in the range of the angle related to the 004 reflection of the cubic crystals of the heterostructure is shown in Fig. 4 as the red curve. While the strongest peak originates from the InP substrate, the peak indicated by the arrow was presumably produced by the QW region. The bar shows the position expected for bulk InAs. The broad peak in the background with a width of several degrees, which is marked by the gray rectangles, is associated with the buffer layer. Curves simulated for the heterostructure for fully strained and fully relaxed situations are shown by the blue and cyan curves, respectively. The calculations were performed using the X'pert Epitaxy software package. A partial relaxation of the strain is manifested by the difference in the angle range for the broad peak.

Fig. 4 X-ray diffraction characterization of InAs QW structure. An ω–2θ-scan curve associated with the 004 reflection of the cubic crystals is shown by the red curve for the heterostructure #2. A simulated curve using the profile of the relaxation R in the inset is shown by the green curve. The blue and cyan curves show simulated curves for the cases of no relaxation (R = 0 for all layers) and full relaxation (R = 1 for all layers), respectively. The bar indicates the peak position expected for bulk InAs.

In the simulations, the relaxation in each heterointerface needs to be specified as fit parameters. The fitting alone was, therefore, unable to identify the relaxation profile since similar agreements with the experimental curve were achieved by a number of parameter sets due to the large number of fit parameters. The curve shown in green was obtained by incorporation the manner of the strain relaxation revealed by TEM in the modeling, as will be discussed later.

Before we proceed further with the analysis of the structural properties, we present in Fig. 5 the transport properties of the 2DEGs in order to emphasize an issue that turns out to be important concerning the relaxation. In Fig. 5(a) and (b), the temperature dependencies of the mobility and sheet concentration n_s of the 2DEGs, respectively, are plotted using filled symbols. The black circles and triangles correspond to undoped heterostructures #1 and #2, respectively, whereas the heterostructures were doped for the colored circles. For comparison, the results for (Ga,In)As-based QWs grown by the same MBE system are shown by open symbols. Here, a 25 nm-thick Ga_0.4In_0.6As layer was inserted in an Al_0.48In_0.52As layer. A number of samples with different concentrations of Si δ-doping were examined.

Fig. 5 Temperature dependencies of (a) mobility and (b) sheet concentration of 2DEGs in InAs quantum wells. The heterostructure is undoped for #1 and #2 and doped for #3–#7. The results for (Ga,In)As quantum wells for comparison are shown by the open circles.

The alloy scattering of (Ga,In)As restricts the mobility to be lower than 10 m² V⁻¹ s⁻¹ for the (Ga,In)As-based QWs, as shown by the open circles in Fig. 5(a). The low-temperature mobility in the InAs-based QWs is not only larger than that in the (Ga,In)As-based QWs due to the absence of the alloy scattering but even comparable with that typically obtained for the 2DEGs in GaAs-(Al,Ga)As heterostructures, for which the mobility is limited by the concentration of the background impurities. As a matter of fact, a mobility exceeding 100 m² V⁻¹ s⁻¹ has been reported by Hatke et al.⁶ for identical InAs QW structures. The epitaxial growth of the GaAs–(Al,Ga)As heterostructures generally takes place coherently since the lattice mismatch of the (Al,Ga)As layers with the GaAs substrates is insignificant. The result that the mobility in the InAs-based QWs appears to be controlled by the background impurities implies that the misfit dislocations generated in the strain relaxation do not cause scattering for the 2DEGs.

In addition to the improvement of the mobility at low temperatures, it is worth pointing out that the RT mobility for the InAs QWs is twice as large as that for the (Ga,In)As QWs. This reflects primarily the difference in the electron effective mass shown in Table 2. The (Ga,In)As-based heterostructures are widely used for high-frequency and optoelectronic devices because of the high mobility. The InAs-based heterostructures may further improve their performance.²³

Table 2 Comparison of electron effective mass m* divided by free electron mass m₀

	GaAs	Ga0.47In0.53As	Ga0.25In0.75As	InAs
m*/m0	0.063	0.041	0.032	0.023

---

For understanding why the 2DEGs were not scattered by the misfit dislocations, which must have been generated in the strain relaxation, we have employed scanning TEM. The lamella with a size of 6 μm × 0.3 μm for the observation was prepared using the focused ion beam etching. In Fig. 6(a), a bright-field image showing the epitaxial layer over the whole thickness is displayed. Here, the growth took place from left to right. It is revealed that misfit and threading dislocations were generated exclusively in the compositional grading part of the buffer layer (one can find an image showing a larger area in ESI†). The bottom part of the buffer layer enclosed by the dotted rectangle is shown with a magnified scale in Fig. 6(b). Fig. 6(c) shows a high-resolution annular dark-field image of the top part of the layer. The QW structure is found to be without defects.

Fig. 6 Cross-sectional scanning TEM images of strain relaxation. A bright-field image of the layer is shown in (a). The area marked by the dotted rectangle is shown in (b) with an expanded scale. A high-resolution annular dark-field image of the quantum well region is shown in (c).

Although the gradual composition variation was unable to avoid the strain relaxation, the confinement of the dislocations in the buffer layer was driven by the compositional grading.²⁴ The dislocations would have extended to the surface and threaded through the QW if the buffer layer was grown with a uniform composition. The introduction of the composition grading in the buffer layer is, therefore, crucial regardless of whether the buffer layer relaxes or not.

The TEM investigation has explicitly identified the manner the strain relaxed in the growth of the heterostructures. We have, therefore, modeled a relaxation profile to be consistent with the TEM image in fitting the experimental curve in Fig. 4. The green curve is the outcome of such a simulation. The distribution of the relaxation was assumed as illustrated in the inset, where R (0 ≤ R ≤ 1) is the degree of the lattice relaxation in each layer with respect to the in-plane lattice parameter of the underlying adjacent layer. Here, R was assumed to be identical within the relaxed section since the fitting was otherwise not possible. The agreement between the experimental and theoretical curves is seen to be good. It needs to be pointed out that, for the step-like depth profile of R shown in the inset, the deterioration of the agreement with the experimental curve is not large when the value of R in the relaxed layers is further increased, i.e., the simulated curves become nearly indistinguishable for R ≥ 0.6. We hence deduce a conclusion that the extent of the relaxation in the relaxed part is estimated to be about or larger than 0.6.

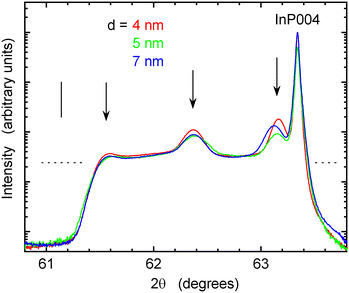
In Fig. 7, ω–2θ-scan curves are compared between the thicknesses d of the InAs layer of 4, 5, and 7 nm. The part below the dotted lines is almost identical as it is associated with the partial strain relaxation in the buffer layer. The consequences due to the difference in the QW region are expected to be manifested in the features above the dotted lines, such as the three peaks indicated by the arrows. The peak at 2θ = 63.1–63.2° seems to shift to smaller angles with increasing d. On the other hand, the variations in the position of the other peaks with d are not significant. It is plausible that the overshoot (Al,In)As layer where the In content was reduced from 0.84 to the required final value of 0.75 roughly nullified the residual strain for the InAs layer.²⁴

Fig. 7 Comparison of ω–2θ-scan curves for different thicknesses of InAs QW layer. The red, green, and blue curves were obtained from the heterostructures #2, #5, and #7, for which the thickness d of the InAs layer is 4, 5, and 7 nm, respectively. The curves are vertically offset to make them overlap with each other.

The lattice mismatch does not generate crystalline defects in the QW region, and so the 2DEGs merely experience the meandering of the conduction plane in the depth direction with an amplitude of ≤10 nm. The role of the meandering is insignificant for the mobility as the lateral scale of the height modulation is much larger than its amplitude. In Fig. 3(c), we show the lateral autocorrelation C(δ) of the height modulation δh defined as

C(δ) = 〈δh(x)δh(x + δ)〉, (1)

where δh(x) = h(x) − h_av with h(x) being the height at position x and h_av the average height. The angular bracket denotes the averaging over x. The red and green curves show C(δ) calculated for the horizontal and vertical directions of Fig. 3(a), respectively, which are nearly parallel to the [110] and [11̄0] directions of the surface, respectively. The correlation length δ_cor defined as is 0.39 and 0.85 μm in the approximate [110] and [11̄0] directions, respectively. The largest value of l_e for the data in Fig. 5 is 3.9 μm, and so a condition l_e ≫ δ_cor is realized. This may be regarded as evidence that the InAs–Ga_0.25In_0.75As interface is not rough.

3.2 Occupation of second subband

In general, the carrier mobility increases with increasing n_s as the screening of scattering potentials is enhanced. No improvement of the mobility was, however, accomplished by the doping in Fig. 5. The absence of the change in the mobility may be attributed to the inter-subband scattering caused by the second subband. The threshold energy of the second subband in the QW was not far from the Fermi level even in the undoped situation. In Fig. 8, we demonstrate that the second subband was occupied for n_s = 5.7 × 10¹⁵ m⁻². Here, the Shubnikov–de Haas (SdH) oscillation in the longitudinal resistance R_xx and the quantum Hall effect in the transverse resistance R_xy at a temperature of T = 4.2 K are shown for the 2DEG in the heterostructure #5. The resistance peaks indicated by the arrows manifest the occupation of the second subband. The Landau level filling factor ν is associated with the ground-state subband. The peaks indicated by the arrows emerged when the Fermi level was located in the energy gap between the Landau levels of the ground-state subband. That is, electrons were transferred from the Landau level of the ground-state subband to the bottom Landau level of the second subband at the magnetic depopulation associated with the change of ν.^25,26

Fig. 8 Electron occupation in second subband. The longitudinal resistance R_xx and transverse resistance R_xy at a temperature of T = 4.2 K are shown for the sample #5. The Landau filling factor ν associated with the ground-state subband is indicated. The peaks indicated by the vertical arrows manifest the population of electrons in the second subband.

The threshold sheet electron density for the population of the second subband is low in our heterostructures since the confinement of the second subband is imposed by the Al_0.25In_0.75As layers instead of the Ga_0.25In_0.75As layers that surround the InAs QW layer. We indicate in Fig. 9 the quantized electronic levels calculated using the effective mass approximation.⁵ The space-charge potential was taken into account within the Hartree approximation, where the Fermi level was assumed to be fixed at the threshold level of the second subband. The quantized energy levels for the excited-state subbands exceed the conduction-band edge of the Ga_0.25In_0.75As barrier layers. The quantized levels are lowered in energy significantly in comparison to when the excited-state subbands are confined by the Ga_0.25In_0.75As layers as the confining QW width is 26 nm instead of 5 nm. The second subband is occupied in the simulation at n_s = 8.7 × 10¹⁵ m⁻², which is in reasonable agreement with the experimental observation. The discrepancy with the experimental value is attributed to the fact that the conduction-band minimum of Al_0.25In_0.75As is not located at the Γ point, and so its effective potential height in the simulation is not simple to estimate.

Fig. 9 Quantized energy levels in QW structure. The threshold energies E_i and the probability density |φ_i(z)|² are illustrated for the bottom three subbands i = 0, 1, and 2. The black curve shows the confinement potential V(z), which includes the space-charge potential.

Before ending, we note that a parallel conduction in the barrier layer was additionally manifested in the SdH oscillations for n_s > 1 × 10¹⁶ m⁻² (not shown), giving rise to the drastic reduction in the nominal mobility for #6 and #7 in Fig. 5(a).

4 Conclusions

We have grown InAs QWs as being incorporated in Al_0.25In_0.75As–Ga_0.25In_0.75As–Al_0.25In_0.75As double heterojunctions on InP(001). Despite the gradual compositional variation in the buffer layer implemented over a thickness of ≈1 μm, the layers relaxed due to the large strain resulting from the high In contents. It has turned out, however, that the mobility of the 2DEGs is hardly reduced by the strain relaxation. We have shown that the presence of the misfit and threading dislocations is restricted to be only in the buffer layer as the propagation of the dislocations towards the surface is blocked by the composition grading. In other words, the low-temperature-grown buffer layer serves to prevent the strain relaxation in the QW section. The 2DEGs thus do not encounter the defects generated in the relaxation. The second subband of the 2DEGs has been identified to be occupied at a relatively low 2DEG density since the quantized energies of the excited-state subbands exceed the barrier height of the Ga_0.25In_0.75As layers. The higher subbands are confined by the Al_0.25In_0.75As layers. The inter-subband scattering is presumably responsible for the lack of the mobility improvement when the electron concentration was increased.

Author contributions

Anna Aleksandrova: investigation, writing and original draft preparation. Christian Golz: investigation. Klaus Biermann: investigation. Achim Trampert: investigation. Mykhaylo Semtsiv: project administration. Helmut Weidlich: conceptualization, project administration. William Ted Masselink: project administration. Yukihiko Takagaki: conceptualization, writing and original draft preparation.

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. I. Žutić, J. Fabian and S. D. Sarma, Rev. Mod. Phys., 2004, 76, 323–410.
2. K. Premasiri and X. P. A. Gao, J. Phys.: Condens. Matter, 2019, 31, 193001.
3. J. Nitta, T. Akazaki, H. Takayanagi and T. Enoki, Phys. Rev. Lett., 1997, 78, 1335–1338.
4. M. Gmitra and J. Fabian, Phys. Rev. B, 2016, 94, 165202.
5. A. Richter, M. Koch, T. Matsuyama, C. Heyn and U. Merkt, Appl. Phys. Lett., 2000, 77, 3227–3229.
6. A. T. Hatke, T. Wang, C. Thomas, G. C. Gardner and M. J. Manfra, Appl. Phys. Lett., 2017, 111, 142106.
7. Y. Iwasaki, Y. Hashimoto, T. Nakamura and S. Katsumoto, Sci. Rep., 2017, 7, 7909.
8. J. S. Lee, B. Shojaei, M. Pendharkar, M. Feldman, K. Mukherjee and C. J. Palmstrøm, Phys. Rev. Mater., 2019, 3, 014603.
9. S. J. Pauka, J. D. S. Witt, C. N. Allen, B. Harlech-Jones, A. Jouan, G. C. Gardner, S. Gronin, T. Wang, C. Thomas, M. J. Manfra, J. Gukelberger, J. Gamble, D. J. Reilly and M. C. Cassidy, J. Appl. Phys., 2020, 128, 114301.
10. C. L. Hsueh, P. Sriram, T. Wang, C. Thomas, G. Gardner, M. A. Kastner, M. J. Manfra and D. Goldhaber-Gordon, Phys. Rev. B, 2022, 105, 195303.
11. W. M. Strickland, M. Hatefipour, D. Langone, S. M. Farzaneh and J. Shabani, Appl. Phys. Lett., 2022, 121, 092104.
12. H. Akinaga, Jpn. J. Appl. Phys., 2020, 59, 110201.
13. S. Hemour and K. Wu, Proc. IEEE, 2014, 102, 1667–1691.
14. T. Sanislav, G. D. Mois, S. Zeadally and S. C. Folea, IEEE Access, 2021, 9, 39530–39549.
15. V. Hortelano, H. Weidlich, W. T. Masselink, G. Mahler and Y. Takagaki, Semicond. Sci. Technol., 2017, 32, 125005.
16. Y. Takagaki, T. Kosugi, K. Gamo, S. Namba and K. Murase, Semicond. Sci. Technol., 1990, 5, 634–637.
17. A. Aleksandrova, C. Golz, H. Weidlich, M. Semtsiv, W. T. Masselink and Y. Takagaki, Semicond. Sci. Technol., 2023, 38, 055017.
18. V. Hortelano, H. Weidlich, M. P. Semtsiv, W. T. Masselink, M. Ramsteiner, U. Jahn, K. Biermann and Y. Takagaki, Appl. Phys. Lett., 2018, 112, 151602.
19. K. H. Chang, R. Gibala, D. J. Srolovitz, P. K. Bhattacharya and J. F. Mansfield, J. Appl. Phys., 1990, 67, 4093–4098.
20. M. K. Hudait, Y. Lin, M. N. Palmisiano, C. Tivarus, J. P. Pelz and S. A. Ringel, J. Appl. Phys., 2004, 95, 3952–3960.
21. V. A. Kovalskiy, V. G. Eremenko, P. S. Vergeles, O. A. Soltanovich, I. I. Khodos, M. V. Dorokhin and Y. A. Danilov, Appl. Surf. Sci., 2019, 479, 930–941.
22. R. S. Goldman, H. H. Wieder and K. L. Kavanagh, Appl. Phys. Lett., 1995, 67, 344–346.
23. J. K. Zahurak, A. A. Iliadis, S. A. Rishton and W. T. Masselink, IEEE Electron Device Lett., 1994, 15, 489–492.
24. J. Tersoff, Appl. Phys. Lett., 1993, 62, 693–695.
25. R. M. Kusters, J. Singleton, G. Gobsch, G. Paasch, D. Schulze, F. A. Wittekamp, G. A. C. Jones, J. E. F. Frost, D. C. Peacock and D. A. Ritchie, Superlattices Microstruct., 1991, 9, 55–58.
26. Y. Takagaki, K. Muraki and S. Tarucha, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 1057–1060.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ce00010a

---