The pressure and temperature evolution of the Ca₃V₂O₈ crystal structure using powder X-ray diffraction

Abstract

We present a comprehensive experimental study of the crystal structure of calcium vanadate (Ca₃V₂O₈) under systematic temperature and pressure conditions. The temperature evolution (4–1173 K) of the Ca₃V₂O₈ structural properties is investigated at ambient pressure. The pressure evolution (0–13.8 GPa) of the Ca₃V₂O₈ structural properties is investigated at ambient temperature. Across all pressures and temperatures used in the present work, the Ca₃V₂O₈ crystal structure was determined by Rietveld refinement of powder X-ray diffraction data. The experimental high-pressure data are also supported by density-functional theory calculations. According to the high-pressure results, Ca₃V₂O₈ undergoes a pressure-induced structural phase transition at a pressure of 9.8(1) GPa from the ambient pressure trigonal structure (space group R3c) to a monoclinic structure (space group Cc). The experimentally determined bulk moduli of the trigonal and monoclinic phases are, respectively, B₀ = 69(2) GPa and 105(12) GPa. The trigonal to monoclinic phase transition appears to be prompted by non-hydrostatic conditions. Whilst the trigonal and monoclincic space groups show a group/subgroup relationship, the discontinuity in the volume per formula unit observed at the transition indicates a first order phase transition. According to the high-temperature results, the trigonal Ca₃V₂O₈ structure persists over the entire range of studied temperatures. The pressure-volume equation of state, axial compressibilities, Debye temperature (264(2) K), and thermal expansion coefficients are all determined for the trigonal Ca₃V₂O₈ structure.

---

1. Introduction

Calcium vanadate materials exhibit a wide variety of chemical compositions, including calcium orthovanadate (Ca₃V₂O₈), metavanadate (CaV₂O₆) and pyrovanadate (Ca₂V₂O₇).^1–3 Based on their electronic, transport and dielectric properties, calcium vanadates are used in ceramics for potential applications such as electrode materials for green energy storage devices.^4–6 In particular, calcium orthovanadate (Ca₃V₂O₈) has been studied as a potential medium for solid-state lasers,⁷ and it has therefore been doped with various cations, including Sm³⁺,⁸ Eu³⁺,⁹ Tb³⁺,¹⁰ (Li⁺, Nd³⁺),¹¹ and (Tm³⁺/Ho³⁺),¹² to enhance its lasing properties.

At ambient conditions, Ca₃V₂O₈ crystallizes in a trigonal crystal structure (space group R3c).¹³ Additionally, a monoclinic polymorph of Ca₃V₂O₈ (space group C2/m) has been synthesized under high-pressure (HP) and high-temperature (HT) conditions of 11 GPa and 1373 K.¹⁴ This monoclinic polymorph can be recovered from high temperature to ambient conditions. HT experiments have previously been conducted to study the dielectric constant^4,15 and vibrational properties^16,17 of the monoclinic Ca₃V₂O₈. Temperature-induced changes observed in the experimental Raman spectra have been attributed to structural phase transitions between 550 and 800 K,¹⁶ and between 1123 and 1148 K.¹⁷ To the best of the authors' knowledge, no low-temperature studies have been reported for Ca₃V₂O₈. Regarding HP Ca₃V₂O₈ studies, room-temperature (RT) HP X-ray diffraction (XRD) and Raman experiments have been reported, finding pressure-induced amorphization between 8.1 and 14.8 GPa.¹⁸ One Raman study on the related compound Ca_9−xR(VO₄)₇ (R = La, Nd, Gd) reported signs of partial amorphization around 9–10 GPa.¹⁹ According to the results summarized above, the HP behavior of Ca₃V₂O₈ is different from that of other orthovanadates with equivalent chemical formulae. For instance, Zn₃V₂O₈, Ni₃V₂O₈, and Ba₃V₂O₈ remain stable up to at least 15,²⁰ 23²¹ and 29 GPa²² respectively. Mn₃V₂O₈ and Sr₃V₂O₈ exhibit pressure-induced phase transitions around 10 GPa²³ and 13.8 GPa^22,24 respectively, and Cu₃V₂O₈ chemically decomposes at 1.35 GPa.²⁵ Such different results from various HP studies in the M₃V₂O₈ family, and the apparent contradictions between different HT studies, clearly show that further investigation into the pressure and temperature evolution of the Ca₃V₂O₈ is needed to understand its structural behavior under extreme conditions of pressure and temperature.

In the present study, we characterize the pressure and temperature evolution of the whitlockite-related Ca₃V₂O₈ polymorph by performing synchrotron and in-house X-ray diffraction (XRD) experiments. Firstly, Ca₃V₂O₈ was studied at ambient temperature under high pressure conditions (up to 13.8(1) GPa). Secondly, Ca₃V₂O₈ was studied at ambient pressure between 4(1) and 292(1) K using a synchrotron X-ray source, and at ambient pressure between 300(1) and 1173(1) K using an in-house X-ray diffractometer. The structural models were refined against the observed diffraction data via the Rietveld refinement method.^26,27 The structural data extracted from the refined models was used to determine equation of state (EOS) parameters and thermal expansions coefficients. Density-functional theory calculations have been also performed which support the experimental HP observations.

2. Methods

2.1 Experimental details

Ca₃V₂O₈ was synthesized by a solid-state reaction between V₂O₅ and CaCO₃ (99.6% purity). The reactants were mixed in the stoichiometric proportion and formed into a pellet. The pellet was annealed over three consecutive 5 hour periods, with the temperature being 1100(1) K for the first 5 hour period, and 1150(1) K for the other two. The obtained sample was used for all reported experiments. Energy dispersive X-ray spectroscopy analysis, using a scanning electron microscope (Thermo Fisher Scios 2 Dual Beam) equipped with an Oxford Ultima Max 170 detector, confirmed the stoichiometry of the material. No impurities were detected within an accuracy of approximately 1 atomic%. Within this accuracy, the relative ratio of Ca : V was 3 : 2 in agreement with the stoichiometry of the compound.

The crystal structure of the Ca₃V₂O₈ sample at ambient conditions was verified by powder XRD using a Philips X'Pert Pro Alpha1 diffractometer with a Bragg–Brentano geometry, working in continuous scanning mode, and using Cu K_α1 radiation (λ = 1.54056 Å). The set-up is equipped with a linear photon-counting detector and a primary-beam Johansson monochromator. Powder XRD data were collected over the range of 6–159° (2θ) and recorded increments of 0.0167°. The crystal structure of the obtained compound was refined by the Rietveld method^26,27 using the Fullprof software.²⁸ HT XRD experiments were performed in the temperature range 300(1)–1173(1) K using the same set-up and an HTK 1200 N (Anton Paar) temperature stage. In this experiment, XRD data were collected at high temperatures over the range 2θ = 9–87° (2θ).

Low temperature (LT) powder diffraction measurements were performed by high-resolution X-ray powder diffraction at the ID22 beamline at the European Synchrotron Radiation Facility (ESRF) in the temperature range 4(1)–292(1) K using a helium cryostat. The high-resolution diffraction data were collected at LT over the range of 2–40° (2θ) using a wavelength of 0.3998 Å and a nine-crystals multi-analyzer stage.²⁹ XRD patterns were measured from a fine powder of Ca₃V₂O₈ sealed in a 0.5 mm diameter borosilicate glass capillary.

HP powder XRD measurements up to 13.8(1) GPa were carried out at room temperature (RT) using a membrane-type diamond-anvil cell (DAC). A 4 : 1 ratio methanol–ethanol mixture (ME) was used as the pressure-transmitting medium (PTM). The pressure was determined using the equation of state of copper (Cu)³⁰ with a precision of ±0.1 GPa. We performed angle-dispersive powder XRD measurements under HP at the MSPD beamline of the ALBA synchrotron³¹ using a monochromatic beam of wavelength 0.4246 Å. The X-ray beam was focused to a 20 μm × 20 μm (FWHM) spot. A Rayonix CCD detector was used to collect XRD patterns, with a sample-detector distance of 280 mm. The structural analysis was performed using FullProf²⁸ and PowderCell.³²

2.2 Ab initio density-functional theory calculations

First-principles simulations have proven to be a very powerful technique for studying materials under high pressure.³³ In this study ab initio simulations were carried out within the framework of density-functional theory (DFT) with the Vienna ab initio Simulation Package (VASP).^34–36 Calculations were implemented within the framework of the generalized-gradient approximation (GGA) using the Perdew–Burke–Ernzerhof for solids (PBEsol) functional³⁷ to describe the exchange-correlation energy. Interactions between valence and core electrons were treated using the projector-augmented-wave (PAW) scheme.³⁸ All calculations have been carried out with temperature T = 0 K and without including dispersion corrections. We have tested including the Grimme D3 corrections, but under this approximation we obtained an equilibrium volume which agrees worse with experiments than the volume obtained without dispersive corrections. The equilibrium volume is 2% larger than in experiments when the Grimme D3 corrections are included and only 0.5% smaller than in experiments when they are not included. Based on this result and the fact that calculations without dispersive corrections usually works well to describe the changes induced by pressure in the crystal structure of vanadates,^39,40 we decided to neglect dispersion corrections in our simulations. Finite temperature calculations are beyond the scope of the present work. To solve the Schrödinger equation with high accuracy we used a plane wave basis set using an energy cutoff of 540 eV. The integrations over the Brillouin zone (BZ) of the two studied structures were calculated with a dense Monkhorst–Pack⁴¹ grid of 4 × 4 × 4 special k-points. The unit-cell parameters and the atomic positions were fully optimized at different volumes to obtain, at selected fixed volumes, the crystal structure. Pressure is obtained in our simulations from the stress tensor. During optimization we requested that the forces on the atoms were less than 0.003 eV Å⁻¹, and the deviations of the stress tensors from a diagonal hydrostatic form were lower than 0.1 GPa. This procedure allows us to obtain a set of volume, energy, and pressure data from our simulations determining the crystal structure at different pressures.⁴² Lattice-dynamics calculations were performed using the direct force constant approach using the Phonopy package.⁴³ To calculate the phonon dispersion, we used a 2 × 2 × 2 supercell to study the dynamical stability of the system under pressure. These calculations were performed with the aim of testing the dynamical stability of the calculated crystal structure. The mechanical properties were evaluated by computing the elastic constants with the method implemented in the VASP code.⁴⁴

3. Results and discussion

3.1 Crystal structure at ambient conditions

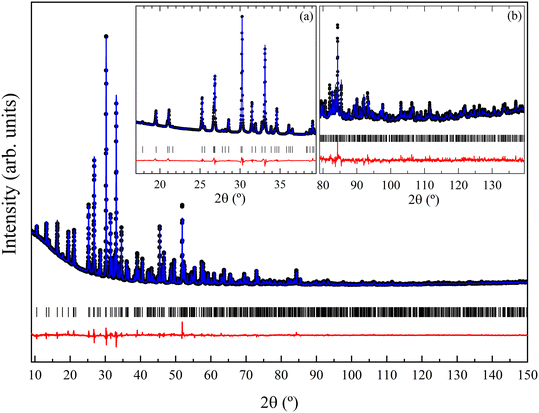
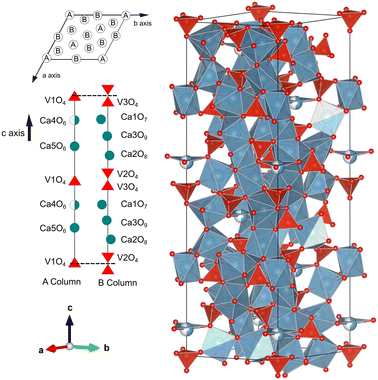
XRD patterns acquired at ambient conditions (using Cu K_α1 radiation) confirm the known trigonal structure of Ca₃V₂O₈ with space group R3c (space group number 161). The results of Rietveld refinement are shown in Fig. 1. The diffraction peaks are well matched to the Ca₃V₂O₈ structure reported in the literature.¹³ The atomic coordinates, atomic displacement parameters and peak shape parameters were refined using initial values given in ref. 13. The refined lattice parameters of Ca₃V₂O₈ are a = 10.81221(8) Å and c = 38.0262(3) Å, which are consistent with earlier reported values.^{13,15,18,45–49} The refined atomic positions, reported in Table S1 in the ESI,† are also in agreement with those reported in the literature. In Table 1 we compare unit-cell parameters at ambient conditions from our four experiments (ambient conditions, HP, HT, and LT) to show the mutual agreement. Fig. 2 shows the crystal structure of Ca₃V₂O₈. The structure is known to be composed of only two building units, namely columns called A and B.^50,51 Each A column is surrounded by 6 B columns and the 5 cationic sites (Ca1–Ca5) are divided between columns A and B. The proportion of columns A : B is 1 : 3. The A column has the cation site sequence described by the following order of polyhedra: V1O₄–Ca4O₆–Ca5O₆–V1O₄ and the corresponding sequence in column B is V3O₄–Ca1O₇–Ca3O₈–Ca2O₈–V2O₄ (see Fig. 2). The VO₄ tetrahedral units are isolated from each other. In this Ca₃V₂O₈ structure there is also a position half-occupied by Ca atoms (Ca4), which is surrounded by three oxygen atoms in a triangular coordination.

Fig. 1 Rietveld refinement of trigonal Ca₃V₂O₈ at RT. black dots correspond to the experimental data, the blue line to the calculated profile, ticks to the Bragg reflections, and the red line to the residual. The R-factors are: R_wp = 4.46%, R_exp = 1.61%, and R_p = 3.08%. The insets present an enlarged view of the 20–40° region of the refinement (a) and an enlarged view of the 80–140° region (b) in order to illustrate the quality of refinement.

Table 1 Trigonal Ca₃V₂O₈ lattice parameters at ambient conditions as obtained from different measurements performed in this work art various experimental facilities

Type of measurement	λ (Å)	a (Å)	c (Å)	V (Å^3)	T (K)
Amb. Cond. Exp. (laboratory)	1.5406	10.81221(8)	38.0262(3)	3849.84(5)	298(2)
HT experiment (laboratory)	1.5406	10.8133(3)	38.031(1)	3851.1(2)	300(1)
LT experiment (ESRF)	0.3998	10.81370(2)	38.03276(8)	3851.56(1)	292(1)
HP experiment (ALBA)	0.4246	10.807(1)	38.073(4)	3850.8(5)	296(1)

---

Fig. 2 (Right) Crystal structure of trigonal Ca₃V₂O₈ at ambient conditions. The coordination polyhedra of Ca are shown in blue and the VO₄ tetrahedra in red. The sites with partial occupation of Ca atoms are shown with half blue/half white spheres. (Left) The layout of A and B columns and column composition. The red triangles represent the vanadium centered V1, V2, and V3 tetrahedra, and the circles show the calcium-centered polyhedral located at the Ca1–Ca5 sites.

3.2 Variable-temperature measurements at ambient pressure

The low-temperature Ca₃V₂O₈ XRD patterns from 4(1) to 292(1) K (λ = 0.3998 Å) are very similar to those acquired at ambient temperature. They can be described by the same R3c crystal structure, as confirmed by the Rietveld refinements (see Fig. 3(b)). Therefore, Ca₃V₂O₈ always maintains its trigonal structure in the temperature range of 4(1)–292(1) K at ambient pressure, and no structural phase transition occurs. Lattice parameters and the crystal structure were refined for all LT XRD patterns using the ambient temperature structure as starting model.

Fig. 3 Variable-temperature X-ray diffractograms of Ca₃V₂O₈ in the temperature range of (a) 300(1)–1173(1) K and (b) 4(1)–292(1) K. The inset in (b) shows the most intense reflection marked with an asterisk peak (0, 2, 10). Due to the use of an ateanuator at the lowest temperature the observed intensity is reduced by 50% from 50(1) to 4(1) K.

X-ray diffraction patterns of Ca₃V₂O₈ at HT can be all explained with the same R3c crystal structure as that of the ambient-conditions XRD patterns. The evolution with temperature of XRD is gradual with no new peaks appearing up to the highest temperature covered by this study; see Fig. 3(a). Consequently, there is no phase transition up to 1173(1) K. This observation is in line with previous Raman scattering studies. The only reported phase transition reported is ferroelectric–paraelectric and it occurs at 1383 K.¹⁶ In whitlockite-related materials, a change of symmetry from R3c to R3̄m occurs at high temperatures.^52,53 Attempts to use the space group R3̄m for refinement of Ca₃V₂O₈ XRD patterns acquired at high temperature have not been successful. Therefore, the change of symmetry from R3c to R3̄m is ruled out for Ca₃V₂O₈. In particular, the structure with space group R3̄m fails to explain several peaks experimentally observed which can be identified with Miller indexes (223), (315), (137), (1115), and (2113) in the structure described by space group R3c.

From the low-temperature and high-temperature diffraction experiments, we have determined the temperature dependence of the unit-cell parameters. In the case of the LT experiments atomic positions have also been refined. The Ca₃V₂O₈ unit cell parameters and atomic positions for the low-temperature and high-temperature diffraction experiments are given in Table S2 of the ESI.† The temperature evolution of lattice parameters and unit cell volume are shown in Fig. 4. The variation of the lattice parameters over the whole temperature range are at the level of 1.742% for a and 1.640% for c. There is a weakly anisotropic expansion which can be better seen in the variation of axial ratio (c/a) with temperature. From 4 K to 306(5) K the expansion of c is larger than the expansion of a. Above 306(5) K, and up to 888(10) K, the sign of anisotropy is reversed with larger expansion along the a-axis than that along c-axis. The behavior changes once again beyond 888(10) K, whereafter it becomes isotropic. Notice that changes in c/a are included within the range of 3.5124 and 3.5172; i.e., the maximum variation is quite low, 0.1%. We attribute the nonlinear behavior of c/a to changes in the vibrations of polyhedral units forming the crystal structure⁵⁴ and/or to the hypothetical variation in occupancies of Ca sites due to the migration of Ca atoms to the half-occupied Ca4 site just at the highest temperatures.⁵⁵ In Fig. 5, linear (α_a and α_c) and volumetric (α_V) thermal expansion coefficients (TEC) are shown. They have been obtained from experiments using a Lagrange interpolation.⁵⁶

Fig. 4 Temperature evolution of the trigonal Ca₃V₂O₈ unit-cell parameters (top), volume/Z (bottom), and c/a axial ratio (inset). Solid symbols correspond to the LT experiment and empty symbols to the HT experiment. The results of modeling by a second order Grüneisen approximation, discussed in the text, are shown with a solid line. Vertical dashed lines separate the regions of different c/a evolution.

Fig. 5 Thermal expansion coefficients (TEC) of unit-cell parameters and unit-cell volume of Ca₃V₂O₈. Solid dots are from the LT experiment and empty dots are from the HT experiment. The solid line represents the result of modeling by a second order Grüneisen approximation, discussed in the text. Vertical dashed lines separate the regions where the behavior of c/a varies.

At low-temperature, the variation of unit-cell volume with temperature can be modeled by a second order Grüneisen approximation.^57,58 Using this model to fit low-temperature experiments (4–292 K), the Debye temperature (θ_D) was evaluated as θ_D = 264(2) K. In Fig. 4 and 5 we show that the Grüneisen approximation agrees quite well with the experimental data. There are few reports concerning the Debye temperature using DFT calculations for materials related to Ca₃V₂O₈ but described by different space groups. For example, in Sr₃P₂O₈ (space group R3m)⁵⁹ the calculated Debye is 559 K. The structure rigidity will increase by replacing Ca with the heavier atom Sr, which could cause the differences in Debye temperatures. A similar difference in Debye temperatures is observed when comparing Ca₃(PO₄)₂ : 0.07Ce³⁺ (θ_D = 541 K) to Ca_1.5Sr_1.5(PO₄)₂ : 0.07Ce³⁺ (θ_D = 730 K).⁶⁰

3.3 High-pressure studies

The trigonal Ca₃V₂O₈ crystal structure model was successfully refined against the observed powder XRD patterns acquired under high pressure conditions from 0.1(1) to 9.3(1) GPa. The Rietveld refinement results are shown in Fig. 6 for selected pressures. The fit indicators of the Rietveld refinement obtained at the lowest pressure were R_p = 6.55%, R_exp = 5.24% and R_wp = 9.80%. Similar goodness-of-fit quantities were obtained at all pressures. At 9.8(1) GPa, we notice a partial splitting, broadening of some reflections, and the appearance of extra peaks at low angles. The phenomenon becomes more evident as pressure is increased. To highlight the changes of XRD patterns, Fig. 7 shows enlarged versions of the XRD patterns measured at 9.3(1) and 13.8(1) GPa for 2θ ≤ 10°. In particular, the broadening and splitting of peaks are noticeable at 6° and around 7–8° (see the peaks marked with arrows in Fig. 7). The extra peaks are marked with asterisks in Fig. 7. The phenomenon described above can be interpreted as the occurrence of a phase transition into a monoclinic structure (space group Cc). In Fig. 7 it can be seen that the trigonal structure cannot index all the peaks observed at 13.8(1) GPa. In particular, the trigonal structure does not explain the four peaks marked with asterisks in Fig. 7. The structural information of the monoclinic HP phase can be found in the ESI† (Table S3). The crystallographic information file for the monoclinic Ca₃V₂O₈ is structure can be obtained from the Cambridge Crystallographic Data Centre under deposition number 2192772. The crystal structure of the monoclinic phase is shown in Fig. 8. The HP structure was inferred from the low-pressure structure by means of group-subgroup relations. The HP–HT structure reported in the literature¹⁶ does not explain any of our XRD patterns thus it was excluded from the search for the Ca₃V₂O₈ structure at HP and room temperature. The room-temperature HP phase reported here has a similar structural framework to the trigonal phase, but with a monoclinic distortion of the β angle and subtle changes of the unit-cell parameters which indicate a symmetry reduction of the structure. The same kind of transformations have been observed in piezoelectric materials, which are associated with a disorder induced by external fields.⁶¹ The subsequent analysis of the unit-cell parameters shows a small discontinuity in the volume per formula unit at the phase transition. Therefore, despite the continuous symmetry change from R3c to Cc, the structural transformation can be interpreted as a first-order phase transition. From 9.8(1) to 13.8(1) GPa the XRD patterns can be fitted with the HP monoclinic structure. Two Ca₃V₂O₈ diffraction patterns were collected on pressure-release at 9.7(1) GPa and 4.3(1) GPa. The pattern at 9.7(1) GPa remains in the monoclinic structure, while the other at 4.3(1) GPa can be assigned to the original trigonal structure, indicating that the phase transition is reversible and the return to the trigonal phase occurs on decompression somewhere between 9.7(1) and 4.3(1) GPa.

Fig. 6 XRD patterns at selected pressures (black symbols). Rietveld fits, and residuals are shown with blue and red lines, respectively. Ticks indicate the positions of the Bragg peaks for the phase indicated in the figure. Pressures are indicated in the figure. The top trace corresponds to data acquired on sample decompression.

Fig. 7 Enlarged view of the low-angle region of XRD patterns acquired from Ca₃V₂O₈ at 9.3(1) and 13.8(1) GPa. The figure highlights the broadening and splitting of peaks described in the text. The phenomena are noticeable for the peaks located at 6° between 7° and 8°. The figure also highlights the presence of extra peaks which are a fingerprint of the occurrence of a phase transition. The ticks give the position of Bragg peaks according to indexation. The trigonal structure (space group R3c) cannot explain the peaks marked with asterisks at 13.8(1) GPa.

Fig. 8 Crystal structure of the monoclinic phase Ca₃V₂O₈. The coordination polyhedra of Ca are shown in blue and the VO₄ tetrahedra in red.

Interestingly, the phase transition takes place at a pressure that coincides with the limit of quasi-hydrostatic conditions for the used pressure medium (9.8(1) GPa).⁶² Therefore, one possibility is that the pressure-driven transition could be triggered by non-hydrostatic stresses. A similar phenomenon has previously been observed in other vanadates.⁶³ Our density functional theory (DFT) calculations support this hypothesis. For example, when considering the two polymorphs observed in our experiments, DFT calculations found that the low-pressure trigonal structure is the stable structure within the pressure range covered by our studies. In particular, when calculations were performed for the HP monoclinic structure (described by a subgroup (Cc) of the space group of the trigonal structure (R3c)), we found that under hydrostatic conditions optimization of the monoclinic structure always led to the trigonal structure (i.e. the structural parameters of the lower monoclinic structure satisfy the conditions to allow it to be described by the higher symmetry trigonal structure (R3c)), which means that the trigonal structure is the ground state in the pressure range covered in our studies. Lattice dynamics calculations also show that the trigonal structure is dynamically stable at 0 GPa and at pressures where we experimentally observed the monoclinic phase. In the calculated phonon dispersion plots (see Fig. S1 in the ESI†) all phonon branches are positive at 0 and 11.2 GPa, supporting the dynamical stability of the trigonal structure also under HP. In addition, elastic constants calculations (see results in Table S4 in ESI†) show that the generalized Born stability criteria are fulfilled at 0 and 11.2 GPa. This means that the trigonal structure is also mechanically stable. Based on calculations we believe that the observed phase transition could have been triggered by non-hydrostatic stresses. In particular, our DFT calculations show that a uniaxial stress of 1.2 GPa is sufficient to trigger the transition from trigonal to monoclinic. This hypothesis should be confirmed by future experiments using different pressure transmitting media.

We report the pressure dependence of the unit-cell parameters and corresponding volume per formula unit of both phases of Ca₃V₂O₈ and the results of the DFT calculations for the trigonal phase in Fig. 9. Theoretical results for the monoclinic HP phase are not reported because under hydrostatic conditions this phase is not stable in the pressure range covered by our studies as discussed before. For the low-pressure phase, the agreement between calculations and experiments is good. According to experiments, at 9.8(1) GPa we detected a 1% volume reduction associated with the phase transition into the monoclinic structure. This volume discontinuity is consistent with the existence of the phase transition. Notice that for proper comparison volumes per formula unit are used. We have analyzed the unit-cell volume using a third-order Birch–Murnaghan equation of state (EOS)⁶⁴ employing the EosFit7 software.⁶⁵ The third order EOS was determined from the Eulerian strain-normalized pressure dependence of the data.⁶⁶ All EOS parameters of this work are shown and compared to the literature in Table 2. As discussed in the next paragraph, the bulk modulus at zero pressure (B₀) and its pressure derivative () agree within confidence ellipses with the values obtained from the second-order EOS. The B₀ obtained is close to the bulk moduli found for other calcium compounds with the whitlockite-related structure, such as Ca₉R(VO₄)₇ (R = La, Nd, Gd)¹⁹ and β-Ca₃P₂O_8.^67,68 The reported bulk modulus for the low-pressure trigonal Ca₃V₂O₈ phase is much smaller that of other orthovanadates with similar chemical formulae, for example: Mn₃V₂O₈, Co₃V₂O₈, Ni₃V₂O₈, and Zn₃V₂O₈, however these compounds have different crystal structures which have been recently systematically studied.⁶⁹ The higher compressibility of whitlockite-related compounds is related to its lower packing efficiency. For the monoclinic Ca₃V₂O₈ phase, based on the conclusions obtained from the trigonal phase EOS and because we have only six data points, we have used a second-order EOS. The corresponding EOSs are also plotted in Fig. 9. The observed increase of the bulk modulus after the transition is comparable with results from other vanadates, such as CeVO₄, TbVO₄, BiVO₄ and other zircon, scheelite, or fergusonite structured orthovanadates, where phase transitions near 10 GPa induce an increase of the bulk modulus.^70,71

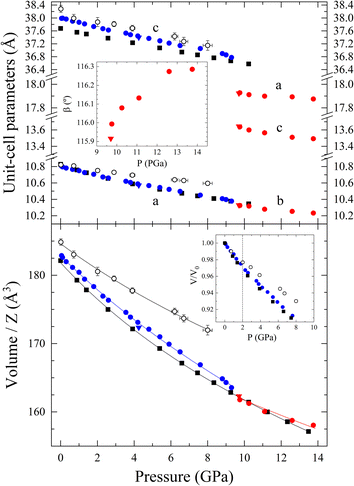Fig. 9 Pressure dependence of the Ca₃V₂O₈ unit-cell parameters (top), beta angle (top inset), volume/Z (bottom), and normalized volume (bottom inset). Blue and red symbols represent the trigonal and monoclinic phases, respectively. Black empty symbols represent literature data from the trigonal phase,¹⁸ and black squares represent DFT calculations. Circles represent upward pressure, while triangles releasing pressure data. The calculated EOS are shown with solid lines. The vertical dashed line in the inset shows the pressure where non-hydrostatic experiments deviate from quasi-hydrostatic experiments. Z = 21/14 for the trigonal/monoclinic phase.

Table 2 EOS parameters (cell volume per formula unit (V₀/Z), bulk modulus (B₀), and its pressure derivative ()) for trigonal Ca₃V₂O₈ from this work and from the literature. Data of structurally related vanadates and phosphates are included for comparison. The first line shows the results of the HP phase here reported

	V 0/Z (Å^3)	B 0 (GPa)
Monoclinic Ca3V2O8 (HP experiment)	175.4(16)	105(12)	4 (fixed)
Trigonal Ca3V2O8 (HP experiment)	182.83(15)	69(2)	3.7(6)
	182.88(12)	68.2(8)	4 (fixed)
Trigonal Ca3V2O8 (DFT calculations)	181.83(10)	61.9(7)	5.5(2)
	181.53(16)	68.2(9)	4 (fixed)
Trigonal Ca3V2O8 ^18	184.6(2)	92.50(8.23)	5.89(2.38)
	184.49(17)	99.08(2.25)	4 (fixed)
Trigonal Ca9La(VO4)7 ^19	186.71(19)	63(4)	4(1)
	186.7(3)	63(1)	4 (fixed)
Trigonal Ca9Nd(VO4)7 ^19	185.05(10)	63(2)	5.6(6)
	185.38(14)	69.2(7)	4 (fixed)
Trigonal Ca9Gd(VO4)7 ^19	184.29(19)	61(5)	6(1)
	184.7(3)	69(1)	4 (fixed)
Trigonal Ca3P2O8 ^67	167.1(3)	79.5(20)	4 (fixed)

---

The confidence ellipses of B₀vs. for the trigonal phase are shown in Fig. 10. We include in the plot the results of 2nd and 3rd order Birch–Murnaghan EOS, results from a previous study¹⁸ as well as the DFT calculations from this work. Fig. 10 shows that both experimental fits lead to similar parameters. In particular, the result of the 2nd order EOS is within the 68.3% confidence level ellipse of the 3rd order EOS; i.e. both EOSs describe equally well the pressure dependence of the volume. For the fits of the DFT calculations, the 2nd order EOS overlaps with the experimental one, while the 3rd order EOS ends up being inside the 99.7% confidence level ellipse of the experimental fitting. Therefore, the DFT calculations are in a good agreement with the results of this work. Fig. 10 shows that the bulk modulus of previous studies¹⁸ is probably overestimated. This could be related to non-hydrostatic effects. In the V/V₀ figure (inset of the bottom panel of Fig. 9) we show that the results of this experiment depart from our results at 2 GPa. The PTM used in that work was silicone oil, which is hydrostatic only up to 2 GPa.⁶² Otherwise, the ME 4 : 1 mixture we have used is quasi-hydrostatic up to 10 GPa.⁶² This substantial difference, which makes deviatoric stresses larger under silicone oil than under ME 4 : 1, might explain the previously overestimated B₀.⁶² In fact, there are many studies in oxides where non-hydrostatic effects have induced a decrease of compressibility as an artifact.⁷² For instance, in YBO₃ and GdYO₃ non-hydrostatic effects induce an overestimation by 50% of the bulk modulus.⁷³ In HoVO₄, non-hydrostatic experiments give a bulk modulus 25% larger than quasi-hydrostatic experiments.⁷⁴ Then it is quite reasonable to assume the non-hydrostatic effects could lead to a 30% overestimation of the bulk modulus of Ca₃V₂O₈. They can be also the cause of the previously observed amorphization, which could have been triggered by large non-hydrostatic effects, as those created when silicone oil is used as pressure medium, as previously observed in ternary oxides.⁷⁵ Generally, under non-hydrostatic conditions, the EOS fitting provides an overestimated value of B₀.⁷⁵

Fig. 10 versus B ₀ plot from results of the trigonal phase of Ca₃V₂O₈ are represented with blue empty circles. Confidence ellipses from the present experiment are shown. The black empty circles are previous results from the literature,¹⁸ and the red empty squares are DFT calculations.

From our experiments, we have also derived the linear isothermal compressibility coefficients for the a and c axis of the trigonal structure; , where x = a or c. The linear compressibilities obtained are κ_a = 5.2(4) 10⁻³ GPa⁻¹ and κ_c = 3.8(2) 10⁻³ GPa⁻¹. The region used for the fits is from 0.1(1) to 4.8(1) GPa to guarantee that only hydrostatic data are used. Compared to the results of previous experiments¹⁸ (κ_a = 2.6(5) 10⁻³ GPa⁻¹ and κ_c = 3.4(7) 10⁻³ GPa⁻¹) we have obtained a similar compressibility for the c-axis but a two times larger compressibility along the a-axis. Thus, the axis along the hexagonal planes of the structure seems to be more sensitive to non-hydrostatic stresses than the perpendicular axis.

4. Conclusions

In the present study, polycrystalline calcium orthovanadate Ca₃V₂O₈ (space group R3c) was investigated via synchrotron powder XRD as a function of pressure up to 13.8(1) GPa at ambient temperature, and as a function of temperature between 4(1) and 1173(1) K at ambient pressure. Experiments at room temperature confirm the previously reported trigonal low-pressure structure of the studied crystal and confirms its phase purity. The high-pressure experiments provide information on the compressibility of both the trigonal and monoclinic Ca₃V₂O₈ phases and show the occurrence of a reversible phase transition between these two polymorphs at 9.8(1) GPa on compression. The phase transition is interpreted based on the results of Rietveld refinements. The experimental conditions and ab initio calculations suggest that the transition could be triggered by non-hydrostatic stresses. The trigonal structure of Ca₃V₂O₈ remains stable at ambient pressure throughout the wide range of temperatures studied in this work (4(1)–1173(1) K). The results obtained via X-ray diffraction have enabled the determination of the Birch–Murnaghan equation of state and thermal expansion coefficients. We have determined a bulk modulus B₀ = 69(2) GPa for the trigonal phase and B₀ = 105(12) GPa for the monoclinic phase. The value obtained for the trigonal phase under quasi-hydrostatic conditions shows that the bulk modulus of Ca₃V₂O₈ was previously overestimated by more than 20%. The value of the Debye temperature is evaluated as 264(2) K. Thermal expansion coefficients have also been reported, clearly finding three distinct temperature regions in which the c/a ratio exhibits distinct behaviors. The acquired knowledge for this compound will facilitate analysis of the properties of such compounds, treating it as a reference material.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Author contributions

J. Sánchez-Martín, D. Errandonea, R. Turnbull, J. Ibáñez, and C. Popescu were involved in the pressure experiments and analysis. H. Sadat Rahimi Mosafer, W. Paszkowicz, R. Minikayev, and A. Fitch were involved in the temperature experiments and analysis. M. Berkowski was responsible for the material synthesis. P. Rodríguez-Hernández and A. Muñoz were involved in the DFT calculations. The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

Conflicts of interest

The authors declare no competing interests.

Acknowledgements

The authors acknowledge financial support from the Spanish Research Agency (AEI) and Spanish Ministry of Science and Investigation (MCIN) under grant PID2019-106383GB-41/43 (DOI: https://doi.org/10.13039/501100011033). This work was also supported by the Generalitat Valenciana under Grant No. PROMETEO CIPROM/2021/075-GREENMAT. This study forms part of the Advanced Materials Programme and was supported by MCIN with funding from European Union NextGenerationEU (PRTR-C17.I1) and by Generalitat Valenciana (Grant MFA/2022/007). J. S.-M. acknowledges the Spanish Ministry of Science, Innovation and Universities for the PRE2020-092198 fellowship. The authors thank ALBA synchrotron for providing beam time for the HP XRD experiments (Proposal 2021085271). The high-resolution powder diffraction at low-temperature experiments were performed on beamline ID22 at the European Synchrotron Radiation Facility (ESRF), Grenoble, France. The access to ESRF was financed by the Polish Ministry of Education and Science – decision number 2021/WK/11. R.T. acknowledges funding from the Generalitat Valenciana through the APOSTD postdoctoral Fellowship No. CIAPOS/2021/20.

References

1. Y. Yang, H. Mao and M. Selleby, An Assessment of the Ca-V-O System, Calphad, 2017, 56, 29–40.
2. Z. Cao, N. Wang, W. Xie, Z. Qiao and I. H. Jung, Critical Evaluation and Thermodynamic Assessment of the MgO-V₂O₅ and CaO-V₂O₅ Systems in Air, Calphad, 2017, 56, 72–79.
3. J. Xiang, X. Wang, G. Pei, Q. Huang and X. Lü, Solid-State Reaction of a CaO−V₂O₅ Mixture: A Fundamental Study for the Vanadium Extraction Process, Int. J. Miner., Metall. Mater., 2021, 28, 1462–1468.
4. H. Ning, H. Yan and M. A. Reece, High Curie Point Ferroelectric Ceramic Ca₃(VO₄)₂, Ferroelectrics, 2015, 487, 94–100.
5. G. Yao, C. Pei, J. Xu, P. Liu, J. Zhou and H. Zhang, Microwave Dielectric Properties of CaV₂O₆ Ceramics with Low Dielectric Loss, J. Mater. Sci.: Mater. Electron., 2015, 26, 7719–7722.
6. K. Thiagarajan, J. Theerthagiri, R. A. Senthil and J. Madhavan, Simple and Low Cost Electrode Material Based on Ca₂V₂O₇/PANI Nanoplatelets for Supercapacitor Applications, J. Mater. Sci.: Mater. Electron., 2017, 28, 17354–17362.
7. L. H. Brixner and P. A. Flournoy, Calcium Orthovanadate Ca₃(VO₄)₂ - A New Laser Host Crystal, J. Electrochem. Soc., 1965, 112, 303.
8. C. Li, W. Yang and Y. Chang, Fluorescence Spectrum of Calcium Orthovanadate Doped with Samarium, Ferroelectrics, 1993, 142(1), 131–135.
9. H. Lin, Y. Fang, X. Huang and S. Chu, Luminescence and Site Symmetry Studies of New Red Phosphors (Ca, Ba)₃(VO₄)₂:Eu³⁺ Under Blue Excitation, J. Am. Ceram. Soc., 2010, 93, 138–141.
10. S. S. Parab and A. V. Salker, Structural and Optical Properties of Tb and Na-Tb Co-doped Ca₃V₂O₈ Phosphors Prepared by Sol-gel Process, Mater. Res. Express, 2018, 5, 016302.
11. M. B. Kosmyna, B. P. Nazarenko, V. M. Puzikov, A. N. Shekhovtsov, W. Paszkowicz, A. Behrooz, P. Romanowski, A. S. Yasukevich, N. V. Kuleshov and M. P. Demesh, et al. Ca10Li(VO4)7:Nd3+, a Promising Laser Material: Growth, Structure and Spectral Characteristics of a Czochralski-Grown Single Crystal, J. Cryst. Growth, 2016, 445, 101–107.
12. L. I. Ivleva, E. E. Dunaeva, I. S. Voronina, M. E. Doroshenko, A. G. Papashvili, J. Sulc, J. Kratochvíl and H. Jelinkova, Impact of Tm³⁺/Ho³⁺ Co-Doping on Spectroscopic and Laser Properties of Ca₃(VO₄)₂ Single Crystal, J. Cryst. Growth, 2019, 513, 10–14.
13. R. Gopal and C. Calvo, The Structure of Ca₃(V0₄)₂, Z. Kristallogr., Kristallgeom., Kristallphys., Kristallchem., 1973, 137, 7–85.
14. A. Grzechnik, Crystal Structure of Ca₃(VO₄)₂ Synthesized at 11 GPa and 1373 K, Solid State Sci., 2002, 4, 523–527.
15. A. M. Glass, S. C. Abrahams, A. A. Ballman and G. Loiacono, Calcium Orthovanadate, Ca₃(VO₄)₂-a New High-temperature Ferroelectric, Ferroelectrics, 1978, 17, 579–582.
16. A. Grzechnik, High-Temperature Transformations in Calcium Orthovanadate Studied with Raman Scattering, Chem. Mater., 1998, 10, 1034–1040.
17. M. K. Ryu, J. G. Choi, G. H. Kim, S. Kojima, M. Takashige and M. S. Jang, Raman Scattering Study in Ca₃V₂O₈, Ferroelectrics, 2006, 332, 1–5.
18. A. Grzechnik, Amorphization of Ca₃(VO₄)₂ at High Pressure, J. Solid State Chem., 1998, 139, 161–167.
19. K. M. Kosyl, W. Paszkowicz, O. Ermakova, D. Wlodarczyk, A. Suchocki, R. Minikayev, J. Z. Domagala, A. N. Shekhovtsov, M. Kosmyna and C. Popescu, et al. Equation of State and Amorphization of Ca9R(VO4)7 (R = La, Nd, Gd): A Combined High-Pressure X-ray Diffraction and Raman Spectroscopy Study, Inorg. Chem., 2018, 57, 13115–13127.
20. D. Diaz-Anichtchenko, D. Santamaría-Pérez, T. Marqueño, J. Pellicer-Porres, J. Ruíz-Fuertes, R. Ribes, J. Ibáñez, S. N. Achary, C. Popescu and D. Errandonea, Comparative study of the high-pressure behavior of ZnV₂O₆, Zn₂V₂O₇, and Zn₃V₂O₈, J. Alloys Compd., 2020, 837, 155505.
21. D. Diaz-Anichtchenko, R. Turnbull, E. Bandiello, S. Anzellini and D. Errandonea, High-Pressure Structural Behavior and Equation of State of Kagome Staircase Compound, Ni₃V₂O₈, Crystals, 2020, 10, 910.
22. A. Grzechnik and P. F. McMillan, High-pressure X-ray diffraction of Sr₃(VO₄)₂ and Ba₃(VO₄)₂, Phys. B, 1998, 252, 268–273.
23. S. Kesari, A. B. Garg, O. Clemens, B. Joseph and R. Rao, Pressure-Induced Structural Behavior of Orthorhombic Mn₃(VO₄)₂: Raman Spectroscopic and X-ray Diffraction Investigations, ACS Omega, 2022, 7, 3099–3108.
24. A. Grzechnik and P. F. McMillan, High Pressure Behavior of Sr₃(VO₄)₂ and Ba₃(VO₄)₂, J. Solid State Chem., 1997, 132, 156–162.
25. D. Diaz-Anichtchenko, R. Turnbull, E. Bandiello, S. Anzellini, A. N. Achary and D. Errandonea, Pressure-Induced Chemical Decomposition of Copper Orthovanadate (α-Cu₃V₂O₈), J. Mater. Chem. C, 2021, 9, 13402.
26. B. O. Loopstra and H. M. Rietveld, The Structure of Some Alkaline-Earth Metal Urinates, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1969, 25, 787–791.
27. H. M. Rietveld, A Profile Refinement Method for Nuclear and Magnetic Structures, J. Appl. Crystallogr., 1969, 2, 65–71.
28. J. Rodrígez-Carvajal, Recent Advances in Magnetic Structure Determination by Neutron Powder Diffraction, Phys. B, 1993, 192, 55.
29. J. L. Hodeau, P. Bordet, M. Anne, A. Prat, A. N. Fitch, E. Dooryhee, G. Vaughan and A. Freund, Nine Crystal Multi-Analyser Stage for High-Resolution Powder Diffraction Between 6 and 40 keV, in Crystal and Multilayer Optics, Proceedings 3448, 353 of the SPIE's International Symposium on Optical Science, Engineering, and Instrumentation, San Diego, CA, United States, 1998.
30. A. Dewaele, P. Loubeyre and M. Mezouar, Equations of State of Six Metals Above 94 GPa, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 094112.
31. F. Fauth, I. Peral, C. Popescu and M. Knapp, The New Material Science Powder Diffraction Beamline at ALBA Synchrotron, Powder Diffr., 2013, 28, S360–S370.
32. W. Kraus and G. Nolze, POWDER CELL – a Program for the Representation and Manipulation of Crystal Structures and Calculation of the Resulting X-ray Powder Patterns, J. Appl. Crystallogr., 1996, 29, 301–303.
33. A. Mujica, A. Rubio, A. Muñoz and R. J. Needs, High-Pressure Phases of Group-IV, III-V, and II-VI Compounds, Rev. Mod. Phys., 2003, 75, 863.
34. G. Kresse and J. Hafner, Ab Initio Molecular Dynamics for Liquid Metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558.
35. G. Kresse and J. Furthmüller, Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set, Comput. Mater. Sci., 1996, 6, 15.
36. G. Kresse and J. Furthmüller, Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
37. J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces, Phys. Rev. Lett., 2008, 100, 136406.
38. P. E. Blöchl, Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
39. S. López-Moreno, D. Errandonea, J. Pellicer-Porres, D. Martínez-García, S. J. Patwe, S. N. Achary, A. K. Tyagi, P. Rodríguez-Hernández, A. Muñoz and C. Popescu, Stability of FeVO₄ under Pressure: An X-ray Diffraction and First-Principles Study, Inorg. Chem., 2018, 57, 7860–7876.
40. T. Marqueño, D. Errandonea, J. Pellicer-Porres, D. Santamaría-Pérez, P. Rodríguez-Hernández and A. Muñoz, Competing dynamical and lattice instabilities in RVO₄ rare-earth vanadium oxides under high pressure, Phys. Rev. Mater., 2020, 6, L060601.
41. H. J. Monkhorst and J. D. Pack, Special Points for Brillouin-Zone Integration, Phys. Rev. B: Solid State, 1976, 13, 5188.
42. E. Bandiello, P. Rodríguez-Hernández, A. Muñoz, M. Bajo Buenestado, C. Popescu and D. Errandonea, Electronic properties and high-pressure behavior of wolframite-type CoWO₄, Mater. Adv., 2021, 2, 5955–5966.
43. A. Togo and I. Tanaka, First Principles Phonon Calculations in Materials Science, Scr. Mater., 2015, 108, 1.
44. Y. Le Page and P. Saxe, Symmetry-General Least-Squares Extraction of Elastic Data for Strained Materials from Ab Initio Calculations of Stress, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 104104.
45. V. D. Zhuravlev, V. A. Makarov and A. A. Fotiev, Binary Systems of Calcium, Strontium, and Barium Orthovanadates, Russ. J. Inorg. Chem., 1976, 21(1218), 1221.
46. I. A. Leonidov, M. Y. Khodos, A. A. Fotiev and A. S. Zhukovskaya, Effect of Vacancies on ⁴⁵Ca Diffusion in the Solid Solutions Ca/sub 3(1-x)/Eu/sub 2x/square/sub x/(VO₄)₂, Izv. Akad. Nauk SSSR, Neorg. Mater., 1988, 24, 347–348.
47. B. I. Lazoryak, L. O. Dmitrienko and S. V. Grechkin, Zh. Neorg. Khim., 1990, 35, 1095 . ICDD database 04-005-5987.
48. J. Macicek, Data Base, International Centre for Diffraction Data, Newton Square, PA, 1995, JCPDS-ICDD database 00–046-0756.
49. G. M. Kuz'micheva, L. I. Ivleva, I. A. Kaurova, E. V. Khramov, V. B. Rybakov and M. E. Doroshenko, Pure and Tm³⁺-doped Ca₃(VO₄)₂ crystals: Growth, Statistical and Local Structure, and Luminescent Properties, J. Alloys Compd., 2021, 854, 155918.
50. B. L. Dickens, W. Schroeder and W. E. Brown, Crystallographic Studies of the Role of Mg as a Stabilizing Impurity in β-Ca₃(PO₄)₂. The Crystal Structure of pure β-Ca₃(PO₄)₂, J. Solid State Chem., 1974, 10, 232–248.
51. M. Yashima, A. Sakai, T. Kamiyama and A. Hoshikawa, Crystal Structure Analysis of β-tricalcium phosphate Ca₃(PO₄)₂ by Neutron Powder Diffraction, J. Solid State Chem., 2003, 175, 272–277.
52. B. I. Lazoryak, S. M. Aksenov, S. Y. Stefanovich, N. G. Dorbakov, D. A. Belov, O. V. Baryshnikova, V. A. Morozov, M. S. Manylov and Z. Lin, Ferroelectric Crystal Ca₉Yb(VO₄)₇ in the Series of Ca₉R(VO₄)₇ Non-Linear Optical Materials (R = REE, Bi, Y), J. Mater. Chem. C, 2017, 5, 2301–2310.
53. B. I. Lazoryak, V. A. Morozov, A. A. Belik, S. Y. Stefanovich, V. V. Grebenev, I. A. Leonidov, E. B. Mitberg, S. A. Davydov, O. I. Lebedev and G. V. Tendeloo, Ferroelectric Phase Transition in the Whitlockite-Type Ca₉Fe(PO₄)₇; Crystal Structure of the Paraelectric Phase at 923 K, Solid State Sci., 2004, 6, 185–195.
54. F. Datchi, A. Dewaele, Y. Le Godec and P. Loubeyre, Equation of State of Cubic Boron Nitride at High Pressures and Temperatures, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 214104.
55. H. S. R. Mosafer, W. Paszkowicz, R. Minikayev, M. Kozłowski, R. Diduszko and M. Berkowski, The Crystal Structure and Thermal Expansion of Novel Substitutionally Disordered Ca₁₀TM_0.5(VO₄)₇ (TM = Co, Cu) orthovanadates, Dalton Trans., 2021, 50, 14762.
56. E. Sülli and D. F. Mayers, An Introduction to Numerical Analysis, Cambridge University Press, Cambridge, U.K., 2003.
57. D. C. Wallace, Thermodynamics of Crystals, Am. J. Phys., 1972, 40, 1718–1719.
58. L. Vočadlo, K. S. Knight, G. D. Price and I. G. Wood, Thermal Expansion and Crystal Structure of FeSi Between 4 and 1173 K Determined by Time-of-Flight Neutron Powder Diffraction, Phys. Chem. Miner., 2002, 29, 132–139.
59. Z. Sun, B. Sun, X. Zhang, D. Wen and P. Dai, Superb Thermal Stability Purple-Blue Phosphor Through Synergistic Effect of Emission Compensation and Nonradiative Transition Restriction of Eu²⁺, Mater. Today Chem., 2022, 24, 100877.
60. X. Pan, L. Mei, Y. Zhuang, T. Seto, Y. Wang, M. Plyaskin, W. Xi, C. Li, Q. Guo and L. Liao, Anti-Defect Engineering Toward High Luminescent Efficiency in Whitlockite Phosphors, Chem. Eng. J., 2022, 434, 134652.
61. E. Aksel, J. S. Forrester, B. Kowalski, J. L. Jones and P. A. Thomas, Phase Transition Sequence in Sodium Bismuth Titanate Observed Using High-Resolution X-Ray Diffraction, Appl. Phys. Lett., 2011, 99, 222901.
62. S. Klotz, J.-C. Chervin, P. Munsch and G. L. Marchand, Hydrostatic Limits of 11 Pressure Transmitting Media, Phys. Rev. D: Part., Fields, Gravitation, Cosmol., 2009, 42, 075413.
63. A. B. Garg, D. Errandonea, P. Rodríguez-Hernández and A. Muñoz, ScVO₄ under non-hydrostatic compression: a new metastable polymorph, J. Phys.: Condens. Matter, 2017, 29, 055401.
64. F. Birch, Finite Elastic Strain of Cubic Crystals, Phys. Rev., 1947, 71, 809–824.
65. J. Gonzalez-Platas, M. Alvaro, F. Nestola and R. Angel, EosFit7-GUI: a New Graphical User Interface for Equation of State Calculations, Analyses and Teaching, J. Appl. Crystallogr., 2016, 49, 1377–1382.
66. R. J. Angel, Equations of State, Rev. Mineral. Geochem., 2000, 41, 35–59.
67. S. Zhai and X. Wu, X-Ray Diffraction Study of β-Ca₃(PO₄)₂ at High Pressure, Solid State Commun., 2010, 150, 443–445.
68. L. Liang, P. Rulis and W. Y. Ching, Mechanical Properties, Electronic Structure and Bonding of α- and β-Tricalcium Phosphates with Surface Characterization, Acta Biomater., 2010, 6, 3763–3771.
69. D. Díaz-Anichtchenko and D. Errandonea, Comparative Study of the Compressibility of M₃V₂O₈ (M = Cd, Zn, Mg, Ni) Orthovanadates, Crystals, 2022, 12, 1544.
70. T. Xie, S. E. Nikitin, A. I. Kolesnikov, E. Mamontov, L. M. Anovitz, G. Ehlers, I. Huskić, T. Friščić and A. Podlesnyak, Direct Determination of the Zero-Field Splitting for the Fe³⁺ Ion in a Synthetic Polymorph of NaMgFe(C₂O₄)₃·9H₂O: A Natural Metal-Organic Framework, Phys. Rev. B, 2021, 103, 024402.
71. J. Sánchez-Martín, D. Errandonea, J. Pellicer-Porres, D. Vázquez-Socorro, D. Martínez-García, S. N. Achary and C. Popescu, Phase Transitions of BiVO₄ under High Pressure and High Temperature, J. Phys. Chem. C, 2022, 126, 7755–7763.
72. D. Errandonea, A. Muñoz and J. Gonzalez-Platas, Comment on “High-Pressure X-Ray Diffraction Study of YBO₃/Eu³⁺, GdBO₃, and EuBO₃: Pressure-Induced Amorphization in GdBO₃”, J. Appl. Phys., 2014, 115, 216101.
73. R. Turnbull, D. Errandonea, J. A. Sans, V. P. Cuenca-Gotor, R. I. Vilaplana, J. Ibáñez, C. Popescu, A. Szczeszak, S. Lis and F. J. Manjón, GdBO₃ and YBO₃ Crystals under Compression, J. Alloys Compd., 2021, 866, 158962.
74. A. B. Garg, D. Errandonea, P. Rodríguez-Hernández, S. López-Moreno, A. Muñoz and C. Popescu, High-Pressure Structural Behaviour of HoVO₄: Combined XRD Experiments and Ab Initio Calculations, J. Phys.: Condens. Matter, 2014, 26, 265402.
75. D. Errandonea, M. Somayazulu and D. Häusermann, Phase Transitions and Amorphization of CaWO₄ at High Pressure, Phys. Status Solidi B, 2002, 235, 162–169.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ce01676a

---