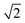Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Phase field modelling of crystal growth of NaCl in two dimensions†
Chao Dun
Tan
 and
Georg
Hähner
and
Georg
Hähner
 *
*
EaStCHEM School of Chemistry, University of St Andrews, North Haugh, St Andrews, KY16 9ST, UK. E-mail: gh23@st-andrews.ac.uk
First published on 24th April 2023
Abstract
Modelling crystal growth is important for example in crystal engineering, materials science, and the life sciences. Molecular modelling techniques can provide fundamental insights into the atomic processes underlying crystal growth but do not always give direct information about growth rates and growth modes on spatial and temporal scales relevant in nature and for applications. The phase-field (PF) approach is a relatively simple model that can provide results on length and time scales directly comparable to experiments, but it has not extensively been employed to investigate crystallization of ionic solids, and not many quantitative results have been reported. In the present study we model the growth of cubic NaCl crystals in two dimensions. We have used small crystal seeds with an appropriate anisotropy term to investigate both the growth speed and the growth mode. Results are compared to experimental data from the literature. The PF model displays the concentration dependent transition from compact to non-compact growth of NaCl reasonably well on spatial and temporal scales that are not easily accessible with other theoretical models.
1. Introduction
The crystallization and solidification of materials play an important role in nature and are also relevant in relation to some industrial processes.1 Crystallization properties such as the growth speed and growth mode have been studied experimentally on microscopic and macroscopic scales for periods of milliseconds up to several hours.2–4 These studies involve the controlled evaporation of the solvent of salt solutions – often in microchannels – and have revealed some insights into the crystallization process. It was found that crystallization of NaCl in confinement typically starts at high supersaturation values, Ω, of 1.6–1.7.3,5 Furthermore, growth was observed to be ultrafast during the first few milliseconds slowing down on longer time scales.3,6 The rates of both nucleation and growth determine the product crystal shape, its size, and the size distribution and are therefore of high interest in relation to industrial applications involving crystallization.Modelling the crystallization of salts is in general challenging since the processes underlying nucleation and growth are complex. Precipitation and dissolution as well as the growth rate and growth mode of NaCl have been studied theoretically on the molecular scale using different methods.7–13 Molecular dynamics (MD) simulations can give insights on atomic scale processes,7,14–18 leading to a fundamental understanding of the growth mechanism. It was found, for example, that the growth rate scales with solvent residence times near ions and surface sites.7 Atomistic simulations can also predict nucleation rates,16–18 and even reveal a change in the nucleation mechanism in aqueous NaCl solution indicated by a transition to a phase separation via spinodal decomposition.18 However, such calculations are in general time consuming and often require significant additional effort to provide information on time scales and spatial dimensions that are of practical interest or are directly comparable with experiments. At low supersaturation, steady-state growth models provide an excellent quantitative description of growth rates and morphologies,19 which can be directly compared to population balance models for crystallization at industrial scales.20,21
The conventional phase-field (PF) approach is a diffuse interface model including diffusion and reaction kinetics that can be used to facilitate interface tracking but does not provide an accurate physical model of the interface on the atomic scale.22 It can capture length scales between the atomistic approaches and the steady state growth models, as well as high-supersaturation morphologies. However, the PF approach is not a first-principles method and often an unphysical thickness of the interface has to be used. In the conventional approach it is limited to the diffusion limited growth regime. It is based on a set of differential equations. The PF model has been extensively applied to simulate the solidification of liquid phases of pure substances in an undercooled melt that is controlled by a continuous temperature field across the solid–liquid interface with a discontinuous temperature gradient, e.g., ref. 22–24. It has to a much lesser extent been employed in relation to the precipitation and dissolution processes involved in crystallization that is controlled by a discontinuous solute concentration at the solid–liquid interface,25–28 and PF modelling of the crystallization of real systems with direct quantitative comparison to experimental data is rare.29–31 According to reaction diffusion theory ionic crystals develop a diffuse interface of several tens of micrometres in solution32,33 and the PF model is in principle well suited to provide quantitative results on microscopic and macroscopic scales for such systems. The model is appealing because it can provide information about properties such as the crystal growth rate and the growth mode.26 In addition, it can visualise the solid structures resulting from crystallization.34
In the present study we investigate the crystallization of NaCl in two dimensions based on the PF approach as described in ref. 25 and 26.
The crystallization process is often complex on the atomic scale and is still debated for many systems. It can phenomenologically be decomposed into nucleation and growth. The conventional PF model does not include nucleation. We therefore used small starting seeds to simulate the growth of NaCl. The growth proceeds via reaction at the solid–liquid interface and involves precipitation and dissolution. Although the equations of the PF model do only provide a phenomenological description of the atomic processes underlying precipitation and dissolution at the solid–liquid interface the approach can reveal information about some of the essential features in relation to crystal growth, for example about the growth speed and growth mode such as compact and non-compact growth. The goal of the present study was to test how well the PF model can describe these aspects on the mesoscale by comparison with some of the experimental results reported in the literature. We demonstrate that some features of the crystal growth of NaCl are well reproduced and are in good agreement with experimental findings.
2. Modelling of the system
2.1 Simulation parameters
Physical parameters relevant for the simulation of the crystal growth of the salt are the diffusion constant of the ions in solution, D, the density of the solid, ρc, the solute concentration at equilibrium with the solid, Ceq, the ‘rate of reaction’, kR, the surface energy, S, and the interface mobility, L. Table 1 summarises the parameters and the values used in the simulations.| Parameter | Symbol | Value | Ref. |
|---|---|---|---|
| Diffusion constant | D | 1.3 × 10−9 m2 s−1 | 40 |
| Solid density | ρ c | 37.04 mol l−1 (≡ 2165 kg m−3) | 2, 41 |
| Equilibrium concentration | C eq | 5.55 mol l−1 (at room temperature) | 3, 7 |
| Rate of reaction | k R | 2.33 × 10−3 m s−1 | 3 |
| Surface energy | S | 0.114 J m−2 along (111) direction of NaCl | 29, 35 |
| 0.100 J m−2 along (100) direction of NaCl | |||
| Interface mobility | L | 4.11 × 10−3 m3 J−1 s−1 | 29 |
Both S and L are physical parameters that can be determined experimentally34 or computationally.29,35 The surface energy S (ref. 35) depends on the direction of the Miller planes. For NaCl S = 0.100 J m−2 in the direction of the (1 0 0) plane and S = 0.114 J m−2 in the direction of the (1 1 1) plane.35 The interface mobility, L, is related to the interface velocity.29,34 In some cases it can be determined experimentally. The value we used is from the literature and was determined by modelling the dissolution of NaCl with the PF model.29
2.2 Phase-field equations and initial phase field and concentration
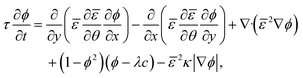 | (2.1) |
 | (2.2) |
![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) (θ) = εσ(θ),22,36 where σ is the anisotropy term:22
(θ) = εσ(θ),22,36 where σ is the anisotropy term:22σ(θ) = 1 + δ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(j(θ − θ0)). cos(j(θ − θ0)). | (2.3) |
 .25α = 1/2b is a dimensionless constant25–27 with b = Ceq/ρc the ratio of solute concentration at equilibrium with the solid and the density of the solid. ε is a length parameter related to the interface width of the phase field.25τ is a characteristic time parameter25–27 that is related to the interface mobility L, the surface energy S,29,34,37 and ε (see ESI†):
.25α = 1/2b is a dimensionless constant25–27 with b = Ceq/ρc the ratio of solute concentration at equilibrium with the solid and the density of the solid. ε is a length parameter related to the interface width of the phase field.25τ is a characteristic time parameter25–27 that is related to the interface mobility L, the surface energy S,29,34,37 and ε (see ESI†):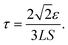 | (2.4) |
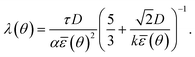 | (2.5) |
We approximated the mean curvature κ = ∇·(∇ϕ/|∇ϕ|) as described in ref. 26. In the PF model we used the phase field ϕ can adopt values between −1 and +1, with −1 < ϕ < −(1 − ξ) indicating the solid phase, and 1 − ξ < ϕ < 1 liquid phase. We set the cut-off ξ = 10−6. Diffusion in the solid is neglected. Note that the concentration in this model is zero in regions of the solid and is not equal to the density of the solid, i.e., there is no discontinuity in the concentration at the position of the interface.
The free parameter ε has to be small enough such that the results obtained are in good agreement with those for a sharp interface and experimentally observed results. On the other hand, in order to obtain results on the mesoscale in a reasonable amount of computing time, ε should be ‘large’ since the limit for the numerical time step, Δt, given by the instability condition is34 where Δx is the grid size, and Δx has to be ≤0.5ε to achieve sufficiently accurate results.26,42 Therefore, a small ε implies a small Δx and hence a small Δt. This dichotomy is one of the main reasons why the application of the PF model can be a challenge on scales relevant for many experiments.
where Δx is the grid size, and Δx has to be ≤0.5ε to achieve sufficiently accurate results.26,42 Therefore, a small ε implies a small Δx and hence a small Δt. This dichotomy is one of the main reasons why the application of the PF model can be a challenge on scales relevant for many experiments.
Our simulations were run with home-written MATLAB® routines. The numerical cell size Δx of the grid and the time step Δt had to be determined such that the calculations are numerically stable and provide insights on the spatial–temporal scale of interest. We tested various grid sizes Δx < ε to see if this had an influence on the resulting diffuse interface of the phase field. It has been reported that Δx = 0.5ε provides a sufficiently accurate shape of the phase field profile.42 Our results were independent of Δx if Δx ≤ 0.5ε. Therefore, we set Δx = 0.5ε similar to ref. 26. We set the time step, Δt, for the iterations well below the value given by the instability condition.34
In the calculations we used the finite difference method with Nx × Ny square cells of equal length Δx.26 The time discretization of eqn (2.1) and (2.2) was implemented using the finite difference mid-point method to improve accuracy.43 For the discretised Laplace operator, ∇2, we employed the 9-point stencil method to reduce anisotropy effects that can be caused by the finite grid size of the lattice.23,38,39 In addition, the anisotropy term helps to minimise potential anisotropy effects that can be induced by the simulation grid.
 , which can adopt values between +1 (solid) and 0 (liquid) and setting the concentration c equal to the equilibrium concentration (ceq = 0) in the entire simulation domain. In all cases studied the initially sharp phase interface converged to a hyperbolic tangent profile after around a few thousand iterations and remained essentially stable afterwards,42 with the interface width of ϕ determined by ε (see ESI†).
, which can adopt values between +1 (solid) and 0 (liquid) and setting the concentration c equal to the equilibrium concentration (ceq = 0) in the entire simulation domain. In all cases studied the initially sharp phase interface converged to a hyperbolic tangent profile after around a few thousand iterations and remained essentially stable afterwards,42 with the interface width of ϕ determined by ε (see ESI†).
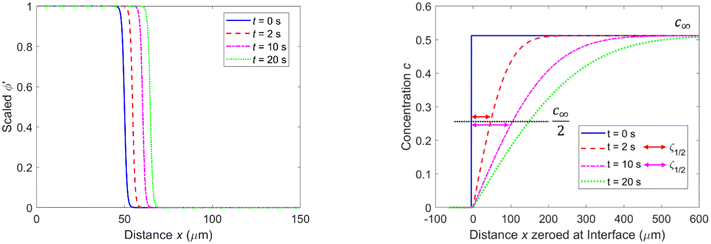
We used these numerically determined stable phase field profiles as the starting profiles in combination with a ‘sharp interface’ in the initial concentration field (see Fig. 1c) and d)) when studying growth, i.e., the initial concentration in our simulations changed from ceq = 0 (solid) to c∞ (solution) over one Δx at the position of the interface (ϕ′ = 1/2). The concentration profile changes its shape as long as the solid grows or is dissolved, i.e., if c∞ ≠ 0 in the solution. The concentration in our PF model is constant (=0) at the position of the solid. We set the concentration c∞ > 0 in the bulk of the solution at t = 0. During growth ions are removed from the solution and are attached to the solid. Consequently, during growth the concentration profile of the solution changes with time while the phase profile moves due to the growth of the solid but the solid–liquid interface shape is essentially constant (see ESI†).
3. Results and discussion
3.1 Growth speed in 2D
To study the influence of ε on the growth speed we initialised the simulations with the equilibrium profile of the phase corresponding to ε, and the sharp concentration profile as described in section 2.2.
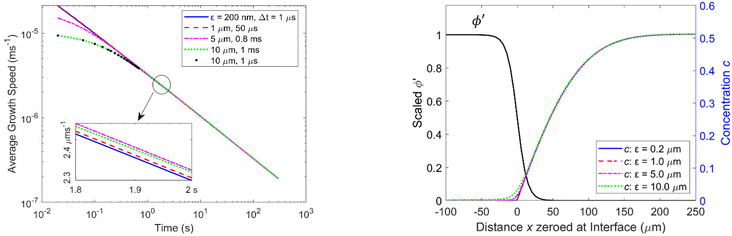
Crystal growth was simulated for periods from 10 ms up to 5 minutes using a range of ε and Δt values to test the influence of both on the resulting crystal growth speeds. The timescales and bulk concentrations c∞ are based on experimental conditions reported in the literature.2,3,6,46 We first investigated the influence of ε on both the resulting concentration distribution after 10 ms and the resulting average growth speed, ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) gr:
gr:
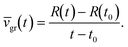 | (3.1) |
Fig. 2 (left) shows the determined growth speeds over 10 ms for Ω = 1.72 (c∞ = 0.61) and different values of ε, and the concentration profiles that result after 10 ms (right). Also shown is the scaled phase profile ϕ′.
Table 2 summarises the different values of ε and Δt studied, as well as the resulting τ and λ values, and the average growth speeds. There is a small increase of ∼3% in the growth speed with increasing ε over the range of values tested.
| ε (nm) | Δt used (μs) | τ (ms) | λ |
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) gr (μm s−1)
gr (μm s−1) |
|---|---|---|---|---|
| 80 | 0.05 | 0.167 | 0.871 | 34.0 |
| 100 | 0.5 | 0.209 | 0.841 | 34.2 |
| 200 | 0.5 | 0.417 | 0.717 | 34.6 |
| 400 | 5 | 0.834 | 0.554 | 35.0 |
Experimentally determined growth speeds have also been reported for longer periods of 2 s, 20 s, and 5 minutes,2,6,46 and we have run simulations for those periods and the reported experimental concentrations as well. Fig. 3 shows as an example the average growth speed over a period of 5 min for Ω = 1.6 (c∞ = 0.51) and various ε values. The behavior is similar to that found for 10 ms: while there is some deviation between the average growth speeds depending on ε for periods of less than 1 s corresponding to the first few thousand iterations, they are virtually identical for longer periods (see inset of Fig. 3 left): for example, the average growth speed after 2 s is 2.31 μm s−1 with an error of 0.4%, for the four ε values tested. The concentration profiles that result after 2 s are shown in Fig. 3, right.
Table 3 summarises the periods and the concentrations studied, the ε range tested for each concentration, and the periods after which the average growth speeds for larger ε values are essentially identical to the growth speed for ε = 200 nm. The table also shows the average growth speeds obtained from the modelling together with the experimental values reported in the literature. A smaller ε and therefore a sharper interface is preferable in general but can increase computing time significantly and would not provide additional physical insights here.
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) gr, for the ε range tested, their relative standard deviation, Δ
gr, for the ε range tested, their relative standard deviation, Δ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) gr/
gr/![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) gr, and experimental growth speeds, vExp (ref. 2, 3, 6 and 46)
gr, and experimental growth speeds, vExp (ref. 2, 3, 6 and 46)
Precipitation in the absence of fluid flow is similar to diffusion-limited aggregation. Diffusion is the only mechanism responsible for solute transport to the solid–liquid interface for growth without liquid agitation. Diffusion theories presume that during crystal growth matter is deposited continuously on the crystal faces at a rate proportional to the concentration difference between the bulk of the solution and the point of deposition, C∞ − Ceq. This predicts a linear increase of the instantaneous growth speed,  , with concentration, c∞, in the solution:32
, with concentration, c∞, in the solution:32
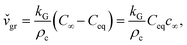 | (3.2) |
 , depends on the diffusion constant, D, and ζ1/2, which evolves with time. ζ1/2 is related to the diffuse length. We set ζ1/2 to the distance over which the concentration profile from ceq at the solid–liquid interface reaches half of the bulk value, c∞/2 (see Fig. 4). The increase of ζ1/2 with time leads to a decrease of kD such that after longer periods kD ≪ kR and therefore kG ≈ kD. The instantaneous growth speed decreases with time due to the increase of ζ1/2 (Fig. 4).3,32 The average growth speed,
, depends on the diffusion constant, D, and ζ1/2, which evolves with time. ζ1/2 is related to the diffuse length. We set ζ1/2 to the distance over which the concentration profile from ceq at the solid–liquid interface reaches half of the bulk value, c∞/2 (see Fig. 4). The increase of ζ1/2 with time leads to a decrease of kD such that after longer periods kD ≪ kR and therefore kG ≈ kD. The instantaneous growth speed decreases with time due to the increase of ζ1/2 (Fig. 4).3,32 The average growth speed, ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) gr, that is measured in experiments is related to the instantaneous growth speed via:
gr, that is measured in experiments is related to the instantaneous growth speed via: | (3.3) |
![[v with combining caron]](https://www.rsc.org/images/entities/i_char_0076_030c.gif) gr it also increases linearly with the concentration, c∞, for a fixed time, t, and decreases with time for a fixed c∞.
gr it also increases linearly with the concentration, c∞, for a fixed time, t, and decreases with time for a fixed c∞.
Crystallization comprises nucleation and growth. Nucleation is not included in the conventional PF model and we initiated growth by starting with small crystal seeds. The concentration profile immediately following nucleation is not known. It might display an abrupt transition from the value in the liquid to that at the interface, i.e., a change from the solution value c∞ to ceq = 0 at the solid–liquid interface over a very short distance, similar to the initial distribution we used. In our initial setup ζ1/2 = Δx/2 (abrupt change in the concentration from liquid bulk to solid–liquid interface over one Δx). When ζ1/2 is ‘small’ and kD large the reaction rate, kR, can potentially dominate the overall growth, kG. ζ1/2 then increases quickly to larger values compatible with the profile of the concentration under the given conditions.
Based on an asymptotic sharp interface analysis the PF equations provide reliable results if the diffusion length is much greater than the interface width, i.e., ζ1/2 ≫ ε.25,38,39 Since in our initial setup ζ1/2 is of comparable size to ε (see Fig. 4, right, t = 0 s), the determined growth speeds for very short periods (corresponding to the first few thousand iterations) are not reliable. This is reflected by the ε dependence of the growth speed during the initial period (Fig. 2 and 3) and the subsequent convergence to values similar to those for smaller ε (and independent from ε) once ζ1/2 is sufficiently large.
For diffusion limited growth the distance, R(t), that a plane face of the crystal moves increases with 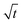 ,32,47 and the instantaneous growth speed
,32,47 and the instantaneous growth speed  is proportional to
is proportional to  . This also holds for the average growth speed,
. This also holds for the average growth speed, ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) gr, because of eqn (3.3). Fig. 5 shows R(t) vs.
gr, because of eqn (3.3). Fig. 5 shows R(t) vs. for a supersaturation Ω = 1.6 (c∞ = 0.51) over 20 s. R(t) displays linear behaviour for the whole period studied confirming that growth is diffusion limited from the start and there is no indication of non-diffusion limited growth in our model despite the sharp initial concentration profile.
for a supersaturation Ω = 1.6 (c∞ = 0.51) over 20 s. R(t) displays linear behaviour for the whole period studied confirming that growth is diffusion limited from the start and there is no indication of non-diffusion limited growth in our model despite the sharp initial concentration profile.
An ideal planar surface in two or three dimensions moves during growth with the same speed in the direction normal to the face as in one dimension if under the same conditions, and the values from Table 3 can be directly compared to experimental values reported for the growth normal to planar surfaces (experiments B and D in Table 3). For some of the experimental growth speeds reported, however, (A and C in Table 3) it is not clear if they were obtained strictly normal to a crystal face or in another direction. In all cases studied the values obtained with the PF model are on the same order of magnitude but significantly smaller than the experimentally observed values. For periods of a few seconds up to several minutes the simulated growth speeds are three to five times smaller than the experimental values. The growth of NaCl during the initial stage of crystallization has been reported to be particularly ‘fast’ with an average value of at least 271 μm s−1 over the first 10 ms.3 For this short period the simulated growth speed is around eight times smaller than the experimental value (Table 3).
It has been shown experimentally that during the initial phase of crystallisation and the early stages following nucleation (first few seconds) the growth rate can be dominated by the reaction rate3,4 for the concentrations studied, while over longer periods growth becomes diffusion limited. This could explain the bigger deviation seen for 10 ms.
Another factor that can play a role in the growth speed is convection, which is not included in the model we used but can contribute to the transport of the ions to the solid–liquid interface. In addition, something that could be particularly important during the initial stages when the crystal is small is the pushing of the liquid by the fast growing crystal causing movement in the liquid, potentially leading to a faster transport of ions from the solution to the solid–liquid interface and hence a higher growth speed.48,49 We have assumed simple first order reaction kinetics to be valid, which might be adequate when diffusion limited growth dominates. However, dissolution and precipitation are complex processes and likely to follow other reaction kinetics. Therefore, first order kinetics might in particular not be a good assumption during the very early stages following nucleation. This might also explain some of the deviation observed in the growth speed between the modelling and the experiments. All the points mentioned might contribute to the higher values observed in the experiments.
In addition, when simulating growth in two or three dimensions with the PF model, effects that arise from a curved surface in combination with the overestimation of the diffuse width of the interface of the phase field can result in non-physical curvature driven interface motion, and therefore potentially be a problem.25,50 The last term in eqn (2.1) counteracts this non-physical effect due to curvature to first order such that a stationary hyperbolic tangent profile across the interface results.25,42,50 On the other hand, curvature driven interface motion in relation to excess surface free energy is an important contribution to diffusion limited growth.51
We have used a simple model to estimate potential non-physical contributions in our PF simulations. When the time scale over which the concentration profile around the solid reaches equilibrium is short compared to the time scale over which the size of the solid changes appreciably then the diffusion process around the solid reaches steady state, i.e., there is a balance between the solute flux density at the solid–liquid interface and the rate of precipitation or dissolution, and the steady state model is a good approximation. The rate of mass transfer from the fluid to the solid can then be used to calculate the time evolution of the size of the solid.51 The ratio of the two timescales is  in our PF model. Using the steady state model we have derived expressions for the instantaneous growth speeds,
in our PF model. Using the steady state model we have derived expressions for the instantaneous growth speeds, ![[v with combining breve]](https://www.rsc.org/images/entities/i_char_0076_0306.gif) , of spherical crystals in two and three dimensions, respectively:
, of spherical crystals in two and three dimensions, respectively:
 | (3.4) |
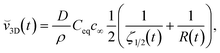 | (3.5) |
![[v with combining breve]](https://www.rsc.org/images/entities/i_char_0076_0306.gif) 2D and
2D and ![[v with combining breve]](https://www.rsc.org/images/entities/i_char_0076_0306.gif) 3D converge to
3D converge to  , which is
, which is ![[v with combining breve]](https://www.rsc.org/images/entities/i_char_0076_0306.gif) 1D(t) and is identical to eqn (3.2) if kG ≈ kD.
1D(t) and is identical to eqn (3.2) if kG ≈ kD.
In order to estimate potential non-physical contributions to the growth speed we simulated isotropic growth of circular seeds with different radii with the PF model and also used eqn (3.4) to compare the curvature dependent contributions in both models (see ESI†). The PF model and the steady state approximation gave very similar results. We therefore conclude that curvature dependent growth is adequately described in the PF model and artefacts due to curvature do not contribute significantly.
3.2 Growth modes
The growth speed of a crystal depends on the crystallographic direction if the surface energy, S, is direction dependent. Faster growth along energetically favourable directions is the reason for non-compact growth such as Hopper and dendritic growth.4,52 Therefore, when modelling growth the symmetry of the crystal has to be properly taken into account. In our model the crystal symmetry is superimposed by the anisotropy terms in eqn (2.1). The terms also help to minimise unwanted effects that can be induced by the symmetry of the simulation grid.23,26,38,39For NaCl with fourfold symmetry, i.e., j = 4, we determined δ using the known interfacial energies for different Miller planes:35 if ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) (θ) = Sσ(θ) is the angle dependent interfacial energy and θ0 indicates the direction of the (1 1 1) plane with
(θ) = Sσ(θ) is the angle dependent interfacial energy and θ0 indicates the direction of the (1 1 1) plane with ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) (θ0) = 0.114 J m−2, then (θ0 + 45°) indicates the direction of a (1 0 0) plane with
(θ0) = 0.114 J m−2, then (θ0 + 45°) indicates the direction of a (1 0 0) plane with ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) (θ0 + 45°) = 0.100 J m−2. Therefore, S = 0.107 J m−2 and δ = 0.0654. Note that
(θ0 + 45°) = 0.100 J m−2. Therefore, S = 0.107 J m−2 and δ = 0.0654. Note that  is a condition for the equilibrium shape of an anisotropic four-fold crystal to be well described.53–56 For higher values of δ, missing orientations will occur and the phase-field problem becomes ill-posed.55,57–60
is a condition for the equilibrium shape of an anisotropic four-fold crystal to be well described.53–56 For higher values of δ, missing orientations will occur and the phase-field problem becomes ill-posed.55,57–60
A spherical shape has been reported to be a reasonable assumption for initial small NaCl clusters.35 Due to the square cells of the grid however a spherical shape of the seed is not perfect. To ensure that initial growth is driven by energetics and not the non-perfect shape of the seed due to the grid we tested circular seeds of different size and under different conditions (see ESI†). The imposed symmetry causes the seed to develop in such a way that one of the vertices of the crystal points in a direction θ0 degrees off the x-axis. However, which grid cell of the edge of the seed develops into the vertex depends on the size of the initial seed relative to the cell size and ε, because of the non-ideal circular shape. As a result, the shape after several seconds shows minor variations depending on the initial deviation from the ideal circular shape. It displays four-fold rotational symmetry but does not always show four-fold symmetry including mirror symmetry (see ESI†). Therefore, we initiated corner growth by tiny protrusions on the seed. This makes it much less likely for the crystal to develop only four-fold rotational and not four-fold symmetry.
The simulations were performed in a quadrant of the overall area of interest26,39 with no-flux Neumann conditions applied on the outer boundaries, exploiting the fourfold rotational symmetry of both the simulation grid and the crystal. For simulations with ε = 700 nm, the area of the simulation grid was 240 × 240 μm2, corresponding to a finite reservoir of overall size 480 × 480 μm2, conditions similar to those in a microchannel. For the simulations performed with ε = 1 μm, a square grid 400 × 400 μm2 was used, corresponding to an overall area of 800 × 800 μm2 (see details in ESI†).
Fig. 6 displays the initial shape of a spherical seed of radius 15 μm and its final shape after 10 s of growth together with the contour lines of the concentration for a range of values of concentration. The crystal develops fourfold symmetry and it can be seen that for Ω ∼ 1.3 a circular seed with fourfold symmetry develops into a square that grows in size but stays a square over the period studied, indicating compact growth. For Ω ∼ 1.6 however the crystal grows faster in the direction of the edges resulting in a transition from compact to non-compact growth due to the higher concentration. This is supported by Fig. 7, which shows the ratio of the distances the crystals have grown in the directions of the (1 1 1) and the (1 0 0) planes depending on time for the different concentrations. There is a transition from compact to non-compact growth for Ω between 1.3 and 1.6 (if the ratio is > ) with non-compact growth for higher concentrations.
) with non-compact growth for higher concentrations.
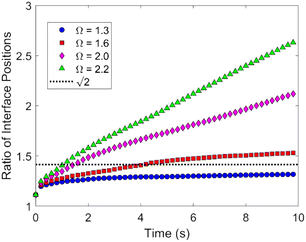 | ||
Fig. 7 Ratio of distances the crystal has grown in the direction of the edges to the direction of the faces for Ω = 1.3, 1.6, 2.0 and 2.2. A ratio below 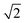 indicates compact growth. indicates compact growth. | ||
Fig. 8 (left) displays the initial shape of the same spherical seed as in Fig. 6 and its final shape for Ω < 1.3 (c∞ < 0.26) after an extended period of 60 s of growth together with the contour lines of the concentration. For this concentration the circular seed with fourfold symmetry develops into a square that grows in size but stays a square even after longer periods, clearly indicating compact growth under these conditions. This is supported by Fig. 8 (right) showing the ratio of the distances the crystal has grown in the direction of the (1 1 1) face (corner) and the direction of the (1 0 0) face (plane). The ratio of the interface positions along both directions is clearly <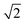 even after 60 s supporting compact growth for this concentration value.
even after 60 s supporting compact growth for this concentration value.
For NaCl both compact and non-compact growth have been observed experimentally for high supersaturation values.2–4 Non-compact growth occurs if growth at the edges of the crystal is faster than at the centre of each face, i.e., more material is added to edges compared to the interior sections of the crystal. As a result, the edges and faces of the crystal experience different concentration gradients and therefore grow with different speeds.4,52,61,62
Under high supersaturation secondary nucleation may occur at the edges of the growing primary nuclei, i.e., nucleation is re-initiated4,5 at the edges with a high frequency. This leads to rapid growth of non-compact crystals due to a disparity of growth rates between the crystal edges and the crystal faces. This can then result in a chain-like structure of non-compact (Hopper) crystals often followed by compact growth resulting in a hybrid shape.2–4 Since nucleation is not included in our model such chain-like growth is not revealed.
The overall size of the crystals after tens of seconds up to several minutes depends on how long nucleation occurred and for how long non-compact growth dominated, potentially followed by compact growth. This makes it difficult to compare the overall size of experimentally studied crystal growth with results from our modelling and could explain the variety of experimentally obtained growth rates for longer periods reported in the literature.2,3,6,46,63 While the PF model has its limitations in describing accurately the experimentally observed growth speeds, it shows a transition from compact to non-compact growth for concentrations Ω ∼ 1.4 in good agreement with experiments.4 This is illustrated in Fig. 9, which displays the ratio of the average growth speeds in the direction of the edges and that normal to the faces, indicating a transition at Ω ∼ 1.4.
An extension of the simulations to 3D by appropriate modification of eqn (2.1)–(2.3) and a modelling of more complex systems is possible39 but comes with a significant increase in complexity and computing time. It would however not provide fundamentally new insights here if not other effects such as nucleation, convection, or a different order of the kinetics are included, too.
4. Conclusions
We studied the growth speed and the growth modes of NaCl in two dimensions for a range of high concentration values. Such high supersaturation has been reported to prevail in microchannels. The PF model is not suited to describe adequately characteristics related to molecular processes such as the fast decrease of the initial growth rate and the change from non-diffusion to diffusion limited growth on very short time scales.34 Apart from the very short time scale (10 ms) the average growth speeds obtained with the PF model are of the same order of magnitude as the experimentally determined values but the values obtained from modelling are consistently too low. This is most likely due to the model only capturing diffusion limited growth, while nucleation followed by a period of non-diffusion limited high growth speed as well as other phenomena such as a pushing of the liquid due to the growing crystal or convection are not included. The PF model does however correctly show a transition from compact to non-compact growth depending on the concentration for high supersaturation values as has been found in experiments. The model we used does not include nucleation and convection. It is quantitatively not accurate but predicts some characteristics in relation to the growth of NaCl correctly and might be useful in connection with the modelling of the establishment of macroscopic structures and patterns, something that is difficult to simulate in general. It might for example help to better understand and to determine under which conditions ordered crystal patterns on the mesoscale are established in quasi two dimensions.64,65Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support from the University of St. Andrews under a St Leonard's College Scholarship (CDT) is gratefully acknowledged.Notes and references
- M. A. McDonald, H. Salami, P. R. Harris, C. E. Lagerman, X. Yang, A. S. Bommarius, M. A. Grover and R. W. Rousseau, React. Chem. Eng., 2021, 6, 364–400 RSC
.
- A. Naillon, P. Duru, M. Marcoux and M. Prat, J. Cryst. Growth, 2015, 422, 52–61 CrossRef CAS
.
- A. Naillon, P. Joseph and M. Prat, J. Cryst. Growth, 2017, 463, 201–210 CrossRef CAS
.
- J. Desarnaud, H. Derluyn, J. Carmeliet, D. Bonn and N. Shahidzadeh, J. Phys. Chem. Lett., 2018, 9, 2961–2966 CrossRef CAS PubMed
.
- J. Desarnaud, H. Derluyn, J. Carmeliet, D. Bonn and N. Shahidzadeh, J. Phys. Chem. Lett., 2014, 5, 890–895 CrossRef CAS PubMed
.
- R. Grossier, A. Magnaldo and S. Veesler, J. Cryst. Growth, 2010, 312, 487–489 CrossRef CAS
.
- M. N. Joswiak, B. Peters and M. F. Doherty, Cryst. Growth Des., 2018, 18, 6302–6306 CrossRef CAS
.
- A. C. Levi and M. Kotrla, J. Phys.: Condens. Matter, 1997, 9, 299–344 CrossRef CAS
.
- L. M. Sander, P. Ramanlal and E. Ben-Jacob, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 32, 3160–3163 CrossRef CAS PubMed
.
- A. G. Stack, P. Raiteri and J. D. Gale, J. Am. Chem. Soc., 2012, 134, 11–14 CrossRef CAS PubMed
.
- T. Mori, R. J. Hamers, J. A. Pedersen and Q. Cui, J. Chem. Theory Comput., 2013, 9, 5059–5069 CrossRef CAS PubMed
.
- M. N. Joswiak, M. F. Doherty and B. Peters, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 656–661 CrossRef CAS PubMed
.
- M. W. Anderson, J. T. Gebbie-Rayet, A. R. Hill, N. Farida, M. P. Attfield, P. Cubillas, V. A. Blatov, D. M. Proserpio, D. Akporiaye, B. Arstad and J. D. Gale, Nature, 2017, 544, 456–459 CrossRef CAS PubMed
.
- K. Kobayashi, Y. F. Liang, T. Sakka and T. Matsuoka, J. Chem. Phys., 2014, 140, 8 Search PubMed
.
- J. Zhang, M. K. Borg, K. Sefiane and J. M. Reese, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 052403 CrossRef PubMed
.
- G. Lanaro and G. N. Patey, J. Phys. Chem. B, 2016, 120, 9076–9087 CrossRef CAS PubMed
.
- N. E. R. Zimmermann, B. Vorselaars, J. R. Espinosa, D. Quigley, W. R. Smith, E. Sanz, C. Vega and B. Peters, J. Chem. Phys., 2018, 148, 222838 CrossRef PubMed
.
- H. Jiang, P. G. Debenedetti and A. Z. Panagiotopoulos, J. Chem. Phys., 2019, 150, 124502 CrossRef PubMed
.
- M. Uwaha, Prog. Cryst. Growth Charact. Mater., 2016, 62, 58–68 CrossRef CAS
.
-
M. Mazzotti, T. Vetter and D. R. Ochsenbein, in Polymorphism in the Pharmaceutical Industry, ed. R. Hilfiker and M. von Raumer, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2018, ch. 10, pp. 285–304 Search PubMed
.
- V. Bal and B. Peters, Cryst. Growth Des., 2021, 21, 227–234 CrossRef CAS
.
- R. Kobayashi, Phys. D, 1993, 63, 410–423 CrossRef
.
- B. Echebarria, R. Folch, A. Karma and M. Plapp, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 061604 CrossRef PubMed
.
- C. Beckermann, H. J. Diepers, I. Steinbach, A. Karma and X. Tong, J. Comput. Phys., 1999, 154, 468–496 CrossRef CAS
.
- Z. Xu and P. Meakin, J. Chem. Phys., 2008, 129, 014705 CrossRef PubMed
.
- Z. Xu and P. Meakin, J. Chem. Phys., 2011, 134, 044137 CrossRef PubMed
.
- Z. Xu, H. Huang, X. Li and P. Meakin, Comput. Phys. Commun., 2012, 183, 15–19 CrossRef CAS
.
-
S. B. Biner, Programming Phase-Field Modeling, Springer International Publishing, Cham, 2017 Search PubMed
.
- S. Yang, N. Ukrainczyk, A. Caggiano and E. Koenders, Appl. Sci., 2021, 11, 2464 CrossRef CAS
.
- C. Hawkins, L. Angheluta, Y. Hammer and B. Jamtveit, Europhys. Lett., 2013, 102, 54001 CrossRef
.
- C. Hawkins, L. Angheluta and B. Jamtveit, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 022402 CrossRef PubMed
.
-
J. W. Mullin, Crystallization, Elsevier, Oxford, 4th edn, 2001 Search PubMed
.
- J. P. Silva, L. Stragevitch, G. M. Vinhas and J. M. F. Silva, Theor. Found. Chem. Eng., 2017, 51, 458–463 CrossRef CAS
.
- R. S. Qin and H. K. Bhadeshia, Mater. Sci. Technol., 2010, 26, 803–811 CrossRef CAS
.
- J. R. Espinosa, C. Vega, C. Valeriani and E. Sanz, J. Chem. Phys., 2015, 142, 194709 CrossRef PubMed
.
- G. B. McFadden, A. A. Wheeler, R. J. Braun, S. R. Coriell and R. F. Sekerka, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 48, 2016–2024 CrossRef CAS PubMed
.
- A. A. Wheeler, J. Stat. Phys., 1999, 95, 1245–1280 CrossRef
.
- A. Karma and W.-J. Rappel, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 53, R3017–R3020 CrossRef CAS PubMed
.
- A. Karma and W.-J. Rappel, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 57, 4323–4349 CrossRef CAS
.
- P. Passiniemi, J. Solution Chem., 1983, 12, 801–813 CrossRef CAS
.
-
S. R. Feldman, Sodium Chloride, in Kirk-Othmer Encyclopedia of Chemical Technology, John Wiley & Sons, Inc., Hoboken, NJ, 2011, p. 27 Search PubMed
.
- Y. Sun and C. Beckermann, J. Comput. Phys., 2007, 220, 626–653 CrossRef
.
-
R. L. Burden and J. D. Faires, Numerical Analysis, Richard Stratton, Boston, MA, 9th edn, 2011 Search PubMed
.
- I. Steinbach, Annu. Rev. Mater. Res., 2013, 43, 89–107 CrossRef CAS
.
- N. Provatas, N. Goldenfeld and J. Dantzig, J. Comput. Phys., 1999, 148, 265–290 CrossRef
.
- N. Shahidzadeh and J. Desarnaud, Eur. Phys. J.: Appl. Phys., 2012, 60, 24205 CrossRef
.
- H. B. Aaron, D. Fainstein and G. R. Kotler, J. Appl. Phys., 1970, 41, 4404–4410 CrossRef
.
- A. E. Nielsen, Croat. Chem. Acta, 1980, 53, 255–279 CAS
.
- F. Rosenberger and G. Müller, J. Cryst. Growth, 1983, 65, 91–104 CrossRef CAS
.
- T. Biben, C. Misbah, A. Leyrat and C. Verdier, Europhys. Lett., 2003, 63, 623–630 CrossRef CAS
.
-
Y. Saito, Statistical Physics of Crystal Growth, World Scientific, Singapore, 1996 Search PubMed
.
- Z. Yang, J. Zhang, L. Zhang, B. Fu, P. Tao, C. Song, W. Shang and T. Deng, Adv. Funct. Mater., 2020, 30, 1908108 CrossRef CAS
.
- R. F. Sekerka, J. Cryst. Growth, 2005, 275, 77–82 CrossRef CAS
.
- R. F. Sekerka, Cryst. Res. Technol., 2005, 40, 291–306 CrossRef CAS
.
- J. J. Eggleston, G. B. McFadden and P. W. Voorhees, Phys. D, 2001, 150, 91–103 CrossRef CAS
.
-
C. Herring, in Fundamental Contributions to the Continuum Theory of Evolving Phase Interfaces in Solids, ed. J. M. Ball, D. Kinderlehrer, P. Podio-Guidugli and M. Slemrod, Springer, Berlin, Heidelberg, 1999, ch. 8, pp. 33–69 Search PubMed
.
- J. E. Taylor and J. W. Cahn, Phys. D, 1998, 112, 381–411 CrossRef CAS
.
- S. Torabi, J. Lowengrub, A. Voigt and S. Wise, Proc. R. Soc. A, 2009, 465, 1337–1359 CrossRef
.
- A. Miranville, Cubo, 2015, 17, 73–88 CrossRef
.
- O. Tschukin, A. Silberzahn, M. Selzer, P. G. K. Amos, D. Schneider and B. Nestler, Geotherm. Energy, 2017, 5, 19 CrossRef
.
- J. Zhang, S. Zhang, Z. Wang, Z. Zhang, S. Wang and S. Wang, Angew. Chem., Int. Ed., 2011, 50, 6044–6047 CrossRef CAS PubMed
.
- S. K. Chan, H. H. Reimer and M. Kahlweit, J. Cryst. Growth, 1976, 32, 303–315 CrossRef CAS
.
- J. Zhao, H. Miao, L. Duan, Q. Kang and L. He, Opt. Lasers Eng., 2012, 50, 540–546 CrossRef
.
- J. H. Wu, S. G. Ang and G. Q. Xu, J. Phys. Chem. C, 2008, 112, 7605–7610 CrossRef CAS
.
- G. F. Harrington, J. M. Campbell and H. K. Christenson, Cryst. Growth Des., 2013, 13, 5062–5067 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ce01640k |
| This journal is © The Royal Society of Chemistry 2023 |