Open Access Article
Open Access ArticleDesign of diastereomeric salt resolution via multicomponent system characterization: a case study with hydrate formation†
Miklós H.
Bosits
 ab,
Laura
Bereczki
c,
Petra
Bombicz
ab,
Laura
Bereczki
c,
Petra
Bombicz
 c,
Zsófia
Szalay
b,
Hajnalka
Pataki
*a and
Ádám
Demeter
b
c,
Zsófia
Szalay
b,
Hajnalka
Pataki
*a and
Ádám
Demeter
b
aDepartment of Organic Chemistry and Technology, Faculty of Chemical Technology and Biotechnology, Budapest University of Technology and Economics, Műegyetem rkp. 3., H-1111 Budapest, Hungary. E-mail: pataki.hajnalka@vbk.bme.hu
bGedeon Richter Plc, P.O. Box 27, H-1475 Budapest, Hungary
cCentre for Structural Science, Research Centre for Natural Sciences, Magyar tudósok körútja 2., H-1117 Budapest, Hungary
First published on 19th December 2022
Abstract
Diastereomeric salt crystallization is a convenient method to resolve chiral drug substances when other separation methods like preferential crystallization and solid-state deracemization cannot be applied directly. This is the case of the antiepileptic pregabalin, which is a racemate-forming compound with recently discovered hydrate-forming activity. In this study, the quaternary system of pregabalin enantiomers, L-tartaric acid and water was investigated by the characterization of relevant solid forms and the measurement of solubilities and solid–liquid equilibria. This information was used to outline phase diagrams in the specific quaternary space and create a thermodynamic model based on solubility product constants to simulate the effect of variable parameters on the resolution process. Thus, a set of optimal temperature pairs were identified with similar selectivity along the so-called purity line in the region of 10–40 °C. This line was adjusted experimentally, and a realistic correction of 3 °C was made. Our method provided a quick process with low material requirements to design diastereomeric salt resolution. Finally, a proof of concept resolution experiment was conducted, where a diastereomerically pure product was obtained with 51.6% yield and 153 mg (g water)−1 productivity.
Introduction
More than half of pharmaceutically active compounds (e.g., amino acid derivatives) contain an asymmetric center. Such chiral drugs usually have stereoisomers that are mirror images of each other (enantiomers). Although enantiomers have the same chemical structure, their biological activities could differ due to differences in configuration. Thus, producing an enantiomerically pure drug substance is favorable for increasing therapeutic efficiency and/or avoiding potential toxicological side effects.1,2The most classical and widespread chiral resolution technique is diastereomeric salt crystallization.3 It requires an enantiopure chiral additive (resolving agent) that forms a salt pair with the two enantiomers. These diastereomerically related salts have different physical properties like solubility, which makes their separation possible by selective crystallization. Diastereomeric salt resolution is easy to scale up and implement in industrial processes.4 Contrary to other methods like preferential crystallization and solid-state deracemization, it can be applied to any material that has an acidic/basic functional group.5 Therefore, its application in intensively researched innovative crystallization procedures (e.g., continuous crystallization6 and Viedma-ripening7) is actively studied as well.
Knowledge about the physicochemical properties of our system is the key to the development of an efficient resolution process. Thus, in crystallization-based separation techniques, understanding the structure of the relevant phase diagrams is essential to interpret the solid–liquid phenomena properly. Several phase diagrams were designed related to chiral separation methods: crystallization of conglomerate-forming enantiomers,8 cocrystal formation with chiral9 or achiral10,11 coformers, and diastereomeric salt crystallization.12,13 The construction of detailed experimental phase diagrams can help to identify new crystal phases,14 but it also requires a large number of measurements, especially in quaternary systems like diastereomeric salt resolution.15 On the other hand, a detailed investigation of the components' thermodynamical behavior supports outlining the model phase diagram that can be used in further research.10,11,16 Recent studies focus on creating short-cut procedures considering basic knowledge about phase diagrams. W. Li et al. described a quick process using saturation temperature measurements to identify cocrystal types and resolution possibilities in multicomponent systems.17 L. Codan et al. introduced a methodology using temperature maps to design the cooling preferential crystallization of conglomerate-forming compounds.18
Pregabalin (PG) is a chiral, alkylated analogue of γ-aminobutyric acid (GABA) with anticonvulsant and anxiolytic effects. It was developed by Pfizer and became a blockbuster for treating epilepsy, generalized anxiety disorder, neuropathic pain, and other pain-related problems.19,20 Since the expiration of relevant patents,21,22 PG has been available as a generic medication in most countries, including the United States, as of 2019. As (S)-enantiomer of PG exhibits the desired pharmacological activity,23,24 it is produced and commercialized in enantiomerically pure form. Several enantioselective processes were developed using chiral pool synthesis,25 asymmetric catalysis,26–29 chemoenzymatic reaction,30–33 or chiral auxiliaries,34,35 but a classical chiral resolution method like diastereomeric salt formation can be their favorable, low-cost alternative in a scaled-up, commercial process.25 Such PG resolution processes are known using (S)-mandelic acid,36L-tartaric acid,37O,O′-dibenzoyl-L-tartaric acid,38 and their mixtures39 mostly in alcohol–water mixtures. Resolving agents are used in 0.5–1.5 equivalent with optional additional achiral acids (hydrochloric acid, formic acid, benzoic acid, etc.) for complete dissolution. L-Tartaric acid (L-TA) can also be applied in pure water, which is beneficial for productivity due to the high solubility of diastereomeric salts.40 The less bioactive (R)-enantiomer can be racemized and recycled or used as a resolving agent to produce other asymmetric chemicals.41–43
(S)-Pregabalin has a thermodynamically stable anhydrous form44,45 produced worldwide and two recently discovered monohydrates.46,47 (S)-PG hydrates can nucleate in water-containing solvents, but they are unstable in solid state and transform to anhydrate rapidly.48 Contrary to enantiopure PG, racemic pregabalin is known as a stable hydrate with water content ranging 0.5–1.0 equivalent,36,49 but no further investigation was made about its structure.
This study aims to describe the multicomponent system of pregabalin enantiomers, L-tartaric acid, and water using solid-state analytical techniques and phase diagrams. We will also present a short-cut method using thermodynamic information to design a diastereomeric salt resolution process.
Materials and methods
Starting materials
(S)-Pregabalin was obtained from Gedeon Richter Plc. in pharmaceutical grade. Racemic pregabalin was obtained from Gedeon Richter Plc. as a raw intermediate (purity ≥97%). L-Tartaric acid was purchased from Industria Chimica Valenzana (purity ≥99.9%). D-Tartaric acid was bought from Sigma-Aldrich (purity ≥99%).Preparation of pure components
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 volume unit, respectively). Solids were dissolved in a 9× amount of solvent mixture, then cooled to 5 °C, filtered, and dried as described above. Finally, 0.44 g (R)-PG was obtained with a total yield of 10%. The salt formation was performed by dissolving the 0.44 g (R)-PG with 0.42 g L-TA in 1.8 mL of water. Then, linear cooling was applied from 40 to 2 °C with a 0.5 °C min−1 cooling rate. The white solid product was filtered and dried in a vacuum drying chamber at 100 mbar and 40 °C. (R)-Pregabalin L-tartrate hydrate was obtained with a 91% yield (0.82 g).
2 volume unit, respectively). Solids were dissolved in a 9× amount of solvent mixture, then cooled to 5 °C, filtered, and dried as described above. Finally, 0.44 g (R)-PG was obtained with a total yield of 10%. The salt formation was performed by dissolving the 0.44 g (R)-PG with 0.42 g L-TA in 1.8 mL of water. Then, linear cooling was applied from 40 to 2 °C with a 0.5 °C min−1 cooling rate. The white solid product was filtered and dried in a vacuum drying chamber at 100 mbar and 40 °C. (R)-Pregabalin L-tartrate hydrate was obtained with a 91% yield (0.82 g).
Single-crystal X-ray diffraction (SC-XRD)
Single crystals were grown: 150 mg racemic pregabalin hydrate was dissolved in 5 mL pure water at 45 °C, then the clear solution was left at room temperature. Colourless platelet-like single crystals were collected after two weeks, and tested by polarized light under optical microscope. As the platelet crystals were too soft to cut them, a crystal with the size of 1.7 × 0.9 × 0.3 mm was selected. Intensity data were collected on an RAXIS-RAPID II diffractometer (graphite monochromator; MoKα radiation) at a low temperature of 143(2) K. The atomic positions were determined by direct methods, all hydrogen atoms were found on the difference Fourier maps.50CCDC-2215531 contains the supplementary crystallographic data of (RS)-PG hydrate.
X-ray powder diffraction (XRPD)
X-ray powder data were collected on a PANalytical X'Pert PRO MPD diffractometer. Samples were measured in transmission mode with 1 round per s spinning rate. A scanning range of 2θ values from 2° to 40° at a scan rate of 0.0305° s−1 was applied.Variable-temperature X-ray powder diffraction (VT-XRPD)
Variable-temperature X-ray powder data were collected in reflection mode on a PANalytical X'Pert PRO MPD diffractometer equipped with the Anton Paar TTK-450 temperature chamber. The temperature was varied between 25 °C and 120 °C with 5–10 °C steps between XRPD measurements. A scanning range of 2θ values from 5° to 24° at a scan rate of 0.0309° s−1 was applied at each stage.Differential scanning calorimetry (DSC)
Calorimetric measurements were performed on a TA Instruments Discovery DSC 2500 instrument. Typically, 3–5 mg of sample was accurately weighed into an open aluminum pan and heated at a 10 °C min−1 heating rate under a nitrogen gas flow of 50 mL min−1.Thermogravimetric analysis (TG)
Thermograms were measured with a TA Instruments Discovery TGA 5500 instrument at a heating rate of 10 °C min−1 under a nitrogen gas flow of 25 mL min−1.Dynamic vapor sorption (DVS)
Water vapor sorption measurements were performed on an SMS DVS Advantage 1 instrument between 0–90% relative humidity (RH) under a nitrogen gas flow of 150 mL min−1. Two cycles were measured with 10% RH steps. Criterion for dm/dt value was 0.002% min−1.Optical microscopy (OM)
Images of the prepared crystals were captured using a Carl Zeiss Axio Imager M2 stereomicroscope.Solubility measurements
Solubility measurements of (S)-PG-L-TA, and (S)-PG-D-TA hydrates in water were performed using a polythermal method in Crystal16 equipment (Technobis BV). Suspensions of known concentrations were prepared from the pure components and water. Concentrations were calculated as the mass of dissolved pregabalin tartrate per mass of solvent (water). 1.0–1.5 g suspension was linearly heated (0.3 °C min−1) until complete dissolution (clear point) and then cooled for recrystallization. The clear point temperature was considered as the saturation temperature of the corresponding concentration. Suspensions were stirred by magnetic stirrer with 1000 rpm. The heating–cooling cycle was repeated three times. The solid phase was analysed by XRPD after the last cycle to exclude the change of crystalline form in each case.Solid–liquid equilibrium measurements
Equilibrium data was obtained by preparing a set of vials with specific compositions of (RS)-PG, L-TA, and water. All vials were sealed, and mixtures were heated up to 40 °C until complete dissolution. They were cooled down to predetermined temperatures between 16 to 36 °C. Then, they were stirred at constant temperature for a day and seeded with (S)-PG-L-TA and (R)-PG-L-TA diastereomeric salts. After two weeks, the system was assumed to have reached equilibrium. The final phases were analyzed for each vial using HPLC to determine the equilibrium composition. Total concentrations of pregabalin tartrates in the liquid phases were measured gravimetrically. The suspensions were sampled using a preheated syringe and filtered into a preweighted dry glass vial using a PTFE (0.22 μm) membrane syringe filter. Total masses were measured directly after sampling and after evaporating the solvent. The residual water content of solid crystals was measured by TG. Equilibrium concentrations were calculated as the mass of dissolved pregabalin tartrate per mass of solvent (water). Some mixtures could not reach equilibrium due to the nucleation of (R)-PG-L-TA monohydrate; those were marked as failed experiments.High-performance liquid chromatography (HPLC)
Diastereomeric excess of pregabalin tartrate salts was determined by HPLC after derivatization with Marfey's reagent (bought from Thermo Scientific).51 A mixture of 200–200 μL pregabalin tartrate (10 mg mL−1 water), Marfey's reagent (3 mg mL−1 acetone), NaHCO3 (1 M in water), and acetonitrile were stirred at 50 °C for 2 hours. After cooling, 200 μL of hydrochloric acid (1 M in water) was added and stirred until the end of bubble formation. Aliquots of the formed pregabalin derivative were injected within 12 hours.A reverse HPLC method was applied using a Kinetex EVO C18 analytical column (150 mm × 4.6 mm, particles 5 μm). The column temperature was kept at 50 °C. Linear gradient elution mode with a total flow rate of 1 mL min−1 was used. The ‘A’ eluent was water + 0.1% trifluoroacetic acid (TFA), and the ‘B’ eluent was pure acetonitrile. Eluent composition was changed from 0% ‘B’ to 90% in 15 min. Area of peaks at 9.6 and 9.8 min retention time were compared to calculate diastereomeric purity: de = (A9.6min − A9.8min)/(A9.6min + A9.8min).
Results and discussion
Results are discussed in three consecutive sections. First, relevant components of the quaternary system are characterized. The second part focuses on understanding the complex, hydrate-forming system of diastereomeric salt resolution. Based on solid-state information, the specific phase diagrams of the system are outlined. Finally, our mathematical model and experimental work are described, which aim to investigate the relevant parameter space for the optimal resolution process.Solid-state characterization of the components
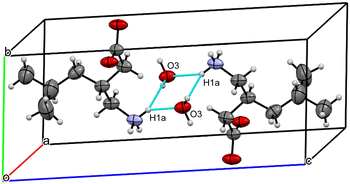
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) (#2). Two enantiomerically related pregabalin molecules in the unit cell (Z = 2, Z′ = 1) are connected by strong N–H⋯O type hydrogen bonds forming a dimer via two water molecules arranged by a symmetry centre (Fig. 2), which verifies the presence of the strongly bound structural water indicated by DVS. Detailed crystallographic analysis is attached in the ESI.†
(#2). Two enantiomerically related pregabalin molecules in the unit cell (Z = 2, Z′ = 1) are connected by strong N–H⋯O type hydrogen bonds forming a dimer via two water molecules arranged by a symmetry centre (Fig. 2), which verifies the presence of the strongly bound structural water indicated by DVS. Detailed crystallographic analysis is attached in the ESI.†
Description of the multicomponent system considering hydrate formation
The system of a diastereomeric salt resolution can be described in a quaternary phase diagram assuming pure solvent and the absence of other excipients (e.g., inorganic acid/base, second resolving agent). The four pure components define a tetrahedron with (R)-PG, (S)-PG, L-TA, and water in the corners. Based on solid-state characterizations, seven additional solid phases are known with stoichiometric composition. Racemic pregabalin and the two diastereomeric salt anhydrates are in the center of the bottom edges (Fig. 7). All three compounds have monohydrates located in the center of the faces (X, Y, Z). These specific compositions determine the solidus line with no liquids below it (netted). Solubilities can be used to outline the ternary phase diagrams on the faces. The solubility difference (Δx) between the diastereomeric salts is highlighted as it is a fundamental condition of their separation. The area between the solidus and liquidus lines is divided into zones based on which crystal phases (I–VI) are present in equilibrium. | ||
| Fig. 7 Scheme of the ternary phase diagrams in the (R)-pregabalin – (S)-pregabalin – L-tartaric acid – water quaternary system. | ||
However, the resolution process cannot be demonstrated on these ternary phase diagrams but on the quaternary space between them. The complete description of the tetrahedron is complex and time-consuming work, especially with the numerous hydrate crystal forms. Alternatively, pseudo-phase diagrams on specific slices can be examined. Firstly, a racemic mixture should be resolved so the composition will be selected on the (RS)-PG – L-TA – H2O diagram (Fig. 8). The individual points represent the two most relevant parameters regarding resolutions: the molar ratio of the resolving agent and total concentration. In our case, the low solubility of racemic pregabalin required a minimum equivalent resolving agent for complete dissolution. From a thermodynamic point of view, zone IV is the best for resolution where only one diastereomer is stable in the crystalline phase. The (RS)-PG – L-TA – H2O slice helps to choose the initial composition but does not provide quantitative information about the new, divided phases. (S)-Pregabalin L-tartrate monohydrate (point ‘Y’) is not part of this slice, although the lever rule can only be used in diagrams that contain all the crystallized phases.
 | ||
| Fig. 8 Scheme of the pseudo-phase diagram on the (RS)-pregabalin – L-tartaric acid – water slice of the tetrahedron. | ||
The slice of (R)-PG-L-TA – (S)-PG-L-TA – H2O in the quaternary phase diagram is suitable to describe the separation of diastereomeric salts using an equivalent amount of resolving agent (Fig. 9). Pseudo-phase diagrams neglecting the area below the solidus line can also be used, especially at a higher ratio of the resolving agent. Pseudo-phase diagrams neglecting the area below the solidus line can also be used, especially at a higher ratio of the resolving agent. However, the excess of the L-tartaric acid would decrease the solubility of both pregabalin salts via counter-ion effect thus the productivity will decrease without any change in their relative solubility.
 | ||
| Fig. 9 Scheme of the pseudo-phase diagram on the (R)-pregabalin L-tartrate – (S)-pregabalin L-tartrate – water slice of the tetrahedron. | ||
Generally, the racemic composition is represented by the altitude of the triangle and a concentration along that is selected for the best separation (Fig. 10). Pseudo-phase diagrams are temperature-dependent, like the entire quaternary phase diagram. Thus, knowledge about the system at one temperature is not enough during a cooling crystallization. The selected composition (point ‘A’) should correspond to a saturated, clear solution at the upper temperature (T1) of the crystallization and be on the edge of zone IV at the lower temperature (T2).
Assuming equilibrium composition and neglecting the effect of cooling attributes, resolution can be optimized by monitoring the borders of zone IV at different temperatures. Here we describe a method to estimate the resolution attributes and use it for focused experimental research.
Design of diastereomeric salt resolution of pregabalin
Solubility is essential information for designing a crystallization process. It can vary with temperature, solvent quality (antisolvent ratio), and presence of other chemicals (excipients, impurities). The selection of the most suitable crystallization technique depends on which parameter has the most significant effect on the solubility. Cooling crystallization is preferred when the solute has a steep temperature-based solubility curve. Thus, high yield can be achieved in a realistic, narrow temperature range.In classical resolutions, the crystallized products are diastereomeric salts. These are dissociable compounds with a common counterion, so their solubilities are related. Moreover, solubility can hardly be defined and used in crystallization design when the ratio of the cation and anion is not stochiometric and changes over time. In such a multicomponent system, the solid–liquid equilibrium is determined by the components' solubility product constants (Ksp).
The solubility product constant of any diastereomeric salt can be calculated from the measured solubility of the pure compound. Therefore, the solubility curves of the prepared (S)-pregabalin L-tartrate monohydrate and (S)-pregabalin D-tartrate monohydrate were measured (Fig. 11). As (S)-PG-D-TA and (R)-PG-L-TA are enantiomerically related, their solubilities are identical. The measured solubility points showed good fitting with the modified Apelblat equation (ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c = A + B/T + C
c = A + B/T + C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c). Both diastereomer salts are highly soluble in water with strong temperature dependence. Even so, there is a significant solubility difference between the salts. Solubility of (S)-PG-D-TA can be 2–3 times higher in the investigated temperature range (10–40 °C), which makes the process suitable for chiral separation.
c). Both diastereomer salts are highly soluble in water with strong temperature dependence. Even so, there is a significant solubility difference between the salts. Solubility of (S)-PG-D-TA can be 2–3 times higher in the investigated temperature range (10–40 °C), which makes the process suitable for chiral separation.
 | ||
Fig. 11 Solubility curves of (S)-pregabalin L-tartrate monohydrate (A = −729, B = 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 310, C = 112) and (S)-pregabalin D-tartrate monohydrate (A = −1484, B = 61 310, C = 112) and (S)-pregabalin D-tartrate monohydrate (A = −1484, B = 61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 720, C = 225). 720, C = 225). | ||
Solubility product constants of (S)-PG-L-TA (KSLsp) and (R)-PG-L-TA (KRLsp) were calculated from fitted solubilities in the investigated temperature range. Activities of ionic (S)-PG, (R)-PG, and L-TA (aS+, aR+, and aL−, respectively) were estimated by using their mol fraction (xS+, xR+, and xL−, respectively). Water activity (aH2O) was considered 1 due to the aqueous solution (eqn (1)). These estimations can be generally used, but their accuracy should be handled with caution at high ionic strength. In our case, this model was only used to gain preliminary data to shorten the design process.
| Ksp = aS/R+ × aL− × aH2O ≈ xS/R+ × xL− | (1) |
 | (2) |
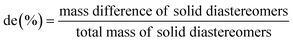 | (3) |
| S(−) = Y × de | (4) |
| P(mg (g water)−1) = total concentration × S | (5) |
The Ksp-based model could simulate resolution processes over the investigated temperature range and estimate parameter combinations for the best chiral separation. This prediction was used to design experiments focusing on the diastereomerically pure zone and adjusting its lower boundary, the purity line. Small-scale solid–liquid equilibrium measurements were executed at T1 − T2 combinations visualized in Fig. 13. Combinations were evaluated based on the crystallization of one or two diastereomers (green circles and red diamonds, respectively). The dashed line represents the experimental boundary of the diastereomerically pure zone. This line is above the calculated purity line by 3 °C, which is a realistic difference considering the rough estimation in the simulation for concentrated solutions. Thus, the calculation can save both time and material by focusing on adjusting the simulated purity line.
Experiments with both diastereomers in the solid phase could not reach equilibrium due to insufficient mixing. A similar problem emerged during (S)-PG-D-TA monohydrate preparation. Due to the fibrous crystal habit and concentrated (0.3–1.0 g (g water)−1) solutions, the produced crystals had extensive surfaces, and after reaching a critical suspension density, stirring was no longer possible. In equilibrium experiments, the nucleation of (R)-PG-L-TA monohydrate occurred in the presence of (S)-PG-L-TA crystals with high suspension density. Thus, the appearance of a minimal quantity of fibrous crystals was enough to fail proper mixing. This phenomenon emphasizes the role of the pure region, and it is recommended to consider the risk of undesired nucleation of (R)-PG-L-TA diastereomer when (S)-PG-L-TA is crystallized at a lower temperature for higher yield.
The solubility of the crystallized component depends on the quantity of counter diastereomer dissolved in the liquid phase. Thus, equilibrium concentrations cannot be measured independently with the classical clear-point method. Alternatively, the concentration of pregabalin tartrate was determined from the solid–liquid equilibrium experiments by analyzing their liquid phase. Equilibrium concentrations of suspensions with the same total composition describe an effective solubility curve. This curve is valid for cooling crystallizations starting from a saturated solution at T1. Trends for different total compositions (corresponding to the signed upper temperatures) are presented in Fig. 14. Concentrations at T2 = T1 represent saturated solutions. Results show linear descending concentration profiles during the cooling process with a predicted maximum yield of 40–50% for the desired diastereomer salt.
Based on theoretical and experimental research, a set of parameter combinations was suggested (the so-called purity line) for chiral separation between 10–40 °C. Besides productivity, other technological factors or preferences can affect the selection of operating parameters. Hereby, a resolution experiment is demonstrated in the center of the purity line (T1 = 31 °C, T2 = 20 °C), and detailed investigations will be discussed in later publications. The pseudo-phase diagram at the lower temperature (20 °C) could also be calculated from the solid–liquid equilibrium measurements (Fig. 15). The total composition was chosen to be on the border of zone IV and zone VI + IV in the following experiment.
A diastereomeric salt resolution was executed by cooling 56 g saturated solution (600 mg (g water)−1) from 31 °C to 20 °C in a 100 mL EasyMax reactor. The solution was seeded with pure (S)-PG-L-TA monohydrate crystals at 30 °C and cooled to 20 °C with a 0.07 °C min−1 cooling rate. After 90 min agitation, pure (S)-PG-L-TA monohydrate crystals were obtained with 51.6% yield and 153 mg (g water)−1 productivity (Fig. 16). The product suspension was dense but easy to be mixed and filtered due to the isometric crystal habit with good fluidity. Yield and productivity were close to the estimated values.
Conclusions
This paper presents how a diastereomeric salt resolution of hydrate forming system can be characterized thermodynamically and how to incorporate this information in phase diagram construction to facilitate resolution design.Knowledge of the relevant solid phases could be used to describe the specific multicomponent system in a quaternary space. Recommendations were made on how to choose relevant faces or slices of the tetrahedron regarding process design. Our Ksp-based model could simulate the diastereomeric salt crystallization of pregabalin tartrate and estimate the boundary of the diastereomerically pure zone. Working on this line can be optimal when the process is thermodynamically controlled and/or nucleation of the counter diastereomer negatively affects the process. As in our case, the fibrous crystals of (R)-PG-L-TA monohydrate could destroy the fluidity of the suspension, making production extremely difficult. To prove our concept, a resolution experiment was conducted with process parameters selected from the recommended rage and a diastereomerically pure product was obtained without any fluidity problem.
Author contributions
Miklós H. Bosits: conceptualization, investigation, visualization, and writing. Laura Bereczki: investigation. Petra Bombicz: formal analysis. Zsófia Szalay: methodology and project administration. Hajnalka Pataki: supervision. Ádám Demeter: supervision.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been implemented with the support provided by the Ministry of Innovation and Technology of Hungary from the National Research, Development and Innovation Fund, financed under the [FK-143019 and K-124544] funding scheme. H. P. is thankful for the János Bolyai Research Scholarship of the Hungarian Academy of Sciences. The authors greatly acknowledge the continuous support of colleagues from the Polymorphism Research Team at Gedeon Richter Plc., who contributed to this work with numerous daily technical help.References
- L. A. Nguyen, H. He and C. Pham-Huy, Int. J. Biomed. Sci., 2006, 2, 85–100 CAS.
- A. Calcaterra and I. D'Acquarica, J. Pharm. Biomed. Anal., 2018, 147, 323–340 CrossRef CAS PubMed.
- C. Viedma, G. Coquerel and P. Cintas, in Handbook of Crystal Growth, ed. T. Nishinaga, Elsevier, 2nd edn, 2015, pp. 951–1002 Search PubMed.
- J. Jacques, A. Collet and S. H. Wilen, Enantiomers, racemates, and resolutions, J. Wiley & Sons, Inc., New York, 1981 Search PubMed.
- R. Siedlecka, Tetrahedron, 2013, 69, 6331–6363 CrossRef CAS.
- L. Marc, S. Guillemer, J. M. Schneider and G. Coquerel, Chem. Eng. Res. Des., 2022, 178, 95–110 CrossRef CAS.
- T. Lerdwiriyanupap, G. Belletti, P. Tinnemans, H. Meekes, F. P. J. T. Rutjes, E. Vlieg and A. E. Flood, Eur. J. Org. Chem., 2021, 2021, 5975–5980 CrossRef CAS.
- N. Wermester, E. Aubin, M. Pauchet, S. Coste and G. Coquerel, Tetrahedron: Asymmetry, 2007, 18, 821–831 CrossRef CAS.
- G. Springuel and T. Leyssens, Cryst. Growth Des., 2012, 12, 3374–3378 CrossRef CAS.
- C. Neurohr, M. Marchivie, S. Lecomte, Y. Cartigny, N. Couvrat, M. Sanselme and P. Subra-Paternault, Cryst. Growth Des., 2015, 15, 4616–4626 CrossRef CAS.
- L. C. Harfouche, N. Couvrat, M. Sanselme, C. Brandel, Y. Cartigny, S. Petit and G. Coquerel, Cryst. Growth Des., 2020, 20, 3842–3850 CrossRef CAS.
- F. Querniard, J. Linol, Y. Cartigny and G. Coquerel, J. Therm. Anal. Calorim., 2007, 90, 359–365 CrossRef CAS.
- P. Marchand, L. Lefèbvre, F. Querniard, P. Cardinaël, G. Perez, J. J. Counioux and G. Coquerel, Tetrahedron: Asymmetry, 2004, 15, 2455–2465 CrossRef CAS.
- K. Chadwick, R. Davey, G. Sadiq, W. Cross and R. Pritchard, CrystEngComm, 2009, 11, 412–414 RSC.
- G. Springuel, L. Collard and T. Leyssens, CrystEngComm, 2013, 15, 7951–7958 RSC.
- P. Thorey, P. Bombicz, I. M. Szilágyi, P. Molnár, G. Bánsághi, E. Székely, B. Simándi, L. Párkányi, G. Pokol and J. Madarász, Thermochim. Acta, 2010, 497, 129–136 CrossRef CAS.
- W. Li, M. De Groen, H. J. M. Kramer, R. De Gelder, P. Tinnemans, H. Meekes and J. H. Ter Horst, Cryst. Growth Des., 2021, 21, 112–124 CrossRef CAS.
- L. Codan, M. U. Bäbler and M. Mazzotti, Org. Process Res. Dev., 2012, 16, 294–310 CrossRef CAS.
- R. Andruszkiewicz and R. B. Silverman, Synthesis, 1989, 1989, 953–955 CrossRef.
- R. B. Silverman, Angew. Chem., Int. Ed., 2008, 47, 3500–3504 CrossRef CAS PubMed.
- R. B. Silverman, R. Andruszkiewicz, P.-W. Yuen, D. M. Sobieray, L. C. Franklin and M. A. Schwindt, WO/1993/023383, 1993.
- L. Singh, WO/1998/003167, 1998.
- C. P. Taylor, M. G. Vartanian, Y. Po-Wai, C. Bigge, N. Suman-Chauhan and D. R. Hill, Epilepsy Res., 1993, 14, 11–15 CrossRef CAS PubMed.
- P. Yuen, G. D. Kanter, C. P. Taylor and M. G. Vartanian, Bioorg. Med. Chem. Lett., 1994, 4, 823–826 CrossRef CAS.
- M. S. Hoekstra, D. M. Sobieray, M. A. Schwindt, T. A. Mulhern, T. M. Grote, B. K. Huckabee, V. S. Hendrickson, L. C. Franklin, E. J. Granger and G. L. Karrick, Org. Process Res. Dev., 1997, 1, 26–38 CrossRef CAS.
- M. J. Burk, O. P. Goel, M. S. Hoekstra, T. F. Mich, T. A. Mulhern and J. A. Ramsden, WO/2001/055090, 2001.
- M. J. Burk, P. D. De Koning, T. M. Grote, M. S. Hoekstra, G. Hoge, R. A. Jennings, W. S. Kissel, T. V. Le, I. C. Lennon, T. A. Mulhern, J. A. Ramsden and R. A. Wade, J. Org. Chem., 2003, 68, 5731–5734 CrossRef CAS PubMed.
- G. M. Sammis and E. N. Jacobsen, J. Am. Chem. Soc., 2003, 125, 4442–4443 CrossRef CAS PubMed.
- M. Moccia, M. Cortigiani, C. Monasterolo, F. Torri, C. Del Fiandra, G. Fuller, B. Kelly and M. F. A. Adamo, Org. Process Res. Dev., 2015, 19, 1274–1281 CrossRef CAS.
- C. A. Martinez, S. Hu, Y. Dumond, J. Tao, P. Kelleher and L. Tully, Org. Process Res. Dev., 2008, 12, 392–398 CrossRef CAS.
- C. K. Winkler, D. Clay, S. Davies, P. O'Neill, P. McDaid, S. Debarge, J. Steflik, M. Karmilowicz, J. W. Wong and K. Faber, J. Org. Chem., 2013, 78, 1525–1533 CrossRef CAS PubMed.
- Q. Zhang, Z.-M. Wu, S. Liu, X.-L. Tang, R.-C. Zheng and Y.-G. Zheng, Org. Process Res. Dev., 2019, 23, 2042–2049 CrossRef CAS.
- Q. Zhang, Z. M. Wu, C. L. Hao, X. L. Tang, R. C. Zheng and Y. G. Zheng, Appl. Microbiol. Biotechnol., 2019, 103, 5617–5626 CrossRef CAS PubMed.
- C. He, Z. Zhai, Y. Zhou, J. Li and G. Wang, Synth. Commun., 2021, 51, 2034–2040 CAS.
- A. P. Tiwari, V. K. Kansal, B. P. Chaurasia and V. G. Rao, WO/2007/035890, 2007.
- T. M. Grote, B. K. Huckabee, T. Mulhern, D. M. Sobieray and R. D. Titus, WO/1996/040617, 1996.
- V. Gore, D. Datta, M. Gadakar, K. Pokharkar, V. Mankar and S. Wavhal, WO/2009/122215, 2009.
- R. Tufaro and G. Marras, WO/2008/138874, 2008.
- D. F. Bánhegyi and E. Pálovics, Chemical & Pharmaceutical Research, 2020, 2, 1–5 Search PubMed.
- J. Neu, E. Fogassy, N. Szalma, P. Kálvin, J. Schindler, G. Jakab, S. Garadnay and E. Pálovics, WO/2011/124934, 2011.
- Z. Szeleczky, P. Bagi, E. Pálovics and E. Fogassy, Tetrahedron: Asymmetry, 2014, 25, 1095–1099 CrossRef CAS.
- Z. Szeleczky, P. Bagi, E. Pálovics and E. Fogassy, Tetrahedron: Asymmetry, 2015, 26, 377–384 CrossRef CAS.
- Z. Szeleczky, P. Bagi, E. Pálovics, F. Faigl and E. Fogassy, J. Chem. Res., 2016, 40, 21–25 CrossRef CAS.
- A. Perez-Benitez, I. Angel Nieto and S. Bernes, CSD Communication (Private Communication) CCDC 2059215, 2021.
- N. Venu, P. Vishweshwar, T. Ram, D. Surya and B. Apurba, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2007, 63, o306–o308 CrossRef CAS PubMed.
- A. Perez-Benitez, I. Angel Nieto and S. Bernes, CSD Communication (Private Communication) CCDC 2059213, 2021.
- U. B. R. Khandavilli, M. Lusi and P. J. Frawley, IUCrJ, 2019, 6, 630–634 CrossRef CAS PubMed.
- R. R. E. Steendam, U. B. R. Khandavilli, L. Keshavarz and P. J. Frawley, Cryst. Growth Des., 2019, 19, 4483–4488 CrossRef CAS.
- J. Aronhime, S. Levi and L. Hedvati, WO/2006/108151, 2006.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2007, 64, 112–122 CrossRef PubMed.
- R. Bhushan and H. Brückner, Amino Acids, 2004, 27, 231–247 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2215531. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2ce01490d |
| This journal is © The Royal Society of Chemistry 2023 |