Structural stability, optical and thermoelectric properties of the layered RbSn₂Br₅ halide synthesized using mechanochemistry

Abstract

Two-dimensional (2D) layered metal halide perovskites have recently received a lot of attention due to their possible applications as photovoltaic and optoelectronic materials. Rubidium di-tin pentabromide, RbSn₂Br₅, is a promising lead-free alternative to its RbPb₂Br₅ counterpart. Its lack of toxic lead, improved stability, and tolerance to ambient conditions are a great step forward to be used in electronic devices. In contrast with lead-based halides, this sample has received less attention up to now. There have been no experimental studies on its transport parameters such as electronic conductivity, Seebeck coefficient, or thermal transport. Here, we describe how this material can be easily synthesized using a ball milling procedure, obtaining specimens with high crystallinity. TG measurements indicate total decomposition above ∼673 K, whereas DSC curves suggest melting and recrystallization at 562 K (heating run, endothermic) and 523 K (cooling run, exothermic), respectively. A structural analysis from room temperature up to 548 K from neutron powder diffraction (NPD) data allowed the determination of the Debye model parameters, providing information on the relative Rb–Br and Sn–Br chemical bonds. Synchrotron X-ray diffraction experiments confirmed a tetragonal structure (space group I4/mcm) and provided evidence on the presence of the Sn²⁺ lone electron pair (5s²) from a X–N study. Diffuse reflectance UV-vis spectroscopy yields an indirect optical gap of ∼3.08 eV, coincident with the literature and ab initio calculations. A maximum positive Seebeck coefficient of ∼2.3 × 10⁴ μV K⁻¹ is obtained at 440 K, which is one order of magnitude higher than those reported for other halide perovskites. We obtain an ultra-low thermal conductivity, below 0.2 W m⁻¹ K⁻¹ from 300 up to 550 K.

---

1. Introduction

Hybrid halide organic–inorganic perovskites have gained important popularity in the past years due to their promising potential for photovoltaic applications, reaching over 22% of power conversion efficiency.¹ All-inorganic perovskite derivatives are also excellent materials for solar cell applications, because of their interesting optical properties (i.e. bandgap tuning and quantum efficiency). With a bandgap of 1.73 eV,² cubic CsPbI₃ is a great candidate; moreover, it has a high fluorescence quantum yield and a better tolerance to degradation when exposed to ambient atmosphere and humidity. However, there is a major drawback, which prevents its commercialization: the stabilization of the cubic α-CsPbI₃ phase at room temperature (RT) is still a challenge, since the cubic phase undergoes transitions to an undesirable orthorhombic (δ) polymorph.³

By the replacement, complete or partial, of I with Br, it is possible to reach a more stable state; this is the case of the orthorhombic CsPbBr₃ perovskite.^4–12 These chemical modifications lead to a change in the opto-electronic properties, such as high and constant photo-response, and an improved stability under ambient conditions. Unfortunately, the replacement of the I atoms increases the bandgap of the CsPbBr₃ perovskite, up to a value of 2.3 eV. Although it can still be applied in a variety of optoelectrical systems,¹³ the relatively large bandgap would prevent its use in solar cell devices.

Recently, various techniques for achieving greater photoefficiencies in these halide perovskites have been explored, including structural ordering and various topologies for the octahedral arrangements; this is the case of CsPb₂Br₅,^10,13–16 belonging to the APb₂X₅ family where A = K, Rb, Cs and X = Cl, Br. Instead of the classical 3D network of corner-sharing [PbBr₆] units, CsPb₂Br₅ has a 2D dimensionality with an interesting layered structure.^10,17,18 RbPb₂Br₅ is also part of this family of layered lead-containing halides; this specimen has been found to be a promising low-phonon energy material for tunable middle-and long-wavelength infrared laser sources for applications such as remote sensing.^19,20 However, the presence of toxic Pb is a major drawback and a huge restriction for its final application and commercialization.

Consequently, great efforts have been addressed to the development of Pb-free alternatives. It is the case of rubidium di-tin pentabromide, RbSn₂Br₅, belonging to the 2D layered tin-containing halide family. Although the optical and dielectric properties were estimated recently,²¹ no extensive research on its crystallographic structure and transport properties has been reported yet, such as the electronic conductivity, Seebeck coefficient or thermal transport. Moreover, it turns out that many layered materials present interesting properties for thermoelectric applications.^22–25 High thermoelectric performances can be achieved depending on the plane direction thanks to their layered nature.^26,27 This fact has become evident in compounds like NaCo₂O₄,²⁸ Bi₂Te₃,²⁹ CaSi₂, or even in the recently rediscovered SnSe, which reaches a thermoelectric figure of merit (ZT = S²σT/κ) of ∼2.8 due to the ultra-low thermal conductivity of ∼0.2 W m⁻¹ K⁻¹ measured in the out-of-plane direction.³⁰ The thermoelectric figure of merit involves the Seebeck coefficient (S), the electrical conductivity (σ), the thermal conductivity (κ) and the absolute temperature (T), and offers a way to characterize the thermoelectric performance of a certain material at a given temperature.³¹ All-inorganic halide perovskites in their polycrystalline bulk form, such as the CsSnBr_3−xI_x, were recently proposed by H. Xie et al. as potential thermoelectric materials.³² Although the figure of merit of this series barely reaches ∼0.15, their extremely low thermal conductivity (0.32 W m⁻¹ K⁻¹ for the CsSnBrI₂) makes them promising candidates for future thermoelectric applications.³³ As paradigmatic examples of extremely low thermal conductivity in these polycrystalline halide perovskites, we can highlight the 0.3–0.5 W m⁻¹ K⁻¹ reported for the MAPI (CH₃NH₃PbI₃) perovskite,³⁴ the 0.43 and 0.33 W m⁻¹ K⁻¹ for CsPbBr₃ and CsPb₂Br₅ respectively,³⁵ and the 0.74 W m⁻¹ K⁻¹ reported for the CsSnI₃ compound.³⁶

Here, we have managed to synthesize a well-crystallized powder of RbSn₂Br₅ by a solvent-free mechano-chemical method using a planetary ball-mill. A neutron powder diffraction (NPD) experiment was carried out to accurately study the crystallographic structure in a broad temperature range (295–550 K), complemented with synchrotron X-ray diffraction (SXRD) data at 100 K and 295 K. This specimen presents a tetragonal symmetry described by the I4/mcm (#140)³⁷ space group, and no phase transitions have been observed below the melting point. A study of the thermal evolution of the atomic mean square displacement factors was carried out, from which we were able to describe the Debye temperatures and to estimate the bonding stiffness in RbSn₂Br₅. An optical gap of 3.08 eV is determined from UV-vis spectra that was corroborated by ab initio calculations (indirect bandgap of 2.9 eV). The characterization of this ball-milled specimen is complemented with DSC measurements and transport properties, revealing a huge Seebeck coefficient of ∼2 × 10⁴ μV K⁻¹ at 400 K.

2. Experimental methods

Mechano-chemical synthesis

RbSn₂Br₅ was synthesized in polycrystalline powder form by mechano-chemical synthesis using a planetary ball mill from stoichiometric amounts of SnBr₂ and RbBr. The total mass of reactants was 1 g, which were weighed and mixed with 20 zirconia balls (5 mm diameter) in a N₂-filled glove box. The reaction took place in a Retsch PM100 mill for 3 h at 450 rpm, in a sealed zirconia-lined jar with N₂ atmosphere.

Structural characterization and analysis

A Bruker D5 diffractometer with Cu-K_α (λ = 1.5418 Å) radiation was used to collect a laboratory XRD pattern at room temperature. The thermal evolution of the crystallographic structure was studied by neutron powder diffraction (NPD) in D2B, a high-resolution two-axis diffractometer at the Institut Laue-Langevin in Grenoble, France. The NPD patterns were collected at room temperature (295 K) and above (403, 473, 513 and 548 K) with a wavelength of λ = 1.594 Å. The sample was contained in a cylindrical vanadium holder of 6–8 mm diameter coupled to a vanadium furnace working under vacuum. SXRD experiments were conducted at the 11-BM beamline in APS, at the Argonne National Laboratory, Illinois, USA. The SXRD patterns were collected at room temperature (295 K) and at 100 K with a wavelength of λ = 0.45894 Å. The SXRD and NPD data were analysed with the Rietveld method using the FullProf program.^38,39 The refined parameters were the following: zero-point error, background coefficients, scale factor, asymmetry factors, lattice parameters (a, c), atomic fractional coordinates (x, y, z), and isotropic thermal displacements (u_iso).

Thermal and morphological characterizations

Differential scanning calorimetry (DSC) measurements were carried out in the range 130 K up to 520 K in a Mettler TA3000 system equipped with a DSC30 unit. The heating and cooling rates were 10 K min⁻¹, using about 70 mg of sample in each run. The specific heat was recorded in the PPMS with an adiabatic heat pulse method, starting from pressed pellets cut with a diamond saw to fit into the sample-holder dimension. The c_p curve is shown and discussed in the ESI.†

Field-effect Scanning Electron Microscopy (FE-SEM) images were obtained using an FEI Nova microscope, with an acceleration potential of 5 kV, coupled to an energy-dispersive X-ray spectrometer (EDX), working with an accelerating voltage of 18 kV and 60 s of acquisition time. A UV-vis spectrophotometer Varian Cary 5000 was employed to measure the optical diffuse reflectance spectrum at room temperature.

Thermoelectric characterization

The resulting powder was cold pressed into a pellet using an 8 mm die to perform transport measurements. The achieved density was around 93% of the theoretical crystallographic density, calculated geometrically. The Seebeck coefficient was derived by measuring simultaneously drop voltages across the sample and a constantan reference wire with an electrometer (Keithley 6517B) and nanovoltmeter (Keithley 2182A) under vacuum (10⁻³ mbar). The electrical resistivity was measured in an Agilent E4980A LCR meter. The total thermal conductivity was obtained by the laser-flash technique, calculated from the thermal diffusivity (α) in a Linseis LFA 1000 equipment. The thermal conductivity (κ) was determined using κ = α × c_p × d, where c_p is the specific heat and d is the sample density.

3. Computational methods

Theoretical models based on density functional theory were built in order to assist the understanding of the electronic transitions and the chemical environment. The models were created using the CRYSTAL17 package⁴⁰ with the HSE06 functional.⁴¹ The atomic bases of all atoms used in the calculations were the Triple-Zeta valence with the polarization Gaussian basis (POB-TZVP) sets developed by Laun et al.⁴² The Coulomb and exchange series thresholds are controlled according to five parameters (overlap and penetration for Coulomb integrals, the overlap for HF exchange integrals, and the pseudo-overlap), which were set as 8, 8, 8, 8, and 16, respectively. The shirking factors (Pack–Monkhorst and Gilat net) were 6 and 6, respectively. The gradient component and the nuclear displacement of the structure optimization were set with a tolerance on their root-mean-square of 0.0003 and 0.0012 a.u., respectively. The topological analysis of the critical points of the chemical bonds was performed according to the “quantum theory: atoms in molecules” (QTAIM) with the TOPOND program, which is part of the CRYSTAL17 package.

4. Results and discussion

Initial characterization

RbSn₂Br₅ was stabilized as a pale-cream polycrystalline powder. An initial identification of the sample was carried out on a laboratory X-ray diffractometer at room temperature (RT) confirming the presence of RbSn₂Br₅, as described below.

Fig. 1a shows the thermogravimetric curve, exhibiting the beginning of the sample decomposition above ∼523 K by weight loss due to Br elimination. The inset illustrates one cycle of a DSC curve, with their respective cooling and heating runs. Fig. 1b displays an amplified area of the DSC graph, highlighting a reversible peak with non-negligible hysteresis at 562 K (heating run, endothermic) and 523 K (cooling run, exothermic), probably related to the melting and recrystallization of the sample, respectively.

Fig. 1 a) Thermogravimetric curve, showing weight loss upon decomposition of the sample above 523 K. Inset: First and second cycle of DSC curves. b) Enlarged area of the DSC curve showing a reversible peak at 562 K (endothermic in the heating run) and 523 K (exothermic in the cooling run).

Fig. S2a–d (ESI†) illustrate some representative micrographs from FE-SEM images, giving insight into the microstructure of this product as-synthesized by ball milling. An overall view with low magnification (7000×) revealed irregular-shaped clusters of particles of different sizes (Fig. S2a†). Some other micrographs depicted regular edges and faces (Fig. S2b† at 25.000×). However, large magnification views (Fig. S2c and d† up to 86.610×) unveil that they are indeed formed by tiny nano-particles of uneven form, with typical size about 50 nm, which are grown during the ball milling process.

EDX analysis coupled to the FE-SEM images confirmed the homogeneity of the composition across the particles, and the analysis yields an atomic composition close to 1 : 2 : 5 for the Rb : Sn : Br ratio. A typical EDX spectrum is included in Fig. S2 in the ESI.†

Crystal structure analysis

As mentioned above, the sample structural characterization was carried out on a laboratory X-ray diffractometer at room temperature (RT). In agreement with previous studies, the RbSn₂Br₅ sample presented a tetragonal unit-cell indexable within the I4/mcm space group (#140), belonging to the (NH₄)Pb₂Br₅ structural type.⁴³ A preliminary Rietveld refinement was carried out from XRD data, with unit-cell parameters a = 8.4260(13) Å and c = 14.717(3) Å. Fig. 2a displays the Rietveld refinement fit.

Fig. 2 Observed (red crosses), calculated (full black line), difference (blue line), Bragg position (green vertical bars) Rietveld profiles for RbSn₂Br₅ at room temperature as extracted from a) XRD and b) NPD data.

The crystal structure evolution was investigated from neutron powder diffraction data. Diffraction patterns were collected as a function of temperature (300–548 K) in the D2B diffractometer at the ILL, Grenoble. As mentioned, the sample presents a tetragonal symmetry defined in the I4/mcm space group. Within this model, Rb⁺ and Sn²⁺ ions are located at 4a (0,0,1/4) and 8h (x, x + 0.5,0) Wyckoff sites, respectively. The two types of bromine, Br1 and Br2, are located at 4c (0,0,0) and at 16l (x,y,z) positions. The refined unit-cell parameters at RT are a = 8.4328(10) Å, c = 14.735(2) Å, and V = 1047.9(2) ų, which resemble those reported: a = 8.4339(1) Å, c = 14.7502(2) Å, and V = 1049.19 ų.³⁰ The corresponding Rietveld refinement at RT is presented in Fig. 2b. Table 1 displays the main crystallographic parameters at RT.

Table 1 Crystallographic parameters for the RbSn₂Br₅ phase in the tetragonal system (I4/mcm) from NPD data at RT. a = 8.4328(10) Å, c = 14.735(2) Å and V = 1047.9(2) ų

	x	y	z	U iso	f occ
R p = 1.80%, Rwp = 2.30%, χ^2 = 1.54, RBragg = 6.94%
Rb	0	0	0.25	0.033(3)	1
Sn	0.1763(6)	0.6763(6)	0	0.051(3)	1
Br1	0	0	0	0.040(5)	1
Br2	0.1625(3)	0.6625(3)	0.37000	0.0338(18)	1
Anisotropic atomic displacement parameters (Å^2)
	U ^11	U ^22		U ^33
Sn	0.051(3)	0.051(3)		0.051(3)
Br1	0.033(3)	0.033(3)		0.054(7)
Br2	0.0358(14)	0.0358(14)		0.030(2)

---

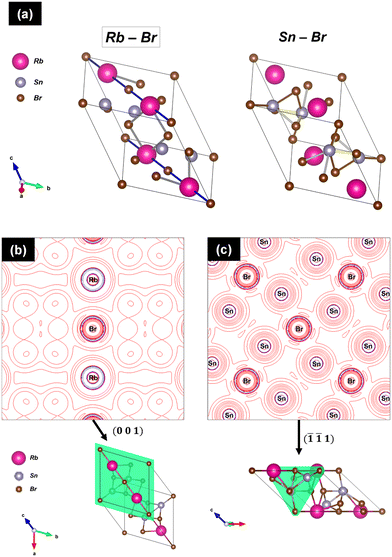
Fig. 3 displays three views of the crystal structure of RbSn₂Br₅ at room temperature. The structure consists of layers of [SnBr₈] polyhedra sharing edges and triangular faces, connected by Rb⁺ ions. The greatly distorted Sn–Br polyhedra contain four short bond-lengths of Sn–Br1 = 3.108(4) Å and Sn–Br2 = 2.713(3) Å, forming a square pyramid with Sn in the apex (Fig. 3b), and four additional Br2 at superior distances of Sn–Br2 = 3.442(5) Å, completing the polyhedra. This asymmetrical configuration is probably driven by the stereochemical effect of the 5s² lone electron pair of Sn²⁺. The distance between Sn atoms is 4.396(8) Å. Rb⁺ ions are coordinated with bromine anions as Rb–Br1 = 3.6837(6) Å (×2) and Rb–Br2 = 3.620(3) Å (×10). The bond valence^44,45 of Rb is fully satisfied in this compound, with a calculated value of v_Rb = 1.001(1), whereas Sn atoms are slightly underbonded, with v_Sn = 1.864(9), at RT.

Fig. 3 Views of the layered crystal structure of RbSn₂Br₅; a) the SnBr₈ polyhedra constitute layers within the ab plane that alternate with Rb atoms; b) the four short Sn–Br bonds conform square pyramids, driven by the 5s² lone pair repulsion; c) SnBr₈ units share edges and faces within the layers.

No major structural changes were observed above room temperature. Fig. 4 shows the unit-cell parameters and volume evolution with temperature, exhibiting the expected positive thermal expansion behaviour. Even the last NPD diagram, collected at 548 K, just below the thermal event identified in the DSC curves at 562 K (Fig. 1b) and assigned to the sample melting, can be properly refined in the same structural type, with no symptoms of phase transition, decomposition or deviation of the main structural parameters.

Fig. 4 Plots of the evolution of the lattice constants a, c and, V of RbSn₂Br₅ with temperature as obtained from neutron powder diffraction data. The error bars are smaller than the size of the symbols.

The crystal structure analysis at RT (295 K) and at low temperature (100 K) was completed from SXRD data. Both high-resolution patterns were properly fitted in the described tetragonal structure (I4/mcm space group), thus confirming the previous NPD results. The high resolution of synchrotron data allowed the identification of a minor amount of Rb₂SnBr₆. This phase was included in the refinements and its amount was less than 2% w/w. Fig. S3† shows the fitted patterns and Tables S1 and S2† list the crystallographic parameters. These results reveal the high stability of the tetragonal phase over a wide temperature range of at least 448 K (from 100 to 548 K). Moreover, the importance of having both synchrotron and neutron diffraction data resides in the possibility of analysing jointly the electronic and nuclear density of the crystal structure. This is particularly interesting in the RbSn₂Br₅ halide, because it allows searching density deviations due to the lone pair effect in Sn²⁺. To accomplish this, the so-called X–N method was used. Thus, the positions of the nuclei determined from neutron data are utilized to perform difference Fourier syntheses from SXRD data, which contain information on the electron distribution in the crystal. Then, difference Fourier maps were drawn and asymmetric densities were searched around Sn²⁺ cations. Fig. 5 displays the difference electron density obtained over the (001) plane, where an appreciable density is observed close to Sn²⁺ ions and opposite of Sn–Br bonds. The position and intensity of these densities allow the confirmation of the stereochemical effect of the 5s² lone electron pair of Sn²⁺ on the distribution of the chemical bonds. Thus, the Sn²⁺ lone electron pairs tend to occupy the empty space of the crystal structure and are responsible for the distorted coordination polyhedra of these cations, in pseudo-square pyramids, as shown in Fig. 3 and 5.

Fig. 5 Electron density obtained from the X–N procedure along the (001) plane overlaid with the SnBr₄ polyhedral structure.

Mean-square displacements

The temperature-dependence of the mean-square displacements (MSDs) of the atomic species Rb, Sn, and Br within the system RbSn₂Br₅ was analysed by the Debye model.^46–48 This model employs the isotropic displacement parameters (U_eq, in units of Ų) as derived from the neutron powder diffraction at 300–548 K, as follows:where m is the atomic mass, k_B the Boltzmann constant, ℏ the reduced Planck constant, and T the absolute temperature. Both the Debye temperature (θ_D) and quadratic static displacement (d²_S) are the parameters to be obtained after the non-linear regression. The precise evaluation of the static displacements is strongly dependent on the low-temperature data, being not the case of this work; therefore, such a parameter was kept equal to zero and only room to high-temperature range were used in eqn (1).

Fig. 6 represents the temperature-dependence of the MSDs for Rb, Sn, and Br with their respective best fittings to the Debye equation. The present crystal structure has two bromide atoms at two non-equivalent sites (Br1 and Br2); therefore, they were independently evaluated. The Debye temperatures were calculated, namely: Rb (104.4 K), Sn (91.9 K), Br1 (131.9 K), and Br2 (121.6 K). Since tin is heavier than rubidium, its Debye temperature is smaller than that of Rb. The Debye temperature of RbSn₂Br₅ was estimated by averaging the individual temperature values for each site, considering the site multiplicity and atomic masses. It leads to an average Debye temperature of 110.9 K, which is a value ranging within that already reported for Rb- and Br-based halides.^49,50 The bonding stiffness evaluation for Rb–Br and Sn–Br can be conducted by the harmonic one-particle potential model (h-OPP),^51,52 where a force constant is defined from θ_D and atomic mass:

here, K_D is the force constant in units of eV Å⁻². The as-obtained K_D values are the next ones: 0.55 eV Å⁻² for Rb, 0.59 eV Å⁻² for Sn, 0.82 eV Å⁻² for Br1, and 0.70 eV Å⁻² for Br2. It means that the potential values of Rb and Sn are quite similar to each other. Although the average bond distance Rb–Br (〈d〉 = 3.63 Å) is around 1.25 times greater than Sn–Br (〈d〉 = 2.91 Å), meaning that Rb atoms have a huge cavity with free-space to move along the Rb–[SnBr₄] beating mode, the tetrahedral coordination (T_d-fold) is an important factor to decrease the harmonic potential of the Sn–Br bond.

Fig. 6 Temperature dependence of U_eq (MSDs) for Rb, Sn, Br1, and Br2 atoms. Open symbols denote the MSD values extracted from the Rietveld refinement of NPD data. The dotted lines are the best fittings to the experimental data using the Debye equation. Standard deviations are smaller than the size of the symbols.

The critical points parameters of each kind of bond present in RbSn₂Br₅ were calculated and are listed in Table 2. The different bonds are highlighted in Fig. 7a, where Rb–Br1 and Rb–Br2 are the blue and grey bonds, respectively, in the unit-cell on the left; Sn–Br1, Sn–Br2, and Sn–Br3 are yellow, brown and light grey bonds, respectively, in the unit-cell representation on the right. One may notice that the electron density is more localized along the Sn–Br pair-bond than that along Rb–Br, which agrees with the Debye analysis performed using the MSD data.

Table 2 Critical points parameters from topological analysis of RbSn₂Br₅: bond length, electron density (ρ), Laplacian of electron density (∇²ρ), virial field density (v), Lagrangian kinetic energy density (G), and the total energy (H) of the bonds

Bond	Length (Å)	ρ (×10^−3)	∇ ^2 ρ (×10^−2)	G (×10^−3)	v (×10^−3)	H (×10^−3)	|v|/G
Rb–Br1	3.5905	7.47	2.55	5.15	−3.91	1.24	0.76
Rb–Br2	3.7676	5.21	1.93	3.76	−2.68	1.08	0.71
Sn–Br1	2.7636	45.2	7.73	27.1	−34.9	−7.79	1.29
Sn–Br2	2.9827	28.2	5.54	15.5	−17.2	−1.67	1.11
Sn–Br3	3.1687	21.2	4.28	10.9	−11.1	−0.18	1.02

---

Fig. 7 (a) Rb–Br and Sn–Br pair-bonds within the RbSn₂Br₅ unit-cell. ∇²ρ isolines of the (b) (001) plane with the Rb–Br bonds and (c) (−1−11) plane with the Sn–Br bonds. Those planes were chosen so as to provide a better visualization of the topochemical isolines.

The topological parameters listed in Table 2 were used to estimate the types of bonds present in the structure. All the bonds exhibit small values of ρ with positive values of ∇²ρ, which suggests that the bonds have a predominant ionic character.^53,54 However, there are relevant differences between the two types of bonds (Rb–Br and Sn–Br): the H parameters have opposite magnitudes, with positive values for Rb–Br bonds and negative for the Sn–Br bonds. In the same way, the |v|/G parameters are lower than 1 for the Rb–Br bonds and greater than 1 and less than 2 for the Sn–Br bonds. The behavior of the Rb–Br critical points still indicates values directly related to ionic-type bonds. On the other hand, the different tendencies for the critical-point parameters found in the Sn–Br bonds suggest a transient behaviour, meaning that a certain covalent character cannot be neglected. These theoretical observations are in agreement with experimental estimations made from the Debye analysis. The ∇²ρ isolines with the highlighted selected planes containing the Rb–Br and Sn–Br bonds of the unit-cell are represented in Fig. 7b and c. In addition to the evaluation of the critical point described above, it is possible to see the isolated isolines at the Rb sites (Fig. 7b) as resulting from its predominant ionic character. In Fig. 7c, the Sn presents shared isolines with the Br sites.

Thermoelectric properties

As we mentioned before, there is still not much information about the transport properties of this halide. It is enlightening to compare it with other similar compounds such as RbPb₂Br₅, also prepared by ball-milling⁵⁵Fig. 8 shows the transport thermoelectric properties measured near RT, 8a exhibits the resistivity, 8b the Seebeck coefficient and 9c the power factor. The resistivity continually diminishes from 2.5 × 10⁶ Ω m at 320 K, down to 8 × 10² Ω m at 560 K, a decrease which is very similar to that shown by the RbPb₂Br₅ halide, and we conclude that it is caused by the thermal activation of the minority carriers. The activation energy of these carriers is calculated from the electrical conductivity, yielding a result of approximately 451 meV (Fig. S4 and S5†). Although the resistivity is reduced by several orders of magnitude as the temperature increases, it is still too high to be competitive with other thermoelectric materials, including some halide perovskites.⁵⁶ However, this resistivity is close to the ∼3.3 × 10⁶ Ω m reported for undoped MAPbBr₃ single crystals.⁵⁷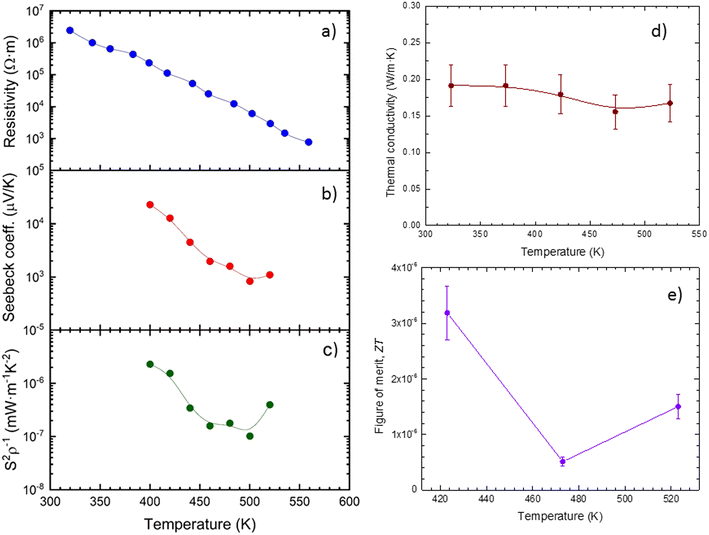

Fig. 8 a) Electrical resistivity, b) Seebeck coefficient, c) power factor, d) thermal conductivity (κ) and e) thermoelectric figure of merit (ZT) of RbSn₂Br₅.

Regarding the Seebeck coefficient, the RbSn₂Br₅ halide shows a Seebeck coefficient of ∼2.3 × 10⁴ μV K⁻¹ at 440 K, which is quite similar (in absolute value) to that reported for the ball milled RbPb₂Br₅ (−1.3 × 10⁴ μV K⁻¹ at 440 K). However, unlike for RbPb₂Br₅, the Seebeck coefficient is always positive from 400 K up to 520 K, indicating a p-type conductivity, and lying between ∼2 × 10⁴ μV K⁻¹ and ∼10³ μV K⁻¹ for all the measured temperature range.

We can notice that the maximum value is about two orders of magnitude higher than the Seebeck coefficients reported for other halide perovskites like CsSnBr₃, and hybrid perovskites like MAPbBr₃,^56,57 probably due to a lower carrier density. Despite this huge Seebeck coefficient, and as happens in RbPb₂Br₅, the power factor remains between 3 × 10⁻⁶ and 10⁻⁷ mW m⁻¹ K⁻¹ due to the high resistivity (see Fig. 8c). These are very low values if compared with other layered materials known for their thermoelectric applications, such as Bi₂Te₃, CaSi₂ or SnSe, which can reach a power factor of ∼400 mW m⁻¹ K⁻¹.^29,58,59

As Fig. 8d illustrates, the thermal conductivity κ is lower than that reported for other halide and hybrid perovskites;^56,57 it always remains between 0.20 and 0.15 W m⁻¹ K⁻¹ at all the measured temperatures, from 323 K up to 523 K; this thermal conductivity is even lower than that reported for RbPb₂Br₅, ∼0.25 W m⁻¹ K⁻¹ at room temperature, and is similar to that shown even by organic materials like Teflon.⁶⁰ Moreover, this thermal conductivity is lower than that, already low, of, for instance, GeH⁶¹ and most of the SnSe specimens, of which only the SnSe thin films can achieve a thermal conductivity lower than 0.2 W m⁻¹ K⁻¹.⁶² Those values derive from the low Debye temperatures for Rb, Sn, and Br, as we will detail next.

As we stated before, the Sn²⁺ lone electron pairs are driving the distortion of the coordination polyhedra of these cations, as shown in Fig. 4 and 6. In the mixed halide CsSnBr_3−xI_x, the distortion of the SnX₆ octahedra has been proven to produce a highly dynamic and disordered structure in this compound,³² which gives rise to a very low Debye temperature (between 103 and 107 K) and phonon velocity. The Debye temperature that we have calculated from our experimental data is also very low, an average of 110.9 K, which suggests that the distortion caused by the Sn²⁺ lone electron pairs produces a similar effect in the thermal conductivity, as reported by H. Xie et al.⁵⁶ Our thermal conductivity of ∼0.2 W m⁻¹ K⁻¹ measured in RbSn₂Br₅ is even lower than that reported by H. Xie et al. for the CsSnBr_3−xI_x series, where values as low as 0.32 W m⁻¹ K⁻¹ are achieved.

This ultra-low thermal conductivity^56,63 can be considered as a major finding regarding the thermoelectric properties of RbSn₂Br₅, making possible the future improvement of this compound for practical thermoelectric applications.

All these magnitudes are combined in a ZT figure of merit, Fig. 8e, defined as ZT = S²σT/κ. Despite this ultra-low thermal conductivity, the power factor limits the resulting figure of merit, which yields ZT = 1.5 × 10⁻⁶ at 523 K. Although it is very low compared with state-of-the-art thermoelectric materials, it is comparable to other reported values for halide perovskites, like Bi-doped MAPbBr₃, which shows a ZT of 1.8 × 10⁻⁶ at 293 K,⁵⁷ or RbPb₂Br₅, showing a ZT of ∼10⁻⁶ at 573 K.

Optical gap by UV-vis spectra

By performing diffuse reflectance UV/vis spectroscopy, it is possible to study the absorption capacity of RbSn₂Br₅. Fig. 9 shows the optical absorption coefficient related to the Kubelka–Munk function versus wavelength in units of electron-volts. The bandgap has been calculated by extrapolating the linear region to the abscissa, obtaining a value of 3.08 eV; this value is in agreement with that reported in the literature of 3.2 eV.²¹ The nature of this bandgap was evaluated by DFT methods, as shown in Fig. 9a. Such a density of states for RbSn₂Br₅ has both the top of the valence band (VB) and the bottom of the conduction band (CB) composed mainly of Br and Sn orbitals. However, in the VB the density of Br states stands out concerning the Sn states and, in the CB, the inverse is observed. The theoretical bandgap from this structural model was 2.9 eV with an indirect characteristic.

Fig. 9 a) Kubelka−Munk (KM) transformed diffuse reflectance spectrum of RbSn₂Br₅. b) Density of states projection of the RbSn₂Br₅ as calculated from DFT methods.

Conclusions

By a mechano-chemical method using a ball mill, RbSn₂Br₅ has been successfully synthesized in a well-crystallized powder form. The crystal structure evolution has been studied and followed from SXRD and NPD data, presenting a I4/mcm tetragonal phase with no phase transitions in the 100–548 K range. The Sn coordination polyhedron contains four relatively short distances in a distorted square pyramid with Sn at the top; this is completed with four much longer Sr–Br bond lengths in distorted [SrBr₈] polyhedra; this configuration is driven by the stereochemical effect of the 5s² lone electron pair of Sn²⁺ ions, as it was confirmed from X–N analysis using both NPD and SXRD data. By combining the thermal evolution of the atomic mean square displacements and the Debye model, it was possible to determine the Debye temperatures of the atoms in the system, the relative stiffness of the Rb–Br vs. Sn–Br chemical bonds, following the harmonic one-particle potential OPP model. It was determined that the bonding nature of the Rb–Br and Sn–Br bonds is similar but, since the bonding distances differ, the Rb atoms present a larger space to move along. The thermoelectric properties are appealing, regarding a large Seebeck coefficient and an ultra-low thermal conductivity below 0.2 W m⁻¹ K⁻¹, although the large electrical resistivity leads to a negligible figure of merit. An indirect optical band gap of 3.08 eV was measured from the UV-vis spectrum, comparable to the values determined by DFT methods and those reported in the literature.

Author contributions

Conceptualization, C. A., J. L. M., M. T. F. D. and J. A. A.; methodology, J. E. R., J. G., N. M. N., O. J. D., J. L. M., M. T. F. D. and J. A. A.; formal analysis, C. A., C. A. L., J. E. R., B. F., M. M. F., and J. G.; resources, J. L. M. and J. A. A.; writing—original draft preparation, C. A., C. A. L., J. E. R., J. A. A., and J. G.; funding acquisition, J. L. M. and J. A. A. All authors have read and agreed to the published version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank funding from the Spanish Ministry for Science and Innovation (MCIN/AEI/10.13039/501100011033) with grant numbers PID2021-122477OB-I00 and TED2021-129254B-C22. CA thanks financial support from the Institut Laue-Langevin through the DA/SRH/GRI/AS/19-214 contract. J. G. thanks MICINN for granting the contract PRE2018-083398. M. M. F. acknowledges the financial support from the Brazilian agency FAPERGS. The authors wish to express their gratitude to ILL for making all facilities available for the neutron diffraction experiments. We thank Dr. Silvina Pagola for collecting the SXRD data at APS (Argonne National Laboratory, USA).

References

1. W. S. Yang, B.-W. Park, E. H. Jung, N. J. Jeon, Y. C. Kim, D. U. Lee, S. S. Shin, J. Seo, E. K. Kim, J. H. Noh and S. I. Seok, Iodide Management in Formamidinium-Lead-Halide–Based Perovskite Layers for Efficient Solar Cells, Science, 2017, 356(6345), 1376–1379,  DOI:10.1126/science.aan2301.
2. D. B. Straus, S. Guo and R. J. Cava, Kinetically Stable Single Crystals of Perovskite-Phase CsPbI ₃, J. Am. Chem. Soc., 2019, 141(29), 11435–11439,  DOI:10.1021/jacs.9b06055.
3. Z. Chen, L. Dong, H. Tang, Y. Yu, L. Ye and J. Zang, Direct Synthesis of Cubic Phase CsPbI ₃ Nanowires, CrystEngComm, 2019, 21(9), 1389–1396,  10.1039/C8CE02111B.
4. J. Peng, C. Q. Xia, Y. Xu, R. Li, L. Cui, J. K. Clegg, L. M. Herz, M. B. Johnston and Q. Lin, Crystallization of CsPbBr3 Single Crystals in Water for X-Ray Detection, Nat. Commun., 2021, 12(1), 1531,  DOI:10.1038/s41467-021-21805-0.
5. F. Li, S. Huang, X. Liu, Z. Bai, Z. Wang, H. Xie, X. Bai and H. Zhong, Highly Stable and Spectrally Tunable Gamma Phase Rb_x Cs_1−x PbI ₃ Gradient-Alloyed Quantum Dots in PMMA Matrix through A Sites Engineering, Adv. Funct. Mater., 2021, 31(11), 2008211,  DOI:10.1002/adfm.202008211.
6. L. Peng, A. Dutta, R. Xie, W. Yang and N. Pradhan, Dot–Wire–Platelet–Cube: Step Growth and Structural Transformations in CsPbBr ₃ Perovskite Nanocrystals, ACS Energy Lett., 2018, 3(8), 2014–2020,  DOI:10.1021/acsenergylett.8b01037.
7. B. J. Bohn, Y. Tong, M. Gramlich, M. L. Lai, M. Döblinger, K. Wang, R. L. Z. Hoye, P. Müller-Buschbaum, S. D. Stranks, A. S. Urban, L. Polavarapu and J. Feldmann, Boosting Tunable Blue Luminescence of Halide Perovskite Nanoplatelets through Postsynthetic Surface Trap Repair, Nano Lett., 2018, 18(8), 5231–5238,  DOI:10.1021/acs.nanolett.8b02190.
8. Y. Gao, L. Zhao, Q. Shang, Y. Zhong, Z. Liu, J. Chen, Z. Zhang, J. Shi, W. Du, Y. Zhang, S. Chen, P. Gao, X. Liu, X. Wang and Q. Zhang, Ultrathin CsPbX ₃ Nanowire Arrays with Strong Emission Anisotropy, Adv. Mater., 2018, 30(31), 1801805,  DOI:10.1002/adma.201801805.
9. J. Song, J. Li, L. Xu, J. Li, F. Zhang, B. Han, Q. Shan and H. Zeng, Room-Temperature Triple-Ligand Surface Engineering Synergistically Boosts Ink Stability, Recombination Dynamics, and Charge Injection toward EQE-11.6% Perovskite QLEDs, Adv. Mater., 2018, 30(30), 1800764,  DOI:10.1002/adma.201800764.
10. J. Duan, Y. Zhao, X. Yang, Y. Wang, B. He and Q. Tang, Lanthanide Ions Doped CsPbBr ₃ Halides for HTM-Free 10.14%-Efficiency Inorganic Perovskite Solar Cell with an Ultrahigh Open-Circuit Voltage of 1.594 V, Adv. Energy Mater., 2018, 8(31), 1802346,  DOI:10.1002/aenm.201802346.
11. Y. He, L. Matei, H. J. Jung, K. M. McCall, M. Chen, C. C. Stoumpos, Z. Liu, J. A. Peters, D. Y. Chung, B. W. Wessels, M. R. Wasielewski, V. P. Dravid, A. Burger and M. G. Kanatzidis, High Spectral Resolution of Gamma-Rays at Room Temperature by Perovskite CsPbBr3 Single Crystals, Nat. Commun., 2018, 9(1), 1609,  DOI:10.1038/s41467-018-04073-3.
12. C. A. López, M. C. Alvarez-Galván, M. V. Martínez-Huerta, F. Fauth and J. A. Alonso, Crystal Structure Features of CH₃ NH₃ PbI_3−x Br_x Hybrid Perovskites Prepared by Ball Milling: A Route to More Stable Materials, CrystEngComm, 2020, 22(4), 767–775,  10.1039/C9CE01461F.
13. P. Acharyya, K. Kundu and K. Biswas, 2D Layered All-Inorganic Halide Perovskites: Recent Trends in Their Structure, Synthesis and Properties, Nanoscale, 2020, 12(41), 21094–21117,  10.1039/D0NR06138G.
14. H. Wang, H. Liu, W. Li, L. Zhu and H. Chen, Inorganic Perovskite Solar Cells Based on Carbon Electrodes, Nano Energy, 2020, 77, 105160,  DOI:10.1016/j.nanoen.2020.105160.
15. Y. Wang, M. I. Dar, L. K. Ono, T. Zhang, M. Kan, Y. Li, L. Zhang, X. Wang, Y. Yang, X. Gao, Y. Qi, M. Grätzel and Y. Zhao, Thermodynamically Stabilized β-CsPbI ₃-Based Perovskite Solar Cells with Efficiencies >18%, Science, 2019, 365(6453), 591–595,  DOI:10.1126/science.aav8680.
16. Y.-Q. Zhou, J. Xu, J.-B. Liu and B.-X. Liu, Green Emission Induced by Intrinsic Defects in All-Inorganic Perovskite CsPb ₂ Br ₅, J. Phys. Chem. Lett., 2019, 10(20), 6118–6123,  DOI:10.1021/acs.jpclett.9b02367.
17. X. Tang, S. Han, Z. Zu, W. Hu, D. Zhou, J. Du, Z. Hu, S. Li and Z. Zang, All-Inorganic Perovskite CsPb2Br5 Microsheets for Photodetector Application, Front. Phys., 2018, 5, 69,  DOI:10.3389/fphy.2017.00069.
18. G. Tong, T. Chen, H. Li, W. Song, Y. Chang, J. Liu, L. Yu, J. Xu, Y. Qi and Y. Jiang, High Efficient Hole Extraction and Stable All-Bromide Inorganic Perovskite Solar Cells via Derivative-Phase Gradient Bandgap Architecture, Sol. RRL, 2019, 3(5), 1900030,  DOI:10.1002/solr.201900030.
19. K. Rademaker, E. Heumann, G. Huber, S. A. Payne, W. F. Krupke, L. I. Isaenko and A. Burger, Laser Activity at 118, 107, and 097??M in the Low-Phonon-Energy Hosts KPb_2Br_5 and RbPb_2Br_5 Doped with Nd^3+, Opt. Lett., 2005, 30(7), 729,  DOI:10.1364/OL.30.000729.
20. K. Rademaker, W. F. Krupke, R. H. Page, S. A. Payne, K. Petermann, G. Huber, A. P. Yelisseyev, L. I. Isaenko, U. N. Roy, A. Burger, K. C. Mandal and K. Nitsch, Optical Properties of Nd^3+− and Tb^3+-Doped KPb_2Br_5 and RbPb_2Br_5 with Low Nonradiative Decay, J. Opt. Soc. Am. B, 2004, 21(12), 2117,  DOI:10.1364/JOSAB.21.002117.
21. K. Kundu, P. Dutta, P. Acharyya and K. Biswas, Pb-Free Layered All-Inorganic Metal Halides RbSn2Br5: Mechanochemical Synthesis, Band Gap Tuning, Optical and Dielectric Properties, Mater. Res. Bull., 2021, 140, 111339,  DOI:10.1016/j.materresbull.2021.111339.
22. M. Gharsallah, F. Serrano-Sánchez, J. Bermúdez, N. M. Nemes, J. L. Martínez, F. Elhalouani and J. A. Alonso, Nanostructured Bi2Te3 Prepared by a Straightforward Arc-Melting Method, Nanoscale Res. Lett., 2016, 11(1), 142,  DOI:10.1186/s11671-016-1345-5.
23. J. Gainza, F. Serrano-Sánchez, J. E. F. S. Rodrigues, Y. Huttel, O. J. Dura, M. M. Koza, M. T. Fernández-Díaz, J. J. Meléndez, B. G. Márkus, F. Simon, J. L. Martínez, J. A. Alonso and N. M. Nemes, High-Performance n-Type SnSe Thermoelectric Polycrystal Prepared by Arc-Melting, Cell Rep. Phys. Sci., 2020, 1(12), 100263,  DOI:10.1016/j.xcrp.2020.100263.
24. J. E. F. S. Rodrigues, J. Gainza, F. Serrano-Sánchez, C. López, O. J. Dura, N. Nemes, J. L. Martinez, Y. Huttel, F. Fauth, M. T. Fernández-Diaz, N. Biškup and J. A. Alonso, Structural Features, Anisotropic Thermal Expansion, and Thermoelectric Performance in Bulk Black Phosphorus Synthesized under High Pressure, Inorg. Chem., 2020, 59(20), 14932–14943,  DOI:10.1021/acs.inorgchem.0c01573.
25. C. Zhou, Y. K. Lee, Y. Yu, S. Byun, Z.-Z. Luo, H. Lee, B. Ge, Y.-L. Lee, X. Chen, J. Y. Lee, O. Cojocaru-Mirédin, H. Chang, J. Im, S.-P. Cho, M. Wuttig, V. P. Dravid, M. G. Kanatzidis and I. Chung, Polycrystalline SnSe with a Thermoelectric Figure of Merit Greater than the Single Crystal, Nat. Mater., 2021, 20(10), 1378–1384,  DOI:10.1038/s41563-021-01064-6.
26. J. Zhang, L. Song, G. K. H. Madsen, K. F. F. Fischer, W. Zhang, X. Shi and B. B. Iversen, Designing High-Performance Layered Thermoelectric Materials through Orbital Engineering, Nat. Commun., 2016, 7(1), 10892,  DOI:10.1038/ncomms10892.
27. L.-D. Zhao, S.-H. Lo, Y. Zhang, H. Sun, G. Tan, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, Ultralow Thermal Conductivity and High Thermoelectric Figure of Merit in SnSe Crystals, Nature, 2014, 508(7496), 373–377,  DOI:10.1038/nature13184.
28. I. Terasaki, Y. Sasago and K. Uchinokura, Large Thermoelectric Power in NaCo 2 O 4 Single Crystals, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56(20), R12685–R12687,  DOI:10.1103/PhysRevB.56.R12685.
29. T. Caillat, M. Carle, P. Pierrat, H. Scherrer and S. Scherrer, Thermoelectric Properties of (BixSb1−x)2Te3 Single Crystal Solid Solutions Grown by the T.H.M. Method, J. Phys. Chem. Solids, 1992, 53(8), 1121–1129,  DOI:10.1016/0022-3697(92)90087-T.
30. C. Chang, M. Wu, D. He, Y. Pei, C.-F. Wu, X. Wu, H. Yu, F. Zhu, K. Wang, Y. Chen, L. Huang, J.-F. Li, J. He and L.-D. Zhao, 3D Charge and 2D Phonon Transports Leading to High Out-of-Plane ZT in n-Type SnSe Crystals, Science, 2018, 360(6390), 778–783,  DOI:10.1126/science.aaq1479.
31. G. J. Snyder and E. S. Toberer, Complex Thermoelectric Materials, Nat. Mater., 2008, 7(2), 105–114,  DOI:10.1038/nmat2090.
32. H. Xie, S. Hao, J. Bao, T. J. Slade, G. J. Snyder, C. Wolverton and M. G. Kanatzidis, All-Inorganic Halide Perovskites as Potential Thermoelectric Materials: Dynamic Cation off-Centering Induces Ultralow Thermal Conductivity, J. Am. Chem. Soc., 2020, 142(20), 9553–9563,  DOI:10.1021/jacs.0c03427.
33. M. A. Haque, S. Kee, D. R. Villalva, W. Ong and D. Baran, Halide Perovskites: Thermal Transport and Prospects for Thermoelectricity, Adv. Sci., 2020, 7(10), 1903389,  DOI:10.1002/advs.201903389.
34. A. Pisoni, J. Jaćimović, O. S. Barišić, M. Spina, R. Gaál, L. Forró and E. Horváth, Ultra-Low Thermal Conductivity in Organic–Inorganic Hybrid Perovskite CH ₃ NH ₃ PbI₃, J. Phys. Chem. Lett., 2014, 5(14), 2488–2492,  DOI:10.1021/jz5012109.
35. T. Haeger, M. Wilmes, R. Heiderhoff and T. Riedl, Simultaneous Mapping of Thermal Conductivity, Thermal Diffusivity, and Volumetric Heat Capacity of Halide Perovskite Thin Films: A Novel Nanoscopic Thermal Measurement Technique, J. Phys. Chem. Lett., 2019, 10(11), 3019–3023,  DOI:10.1021/acs.jpclett.9b01053.
36. A. K. Baranwal, S. Saini, Z. Wang, D. Hirotani, T. Yabuki, S. Iikubo, K. Miyazaki and S. Hayase, Interface Engineering Using Y2O3 Scaffold to Enhance the Thermoelectric Performance of CsSnI3 Thin Film, Org. Electron., 2020, 76, 105488,  DOI:10.1016/j.orgel.2019.105488.
37. O. Nazarenko, M. R. Kotyrba, M. Wörle, E. Cuervo-Reyes, S. Yakunin and M. V. Kovalenko, Luminescent and Photoconductive Layered Lead Halide Perovskite Compounds Comprising Mixtures of Cesium and Guanidinium Cations, Inorg. Chem., 2017, 56(19), 11552–11564,  DOI:10.1021/acs.inorgchem.7b01204.
38. H. M. Rietveld, A Profile Refinement Method for Nuclear and Magnetic Structures, J. Appl. Crystallogr., 1969, 2(2), 65–71,  DOI:10.1107/S0021889869006558.
39. J. Rodríguez-Carvajal, Recent Advances in Magnetic Structure Determination by Neutron Powder Diffraction, Phys. B, 1993, 192(1–2), 55–69,  DOI:10.1016/0921-4526(93)90108-I.
40. R. Dovesi, A. Erba, R. Orlando, C. M. Zicovich-Wilson, B. Civalleri, L. Maschio, M. Rérat, S. Casassa, J. Baima, S. Salustro and B. Kirtman, Quantum-mechanical Condensed Matter Simulations with CRYSTAL, WIREs Comput. Mol. Sci., 2018, 8(4), e1360,  DOI:10.1002/wcms.1360.
41. A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, Influence of the Exchange Screening Parameter on the Performance of Screened Hybrid Functionals, J. Chem. Phys., 2006, 125(22), 224106,  DOI:10.1063/1.2404663.
42. J. Laun, D. V. Oliveira and T. Bredow, Consistent Gaussian Basis Sets of Double- and Triple-Zeta Valence with Polarization Quality of the Fifth Period for Solid-State Calculations: Fifth Period for Solid-State Calculations, J. Comput. Chem., 2018, 39(19), 1285–1290,  DOI:10.1002/jcc.25195.
43. D. Becker and H. P. Beck, High Pressure Study of NH4Pb2Br5 Type Compounds. I Structural Parameters and Their Evolution under High Pressure, Z. Anorg. Allg. Chem., 2004, 630(12), 1924–1932,  DOI:10.1002/zaac.200400207.
44. I. D. Brown and D. Altermatt, Bond-Valence Parameters Obtained from a Systematic Analysis of the Inorganic Crystal Structure Database, Acta Crystallogr., Sect. B: Struct. Sci., 1985, 41(4), 244–247,  DOI:10.1107/S0108768185002063.
45. S.-Z. Hu, L.-D. Tu, Y.-Q. Huang and Z.-X. Li, Studies on the Antitumor Antimony(III) Aminopolycarboxylic Acid Chelates. Crystal Structures of M[Sb(Pdta)]·H2O (M = Na+, NH4+; Pdta = Propylenediaminetetraacetic Acid), Inorg. Chim. Acta, 1995, 232(1–2), 161–165,  DOI:10.1016/0020-1693(94)04391-8.
46. J. L. Feldman and G. K. Horton, Interpretation of Debye-Waller Factors, Phys. Rev., 1963, 132(2), 644–647,  DOI:10.1103/PhysRev.132.644.
47. J.-L. Mi, M. Christensen, E. Nishibori and B. B. Iversen, Multitemperature Crystal Structures and Physical Properties of the Partially Filled Thermoelectric Skutterudites M 0.1 Co 4 Sb 12 (M = La, Ce, Nd, Sm, Yb, and Eu), Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84(6), 064114,  DOI:10.1103/PhysRevB.84.064114.
48. J. E. F. S. Rodrigues, C. A. Escanhoela, B. Fragoso, G. Sombrio, M. M. Ferrer, C. Álvarez-Galván, M. T. Fernández-Díaz, J. A. Souza, F. F. Ferreira, C. Pecharromán and J. A. Alonso, Experimental and Theoretical Investigations on the Structural, Electronic, and Vibrational Properties of Cs ₂ AgSbCl ₆ Double Perovskite, Ind. Eng. Chem. Res., 2021, 60(51), 18918–18928,  DOI:10.1021/acs.iecr.1c02188.
49. P. G. Krishna, K. G. Subhadra, T. K. Swamy and D. B. Sirdeshmukh, Debye-Waller Factors and Debye Temperatures of Alkali Halide Mixed Crystals, Pramana - J. Phys., 1999, 52(5), 503–509,  DOI:10.1007/BF02830096.
50. A. V. Sharko and A. A. Botaki, Debye Temperature Variations in Alkali-Halide Single Crystals as a Function of Their Chemical Compositions, Sov. Phys. J., 1971, 14(6), 765–770,  DOI:10.1007/BF00822167.
51. P. Coppens, Thermal Vibrations in Crystallography by B. T. M. Willis and A. W. Pryor, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1975, 31(6), 879,  DOI:10.1107/S0567739475001969.
52. A. Nakatsuka, A. Yoshiasa, K. Fujiwara and O. Ohtaka, Variable–Temperature Single–Crystal X–Ray Diffraction Study of SrGeO₃ High–Pressure Perovskite Phase, J. Mineral. Petrol. Sci., 2018, 113(6), 280–285,  DOI:10.2465/jmps.180605.
53. C. Gatti, V. R. Saunders and C. Roetti, Crystal Field Effects on the Topological Properties of the Electron Density in Molecular Crystals: The Case of Urea, J. Chem. Phys., 1994, 101(12), 10686–10696,  DOI:10.1063/1.467882.
54. C. Gatti, Chemical Bonding in Crystals: New Directions, Z. Kristallogr., 2005, 220(5–6), 399–457,  DOI:10.1524/zkri.220.5.399.65073.
55. C. Abia, C. A. López, J. Gainza, J. E. F. S. Rodrigues, M. M. Ferrer, N. M. Nemes, O. J. Dura, J. L. Martínez, M. T. Fernández-Díaz, C. Álvarez-Galván, G. Németh, K. Kamarás, F. Fauth and J. A. Alonso, The Structural Evolution, Optical Gap, and Thermoelectric Properties of the RbPb ₂ Br ₅ Layered Halide, Prepared by Mechanochemistry, J. Mater. Chem. C, 2022, 10(17), 6857–6865,  10.1039/D2TC00653G.
56. H. Xie, S. Hao, J. Bao, T. J. Slade, G. J. Snyder, C. Wolverton and M. G. Kanatzidis, All-Inorganic Halide Perovskites as Potential Thermoelectric Materials: Dynamic Cation off-Centering Induces Ultralow Thermal Conductivity, J. Am. Chem. Soc., 2020, 142(20), 9553–9563,  DOI:10.1021/jacs.0c03427.
57. W. Tang, J. Zhang, S. Ratnasingham, F. Liscio, K. Chen, T. Liu, K. Wan, E. S. Galindez, E. Bilotti, M. Reece, M. Baxendale, S. Milita, M. A. McLachlan, L. Su and O. Fenwick, Substitutional Doping of Hybrid Organic–Inorganic Perovskite Crystals for Thermoelectrics, J. Mater. Chem. A, 2020, 8(27), 13594–13599,  10.1039/D0TA03648J.
58. T. Terada, Y. Uematsu, T. Ishibe, N. Naruse, K. Sato, T. Q. Nguyen, E. Kobayashi, H. Nakano and Y. Nakamura, Giant Enhancement of Seebeck Coefficient by Deformation of Silicene Buckled Structure in Calcium-Intercalated Layered Silicene Film, Adv. Mater. Interfaces, 2022, 9(1), 2101752,  DOI:10.1002/admi.202101752.
59. L.-D. Zhao, G. Tan, S. Hao, J. He, Y. Pei, H. Chi, H. Wang, S. Gong, H. Xu, V. P. Dravid, C. Uher, G. J. Snyder, C. Wolverton and M. G. Kanatzidis, Ultrahigh Power Factor and Thermoelectric Performance in Hole-Doped Single-Crystal SnSe, Science, 2016, 351(6269), 141–144,  DOI:10.1126/science.aad3749.
60. S. P. Andersson, O. Andersson and G. Bäckström, Thermal Conductivity of Amorphous Teflon (AF 1600) at High Pressure, Int. J. Thermophys., 1997, 18(1), 209–219,  DOI:10.1007/BF02575208.
61. Y. Uematsu, T. Terada, K. Sato, T. Ishibe and Y. Nakamura, Low Thermal Conductivity in Single Crystalline Epitaxial Germanane Films, Appl. Phys. Express, 2020, 13(5), 055503,  DOI:10.35848/1882-0786/ab8726.
62. M. R. Burton, T. Liu, J. McGettrick, S. Mehraban, J. Baker, A. Pockett, T. Watson, O. Fenwick and M. J. Carnie, Thin Film Tin Selenide (SnSe) Thermoelectric Generators Exhibiting Ultralow Thermal Conductivity, Adv. Mater., 2018, 30(31), 1801357,  DOI:10.1002/adma.201801357.
63. C. Chang, G. Tan, J. He, M. G. Kanatzidis and L.-D. Zhao, The Thermoelectric Properties of SnSe Continue to Surprise: Extraordinary Electron and Phonon Transport, Chem. Mater., 2018, 30(21), 7355–7367,  DOI:10.1021/acs.chemmater.8b03732.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ce01488b

---