Energy partitioning of pharmaceutical co-crystal structures†‡
Birger
Dittrich
 *ab,
Lauren E.
Connor
a,
Dominic
Werthmueller
a,
Nicole
Sykes
a and
Anikó
Udvarhelyi
a
*ab,
Lauren E.
Connor
a,
Dominic
Werthmueller
a,
Nicole
Sykes
a and
Anikó
Udvarhelyi
a
aNovartis Campus, Novartis Pharma AG, Postfach, Basel CH-4002, Switzerland. E-mail: birger.dittrich@novartis.com
bMathematisch Naturwiss. Fakultät, Chemie, Universität Zürich, Winterthurer Str. 190, CH-8057 Zürich, Switzerland
First published on 13th January 2023
Abstract
Active pharmaceutical ingredients (APIs) and selected coformers were studied in crystalline self-environment, in selected co-crystal structures, and gas phase. To obtain comparable geometries from experimental crystal structures, we rely on fast quantum mechanical GFN2-XTB molecule-in-cluster optimizations. Optimized crystal structures are first analysed in terms of molecule-pair interaction energies, by subdividing a cluster generated from asymmetric unit content through space-group symmetry into pairs of molecules. Accurate energies are then obtained by single-point molecular orbital (MO/MO) two layer “ONIOM” energy partitioning, comparing the same molecules in different crystal environments. Clusters approximate the local environment of a crystal structure for ONIOM. The pre-processor program BAERLAUCH (Acta. Cryst. A 2012) was used to set up all cluster computations. Solid-state computations using dispersion-corrected density functional theory provide reference results. ONIOM partitioned energies shed light on the driving force of co-crystal formation, with the energy gain from the complementarity of molecule-pair wavefunctions in such structures being the main driving force. It follows that improving prediction of co-crystal structure formation beyond current approaches, e.g. COSMO-RS excess enthalpies, statistics from structural databases or full crystal structure prediction is possible by finding complementary molecule-pairs through conformational sampling, as ultimately exemplified.
1. Introduction
1.1. Co-crystal structures in the pharmaceutical industry
Rather than using classical salts1 or pure API (active pharmaceutical ingredient) material, advantages to using co-crystals2,3 in pharmaceutical formulations have been discussed intensively throughout the last decade.4–8 Co-crystals permit to increase or decrease API bioavailability through solubility, and thereby mitigate the risk of developing amorphous material which might eventually crystallize. If they do not decompose into constituents in a formulation, they can also enable a desired form stability of an API in a drug product. Although the promise of a predicted wave of new co-crystal drug substances9 remains unfulfilled, there is an ever-increasing number of studies describing API co-crystal structures and their properties related to co-crystal development. It is thus fair to say that co-crystals have gained in overall importance, and this is reflected in work leading to a revision10 of FDA regulations in 2018 (ref. 11) (Document FDA-2011-D-0800, revision 1).An important characteristic of a coformer is that it matches and complements the API in modulating donor and/or acceptor hydrogen bonding (HB) capabilities in 3D. In an API lacking donor groups, water as a coformer can e.g., convert an acceptor functional group into a donor by forming one HB to the acceptor, and another HB by providing a donor water hydrogen atom to an adjacent molecule. However, one needs to go beyond distance-based HB analysis to understand cocrystal formation.
Co-crystallization needs to lead to an overall free energy gain to happen. It was emphasized that there is an enthalpy as well as an entropy contribution to co-crystal formation.12,13 Focusing on enthalpy in the molecular orbital picture of quantum chemistry, an API–coformer wavefunction has lower energy when good orbital overlap occurs, with orbital energies and phases alike. A reliable prediction of co-crystal formation needs to include low-energy wavefunctions to provide guidance how to make a particular co-crystal experimentally.
QSAR,14 electrostatic potentials15–17 or excess enthalpy18,19 take intermolecular interactions, but not low-energy conformations, crystal packing, and wavefunction complementarity into account. Rather than relying on more approximate methods, the pKa rule,20 the Hansen solubility parameter21 or experimental methodology,22–28 we are thus interested in contributions of ab initio quantum mechanical (QM) computations for predicting co-crystal formation.
The PIXEL approach29 was used in this context, and an energetic drive for hetero recognition30 was identified and discussed from analysis of an impressive database of co-crystal structures. However, in the PIXEL approach, experimental solid-state structures are not optimized, and only molecular but not oligomer wavefunctions are used. The attainable accuracy is therefore limited. In general, it is not straightforward to disentangle symmetry, lattice energies, dimer energies, and their mutual influence.
Descriptive reference results on the cause of co-crystal formation have been reported using predictive tools of crystal structure prediction (CSP), namely full periodic solid-state computations after putative-structure generation,31,32 and a flavour of the latter using conformation-dependent multipole moments.33 Efforts relying on CSP methodology have shown that A:B enthalpies of an API co-crystal are lower than the sum of the A (API) and B (coformer alone) energies, with 8 kJ mol−1 stabilization on average.32 Most recently, a crystallinity contribution is discussed and considered.34 CSP methods were also combined with mechano-chemical ball milling.35
Unfortunately, predictions of a larger series of co-crystal structures using CSP methods, and classical quantum chemical full-periodic solid-state computations, incur a very high computational cost and take time, since they involve full CSP runs for putative coformer, API and cocrystal structures. Developing a faster alternative to CSP studies and the computationally involved full-periodic approach is therefore desirable. Applying CSP methods is thus currently impractical in early-phase drug development, where impact of theoretical prediction could be highest in influencing solid form selection36 and where guidance is required within days. To meet the requirement of faster predictability is our goal. Since experimental screening efforts have usually already been performed at the stage of drug development when co-crystals are being considered, experimental structures of candidates with beneficial solid-state properties are very often available. In addition, numerous coformer structures have already been determined and are accessible in the Cambridge Structural Database (CSD).37 These are the data we rely upon for gaining insight.
Single-crystal X-ray diffraction (SC-XRD) provides coordinates, but not energies. Combining experimental structure with quantum chemical computations in quantum crystallography38 can. Following this path, insight into the main driving force why co-crystals form can be gained.
Methodologically, fast molecule-in-cluster39 (MIC) optimizations of experimental structures, molecule-pair interaction energy analysis with subsequent ONIOM energy partitioning, meta-dynamic sampling and full-periodic computations are the analytical tools we employ in this study. MIC optimizations make experimental structures comparable and lead to verified H-atom positions. While full-periodic computations provide reference results on the established state of the art, the ONIOM approach40 permits energy decomposition,41 which is crucial for further insight. Simply analysing molecule-pair interaction energies generated from the asymmetric unit of the unit cell (ASU) by symmetry, as well as ONIOM high-layer energies of a coformer–API dimer/oligomer in an ASU of a co-crystal with API/coformer in their own crystal structure (“self-environments”), will then provide a new perspective on co-crystallization. Results are provided for co-crystals containing the APIs piracetam, piroxicam, aspirin and theophylline. The methods used here are applicable to “beyond rule of five”42,43 drug molecules. As a consequence of our findings, it follows that predictive methods for co-crystallization should only require conformational sampling of an API with a series of coformers, optionally in continuous solvent environment, like in the CREST (see below) approach.44 We next introduce key methods, i.e., molecule-in-cluster optimization, new molecule-pair interaction energies and ONIOM energy partitioning of crystal structures.
1.2. QM/MM, MO/MO and molecule-in-cluster computations in crystallography
We first ensured that experimental input structures were validated, and suitable as input for computation in the series of crystal structures listed below in section 2.3. Structure optimization was achieved by the semi-empirical DFT parameterized GFN2-XTB approach,45 providing coordinates of comparable quality. By only optimizing the ASU of the unit cell in a cluster of molecules39 around it, crystal structures of surprising complexity can be optimized, and much more rapidly than with solid-state DFT computations. It is emphasized that treating the ASU as system, which can be optimized repeatedly and iteratively, and keeping the surrounding molecules and their atomic coordinates fixed, leads to optimization of a whole crystal structure, which is generated from the ASU molecule(s) by symmetry. The molecule-in-cluster (MIC) approach of stepwise optimization, re-generating the cluster each time and repetition to convergence was already used for structure validation39 and for studying disorder with restraints46 earlier.The MIC approach is closely related to combining quantum mechanics and molecular mechanics (QM/MM), as has been established in the final decade of the last century.40 Combining quantum chemical ab initio molecular orbital (MO/MO) methods of different sophistication is also possible. Earlier studies of drug–receptor complexes47–49 and accurate active-site macromolecular refinement50,51 have shown that ONIOM methods are suitable to study macromolecules. QM/MM and MO/MO methods have also found use in small-molecule crystallography, e.g., for studying structure and geometry,52 for computing H-atom or all-atom atomic displacement parameters (ADPs),53,54 and to optimize excited state molecules in the surrounding of ground state molecules.55 Further applications were in crystal structure prediction,56 and in comparing X/H-atom ADP ratios57 and X–H bond distances from theory with SC-XRD and neutron diffraction results.58 ONIOM computations are attractive every time a full high-level QM treatment of a system is computationally impractical or infeasible, and when partitioning a system into a high and a low layer is a good approximation, especially when no covalent bonds need to be broken or modified. The ONIOM philosophy is thus very well suited for crystallographic applications since covalent interactions (excluding bonds in coordination compounds) and intermolecular interactions are considered different conceptual levels in a crystal structure. Combining different levels of model quality can provide, in principle, the accuracy in the description of the ASU achieved in more sophisticated solid-state computations.56 However, the high-layer ONIOM energy focused on later is the energy of a molecule in the cluster, not the lattice energy, although both can be related through sublimation enthalpy.59 The MIC, QM/MM or MO/MO approaches are thus different to the approach usually taken in solid-state physics, where the whole unit cell or a supercell is the system investigated. Solid-state computations usually use plane-wave basis sets, a combination of a Gaussian-type and a plane-wave basis set, or numerically tabulated atom-centred orbitals60 [for an overview of modelling solid-state structure see ref. 61]. Especially when a refinement model of an experimental crystal structure is available as starting point, efficient QM/MM62 or MO/MO approaches are clearly attractive and provide extrapolated energy as well as partitioning into high/medium/low layer.63
We here combine clusters methods, i.e., fast MIC optimization, molecule-pair interaction energy calculation and ONIOM, for providing rapid energy partitioning on pre-validated structures from experimental input of possibly varying quality at the same level of theory.
1.3. Molecule-pair interaction energies
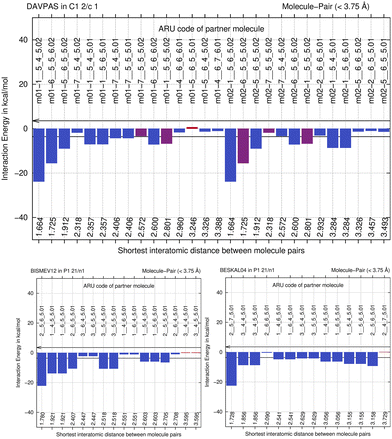
By computing energies of molecule pairs (sometimes also called “dimers” here), we can examine a crystal structure better than by focusing on hydrogen bonding only. To do so, we subdivide a cluster of molecules generated by space group symmetry into pairs of molecules. Taking the Z′ = 1 structure of L-alanine as example, expanding the one ASU molecule into a cluster with a 3.75 Å distance threshold provides a 15-molecule cluster. We can “unpack” this cluster and expand it into pairs of molecules, maintaining the central ASU molecule throughout (see Fig. 1). Calculating the interaction energy as Eint = [E(molecule pair) − E(monomers)], each molecule pair in the cluster then gives us stabilizing or de-stabilizing molecule-pair interaction energy E(MPIE). These energies [here at the DFT level using APFD/6-31G(d,p) at the GFN2-XTB geometry] are also plotted, ordered by the shortest atom–atom distance between each of the ASU atoms and the symmetry generated ones. From Fig. 1 we can easily identify the most stabilizing E(MPIE), which corresponds to adjacent orange doubly hydrogen bonded molecules (right side in figure). We can also see that the turquoise molecules further apart in the lower left of the figure can interact in a stabilizing manner, here though dipole–dipole interactions, but similar situations arise in e.g., π–π stacking. E(MPIE) analysis thus provides insight beyond hydrogen bonding and facilitates the identification of structure determinants64 through energy.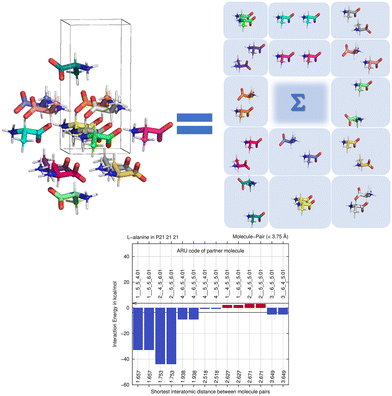 | ||
| Fig. 1 Unpacking a 15-molecule cluster of L-alanine molecules into molecule-pairs (top) for analysis of molecule-pair interaction energies E(MPIE) (bottom). | ||
A symmetry code to identify how the second molecule in a pair is generated as part of the analysis with BAERLAUCH and is provided in the bar-graph. Molecules can be identified by this ARU (asymmetric residue unit) code as also used in the PLATON65 program. The string of the molecule permits to identify the molecule and its symmetry. The first integer in the string 1__ is the number of the symmetry operation used in BAERLAUCH, 5_5_5 then means no translation w.r.t the ASU (6_5_5 would, e.g., mean a +1 translation in a direction). If there is more than one molecule in the ASU, the string allows to identify them, the first molecule being .01; .02 (at the end of the string) would be a possible second molecule.
1.4. E(MPIE), ONIOM compared to PIXEL and energy frameworks
To put the molecule-pair interaction energy and ONIOM methods into a bigger context of energy decomposition41 methods, a shared aim is to reduce computational cost for systems that are too expensive to be calculated, but to still allow an accurate description, reproducing high-level ab initio results. Two-layer ONIOM energy is obtained through E(ONIOM2) = E(high, model) + E(low, real) − E(low, model).63Two related approaches to ONIOM are next discussed in more detail. (1) The PIXEL method29,66 has been the pioneering method devised to gain insight into solid-state phenomena via approximate lattice energies. (2) Energy frameworks67,68 refined this conceptual approach through improvements in the computational approaches69 and more user-friendly software. Both approaches sum up lattice energy from a. electrostatic, b. polarization, c. dispersion and d. Pauli-repulsion contributions, whereas the ONIOM high-layer energy in a crystal-like surrounding is the quantity focused on here. PIXEL and energy frameworks can provide lattice energies within the accuracy of the underlying approximations, whereas we report and compare the E(MPIE) or ONIOM high-layer energy of a molecule or system wavefunction of interest. ONIOM does not currently permit to easily correct a basis-set superposition error (BSSE). The importance of this error has not been investigated but might be growing with the size of the system and the number of basis functions. Moreover, it has been shown that to provide most accurate (lattice) energies, e.g., for ranking polymorphs, lattice sums are required.56 Compared to PIXEL and energy frameworks, the accuracy of ONIOM computations is less limited by underlying approximations and should be comparably high (on the MO/MO level including empirical dispersion correction) than more established solid-state computations, which provide lattice, and not molecule-in-crystal energies and do not permit or include straightforward molecular energy partitioning (except via atomic basins70).
2. Method details
2.1. Pre-processing with BAERLAUCH
Technically, there are several key functionalities of the pre-processor program BAERLAUCH54 relevant to this work. 1. It can provide input and process output of the quantum chemical ‘engines’ GAUSSIAN09/16,71 TURBOMOLE,72 CP2K73 and XTB.74 2. It can interpret Hermann–Mauguin symbols of space-group symmetry and generate clusters of molecules from asymmetric-unit content, separately considering individual molecules. 3. It performs transformations between fractional and Cartesian coordinates and back. The latter is required in the generation of clusters or pairs of molecules for quantum chemical input, where Cartesian coordinates are used, as well as for back converting the Cartesian coordinates of the optimized structure in the cluster into the respective fractional crystal coordinate system used in experimental structure determinations [crystallographic information files (CIF)]. Pre-processing of different input/output formats thus permits to change between and to combine different methods. Here lower-level semi-empirical MIC, or alternatively QM/MM computations58 are combined to provide optimized molecular geometry from experimental input. Program output provides energies from E(MPIE) or MO/MO ONIOM computations at the DFT-D level. The accuracy required to study intermolecular interactions is expected to be better than 1 kcal mol−1 in the latter case. Going back and forth from theoretical computation to experimental least-squares refinement is also possible through the generation of ‘hard’ bond distance and angle restraints and by writing input files for the program SHELXL,75 but would not provide such accuracy.2.2. Input coordinates, useability, and hydrogen-atom positions
2-Layer clusters including atoms in molecules within 3.75 Å of any ASU atom54 are used throughout. Concerning the best initial starting structure for a molecule-in-cluster optimisation, SC-XRD structures refined with the independent atom model (IAM) can already provide suitable input – more so after simple modification of the hydrogen-atom positions elongating their bond distances or after aspherical-atom refinement.76 When IAM coordinates are used, extending along the X–H bond vector by a factor of 1.135 is recommended before a molecule-in-cluster optimization or ONIOM computation is performed. When results from neutron diffraction, or more accurate coordinates from aspherical-atom refinement of high-resolution X-ray data (where hydrogen positions are modelled carefully) are available, this step is not necessary. Since most structure refinements use the IAM, elongating X–H bond distances is part of BAERLAUCH functionality. An alternative procedure available is to keep the non-hydrogen atom positions fixed, and to pre-optimise the coordinates of the hydrogen atoms only, and to provide required input for GAUSSIAN09/16. However, this latter procedure might fail for zwitterionic molecules like amino acids, where it can lead to non-zwitterionic molecules. Another solution offered in BAERLAUCH is to generate constraints/restraints for experimental IAM least-squares refinement. When Bragg intensity data are available, one can use an optimized geometry as input for another round of restrained refinement.2.3. Structures investigated
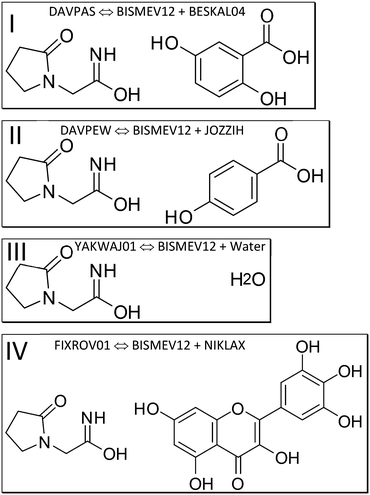
We next discuss which structures were studied, and under which measurement conditions these were obtained. We specify co-crystal structures first, followed by the contributing coformer and the API structures. We rely on deposited structures measured at a temperature close to 100 K whenever possible to ensure comparable measurement conditions in the SC-XRD measurements for datasets retrieved from the CSD as computational input. Low-temperature structures were chosen, since the computational approach approximates Gibbs free energies as enthalpies, assuming a temperature of 0 K; entropy is not explicitly considered. Experimental lattice constants are used without optimization. Since these incorporate entropy via atomic displacements and resulting intramolecular spacing, molecular entropy is implicitly assumed to be constant in related API and co-crystal structures when experimental temperature and pressure are similar.To separately determine the energies of the coformers in their self-environment, coformer structures and their polymorphism (when applicable) were considered. Gentisic acid (2,5-dihydroxybenzoic acid) was part of a multi-temperature study, and we use refcode BESKAL04 (ref. 78) at 100 K. All data sets involving piracetam listed so far were also measured at 100 K. For myricetin solely a monohydrate structure measured at 140 K (ref. 79) was available. Since there was no structure of this molecule in its pure self-environment, we used this monohydrate structure, refcode NIKLAX, for further analysis. For para-hydroxybenzoic acid only a room temperature structure was available,80 where the carboxyl hydrogen atom is disordered, refcode JOZZIH, so this was used in two different conformations for computation and analysis. To see if there is a difference between co-crystals and hydrates from the point of view of computation, we include the hydrate structures refcode YAKWAY81/YAKWAY01 (ref. 77) in our analysis.
Now to pure piracetam. Four polymorphs of this API molecule were reported. Two ambient condition structures were further analysed here, namely forms II (triclinic, space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , refcode BISMEV11) and III (monoclinic, P21/n, refcode BISMEV12),82 here with the lowest high-layer energy. These can be prepared by re-crystallisation from various solvents (e.g., methanol, propan-2-ol), and crystal structures for both forms have been reported.82,83 Both forms transform above 400 K into the high-temperature phase denoted as form I (triclinic, P
, refcode BISMEV11) and III (monoclinic, P21/n, refcode BISMEV12),82 here with the lowest high-layer energy. These can be prepared by re-crystallisation from various solvents (e.g., methanol, propan-2-ol), and crystal structures for both forms have been reported.82,83 Both forms transform above 400 K into the high-temperature phase denoted as form I (triclinic, P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) not considered here. Neither were the high-pressure forms IV and V84 included. We follow the naming conventions in this earlier and a subsequent high-pressure study.81 A structure reported from microfluidic chip crystallization directly measured with synchrotron radiation (refcode BISMEV14) has space group P21 assigned in the CIF deposition (but not in the publication85) and is most probably the known form III in P21/n. Further structures containing piracetam are provided in a study that includes a conformational analysis of the molecule.86
) not considered here. Neither were the high-pressure forms IV and V84 included. We follow the naming conventions in this earlier and a subsequent high-pressure study.81 A structure reported from microfluidic chip crystallization directly measured with synchrotron radiation (refcode BISMEV14) has space group P21 assigned in the CIF deposition (but not in the publication85) and is most probably the known form III in P21/n. Further structures containing piracetam are provided in a study that includes a conformational analysis of the molecule.86
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 water
1 water![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) piroxicam stoichiometry.89 We studied form III (BIYSEH11) and IV (BIYSEH12)88 from the several polymorphs available. An earlier study where form III was solved from powder X-ray diffraction data should be mentioned,90 since this method could have also provided input for computation.
piroxicam stoichiometry.89 We studied form III (BIYSEH11) and IV (BIYSEH12)88 from the several polymorphs available. An earlier study where form III was solved from powder X-ray diffraction data should be mentioned,90 since this method could have also provided input for computation.
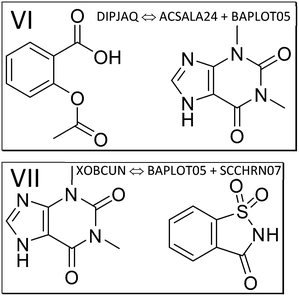 | ||
| Fig. 4 The components of the theophylline co-crystals with aspirin (VI, refcode DIPJAQ) and saccharin (VII, XOBCUN). | ||
Form II was reported to be enantiotropically related to form I, and more stable at room temperature. For form IV, BAPLOT03, the measurement was carried out at 100 K.94 It was found by experiment to be the most stable known polymorph at room temperature. Metastable form III (refcode KOJNIJ) was recently characterized with the help of molecular dynamics simulations95 and is not further considered here. Another form not further considered was characterized at 290 K, deposited as DUWXEA and termed form V. To focus on the forms most stable at room temperature (using high-quality low temperature data), we further computed and analysed form I, II and IV. For the comparisons of the co-crystal of theophylline with saccharin, and the self-environment of saccharin, we can again rely on the abovementioned structure with refcode SCCHRN07.
For pure aspirin and its self-environment as the main API in this co-crystal, coordinates for three polymorphs are available to date. Discovering polymorphism in this classic drug molecule raised interest beyond solid state chemists.96,97 For polymorph I we used refcode ACSALA14 measured at 123 K, for polymorph II ACSALA15 measured at 180 K. For polymorph III, the most recent determination, we relied on a structure solution from powder diffraction data,98 refcode ACSALA24 at 240 K.
3. Results
We start the results section by mentioning characteristics of ONIOM energy partitioning and differences to other approaches. For the ONIOM molecule-in-cluster approach we start with the asymmetric unit. As mentioned, the ASU is surrounded by other molecules generated by symmetry, which provide an approximation of the crystal environment. Different possible choices of the coordinates of the ASU within the unit cell led to formally different clusters, which all give the same high-layer energy. This was confirmed using α-glycine in P21/n: all four possible ASU choices led to identical results within the numerical accuracy. In the PIXEL approach, approximating a structure via symmetry-generated dimers and their energies entails a larger number of pairs of molecules, where each energetic contribution is added to give lattice energy. In full-periodic computations, lattice energies are obtained ‘all at once’. Earlier results from directly analysing lattice energies31,32 do not provide the information required for a thorough understanding, namely how energies of a system change from molecular state in the gas phase, via solution, dimers, or oligomers, to the energy in a crystal packing. In full periodic computations, contributing factors are not looked at separately, only in their entirety. From molecule-pair interactions energies E(MPIE) we can identify the molecule pair that contributes the most stabilizing interaction. Via ONIOM partitioning we can then obtain the energy of a molecule (or several, interacting molecules) in a crystal environment approximated by the cluster molecules, and alternatively the extrapolated energy of the whole cluster. While (like in PIXEL) different choices can be made for a representative ASU dimer/oligomer in ONIOM, the resulting high-layer energy is very similar, since like in full-periodic computations the ASU is surrounded by (symmetry-equivalent) other molecules. In the current study we apply a distance threshold for molecules constituting the environment, and do not perform a lattice sum as in ref. 56. ONIOM partitioning thus provides information only approximated in E(MPIE), PIXEL and energy frameworks, in a computationally more efficient manner than in solid-state computations.3.1. Energy partitioning and co-crystal formation in piracetam
We next perform E(MPIE) analyses for the cocrystal structures I–IV and the API and their coformer components after GFN2-XTB molecule-in-cluster optimization.39 In these first four co-crystal structures piracetam is the API molecule. The analyses can also be performed at the GFN2-XTB level of theory or with APFFD/6-31G(d,p) (ESI‡) using Gaussian09 (ref. 71) as shown in Fig. 5.For DAVPAS, intermolecular interactions are listed from the perspective of the first ASU molecule m01_1__5_5_5.01, the API, so interaction m01_1__5_4_6.02 would be the interaction with the coformer after that is translated −1 in b direction and +1 in c direction. When moving in the plot to molecule m02, the coformer, the perspective changes and the API molecule m01 becomes the one ending with .02, so interaction m02_1__5_6_5.02 is the API translated by +1 in b direction seen from molecule m02, the coformer. Both interacting molecules are outside of the unit cell. Those molecules that are within the unit cell share the absence of a translation as shown by the 5_5_5 part of the ARU code and are emphasized by purple color in the top of Fig. 5. Further E(MPIE) plots for piracetam cocrystals II, III (the hydrate) and IV all show (ESI‡ Fig. S1 and S4) that the sum of the strongest molecule-pair interaction energies is usually between API and coformer, rather than between API–API or coformer–coformer. Although this is different for the hydrates YAKWAJ01 and NIKLAX (Fig. S2 and S3‡), where for the driving force of hydrate formation the small volume of water needs to be considered, the strongest E(MPIE) rule again – in hydrates from the perspective of the water molecule.
This means that we can focus on the ASU content, consisting of the API and the coformer, as high layer for ONIOM partitioning (Fig. 6). ONIOM also permits to go beyond E(MPIE), which both entail the approximation to work in the gas phase.
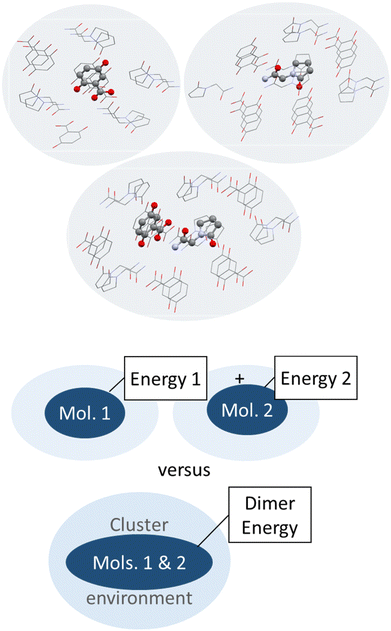 | ||
| Fig. 6 Schematic illustration (top) and depiction of molecules surrounding a central piracetam molecule in a heterogenic cluster taken out of the co-crystal structure of piracetam and gentisic acid (refcode DAVPAS) generated with Mercury.99 Hydrogen atoms omitted for clarity. | ||
So next, we quantify the energy gain more accurately, and MIC ONIOM high-layer energies were compared for that purpose. Fig. 6 shows a representative cluster of piracetam in a cluster of surrounding piracetam and gentisic acid molecules in structure DAVPAS. ASU high-layer molecular energies were computed using MO/MO ONIOM single-point computations throughout. By ONIOM, accurate high-layer energies can be obtained separately for the API or coformer molecules, or their molecule pair. Full results reported next (see Tables S1–S4‡) correspond to APFD/6-31G(d,p):APFD/3-21G [high layer:low layer] computations, which were performed with Gaussian09.71 Basis set choices involve a less sophisticated level of theory for the low layer but make these computations fast to perform even for larger molecules. Using the 3-21G basis e.g. for sulphur is limiting, but better than a QM/MM treatment with point charges in a MM part. Should convergence run into problems, the program option SCF = YQC can be evoked. The APFD/6-31G(d,p):APFD/3-21G ONIOM method combination includes dispersion correction already in the DFT functional100 and shows that the high-layer energy form II and III of piracetam differ by +1.19 kcal mol−1 from each other, and by a maximum of −1.51 kcal mol−1 when the high-layer is chosen to be the coformer in the co-crystal of piracetam and myricetin (refcode FIXROV01) rather than the full ASU. Hence, whether a neutral molecule is in a self- or a co-crystal environment does not usually change its energy considerably. In contrast, the energy gain from cocrystal formation with respect to the sum of the components (lowest energy polymorphs used as reference) is usually considerable. For example, in the DAVPAS ASU it is −18.14 kcal mol−1 (see Table S1‡ for other piracetam results and ESI‡ Tables S1–S4 for all high-layer ONIOM energies of the abovementioned piracetam cocrystal structures).
The question arises, which reference energy to choose to calculate energy gains from co-crystal formation in case there are several polymorphs. We always chose the energy of the most stable individual polymorph in its self-environment, so e.g., piracetam form III was taken as reference for DAVPAS.
From the observation that the ONIOM high-layer energy of the same molecule in different crystal structures is similar, it follows that polymorph energy ranking is of minor relevance in the co-crystal context. Polymorph ranking can be temperature-dependent, and a 2-layer ONIOM approach without lattice sums may not be the optimal choice for this purpose. Whether ranking agrees with experimental or other computational results from the literature is not the decisive factor concerning our main question, the driving force of co-crystal formation.
We continue by discussing the numerical reproducibility of the high-layer ONIOM energy. Here two independent structure determinations of piracetam monohydrate YAKWAJ (data collected at 150 K) and YAKWAJ01 (100 K) were separately MIC optimized and then compared, and the high-layer ONIOM results for the ASU agree favorably within 0.06 kcal mol−1. Differences in lattice constants thus do not seem to have a strong influence on the energies in this temperature range. Moreover, two independent piracetam structure determinations below (BIYSEH13 and 14, same temperature) give almost identical results, adding substance to the assumption that our results are accurate. Neither did increasing cluster size and therefore the number of molecules leads to significant energetic differences, so a 3.75 Å threshold for atom–atom distances to include molecules in cluster generation seems a good choice.
A possible source of error is the quality of the input coordinates. To ensure that MIC optimizations with XTB have indeed converged (there is currently no automatic check for convergence), ten optimization and cluster re-generation steps were performed. Usually, fewer steps are required. The possibly limited accuracy of the geometry optimization step with GFN2-XTB, where inaccurate geometries of a planar amide have been discussed before,39 should be kept in mind and might lead to less accurate MO/MO energies.
We emphasize that for the co-crystals the entire ASU content was simultaneously optimized together in the MIC approach. Separately optimizing molecule by molecule might not allow to reach the reproducibility provided here.
For improving accuracy one can systematically increase the basis-set size and try different DFT functionals. While confirming that the results remain qualitatively the same for different functionals (B3LYP and APFD), we did not attempt an exhaustive coverage of all possible combinations. Rather, moving to full-periodic optimization can provide an alternative and independent benchmark.
Full-periodic computations provide the energy difference between the lattice energies of the contributing crystal structures. They confirm the trend of the energy gains seen in Table 1, where energy gains from ONIOM high-layer and VASP101 are compared. It is emphasized that periodic computations cannot provide partitioned energy of molecules in different structures but their lattice energies. We also note that since the energy gain is here computed via the difference of lattice energies, these values are not directly comparable and differ in magnitude, since the number of molecules in the ASU as well as the multiplicity need to be matched in the full periodic case to get to a result. Also, since energy partitioning is not feasible in the full-periodic approach chosen, only two values are provided for DAVPAS and DAVPEW, since YAKWAJ01 and NIKLAX (used for FIXROV01) contain water.
| Co-crystal structure (REFCODE) | Method | ΔE (kcal mol−1) energy gain w.r.t. to lowest energy self-environment |
|---|---|---|
| DAVPAS | ONIOM (G09) | −7.03 |
| VASP | −0.67 | |
| CREST (G09) | −21.44 | |
| DAVPEW | ONIOM (G09) | −6.71 |
| VASP | −0.80 | |
| CREST (G09) | −21.77 | |
| YAKWAJ01 | ONIOM (G09) | −9.16 |
| FIXROV01 | ONIOM (G09) | −18.14 |
Thus, for piracetam cocrystals a result of the study, confirming earlier findings,31,32 is that there is indeed usually an energy gain of co-crystal formation, not only when looking at lattice energies, but when considering the difference between a.) sum of molecular energies in the self-environment and b.) the dimer energies in the co-crystal with ONIOM (Table 1). For piracetam:p-hydroxybenzoic DAVPEW there is an energy gain of −6.71 kcal mol−1 from our ONIOM computations. Earlier authors31,32 thus compared lattice energies “as a whole”, but not the individual contributions in connection with intermolecular interactions of the high-layer ONIOM energy of an ASU dimer vs. a monomer wavefunction or the related molecule-pair interaction energies.
We also note that for the co-crystal with p-hydroxybenzoic acid there were two structural archetypes103 for the coformer structure since carboxylate H atoms are disordered. Therefore, two computations were performed, which both lead to the same energetic outcome (Table S1‡).
Another aspect is that it is not a requirement for co-crystal formation that both components A and B of a A:B co-crystal have a lower conformational energy than in their self-environment. This can e.g., be concluded from the higher molecular ONIOM high-layer energy of separate gentisic acid and p-hydroxybenzoic acid molecules in their co-crystal with piracetam, when compared to their crystal self-environment. This is less surprising when considering that the energy available for crystallization is around R·T (0.593 kcal mol−1) at ambient conditions. Temperature is relevant for how crystallization experiments are performed, i.e., usually at normal temperature (and pressure, so that a p·V correction can be avoided). If an energy difference is within this amount, crystallization is expected to be favored, since there is an overall Gibbs free energy gain from co-crystal formation. The driving force for co-crystallization should thus exceed R·T at ambient conditions.
Another interesting aspect is that hydrates can be seen as just another co-crystal, with an ASU energy gain of YAKWAJ01 of −9.16 kcal mol−1. Since the crystal structure of ice Ih is disordered104 we use the average high-layer energy of the two water molecules studied in NIKLAX and YAKWAJ01, which give the same high-layer energy in the different crystal structures. What might be special about water as a coformer is its donor–acceptor modulation mentioned in the introduction, that the molecule is small, and that conformational-energy differences for water are expected to be less pronounced than for other, larger molecules. Here we only compare two molecule-in-cluster high-layer energies, but waters' energetic similarity would permit to compare energies between hydrate and anhydrate structures from their components more generally, assuming a similar energy gain from formation of a solid.
The findings for co-crystals I, II and III, the monohydrate, agree well with the fourth example, co-crystal IV of piracetam with myricetin, refcode FIXROV01. Here there was no structure available for the pure self-environment of myricetin, so the monohydrate NIKLAX was chosen. Again, there is a substantial ASU energy gain of −9.85 kcal mol−1 when using the myricetin molecular energy from the monohydrate as reference for the self-energy of myricetin (not listed as cocrystal in Table 1).
After having emphasized the difference between lattice energies and ONIOM molecular energies, it is worthwhile to contemplate on another method detail. ONIOM partitioning can provide the energy of a monomer, dimer, or oligomer (the choice of the high layer) in the cluster (approximating the solid). Different choices of placing the molecules in the asymmetric unit therefore lead to essentially the same energy in ONIOM partitioning. Therefore, one choice of asymmetric unit is approximately representative for all symmetry-related dimers. This was verified by choosing two possible dimers-in-cluster from the next co-crystal example structure in Table S2,‡ which is not dominated by classical strong hydrogen bonding. A different choice of ASU can still lead to numerically different results, and this would be due to ONIOM partitioning and the different basis sets used for high and low layer.
3.2. Energy partitioning and co-crystal formation in piroxicam
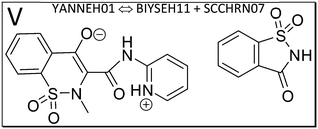
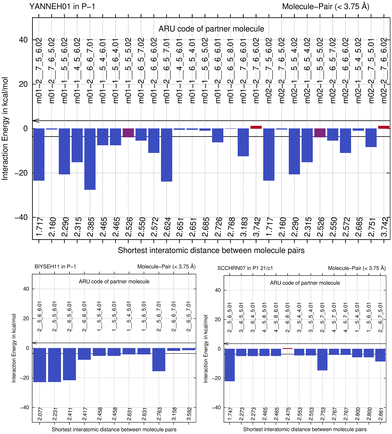
We next study the driving force of co-crystal formation in system V (refcode YANNEH01 (ref. 87)), the co-crystal of piroxicam and saccharin, where no classical hydrogen bonding is present. We start again with the E(MPIE) plot (Fig. 7). Rather than in the plots provided for piracetam, the single strongest interaction is not between the coformer and the API. Still the sum of the API–coformer interactions is larger than the API–API interactions in the API and coformer structures. Moreover, when one considers that the three second-lowest E(MPIE) are for interactions with a single functional group, the sulfonamide, it is valid to “think like chemists do”, i.e. in the context of functional groups. Adding all API–coformer interactions together, API–coformer interactions do again constitute the dominant interactions between these molecules, permitting us the rationale for performing the ONIOM analysis.The abovementioned charge-density diffraction data for co-crystal and its constituents (form I of the API piroxicam, refcode BIYSEH14 [reported to have been measured at 150 K in the CIF, but at 100 K in the publication], and monomorphic co-former saccharin, refcode SCCHRN07) were evaluated by 2-layer ONIOM in a next step. In the co-crystal structure, the main intermolecular interaction is π–π stacking between piroxicam and saccharin. Other authors89 measured form I at 100 K (refcode BIYSEH13) to high resolution. Structures of form I, BIYSEH13 and BIYSEH14, gave identical high-layer ONIOM energies to the precision given. Fig. 7(bottom) shows the energies of the pairwise intermolecular interactions in the coformer self-environments.
Piroxicam can be a zwitterion and likewise a neutral molecule without charge separation. From the several polymorphs we add form III (BIYSEH11) and IV (BIYSEH12) for study.88 Form IV contains five molecules in the ASU. Computed high-layer energies better characterize possible self-environments of the molecule and its conformation as a zwitterion.
What is the energetic driving force of co-crystal formation in the co-crystal structure V? Dimer or molecule-pair formation again leads to a significant energy gain of −13.68 kcal mol−1, but interestingly the piroxicam self-environment energies are significantly more favorable in uncharged form III than in the co-crystal. Co-crystal dimer formation compensates this energy penalty. Full periodic computations give −2.39 kcal mol−1, respectively.
To better understand this driving force in structure V, the zwitterionic nature of piroxicam in the co-crystal needs to be considered. Since we crystallize from solution, the solvent polarity and dielectric constant for stabilization of piroxicam's zwitterionic state play an important role. One can see from a +12.74 kcal mol−1 energy difference between zwitterion and uncharged molecule in form IV (see Table S2‡) that the experimental procedure to obtain the co-crystal requires polar solvent, making piroxicam a zwitterion first. Then the co-crystal can be accessed based on the zwitterion, thereby avoiding an energy penalty with respect to the uncharged self-environment. Similar considerations apply in making pure form IV of the API. Most important for understanding co-crystal V is the role of solvent or, in general, crystallization conditions.
The role of π–π stacking might be a factor in crystallization kinetics,105 as discussed also in the context of hetero-aromatic additives in “multi-component enabled crystallisation”.88 It can also be suspected that systems with classical hydrogen bonding and those dominated by only aromatic interactions behave differently.
When one focusses on the closest intermolecular atom–atom distance as guidance to select the ASU choice, a NH–O hydrogen bond in between API and coformer, the center of mass of the coformer saccharine lies outside the unit cell. An alternative, crystallographically equally valid ASU arrangement is when both molecules have their center of mass inside the unit cell. We have thus optimized both possible input-coordinate sets and compared their energies (Table S2‡). Energies of symmetry-equivalent dimers are within 0.88 kcal mol−1. Despite the change in coordinates, this is in a similar range than the identical energies for BIYSEH13 and 14, or YAKWAJ at 150 K and YAKWAJ01 at 100 K, and close enough to be considered equivalent. It is recommended that when symmetry-equivalent molecular sites are possible in cluster computations, both molecule's center of mass should be inside of the unit cell, adding proximity of molecules (or, if applicable, ion pairs) as second criterion only for ASU choices, although differences seen do not influence or change our conclusion that an ASU energy gain is the driving force of co-crystal formation from ONIOM.
3.3. Energy partitioning and co-crystal formation applied to theophylline co-crystals
Next, we study the API aspirin, which crystallizes together with co-former theophylline (structure VI, refcode DIPJAQ) and then consider theophylline and API in the co-crystal with saccharin (structure VII, refcode XOBCUN). Lewis structures of the contributing molecules in these two co-crystal structures are illustrated in Fig. 4. Again, the molecule-pair interaction energy analysis in Fig. S5‡ (DIPJAQ vs. ACSALA24 and BAPLOT05) and S6‡ (XOBCUN vs. BAPLOT05 and SCCHRN07) precede the 2-layer ONIOM analysis. In the former, we again find that the sum of the E(MPIE) in between API and coformer exceeds the API–API or coformer–coformer interactions. In the latter ONIOM analysis, the high-layer energy in the crystal structure of aspirin (refcode ACSALA24) alone is compared, molecule in self-environment, to corresponding monomer and dimer energies in co-crystal structures VI and VII, the latter involving theophylline (refcode BAPLOT05) and saccharin (SCCHRN07, Table S3‡). For the numerical details of the energy gain through co-crystal formation, all relevant comparative co-former high-layer ONIOM energies in self-environment and cocrystals containing aspirin are provided in the ESI‡ Table S3. Pure aspirin structures are monoclinic and crystallize in space group P21/c with one molecule (polymorph I and II) or two molecules (polymorph III) in the ASU. Just like for the earlier cases involving piracetam and piroxicam, co-crystallization propensity can be put into the bigger context using ONIOM energy partitioning after MIC optimization and confirmation by full-periodic computations. Concerning this driving force of co-crystal formation, we see that the dimer energy of aspirin with theophylline in the co-crystal VI DIPJAQ is, with −26.95 kcal mol−1, again significantly stabilizing compared to the sum of the individual molecules. This also holds for the last example VII XOBCUN of the theophylline:saccharin co-crystal, which again shows a pronounced energy gain of −23.22 kcal mol−1, far exceeding R·T. Full periodic computations, although not directly comparable, also give −1.00 and −0.78 kcal mol−1, respectively, and confirm an energy gain like in piracetam cocrystals (Table 1). Like seen throughout, the individual molecules themselves, when compared in the different self- and co-crystal environments, except for neutral/zwitterionic piroxicam, are energetically rather similar to each other, their differences usually being below R·T.103 This energy “quantum” is thus the range to assess results in terms of macroscopic significance, even when computations provide higher accuracy. However, we want to point out a possible exception to this rule of thumb: when a co-crystal structure is disordered, and different oligomer disorder conformations within R·T are present at the time a co-crystal forms, energies can span a wider range, since R·T can be extended by the number of oligomer conformations involved. Hence, the spread of energies available to a system will increase with molecular size and the number of spatially independent disordered conformations.3.4. Z′ > 1 structures, ASU high-layer energy and lattice energy
Can the ASU energy gain perspective of co-crystal formation also be applied to high Z′ structures (Z′ being the number of ASU molecules)? This would be seeing such structures as co-crystals with themselves, e.g., when the same molecule is present in different conformations. In such cases, we also expect dominating E(MPIE) contributions between the Z′ ASU molecules, and an ASU energy gain with respect to a hypothetical polymorph with only one ASU molecule. There are several aspects to consider for ONIOM work in this context: so far, we have only compared 2-layer ONIOM high-layer energies of molecules and API-co-crystal heterodimers in their respective crystal environment, being provided by the cluster low-layer. When the same molecule is both high-layer system and low-layer crystal environment in a Z′ > 1 structure, we stop comparing like (high-layer) with like (low-layer). Our current efforts only provide relative energies for a particular system, also across a series of crystal structures with different stoichiometry (e.g., an API in anhydrate and hydrate structures, if the API ionization state is the same). What we do not provide with the ASU high-layer energy are lattice energies of the entire system on an absolute scale (e.g., an answer to whether an anhydrate or hydrate would be more stable), which would be relevant and interesting. Future work will need to clarify this, together with the relation between ASU high-layer, solution- and solid-state energy.3.5. Using gas-phase computations for predicting co-crystal formation
We note that one does not really need crystal structure information (unit-cell parameters, space group symmetry), i.e., the reference self-environments, to find a molecule-pair energy gain. Computations in the gas phase or in average solvent environments can provide qualitatively similar results, do not require an already known result in form of a crystal structure and are faster to perform than ONIOM or full periodic DFT-D computations. Having disentangled the driving force of co-crystal formation as dimer (oligomer) recognition as part of the overall lattice energy here, this reasoning permits predictions of co-crystal formation—without knowing crystal structures in advance. We are a step closer to increasing the hit-rate of the earlier promise of “virtual co-crystal screening”.15 Based on our results, an obvious suggestion for a predictive procedure of co-crystal formation is therefore to compute gas-phase energies of dimers (oligomers) in confined space by meta-dynamics and to subtract the energies of the constituent monomers of APIs and suitable coformer molecules from a series to be screened. Computations can optionally be carried out in a dielectric continuum solvation state to take the role of solvent into account. Such computations can easily be carried out using the CREST44 (conformer–rotamer ensemble sampling tool) in silico sampling approach. CREST sampling can overcome the challenge to identify favorable low-energy mutually fitting orientations of the conformations of molecules in the correct protonation state. To show the feasibility of this procedure predicting co-crystal formation, we performed such computations for the two piracetam co-crystal systems DAVPAS and DAVPEW studied above. The best mutual conformation of the API–coformer pair or the best (lowest energy) individual API or coformer conformation were taken after the CREST run, and a subsequent single-point Gaussian calculation with APFD/6-31G(d,p) computation was performed to provide an analogous treatment to the one applied to the input crystal structures. We found that computational sampling can indeed identify those cases, where dimer energies are substantially lower than the sum of the energies of low-energy conformations of the individual molecules, confirming once more the main driving force of dimer (oligomer) formation (CREST → Gaussian single-point energy gain provided in Table 1). Practical aspects, like the best energy threshold for identifying a fitting pair of molecules in high likelihood, whether they really crystallize together, increasing the number of examples, distinguishing, and considering protomers, finding the best solvent, providing an automated workflow for use, or our ability to predict co-crystallization for classical hydrogen-bonded systems compared to those dominated by π–π interactions, will require further study outside the scope of this work, but tasks are facilitated by the fact that CREST/XTB are open-source solutions that only require xyz file format as input.4. Overall discussion
We have shown there to be value in new quantum crystallographic38 combinations of methods involving experimental diffraction, MIC optimization, molecule-pair interaction energy E(MPIE) calculation, and ONIOM energy partitioning via BAERLAUCH pre-processing. Combined SC-XRD/in silico work has the benefit of not requiring laboratory experiments other than crystallization and diffraction. E(MPIE)s allows to rapidly identify the main intermolecular interactions, a tool that can be applied more generally in structure analysis. ONIOM energy partitioning then permits a more accurate quantification in qualitative agreement with full-periodic computations. Computations consistently show that co-crystal formation is indeed accompanied by an overall energy gain, and we learned that the dominant part of it is due to an ASU energy gain, which is distinguishable from a lattice energy gain. Lattice energy of co-crystals containing main API molecule A (with a particular conformational flexibility) and coformer B combined are also lower than their individual contributions. Overall, these findings are mainly due to an improved wavefunction interaction in between the dimer (oligomer) molecules in the fitting mutual conformation. Such ASU energy gains can happen prior to packing in a crystal, and this is in line with recent findings on the origins of symmetry in olanzapine in solution.106 Therefore, our findings suggest performing co-former screening in silico prior to crystallization to guide experimental screening to increase the hit-rate.4.1. Conformation (adjustment energy) or electrostatic complementarity?
For both API molecules and their co-crystals, changes in molecular energy are usually connected with a differing conformation. One can see conformational change as an investment of a molecule to better adapt to a particular solid-state environment. The better (more complementary) a co-crystal environment, the less a molecule must deviate from its energy minimum conformation in the gas phase, and the investment pays off. The geometry of a molecule in a crystal structure is thus related to its energy, like different sides of the same coin, and it indirectly carries the information of the suitability of the crystal environment. This side of the coin corresponds to the concept of adjustment energy,107 where crystal minimal energy conformations are compared to (usually lower-energy) local gas-phase minima. Conformational change is of course not the only way to rationalise co-crystallization. The availability of lock-and-key-like complementary functional groups108 in terms of wavefunction, or simplified: electrostatics, are the other side of the coin and another way at looking at co-crystallization, accompanying, or causing conformational change. It is, therefore, not useful to conceptualise co-crystal formation only from the perspective of conformation, since re-distribution of electron density likewise slightly changes molecular geometry. In other words, is the conformation adopted in a crystal structure a compromise between minimum energy conformation, the suitability of the self-environment and the one in a co-crystal. Conformational adjustments can make such interactions more favourable but are not usually the main driving force.ONIOM energy partitioning contributes to our understanding of the overall picture of co-crystal formation by disentangling this chicken and egg situation, because the high-layer energy in the self-environment of a molecule can directly be compared to its co-crystal environments, without the need of invoking gas-phase conformation in the adjustment-energy picture. ONIOM high-layer energies also include electrostatic influences already at the QM/MM level of theory and, since the molecule-in-cluster calculation involves optimization, conformational change. On the DFT-D MO/MO level, dispersion and Pauli-repulsion are also included, so that we think that the ONIOM method is an attractive way to study co-crystal formation and other solid-state phenomena.
For predictive conformational sampling, the adjustment energy that will need to be invested to form a crystal will also need to be studied.
5. Conclusion and outlook
To summarize the approach taken to better understand the driving force of co-crystal formation, a first aspect to emphasize is the combination of methods. We rely on (1) experimental SC-XRD structures, which are (2) validated and optimized in a computationally efficient manner. Then (3) E(MPIE), molecule-pair interaction energies allow identification of strong interactions in a co-crystal. (4) ONIOM energy partitioning of a molecule in a cluster, representing its crystal structure, provides accurate high-layer molecular, dimer, oligomer (up to the entire asymmetric unit content) energies in the low-layer crystal surrounding. These high-layer energies can be compared in between crystal structures of different composition at low computational cost. Comparing E(MPIE) and high-layer energies provides insight into the driving force of co-crystal formation: energy gains do not only come from enabling a lower-energy conformation or an electrostatically more favorable environment alone. The energy gain from the wavefunction of an ASU dimer (oligomer) in a co-crystal structure, compared to a self-environment of single-component crystal structures, needs to be considered. Through ONIOM, this energy gain can be quantified per dimer, oligomer or per asymmetric unit, analogous to a gas-phase computation. We point out that ONIOM energy partitioning is not possible in (5) plane-wave solid-state computations, as used for comparison purposes. Both E(MPIE) and ONIOM are powerful extensions to molecule-in-cluster geometry optimizations but do not provide lattice energy. (6) Since the energy gain in the solid is most likely first achieved in solution, mutual coformer–API sampling is possible in confined-space, with or without dielectric continuum solvation state modeling, pairing API molecules with suitable coformers. Future work will attempt to more make practical use of these findings and the CREST program for predicting co-crystal formation.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We would like to acknowledge T. Wagner for her important support in the last years, and for many suggestions, and H. Moebitz, T. Grecu, M. Mutz, A. Kordikowski, A. Grandeury, A. Perlberg, M. Kosa, F.P.A. Fabbiani, M. Krack, G. Woollam as well as R. Lewis for helpful discussions.Notes and references
- Handbook of Pharmaceutical Salts: Properties, Selection, and Use, ed. P. H. Stahl and C. G. Wermuth, VHCA, Verlag Helvetica Chimica Acta, Zürich, Switzerland, and Wiley-VCH, Weinheim, Germany, 2nd, revised edn, 2011 Search PubMed.
- M. C. Etter, Acc. Chem. Res., 1990, 23, 120–126 CrossRef CAS.
- C. B. Aakeröy and D. J. Salmon, CrystEngComm, 2005, 7, 439 RSC.
- O. Almarsson and M. J. Zaworotko, Chem. Commun., 2004, 1889–1896 RSC.
- P. Vishweshwar, J. A. McMahon, J. A. Bis and M. J. Zaworotko, J. Pharm. Sci., 2006, 95, 499–516 CrossRef CAS PubMed.
- N. Schultheiss and A. Newman, Cryst. Growth Des., 2009, 9, 2950–2967 CrossRef CAS PubMed.
- D. P. Kale, S. S. Zode and A. K. Bansal, J. Pharm. Sci., 2017, 106, 457–470 CrossRef CAS PubMed.
- O. N. Kavanagh, D. M. Croker, G. M. Walker and M. J. Zaworotko, Drug Discovery Today, 2019, 24, 796–804 CrossRef CAS PubMed.
- H. G. Brittain, J. Pharm. Sci., 2013, 102, 311–317 CrossRef CAS PubMed.
- S. Aitipamula, R. Banerjee, A. K. Bansal, K. Biradha, M. L. Cheney, A. R. Choudhury, G. R. Desiraju, A. G. Dikundwar, R. Dubey, N. Duggirala, P. P. Ghogale, S. Ghosh, P. K. Goswami, N. R. Goud, R. R. K. R. Jetti, P. Karpinski, P. Kaushik, D. Kumar, V. Kumar, B. Moulton, A. Mukherjee, G. Mukherjee, A. S. Myerson, V. Puri, A. Ramanan, T. Rajamannar, C. M. Reddy, N. Rodriguez-Hornedo, R. D. Rogers, T. N. G. Row, P. Sanphui, N. Shan, G. Shete, A. Singh, C. C. Sun, J. A. Swift, R. Thaimattam, T. S. Thakur, R. Kumar Thaper, S. P. Thomas, S. Tothadi, V. R. Vangala, N. Variankaval, P. Vishweshwar, D. R. Weyna and M. J. Zaworotko, Cryst. Growth Des., 2012, 12, 2147–2152 CrossRef CAS.
- Fda and Cder, Regulatory Classification of Pharmaceutical Co-Crystals Guidance for Industry, 2018.
- G. L. Perlovich, CrystEngComm, 2018, 20, 3634–3637 RSC.
- G. L. Perlovich, Cryst. Growth Des., 2020, 20, 5526–5537 CrossRef CAS.
- L. Fábián, Cryst. Growth Des., 2009, 9, 1436–1443 CrossRef.
- D. Musumeci, C. A. Hunter, R. Prohens, S. Scuderi and J. F. McCabe, Chem. Sci., 2011, 2, 883–890 RSC.
- T. Grecu, C. A. Hunter, E. J. Gardiner and J. F. McCabe, Cryst. Growth Des., 2014, 14, 165–171 CrossRef CAS.
- T. Grecu, R. Prohens, J. F. McCabe, E. J. Carrington, J. S. Wright, L. Brammer and C. A. Hunter, CrystEngComm, 2017, 19, 3592–3599 RSC.
- Y. A. Abramov, C. Loschen and A. Klamt, J. Pharm. Sci., 2012, 101, 3687–3697 CrossRef CAS PubMed.
- C. Loschen and A. Klamt, J. Pharm. Pharmacol., 2015, 67, 803–811 CrossRef CAS PubMed.
- A. J. Cruz-Cabeza, CrystEngComm, 2012, 14, 6362–6365 RSC.
- A. Salem, S. Nagy, S. Pál and A. Széchenyi, Int. J. Pharm., 2019, 558, 319–327 CrossRef CAS PubMed.
- A. J. Cruz-Cabeza, G. M. Day and W. Jones, Chem. – Eur. J., 2008, 14, 8830–8836 CrossRef CAS PubMed.
- R. M. Vrcelj, N. I. B. Clark, A. R. Kennedy, D. B. Sheen, E. E. A. Shepherd and J. N. Sherwood, J. Pharm. Sci., 2003, 92, 2069–2073 CrossRef CAS PubMed.
- M. Mukaida, H. Sato, K. Sugano and K. Terada, J. Pharm. Sci., 2017, 106, 258–263 CrossRef CAS PubMed.
- J. H. ter Horst, M. A. Deij and P. W. Cains, Cryst. Growth Des., 2009, 9, 1531–1537 CrossRef CAS.
- M. Svärd, D. Ahuja and Å. C. Rasmuson, Cryst. Growth Des., 2020, 20, 4243–4251 CrossRef.
- C. C. Seaton, CrystEngComm, 2011, 13, 6583–6592 RSC.
- M. Karimi-Jafari, L. Padrela, G. M. Walker and D. M. Croker, Cryst. Growth Des., 2018, 18, 6370–6387 CrossRef CAS.
- A. Gavezzotti, J. Phys. Chem. B, 2002, 106, 4145–4154 CrossRef CAS.
- A. Gavezzotti, V. Colombo and L. lo Presti, Cryst. Growth Des., 2016, 16, 6095–6104 CrossRef CAS.
- H. C. S. Chan, J. Kendrick, M. A. Neumann and F. J. J. Leusen, CrystEngComm, 2013, 15, 3799–3807 RSC.
- C. R. Taylor and G. M. Day, Cryst. Growth Des., 2018, 18, 892–904 CrossRef CAS PubMed.
- P. G. Karamertzanis, A. v. Kazantsev, N. Issa, G. W. A. Welch, C. S. Adjiman, C. C. Pantelides and S. L. Price, J. Chem. Theory Comput., 2009, 5, 1432–1448 CrossRef CAS PubMed.
- G. Sun, Y. Jin, S. Li, Z. Yang, B. Shi, C. Chang and Y. A. Abramov, J. Phys. Chem. Lett., 2020, 8832–8838 CrossRef CAS PubMed.
- A. F. Shunnar, B. Dhokale, D. P. Karothu, D. H. Bowskill, I. J. Sugden, H. H. Hernandez, P. Naumov and S. Mohamed, Chem. – Eur. J., 2020, 26, 4752–4765 CrossRef CAS PubMed.
- S. L. Price and S. M. Reutzel-Edens, Drug Discovery Today, 2016, 21, 912–923 CrossRef PubMed.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179 CrossRef CAS PubMed.
- S. Grabowsky, A. Genoni and H. B. Burgi, Chem. Sci., 2017, 8, 4159–4176 RSC.
- B. Dittrich, S. Chan, S. Wiggin, J. S. Stevens and E. Pidcock, CrystEngComm, 2020, 22, 7420–7431 RSC.
- S. Dapprich, I. Komáromi, K. S. Byun, K. Morokuma and M. J. Frisch, J. Mol. Struct.: THEOCHEM, 1999, 461, 1–21 CrossRef.
- M. J. Phipps, T. Fox, C. S. Tautermann and C. K. Skylaris, Chem. Soc. Rev., 2015, 44, 3177–3211 RSC.
- B. C. Doak, J. Zheng, D. Dobritzsch and J. Kihlberg, J. Med. Chem., 2016, 59, 2312–2327 CrossRef CAS PubMed.
- D. A. Degoey, H. J. Chen, P. B. Cox and M. D. Wendt, J. Med. Chem., 2018, 61, 2636–2651 CrossRef CAS PubMed.
- P. Pracht, F. Bohle and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192 RSC.
- C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS PubMed.
- B. Dittrich, IUCrJ, 2021, 8, 305–318 CrossRef CAS PubMed.
- H. M. Senn and W. Thiel, Curr. Opin. Chem. Biol., 2007, 11, 182–187 CrossRef CAS PubMed.
- H. M. Senn and W. Thiel, Angew. Chem., Int. Ed., 2009, 48, 1198–1229 CrossRef CAS PubMed.
- U. Ryde, Methods Enzymol., 2016, 577, 119–158 CAS.
- O. Y. Borbulevych, J. A. Plumley, R. I. Martin, K. M. Merz Jr. and L. M. Westerhoff, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2014, 70, 1233–1247 CrossRef CAS PubMed.
- O. Borbulevych, R. I. Martin and L. M. Westerhoff, Acta Crystallogr., Sect. D: Struct. Biol., 2018, 74, 1063–1077 CrossRef CAS PubMed.
- R. Bjornsson and M. Buhl, J. Chem. Theory Comput., 2012, 8, 498–508 CrossRef CAS PubMed.
- A. E. Whitten and M. A. Spackman, Acta Crystallogr., Sect. B: Struct. Sci., 2006, 62, 875–888 CrossRef PubMed.
- B. Dittrich, S. Pfitzenreuter and C. B. Hübschle, Acta Crystallogr., Sect. A: Found. Crystallogr., 2012, 68, 110–116 CrossRef CAS PubMed.
- R. Kaminski, M. S. Schmøkel and P. Coppens, J. Phys. Chem. Lett., 2010, 1, 2349–2353 CrossRef CAS.
- P. Mörschel and M. Schmidt, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 26–35 CrossRef PubMed.
- J. Lübben, C. Volkmann, S. Grabowsky, A. Edwards, W. Morgenroth, F. P. A. Fabbiani, G. M. Sheldrick and B. Dittrich, Acta Crystallogr., Sect. A: Found. Adv., 2014, 70, 309–316 CrossRef PubMed.
- B. Dittrich, J. Lübben, S. Mebs, A. Wagner, P. Luger and R. Flaig, Chem. – Eur. J., 2017, 23, 4605–4614 CrossRef CAS PubMed.
- A. Gavezzotti, CrystEngComm, 2018, 20, 2511–2518 RSC.
- V. Blum, R. Gehrke, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter and M. Scheffler, Comput. Phys. Commun., 2009, 180, 2175–2196 CrossRef CAS.
- K. Jug and T. Bredow, J. Comput. Chem., 2004, 25, 1551–1567 CrossRef CAS PubMed.
- T. L. Teuteberg, M. Eckhoff and R. A. Mata, J. Chem. Phys., 2019, 150, 154118 CrossRef PubMed.
- M. Svensson, S. Humbel, R. D. J. Froese, T. Matsubara, S. Sieber and K. Morokuma, J. Phys. Chem., 1996, 100, 19357–19363 CrossRef CAS.
- A. Gavezzotti and G. Filippini, J. Am. Chem. Soc., 1995, 117, 12299–12305 CrossRef CAS.
- A. L. Spek, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2009, 65, 148–155 CrossRef CAS PubMed.
- A. Gavezzotti, J. Phys. Chem. B, 2003, 107, 2344–2353 CrossRef CAS.
- M. J. Turner, S. P. Thomas, M. W. Shi, D. Jayatilaka and M. A. Spackman, Chem. Commun., 2015, 51, 3735–3738 RSC.
- S. P. Thomas, P. R. Spackman, D. Jayatilaka and M. A. Spackman, J. Chem. Theory Comput., 2018, 14, 1614–1623 CrossRef CAS PubMed.
- C. F. Mackenzie, P. R. Spackman, D. Jayatilaka and M. A. Spackman, IUCrJ, 2017, 4, 575–587 CrossRef CAS PubMed.
- R. F. W. Bader, Theor. Chem. Acc., 2001, 276–284 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. B. C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. v. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Pittsburgh PA, 2013 Search PubMed.
- F. Furche, R. Ahlrichs, C. Hättig, W. Klopper, M. Sierka and F. Weigend, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 91–100 Search PubMed.
- J. Hutter, M. Iannuzzi, F. Schiffmann and J. VandeVondele, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 15–25 Search PubMed.
- S. Grimme, C. Bannwarth and P. Shushkov, J. Chem. Theory Comput., 2017, 13, 1989–2009 CrossRef CAS PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122 CrossRef CAS PubMed.
- J. Lübben, C. M. Wandtke, C. B. Hübschle, M. Ruf, G. M. Sheldrick and B. Dittrich, Acta Crystallogr., Sect. A: Found. Adv., 2019, 74, 50–62 CrossRef PubMed.
- P. Vishweshwar, J. A. McMahon, M. L. Peterson, M. B. Hickey, T. R. Shattocka and M. J. Zaworotko, Chem. Commun., 2005, 4601–4603 RSC.
- M. S. Adam, M. J. Gutmann, C. K. Leech, D. S. Middlemiss, A. Parkin, L. H. Thomas and C. C. Wilson, New J. Chem., 2009, 34, 85–91 RSC.
- S. Ren, M. Liu, C. Hong, G. Li, J. Sun, J. Wang, L. Zhang and Y. Xie, Acta Pharm. Sin. B, 2019, 9, 59–73 CrossRef PubMed.
- E. A. Heath, P. Singh and Y. Ebizusaki, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1992, 48, 1960–1965 CrossRef.
- F. P. A. Fabbiani, D. R. Allan, W. I. F. David, A. J. Davidson, A. R. Lennie, S. Parsons, C. R. Pulham and J. E. Warren, Cryst. Growth Des., 2007, 7, 1115–1124 CrossRef CAS.
- M.-H. Chambrier, N. Bouhmaida, F. Bonhomme, S. Lebegue, J.-M. Gillet, C. Jelsch and N. E. Ghermani, Cryst. Growth Des., 2011, 11, 2528–2539 CrossRef CAS.
- G. Admiraal, J. C. Eikelenboom and A. Vos, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1982, 38, 2600–2605 CrossRef.
- F. P. A. Fabbiani, D. R. Allan, S. Parsons and C. R. Pulham, CrystEngComm, 2005, 7, 179–186 RSC.
- E. M. Horstman, S. Goyal, A. Pawate, G. Lee, G. G. Z. Zhang, Y. Gong and P. J. A. Kenis, Cryst. Growth Des., 2015, 15, 1201–1209 CrossRef CAS.
- A. Tilborg, D. Jacquemin, B. Norberg, E. Perpete, C. Michauxa and J. Wouters, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 2011, 67, 499–507 CrossRef CAS PubMed.
- J. J. Du, L. Váradi, P. A. Williams, P. W. Groundwater, J. Overgaard, J. A. Platts and D. E. Hibbs, RSC Adv., 2016, 6, 81578–81590 RSC.
- L. H. Thomas, C. Wales and C. C. Wilson, Chem. Commun., 2016, 52, 7372–7375 RSC.
- X. Shi, N. el Hassan, A. Ikni, W. Li, N. Guiblin, A. Spasojević de-Biré and N. E. Ghermani, CrystEngComm, 2016, 18, 3289–3299 RSC.
- K. Naelapaa, J. van de Streek, J. Rantanen and A. D. Bond, J. Pharm. Sci., 2012, 101, 4214–4219 CrossRef PubMed.
- E. Lu, N. Rodríguez-Hornedo and R. Suryanarayanan, CrystEngComm, 2008, 10, 665–668 RSC.
- S. Darwish, J. Zeglinski, G. Rama Krishna, R. Shaikh, M. Khraisheh, G. M. Walker and D. M. Croker, Cryst. Growth Des., 2018, 18, 7526–7532 CrossRef CAS.
- K. Fucke, G. J. McIntyre, C. Wilkinson, M. Henry, J. A. K. Howard and J. W. Steed, Cryst. Growth Des., 2012, 12, 1395–1401 CrossRef CAS.
- D. Khamar, R. G. Pritchard, I. J. Bradshaw, G. A. Hutcheon and L. Seton, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2011, 67, o496–o499 CrossRef CAS PubMed.
- A. S. Larsen, M. A. Olsen, H. Moustafa, F. H. Larsen, S. P. A. Sauer, J. Rantanen and A. Madsen, CrystEngComm, 2019, 21, 4020–4024 RSC.
- P. Vishweshwar, J. A. McMahon, M. Oliveira, M. L. Peterson and M. J. Zaworotko, J. Am. Chem. Soc., 2005, 127, 16802–16803 CrossRef CAS PubMed.
- A. D. Bond, R. Boese and G. R. Desiraju, Angew. Chem., Int. Ed., 2007, 46, 618–622 CrossRef CAS PubMed.
- A. G. Shtukenberg, C. T. Hu, Q. Zhu, M. U. Schmidt, W. Xu, M. Tan and B. Kahr, Cryst. Growth Des., 2017, 17, 3562–3566 CrossRef CAS.
- C. F. Macrae, I. Sovago, S. J. Cottrell, P. T. A. Galek, P. McCabe, E. Pidcock, M. Platings, G. P. Shields, J. S. Stevens, M. Towler and P. A. Wood, J. Appl. Crystallogr., 2020, 53, 226–235 CrossRef CAS PubMed.
- A. Austin, G. A. Petersson, M. J. Frisch, F. J. Dobek, G. Scalmani and K. Throssell, J. Chem. Theory Comput., 2012, 8, 4989–5007 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- B. Dittrich, C. Server and J. Lübben, CrystEngComm, 2020, 22, 7432–7446 RSC.
- L. Pauling and O. Brockway, J. Am. Chem. Soc., 1935, 57, 2680–2684 CrossRef CAS.
- A. J. Cruz-Cabeza, R. J. Davey, S. S. Sachithananthan, R. Smith, S. K. Tang, T. Vetter and Y. Xiao, Chem. Commun., 2017, 53, 7905–7908 RSC.
- M. Warzecha, L. Verma, B. F. Johnston, J. C. Palmer, A. J. Florence and P. G. Vekilov, Nat. Chem., 2020, 12, 914–920 CrossRef CAS PubMed.
- A. J. Cruz-Cabeza and J. Bernstein, Chem. Rev., 2014, 114, 2170–2191 CrossRef CAS PubMed.
- M. A. Spackman, J. J. McKinnon and D. Jayatilaka, CrystEngComm, 2008, 10, 377–388 CAS.
Footnotes |
| † Dedicated to the memory of Prof. Tibor Koritsánszky. |
| ‡ Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ce00148a |
| This journal is © The Royal Society of Chemistry 2023 |