Ferrimagnetic and spin glass behaviour in SrMn²⁺₃Ti⁴⁺₁₄M³⁺₄O₃₈ (M = Ti and Fe) synthetic crichtonites

Abstract

Novel SrMn₃Ti₁₄M₄O₃₈ (M = Ti and Fe) compounds with a crichtonite-type structure are reported herein. M = Ti shows a ferrimagnetic behavior at T_N = 15 K, while M = Fe creates a ferromagnetic cluster-glass at T_f = 8 K via positional disorder. This family offers a promising magnetic playground.

---

Minerals have been the primary inspirational source for materials discoveries, and the ne plus ultra example is the perovskite family,¹ showing one of the widest ranges of properties and structural variations, e.g. ferroelectricity, photovoltaic, superconducting or magnetic properties.^1–3 Following these lessons and in the search for magnetic materials, this article focuses on the scarcely studied crichtonite-type family of compounds.

The crichtonite family can be represented with an AB₃C₁₈O₃₈ simplified formula. This mineral group includes for instance loveringite, crichtonite, senaite, davidite, landauite, lindsleyite, or matiasite with A = Ca, Sr, Pb, U, Na, Ba and K, respectively.^4–7

Natural crichtonites have been studied mostly in terms of their crystal structure, complex isomorphic substitutions and their hardness.^5,7–10 Synthetic crichtonites have been observed as predominant or secondary phases in high pressure experiments,^11–13 often coexisting with AM₁₂O₁₉ magnetoplumbites for the K(Ti₁₃Cr₄FeZrMg₂)O₃₈, Ba(Ti₁₂Cr₄Fe₂ZrMg₂)O₃₈ and (Ba_0.5K_0.5)(Ti₁₃Cr_3.5FeZrMg_2.5)O₃₈ compositions prepared at 11–12 GPa and 1500–1600 °C.¹⁴ Solid-state, sol–gel or hydrothermal methods have also been applied successfully in the synthesis of BaMn₃Ti₁₈O₃₈, Ca₂Zn₄Ti₁₆O₃₈, Ca(Ca,Mn,Ti)₂₁O₃₈, BiMg₃V₁₈O₃₈ and SrFe₃V₁₈O₃₈.^6,15–18 The latter show either Ti³⁺/Ti⁴⁺ or V³⁺/V⁴⁺ mixed-valence oxidation states in the C site, and together with B = Mn²⁺ or Fe³⁺ open the possibility for the occurrence of complex magnetic behavior.

In this work we report two new compounds, SrMn₃Ti₁₈O₃₈ (SMTO) and SrMn₃Ti₁₄Fe₄O₃₈ (SMTFO), which belong to the crichtonite family. Their crystal structures were characterized with X-ray (XRD) and neutron powder diffraction (NPD) along with their magnetic properties at low temperature. They illustrate the potential of this family group as a novel playground for magnetic materials with cations in different environments and oxidation states.

SMTO and SMTFO were synthesized by solid-state reaction under vacuum. Their respective precursors SrTi_16.5O₃₄ and SrTi₁₄O₂₉ were obtained from stoichiometric amounts of SrCO₃ and TiO₂ heated in air at 900 °C for 12 h. Afterwards, they were stoichiometrically mixed with MnO, Ti metal and TiO₂ for SMTO and with MnO₂, Fe and Fe₂O₃ for SMTFO. The powders were compressed into 80 mg pellets and placed into quartz tubes and sealed under vacuum. The synthesis temperature was increased to 950 °C in 3 h and held for 12 h; it was then raised to 1100 °C in 1.5 hours with a dwell time of 48 h. Finally, the samples were cooled to room temperature by turning off the furnace.

Initial powder XRD characterization shows that both compounds crystallize with the crichtonite-type structure (space group R3̄), see Fig. S1 (ESI†). The SMTO phase shows a small amount of TiO₂ precursor [7.2(4) wt%], while SMTFO is phase pure. High-resolution NPD was carried out at the Institut Laue-Langevin (ILL) in the D20 beamline with λ = 1.36 Å (118° take-off angle) for an accurate crystal structure determination since the different scattering factor between Ti (−3.43 fm), Mn (−3.73 fm) and Fe (9.45 fm) allows the identification of a possible cation ordering. NPD analyses were made through the Fullprof suite.¹⁹

Rietveld refinements of the NPD data are summarized in Table 1 and are shown in Fig. 1d and e. Both compounds crystallize in the desired crichtonite-type structure, with a small amount of unreacted TiO₂ precursor (7.22 wt%) for SMTO as observed from XRD. The crichtonite structure has general formula ^XIIA1^VIB1^IVB2₂^VIC1₆^VIC2₆^VIC3₆O₃₈, where the roman numerals indicate the coordination with oxygen atoms. The large A1 position is occupied in this case by Sr²⁺, whereas Mn²⁺ is located at the B1 and B2 positions in octahedral and tetrahedral coordination, respectively. Ti³⁺(Fe³⁺) cations are located in the C1–3 octahedral positions (see Fig. 1a). The structure comprises two different T and O layers in a (TOT*)₃ rhombohedral sequence with T* related to T by an inversion centre. The latter consists of C1–C2 octahedra sharing edges (Ti1 and Ti2 in Table 1) which form hexagonal rings linked together by B2 tetrahedra (Mn2) and A1 (Sr), as shown in Fig. 1b. Layer O involves twelve C3 (Ti3 and Fe3) octahedra describing a larger hexagonal unit with a B1 (Mn1) octahedron at the center, see Fig. 1c. The linkage between T and O layers is only through vertices while between T and T* is through Ti1–Ti2 edges. The cell parameters for SMTO (a = 10.4282(1) Å, c = 20.8410(3) Å, space group R3̄) are larger in comparison with SMFTO (a = 10.4200(1) Å, c = 20.8147(4) Å) due to the different ionic radii and this suggests that Fe³⁺ (0.645 Å) substitutes Ti³⁺ (0.67 Å) and not Ti⁴⁺ (0.605 Å). Neutron diffraction refinements confirmed the preferential occupation of Fe into the Ti3 position after several trials considering Fe in the other available positions. This is also supported by bond valence sum (BVS) calculations as Ti1 and Ti2 positions confirm a 4+ oxidation state but a smaller ∼3.5 + /3.1+ for Ti3/Fe3. Thus, the nominal formula results in Sr²⁺Mn₃²⁺Ti₁₄⁴⁺Ti₄³⁺O₃₈ and Sr²⁺Mn₃²⁺Ti₁₄⁴⁺Fe₄³⁺O₃₈ for SMTO and SMFTO respectively, with a Ti3(Fe3) 4+ : 3+ mixed valence position in a 1 : 2 ratio.

Table 1 Structural parameters obtained from the Rietveld fitting made to the NPD (λ = 1.36 Å) patterns for SMTO and SMTFO compounds at 300 K. BVS Σ(s_ij) were obtained considering the relation s_ij = exp[(r₀ − r_ij)/b], where r_ij are the bond lengths, b = 0.37 and r₀ is an empirical parameter

	SMTO	SMTFO
a Refined site occupancy factors for Ti3/Fe3 were 0.548(3)/0.451(3)%.Biso (Å^2) were constrained by elements with Sr = 0.9(1)|1.3(2), Mn = 0.7(1)|0.7(1), Ti,Fe = 0.45(4)|1.13(7) and O = 0.59(2)|0.59(2) for SMTO|SMTFO.
a (Å)	10.4282(1)	10.4200(1)
c (Å)	20.8410(3)	20.8147(4)
c/a	1.9985(1)	1.9976(1)
Volume (Å^3)	1962.78(4)	1957.17(5)
Crichtonite (wt%)	92.8 (0.7)	100.0
TiO2 (wt%)	7.2(0.4)	—
R wp (%)	7.61	11.10
R Bragg (%)	2.43	5.36
R exp (%)	3.56	4.77
χ ^2 (%)	4.57	5.38

---

SMTO
	Wyckoff	x	y	z	BVS
Sr1	3a	0	0	0	1.83(6)
Mn1	6c	0	0	1/2	1.87(8)
Mn2	3b	2/3	1/3	0.6454(4)	2.07(1)
Ti1	18f	0.2394(7)	0.3142(7)	0.3985(2)	4.08(4)
Ti2	18f	0.3278(6)	0.0841(7)	0.3928(2)	3.93(3)
Ti3	18f	0.5222(5)	0.3754(6)	0.4970(3)	3.52(3)
O1	18f	0.1922(4)	0.1324(4)	0.4358(2)	1.88(2)
O2	18f	2/3	1/3	0.5450(3)	2.12(2)
O3	18f	0.7211(4)	0.5409(3)	0.6711(2)	2.21(2)
O4	18f	0.4009(4)	0.4388(4)	0.4494(1)	2.12(2)
O5	18f	0.3611(4)	0.2612(4)	0.5589(1)	1.99(2)
O6	18f	0.3647(4)	0.2649(4)	0.3411(1)	1.84(2)
O7	6c	0.4973(4)	0.2039(5)	0.4418(2)	2.10(2)

---

SMTFO
	Wyckoff	x	y	z	BVS
Sr1	3a	0	0	0	1.788(8)
Mn1	6c	0	0	1/2	1.98(1)
Mn2	3b	2/3	1/3	0.6456(5)	2.29(3)
Ti1	18f	0.2446(1)	0.3163(1)	0.4014(3)	4.10(6)
Ti2	18f	0.3335(9)	0.0867(1)	0.3908(4)	3.90(5)
Ti3/Fe3^a	18f	0.5250(1)	0.3740(2)	0.4989(7)	3.56/3.06(6)
O1	18f	0.1923(5)	0.1318(6)	0.4375(2)	1.78(4)
O2	18f	2/3	1/3	0.5453(4)	2.26(3)
O3	18f	0.7202(7)	0.5364(5)	0.6709(3)	2.04(3)
O4	18f	0.4052(6)	0.4378(7)	0.4503(2)	2.13(4)
O5	18f	0.3570(6)	0.2538(6)	0.5594(2)	1.95(4)
O6	18f	0.3671(6)	0.2704(6)	0.3414(2)	1.99(8)
O7	6c	0.4939(6)	0.2045(7)	0.4426(2)	2.09(3)

---

Fig. 1 Crystal structure of SrMn₃Ti₁₈O₃₈ seen on the (a) (110) plane, (b) a and b plane at z = 0.9 and (c) a and b plane at z = 0.2; green, purple, light blue and red balls are the Sr, Mn, Ti and O atoms, respectively. Rietveld refinement to HR (λ = 1.36 Å) NPD at room temperature for (d) SrMn₃Ti₁₈O₃₈ and (e) SrMn₃Ti₁₄Fe₄O₃₈ compounds are shown; red empty circles, black and blue lines and vertical bars are observed data, fitted, difference and Bragg reflections, respectively.

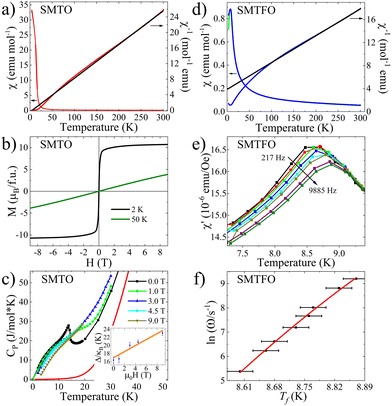
Magnetic properties were measured in a Dynacool-PPMS from Quantum Design. Temperature dependence of the magnetic susceptibility (χ) of SMTO shows a magnetic transition at T_N = 15 K without any FC-ZFC divergence under 1 kOe applied field, see Fig. 2a. The fit of the reciprocal susceptibility to the Curie–Weiss law above 210 K suggests predominant ferromagnetic (FM) interactions with θ_C = 5.0(1) K. The calculated effective magnetic moment of 9.6(1)μ_B/f.u. is slightly reduced from the expected value of 10.82μ_B for 3 Mn²⁺ (S = 5/2) and 4 Ti³⁺ (S = 1/2); this could be due to the small amount of unreacted TiO₂ and thus an error in the considered mass, but it could also be due to an orbital contribution from the t_2g degeneracy of the 3d¹ electrons in Ti³⁺ or to a reduced fitted range. Field dependent magnetization measurements at 2 and 50 K are shown in Fig. 2b. No hysteresis was detected, in accordance with the χ(T) behavior. At low temperature, a sharp increase of the magnetization can be observed and it can access 9μ_B with only 0.4 T and reaches 10.7μ_B at 9 T. NPD in the absence of a magnetic field confirms the ferrimagnetic (FiM) behavior of SMTO as described later.

Fig. 2 Magnetic measurements. SrMn₃Ti₁₈O₃₈: (a) χ and χ⁻¹ as a function of temperature; the Curie Weiss law fitted at high temperature is shown with a black straight line. (b) M vs. H at 2 and 50 K and (c) C_pvs. T (the inset shows the Δ/k_B). SrMn₃Ti₁₄Fe₄O₃₈: (d) χ and χ⁻¹ as a function of temperature, where the Curie Weiss law fitted at high temperature is shown with a black straight line, (e) χ′ vs. T and (f) the T_f change fitted with the Vogel–Fulcher equation.

Heat capacity measurements for SMTO show a sharp transition at T_C = 15 K in agreement with the FiM transition, see Fig. 2c. After the phonon contribution was subtracted (see Fig. S2 for details, ESI†), the magnetic entropy released of 47.65 J mol⁻¹ K⁻¹ accounts for around 70% of the theoretical value S = R(3 ln(2S + 1) + 4 ln(2S + 1)) = 67.74 J mol⁻¹ K⁻¹ for three Mn²⁺ (S = 5/2) and four Ti³⁺ (S = 1/2). A second feature appears at lower temperature, this flattens, broadens and shifts to higher temperatures as a magnetic field is applied. This was attributed to a Schottky anomaly and its contribution was calculated through the equation: C_Sch = NR(Δ/k_BT)²e^Δ/k_BT/(1 + e^Δ/k_BT)², where R is the ideal gas constant (R = 8.314 J mol⁻¹ K⁻¹) and Δ is the Schottky gap. Δ/k_B showed a value of 16.38 K at 2 K. This value reflects a linear relation with the applied field, see inset of Fig. 2c, well-known for a magnetic Schottky term caused by orphan or magnetic impurities.²⁰

For the SMTFO, the magnetic susceptibility presents a transition at 8.0(5) K with a FC-ZFC divergence, pointing towards a canted AFM or spin-glass behavior, see Fig. 2d. Curie–Weiss fit to the inverse susceptibility above 210 K results in θ_WC = −82.6(4) K supporting strong AFM interactions. The calculated effective moment of 13.1(1)μ_B per f.u. is reduced from the expected moment of 15.65μ_B for 3 Mn²⁺ (S = 5/2) and 4 Fe³⁺ (S = 5/2).

It also shows a large frustration index of f = |θ|/T = 10.25. NPD data collected at 2 K showed only short-range order correlations, see Fig. S3 (ESI†). AC-magnetic susceptibility was subsequently measured and revealed a spin-glass behavior, see Fig. 2e. The freezing temperature T_f varies according to the Vogel–Fulcher equation ω = ω₀ exp(E_a/k_B(T_f − T₀)), where ω is the frequency, 1/ω₀ is the intrinsic relaxation time (t₀), E_a is the activation energy, k_B is the Boltzmann constant and T₀ is the Vogel–Fulcher temperature (Fig. 2f). The fittings were made considering the two extreme t₀ values for spin-glass compounds 10⁻⁷s ≤ t₀ ≤ 10⁻¹³ s, obtaining E_a/k_B = 0.5 and 1 with T₀ = 8.22 and 8.02 K, respectively. The very low activation energies in SMTFO reflect that T_f changes only 0.25 K when the frequency changes four orders of magnitude. For spin-glasses, the relative shift per frequency decade, δT_f = ΔT_f/[T_fΔ log (f)], is often calculated. In SMTFO we estimate δT_f = 0.007, which is an order of magnitude smaller than for canonical spin-glass systems and thus suggests the formation of an FM cluster-glass state.^21,22

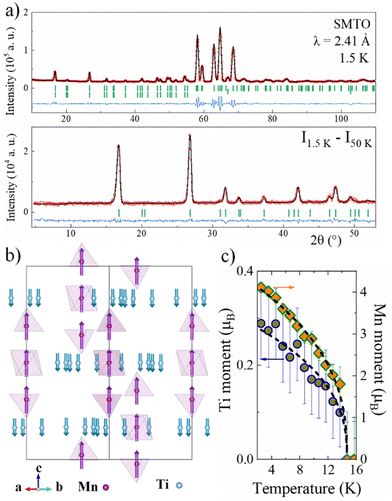
NPD of SMTO collected in D20 with λ = 2.41 Å at low temperature revealed the appearance of magnetic peaks below 15 K, see Fig. S4 (ESI†). These extra reflections coincide with the crystal structure and can be indexed with a k₀ = [0 0 0] propagation vector (Γ point of the first Brillouin zone). ISODISTORT was used to determine the possible magnetic structures and space groups.^23,24 The final Rietveld refinement was obtained with Fullprof with the mΓ1+ irreducible representation with the rhombohedral magnetic space group R3̄ (#148.17). Fig. 3a shows the full pattern with both crystal and magnetic structures at 1.5 K along with the difference pattern between 1.5 and 50 K data to evidence the magnetic intensity gained. The magnetic structure shown in Fig. 3b consists of a ferrimagnetic arrangement between Mn and Ti spins along the z axis. The refined moments at 1.5 K converged to 4.11(2)μ_B and 0.30(2)μ_B for Mn²⁺ and Ti³⁺ respectively (R_mag = 3.02%, χ² = 1.48). Attempts to refine only Mn moments resulted in fits of lower quality (R_mag = 4.93%, χ² = 2.09), thus proving the contribution of the titanium to the model. The slightly reduced moments from the expected 2S_Mn = 5μ_B and 2S_Ti = 1μ_B possibly reflect the disorder of the 3+/4+ mixed valency state in the Ti3 position. However, the ideal FiM disposition of 15μ_B from 3 Mn²⁺ with −4μ_B from 4 Ti³⁺ explains the values of 10.7μ_B at 9 T observed in the M vs. H curve at 2 K. The temperature evolutions of the Mn and Ti moments are shown in Fig. 3c, they follow a critical law μ(T) = μ₁[1 − (T/T_N)]^β with μ₁ = 0.29(3)μ_B and 4.37(5)μ_B for Ti and Mn, T_N = 14.68(1) K and β = 0.39(1). The critical exponent is close to the theoretical value of β = 0.367 for a 3D Heisenberg magnet, which is appropriate for the structure described before. Observation of unsaturated moments is common in Mn²⁺ oxides as observed for instance in Mn₂FeReO₆ (3.5μ_B) or MnTiO₃ (3.9μ_B).^25,26

Fig. 3 SrMn₃Ti₁₈O₃₈ magnetic structure. (a) NPD of SMTO at 1.5 K and intensity difference between 1.5 and 50 K, (b) magnetic structure with moments in Mn and Ti3 atoms and (c) the magnetic moment evolution on Mn and Ti3 atoms adjusted with a critical law as detailed in the text.

Summarizing, the change from a ferrimagnetic spin arrangement in SMTO (T_N = 15 K) to a cluster-glass in SMTFO (T_f = 8 K) originates from cation disorder in the Ti3 position due to Fe³⁺ substitution. However, this opens the possibility for the crichtonite family to be considered as magnetic materials. The AB₃C₁₈O₃₈ formula even further simplified to AM₂₁O₃₈ is in close relation to the industrially important M- and W-hexaferrites, i.e. AM₁₂O₁₉ and AM₁₈O₂₇.²⁷ The mineral family shows a great chemical variety and further directed cationic substitutions may show the full potential as a magnetic playground.

We thank the ILL for beamtime provided at D20 (DOI:https://doi.org/10.5291/ILL-DATA.5-31-2921). A. M. A. L. thanks the ANR-AMANTS project (19-CE08-0002-01). J. L. R. H. thanks the SECTEI/098/2022-Mexico for the post-doctoral fellowship. R. C. thanks Centrale Lille for a PhD scholarship. The Chevreul Institute (FR 2638), Region Hauts-de-France, and FEDER are acknowledged for funding the X-ray diffractometers and the PPMS magnetometer.

Conflicts of interest

There are no conflicts to declare.

References

1. R. J. D. Tilley, Perovskites: Structure-Property relationships, Wiley, 2016, pp. 327.
2. R. H. Mitchell, Perovskites: Modern and Ancient, Almax Press, 2002, pp. 318.
3. N. S. Arul and V. D. Nithya, Revolution of Perovskite, Springer, 2020, pp. 320.
4. B. M. Gatehouse, I. E. Grey, I. H. Campbell and P. Kelly, Am. Mineral., 1978, 63(1–2), 28.
5. P. R. Kelly, I. H. Campbell, I. E. Grey and B. M. Gatehouse, Can. Mineral., 1979, 17, 635.
6. R. C. Peterson and I. E. Grey Csiro, Can. Mineral., 1995, 33(5), 1083.
7. R. K. Rastsvetaeva, S. M. Aksenov, N. V. Chukanov and L. A. D. Menezes, Dokl. Chem., 2014, 455, 53.
8. S. J. Mills, L. Bindi, M. Cadoni, A. R. Kampf, M. E. Ciriotti and G. Ferraris, Eur. J. Mineral., 2012, 24(6), 1061.
9. L. A. D. Menezes Filho, N. V. Chukanov, R. K. Rastsvetaeva, S. M. Aksenov, I. V. Pekov, M. L. S. C. Chaves, R. P. Richards, D. Atencio, P. R. G. Brandão, R. Scholz, K. Krambrock, R. L. Moreira, F. S. Guimarães, A. W. Romano, A. C. Persiano, L. C. A. de Oliveira and J. D. Ardisson, Mineral. Mag., 2015, 79(2), 269.
10. P.-A. Wülser, N. Meisser, J. Brugger, K. Schenk, S. Ansermet, M. Bonin and F. Bussy, Eur. J. Mineral., 2006, 17(6), 933.
11. V. Butvina, A. Spivak, T. Setkova and O. Safonov, Minerals, 2023, 13(2), 192.
12. W. L. Gong, R. C. Ewing, L. M. Wang and H. S. Xie, MRS Online Proc. Libr., 1994, 353, 807.
13. T. H. Green and N. J. Pearson, Mineral. Mag., 1987, 51(359), 145–149.
14. J. Konzett, H. Yang and D. J. Frost, J. Petrol., 2005, 46(4), 749.
15. F. Zhao, Z. Yue, J. Pei, Z. Gui and L. Li, J. Solid State Chem., 2006, 179(6), 1720.
16. R. C. Peterson, I. E. Grey, L. M. D. Cranswick and C. Li, Can. Mineral., 1998, 36, 763.
17. S. Uma and A. W. Sleight, J. Solid State Chem., 2002, 164(1), 138.
18. T. M. Smith Pellizzeri, C. D. McMillen, Y. Wen, G. Chumanov and J. W. Kolis, Eur. J. Inorg. Chem., 2019, 4838.
19. J. Rodríguez-Carvajal, Physica B, 1993, 192(1–2), 55.
20. T. Zhu, B. Zhu, O. Mentré, S. Lee, D. Chen, Y. Jin, W. Zhu, Á. M. Arévalo-López, C. Minaud, K. Y. Choi and M. Lü, Chem. Mater., 2023, 35, 3951.
21. N. Marcano, P. A. Algarabel, L. F. Barquín, J. P. Araujo, A. M. Pereira, J. H. Belo, C. Magén, L. Morellón and M. R. Ibarra, Phys. Rev. B: Condens. Matter Mater. Phys., 2019, 99, 054419.
22. T. Klimczuk, H. W. Zandbergen, Q. Huang, T. M. McQueen, F. Ronning, B. Kusz, J. D. Thompson and R. J. Cava, J. Phys.: Condens. Matter, 2009, 21, 105801.
23. H. T. Stokes, D. M. Hatch and B. J. Campbell, ISODISTORT, ISOTROPY Software Suite, https://iso.byu.edu.
24. B. J. Campbell, H. T. Stokes, D. E. Tanner and D. M. Hatch, J. Appl. Crystallogr., 2006, 39, 607.
25. A. M. Arevalo-Lopez, G. McNally and J. P. Attfield, Angew. Chem., Int. Ed., 2015, 54, 12074.
26. A. M. Arevalo-Lopez and J. P. Attfield, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 104416.
27. T. Kimura, Annu. Rev. Condens. Matter Phys., 2012, 3(93), 110.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cc04336c

---