Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Ideal trigonal prismatic coordination geometry of Co(II) in a honeycomb MOF with a triptycene-based ligand†
Yoshiaki
Shuku
 a,
Rie
Suizu
a,
Rie
Suizu
 ab,
Masahisa
Tsuchiizu
*c and
Kunio
Awaga
ab,
Masahisa
Tsuchiizu
*c and
Kunio
Awaga
 *a
*a
aDepartment of Chemistry & Integrated Research Consortium on Chemical Sciences (IRCCS), Nagoya University, Furo-cho, Chikusa-ku, Nagoya 464-8602, Japan. E-mail: awaga.kunio.h8@f.mail.nagoya-u.ac.jp
bJapan Science and Technology Agency (JST), PRESTO, 4-1-8 Honcho, Kawaguchi, Saitama 332-0012, Japan
cDepartment of Physics, Nara Women's University, Kitauoyanishi-machi, Nara 630-8506, Japan
First published on 27th July 2023
Abstract
A metal–organic framework (MOF) comprised of cobalt ions and triptycene-based 3-fold symmetric bridging ligands 9,10-[1,2]benzenoanthracene-2,3,6,7,14,15(9H,10H)-hexaone (o-TT) was prepared. Single-crystal structure analysis revealed a 2D honeycomb network structure and the ideal trigonal prismatic geometry of the Co(II) ion. The magnetic anisotropy of the Co(II) ion in the trigonal prism coordination geometry was analyzed via magnetic measurements and model calculations.
Six-coordinate complexes with an octahedral coordination geometry are the most frequently observed for the first row transition metal ions. Another representative six-coordinate geometry is the trigonal prism, although far fewer examples of this geometry have been reported.1,2 Ligand field theory predicts that the ligand field stabilization energy (LFSE) of trigonal prismatic geometry is equal to that of octahedral geometry only for the d0, d1, d2 (LS), d5 (HS), d6 (HS) and d10 electronic configurations, and is less stable for the rest.3 The reported structural analyses of 6-coordinate complexes indicate that steric or electronic effects other than the LFSE are important to achieve the trigonal prismatic geometry.1,2 One of the effective strategies to form the trigonal prismatic geometry is to use a multi-dentate (tetra- or hexa-dentate) ligand that can sterically restrain the coordination geometry. In recent years, the syntheses of distorted trigonal prismatic cobalt complexes with hexadentate ligands have been reported, and the resulting complexes show single molecule magnet (SMM) behaviour in the trigonal prismatic geometry.4,5 This unique magnetic behaviour due to the strong anisotropic nature of the cobalt ion motivated us to design a trigonal prismatic coordination geometry for the development of magnetic materials.
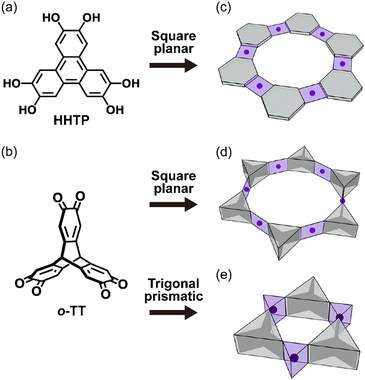
In our previous studies, we demonstrated that triptycene derivatives with π–π interactions can be building blocks for the honeycomb structure in their crystals.6,7 Recently, a triptycene derivative with three o-quinone moieties was reported to form a 2D honeycomb metal–organic framework (MOF) by forming a square planar coordination (Scheme 1d),8 with a packing motif similar to that of the MOFs of planar tris-bidentate bridging ligands such as HHTP (Scheme 1a and c).9,10 Here we would like to emphasize that the trigonal prismatic coordination geometry is also allowed as the building block for the 2D honeycomb network structure when the triptycene-based bridging ligand is used, because of the unique trigonal prismatic arrangement of bidentate coordination sites in the triptycene-based bridging ligand (Scheme 1e). From this point of view, the formation of a honeycomb structure can provide steric effects to stabilize the local trigonal prismatic coordination structure.
In the present work, we prepared a cobalt complex of the 9,10-[1,2]benzenoanthracene-2,3,6,7,14,15(9H,10H)-hexaone ligand (o-TT; Scheme 1b), namely [Co(o-TT)], and showed that it contains a honeycomb network that consists of the o-TT ligand and the trigonal prismatic coordination geometry of the Co ion. Since the anisotropic axes of the trigonal prismatic ions were aligned in the same direction in the crystal structure, magnetic measurements on [Co(o-TT)] clearly revealed the uniaxial magnetic anisotropy of the Co ion, which was consistent with the theoretical model calculations.
o-TT was prepared using the method described in the literature.11 The synthesis and crystal growth of [Co(o-TT)]·3CH3CN is described in the ESI.† Details of the X-ray crystal analysis are also shown in the ESI.†Fig. 1 shows the crystal structure of [Co(o-TT)]·3CH3CN, which belongs to the orthorhombic Pbca space group (#61). The crystal structure consists of a slightly distorted honeycomb lattice, which is compressed along the a axis, with three acetonitrile molecules in the voids. The honeycomb layers are stacked along the b axis by shifting in the a-axis direction relative to their neighbours with an interlayer distance of 5.72 Å. As shown in Fig. 2, the coordination geometry around the Co ion is a trigonal prism. The reported trigonal prismatic geometries around cobalt ions with three-claw ligands are usually distorted with a Bailar twist angle α (Fig. 2b) of 1–30°.4,5 However, the very small values of α (0.33, 0.35 and 0.63°) for [Co(o-TT)]·3CH3CN indicate an ideal trigonal prismatic geometry with a D3h local symmetry; this feature is supported by the finding of almost no variation in the Co–O distance l, the trigonal side distance s, or the trigonal bite distance 2h (Table S2, ESI†). Since there are no specific interactions between bidentate oxygen atoms such as three-claw ligands, the formation of a 2D honeycomb structure is presumably the driving force underlying the formation of an ideal trigonal prismatic coordination geometry. The Co–O distances are in the range from 2.047 to 2.132 Å, which are comparable to the range of Co–O distances for the octahedral Co(II) ion in the high-spin state (S = 3/2).12 Fig. S2a (see ESI†) shows the molecular structure of o-TT in [Co(o-TT)]·3CH3CN, which consists of three o-quinone moieties, A, B and C. Fig. S3 (see ESI†) shows a comparison of the C–O bond distances in o-TT for [Co(o-TT)] and its neutral species, where the three C–O bond distance ranges that are typical of benzoquinones (BQ), semiquinones (SQ) and hydroquinones (HQ) are indicated by pale red, green and blue, respectively. The structure of plane A is close to that of benzoquinone, and the structures of B and C are close to that of semiquinone. We concluded that o-TT in [Co(o-TT)]·3CH3CN is in a dianion state, namely (o-TT)2−, in which each negative charge is localized on planes B and C.
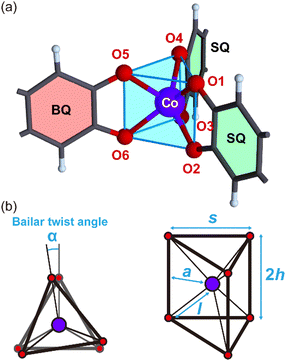 | ||
| Fig. 2 (a) Trigonal prismatic coordination geometry of the Co ions in [Co(o-TT)] and (b) definition of the structural parameters of D3h polyhedra with six vertices. | ||
The g-value anisotropy caused by the crystal electric field (CEF) was calculated for the Co(II) (d7) ion in the trigonal prismatic geometry (see Fig. S4, ESI†). The CEF Hamiltonian of the trigonal prism with D3h symmetry is effectively described by
 | (1) |
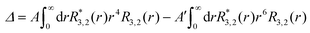 | (2) |
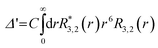 | (3) |
 | (4) |
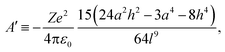 | (5) |
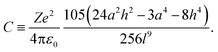 | (6) |
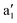 (dz2), e′ (dxy, dx2−y2), and e′′ (dyz, dzx) irreducible representations. For Δ > 0, the e′ orbitals are stabilized while the
(dz2), e′ (dxy, dx2−y2), and e′′ (dyz, dzx) irreducible representations. For Δ > 0, the e′ orbitals are stabilized while the  orbital is destabilized, and vice versa for Δ < 0. For Δ′ > 0, both the a1′ and e′ orbitals are stabilized, while the e′′ orbitals are destabilized, and vice versa for Δ′ < 0.
orbital is destabilized, and vice versa for Δ < 0. For Δ′ > 0, both the a1′ and e′ orbitals are stabilized, while the e′′ orbitals are destabilized, and vice versa for Δ′ < 0.
The electronic states were examined exactly for the standard multi-orbital Hubbard model of the d7 configurations under the CEF with D3h symmetry (see ESI† for details). The phase diagram of the high-spin (S = 3/2) and low-spin (S = 1/2) states is shown on the plane of Δ and Δ′ in Fig. S5 (see ESI†). The high-spin states are obtained in the regions where the energy levels of unoccupied and singly occupied d orbitals become closer, as expected naturally. The g-values were also evaluated for this model, and the ratio of gz/gx is also shown in Fig. 3. The magnetic anisotropy depends significantly on the values of Δ and Δ′. There are three parameter regions of high-spin states: (i) the Heisenberg spin with weak anisotropy gz > gx, gy when Δ > 0 and Δ′ > 0; (ii) a strong uniaxial magnetic anisotropy, namely gz ≫ gx, gy when Δ < 0 and Δ′ > 0; and (iii) the XY-model type anisotropy gz ≈ 0 when Δ ≈ 0 and Δ′ < 0.
 | ||
| Fig. 3 Phase diagram and the contour plot of gz/gx for the model of the Co(II) (d7) ion under the CEF with D3h symmetry. The model parameters are chosen as λ = 0.01 eV and U = 5 eV, U′/U = 0.8, J/U = 0.2 where λ is the spin–orbit coupling, U(U′) is the intra-orbital (inter-orbital) Coulombic repulsion and J is the Hund coupling (see ESI† for details). | ||
The temperature dependence of the magnetic susceptibility for a polycrystalline sample of [Co(o-TT)]·3CH3CN was examined using a Quantum Design MPMS XL SQUID magnetometer in the temperature range of 2–300 K under a magnetic field of 0.1 T. The powder X-ray diffraction pattern of the polycrystalline sample is consistent with the single-crystal structure (Fig. S12, ESI†). The temperature-independent contribution of the sample and cell was estimated by assuming Curie–Weiss behaviour in the high-temperature region, and the estimated contribution was subtracted from the molar susceptibility. The obtained paramagnetic susceptibility χp is shown in Fig. S7 (see ESI†), where the values of χpT are plotted as a function of the temperature T. The values of χpT monotonically decrease with a decrease in T from 300 K. The temperature dependence of χp−1 over the whole temperature range is shown in Fig. S8 (see ESI†). This temperature dependence above 50 K can be fitted to the Curie–Weiss law with the Curie constant of 3.78 cm3 mol−1 K and the Weiss constant of −14.5 K. It is notable that there is no ferrimagnetic behaviour in the low-temperature region, such as a turnover of the Weiss constant from negative to positive with a decrease in temperature. This suggests an S = 0 ground state for (o-TT)2−. The obtained Curie constant corresponds to g = 2.84 for the Co(II) ion, which is a reasonable value for the S = 3/2 HS Co(II) ion with a largely unquenched orbital contribution. Fig. S9 (see ESI†) shows the temperature dependence of χp below 50 K. The value χp shows a monotonic increase with a decrease in temperature, suggesting that there is no magnetic transition down to 2 K.
In order to measure the magnetic anisotropy of Co(II) in the trigonal prismatic coordination, we prepared oriented samples by aligning the thick platelet crystals of [Co(o-TT)]·3CH3CN on a plastic (PVC) plate by hand (see Fig. S10, ESI†) and fixing them with Apiezon N grease. The z axis in this figure is perpendicular to the ac plane of the crystal structure, namely the honeycomb lattice, and the x and y axes are parallel to it. Fig. 4 shows the angular dependence of the magnetization M in the zy plane for the oriented sample at 2, 5, 10, 15, 20 and 25 K. These measurements were obtained under a field of 2 T, using the sample rotator option of Quantum Design. The contribution of the empty rotator was measured and subtracted. The angle φ is the dihedral angle between the magnetic field and the ac plane, so that the magnetic field is parallel to the b axis at φ = 90°. Magnetic anisotropy with a periodicity of 180° clearly appears, and the magnetization exhibits maxima and minima at φ = 90 and 0°, respectively. This behaviour indicates uniaxial magnetic anisotropy with the easy axis parallel to the b axis (φ = 90°). To confirm the uniaxial magnetic anisotropy, the temperature dependence of Mx, My and Mz was examined. The results are shown in Fig. S11 (see ESI†). It is clear that Mz is always larger than Mx and My, and the difference between Mx and My is negligibly small. In addition, the ratio Mz/Mx (or My) is constant 1.38 (or 1.35) and is without any dependence on temperature. This gives gz/gx (or gy) = 1.17 (or 1.16), which corresponds to the light-blue region in Fig. 3. The observed weak uniaxial magnetic anisotropy is quite consistent with theoretical simulations for the Co(II) ion in the present trigonal prismatic coordination geometry.
 | ||
| Fig. 4 Angular φ dependence of the magnetization M in the zy plane for the oriented sample of [Co(o-TT)] (Fig. S10, ESI†) at 2, 5, 10, 15, 20 and 25 K. The angle φ is the dihedral angle between the magnetic field and the ac plane. | ||
In summary, we prepared a MOF with a honeycomb network structure that consists of a 3-fold symmetric triptycene-based bridging ligand (o-TT) and Co(II) ion in the trigonal prismatic coordination geometry. Interestingly, the trigonal prismatic coordination geometry and its orientation were fixed by a 2D honeycomb network structure. CEF calculations on a trigonal prismatic coordination geometry model illustrated the potential of various spin configurations and magnetic anisotropy, including Ising, XY and gz ≳ gx. The angular dependent magnetic measurements of aligned single crystals revealed a uniaxial magnetic anisotropy of gz/gx = 1.17. Although SMM behaviour was not observed on [Co(o-TT)] down to 2 K, presumably due to its weak magnetic anisotropy or intermolecular magnetic interactions, we proposed a novel strategy to prepare an ideal trigonal prismatic coordination geometry by forming a 2D honeycomb MOF structure. This strategy will be broadly applicable to triptycene-based ligands and has the potential to achieve strong magnetic anisotropy that aligns in the same direction in the crystal structure.
Y. S. performed the synthesis and magnetic measurements. R. S. carried out single crystal structural analysis. M. T. carried out theoretical model calculations. All authors contributed to writing and reviewing the manuscript. K. A. directed the project.
The authors acknowledge Japan Society for the Promotion of Science (JSPS) KAKENHI Grants 19K15520 (to Y. S.), 20H02707 (to R. S.) and 20H05621 (to M. T. and K. A.), and Japan Science and Technology Agency (JST) PRESTO Grant JPMJPR21A9 (to R. S.) for funding this work.
Conflicts of interest
There are no conflicts to declare.Notes and references
- E. Cremades, J. Echeverría and S. Alvarex, Chem. – Eur. J., 2010, 16, 10380–10396 CrossRef CAS PubMed.
- S. Alvarez, Chem. Rev., 2015, 115, 13447–13483 CrossRef CAS PubMed.
- J. C. Knight, S. Alvarez, A. J. Amoroso, P. G. Edwards and N. Singha, Dalton Trans., 2010, 39, 3870–3883 RSC.
- B. Yao, M. K. Singh, Y.-F. Deng, Y.-N. Wang, K. R. Dunbar and Y.-Z. Zhang, Inorg. Chem., 2020, 59, 8505–8513 CrossRef CAS PubMed and references cited therein.
- A. Landart-Gereka, M. M. Quesada-Moreno, I. F. Díaz-Ortega, H. Nojiri, M. Ozerov, J. Krzystek, M. A. Palacios and E. Colacio, Inorg. Chem. Front., 2022, 9, 2810–2831 RSC and references cited therein.
- Y. Shuku, A. Mizuno, R. Ushiroguchi, C. S. Hyun, Y. J. Ryu, B.-K. An, J. E. Kwon, S. Y. Park, M. Tsuchiizu and K. Awaga, Chem. Commun., 2018, 54, 3815–3818 RSC.
- R. Ushiroguchi, Y. Shuku, R. Suizu and K. Awaga, Cryst. Growth Des., 2020, 20, 7593–7597 CrossRef CAS.
- J. Lv, W. Li, J. Li, Z. Zhu, A. Dong, H. Lv, P. Li and B. Wang, Angew. Chem., Int. Ed., 2023, 62, e202217958 CrossRef CAS PubMed.
- R. W. Day, D. K. Bediako, M. Rezaee, L. R. Parent, G. Skorupskii, M. Q. Arguilla, C. H. Hendon, I. Stassen, N. C. Gianneschi, P. Kim and M. Dincă, ACS Cent. Sci., 2019, 5, 1959–1964 CrossRef CAS PubMed.
- Y. Misumi, A. Yamaguchi, Z. Zhang, T. Matsushita, N. Wada, M. Tsuchiizu and K. Awaga, J. Am. Chem. Soc., 2020, 142, 16513–16517 CrossRef CAS PubMed.
- S. Langis-Barsetti, T. Maris and J. D. Wuest, J. Org. Chem., 2018, 83, 15426–15437 CrossRef CAS PubMed.
- D. A. Shultz, in Magnetism: Molecules to Materials II, ed. J. S. Miller and M. Drillon, Wiley-VCH, Weinheim, 2001, ch. 8, pp. 281–306 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Details of the sample preparations, crystal structure analysis, model calculation of magnetic anisotropy, magnetic data and PXRD data. CCDC 2255851 and 2281350. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3cc02986g |
| This journal is © The Royal Society of Chemistry 2023 |