Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Machine learning and analytical methods for single-molecule conductance measurements
Yuki
Komoto
 ab,
Jiho
Ryu
ab,
Jiho
Ryu
 a and
Masateru
Taniguchi
a and
Masateru
Taniguchi
 *a
*a
aSANKEN, Osaka University, 8-1 Mihogaoka, Ibaraki, Osaka 567-0047, Japan. E-mail: taniguti@sanken.osaka-u.ac.jp
bArtificial Intelligence Research Center, Osaka University, Ibaraki, Osaka 567-0047, Japan
First published on 2nd May 2023
Abstract
Single-molecule measurements of single-molecule conductance between metal nanogap electrodes have been actively investigated for molecular electronics, biomolecular analysis, and the search for novel physical properties at the nanoscale level. While it is a disadvantage that single-molecule conductance measurements exhibit easily fluctuating and unreliable conductance, they offer the advantage of rapid, repeated acquisition of experimental data through the repeated breaking and forming of junctions. Owing to these characteristics, recently developed informatics and machine learning approaches have been applied to single-molecule measurements. Machine learning-based analysis has enabled detailed analysis of individual traces in single-molecule measurements and improved its performance as a method of molecular detection and identification at the single-molecule level. The novel analytical methods have improved the ability to investigate for new chemical and physical properties. In this review, we focus on the analytical methods for single-molecule measurements and provide insights into the methods used for single-molecule data interrogation. We present experimental and traditional analytical methods for single-molecule measurements, provide examples of each type of machine learning method, and introduce the applicability of machine learning to single-molecule measurements.
Introduction
Machine learning has made remarkable progress in recent years and has attracted attention for its applications in a variety of fields, including chemistry and nanoscience.1–4 New scientific insights can be gained by using machine learning to obtain more information from data. Single-molecule measurement is an area where machine learning is desirable due to the amount of data available, the variability of the data and the difficulty of interpretation. Single-molecule measurement is a technique for assessing the electrical conductance of a single molecule between metal nanogap electrodes (Fig. 1).5–13 It originated from the theoretical proposal of the molecular diode by Aviram and Ratner.14 Subsequent advances in experimental techniques have enabled researchers to actively pursue molecular electronics using functional molecular junctions as devices.8,11,15–21 Notably, molecular junctions composed of functional molecules have been reported as essential components in devices such as diodes,15–18 switches,19,20 and transistors.11,21 In the early stages of research on single-molecule measurements, the primary objective was to develop molecular devices as shown in Fig. 1b and e. Since Di Ventra's group theoretically proposed DNA and RNA sequencing using single-molecule measurements, this novel application of the technique has received attention as shown in Fig. 1c and f.22–24 The research of single-molecule measurements has developed to successfully measure the conductance of nucleotides in DNA and RNA25–30 and amino acids.31–37 As the nature of single-molecule measurements allows for the measurement of the direct conductance of a single molecule, they are expected to flourish as a new analytical method that is highly sensitive, rapid, and requires no pre-treatment steps. Furthermore, single-molecule measurements play a crucial role in the investigating of novel physical and chemical properties in the nanoscale. Recent research has focused on elucidating the mechanisms of electrical38,39 and thermal conduction at the nanoscale,40,41 observing quantum interference,42–44 and detecting and enhancing chemical reactions at the single-molecule level through the nanogap environment Fig. 1d and g.45–47 Regardless of the application, accurately measuring the conductance and identifying the molecular junction structure are critical. However, it is difficult to precisely identify and understand the structures of single-molecule junctions. The typical method of measuring the ensemble average of molecules of the order of Avogadro's number cannot be applied to single-molecule measurements. Electrical conductance measurements are the primary methods used to determine the structure of single-molecule junctions. However, the conductance of a single molecule varies widely, even for repeated measurements of the same molecule.48–53 Moreover, the order of magnitude of conductance differs among reporting groups,54–56 mainly because of variations in single-molecule junction structures and migration of metallic electrodes.48–50,52,53 The molecule-electrode coupling and the energy alignment of the conduction orbital of the bridging molecule determine the single-molecule conductance. Changes in the electrode or adsorption structures of the molecule alter the coupling and conduction orbital levels, which easily affect the conductance owing to noise or external stimuli. Therefore, in single-molecule measurements, conducting only a single trace is insufficient for discussing the properties of single-molecule junctions. Both experimental methods and data analysis need to be developed. Experimental methods for reliable measurements and analytical techniques for obtaining statistical data have been developed for single-molecule measurements. One of examples of experimental development is exploring more stable and well-defined contact with direct bonding between molecule and electrodes via C–C bonding.45,57,58 In aspect of analysis, in broader science, the recent remarkable development of machine learning technology has had a significant impact on a wide range of fields, including nanotechnology.1–3 The development of deep learning, which trains large amounts of data and has nonlinear and highly expressive capabilities, has been particularly noteworthy.2 In addition to deep learning, the accessibility of a wide variety of machine learning analyses has been improved by user-friendly software and the development of new methods such as XGBoost and LightGBM.59–61 Consequently, machine learning-based analysis has also attracted attention in the single-molecule measurements field.62 This review focuses on the development of analysis techniques for single-molecule measurements, particularly those utilising informatics approaches, which have been advancing rapidly in recent years. | ||
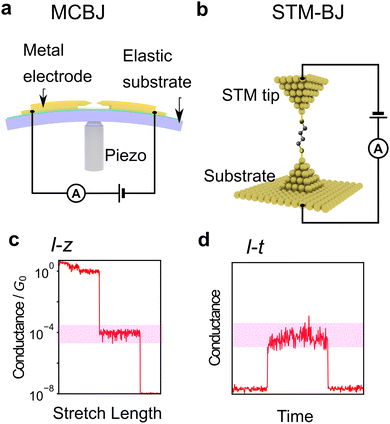
| Fig. 1 (a) Schematic image of single-molecular junction. (b–d) Schematic view of purposes of single-molecule measurement, (b) molecular device, (c) single DNA sequencing, and (d) single-molecule reaction. (e) molecule reported as single-molecule diode. Reprinted with permission from Ref. 18. Copyright 2023 American Chemical Society. (f) Current histogram of DNA nucleobases. Different nucleobases represent different single-molecule current. Reprinted with permission from Ref. 25. CC BY-NC-SA3.0. (g) Example of detection of chemical reaction with single-molecule measurement. Detection ratio between two classes increase with time. Reprinted with permission from Ref. 107 Copyright 2023 Royal Society of Chemistry. | ||
First, the experimental technique is briefly described. The most common method is the break junction (BJ) method, which includes the mechanically controllable break junction (MCBJ)63–67 and the Scanning Tunnelling Microscope (STM)-BJ method68 represented in Fig. 2a and b, respectively. The MCBJ method involves breaking metal wires on an elastic substrate to create a nanogap, while the STM-BJ method measures the conductance of a molecule between the substrate and STM tip. The first report of single-molecule conductance using the MCBJ method showed only several single-molecule conductance measurements.66 The MCBJ's ability to form stable and controllable nanogaps led to the development of methods to measure the vibrational state of molecules by changing voltage, such as point-contact spectroscopy (PCS) and inelastic tunnelling spectroscopy (IETS).67,69–71 These techniques require low-temperature environments for experiments, limiting them to basic research. However, after the STM-BJ method was reported in 2003, single-molecule measurements became executable in a commercially available setup, and various molecules were subsequently measured for their conductance.68 In this report, the authors not only used STM but also performed a statistical treatment of conductance through repeated breakup and formation, thereby increasing the reliability of conductance measurements. There are two types of conductance measurement methods in the BJ method. One is the I–z method, which measures current (I) during the process of breaking the junction by continuously increasing the nanogap distance (z) as shown in Fig. 2c, and the other is the I–t method, which measures conductance-time (t) after nanogap formation by keeping the nanogap distance constant as shown in Fig. 2d. Recently, not only break junction of metallic contact but also the I–t method using graphene electrodes have also attracted attention using, which provide a stable measurement by direct C–C bonding.45,57,58 Subsequently, methods other than conductance measurements have been developed, such as current–voltage (I–V) characteristic measurements,72–76 thermoelectric voltage measurements,77–80 and electrochemical measurement techniques9,81 to investigate electronic structures. Raman spectroscopy is used for spectroscopic measurements of vibrational states,82,83 and shot noise is used for conduction channel measurements.84,85 These measurement techniques have improved the amount of information obtained from single-molecule measurements. However, these elaborate experiments are experimentally costlier in comparison to simple conductance measurements.
Histogram-based analysis
In single-molecule conductance measurements, a plateau observed in the conductance trace is commonly interpreted as an indication of single-molecule conductance. However, similar plateaus are also observed in blank measurements. Although plateaus are more frequently observed in samples containing molecules, a single trace alone is insufficient to determine their presence. Therefore, histogram-based analysis is the most fundamental and important statistical analysis method for single-molecule measurements.5–13 Conductance histograms are typically created by accumulating conductance traces during the rupture process, and single-molecule conductance is then determined from the peak positions of the histogram. Although the single-molecule conductance is the most fundamental information, the peak width also contains information about the molecular junction. A series of conductance values determined from the histograms under different conditions provides more detailed information. The decay constants for the molecular series are determined using single-molecule conductance-molecular length plots. The decay constant depends on the conduction orbital level of the molecular backbone and broadening of the conjugated system.86,87 Experiments are also often performed at varying temperatures. The temperature dependence of the single-molecule conductance obtained at each temperature provides information on the conduction mechanism.39 For example, tunnelling conduction shows no temperature dependence, while hopping conduction shows Arrhenius-type temperature activity. Therefore, the conductance histogram provides basic information about the single-molecule junction under study.In addition to conductance measurements, histograms are a commonly used statistical tool for other parameters related to junction stability. These parameters include the junction plateau length, retention time, and snapback distance.88–91 The snapback distance is the distance travelled by the electrode immediately after breakage, which is defined by the difference between the elongation distance after gold junction breakage and the distance to metal junction re-formation. Additionally, a conductance-stretch length 2D histogram can provide a statistical representation of the overall trace shape.92,93 The 2D histogram displays conductance on the vertical axis and elongation distance on the horizontal axis, which allows for a visualization of the statistical behaviour; 2D histograms reveal the presence of conduction states or illustrate the decay of conductance with increasing distance.
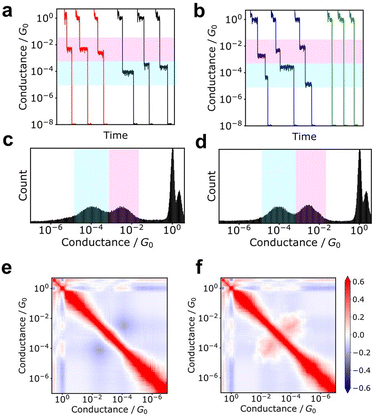
2D correlation histogram
Additionally, the 2D correlation histogram (2DCH) has proven to be a powerful tool for understanding molecular junctions with multiple conduction states.94–97 First, n conductance traces are individually converted into an m-dimensional conductance histogram. From this n × m matrix, an m × m correlation matrix is generated, which is then displayed as a 2D heat map in the 2DCH. The values in the 2DCH range from 1 for strong positive correlation, −1 for negative correlation, and 0 for no correlation at all. The correlation between the two conduction states related to the frequency of occurrence of the other state when one state is observed can be easily determined with the 2DCH. The examples for simulated test data is represented in Fig. 3. The two datasets exhibit similar conductance histograms. In 2DCH, there is clear difference in cross region between the two conductance states. This information is valuable for inferring the relationship between conduction states during the breaking process.Machine learning
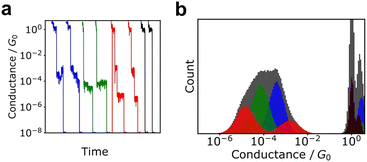
Although histograms are commonly used to analyse single-molecule measurements, they do not capture all information during the breaking process of single-molecule junctions as represented in Fig. 4. To compensate for this large measurement variability, the statistical analysis is applied for single-molecule current profiles. Machine learning algorithms improve the accuracy of discrimination, regression, and clustering with multi-dimensional features. Statistical models are trained and used to identify significant individual measurements to improve data quality. As mentioned, repeated single-molecule measurements can be collected via repeatedly breaking and forming the junction despite the variability of the individual conductance traces. This feature makes single-molecule measurements a promising research area for machine learning applications. In particular, deep learning algorithms can optimize a large number of parameters to improve accuracy,2 a good fit for the large amounts of data generated in single-molecule measurements.Typical machine leaning categories are described in Fig. 5. Machine learning is broadly categorised into supervised and unsupervised learning. Supervised learning is used to predict labels and numerical values for unknown data based on a data set with known labels and values. On the other hand, unsupervised learning is used to provide interpretation for data sets without explicit labels or values. In the next section, we provide examples of the application of machine learning to single-molecule measurements and its use in related research fields.
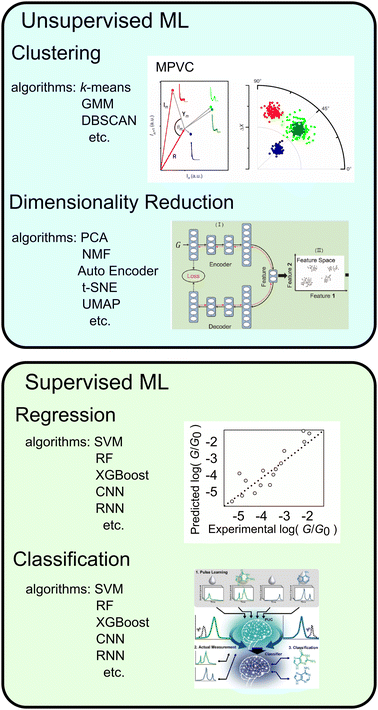 | ||
| Fig. 5 Types of machine learning, typical algorithms, examples and schematic image of application. Reproduced with permission from Ref. 107. Copyright 2023 Royal Society of Chemistry, Ref. 137. Copyright 2023 American Chemical Society, Ref. 109 CC BY-4.0. | ||
Unsupervised learning
In unsupervised learning, no explicitly correct labels or numerical errors are provided to the algorithm, and the probability density of the data is estimated directly from the measured data. The results of unsupervised learning are often evaluated using physical interpretations, and validation is often heuristic. The two main unsupervised learning methods used in single-molecule measurements are clustering, which involves dividing data into several groups,98–112 and feature extraction, which involves reducing the dimensionality of multi-dimensional data.95,99,106,107,113–115Clustering
Clustering is a method used to partition unlabelled data into multiple groups. Commonly used algorithms include k-means, Gaussian mixture models, and DBSCAN.116 The k-means method clusters to determine the centre of gravity of the clusters as the centroid and assigning data to clusters that are closest to the centroid. The application example of k-means are quantization of measurement images and clustering nanoparticle size by mass spectra of nanoparticle.117,118 GMMs clusters by representing probability densities with multiple Gaussian distributions. GMM are used for clustering FRET fluorescence responses and molecular structures obtained from molecular dynamics calculations.119,120 The DBSCAN algorithm clusters data by its probability density using a distance in the feature space. DBSCAN is applied to cluster nanopore current data.121k-means is simple algorithm and widely applied, but cannot be applied to data with different variances between clusters or data that are not spherically distributed since the data are clustered by distance from the centre. GMMs are also effective when each cluster has a different variance. k-Means and GMMs require the number of clusters to be defined in advance. DBSCAN requires distance between the data in advance. DBSCAN can also define outliers or noise points.The pioneering study of the application of clustering to conductance traces of single-molecule measurements is a multiparameter vector-based classification process (MPVC) reported by Lemmer et al.109 In which conductance traces are treated as vectors and features for clustering are extracted by transforming each trace into three characteristic quantities. A reference trace is initially selected, and the traces are transformed into a feature vector with three components: the Euclidean distance, which represents the magnitude of the difference between each trace and the reference vector; the normalised inner product, which indicates the similarity of the shapes; and the degree of fluctuation relative to the reference vector. The vectors are then clustered using an unsupervised learning algorithm. In this study, clustering was performed using the Gustafson-Kessel Fuzzy clustering algorithm, which successfully distinguished conductance traces in 3-D space from the simulation data that peaked at the same location in a conductance histogram. With Fuzzy clustering, data can be assigned to multiple clusters. For the experimental data of oligophenylene ethylene molecules, which did not exhibit a distinct peak in the conductance histogram of all traces due to a low bridging rate, the application of MPVC enabled the identification of populations that displayed a distinct plateau. This technique is not only applicable to conductance traces but also to current–voltage characteristic curves obtained by sweeping the bias voltage during junction formation. By clustering the I–V curves of molecules with tripodal anchors, three states with varying conductive and rectifying properties were distinguished, and their respective structures were identified by comparison to theoretical calculations.100
This MPVC method is visually intuitive because it utilises mapping to a three-dimensional feature space that reflects the shape of the trace. Nonetheless, some drawbacks exist, such as the challenge of identifying reference vectors and managing excessively lengthy traces when contrasting traces of varying sizes. Normal clustering algorithms require feature vectors with identical dimensions. Hence, each conductance trace must be transformed into a vector of the same dimensions. Fig. 6 displays other clustering scheme of single-molecule measurement. The most applicable conversion method is to create a conductance histogram from a single trace, which can easily convert a trace of any length into a vector with dimensions in bins.103,104,111 Vectors representing the histogram are clustered using algorithms such as k-means and spectral clustering. This method cannot distinguish between traces where the single-molecule conductance transitions from a high-conductance state to a low-conductance state and vice versa. In numerous measurements of individual molecules, the conductance tends to decrease as the distance increases.
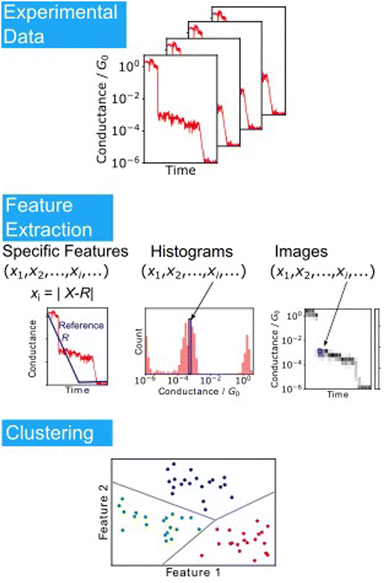 | ||
| Fig. 6 Analysis scheme of single-molecule data clustering. Experimental conductance traces are converted into feature vectors choosing specific features as reported in Ref. 109, using histograms or images. Feature vectors are clustered according to the algorithms. | ||
However, certain molecules, like alkanes, display a rise in conductance just before breaking due to the presence of gauche defects that lead to a decrease in conductance.79,122 It is essential to consider the loss of information, such as conductance increase, which may depend on the choice of feature vectors during the analysis. Another method using deep learning has been proposed, in which traces are treated as ordinary two-dimensional images.99,106,110 This image-based method can directly capture changes in conductance.
Clustering analysis provides valuable insights lost through simple histogram generation. In our study, we utilised Grid-based DBSCAN to analyse octanedithiol conductance traces and obtained histograms that revealed multiple distinct peaks by clustering data points within each trace.112 This approach enabled us to infer changes in the single-molecule junction structure from conductance changes during the rupture process. Clustering, a machine learning method, employs an algorithm to classify data without relying on the researcher's intention. It exposes insights that cannot be extracted through conventional histogram-based analysis.
As previously stated, there is no definitive solution in unsupervised learning, and the results are highly dependent on both pre-processing and model selection.123 In the case of clustering, a distance metric is utilised to group data points. The pre-processing of normalisation also impacts the clustering results. When dealing with multiple quantities of varying physical dimensions, it is necessary to normalise the data to enable proper clustering. Without normalisation, only those quantities with significant numerical variations will be affected, resulting in suboptimal clustering outcomes. Standardisation is the most common normalisation technique, which involves converting each feature's mean to zero and the standard deviation to one to mitigate size-related differences in physical quantities. Additionally, some clustering algorithms require a priori knowledge of the number of clusters; however, choosing an appropriate number of clusters is critical. Performance indices such as the least-squares error are not ideal for determining the number of clusters because they tend to improve as the number increases. A commonly used method involves adjusting the number of clusters and selecting a value that maximises or minimises the performance indicator, including a penalty term that depends on the number of clusters. Examples of such performance indices are the Calinski–Harabasz index, akaike information criterion (AIC), and bayesian information criterion (BIC).111,124 Using this approach, the molecules in chemical reactions, the number of association states of nucleobases, and recognition of small molecules have been clarified.124 Other methods for determining the number of clusters include identifying the point at which the slope of the error decreases with respect to the number of cluster changes, specifying a large number of classes, and assigning physical meanings to each class,125 or determining the classes from a physical model. Furthermore, machine learning emphasises the importance of understanding the data's characteristics. Therefore, associating the data to be clustered with physical interpretations is beneficial.123
Dimensionality reduction
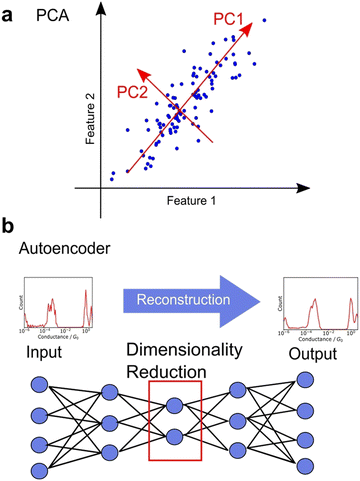
Unsupervised learning involves dimensionality reduction and feature extraction. Principal Component Analysis (PCA) is the most commonly used method for dimensionality reduction,99,106,113–115 in which orthogonal axes are selected to capture large values of variance in increasing order as shown in Fig. 7a. The number of dimensions is reduced by PCA, which mathematically corresponds to the variance-covariance matrix introduced above, a non-standardised matrix of 2DCH, by adopting the eigenvectors of the variance-covariance matrix in the order of increasing eigenvalues. The magnitude of the eigenvalue corresponding to the eigenvector represents the contribution of the component. PCA is widely used because of its ability to provide a unique solution without parameter selection and its ease of interpretation. In various related fields, PCA is used for noise reduction and characteristic feature extraction from GC/MS,126 EELS,127 Raman,128 and 13C-NMR spectra.129 To obtain a characteristic histogram, the histograms generated from each single trace were analysed using PCA, making it useful for spectral analysis. PCA is applied to Raman spectra measured simultaneously during single-molecule measurements.115 Other dimensionality reduction methods include sparse PCA, which emphasises differences, and non-negative matrix factorisation (NMF), which always decomposes data using a vector whose components are non-negative.116 Although NMF is mathematically incapable of defining a unique solution, it is convenient for interpreting physical data, such as conductance histograms and spectra constructed using only non-negative values. Nonlinear representation methods such as t-SNE and U-MAP are also useful for understanding complex data.106,110 These methods are algorithms where the closer the distance between data in the original feature space, the closer the distance after dimensionality reduction. Hence, these methods are powerful for visualisation of multi-dimensional data. Neural networks have also been applied for dimensionality reduction. Autoencoders are neural networks in which the input and output layers are identical. Fig. 7b shows the network structure of autoencoder. The intermediate layer of an autoencoder has a lower dimension than the input layer, and the dimensionality is reduced nonlinearly by the intermediate layer after reconstructing the output from the input training data.95,107 A deep learning-based noise reduction algorithm, known as Noise2Noise,130 has successfully reduced noise in nanopore measurements, leading to improved comprehension.131 Noise reduction and feature extraction through dimensionality reduction are effective tools for data visualization and improve data interpretability.Clustering of dimension-reduced data
Dimensionality-reduction techniques are commonly used as pre-processing methods for clustering to address the curse of dimensionality, which refers to the increase in computational cost when clustering large input data. While supervised learning is the typical approach to discrimination, unsupervised learning techniques, such as clustering, are used as a form of supervised learning by transforming the density estimation problem into a supervised function approximation problem through the comparison of probability densities.116 In single-molecule measurement research, clustering with dimensionality reduction is used to solve discrimination problems, such as chemical reaction detection.107 An autoencoder is applied for dimensionality reduction. The input and output are both I–z traces, and the number of nodes in the layer with the fewest nodes in between is less than the dimensions of the input data. The loss functions of the input and output were minimised to obtain the intermediate layer encoding the input layer, which served as the dimension-reduced feature for clustering using k-means. In the concentration-ratio identification of mixed solutions and the identification of chemical species during chemical reactions, the clustering method is applied for classification with the order of probability densities known. This technique enables the conversion of a conventional all-accumulated histogram with no clear peaks into two histograms with distinct peaks. In a Diels–Alder reaction system at a molecular junction, the ratio of one class decreases and that of the other class increases with time to represent the progress of the chemical reaction. Machine learning is used to analyse the individual trace information that disappears during histogram creation.There is a wide range of techniques for selecting features, reducing dimensionality, and clustering, which have been extensively researched in the context of clustering I–z traces.106 To evaluate these methods, several traces from the OPE experimental data were used to generate test traces with multiple classes. Various methods were employed, including 2D histograms, the method with reference vectors reported by Lemmer et al.,109 PCA, MDS, Samm, t-SNE, UMAP, and Autoencoder as dimensionality reduction techniques, and SOM, FCM, k-means, hierarchical, OPTICS, GMM, and GAL as clustering methods. The Folwkes–Mallows index was used to assess the similarity of the clustering results obtained from all combinations of the methods. The results indicated that GAL and GMM were the best clustering methods. Hierarchical clustering was not as effective, although it is sometimes easier to interpret from a physical and chemical property standpoint. Therefore, it is important to select an appropriate method based on the intended purpose. Feature selection was found to have a greater impact than clustering algorithms, with 2D histograms performing better than raw data. Nonlinear dimensionality reduction methods, such as t-SNE and UMAP, have been found to achieve higher accuracy.106 These results highlight the importance of utilising analysis methods with complex representations of feature selection for the analysis of single-molecule measurement data.
Supervised learning
In supervised learning, the model is provided with both the training data and the correct answer, and it uses this information to predict the objective variable for unknown data. Regression,132–135 which predicts continuous values, and classification,33,136–147 which predicts categorical values, such as chemical species prediction, are included in supervised learning.Regression
In related fields, regression has been employed to predict the performance of organic solar cell devices148,149 and the toxicity of nanoparticles.150 These prediction models aid in the establishment of efficient experimental procedures. Linear single regression, the most straightforward regression method, is widely used, including for single-molecule measurements. Machine learning regression employs multi-dimensional input data, such as vectors with multiple features that represent molecular fingerprints or converting molecular structures into vectors.151 Furthermore, graph neural networks, which directly train and predict graphs, have been developed in the machine learning field.152,153 The ability to predict physical properties directly from molecular structures, without the need for a chemist's input, is evolving, given that molecular structures can be represented as graphs.In the field of single-molecule conduction, machine learning plays an increasingly important role in theoretical calculations to reduce calculation costs.132,135 Convolutional neural networks trained on the outcomes of molecular dynamics (MD) and nonequilibrium green's function (NEGF) calculations are employed to predict the experimental conductance more efficiently than conventional, first-principles, direct calculations of transport properties. Additionally, the regression of experimental data for single-molecule measurements has been reported, with a machine learning-based regression model constructed to predict the conductance of a molecule.134 To obtain information about the molecule, descriptors are used as dependent variables, such as the gradient of kinetic energy, surface integral of kinetic energy, van der Waals surface area, bond stretch energy, and LUMO. 117 molecules were subjected to support vector machine (SVM)-based training and regression, yielding a correlation coefficient of 0.95 for the training set and 0.78 for the blind test set between the predicted and experimental conductance. The support vector regression is an extension of the SVM classifier, which determines discriminative boundaries to maximise the margin from each data point. SVM usually requires tuning of hyperparameters such as the regularisation parameter and the kernel selection. SVM is effective when the sample size is not large. Furthermore, a regression model was developed to predict the snapback distance and plateau length based on the trace geometry and conductance, with the aim of gaining insight into the phenomenon of single-molecule junction breakage with XGBoost.133 XGBoost is the algorithm that shows the highest accuracy of the many algorithms applied in NMR chemical shift prediction models.154 The regression model was constructed using five features, including the maximum conductance at the metal junction formation and the length near 1G0, rather than more general features such as the histogram obtained from a single trace in the clustering section. The machine learning techniques utilised in this study, namely, XGBoost, Adaboost, and Random Forest, train many weak regressors with low accuracy on a subset of features and make predictions by majority voting of these regressors. The importance of these features was determined based on the errors of the weak regressors. The importance comparison of the feature values in this study revealed that the distance to a metal junction rupture is a crucial factor in snapback distance prediction, whereas the plateau length is not a particularly significant parameter. This supports a model in which the molecular junctions are formed before the gold atom junction breaks. Thus, supervised learning can be applied not only to quantitative prediction but also to the interpretation of physical phenomena.
Classification
Another common type of supervised learning involves classifying data into categories. Machine learning classification is widely employed in image recognition and other applications.155,156 As an analytical technique, supervised learning for predicting a definite correct answer is a powerful means of object identification. Nanopore measurement is a technique that enables the measurement of a single particle by detecting the changes in ionic current that occur when a particle passes through a nanopore.157–159 The data obtained through the I–t method, which involves continuously measuring the conductance while maintaining a fixed gap interval in single-molecule conductance measurements, are analogous to the current measurement results obtained in nanopore measurements, as the current changes are observed only when a single molecule or particle passes through the nanopore. In nanopore measurements, machine learning classification is used to learn and categorise the viral species to train the current profile.160,161 DNA sequences are also analysed using recurrent neural network (RNN) to measure the current change when DNA was passed through the nanopore.162Machine learning has proven effective in identifying signals obtained from single-molecule measurements of DNA nucleobases and amino acids. Lindsay et al. utilised the STM-BJ and I–t methods of single-molecule measurements with molecular modifications to measure the conductance of nucleobases, achieving high accuracy in identifying DNA.136 Single-molecule measurements, which directly measure the tunnelling current through a single molecule in a gap, have the potential to be applied to a variety of molecules. The conductance differences among amino acids were also observed using single-molecule measurement.32 The same method was applied to amino acids, and using SVM,33 they successfully identified D-Asn to L-Asn, Gly to mGly, and Leu to Ile with accuracies of 0.87, 0.95, and 0.80, respectively. This method classified the single-molecule signals by analysing cluster of signals not individual signals. One of the ultimate goals of single-molecule measurements of DNA, RNA, and amino acids is to develop sequencing methods to identify individual signals rather than groups of signals. Our research group identified individual single-molecule signals by classification with supervised learning, random forests.137 For the machine learning analysis, the feature was the average of each region of the current signal partitioned along the time domain. The four DNA nucleotides were classified with an F-measure of 0.83. The F-measure is a performance measure for machine learning classification and is defined as the harmonic mean of sensitivity and specificity. This statistical process allowed the identification of single signals derived from single molecules. Furthermore, the targets of this method extend beyond the four DNA nucleobases to include modified bases that are expected to be cancer markers, oligo DNA with varying base lengths, and neurotransmitters.141–144 This method also allows for single-molecule measurements in cases where discrimination by conductance alone is ineffective in the presence of multiple molecules with similar conductance. Using this method, a mixture of modified bases and dG, which are cancer markers, was measured, and the obtained signals were individually discriminated using a machine-learning classifier trained on each solution as shown in Fig. 8.143 Concentration ratios were determined by predicting the class ratios. Mixed solutions of modified bases and dG with concentration ratios of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and 3
3 and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 were obtained, resulting in 1
1 were obtained, resulting in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4.0 and 2.7
4.0 and 2.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, respectively.
1, respectively.
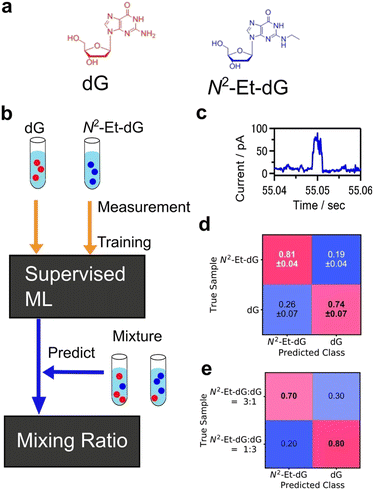 | ||
Fig. 8 Example of single-molecule classification. (a) Molecular structures of target molecules, dG and modified nucleobase N2-Et-dG. (b) Analysis scheme of single-molecule classification. Machine learning classifier was trained with the signals from pure dG, N2-Et-dG solution. The trained classifier predicted the molecule obtained from mixtures individually and determined mixing ratio. (c) Example of single-molecule current profile obtained by MCBJ I–t method. (d) Confusion matrix of validation result of pure solution signal classification. F-Measure is 0.78. (e) Predicted results for N2-Et-dG:dG = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and 1 1, and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 mixing solutions. Reproduced from Ref. 143 Copyright 2023 Royal Society of Chemistry. 3 mixing solutions. Reproduced from Ref. 143 Copyright 2023 Royal Society of Chemistry. | ||
Neural networks with high expressive power when trained on big data have also been utilised for the identification of single-molecule measurement data. Venkataraman et al. converted each conductance trace obtained by the I–z method of STM-BJ into a conductance histogram, and trained the conductance histogram features with a neural network, resulting in 93% accuracy in discriminating molecular traces from tunnel traces.140 In this study, the neural net classifier were trained with more than 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 traces and achieved high classification accuracy. This study demonstrates the potential of machine learning for the efficient analysis of large amounts of data. Classification using recurrent neural networks (RNNs) has also been reported.146 In the I–z traces of the BJ method, metal and molecular junction breaks are often occasional, and the lengths of the data cannot be aligned. However, RNNs are applicable to variable-length input data such as speech identification.163 In this method, RNNs were trained on normalised minimum cross-sectional time series data from MD simulations, and a class of experimental conductance traces was predicted. The results showed that RNNs classify variable-length traces and provide a tool for recognising characteristic motifs in traces that are difficult to find using simple data-selection algorithms.
000 traces and achieved high classification accuracy. This study demonstrates the potential of machine learning for the efficient analysis of large amounts of data. Classification using recurrent neural networks (RNNs) has also been reported.146 In the I–z traces of the BJ method, metal and molecular junction breaks are often occasional, and the lengths of the data cannot be aligned. However, RNNs are applicable to variable-length input data such as speech identification.163 In this method, RNNs were trained on normalised minimum cross-sectional time series data from MD simulations, and a class of experimental conductance traces was predicted. The results showed that RNNs classify variable-length traces and provide a tool for recognising characteristic motifs in traces that are difficult to find using simple data-selection algorithms.
Table 1 summarises the results of machine learning of current data from single-molecule measurements. In general, deep learning is considered capable of handling big data. However, it is difficult to determine a general algorithm because the classification results depend on the nature of the data, such as the dimension and the similarity between classes. It is also important to increase the interpretability of the data or reduce computational costs, even if it slightly reduces discrimination accuracy. Clear purposes and the choice of a suitable method for the purposes are necessary.
| Target | Class | Method | Modification | Accuracy | Algorithm | Dataset sizea | Ref. |
|---|---|---|---|---|---|---|---|
| a Signals, clusters, and traces denotes I–t pulse signals, cluster of I–t pulse signals, I–z traces. b Performance index is F-measure. | |||||||
| dAMP, dGMP, dTMP, dCMP, dmeCMP(5-methyl-cytosine) | 5 | STM-BJ | 4(5)-(2-mercaptoethyl)-1H-imidazole-2-carboxamide (ICA) | 0.84 | SVM | 200 signals | 136 |
| D-Asn, L-Asn | 2 | STM-BJ | ICA | 0.87 | SVM | 3000 clusters | 33 |
| Gly, mGly | 2 | ICA | 0.95 | 3000 clusters | |||
| Leu, Ile | 2 | ICA | 0.8 | 3000 clusters | |||
| dAMP, dGMP, dTMP, dCMP | 4 | MCBJ | — | 0.83b | RF | >4000 signals | 137 |
| Oligo DNA of A | 3 | MCBJ | — | 0.54b | XGBoost | >3000 signals | 141 |
| dG, N2-Et-dG | 2 | MCBJ | — | 0.77b | XGBoost | >1000 signals | 143 |
| Dopamine, serotonin, norepinephrine | 3 | MCBJ | — | 0.52b | XGBoost | >3000 signals | 144 |
| ds-DNA(12-15mer) | 6 | STM-BJ | — | 0.99 | XGBoost | 4200 traces | 138 |
| 8 | — | 0.99 | 5600 traces | ||||
| 1,6-Diaminohexane, 4,4′-bis(methylthiol)biphenyl | 2 | STM-BJ | — | 0.976 | CNN | >100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 traces 000 traces |
140 |
| 4,4′-Bis(methylthiol)biphenyl, 1,6-bis-(methylthiol)hexane | 2 | — | 0.959 | >100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 traces 000 traces |
|||
| 1,6-Diaminohexane, 1,6-bis-(methylthiol)hexane | 2 | — | 0.896 | >100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 traces 000 traces |
|||
| Cis-,trans-[3]cumulene | 2 | — | 0.884 | >100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 traces 000 traces |
|||
| Asp, Leu | 2 | MCBJ | Mercaptoacetic acid | 0.79b | XGBoost | 5280 signals | 36 |
Weakly supervised learning
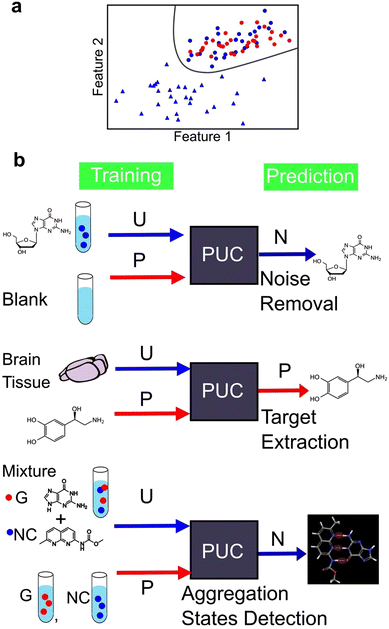
We identified two main types of machine learning, supervised and unsupervised learning. However, there exists a third category called weakly supervised learning that integrates features from both the aforementioned categories. One example of weakly supervised learning is the positive and unlabelled data classification (PUC) approach.164,165 Its objective is to identify data in the same manner as in supervised learning. However, unlike in supervised learning—where the training data include fully labelled data with known correct answers—in weakly supervised learning, the training is conducted without complete labels, that is, objective variables. The PUC was trained using two types of samples. The first sample included only one positive-signal class, similar to supervised learning, and the origin of the data was known. The second sample contained a mixture of positive and negative signals. However, the data were unlabelled and indistinguishable between the two classes. The PUC is trained on both samples and used to classify the positive and negative classes of the unlabelled data as represented in Fig. 9a. As the specific characteristics of single-molecule junctions are often unknown based on the available samples, this approach is useful because of its ability to identify unknown data within the available data.124,137,144 The PUC proposed by Elkan and Noto,164 applied to single-molecule measurements, trains a classifier that outputs the probabilities of being initially labelled with positive and unlabelled examples, under the assumption that labelled examples are randomly selected from the positive examples. Then, the class of unlabelled data is learned and predicted by weighting by labels using learned classifier to predict probability of labelled data. The algorithm can identify protein records that should be included in an incomplete specialized molecular biology database.164Fig. 9b shows an example of the application of PUC in single-molecule measurements. Our research group has developed a novel approach to enhance the accuracy of DNA nucleotide identification by eliminating signals that are present even in blank measurements.137 During single-molecule measurements, a telegraphic noise-like signal, which may be attributed to changes in the electrode structure or contamination, is occasionally observed even in blank measurements. These noise signals are also presumed to be present in DNA nucleotide measurements. However, it is difficult to distinguish between noise signals and signals derived from the sample. To address this issue, we utilised the PUC method to remove noise signals accurately. In this approach, the noise signals are classified as positive and the sample-derived signals are classified as negative. The blank data contained only the positive class, whereas the sample data included both the positive and negative classes that were unlabelled and unknown. Noise-derived signals were removed from the sample data by learning and discriminating using PUC. PUC-based noise reduction improves the discrimination accuracy described in supervised learning section. Although the conductance of noise signals is typically lower than that of molecular signals in such measurements, identifying molecular signals using a current criterion by extracting only the peak currents is feasible. However, this machine learning-based approach reduces the arbitrariness associated with criteria selection. Moreover, this method detects false negative signals originating from the sample. Our PUC-based analysis has the potential to identify signals that cannot be analysed using conventional methods.
Furthermore, it is important to note that noise signal contamination is not solely caused by the nature of single-molecule measurements. Since single-molecule measurements provide the advantage of directly measuring molecules, a direct measurement technique for biological samples is highly desirable. Consequently, single-molecule measurements are often conducted in the presence of various molecules other than the target molecule, contributing to noise signals. Our research group successfully identified neurotransmitters in biological samples using PUC to learn from samples derived from both biological and pure substances.144 By training pure solutions as positive and biological samples as unlabelled, the neurotransmitter signals in biological samples were extracted. The extracted neurotransmitter signals were then discriminated using supervised learning to obtain the concentration ratios of neurotransmitters in the biological samples. This approach is promising for analysing complex biological samples and enables the direct detection of target molecules.
PUC is a powerful analytical technique for identifying novel states. Its application to data obtained from single-molecule measurements has enabled quantitative evaluation of the aggregation ratio between small molecules and nucleobases.124 In a solution containing a mixture of small molecules and nucleobases, both aggregated and unaggregated molecules are present. The experimental isolation of the aggregated state is difficult. The signals of the small molecules and nucleobases were separately measured as positive and the mixed solution as unlabelled. PUC can classify and detect signals of the aggregation state present only in the mixed solution. Through this analysis, we confirmed, at the single-molecule level, that the aggregation ratio was larger for small molecules with more hydrogen bonding sites for guanine. The number of associated states was determined by clustering the signals of guanine and guanine recognition molecules using unsupervised learning, and the optimal cluster was determined using the BIC. Single-molecule measurements with machine learning-based analysis provide insights into molecular interactions at the microscopic level and the development of molecular design guidelines for new drugs. Therefore, machine learning has the potential to not only classify known labelled signals, but also contribute significantly to the discovery of unknown states.
Conclusions and future perspective
In summary, the use of machine learning to develop analytical techniques for single-molecule measurements has resulted in a substantial increase in the amount of information obtained beyond conductance, which is typically determined using conventional histogram-based analysis. Discriminating between multiple similar states obtained from the measurements of a single type of molecule, extracting characteristic features from multiple measurement data, and identifying the molecular species measured with single-molecule measurements have been achieved through machine learning-based analysis. These methods play a major role in understanding single-molecule conduction and utilising single-molecule measurements as a new biomolecule detection technique. The development of analytical techniques is essential for the ultimate goals of single-molecule measurement, such as the creation of molecular devices, investigation of novel phenomena at the nanoscale, and discovery of novel molecule detection, owing to the advantage of single-molecule resolution.Unsupervised learning
Measurement of various physical properties, including thermal and vibrational spectra, are performed in single-molecule experiments. The impact of noise is expected to be significant during measurement due to the microquantity of these physical properties. Numerous noise reduction methods have been developed in the field of informatics and applied to chemical measurements.126–131,166,167 Basic techniques involve dimensionality reduction via PCA,126–129 whereas more advanced techniques include dimensionality reduction using autoencoders and Noise2Noise mentioned above.167,168 Noise reduction methods can further be applied to single-molecule experiments.Since single-molecule measurement data often consists of various types of current traces, clustering is useful for understanding single-molecule phenomena. Since clustering is a heuristic method with no explicit answer, it is essential to select appropriate features. It is desirable to establish an appropriate feature selection method according to the physical properties of the target molecules. Furthermore, clustering methods that directly calculate the distance or similarity between current traces will be utilized for proper interpretation.
Supervised learning
Classification and identification of single-molecule current data is expected to expand to a variety of measurement targets. Further research is necessary for practical applications. It is desirable to identify nucleobases and amino acids in DNA, RNA, and protein sequences. In addition to the conventional identification of individual molecules, identification technology for molecules in sequences is essential. Furthermore, since generalization performance needs to be improved for a wide range of applications, it is necessary to eliminate differences among devices. For this purpose, refinement of the device fabrication process or learning of large-scale data including device differences will be effective. Physical insights gained from feature-dependence in discrimination accuracy would also be helpful for versatile application.Regression models are useful for investigation for high-performance single-molecule junction as molecular devices or identifying the origin of the unknown signals found with PUC. Although regression model for predicting the single-molecule conductance has already been reported,134 a more precise model is necessary and can be achieved by training on a larger dataset. To enable the identification of unknown substances, a machine learning model capable of analysing complex data is required to develop a data assimilation method and a large database of single-molecule conductance measured using a precise single-molecule measurement methodology.
The purpose of applying regression models is not only to predict precise values from large data sets, but also to efficiently search for optimal conditions from small data sets. In the related fields, Gaussian process regression has been reported to obtain high-yield or optimized results with minimal trials of experiments or calculations.169,170 Application of Gaussian process regression to measurement conditions and device fabrication method leads to more efficient and stable experiments.
Weakly supervised learning
Single-molecule junctions possess two metal–molecule interfaces, with the metal surface displaying properties distinct from the bulk, such as catalytic activity.13 Additionally, an immense electric field is applied by a bias voltage in the nanometre-scale gap.47 The unique nature of single-molecule junctions is expected to yield unparalleled chemical reactions. The previous study reported the amplification of chemical reaction rates of Diels–Alder reaction attributable to the electric field across the nanogap using the STM-BJ method.47 In this study, molecule identification before and after the reaction is solely predicted on conductance. The implementation of machine learning-based analytical techniques will improve discrimination accuracy and facilitate the discovery of unknown phenomena. New techniques to identify novel phenomena, such as PUC, are applicable for discovering new chemical reactions, not only for the determination of reaction rates of the same reaction as in bulk. Furthermore, these methods are helpful in identifying molecules that perform specific roles in a sample comprising a multitude of molecules.Application of novel methods
In related fields, there have been efforts to efficiently search for optimal experimental conditions through the utilisation of reinforcement learning.171,172 These applications have the potential to aid in the discovery of appropriate experimental conditions for single-molecule measurements and facilitate the generation of more reliable data.Machine learning has significantly improved the accuracy of discrimination in single-molecule measurements. In addition to expanding the applications of analytical techniques, exploring suitable experimental environments for measurement and analysis is becoming increasingly important. We previously demonstrated that modifying nanogap electrodes improves identification accuracy, even for molecules that cannot be distinguished using conventional machine learning methods alone.36 Further progress in both statistical analysis method and novel and precise measurement technique development will be necessary to achieve these goals.
Author contributions
Conceptualization,Y. K. and M. T.; Visualization, Y. K. and J. R.;Writing original draft, Y. K.; writing – review & editing Y. K. and M. T. All authorshave approved the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by Japan Society for the Promotion of Science (JSPS) KAKENHI Grant Numbers 19H00852, 22K14566, 22H00281 and Japan Science and Technology Agency (JST) Core Research for Evolutional Science and Technology (CREST) Grant Number JPMJCR1666, JPMJCR2234, and JST Support for Pioneering Research Initiated by the Next Generation (SPRING) Grant Number JPMJSP2138, Japan. We would like to thank Editage (www.editage.com) for English language editing.Notes and references
- K. A. Brown, S. Brittman, N. Maccaferri, D. Jariwala and U. Celano, Nano Lett., 2019, 20, 2–10 CrossRef.
- Y. LeCun, Y. Bengio and G. Hinton, Nature, 2015, 521, 436–444 CrossRef CAS.
- A. C. Mater and M. L. Coote, J. Chem. Inf. Model., 2019, 59, 2545–2559 CrossRef CAS.
- M. Meuwly, Chem. Rev., 2021, 121, 10218–10239 CrossRef CAS PubMed.
- X. Xie, P. Li, Y. Xu, L. Zhou, Y. Yan, L. Xie, C. Jia and X. Guo, ACS Nano, 2022, 16, 3476–3505 CrossRef CAS PubMed.
- T. A. Su, M. Neupane, M. L. Steigerwald, L. Venkataraman and C. Nuckolls, Nat. Rev. Mater., 2016, 1, 1–15 Search PubMed.
- H. Song, M. A. Reed and T. Lee, Adv. Mater., 2011, 23, 1583–1608 CrossRef CAS PubMed.
- Y. Komoto, S. Fujii, M. Iwane and M. Kiguchi, J. Mater. Chem. C, 2016, 4, 8842–8858 RSC.
- C. Huang, A. V. Rudnev, W. Hong and T. Wandlowski, Chem. Soc. Rev., 2015, 44, 889–901 RSC.
- F. Evers, R. Korytár, S. Tewari and J. M. Van Ruitenbeek, Rev. Mod. Phys., 2020, 92, 35001 CrossRef CAS.
- J. Bai, X. Li, Z. Zhu, Y. Zheng and W. Hong, Adv. Mater., 2021, 33, 2005883 CrossRef CAS PubMed.
- S. V. Aradhya and L. Venkataraman, Nat. Nanotechnol., 2013, 8, 399–410 CrossRef CAS PubMed.
- Y. Komoto, S. Fujii and M. Kiguchi, Mater. Chem. Front., 2018, 2, 214–218 RSC.
- A. Aviram and M. A. Ratner, Chem. Phys. Lett., 1974, 29, 277–283 CrossRef CAS.
- I. Díez-Pérez, J. Hihath, Y. Lee, L. Yu, L. Adamska, M. A. Kozhushner, I. I. Oleynik and N. Tao, Nat. Chem., 2009, 1, 635–641 CrossRef PubMed.
- R. Yamada, K. Albrecht, T. Ohto, K. Minode, K. Yamamoto and H. Tada, Nanoscale, 2018, 10, 19818–19824 RSC.
- M. L. Perrin, E. Galán, R. Eelkema, J. M. Thijssen, F. Grozema and H. S. J. van der Zant, Nanoscale, 2016, 8, 8919–8923 RSC.
- S. Fujii, T. Tada, Y. Komoto, T. Osuga, T. Murase, M. Fujita and M. Kiguchi, J. Am. Chem. Soc., 2015, 137, 5939–5947 CrossRef CAS PubMed.
- S. Y. Quek, M. Kamenetska, M. L. Steigerwald, H. J. Choi, S. G. Louie, M. S. Hybertsen, J. B. Neaton and L. Venkataraman, Nat. Nanotechnol., 2009, 4, 230 CrossRef CAS PubMed.
- J. L. Zhang, J. Q. Zhong, J. D. Lin, W. P. Hu, K. Wu, G. Q. Xu, A. T. S. Wee and W. Chen, Chem. Soc. Rev., 2015, 44, 2998–3022 RSC.
- B. Xu, X. Xiao, X. Yang, L. Zang and N. Tao, J. Am. Chem. Soc., 2005, 127, 2386–2387 CrossRef CAS PubMed.
- M. Zwolak and M. Di Ventra, Nano Lett., 2005, 5, 421–424 CrossRef CAS PubMed.
- M. Zwolak and M. Di Ventra, Rev. Mod. Phys., 2008, 80, 141–165 CrossRef.
- M. Zwolak and M. Di Ventra, Nat. Nanotechnol., 2016, 11, 117–126 CrossRef PubMed.
- T. Ohshiro, K. Matsubara, M. Tsutsui, M. Furuhashi, M. Taniguchi and T. Kawai, Sci. Rep., 2012, 2, 501 CrossRef PubMed.
- M. Tsutsui, M. Taniguchi, K. Yokota and T. Kawai, Nat. Nanotechnol., 2010, 5, 286–290 CrossRef CAS PubMed.
- T. Ohshiro, M. Tsutsui, K. Yokota and M. Taniguchi, Sci. Rep., 2018, 8, 1–8 CAS.
- T. Ohshiro, A. Asai, M. Konno, M. Ohkawa, Y. Komoto, K. Ofusa, H. Ishii and M. Taniguchi, Sci. Rep., 2022, 12, 1–9 CrossRef PubMed.
- T. Ohshiro, M. Konno, A. Asai, Y. Komoto, A. Yamagata, Y. Doki, H. Eguchi, K. Ofusa, M. Taniguchi and H. Ishii, Sci. Rep., 2021, 11, 19304 CrossRef CAS PubMed.
- Y. Li, J. M. Artés, B. Demir, S. Gokce, H. M. Mohammad, M. Alangari, M. P. Anantram, E. E. Oren and J. Hihath, Nat. Nanotechnol., 2018, 13, 1167–1173 CrossRef CAS PubMed.
- J. Hihath and N. Tao, Nanotechnology, 2008, 19, 265204 CrossRef PubMed.
- T. Ohshiro, M. Tsutsui, K. Yokota, M. Furuhashi, M. Taniguchi and T. Kawai, Nat. Nanotechnol., 2014, 9, 835–840 CrossRef CAS PubMed.
- Y. Zhao, B. Ashcroft, P. Zhang, H. Liu, S. Sen, W. Song, J. Im, B. Gyarfas, S. Manna and S. Biswas, Nat. Nanotechnol., 2014, 9, 466–473 CrossRef CAS PubMed.
- B. Zhang, W. Song, P. Pang, Y. Zhao, P. Zhang, I. Csabai, G. Vattay and S. Lindsay, Nano Futures, 2017, 1, 035002 CrossRef PubMed.
- M. P. Ruiz, A. C. Aragonès, N. Camarero, J. G. Vilhena, M. Ortega, L. A. Zotti, R. Pérez, J. C. Cuevas, P. Gorostiza and I. Díez-Pérez, J. Am. Chem. Soc., 2017, 139, 15337–15346 CrossRef CAS PubMed.
- J. Ryu, Y. Komoto, T. Ohshiro and M. Taniguchi, Chem. – Asian J., 2022, 17, e202200179 CrossRef CAS PubMed.
- B. Zhang, W. Song, P. Pang, H. Lai, Q. Chen, P. Zhang and S. Lindsay, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 5886–5891 CrossRef CAS PubMed.
- R. J. Nichols, W. Haiss, S. J. Higgins, E. Leary, S. Martin and D. Bethell, Phys. Chem. Chem. Phys., 2010, 12, 2801–2815 RSC.
- T. Hines, I. Diez-Perez, J. Hihath, H. Liu, Z.-S. Wang, J. Zhao, G. Zhou, K. Müllen and N. Tao, J. Am. Chem. Soc., 2010, 132, 11658–11664 CrossRef CAS PubMed.
- L. Cui, S. Hur, Z. A. Akbar, J. C. Klöckner, W. Jeong, F. Pauly, S.-Y. Jang, P. Reddy and E. Meyhofer, Nature, 2019, 572, 628–633 CrossRef CAS PubMed.
- L. Cui, W. Jeong, S. Hur, M. Matt, J. C. Klöckner, F. Pauly, P. Nielaba, J. C. Cuevas, E. Meyhofer and P. Reddy, Science, 2017, 355, 1192–1195 CrossRef CAS PubMed.
- J. Bai, A. Daaoub, S. Sangtarash, X. Li, Y. Tang, Q. Zou, H. Sadeghi, S. Liu, X. Huang and Z. Tan, Nat. Mater., 2019, 18, 364–369 CrossRef CAS PubMed.
- J. Liu, X. Huang, F. Wang and W. Hong, Acc. Chem. Res., 2018, 52, 151–160 CrossRef PubMed.
- M. Taniguchi, M. Tsutsui, R. Mogi, T. Sugawara, Y. Tsuji, K. Yoshizawa and T. Kawai, J. Am. Chem. Soc., 2011, 133, 11426–11429 CrossRef CAS PubMed.
- C. Yang, L. Zhang, C. Lu, S. Zhou, X. Li, Y. Li, Y. Yang, Y. Li, Z. Liu and J. Yang, Nat. Nanotechnol., 2021, 16, 1214–1223 CrossRef CAS PubMed.
- X. Huang, C. Tang, J. Li, L.-C. Chen, J. Zheng, P. Zhang, J. Le, R. Li, X. Li and J. Liu, Sci. Adv., 2019, 5, eaaw3072 CrossRef CAS PubMed.
- A. C. Aragones, N. L. Haworth, N. Darwish, S. Ciampi, N. J. Bloomfield, G. G. Wallace, I. Diez-Perez and M. L. Coote, Nature, 2016, 531, 88–91 CrossRef CAS PubMed.
- K.-H. Müller, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 45403 CrossRef.
- X. Li, J. He, J. Hihath, B. Xu, S. M. Lindsay and N. Tao, J. Am. Chem. Soc., 2006, 128, 2135–2141 CrossRef CAS PubMed.
- M. S. Hybertsen, L. Venkataraman, J. E. Klare, A. C. Whalley, M. L. Steigerwald and C. Nuckolls, J. Phys.: Condens. Matter, 2008, 20, 374115 CrossRef PubMed.
- Y. Kim, T. Pietsch, A. Erbe, W. Belzig and E. Scheer, Nano Lett., 2011, 11, 3734–3738 CrossRef CAS PubMed.
- S.-H. Ke, H. U. Baranger and W. Yang, J. Am. Chem. Soc., 2004, 126, 15897–15904 CrossRef CAS PubMed.
- F. Chen, J. Hihath, Z. Huang, X. Li and N. J. Tao, Annu. Rev. Phys. Chem., 2007, 58, 535–564 CrossRef CAS PubMed.
- S. Fujii, H. Cho, Y. Hashikawa, T. Nishino, Y. Murata and M. Kiguchi, Phys. Chem. Chem. Phys., 2019, 21, 12606–12610 RSC.
- S. K. Yee, J. A. Malen, A. Majumdar and R. A. Segalman, Nano Lett., 2011, 11, 4089–4094 CrossRef CAS PubMed.
- Y. Kim, W. Jeong, K. Kim, W. Lee and P. Reddy, Nat. Nanotechnol., 2014, 9, 881–885 CrossRef CAS PubMed.
- C. Yang, Z. Liu, Y. Li, S. Zhou, C. Lu, Y. Guo, M. Ramirez, Q. Zhang, Y. Li and Z. Liu, Sci. Adv., 2021, 7, eabf0689 CrossRef CAS PubMed.
- N. Xin, J. Guan, C. Zhou, X. Chen, C. Gu, Y. Li, M. A. Ratner, A. Nitzan, J. F. Stoddart and X. Guo, Nat. Rev. Phys., 2019, 1, 211–230 CrossRef.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss and V. Dubourg, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- T. Chen and C. Guestrin, in Proceedings of the 22nd acm sigkdd international conference on knowledge discovery and data mining, 2016, pp. 785–794.
- G. Ke, Q. Meng, T. Finley, T. Wang, W. Chen, W. Ma, Q. Ye and T.-Y. Liu, Adv. Neural Inf. Process. Syst., 2017, 30, 52 Search PubMed.
- W. Bro-Jørgensen, J. M. Hamill, R. Bro and G. C. Solomon, Chem. Soc. Rev., 2022, 51, 6875–6892 RSC.
- N. Agraıt, A. L. Yeyati and J. M. Van Ruitenbeek, Phys. Rep., 2003, 377, 81–279 CrossRef.
- J. M. Krans, C. J. Muller, I. K. Yanson, T. C. M. Govaert, R. Hesper and J. M. Van Ruitenbeek, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 14721–14724 CrossRef CAS PubMed.
- C. A. Martin, D. Ding, H. S. J. Van Der Zant and J. M. Van Ruitenbeek, New J. Phys., 2008, 10, 65008 CrossRef.
- M. A. Reed, C. Zhou, C. J. Muller, T. P. Burgin and J. M. Tour, Science, 1997, 278, 252–254 CrossRef CAS.
- R. H. M. Smit, Y. Noat, C. Untiedt, N. D. Lang, M. C. Van Hemert and J. M. Van Ruitenbeek, Nature, 2002, 419, 906–909 CrossRef CAS PubMed.
- B. Xu and N. J. Tao, Science, 2003, 301, 1221–1223 CrossRef CAS PubMed.
- Y. Kim, H. Song, F. Strigl, H.-F. Pernau, T. Lee and E. Scheer, Phys. Rev. Lett., 2011, 106, 196804 CrossRef PubMed.
- M. Taniguchi, M. Tsutsui, K. Yokota and T. Kawai, Nanotechnology, 2009, 20, 434008 CrossRef PubMed.
- J. Hihath and N. Tao, Prog. Surf. Sci., 2012, 87, 189–208 CrossRef CAS.
- E. Lörtscher, H. B. Weber and H. Riel, Phys. Rev. Lett., 2007, 98, 176807 CrossRef PubMed.
- S. Guo, J. Hihath, I. Díez-Pérez and N. Tao, J. Am. Chem. Soc., 2011, 133, 19189–19197 CrossRef CAS PubMed.
- Y. Isshiki, S. Fujii, T. Nishino and M. Kiguchi, J. Am. Chem. Soc., 2018, 140, 3760–3767 CrossRef CAS PubMed.
- J. R. Widawsky, M. Kamenetska, J. Klare, C. Nuckolls, M. L. Steigerwald, M. S. Hybertsen and L. Venkataraman, Nanotechnology, 2009, 20, 434009 CrossRef CAS PubMed.
- Y. Komoto, S. Fujii, H. Nakamura, T. Tada, T. Nishino and M. Kiguchi, Sci. Rep., 2016, 6, 1–9 CrossRef PubMed.
- P. Reddy, S.-Y. Jang, R. A. Segalman and A. Majumdar, Science, 2007, 315, 1568–1571 CrossRef CAS PubMed.
- K. Baheti, J. A. Malen, P. Doak, P. Reddy, S.-Y. Jang, T. D. Tilley, A. Majumdar and R. A. Segalman, Nano Lett., 2008, 8, 715–719 CrossRef CAS PubMed.
- M. Paulsson and S. Datta, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 241403 CrossRef.
- M. Tsutsui, T. Morikawa, Y. He, A. Arima and M. Taniguchi, Sci. Rep., 2015, 5, 11519 CrossRef CAS PubMed.
- R. J. Nichols and S. J. Higgins, Acc. Chem. Res., 2016, 49, 2640–2648 CrossRef CAS PubMed.
- S. Kaneko, E. Montes, S. Suzuki, S. Fujii, T. Nishino, K. Tsukagoshi, K. Ikeda, H. Kano, H. Nakamura and H. Vázquez, Chem. Sci., 2019, 10, 6261–6269 RSC.
- S. Kaneko, D. Murai, S. Marqués-González, H. Nakamura, Y. Komoto, S. Fujii, T. Nishino, K. Ikeda, K. Tsukagoshi and M. Kiguchi, J. Am. Chem. Soc., 2016, 138, 1294–1300 CrossRef CAS PubMed.
- M. A. Karimi, S. G. Bahoosh, M. Herz, R. Hayakawa, F. Pauly and E. Scheer, Nano Lett., 2016, 16, 1803–1807 CrossRef CAS PubMed.
- D. Djukic and J. M. Van Ruitenbeek, Nano Lett., 2006, 6, 789–793 CrossRef CAS PubMed.
- J. He, F. Chen, J. Li, O. F. Sankey, Y. Terazono, C. Herrero, D. Gust, T. A. Moore, A. L. Moore and S. M. Lindsay, J. Am. Chem. Soc., 2005, 127, 1384–1385 CrossRef CAS PubMed.
- L.-L. Peng, B. Huang, Q. Zou, Z.-W. Hong, J.-F. Zheng, Y. Shao, Z.-J. Niu, X.-S. Zhou, H.-J. Xie and W. Chen, Nanoscale Res. Lett., 2018, 13, 1–6 CrossRef PubMed.
- D. Murai, T. Nakazumi, S. Fujii, Y. Komoto, K. Tsukagoshi, C. Motta and M. Kiguchi, Phys. Chem. Chem. Phys., 2014, 16, 15662–15666 RSC.
- Z. Huang, F. Chen, P. A. Bennett and N. Tao, J. Am. Chem. Soc., 2007, 129, 13225–13231 CrossRef CAS PubMed.
- M. Tsutsui, K. Shoji, K. Morimoto, M. Taniguchi and T. Kawai, Appl. Phys. Lett., 2008, 92, 223110 CrossRef.
- J. McNeely, N. Miller, X. Pan, B. Lawson and M. Kamenetska, J. Phys. Chem. C, 2020, 124, 13427–13433 CrossRef CAS.
- M. Kamenetska, M. Koentopp, A. C. Whalley, Y. S. Park, M. L. Steigerwald, C. Nuckolls, M. S. Hybertsen and L. Venkataraman, Phys. Rev. Lett., 2009, 102, 126803 CrossRef CAS PubMed.
- C. A. Martin, D. Ding, J. K. Sørensen, T. Bjørnholm, J. M. Van Ruitenbeek and H. S. J. Van Der Zant, J. Am. Chem. Soc., 2008, 130, 13198–13199 CrossRef CAS PubMed.
- A. S. Paluch, D. L. Mobley and E. J. Maginn, J. Chem. Theory Comput., 2011, 7, 2910–2918 CrossRef CAS PubMed.
- A. Vladyka and T. Albrecht, Mach. Learn. Sci. Technol., 2020, 1, 035013 CrossRef.
- K. Wang, J. M. Hamill, B. Wang, C. Guo, S. Jiang, Z. Huang and B. Xu, Chem. Sci., 2014, 5, 3425–3431 RSC.
- Z. Balogh, P. Makk and A. Halbritter, Beilstein J. Nanotechnol., 2015, 6, 1369–1376 CrossRef CAS PubMed.
- N. D. Bamberger, J. A. Ivie, K. N. Parida, D. V. McGrath and O. L. A. Monti, J. Phys. Chem. C, 2020, 124, 18302–18315 CrossRef CAS.
- D. Cabosart, M. El Abbassi, D. Stefani, R. Frisenda, M. Calame, H. S. J. Van der Zant and M. L. Perrin, Appl. Phys. Lett., 2019, 114, 143102 CrossRef.
- T. Ohto, A. Tashiro, T. Seo, N. Kawaguchi, Y. Numai, J. Tokumoto, S. Yamaguchi, R. Yamada, H. Tada, Y. Aso and Y. Ie, Small, 2021, 17, 1–8 Search PubMed.
- L. Palomino-Ruiz, S. Rodríguez-González, J. G. Fallaque, I. R. Márquez, N. Agraït, C. Díaz, E. Leary, J. M. Cuerva, A. G. Campaña, F. Martín, A. Millán and M. T. González, Angew. Chem., Int. Ed., 2021, 60, 6609–6616 CrossRef CAS PubMed.
- B. H. Wu, J. A. Ivie, T. K. Johnson and O. L. A. Monti, J. Chem. Phys., 2017, 146, 092321 CrossRef.
- P. Yu, L. Chen, Y. Zhang, S. Zhao, Z. Chen, Y. Hu, J. Liu, Y. Yang, J. Shi, Z. Yao and W. Hong, Anal. Chem., 2022, 94, 12042–12050 CrossRef CAS PubMed.
- L. A. Zotti, B. Bednarz, J. Hurtado-Gallego, D. Cabosart, G. Rubio-Bollinger, N. Agrait and H. S. J. van der Zant, Biomolecules, 2019, 9, 1–13 CrossRef PubMed.
- L. Domulevicz, H. Jeong, N. K. Paul, J. S. Gomez-Diaz and J. Hihath, Angew. Chem., Int. Ed., 2021, 60, 16436–16441 CrossRef CAS PubMed.
- M. El Abbassi, J. Overbeck, O. Braun, M. Calame, H. S. J. van der Zant and M. L. Perrin, Commun. Phys., 2021, 4, 1–9 CrossRef.
- F. Huang, R. Li, G. Wang, J. Zheng, Y. Tang, J. Liu, Y. Yang, Y. Yao, J. Shi and W. Hong, Phys. Chem. Chem. Phys., 2020, 22, 1674–1681 RSC.
- M. S. Inkpen, M. Lemmer, N. Fitzpatrick, D. C. Milan, R. J. Nichols, N. J. Long and T. Albrecht, J. Am. Chem. Soc., 2015, 137, 9971–9981 CrossRef CAS PubMed.
- M. Lemmer, M. S. Inkpen, K. Kornysheva, N. J. Long and T. Albrecht, Nat. Commun., 2016, 7, 1–10 Search PubMed.
- D. Lin, Z. Zhao, H. Pan, S. Li, Y. Wang, D. Wang, S. Sanvito and S. Hou, Chem. Phys. Chem., 2021, 22, 2107–2114 CrossRef CAS PubMed.
- L. Lin, C. Tang, G. Dong, Z. Chen, Z. Pan, J. Liu, Y. Yang, J. Shi, R. Ji and W. Hong, J. Phys. Chem. C, 2021, 125, 3623–3630 CrossRef CAS.
- B. Liu, S. Murayama, Y. Komoto, M. Tsutsui and M. Taniguchi, J. Phys. Chem. Lett., 2020, 11, 6567–6572 CrossRef CAS PubMed.
- Q. Ai, J. Zhou, J. Guo, P. Pandey, S. Liu, Q. Fu, Y. Liu, C. Deng, S. Chang, F. Liang and J. He, Nanoscale, 2020, 12, 17103–17112 RSC.
- J. M. Hamill, X. T. Zhao, G. Mészáros, M. R. Bryce and M. Arenz, Phys. Rev. Lett., 2018, 120, 016601 CrossRef CAS PubMed.
- S. Kobayashi, S. Kaneko, T. Tamaki, M. Kiguchi, K. Tsukagoshi, J. Terao and T. Nishino, ACS Omega, 2022, 7, 5578–5583 CrossRef CAS PubMed.
- T. Hastie, R. Tibshirani, J. H. Friedman and J. H. Friedman, The elements of statistical learning: data mining, inference, and prediction, Springer, 2009, vol. 2 Search PubMed.
- A. R. Konicek, J. Lefman and C. Szakal, Analyst, 2012, 137, 3479–3487 RSC.
- X. Bi, S. Lee, J. F. Ranville, P. Sattigeri, A. Spanias, P. Herckes and P. Westerhoff, J. Anal. At. Spectrom., 2014, 29, 1630–1639 RSC.
- W. Khuntawee, M. Kunaseth, C. Rungnim, S. Intagorn, P. Wolschann, N. Kungwan, T. Rungrotmongkol and S. Hannongbua, J. Chem. Inf. Model., 2017, 57, 778–786 CrossRef CAS PubMed.
- M. Dagher, M. Kleinman, A. Ng and D. Juncker, Nat. Nanotechnol., 2018, 13, 925–932 CrossRef CAS PubMed.
- J. H. Zhang, X. L. Liu, Z. L. Hu, Y. L. Ying and Y. T. Long, Chem. Commun., 2017, 53, 10176–10179 RSC.
- M. Fujihira, M. Suzuki, S. Fujii and A. Nishikawa, Phys. Chem. Chem. Phys., 2006, 8, 3876–3884 RSC.
- A. K. Jain, M. N. Murty and P. J. Flynn, ACM Comput. Surv., 1999, 31, 264–323 CrossRef.
- Y. Takashima, Y. Komoto, T. Ohshiro, K. Nakatani and M. Taniguchi, J. Am. Chem. Soc., 2023, 145, 1310–1318 CrossRef CAS PubMed.
- D. Stefani, C. Guo, L. Ornago, D. Cabosart, M. El Abbassi, M. Sheves, D. Cahen and H. S. J. Van Der Zant, Nanoscale, 2021, 13, 3002–3009 RSC.
- M. Statheropoulos, A. Pappa, P. Karamertzanis and H. L. C. Meuzelaar, Anal. Chim. Acta, 1999, 401, 35–43 CrossRef CAS.
- S. Lichtert and J. Verbeeck, Ultramicroscopy, 2013, 125, 35–42 CrossRef CAS PubMed.
- J. Hwang, N. Choi, A. Park, J.-Q. Park, J. H. Chung, S. Baek, S. G. Cho, S.-J. Baek and J. Choo, J. Mol. Struct., 2013, 1039, 130–136 CrossRef CAS.
- Y. Kusaka, T. Hasegawa and H. Kaji, J. Phys. Chem. A, 2019, 123, 10333–10338 CrossRef CAS PubMed.
- J. Lehtinen, J. Munkberg, J. Hasselgren, S. Laine, T. Karras, M. Aittala and T. Aila, arXiv, 1803, 2018, 04189 Search PubMed.
- M. Tsutsui, T. Takaai, K. Yokota, T. Kawai and T. Washio, Small Methods, 2021, 5, 2100191 CrossRef CAS PubMed.
- M. Bürkle, U. Perera, F. Gimbert, H. Nakamura, M. Kawata and Y. Asai, Phys. Rev. Lett., 2021, 126, 177701 CrossRef PubMed.
- T. Fu, K. Frommer, C. Nuckolls and L. Venkataraman, J. Phys. Chem. Lett., 2021, 12, 10802–10807 CrossRef CAS PubMed.
- N. A. Lanzillo and C. M. Breneman, J. Appl. Phys., 2016, 120, 134902 CrossRef.
- R. Topolnicki, R. Kucharczyk and W. Kamiński, J. Phys. Chem. C, 2021, 125, 19961–19968 CrossRef CAS.
- S. Chang, S. Huang, H. Liu, P. Zhang, F. Liang, R. Akahori, S. Li, B. Gyarfas, J. Shumway, B. Ashcroft, J. He and S. Lindsay, Nanotechnology, 2012, 23, 235101 CrossRef PubMed.
- M. Taniguchi, T. Ohshiro, Y. Komoto, T. Takaai, T. Yoshida and T. Washio, J. Phys. Chem. C, 2019, 123, 15867–15873 CrossRef CAS.
- Y. Wang, M. Alangari, J. Hihath, A. K. Das and M. P. Anantram, BMC Genomics, 2021, 22, 1–10 Search PubMed.
- B. Xiao, F. Liang, S. Liu, J. Im, Y. Li, J. Liu, B. Zhang, J. Zhou, J. He and S. Chang, Nanotechnology, 2018, 29, 365501 CrossRef PubMed.
- T. Fu, Y. Zang, Q. Zou, C. Nuckolls and L. Venkataraman, Nano Lett., 2020, 20, 3320–3325 CrossRef CAS PubMed.
- Y. Komoto, T. Ohshiro and M. Taniguchi, Anal. Sci., 2021, 37, 513–517 CrossRef CAS PubMed.
- Y. Komoto, T. Ohshiro and M. Taniguchi, Nanomaterials, 2021, 11, 784 CrossRef CAS PubMed.
- Y. Komoto, T. Ohshiro and M. Taniguchi, Chem. Commun., 2020, 56, 14299–14302 RSC.
- Y. Komoto, T. Ohshiro, T. Yoshida, E. Tarusawa, T. Yagi, T. Washio and M. Taniguchi, Sci. Rep., 2020, 10, 1–7 CrossRef PubMed.
- L. E. Korshoj, S. Afsari, A. Chatterjee and P. Nagpal, J. Am. Chem. Soc., 2017, 139, 15420–15428 CrossRef CAS PubMed.
- K. P. Lauritzen, A. Magyarkuti, Z. Balogh, A. Halbritter and G. C. Solomon, J. Chem. Phys., 2018, 148, 084111 CrossRef PubMed.
- A. Magyarkuti, N. Balogh, Z. Balogh, L. Venkataraman and A. Halbritter, Nanoscale, 2020, 12, 8355–8363 RSC.
- H. Sahu, W. Rao, A. Troisi and H. Ma, Adv. Energy Mater., 2018, 8, 1801032 CrossRef.
- K. Kranthiraja and A. Saeki, Adv. Funct. Mater., 2021, 31, 2011168 CrossRef CAS.
- V. C. Epa, F. R. Burden, C. Tassa, R. Weissleder, S. Shaw and D. A. Winkler, Nano Lett., 2012, 12, 5808–5812 CrossRef CAS PubMed.
- S. Jaeger, S. Fulle and S. Turk, J. Chem. Inf. Model., 2018, 58, 27–35 CrossRef CAS PubMed.
- F. Scarselli, M. Gori, A. C. Tsoi, M. Hagenbuchner and G. Monfardini, IEEE Trans. Neural Networks Learn., 2008, 20, 61–80 Search PubMed.
- J. Zhou, G. Cui, S. Hu, Z. Zhang, C. Yang, Z. Liu, L. Wang, C. Li and M. Sun, AI open, 2020, 1, 57–81 CrossRef.
- K. Ito, Y. Obuchi, E. Chikayama, Y. Date and J. Kikuchi, Chem. Sci., 2018, 9, 8213–8220 RSC.
- T. Nakazawa and D. V. Kulkarni, IEEE Trans. Semicond. Manuf., 2018, 31, 309–314 Search PubMed.
- M. K. Song, S. X. Chen, P. P. Hu, C. Z. Huang and J. Zhou, Anal. Chem., 2021, 93, 2619–2626 CrossRef CAS PubMed.
- D. Branton, D. W. Deamer, A. Marziali, H. Bayley, S. A. Benner, T. Butler, M. Di Ventra, S. Garaj, A. Hibbs and X. Huang, Nat. Biotechnol., 2008, 26, 1146–1153 CrossRef CAS PubMed.
- C. Dekker, Nat. Nanotechnol., 2007, 2, 209–215 CrossRef CAS PubMed.
- S. Howorka and Z. Siwy, Chem. Soc. Rev., 2009, 38, 2360–2384 RSC.
- A. Arima, I. H. Harlisa, T. Yoshida, M. Tsutsui, M. Tanaka, K. Yokota, W. Tonomura, J. Yasuda, M. Taniguchi and T. Washio, J. Am. Chem. Soc., 2018, 140, 16834–16841 CrossRef CAS PubMed.
- A. Arima, M. Tsutsui, T. Washio, Y. Baba and T. Kawai, Anal. Chem., 2020, 93, 215–227 CrossRef PubMed.
- Q. Liu, L. Fang, G. Yu, D. Wang, C.-L. Xiao and K. Wang, Nat. Commun., 2019, 10, 2449 CrossRef PubMed.
- H. Yoo, E. Kim, J. W. Chung, H. Cho, S. Jeong, H. Kim, D. Jang, H. Kim, J. Yoon and G. H. Lee, ACS Appl. Mater. Interfaces, 2022, 14, 54157–54169 CrossRef CAS PubMed.
- C. Elkan and K. Noto, in Proceedings of the 14th ACM SIGKDD international conference on Knowledge discovery and data mining, 2008, pp. 213–220.
- T. Yoshida, T. Washio, T. Ohshiro and M. Taniguchi, Intell. Data Anal., 2021, 25, 57–79 Search PubMed.
- S. Torkamani and V. Lohweg, Wiley Interdiscip. Rev.: Data Min. Knowl. Discov., 2017, 7, e1199 Search PubMed.
- J. Brandt, K. Mattsson and M. Hassellöv, Anal. Chem., 2021, 93, 16360–16368 CrossRef CAS PubMed.
- K. Wu, J. Luo, Q. Zeng, X. Dong, J. Chen, C. Zhan, Z. Chen and Y. Lin, Anal. Chem., 2021, 93, 1377–1382 CrossRef CAS PubMed.
- M. Kondo, H. D. P. Wathsala, M. Sako, Y. Hanatani, K. Ishikawa, S. Hara, T. Takaai, T. Washio, S. Takizawa and H. Sasai, Chem. Commun., 2020, 56, 1259–1262 RSC.
- L. Bassman Oftelie, P. Rajak, R. K. Kalia, A. Nakano, F. Sha, J. Sun, D. J. Singh, M. Aykol, P. Huck and K. Persson, npj Comput. Mater., 2018, 4, 74 CrossRef.
- B. Ramsauer, G. J. Simpson, J. J. Cartus, A. Jeindl, V. García-López, J. M. Tour, L. Grill and O. T. Hofmann, J. Phys. Chem. A, 2023, 127, 2041–2050 CrossRef CAS PubMed.
- Z. Zhou, X. Li and R. N. Zare, ACS Cent. Sci., 2017, 3, 1337–1344 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2023 |