Molecular design of two-dimensional donor–acceptor covalent organic frameworks for intramolecular singlet fission

Abstract

Two-dimensional covalent organic frameworks (2D-COFs) constitute an ideal platform for the design of novel optoelectronic materials. In this work, the donor–acceptor copolymer strategy for intramolecular singlet fission (iSF) is revisited and applied for the tailored design of a functional 2D-COF with iSF capabilities.

---

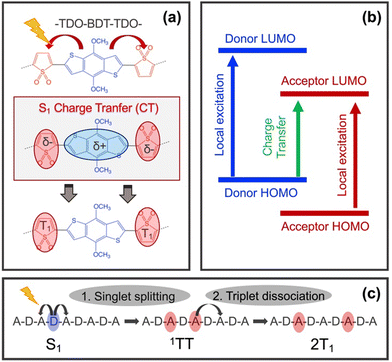
Singlet Fission (SF) is a multiple exciton generation process in which a high energy singlet evolves into two low energy triplets. This phenomenon has great potential to improve the power conversion efficiency of solar cells by reducing the energy loss of the high energy photons generating two profitable low energy excitons. SF is the consequence of two consecutives steps, singlet splitting and triplet–triplet separation (eqn (1)).¹ Photoexcitation promotes the system to the bright S₁ state which decays towards the so-called triplet-pair singlet (¹TT) within a spin-allowed reaction. Then, the ¹TT state dissociates into two independent triplets (2T₁). The success of both processes relies on the proper balance between the energetics and coupling, as well as on the kinetics with respect to the competitive pathways, namely fluorescence, intersystem crossing, or triplet–triplet recombination.²

S₁ ⇌ ¹TT ⇌ 2T₁ (1)

Since the early discovery of SF in molecular crystals of anthracene derivatives,³ continuous effort has been made to develop a molecular strategy to design SF materials with target properties.^4,5 In this context, the modularity of donor–acceptor (D–A) copolymers showed great promise for the development of intramolecular singlet fission (iSF) materials. In particular, pioneer work of Busby and coworkers showed that a triplet quantum yield up to 170% can be obtained for poly(benzodithiophene-alt-thiophene-1,1-dioxide) (BDT–TDO) copolymer chains upon the absorption of light,⁶ and similar conclusions were obtained for other D–A copolymers.^7,8

The D–A copolymer strategy for iSF relies on two main features: (i) strong intramolecular charge transfer (CT) upon light irradiation and (ii) the formation of well localised low-lying triplets in the acceptor core (Fig. 1a). These two characteristics, together with the thermodynamic requirement, E(S₁) ≥ 2E(T₁), have been used to screen large datasets of D–A pairs via cost-effective Density Functional Theory (DFT) calculations and its Linear Response Time-Dependent version (TDDFT), to find appropriate D–A combinations that fulfill these criteria.^9,10 These theoretical studies showed that thermodynamic adequacy in D–A copolymers mostly depends on the appropriate selection of a polymerizable acceptor with a sufficiently low triplet energy (ca. 1–2 eV).^10–12 In addition, the singlet splitting strongly depends on the CT mixing of the S₁ and ¹TT states,^13,14 which can be modulated by the relative position of the HOMO and LUMO of the D and A units (Fig. 1b).^9,10 Finally, intramolecular triplet–triplet dissociation rates rely upon a small acceptor–acceptor interaction through the donor core, and its ability to promote triplet energy transfer along the D–A copolymer chain.¹⁵ In this way, the role of the donor core is two-fold in the iSF process: first, to promote CT for efficient singlet splitting and second, to allow favorable and fast intrachain triplet energy transfer for triplet–triplet dissociation (Fig. 1c). Certainly, finding the proper balance between these two functionalities within a single donor unit may limit the applicability of the D–A copolymer strategy for iSF in the search of possible candidates. Here, this problem is addressed by the selection of two donor cores, one to optimize singlet splitting (D₁), and the other to promote triplet–triplet dissociation (D₂), both encompassed in an extended –A–D₁–A–D₂– two dimensional framework.

Fig. 1 (a) D–A strategy for iSF applied to the BDT–TDO copolymer includes strong CT upon absorption and the formation of S₁ followed by the formation of two low lying triplets in the TDO units. (b) Scheme of the HOMO and LUMO orbital energies of the D and A units required to obtain low lying CT excitation. (c) Scheme of the iSF steps in extended D–A copolymers: 1. Singlet splitting and 2. Triplet dissociation.

Two dimensional copolymers, or 2D covalent organic frameworks (COFs), have attracted great attention in the field of optoelectronics due to their ability to form crystalline periodic networks with the potential to improve the semiconducting properties of less ordered 1D polymers.¹⁶ The formation of π-conjugate sheets organised in π-stacking motifs results in well-structured directional charge (or exciton) carrier pathways that improve their mobility and lifetime.^17,18 Indeed, the D–A strategy has been widely exploited in the synthesis of 2D-COFs to promote effective charge separation and suppress undesired charge recombination within a variety of optoelectronic applications.^19–21 To date however, D–A 2D–COFs have not been proposed for iSF. The approach that is presented here is to rationally select one acceptor and two donors that can serve for the iSF purpose forming a 2D framework. To do that, the database containing the HOMO, LUMO, S₁ and T₁ energies of 92 donors and 32 acceptor units reported by Blaskovits et al. based on DFT and TDDFT calculations has been used,¹⁰ together with the triplet–triplet dissociation energies and triplet energy transfer barriers analysis previously reported.¹⁵ Both datasets are based on ωb97xD/6-31g* calculations benchmarked in front of refence wave function based methods.⁹ First, each unit is selected based on the aforementioned criteria. Then, the properties of the resulting –A–D₁–A–D₂– polymer are computed to ensure that it fulfills the requirements for iSF and finally, the periodic 2D framework is built and its electronic properties analysed.

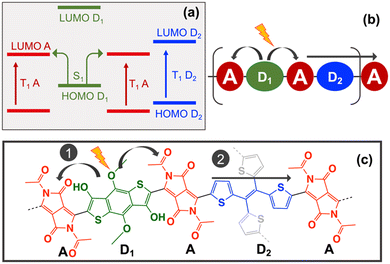
The selection of the A, D₁ and D₂ molecular units was made based on the scheme of Fig. 2a, where D₁ corresponds to the donor unit that assists the singlet splitting process by promoting light-induced CT, and D₂ corresponds to the donor unit that assists the triplet–triplet separation by promoting triplet energy transfer from one acceptor to the next one (Fig. 2b). Previous work showed that donors such as 2,2′-bithiophene and thiophene-vinyl-thiophene (TVT) are able to optimize both the thermodynamics and kinetics of the triplet-pair dissociation process in D–A copolymers due to their ability to adopt pseudo coplanar and non-coplanar conformations.¹⁵ In this case, the TVT unit was selected for D₂ because it can be extended into tetrathienylethene (TTE) as a 4-arms linker to built the 2D network. DFT and TDDFT(TDA) calculations were done for TTE at the same level ωb97xD/6-31g* using Gaussian 09²² to collect the HOMO, LUMO, S₁ and T₁ energies of this ligand (Table 1).

Fig. 2 (a) Scheme of the HOMO and LUMO orbital energies required for the –A–D₁–A–D₂– copolymer strategy for iSF. (b) Scheme of the –A–D₁–A–D₂– 1D sequence. (c) Molecular structure of the –A–D₁–A–D₂– copolymer proposed for iSF. Highlighted in red the DPP acceptor units, in green the BDT D₁ unit, in blue the TVT D₂ unit to form a 1D copolymer, and in grey the extension of D₂ to the TTE derivative for the formation of the 2D COF.

Table 1 S₁, T₁, HOMO and LUMO energies (in eV) obtained with DFT and TDDFT(TDA) at ωb97xD/6-31g* level for the selected molecular building blocks of the –A–D₁–A–D₂–A– polymer

Molecular unit	S1	T1	HOMO	LUMO
a Collected from ref. 10.
TVT^a	4.26	2.47	−7.23	0.23
TTE	3.62	2.34	−6.94	0.05
BDT(R1 = –OH, R2 = –OCH3)^a	4.24	2.87	−6.77	0.80
DPP (R = –COOCH3)^a	4.15	2.08	−8.29	−0.83

---

The next step is to select an appropriate D₁–A pair able to localise T₁ in the A unit and promote CT from D₁ to A when combined with TTE. This can be achieved by ensuring that the energy of T₁ increases following T₁(A) < T₁(D₂) < T₁(D₁) and that the energy of the HOMO (and LUMO) decreases following HOMO(D₁) > HOMO(D₂) > HOMO(A) as shown in Fig. 2a. From the 32 acceptor candidates, 8 have T₁ energies below TTE, which correspond to substituted versions of diketopyrrolopyrrole (DPP) and isoindigo (II) acceptor cores (Table S1.1, ESI†). The II acceptors were discarded due to their tendency to strongly localise not only T₁ but also S₁ state in the A unit, significantly reducing the CT.⁹ From the 92 donor candidates, only 4 have HOMO, LUMO and T₁ energies above TTE. These donors correspond to hydroxyl substituted derivatives of benzodithiophene (BDT) and 2,2′-bithiophene (Table S1.2, ESI†). 2,2′-bithiophene was discarded for D₁ as it has better features for D₂. To promote the largest possible CT within these candidates, the DPP with the largest T₁ and the BDT with the highest HOMO energy were selected for A and D₁, respectively. The resulting –A–D₁–A–D₂–A copolymer sequence (–DPP–BDT–DPP–TTE–) is shown in Fig. 2c.

The S₁ and T₁ excited states of the –DPP–BDT–DPP–TTE– copolymer were computed using a tetramer model (A–D₁–A–D₂), and the local and CT character analised based on the electron and hole transition densities located in the different A, D₁ and D₂ fragments.²³ The S₁ and T₁ vertical energies obtained are 2.60 eV and 1.49 eV, respectively, which leads to a E(S₁)-2E(T₁) energy difference of −0.37 eV, which is larger than the −1.0 eV limit established for the vertical energetic requirement for iSF.⁹ Indeed, optimization of the S₁ and T₁ states stabilises their energies down to 2.38 eV and 1.18 eV, respectively, resulting in a slightly positive E(S₁)-2E(T₁) energy difference. Regarding the excited state character, the local character of T₁ obtained is 0.45 and the CT character of S₁ is 0.22 (Table 2 and Table S2.1, ESI†), both within the range established to accomplish the coupling and separation requirements for iSF.⁹ These results confirm that appropriate energetic, coupling, and separation requirements for iSF can be obtained from the rational selection of the molecular building blocks considering their relative T₁ and HOMO/LUMO energies.

Table 2 Excited state characterization at ωb97xD/6-31g* level: vertical energy (eV), D₁–to–A charge transfer (CT) and A–to–A local character of S₁ and T₁, respectively, obtained for the DPP-BDT-DPP-TTE tetramer model optimized (i) in gas phase, and within (ii) the Kagome lattice and (iii) the rhombic monolayer

	S1 (eV)	T1 (eV)	S1 (CT)	T1 (local)
(i) Gas phase	2.60	1.49	0.22	0.45
(ii) Kagome	2.31	1.24	0.16	0.39
(iii) Rhombic	2.12	1.16	0.23	0.28

---

Two different topologies, Kagome and rhombic, were used to build the 2D copolymer based on the COF structures previously reported for the tetraphenylethylene TPE linker.^24,25 The Kagome lattice displays dual-pore characteristics with a central hexagonal core surrounded by six triangular pores (Fig. 3a), while the rhombic lattice forms a single-pore structure (Fig. 3b). Previous work has shown that these two topologies can be generated using D_2h linkers and C₂ ligands by modulating the solvent and monomer concentration.²⁶ Optimization of the 2D COF monolayers was performed under periodic boundary conditions with PBE including D3 dispersion correction using CP2K.²⁷ The Goedecker–Teter–Hutter pseudopotentials were used with a density cutoff of 400 Ry and DZVP-MOLOPT basis set. The optimized lattice vectors and energies are collected in Table S3 (ESI†). Comparison of the unit cell relative energies indicate that the Kagome lattice is significantly more stable than the rhombic in agreement with previous analysis reported for these two lattices.^26,28 The morphology of both monolayers shows significant torsions originated in the non-coplanarity of the TTE linkers and the bulky substituent groups (–OCH₃ and –COOCH₃) (see Fig. S3, ESI†). This suggests that π-stacking, and therefore through-space electronic coupling between the monolayers, will be relatively weak in favour of intramolecular SF. In this way, the iSF capabilities can be analysed based on a single monolayer.

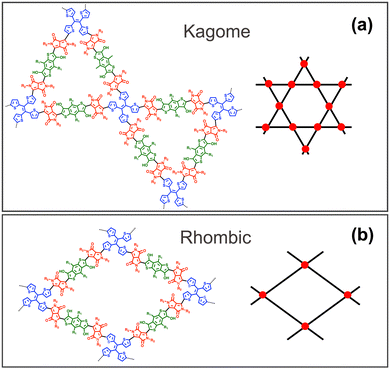Fig. 3 (a) Kagome and (b) rhombic lattices proposed for the –DPP–BDT–DPP–TTE– 2D–COF. R₁: –OCH₃, R₂: –COOCH₃. Color code: red DPP acceptor, green BDT D₁ and blue TTE D₂ linker.

Energy and TDDFT(TDA) calculations were performed in periodic boundary conditions for the 2D optimized structures and for isolated A–D₁–A–D₂ tetramer models extracted from the optimized monolayers. These calculations were first done with PBE0 using the auxiliary density matrix method (ADMM)²⁹ as implemented in CP2K. The S₁ and T₁ energies of the periodic cells are 1.21 and 0.54 eV, respectively, for the Kagome lattice, and 1.18 and 0.54 eV for the rhombic topology. These values become 1.44 and 0.40 (and 1.58 and 0.53, respectively) at PBE0 level for the isolated tetramer models extracted from the unit cells indicating that the 2D periodicity slightly modifies the local environment. Further accuracy of the excited state characterization of the local and CT character of the S₁ and T₁ excitations is obtained at ωb97xD/6-31g* level using Gaussian 09 for the A–D₁–A–D₂ tetramer models extracted from the optimized monolayers (Table 2 and Tables S2.2 and S2.3, ESI†). Comparison with the values obtained at the gas phase optimized geometry (Table 2) indicates that the main local and CT character of the S₁ and T₁ states is preserved in 2D periodic boundary conditions, thus fulfilling the requirements for iSF.

To conclude, in this work two design strategies are proposed for the further development of D–A copolymers for iSF. First, to use two different donors, which each optimizes a fundamental step of iSF, either singlet splitting or triplet–triplet separation, within a –A–D₁–A–D₂– copolymer sequence. This allows to bypass the restrictive need of finding a unique donor unit capable of both functions. Second, to encompass the –A–D₁–A–D₂– copolymer in a 2D framework. Better through-bond exciton and charge carrier mobilities are expected for crystalline 2D COF monolayers with respect to amorphous 1D copolymers resulting in improved iSF efficiencies. Two different 2D topologies are proposed for the iSF –DPP–BDT–DPP–TTE– copolymer candidate fulfilling the energetic, coupling and separation requirements. Further extension of the library of 2D COFs candidates for iSF is envisioned by exploiting more diverse datasets of molecular building blocks, including different possible covalent bond assemblies³⁰ and potentially chiral candidates,³¹ applying accelerated computational screening protocols.

M. F. acknowledges financial support from the Ministerio de Ciencia e Innovación and Agencia Estatal de Investigación MCIN/AEI/10.13039/501100011033 for the Ramón y Cajal research contract (RYC2021-030924-I) and the Unidad de Excelencia María de Maeztu CEX2021-001202-M granted to the IQTCUB, as well as the Generalitat de Catalunya for the 2021SGR00354 grant, and the University of Barcelona/IQTCUB and the Red Española de Supercomputación (RES) for the computational resources (QHS-2022-2-0004 and QHS-2022-3-0014 projects).

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. D. Casanova, Chem. Rev., 2018, 118, 7164.
2. R. J. Hudson, A. N. Stuart, D. M. Huang and T. W. Kee, J. Phys. Chem. C, 2022, 126, 5369.
3. S. Singh, W. J. Jones, W. Siebrand, B. P. Stoicheff and W. G. Schneider, J. Chem. Phys., 1965, 42, 330.
4. T. Ullrich, D. Munz and D. M. Guldi, Chem. Soc. Rev., 2021, 50, 3485.
5. R. Casillas, I. Papadopoulos, T. Ullrich, D. Thiel, A. Kunzmann and D. M. Guldi, Energy Environ. Sci., 2020, 13, 2741.
6. E. Busby, J. Xia, Q. Wu, J. Z. Low, R. Song, J. R. Miller, X. Zhu, L. M. Campos and M. Y. Sfeir, Nat. Mater., 2015, 14, 426.
7. Y. Kasai, Y. Tamai, H. Ohkita, H. Benten and S. Ito, J. Am. Chem. Soc., 2015, 137, 15980.
8. J. Hu, K. Xu, L. Shen, Q. Wu, G. He, J.-Y. Wang, J. Pei, J. Xia and M. Y. Sfeir, Nat. Commun., 2018, 9, 2999.
9. J. T. Blaskovits, M. Fumanal, S. Vela and C. Corminboeuf, Chem. Mater., 2020, 32, 6515.
10. J. T. Blaskovits, M. Fumanal, S. Vela, R. Fabregat and C. Corminboeuf, Chem. Mater., 2021, 33, 2567.
11. M. Fumanal and C. Corminboeuf, J. Phys. Chem. Lett., 2021, 12, 7270.
12. J. T. Blaskovits, M. Fumanal, S. Vela, Y. Cho and C. Corminboeuf, Chem. Commun., 2022, 58, 1338.
13. J. Ren, Q. Peng, X. Zhang, Y. Yi and Z. Shuai, J. Phys. Chem. Lett., 2017, 8, 2175.
14. M. Fumanal and C. Corminboeuf, J. Phys. Chem. Lett., 2020, 11, 9788.
15. M. Fumanal and C. Corminboeuf, Chem. Mater., 2022, 34, 4115.
16. M. Souto and D. F. Perepichka, J. Mater. Chem. C, 2021, 9, 10668.
17. A. Kuc, M. A. Springer, K. Batra, R. Juarez-Mosqueda,C. Wöll and T. Heine, Adv. Funct. Mater., 2020, 30, 1908004.
18. M. Martínez-Abadía, K. Strutyński, C. T. Stoppiello, B. Lerma Berlanga, C. Martí-Gastaldo, A. N. Khlobystov, A. Saeki, M. Melle-Franco and A. Mateo-Alonso, Nanoscale, 2021, 13, 6829.
19. J. Zhao, J. Ren, G. Zhang, Z. Zhao, S. Liu, W. Zhang and L. Chen, Chem. – Eur. J., 2021, 27, 10781.
20. T. Li, X. Yan, W.-D. Zhang, W.-K. Han, Y. Liu, Y. Li, H. Zhu, Z. Li and Z.-G. Gu, Chem. Commun., 2020, 56, 14187.
21. W. Li, X. Huang, T. Zeng, Y. A. Liu, W. Hu, H. Yang, Y.-B. Zhang and K. Wen, Angew. Chem., Int. Ed., 2021, 60, 1869.
22. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. Scuseria and M. A. Robbet al., Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford, CT, 2009.
23. F. Plasser, TheoDORE 1.7: A package for theoretical density, orbital relaxation, and exciton analysis, 2017.
24. D. Cui, X. Ding, W. Xie, G. Xu, Z. Su, Y. Xu and Y. Xie, CrystEngComm, 2021, 23, 5569.
25. J. Xiu, N. Zhang, C. Li, A. Salah and G. Wang, Microporous Mesoporous Mater., 2021, 316, 110979.
26. Z. Zhao, J. Zhao, S. Zhang, W. Chen, Z. Yang, T. Zhang and L. Chen, Nanoscale, 2021, 13, 19385.
27. T. D. Kühne, M. Iannuzzi, M. Del Ben, V. V. Rybkin and P. Seewald, et al. , J. Chem. Phys., 2020, 152, 194103.
28. T.-Y. Zhou, S.-Q. Xu, Q. Wen, Z.-F. Pang and X. Zhao, J. Am. Chem. Soc., 2014, 136, 15885.
29. M. Guidon, J. Hutter and J. VandeVondele, J. Chem. Theory Comput., 2010, 6, 2348.
30. J. Yang, S. Ghosh, J. Roeser, A. Acharjya, C. Penschke, Y. Tsutsui, J. Rabeah, T. Wang, S. Y. D. Tameu, M.-Y. Ye, J. Grüneberg, S. Li, C. Li, R. Schomäcker, R. Van De Krol, S. Seki, P. Saalfrank and A. Thomas, Nat. Commun., 2022, 13, 6317.
31. X. Han, C. Yuan, B. Hou, L. Liu, H. Li, Y. Liu and Y. Cui, Chem. Soc. Rev., 2020, 49, 6248.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cc01554h

---