Improper ferroelastic phase transition in a hydrogen-bonded metallocyanide-based (azetidinium)₂(H₃O)[Co(CN)₆] framework

Abstract

A hydrogen-bonded metallocyanide-based (AZE)₂(H₃O)[Co(CN)₆] framework was obtained by introducing a hydronium cation to the A₂B(1)B(2)CN₆-type structure. Simple K⁺/H₃O⁺ substitution exchange the three-dimensional structure of the double-perovskite into two-dimensional layers containing open inorganic cages with a strongly discontinuous improper ferroelastic phase transition.

---

Organic–inorganic hybrids^1–3 based on coordination complexes are widely used as dielectric, ferroelectric, piezoelectric materials, exhibiting nonlinear optical and photoluminescent properties. These characteristics are the result of combining two opposing poles: an organic guest with changeable, temperature-dependent molecular dynamics, and an inorganic host-type entity that ensures stability and periodicity. The organic–inorganic combination ensures sensitivity of the material to external parameters such as temperature, pressure, electric field strength, or light with the appropriate wavelength or polarization. The aforementioned combinations provide compounds with various crystal structures, changes in which, as a result of the phase transition, generate states that differ in parameters, such as the value of the dielectric constant, spontaneous polarization, and optical activity, to name a few.^4–7 A perfect example of thermally stimulated compounds are cyanide-linked complexes (cyanoelpasolites) with a double-perovskite structure. These coordination polymers usually adopt an architecture with general formula of A₂B₂CN₆. Typically, two metallic cations (mono- and trivalent) form an inorganic cage, whose arm has a B(1)–N≡C–B(2) moiety. Inside this cage resides an organic polar cation. Depending on the size of the inorganic cage, the encapsulated cation may exhibit a multi-step thermally induced transition from a frozen-ordered state to a rotational-disordered state. In order to design modern dielectrics that can be easily switched between low- and high-dielectric states, properties such as size and symmetry, as well as the dipole moment of organic guests and the flexibility of the inorganic cage, must be taken into account.

An additional feature of the materials in discussion is their ferroelasticity.^8,9 Ferroelastic materials are of interest because the abrupt change in physical properties at a ferroelastic domain wall constitutes an interface that reflects optical and acoustic waves. The position of ferroelastic domain walls can also be tuned by subjecting the material to a stress field. The potential applications of these domain arrays are numerous and exciting. They include tuneable: active gratings for lasers, diffraction gratings, Bragg reflection gratings, acoustic filters, optical modulators, and optical domain wall memories.¹⁰ Additionally, ferroelastic materials are particularly promising in the thin-films technology since the ferroelastic twin patterns occur exactly in the nanometric scale and ferroelastic crystals may hold the key for templating electronic thin-films devices.¹¹ Related to ferroelasticity are also memory shape effects and superelasticity.¹²

To date, the most common crystal structures from the family of cyanoelpasolite found in the literature have been based on the K–N≡C–B(2) structural unit, with transition metals, Cr(III),^13,14 Fe(III),^15,16 Co(III)^6,17 in the B(2) position. Some reports show analogues with Na⁺ or Rb⁺, while the H₃O⁺ cation is relatively rarely used.^18–21

Herein we report the completely novel hydrogen-bonded metallocyanide framework, (AZE)₂(H₃O)[Co(CN)₆], 1,. As a result of a simple cation exchange, we obtained a crystal where the azetidinium cation (AZE⁺) is embedded in an open inorganic cage (more detail about synthesis can be found in Section S1 ESI†). Ordering of the AZE⁺ cations located in corner-like niches underlies a phase transition at 295 K, whose mechanisms have been elucidated with structural, thermodynamic and dielectric studies and group-theoretic analysis.

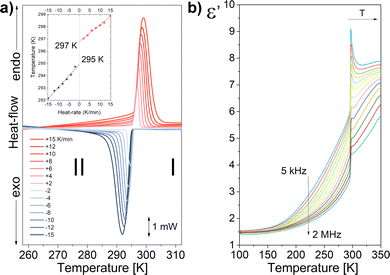
Analysis reveals that the crystal of 1 undergoes one phase transition (PT) in the solid state. As shown in DSC curves (Fig. 1a), one pair of endothermic/exothermic peaks is observed at the range of temperature from 315 to 250 K. In order to estimate the PT's temperature, the thermal anomaly was measured for different temperature ramps between ±2 and ±15 K min⁻¹. Next, the temperature was extrapolated to run with 0 K min⁻¹, obtaining 297/295 K for the heating/cooling cycle. Despite the small value of thermal hysteresis of 2 K, the symmetrical shape of both peaks indicates a first order PT. Additional proof for this assumption can be found in significant enthalpy and entropy change of 4558 J mol⁻¹ and 15.4 J K⁻¹ mol⁻¹, respectively (see Section S2 ESI† for more details). For clarity, the phase above T_PT was labelled as high-temperature phase (HT), while the low-temperature phase (LT) corresponds to the one below T_PT. Changes in velocity of PT were also manifested in an on-step dielectric response.

Fig. 1 (a) DSC curves for 1 (inset: Temperature of PT versus heat-rate between ±2 and ±15 K min⁻¹) b) Temperature dependence of the dielectric constants (ε′) for 1 measured at a frequency of 5 kHz–2 MHz.

Dielectric materials are widely used as standard components in electronics. A measure of the quality of a dielectric is the complex dielectric permittivity (ε* = ε′ − iε′′), which consists of two components: a real part (ε′) and an imaginary part (ε′′). The real part describes how easily the dielectric polarizes under the action of an external electromagnetic field. On the other hand, the imaginary part is related to the relaxation processes of dipole moments and bound electric charges, which cause energy loss (energy dispersion) in the medium. An ideal dielectric has minimal values of the imaginary part and large values of the real part. Fig. 1b, presents the temperature dependence of ε′, measured for the range of frequency from 2 kHz to 2 MHz. The permittivity was studied for a monocrystalline sample with geometry S = 8 mm², d = 1.2 mm. The electrodes were placed along the c_HT-axis. As the temperature decreases, the permittivity also decreases. There is a jump in permittivity around 300 K, related to a structural change in PT (see also Fig. S4 in ESI†). A step-like change of the permittivity points out the transition with the order–disorder mechanism of the polar cation. Additionally, the relaxation processes in the dielectric response in both the LT and HT phases are observed. The frequency dependence of the real and imaginary parts of the electrical permittivity is shown in Fig. S5 (ESI†). The Cole–Cole theoretical model was fitted to the selected temperatures (see Section S3 ESI† for more details). The data obtained in the theoretical fitting are included in Table S1 (ESI†). The obtained relaxation times satisfy the Arrhenius relation in both LT and HT phases. Fig. S6 (ESI†) shows the linear dependence of relaxation times vs. 1000/T on the y-logarithmic scale. From the slope of the lines, the activation energies were determined, which describe the molecular dynamics of the cations in each phase.

We performed the structural analysis in both HT and LT phases to understand the mechanism of the PT. Crystal structures were determined at 308 K (1-HT) and 200 K (1-LT) according to the DSC data. In the HT phase, the symmetry of 1 is described by the trigonal (hexagonal axes, triple obverse cell, primitive cell a′ = 14.656 Å, α′ = 33.65°, V = 862 ų) R3̄m space group (Table S2, ESI†) with the cell parameters a = 8.4901(3) and c = 41.463(2) Å. Analysis revealed, as shown in Fig. 2a, three building units: two types of discrete [Co(CN)₆]³⁻ anions, two types of azetidinium (AZE⁺) and hydronium (H₃O⁺) cations. The AZE⁺ cations are located close to high symmetry sites (3m), thus exhibiting a 6-fold orientationally disordered state. The main structural feature of 1 is a two-dimensional (2D) layer of hydronium cations with one of [Co(CN)₆]³⁻-type anions, denoted as type A (see Fig. 3). Unlike the double-perovskite (AZE)₂[KM(CN)₆]^22,23 (M = Cr^III, Fe^III, Co^III), which exhibits a three-dimensional (3D) framework consisting of [M₄K₄(CN)₁₂] cages formed by M–C ≡ N–K fragments, the H₃O⁺ cations can develop only three-directional hydrogen bonds (Table S3, ESI†), which leads to the 2D hydrogen-bonded layer structure. The second [Co(CN)₆]³⁻-type of anions together with two types of AZE⁺ cations forms the 2D hydrogen-bonded (Table S3, ESI†) (AZE)₄[Co(CN)₆]⁺ layer (denoted as layer type B, Fig. 3). Type A and type B of hydrogen-bonded 2D layers form an A–B–A–B packing along the c_HT-axis. Interestingly, there are no distinct intermolecular interactions between those two layers. In fact, the AZE⁺ cations from layer B build up in the free space of layer A resembles open inorganic cages, see Fig. 3, Type A.

Fig. 2 Unrelated part of the unit cell with the atom-numbering scheme of 1 at (a) 308 and (b) 200 K. Asymmetric part is drawn as displacement ellipsoids with 50% probability. Transparent part completes the chemical formula of 1.

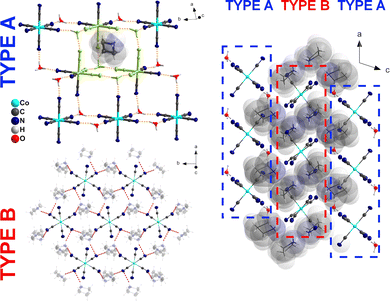Fig. 3 Crystal structure of 1 at 200 K (right side). The type A and type B two-dimensional hydrogen-bond layers are shown on the left. An open inorganic cage is drawn in lime colour.

During the PT from HT phase to the LT phase, the crystal system changes, and at 200 K, 1-LT adopts the P2₁/c monoclinic space group. However, to be able to compare the positions of the atoms in LT with those in HT (Table S4, ESI†), we have transformed the unit-cell from P2₁/c to P2₁/a with cell parameters a = 14.497(3) Å, b = 8.5378(3) Å, c = 14.317(2) Å, β = 108.12(3)° – (a nonstandard setting of the P2₁/c, no. 14, Table S2, ESI†). The geometric relation of the unit cell is given in Fig. S7, and Table S5 ESI.† The change of symmetry occurs with a reduction of the number of symmetry elements of the crystallographic point group from 12 to 4, which corresponds to a ferroelastic transition belonging to the Aizu species 3̄mF2/m.⁸ The full symmetry reduction R3̄m → P2₁/c (P2₁/a) involves, however, doubling of the unit cell i.e. a reduction of translational symmetry. Therefore, the phase transition is an antiferrodistorive improper ferroelastic. (ref. 24 p. 440) The details of the group theoretic analysis of this phase transition are given in Section S5 of ESI.† The AZE⁺ cations which were dynamically disordered in the HT phase, are fully ordered in the LT phase (Fig. 2b). Based on the Boltzmann equation, ΔS = R ln(N), where R is the gas constant and N stands for the ratio of the number of respective geometrically distinguishable orientations. The value of N was calculated as 6.4 (see Section S2 ESI†). Considering that the trigonal phase has 12 orientations and the monoclinic phase has two orientations, the theoretically calculated value of N should be 12/2 = 6, which is very close to our experimental value (6.4) and the observed changes in the disorder of molecules are the major contributors to the mechanism of this transition; thus, the observed changes can be classified as an order–disorder transition.

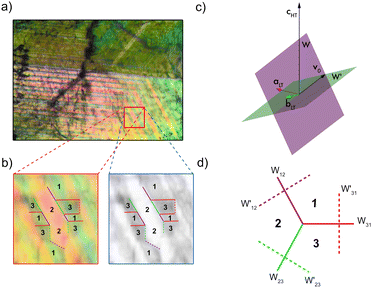
The ferroelastic domains are detectable with the use of polarization microscopy (Movie 1 and Section S6, ESI†). Fig. 4a shows a domain pattern observed in the LT phase at 294 K with the incident light along the [0001] or c_HT direction. The orientation of the domain walls separating two selected ferroelastic domains can be deduced from the strain needed to transform one of the domains into the other. This is always a pure shear. It turns out that one of such domain walls, called W domain wall, coincides with a mirror plane of the R3̄m group. Every mirror plane of R3̄m becomes the unique mirror plane of one of the domains of the P2₁/c structure and, at the same time, transforms the remaining domains into each other. The domain wall W′ is perpendicular to the W one for the same pair of domains and intersects the W wall along the direction corresponding to the zero eigenvalue of the difference strain. The direction is denoted with v₀ in Fig. 4c. The angle subtended by this vector with the c_HT direction amounts to 58.86°. What's worth noting is that the W′ are not perpendicular to the observation plane. Thus, one might expect three W domain walls 120° and 240° apart of each other, and three W′ domain wall traces perpendicular to the W walls. The scheme of the traces of the domain walls in the [0001] projection is represented in Fig. 4d. It is important to remember that reflection in any W wall plane transforms the system of domains into another allowable system as depicted in Fig. 4d. Fig. 4c illustrates an attempt of attributing the domains and domain wall traces to features of the experimental microscopic image.

Fig. 4 (a) Polarization microscopy image of (AZE)₂(H₃O)[Co(CN)₆] recorded at 294 K in LT phase with the light beam parallel to c_HT crystallographic direction. (b) selected area with marked traces of domain walls (colors and achromatic grays), (c) schematic of the W and W′ domain walls orientation for selected domain pair in the reference system (a_LT, b_LT, c_HT), (red, green, blue) respectively, (d) traces of stress free W and W′ domain walls in plane (0001); traces of W walls perpendicular to observation plane continuous, traces of oblique W′ domain walls dashed.

The image is coloured in contradistinction to other observations in compounds with a general formula of A₂B₂CN₆.^13,22,25 This may be a consequence of a non-perpendicularity of the W’ domain walls to the observation plane. Thus, the thickness of both domains that divide the wall varies and may produce standing waves of the length corresponding to the actual thickness. Consequently, some wavelengths may be enhanced or extinguished from the initially white light beam. Under supposition of this origin of the variety of the observed colours we have compared the native image with its grayscale counterpart, see Fig. 4b. The achromatic grayscale image shows the traces of the domain walls in agreement with the group theoretical predictions. Some of the traces have been identified in Fig. 4b. Noteworthy that some of the identified domain walls are not smooth but show a step-like fine structure of a series of rectangular steps significantly larger than the size of the pixels. This suggests a decomposition of a W or W′ wall into a series of mutually perpendicular sequences of W and W′ walls for the same pair of domains. The origin and the nature of this fine structure as well as the mechanism of the tinted domain pattern are worth further studies with more refined means of observation.

In summary, by simply replacing alkali metal cation with a H₃O⁺, we obtained a (AZE)₂(H₃O)[Co(CN)₆] (1) crystal where the azetidinium cations (AZE⁺) are embedded in an inorganic cage-like. The compound shows a phase transition with a large entropy jump, although relatively narrow thermal hysteresis at about 297/295 K. The mechanism of the phase transition involves order–disorder of AZE⁺ cation, which afford a drastic symmetry breaking from trigonal to a monoclinic crystal system. The phase transition belongs to a class of improper antiferrodistortive species, implying three ferroelastic domains with two antiphase domains within each of them. The observed domain structure corresponds to symmetry based predictions. The wave vector on B.z. border (Brillouin zone border) and the symmetry of the order parameter have been determined to indicate the plausible location of anomalies to be observed with neutron scattering methods. We believe that this work not only deepens the understanding of the phase transition mechanisms in a hydrogen-bonded metallocyanide-based 2D framework but also gives an important clue for the further design and understanding of ferroelastic materials.

The MM is grateful for financial support from the National Science Center (Narodowe Centrum Nauki) in Poland under project No. 2021/05/X/ST5/01382.

Conflicts of interest

There are no conflicts to declare.

References

1. W. Li, A. Stroppa, Z.-M. Wang and S. Gao, Hybrid Organic–Inorganic Perovskites, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2020.
2. M. Ptak, A. Sieradzki, M. Šimėnas and M. Mączka, Coord. Chem. Rev., 2021, 448, 214180.
3. W.-J. Xu, Z.-Y. Du, W.-X. Zhang and X.-M. Chen, CrystEngComm, 2016, 18, 7915–7928.
4. W.-J. Xu, P.-F. Li, Y.-Y. Tang, W.-X. Zhang, R.-G. Xiong and X.-M. Chen, J. Am. Chem. Soc., 2017, 139, 6369–6375.
5. C. S. Coates, H. J. Gray, J. M. Bulled, H. L. B. Boström, A. Simonov and A. L. Goodwin, Philos. Trans. R. Soc., A, 2019, 377, 20180219.
6. M. Rok, A. Ciżman, B. Zarychta, J. K. Zaręba, M. Trzebiatowska, M. Mączka, A. Stroppa, S. Yuan, A. E. Phillips and G. Bator, J. Mater. Chem. C, 2020, 8, 17491–17501.
7. W.-J. Xu, K. Romanyuk, Y. Zeng, A. Ushakov, V. Shur, A. Tselev, W.-X. Zhang, X.-M. Chen, A. Kholkin and J. Rocha, J. Mater. Chem. C, 2021, 9, 10741–10748.
8. K. Aizu, J. Phys. Soc. Jpn., 1969, 27, 387–396.
9. K. Aizu, Phys. Rev. B: Solid State, 1970, 2, 754–772.
10. S. W. Meeks and B. A. Auld, in Advances in Electronics and Electron Physics, ed. P. W. Hawkes, Academic Press, 1988, vol. 71, pp. 251–355.
11. V. Nagarajan, A. Roytburd, A. Stanishevsky, S. Prasertchoung, T. Zhao, L. Chen, J. Melngailis, O. Auciello and R. Ramesh, Nat. Mater., 2003, 2, 43–47.
12. M. D. Hollingsworth, M. L. Peterson, J. R. Rush, M. E. Brown, M. J. Abel, A. A. Black, M. Dudley, B. Raghothamachar, U. Werner-Zwanziger, E. J. Still and J. A. Vanecko, Cryst. Growth Des., 2005, 5, 2100–2116.
13. M. Rok, M. Moskwa, M. Działowa, A. Bieńko, C. Rajnák, R. Boča and G. Bator, Dalton Trans., 2019, 48, 16650–16660.
14. M. Mączka, A. Nowok, J. K. Zarȩba, D. Stefańska, A. Ga̧gor, M. Trzebiatowska and A. Sieradzki, ACS Appl. Mater. Interfaces, 2022, 14, 1460–1471.
15. M. Trzebiatowska, A. Gągor, L. Macalik, P. Peksa and A. Sieradzki, Dalton Trans., 2019, 48, 15830–15840.
16. W. Zhang, Y. Cai, R.-G. Xiong, H. Yoshikawa and K. Awaga, Angew. Chem., Int. Ed., 2010, 49, 6608–6610.
17. X. Zhang, X.-D. Shao, S.-C. Li, Y. Cai, Y.-F. Yao, R.-G. Xiong and W. Zhang, Chem. Commun., 2015, 51, 4568–4571.
18. C. Shi, X. Zhang, Y. Cai, Y.-F. Yao and W. Zhang, Angew. Chem., Int. Ed., 2015, 54, 6206–6210.
19. Y.-L. Liu, D.-H. Wu, Z. Wang and Y. Zhang, New J. Chem., 2017, 41, 3211–3216.
20. C. Shi, Y. Wang, X.-B. Han and W. Zhang, Eur. J. Inorg. Chem., 2017, 3685–3689.
21. C. S. de Medeiros, M. Ptak, A. Gągor and A. Sieradzki, J. Mol. Struct., 2022, 1252, 132143.
22. M. Rok, M. Moskwa, J. Hetmańczyk, Ł. Hetmańczyk and G. Bator, CrystEngComm, 2022, 24, 4932–4939.
23. K. Qian, F. Shao, Z. Yan, J. Pang, X. Chen and C. Yang, CrystEngComm, 2016, 18, 7671–7674.
24. V. Wadhawan, Introduction to Ferroic Materials, CRC Press, London, 2014.
25. X.-G. Chen, Z.-X. Zhang, Y.-L. Zeng, S.-Y. Tang and R.-G. Xiong, Chem. Commun., 2022, 58, 3059–3062.

---

Footnote

† Electronic supplementary information (ESI) available: Methods, preparation, PXRD, thermal analysis, crystal morphology, crystal refinement data and dielectric properties. CCDC 2247736 and 2247737.

---