Comment on “Structural transition and superconductivity in hydrothermally synthesized FeX (X = S, Se)” by U. Pachmayr, N. Fehn and D. Johrendt, Chem. Commun., 2016, 52, 194

Abstract

The occurrence of triclinic structural modification of β-FeSe was reported in the literature; in particular this polymorph was claimed to be observed at low temperature in samples prepared by hydrothermal synthesis. The establishment of triclinic symmetry was argued based on peculiar features characterizing some selected X-ray powder diffraction lines. Using high-resolution synchrotron X-ray powder diffraction, the same features were observed for an aged β-FeSe sample prepared by a solid state synthesis technique. Moreover, by refining the anisotropic microstrain parameters it was demonstrated that the diffraction pattern can be fairly fitted by applying the well-recognized orthorhombic structural model adopted for the low temperature phase of β-FeSe. This result indicates that the occurrence of the triclinic polymorph for β-FeSe can be ruled out.

---

Introduction

The class of materials referred to as Fe-based superconductors have attracted many research studies since the discovery of superconducting transition temperatures up to T_c = 26 K in LaFeAs(O_1−xF_x).¹ Among all the compounds belonging to this class, β-FeSe (T_c ∼ 8 K) is characterized by the simplest crystal structure and chemical composition. At room temperature it crystallizes in the tetragonal P4/nmm space group, but on cooling a structural transition takes place (T_s ranging from 100 K down to 70 K^2–5); the symmetry is thus reduced down to the orthorhombic Cmme space group. This compound is generally synthesized by means of a solid state reaction at high temperature under vacuum or an inert atmosphere. Interestingly, Pachmayr et al.⁶ reported the hydrothermal synthesis of β-FeSe; samples prepared in this way are not superconducting and, more relevant, exhibit a triclinic (P1̄ space group) crystal structure below 60 K.

In this article we report the structural properties of an aged β-FeSe sample synthesised using a standard solid state reaction. It is demonstrated that the X-ray powder diffraction patterns collected at low temperature for this sample exhibit the same structural features observed for the hydrothermally synthesized β-FeSe reported in ref. 6. This result questions the real existence of a triclinic polymorph of β-FeSe. As a matter of fact, the orthorhombic Cmme structural model accurately accounts for the observed diffraction pattern when anisotropic strain parameters are included in calculations during Rietveld refinement.

Experimental

Differently to the sample of Pachmayr et al.⁶ (synthesized using a hydrothermal technique), the β-FeSe sample investigated in the present work was prepared by a solid state reaction, annealing stoichiometric amounts of pure powdered elements in an evacuated silica ampoule at high temperature.⁷ In particular, the sample was prepared about 4 years before the structural analysis. During these years the sample was stored in a glovebox under an Ar atmosphere, but it was exposed several times to air for different kinds of analyses and characterization. Each of these analytical sessions in air unavoidably caused the sample to absorb oxygen and moisture. These absorbed impurities cannot be removed by simply storing the sample under argon; conversely, they can trigger oxygen diffusion inward of the sample particles, thus affecting the structural and physical properties of β-FeSe. The sample was analyzed by synchrotron X-ray powder diffraction (XRPD) analysis at the high-intensity–high-resolution ID22 beamline of ESRF using a wavelength λ = 0.3543 Å.⁸ XRPD data were collected in the thermal range of 10–150 K. Structural refinements were carried out according to the Rietveld method⁹ using the program FullProf; in particular, a file describing the instrumental resolution function (obtained by analysing a standard LaB₆ sample) and a Thompson–Cox–Hastings pseudo-Voigt convoluted with axial divergence asymmetry function were used during calculations. In the final cycle, the following parameters were refined: the scale factor; the zero point of detector; the background; the unit cell parameters; the atomic site coordinates not constrained by symmetry; the atomic displacement parameters; and the anisotropic microstrain parameters.

Results and discussion

Structural and microstructural analysis

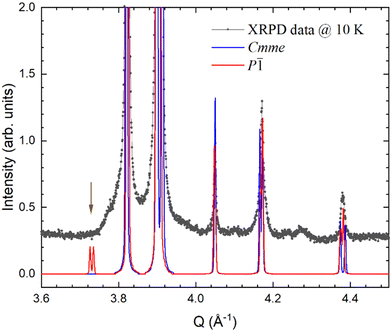
Rietveld refinement reveals that the sample is mainly constituted of tetragonal (P4/nmm) β-FeSe; the hexagonal δ-FeSe polymorph is also observed as a secondary phase (∼7 wt%; Fig. 1).

Fig. 1 Rietveld refinement plot obtained by using data collected at 10 K and applying the Cmme structural model for β-FeSe.

The P4/nmm → Cmme structural transition taking place in β-FeSe can be detected on cooling by the selective splitting affecting the Bragg peaks with strong components in the ab plane. Fig. 2 shows the evolution of the tetragonal 220 diffraction line on cooling. At lower temperature a clear separation of the orthorhombic 400 and 040 lines is not observed; rather, an asymmetric broadening takes place below 50 K. These same features were also observed for β-FeSe samples synthesized using hydrothermal methods. In particular, the asymmetric splitting of the tetragonal 220 diffraction line was related to the occurrence of a triclinic polymorph (P1̄ space group) growing below ∼60 K.⁶

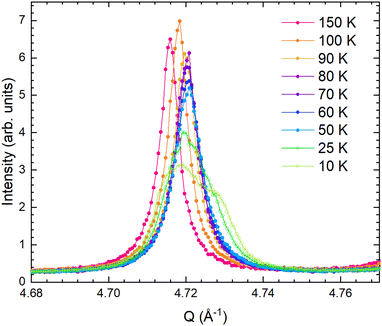Fig. 2 Thermal evolution of the diffraction lines at ∼4.72 Å⁻¹ (full symbols: tetragonal 220 diffraction line; open symbols: orthorhombic 400 and 040 lines).

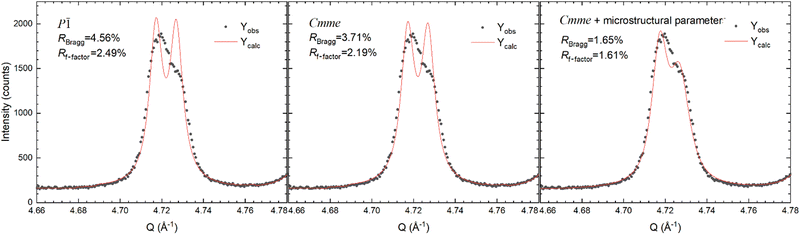
In order to ascertain its real occurrence, the triclinic P1̄ structural model was tested and compared with the Cmme one using the data collected at 10 K. As a matter of fact, both structural models provide a symmetric splitting of the peak (Fig. 3, panels at the centre and on the left); hence the asymmetric shape of the peak cannot be related to a decrease of the crystal symmetry down to the triclinic system. Regardless, significantly better R_Bragg and R_factor factors are obtained using the orthorhombic structural model that should be therefore preferred. Furthermore, the observed asymmetric splitting can be properly modelled by including the anisotropic microstrain parameters in the orthorhombic structural model during refinement (Fig. 3, panel on the right). Remarkably, the calculated diffraction pattern for the triclinic P1̄ structural model is characterized by the presence of several very faint diffraction lines that are missing for the orthorhombic model and that are not actually observed in the experimental data. Fig. 4 shows a magnification of the XRPD pattern at 10 K in the Q-region where some of the triclinic reflections should be observed, but they are actually missing.

Fig. 3 Fitting of the Bragg peak at ∼4.72 Å⁻¹ using the triclinic (panel on the left), orthorhombic (panel at the centre) and orthorhombic with anisotropic strain parameter (panel on the right) structural models (XRPD data collected at 10 K).

Fig. 4 XRPD data collected at 10 K compared with the diffraction patterns calculated for both Cmme and P1̄ structural models; faint diffraction lines (arrowed) are calculated for the monoclinic patterns that are not actually observed in the experimental data.

In this context it is worth noting that in the sample prepared using hydrothermal synthesis the conductive properties were fully suppressed; conversely, in our aged sample superconductivity is still present, although with the transition temperature strongly decreased, down to ∼3 K.

Structural data obtained after refinement at 10 K are listed in Table 1, whereas Fig. 5 shows the thermal evolution of the in-plane lattice parameters for the aged β-FeSe sample; the phase fields of the tetragonal and orthorhombic phases are separated at T_s.

Table 1 Structural parameters of orthorhombic β-FeSe at 10 K (space group Cmme)

Lattice parameters (Å)
A	b	C
5.3170(1)	5.3278(1)	5.4810(1)

---

Atomic positions
Atom	Wyckoff site	x	y	Z
Fe	4g	0	3/4	0.2336(1)
Se	4b	1/4	0	1/2

---

Fig. 5 In-plane lattice parameters (expressed in terms of the primitive unit-cell) as a function of temperature through the P4/nmm → Cmme structural transition (t and o subscripts stand for tetragonal and orthorhombic, respectively). The inset shows the temperature-dependence of the squared value of the order parameter η² for the structural transition.

Remarkably, the anisotropy of the microstrain broadening can reveal the anisotropy of intrinsic properties of the inspected material. In particular, this shows that structural microstrain in the tetragonal phase remains constant along the main tetragonal crystallographic directions on cooling, but increases significantly along [hh0]; this is the same direction of the nesting wave-vector between the electron and hole pockets. This behaviour is in fair agreement with previous analyses of LnFeAsO phases (Ln: lanthanide)^10–14 where the desymmetrisation P4/nmm → Cmme is observed. As a matter of fact, an in-plane 4-fold tensor surface develops on cooling (Fig. 6), whose anisotropy is fully consistent with the microstrain expected for a 4/mmm → mmm point group transition.¹⁵ These results clearly demonstrate that the low temperature phase crystallizes with a Cmme symmetry even though the peak at ∼4.72 Å⁻¹ appears with asymmetric broadening rather than with resolved peak splitting. As a consequence, the occurrence of the triclinic P1̄ polymorph can be ruled out.

Fig. 6 Thermal dependence of the structural strain through the P4/nmm → Cmme structural transition; the upper panel shows the corresponding tensor isosurfaces at selected T (viewed along [001]) representing the microstrain broadening characterizing the tetragonal phase as the structural transition is approached.

Group-theoretical analysis

The possible occurrence of the P1̄ polymorph of β-FeSe would have remarkable consequences from the physical point of view. In fact, in both P4/nmm → Cmme and P4/nmm → P1̄ desymmetrisations reported for β-FeSe a group–subgroup relationship is preserved between the high temperature–high symmetry form, crystallizing in the generic G space group and the low temperature–low symmetry one, crystallizing in the generic H space subgroup. Nonetheless, relevant features should differentiate these transitions if both would occur.

According to the Landau theory of phase transitions, condensation of one or more collective structural degrees of freedom that transform according to a single irreducible representation (IR) of the space group G can drive the structural distortion causing the symmetry breaking. In practice the low symmetry form is equivalent to the high symmetry form, but distorted according to one or more specific modes, i.e. collective atomic displacements fulfilling specific symmetry properties.

For the P4/nmm → Cmme transformation of β-FeSe the proper primary IR is B_2g; as for all the LnFeAsO (Ln: lanthanide) compounds, the displacive B_2g mode is not active at the 2a and 2c Wyckoff sites¹⁶ occupied by Fe and Se atoms in the P4/nmm structure of β-FeSe. This result agrees with theoretical calculations pointing to an electronically driven instability (spin, charge or orbital degrees of freedom).¹⁷

Conversely, the P4/nmm → P1̄ transition should be driven by the primary E_g mode, a structural degree of freedom that is active at both the 2a and 2c Wyckoff sites in the P4/nmm structure of β-FeSe. The formation of the hypothetical P1̄ polymorph deserves a further consideration. In fact, the identity matrix relating the cell edges of the P4/nmm and P1̄ unit cell imposes a P4/nmm → Pmmn → P2₁/m → P1̄ group–subgroup relationship. This is the same group–subgroup relationship observed for the P4/nmm → P2₁/m structural transition in Fe_1+yTe.¹⁶ Notwithstanding, in Fe_1+yTe the structural transition is driven by spin interaction, as clearly demonstrated by the coincident magnetic and structural transitions⁷ as well as by the correlated displacement of Fe atoms with ferromagnetic spin alignment (as sketched in Fig. 7). It is evident that as the nearest neighbouring Fe atoms are ferromagnetically aligned, their bond distance decreases; conversely, for antiferromagnetic coupling Fe atoms move away. It can be thus concluded that the shifting of Fe atoms (required for freezing the primary E_g mode and thus producing the P1̄ symmetry) can be obtained only by the occurrence of magnetic interactions, as in Fe_1+yTe where an antiferromagnetic structure occurs. Conversely, in β-FeSe no magnetic structure develops with structural transition (whatever desymmetrisation is considered) and hence the freezing of the primary E_g mode can be ruled out.

Fig. 7 Primary displacement pattern (on the left) and spin ordering (on the right) characterizing the Fe-substructure in the P2₁/m structure of Fe_1+yTe.

Spontaneous strain analysis

Following the same approach reported already applied for other Fe-based superconductor materials,^11,13 the dependence on temperature of the spontaneous strain was evaluated. By definition, spontaneous strain corresponds to the structural distortion solely induced by the desymmetrisation. It consists of up to six independent components, forming a symmetric second-rank tensor, which are subject to the constraints of symmetry.¹⁸ In particular, the appropriate symmetry-breaking component of the spontaneous strain for the P4/nmm → Cmme structural transition is e₆ that in its general formulation corresponds to:Note that the unit cell of the low-temperature orthorhombic phase is rotated by 45° in the xy plane with respect to that of the high-temperature tetragonal one; as a consequence, a_ortho does not represent the cell edge of the orthorhombic structure, but it is an interplanar distance roughly parallel to the pristine tetragonal [100] direction. For the orthorhombic case e₆ simplifies to:The e₆ component has the same symmetry of the order parameter η of the structural transition. For a second order structural transition η² is linear with temperature and its linear fit extrapolates to zero at T_s ∼ 38.1 K (Fig. 5, inset). Unfortunately, only two sets of data are available for fitting (data collected at T < T_s) and hence this value must be cautiously considered. Nonetheless, it is evident that the structural transition temperature is significantly reduced compared to that normally measured for β-FeSe (T_s ranging from 100 K down to 70 K^2–5), even lower than that ascribed to the P4/nmm → P1̄ transition (∼60 K).⁶

Conclusions

The detrimental effect of oxygen poisoning on both structural and superconductive properties of β-FeSe is a well-known phenomenon, as reported in several investigations.^3,19,20,21 In particular, a small amount of oxygen poisoning was demonstrated to affect both structural and superconductive properties.²¹ Their corruption observed in both samples prepared by hydrothermal synthesis and aged after the solid state reaction can thus be reliably ascribed to oxygen poisoning, mediated by the reaction environment in the first case and by the ambient atmosphere in the second case. This oxygen poisoning determines both the electronic doping of the system as well as structural disordering at the local scale, as evidenced by pair distribution function analysis.²⁰ It can be thus concluded that the occurrence of the non-superconductive P1̄ polymorph of β-FeSe can be excluded, on the basis of structural, microstructural and conductive analyses.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was carried out with the support of the European Synchrotron Radiation Facility, (proposal HC-4366; DOI: http://10.15151/ESRF-ES-445193642); A. M. acknowledges A. Fitch (ESRF-ID22) for his kind assistance during data collection at ID22 and G. Lamura (CNR-SPIN) for magnetization measurements.

References

1. H. Yanagi, T. Kamiya, Y. Kamihara, H. Hiramatsu, M. Hirano and H. Hosono, J. Am. Chem. Soc., 2008, 130, 3296.
2. S. Margadonna, Y. Takabayashi, M. T. McDonald, K. Kasperkiewicz, Y. Mizuguchi, Y. Takano, A. N. Fitch, E. Suard and K. Prassides, Chem. Commun., 2008, 5607–5609.
3. E. Pomjakushina, K. Conder, V. Pomjakushin, M. Bendele and R. Khasanov, Phys. Rev. B, 2009, 80, 024517.
4. T. M. McQueen, A. J. Williams, P. W. Stephens, J. Tao, Y. Zhu, V. Ksenofontov, F. Casper, C. Felser and R. J. Cava, Phys. Rev. Lett., 2009, 103, 057002.
5. R. Khasanov, M. Bendele, K. Conder, H. Keller, E. Pomjakushina and V. Pomjakushin, New J. Phys., 2010, 12, 073024.
6. U. Pachmayr, N. Fehn and D. Johrendt, Chem. Commun., 2016, 52, 194.
7. A. Martinelli, A. Palenzona, M. Tropeano, C. Ferdeghini, M. Putti, M. R. Cimberle, T. D. Nguyen, M. Affronte and C. Ritter, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 094115.
8. A. Martinelli and A. Fitch, 2024, Searching for incommensurability in the FeSe structure at low temperature [Data set], European Synchrotron Radiation Facility DOI:10.15151/ESRF-ES-445193642.
9. R. A. Young, IUCr Monographs on Crystallography, in The Rietveld Method, ed. R. A. Young, Oxford University Press, Oxford, 1993, vol. 5.
10. A. Martinelli, A. Palenzona, M. Putti and C. Ferdeghini, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 224534.
11. A. Martinelli, A. Palenzona, I. Pallecchi, C. Ferdeghini, M. Putti, S. Sanna, C. Curfs and C. Ritter, J. Phys.: Condens. Matter, 2013, 25, 395701.
12. A. Martinelli, Supercond. Sci. Technol., 2019, 32, 015014.
13. A. Martinelli, P. Manfrinetti, A. Provino, C. Ritter and C. Ferdeghini, J. Phys.: Condens. Matter, 2019, 31, 064001.
14. A. Martinelli, P. Carretta, M. Moroni and S. Sanna, Phys. Rev. B, 2021, 103, 014518.
15. A. Leineweber, Z. Kristallogr., 2011, 226, 905.
16. A. Martinelli, J. Phys.: Condens. Matter, 2013, 25, 125703.
17. R. Fernandes, A. Chubukov and J. Schmalian, Nat. Phys., 2014, 10, 97.
18. M. A. Carpenter, E. K. H. Salje and A. Graeme-Barber, Eur. J. Mineral., 1998, 10, 621.
19. T. M. McQueen, Q. Huang, V. Ksenofontov, C. Felser, Q. Xu, H. Zandbergen, Y. S. Hor, J. Allred, A. J. Williams, D. Qu, J. Checkelsky, N. P. Ong and R. J. Cava, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 014522.
20. J. T. Greenfield, S. Kamali, K. Lee and K. Kovnir, Chem. Mater., 2015, 27, 588.
21. B. Rasche, M. Yang, L. Nikonow, J. F. K. Cooper, C. A. Murray, S. J. Day, K. Kleiner, S. J. Clarke and R. G. Compton, Angew. Chem., Int. Ed., 2019, 58, 15401.

---