Non-covalent interactions reveal the protein chain δ conformation in a flexible single-residue model

Abstract

The δ conformation is a local secondary structure in proteins that implicates a π_amide N–H⋯N interaction between a backbone N atom and the NH of the following residue. Small-molecule models thereof have been limited so far to rigid proline-type compounds. We show here that in derivatives of a cyclic amino acid with a sulphur atom in the γ-position, specific side-chain/backbone N–H⋯S interactions stabilize the δ conformation sufficiently to allow it to compete with classical C5 and C7 H-bonded conformers.

---

Nature makes use of non-covalent interactions to stabilize well-defined secondary and tertiary structures in peptides and proteins.¹ Backbone N–H⋯O=C hydrogen bonding is preeminent in the repertoire and provides the basis for the well-known topologies of turns, helices and sheets.² The appreciation of other types of interaction, often found in cooperative combination with classical backbone hydrogen bonding, is still emerging; examples of such phenomena are intra-residue C5 H-bonding,³ C–H⋯O interactions,^4,5 π-stacking,⁶ n → π* hyperconjugative interactions,⁷ C-bonds,⁸ cation–π interactions,⁹ amongst others.¹⁰

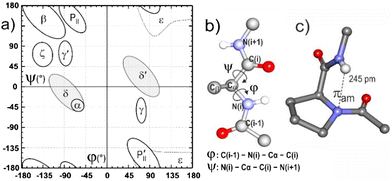
An intriguing feature of folded proteins is a local backbone geometry referred to as the δ conformation,¹¹ that appears on the Ramachandran (φ,ψ) map as an extension of the helix-promoting α region stretching towards the β region, centered at ψ = 0° and φ = −90°, known as the bridge (or δ) region (Fig. 1). It has been suggested that the δ conformation may be stabilized in proteins by a favorable interaction between H(i + 1) of a given residue and the amide π electron density on N(i),^12–15 and this tenet has been consolidated by statistical, theoretical and experimental studies.^16–19 A role for such an NH(i + 1)⋯N(i) interaction, also referred to as a π_amide (π_am) interaction, has been suggested in the enzymatic isomerization of proline,^20,21 and it has recently been evoked in the stabilization of synthetic azapeptides²² and as an accompaniment to β turn conformers in small peptides.^23,24 While the π_am interaction is considered to be very weak, the prevalence of local δ conformations in proteins vindicates further investigation and characterization, in order to better understand its role in protein folding.²⁵

Fig. 1 (a) The classical Ramachandran map, highlighting the δ region and its δ′ mirror image. (b) Definitions of (φ,ψ) protein backbone angles. (c) An example of a π_am interaction implicating a proline residue in a protein; NH(i + 1) is located perpendicular to the plane of the preceding amide bond to interact with the π electron density on N(i).

Small-molecule models (comprising of a single capped α-amino acid) that facilitate experimental spectroscopic characterization of the δ conformation and an assessment of its energetics have remained elusive in the literature. Early pioneering studies on single-residue derivatives of glycine (Gly) and α-aminoisobutyric acid (Aib) suggested that short range C5 and C7 H-bonding interactions preclude the adoption of δ conformations in solution; only with imino acid derivatives could the π_am interaction be detected using IR spectroscopy.²⁶ The dihedral angle φ of proline is advantageously fixed around −60° and the limited panel of small-molecule model systems studied so far has retained a proline-inspired structural constraint in order to impose a δ conformation.^16,20,21,27 To date, no small-molecule model has yet been described for which a δ conformation is shown to compete with accessible C7 and C5 conformers without imposition of covalent constraints.

In order to procure a non-proline δ conformation model, we considered that an α,α-disubstituted amino acid backbone would be auspicious, since a δ-folded conformer has been detected in a gas phase conformational landscape of Cbz-(Aib)₂-OMe,²⁸ and in theoretical²⁹ and experimental³⁰ gas phase studies of 1-aminocyclobutane-1-carboxylic acid (Ac4c), a constrained cyclic analog of Aib (Fig. 2). Local δ conformations implicating Aib residues have been observed in peptide crystal structures on several occasions.³¹

Fig. 2 Rationale for this study and molecules 1–3 investigated. Racemic materials were used experimentally; theoretical calculations were carried out on molecules with the S configuration.

A further conceptual premise was that a local backbone conformation could be influenced through finely-controlled side-chain/backbone interactions, particularly those induced by a sulphur atom in the γ-position of the side-chain (Fig. 2). In this regard, both cysteine (Cys)³² and S-methylcysteine (Cys(Me))³³ can benefit from intra-residue (C5γ) or vicinal (C6γ) NH⋯S H-bonding interactions that stabilize extended or folded forms, respectively, while in the cyclic thioether analog, 3-aminothietane-3-carboxylic acid (Attc), the combination of C6γ (side-chain) and C5 (backbone) H-bonds stabilizes a predominant extended C5–C6γ conformer.³⁴ We reasoned that tailoring the covalent constraints in the cyclic side chain should have a significant impact on the relative strengths of C6γ and C5γ H-bonds as well as their compatibility with canonical backbone C7 and C5 H-bonding regimes.

To substantiate this hypothesis, taking Attc derivative 1 as the starting point, we have made a comparative study of the behavior of compounds 2 and 3, which are derivatives of the corresponding 5- and 6-membered cyclic α,α-disubstituted amino acids, 3-aminothiolane-3-carboxylic acid (Atlc) and 3-aminothiane-3-carboxylic acid (Atc), respectively (Fig. 2).

In the process, we have discovered the ability of the sulphur atom to enable C5γ H-bonds that stabilize δ-folded conformations, both in the gas phase and in weakly polar solution, providing new IR spectroscopic data for a π_am interaction.

We began with a quantum chemistry structural modelling study of molecules 1–3 both isolated in the gas phase (DFT-D level) and in chloroform solution, modelled using a polarizable continuum (see details in the ESI†). Three families of low energy backbone structures characterized by distinct Ramachandran regions were obtained (Fig. 3a–c), with only minor differences between gas and solution phase geometries (Fig. S2.1, ESI†). The classical extended and γ-folded forms, stabilized by C5 and C7 interactions respectively, were accompanied by the quested δ-folded conformations. These latter were characterized by quasi-perpendicular peptide bonds and a weak π_am interaction with a noticeably short NH(2)⋯N(1) distance (ca. 230 pm). A striking feature was the juxtaposition of the S atom with the neighboring NH moiety, featuring short NH⋯S distances and H-bonding interactions that varied significantly with the molecule and the backbone type being considered.

Fig. 3 Most stable theoretical structures of each backbone family of species 1–3 in chloroform solution, illustrated with the gauche− rotamer of the trans benzyl carbamate (a–c). The illustrations show the more stable ring puckering conformers, all of which have the sulphur atom pointing towards N2. For structural comparison, the C1, Cα, and N2 atoms of each conformation have been overlapped. The H-bond NH⋯O/S/N distances are given in pm. The nomenclature indicates the H-bonding status of each NH along the backbone. Within each family, less stable orientations of the ring relative to the backbone also occur, as do backbone mirror structures, e.g. with a δ′-fold (d) or a 7_D H-bond (see Fig. S2.2, ESI†).

The C5 extended forms of each of the three compounds (Fig. 3a) featured an inter-residue NH(2)⋯S C6γ interaction with a short NH⋯S distance (within the range 225–250 pm). The C7 γ-folded (Fig. 3b) and the δ-folded (Fig. 3c) forms of each compound both featured an intra-residue NH(1)⋯S C5γ interaction, for which the H-bonding distance (and thus strength) varied between the three molecules depending on a number of factors: the chirality of the backbone fold (7_L or 7_D, δ or δ′); the ring puckering (depending on whether the S atom is closer to O(1) or N(2)); the local conformation (gauche +/− or trans) of the benzyl carbamate group as well as its configuration (trans or cis). Each type of backbone described above therefore gave rise to a conformational family, wherein all these structural features can vary (see Fig. S2.1 and S2.2, ESI†).

The significance of the stabilizing effects of NH⋯S bonds is reflected in the relative energetics of the three backbone conformation families (Fig. 4 and Fig. S2.4, ESI†). In the series 1→2→3, the energetics suggest that the δ conformer family becomes increasingly favorable and that the accompaniment of an NH⋯S C5γ interaction plays a primordial role (Fig. 3c). The stabilizing effect of the NH⋯S interaction is commensurate with the shortening of the NH⋯S distances highlighted by comparison of the energies of the “mirror-image” δ and δ′ conformer families of 2 and 3 (Fig. 3c and d); the former incorporate the C5γ interaction and are 3–4 kJ mol⁻¹ more stable than the latter, which have no such interaction.

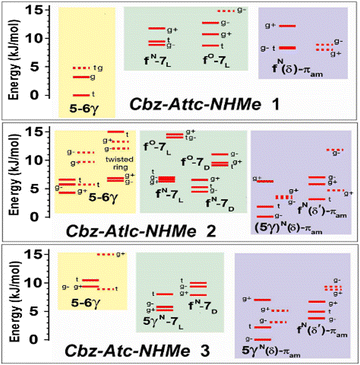Fig. 4 Chloroform solution (300 K) energetic conformational landscape of compounds 1–3 obtained from quantum chemistry calculations (DFT-D level and polarizable continuum; details in ESI,† Section S2), illustrating the three backbone families present in these species – C5/C6γ (yellow), C7 (green) and δ (violet) – and the stabilizing effect of the C5γ interaction on the δ conformer. See Fig. 3 and Fig. S2.2 (ESI†) for the conformational nomenclature. The labels g+, g− and t designate the Cbz orientation.

Despite the presence of a strong C6γ H-bond in the extended form of all three molecules, a progressive destabilization (by ca. 10 kJ mol⁻¹) of the extended (C5/C6γ) form relative to folded (C7 or δ) forms is observed in the series 1 → 2 → 3, indicating that side-chain/backbone H-bonds do not alone control the energetics and that geometric distortions of both backbone and side-chain are also contributing factors.

A gas phase conformation-selective laser spectroscopic study was carried out using UV and IR/UV double-resonance spectroscopies³⁵ and the data were compared to theoretical calculations (see ESI,† Sections S3 and S4). Compounds 1 and 2 behaved similarly, each exhibiting a single conformation assigned to an extended backbone family featuring two red-shifted H-bonds (close to 3360 and 3400 cm⁻¹), consistent with the calculated spectrum for the most stable C5–C6γ structure in the gas phase. In contrast, the numerous UV features of 3 provided five different NH stretch IR spectra (designated A–E; see ESI,† Section S4.2 for details). Comparison with calculated spectra for the most stable forms of each family led us to assign A to the C5–C6γ family and B to the C5γ–C7 family. More interestingly, spectra C-E (Fig. 5) were assigned to conformations belonging to the δ-folded C5γ-π_am family, characterized by a significantly red-shifted band (3345–3405 cm⁻¹ range) and a blue band (3465–3475 cm⁻¹), corresponding respectively to the C5γ H-bond and the π_am features. This important observation demonstrates the existence of and provides spectral characterization for the δ-folded family of compound 3 in the gas phase, albeit in competition with the classical extended and folded forms.

Fig. 5 Gas-phase conformation-selective IR spectra (black) of compound 3, recorded by IR/UV double resonance method: the letter labels (right) refer to the UV band used for conformer selection. For comparison, theoretical IR spectra (sticks) are given for relevant conformations (see details in ESI†).

The search for evidence of δ conformations of compounds 1–3 in solution phase was rewarding. IR absorption spectra were recorded in chloroform (5 mM), without concentration-related effects (Fig S5.2, ESI†), indicating the intramolecular nature of any non-covalent interactions. Considerable differences were observed in the amide NH stretch region in the series: one main band was observed for 1, four were observed for 2 and two were observed for 3 (Fig. 6).

Fig. 6 Solution state IR spectra of compounds 1–3 (5 mM in chloroform) and the calculated IR spectra of their most energetically relevant conformations (a more complete set is shown Fig. S5.3, ESI†). Zones indicate the typical locations of diagnostic spectral features: nearly free (π_am) NH in a δ conformation (violet) and NH engaged in a C5 H-bond (yellow).

The standout feature in the spectrum of 3 was the strong blue-shifted band at 3450 cm⁻¹ (yellow zone in Fig. 6). This band is assigned to NH(2) of δ-folded forms (Fig. 3c), in agreement with the solution state energetics study (Fig. 4). Concomitantly, the H-bonded NH(1) in a C5γ(δ)-π_am conformer of 3 is red-shifted and gives rise to the broad band at 3365 cm⁻¹ (cyan zone in Fig. 6). These assignments are supported by the theoretical solution state spectra (Fig. 6) and demonstrate that the δ-folded conformer family is indeed predominant for compound 3 in solution.

The case of 2 was more complex since several conformer families appear to populate the solution state landscape. While the δ-folded 5γ(δ)-π_am conformer was less prominent than for compound 3 it was still in evidence, giving rise to bands at around 3415 cm⁻¹ for NH(1) (with a weaker C5γ H-bond than in compound 3) and at 3450 cm⁻¹ for NH(2) involved in a π_am interaction. The presence of a C5–C6γ conformer was indicated by the band at 3385 cm⁻¹, typical for N(1) in a C5 interaction (violet zone in Fig. 6),³⁰ with NH(2) appearing in the broad red-shifted region around 3340 cm⁻¹. Furthermore, a f-7 conformer may contribute to the bands observed at 3430 and 3340⁻¹.

The δ conformation was not in evidence in compound 1, whose IR spectrum showed one broad band at 3375 cm⁻¹, assigned to the overlapping NH(1) and NH(2) absorptions of a predominant C5–C6γ conformer. Only previously noted in passing,³⁴ the two minor bands at higher frequencies (3430 and 3450 cm⁻¹) can now be attributed to diminutive contributions from higher energy f(δ)-π_am and/or f-7 conformers of 1.

The prevalence of a δ-folded conformer of 3 in chloroform solution was supported by ¹H NMR experiments. Titration with DMSO-d₆ induced small downfield shifts (Δδ < 0.3 ppm for 10% added DMSO-d₆) indicating limited solvent exposure, while a NOESY experiment showed correlations between the NHs and nearby (within 3.5 Å) CH atoms in a δ-folded conformer (see ESI,† Section S.6).

In summary, these studies provide spectroscopic characterization, supported by theory, of the first example of a single-residue model of the δ conformation of protein secondary structure without recourse to the backbone restriction deployed in previous proline- derived models. Stabilized by a propitious interplay of non-covalent interactions including a C5γ intra-residue NH⋯S interaction, the δ-folded form of derivative 3 competes successfully with the alternative C5–C6γ and C7 conformers. In solution, the NH vibration in δ-folded 3 (and also in δ-folded 2) appears at ca. 3450 cm⁻¹. This compares with an absorption in the 3420-3430 cm⁻¹ range for constrained proline-derived models,^20,21 suggesting that the backbone restrictions in the latter may over-emphasize the red-shift. The present study reiterates that the N–H⋯N interaction should be considered as very weak. In the conformational analysis of many small peptides over the years, NH vibrations around 3450 cm⁻¹ have been designated as “free”; the present findings suggest that such absorbance bands may also include contributions from δ-folded conformations.

Support from the French ANR (Grants ANR-17-CE29-0008 and ANR-10-LABX-0039-PALM) is acknowledged. We thank the computing facilities of GENCI (Grant 2020-A0070807540), CCRT at CEA (Grant CCRT2020-p606bren) and MésoLUM (U. Paris-Saclay).

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. A. Karshikoff, Non-covalent Interactions in Proteins, Imperial College Press, London, UK, 2006.
2. G. A. Jeffrey and W. Sänger, Hydrogen Bonding in Biological Structures, Springer-Verlag, Berlin, Germany, 1991.
3. R. W. Newberry and R. T. Raines, Nat. Chem. Biol., 2016, 12, 1084.
4. Z. S. Derewenda, L. Lee and U. Derewenda, J. Mol. Biol., 1995, 252, 248.
5. S. Horowitz and R. C. Trievel, J. Biol. Chem., 2012, 287, 41576.
6. G. B. McGaughey, M. Gagne and A. K. Rappe, J. Biol. Chem., 1998, 273, 15458.
7. G. J. Bartlett, A. Choudhary, R. T. Raines and D. N. Woolfson, Nat. Chem. Biol., 2010, 6, 615.
8. V. R. Mundlapati, D. K. Sahoo, S. Bhaumik, S. Jena, A. Chandrakar and H. S. Biswal, Angew. Chem., Int. Ed., 2018, 57, 16496.
9. D. A. Dougherty, Science, 1996, 271, 163.
10. R. W. Newberry and R. T. Raines, ACS Chem. Biol., 2019, 14, 1677.
11. S. Hollingsworth and P. Karplus, Biomol. Concepts, 2010, 1, 271.
12. F. M. Pohl, Nature (London), New Biol., 1971, 234, 277.
13. A. Gieren, B. Dederer and F. Schanda, Z. Naturforsch. C, 1980, 35, 741.
14. J. N. Scarsdale, C. Vanalsenoy, V. J. Klimkowski, L. Schafer and F. A. Momany, J. Am. Chem. Soc., 1983, 105, 3438.
15. P. A. Karplus, Protein Sci., 1996, 5, 1406.
16. R. Adhikary, J. Zimmermann, J. Liu, R. P. Forrest, T. D. Janicki, P. E. Dawson, S. A. Corcelli and F. E. Romesberg, J. Am. Chem. Soc., 2014, 136, 13474.
17. M. Holcomb, R. Adhikary, J. Zimmermann and F. E. Romesberg, J. Phys. Chem. A, 2018, 122, 446.
18. J. Dhar, R. Kishore and P. Chakrabarti, Sci. Rep., 2016, 6, 31483.
19. R. Deepak and R. Sankararamakrishnan, Biophys. J., 2016, 110, 1967.
20. C. Cox, V. G. Young and T. Lectka, J. Am. Chem. Soc., 1997, 119, 2307.
21. C. Cox and T. Lectka, J. Am. Chem. Soc., 1998, 120, 10660.
22. K. Baruah, B. Sahariah, S. S. Sakpal, J. K. R. Deka, A. K. Bar, S. Bagchi and B. K. Sarma, Org. Lett., 2021, 23, 4949.
23. K. Scholten and C. Merten, Phys. Chem. Chem. Phys., 2022, 24, 3611.
24. V. C. D’mello, G. Goldsztejn, V. R. Mundlapati, V. Brenner, E. Gloaguen, F. Charnay-Pouget, D. J. Aitken and M. Mons, Chem. – Eur. J., 2022, 28, e202104328.
25. A native protein fold is only 20–50 kJ mol⁻¹ more stable than misfolded or unfolded forms; see: G. D. Rose, P. J. Fleming, J. R. Banavar and A. Maritan, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 16623.
26. M. Marraud, J. Néel and B. Maigret, J. Chim. Phys. Phys.- Chim. Biol., 1975, 72, 1173.
27. T. Vermeyen and C. Merten, Phys. Chem. Chem. Phys., 2020, 22, 15640.
28. J. R. Gord, D. M. Hewett, A. O. Hernandez-Castillo, K. N. Blodgett, M. C. Rotondaro, A. Varuolo, M. A. Kubasik and T. S. Zwier, Phys. Chem. Chem. Phys., 2016, 18, 25512.
29. J. Casanovas, D. Zanuy, R. Nussinov and C. Alemán, Chem. Phys. Lett., 2006, 429, 558.
30. V. R. Mundlapati, Z. Imani, V. C. D’mello, V. Brenner, E. Gloaguen, J.-P. Baltaze, S. Robin, M. Mons and D. J. Aitken, Chem. Sci., 2021, 12, 14826.
31. S. Aravinda, N. Shamala and P. Balaram, Chem. Biodiversity, 2008, 5, 1238.
32. G. Goldsztejn, V. R. Mundlapati, V. Brenner, E. Gloaguen, M. Mons, C. Cabezas, I. Leon and J. L. Alonso, Phys. Chem. Chem. Phys., 2020, 22, 20284.
33. V. R. Mundlapati, Z. Imani, G. Goldsztejn, E. Gloaguen, V. Brenner, K. Le Barbu-Debus, A. Zehnacker-Rentien, J.-P. Baltaze, S. Robin, M. Mons and D. J. Aitken, Amino Acids, 2021, 53, 621.
34. Z. Imani, V. R. Mundlapati, G. Goldsztejn, V. Brenner, E. Gloaguen, R. Guillot, J.-P. Baltaze, K. Le Barbu-Debus, S. Robin, A. Zehnacker, M. Mons and D. J. Aitken, Chem. Sci., 2020, 11, 9191.
35. E. Gloaguen, M. Mons, K. Schwing and M. Gerhards, Chem. Rev., 2020, 120, 12490.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cc06658k

‡ These authors contributed equally to this work.

§ Current address: Département de Chimie, Université de Montréal, Canada.

¶ Current address: Institut de Recherche en Astrophysique et Planétologie, Université de Toulouse, France.

---