Open Access Article
Open Access ArticlePushing up the easy-axis magnetic anisotropy and relaxation times in trigonal prismatic CoII mononuclear SMMs by molecular structure design†
Aritz
Landart-Gereka‡
 a,
María Mar
Quesada-Moreno‡
a,
María Mar
Quesada-Moreno‡
 a,
María A.
Palacios
a,
María A.
Palacios
 *a,
Ismael F.
Díaz-Ortega
*a,
Ismael F.
Díaz-Ortega
 bc,
Hiroyuki
Nojiri
bc,
Hiroyuki
Nojiri
 b,
Mykhaylo
Ozerov
b,
Mykhaylo
Ozerov
 d,
J.
Krzystek
d and
Enrique
Colacio
d,
J.
Krzystek
d and
Enrique
Colacio
 *a
*a
aDepartamento de Química Inorgánica, Facultad de Ciencias, Universidad de Granada, 18071 Granada, Spain. E-mail: ecolacio@ugr.es; mpalacios@ugr.es
bInstitute for Materials Research, Tohoku University, Katahira, Sendai 980-8577, Japan
cDepartamento de Química y Física-CIESOL, Universidad de Almería, Ctra. Sacramento s/n, 04120, Almería, Spain
dNational High Magnetic Field Laboratory, Florida State University, Tallahassee, Florida 32310, USA
First published on 23rd December 2022
Abstract
The replacement of pyridine by 1-methyl-imidazol in the arms of a N6-tripodal ligand allows preparing two new CoII complexes with quasi-ideal triangular prismatic geometry, which behave as SIMs (Single Ion Magnets) at zero dc field with enhanced axial magnetic anisotropy, magnetic relaxation times and magnetic hysteresis.
In the last two decades, the research in the field of the Single-Molecule Magnets (SMMs) has focused on mononuclear complexes, also named Single Ion Magnets (SIMs).1 This is because, in these simple systems, the electronic structure of the complex can be controlled by playing with the features of the metal ion and the coordination environment.2 This control ultimately allows us to fine tune the magnetic anisotropy and, therefore, the SMM properties. Following this approach, very efficient DyIII-based SIMs with large easy-axis magnetic anisotropy have been successfully prepared, which exhibit effective barriers for magnetization reversal, Ueff, and blocking temperatures, TB, as high as 1540 cm−1 and 80 K, respectively.3 Although some 3d mononuclear complexes have also revealed to be very efficient SIMs with Ueff values as large as 450 cm−1 and long relaxation times,4 they are typically air sensitive and so their implementation in devices would be indeed an intricate task. In order to overcome this drawback, the research activity in this area turned its sights on air-stable CoII SIMs, such as trigonal prismatic (TPR-6) CoII complexes, which are able to exhibit large axial easy-axis magnetic anisotropy (D < 0) and SIM behavior at zero field either in the pristine state or after magnetic dilution.5 We have lately reported a series of TPR-6 CoII mononuclear complexes with the N6-tripodal ligand tris(pyridylhydrazonyl)phosphorylsulphide (L) and different counteranions.5j Theoretical and experimental studies have revealed that these compounds exhibit large D < 0 values with very small rhombic zero-field splitting (E), and that the easy-axis magnetic anisotropy decreases with the increase of the distortion from TPR-6 to octahedral OC-6 geometry. Although none of them exhibits SMM behavior at zero field, this behavior can be activated after quenching QTM by magnetic dilution with ZnII (CoII/ZnII = 1/10 molar) ratio. We wondered if the SMM behavior could also be activated at zero-field when the geometry of the CoN6 coordination environment approaches the ideal TPR-6, where E, if any, should be negligible and the fast QTM will be seriously inhibited. In order to try to unveil this point, we have modified the N6-tripodal ligand by replacing the six-membered pyridyl moiety in L by the five-membered 1-methylimidazoyl counterpart. We have chosen this moiety, because it led to minimally distorted TPR-6 CoII complexes with boron-capped tris-arylazooximate tripodal ligands, which exhibit very strong easy-axis anisotropy.5e The reaction between the ligand tris(1-methylimidazolhydrazonyl) phosphorylsulphide (L1) with Co(ClO4)2·6H2O or Co(BF4)2·6H2O, and using methanol and acetonitrile as solvents, respectively, led to dark red crystals of [Co(L1)X (X = ClO4− (1) and BF4−(2)). These compounds crystallise in the hexagonal P63 space group (see Table S1 for crystallographic data, ESI†) and their structures consist of well-isolated cationic mononuclear [Co(L1)]2+ units whose charges are neutralized by the corresponding counteranions. Selected bond lengths and angles for 1 and 2 are given in Table S2 (ESI†).
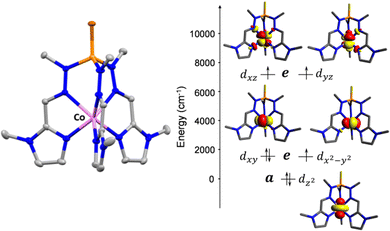
Within the cationic unit (Fig. 1), the cobalt atom is coordinated to six nitrogen atoms belonging to the three arms of the ligand. In this CoN6 coordination environment with strict C3 symmetry, the cobalt ion adopts a slightly distorted (TPR-6) geometry, in which the three nitrogen atoms from the imine groups occupy the vertices of one triangular face with bond distances of 2.225(3) Å for 1 and 2.221(2) Å for 2, while the three nitrogen atoms belonging to the methyl-imidazole groups are located in the vertices of the other triangular and parallel face with bond distances of 2.098(3) and 2.096(2) Å, respectively. Compared to the analogous compounds containing the ligand with the pyridyl moiety, [Co(L)]X2 (X = ClO4−, 1a and BF4−, 2a), the CoN6 coordination spheres of 1 and 2 are less distorted and very close to the ideal TPR-6 geometry, with continues shape measures STPR-6 of 0.533 and 0.486 for 1 and 2, respectively (see ESI†). In good agreement with this, the respective mean Bailar twist angles, θ, for compounds 1 and 2 are 8.94° and 7.69°, which are smaller than those of 1a and 2a. Moreover, the shortest Co⋯Co intermolecular distances of 9.959 Å and 9.879 Å, respectively, are about 1 Å larger than those observed for 1a and 2a. A detailed structural comparison between 1–2 and 1a–2a is provided in the ESI.†
Complexes 1 and 2 were investigated by multiconfigurational ab initio calculations (CASSCF/NEVPT2) based on the experimental X-ray structural data, using the ORCA 5.0.2 program package6 (see Tables S3–S7, ESI†). Calculations for 1 and 2 with and without considering the counteranions yielded very similar results (Table S3, ESI†). Therefore, only the results for the former case are hereafter discussed. The calculated energies of the spin-free states (Table S3, ESI†) point out that the two lowest spin quartet states split by ∼2 cm−1. This gap should be considered as an inherent error of the computational method, because they must be actually degenerate (corresponding to the 4E ground term) due to the C3 symmetry of these compounds. The splitting of the d orbitals for 1 and 2 calculated using the ab initio ligand field theory (AILFT) method together with the electronic configuration corresponding to the 4E ground term are represented in Fig. 1S and Fig. 1, respectively (their energy and one electron wavefunctions are given in Table S6, ESI†). For this kind of pseudotrigonal prismatic CoII complexes, <Lz> is larger than 1.5 and then the first order spin–orbit coupling leads to the expected splitting of the 4E term into four almost equidistant KDs,7 with an energy gap between the ground and first excited KDs of 299.0 and 300.1 cm−1 for 1 and 2, respectively (Table S4, ESI†). Since the second excited KD is located at ∼630 cm−1 above the ground state, it will be barely populated and, therefore, the use of an effective Zero-Field Splitting (ZFS) spin Hamiltonian (eqn (1)) could be appropriate, particularly at low temperatures, to phenomenologically analyze the theoretical results and experimental magnetic data.
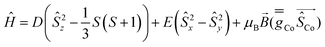 | (1) |
The temperature dependences of the χMT product (χM is the molar susceptibility) measured at 0.1 T in the 300–2 K temperature range for 1 and 2 (Fig. S2 (ESI†) and Fig. 2, respectively) are typical of CoII complexes with unquenched orbital momentum. The M vs. H plots for these complexes in the 2–7 K temperature range (inset Fig. S2 (ESI†) and Fig. 2, respectively), show a continuous increase of the magnetization with the field reaching a value of about 2.45 μB at 2 K. This value is significantly lower than the expected saturation value for an isolated CoII mononuclear complex with S = 3/2, which is supporting evidence of large magnetic anisotropy. Both, the χMT vs. T and the M vs. H data were simultaneously fitted with the PHI program8 using the ZFS Hamiltonian (eqn (1)) with gx = gy and E = 0. The best-fitting procedure afforded the spin Hamiltonian (SH) parameters indicated in Table S8 (ESI†). The extracted D values of −95.2(2) and −98.9(1) cm−1 for 1 and 2, respectively, are similar but smaller than the extracted values from theoretical calculations and FIRMs (see below). It is worth mentioning that poorer quality fits were obtained by imposing D > 0 values.
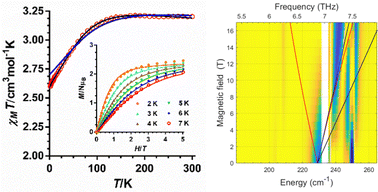 | ||
| Fig. 2 (left) Temperature dependence of χMT and M vs. H isotherms (inset) for compound 2. The solid black line (and colourful lines in the inset) represent the best fit to eqn (1) and the blue line the ab initio calculated values. (right) Experimental (magnetic field vs. energy) heatmaps of FIRMS response for complex 2. Blue and yellow regions represent resonance absorptions sensitive and insensitive to the field, respectively. The lines are simulations of turning points for spin Hamiltonian, using S = 3/2, giso = 2.4, D = 228 cm−1 and E = 0. | ||
The HFEPR spectra of 1 and 2 are silent up to 420 GHz and 14 T, thus indicating the easy-axis anisotropy of these compounds, in good agreement with theoretical calculations. This is because the ΔMs = ±3 transition within the Ms = ±3/2 ground KD doublet is forbidden by the selection rules (only ΔMs = ±1 is allowed) and because the high-lying Ms = ±1/2 KD at about 200 cm−1 is not populated and does not mix with the Ms = ±3/2 ground KD,5j thus supporting the expected E = 0 value.
The FIRMS heatmaps of 2 (Fig. 2) are practically identical to those of compound 1 (Fig. S3, ESI†), with the most prominent spectral feature at 228 cm−1, which can be attributed to the magnetic transition between the ground and first excited KDs in a S = 3/2 system. The precise determination of the |2D*| is hampered by strong spin–phonon coupling effects, resulting in a more complex pattern than the powder spectrum generated for the S = 3/2 spin-Hamiltonian model (see ESI†).
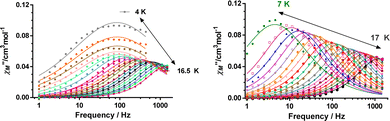
It is worth remarking that 1 and 2 exhibit easy-axis magnetic anisotropies in the upper range of the values observed for CoII based SIMs,1d–f including other pseudo-trigonal prismatic complexes (Table S9, ESI†). In view of this, it is reasonable to presume that these compounds could exhibit slow relaxation of the magnetization at zero field. In good agreement with this expectation, ac magnetic susceptibility measurements of 1 and 2 exhibit temperature and frequency dependent out-of-phase susceptibility (χM′′) peaks in the 10–17 K range, with an upturn below 10 K (Fig. 3 and Fig. S4–S17, ESI†). This upturn is the hallmark of fast quantum tunneling of magnetization (QTM), which can mainly arise from the transverse field created by dipole–dipole and hyperfine interactions.
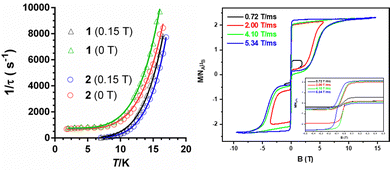
In fact, calculations with the SINGLE-ANISO code implemented in ORCA 5.0.2 program package (ESI), which do not consider these interactions, show that QTM in the ground state can be ruled out. This is because the wave functions of the ground KD state are pure |±3/2〉 (see Tables S10 and S11, ESI†) and the matrix element for the QTM transition is <0.01, which is smaller than the assumed value of 0.1 needed for an efficient relaxation mechanism (Fig. S18 and S19, ESI†). The temperature dependence of the relaxation times (extracted from the frequency dependence of the χM′′ using the generalized Debye model) seems to obey an Arrhenius-like relaxation regime that turns out to be temperature independent below about 7 K due to QTM (Fig. S6 and S13, ESI†). The thermal activated energy barriers, extracted from the barely linear high temperature region, of 38(2) cm−1 and 41(2) cm−1 for 1 and 2, respectively, are much lower than the values extracted from theoretical and experimental magnetic and FIRMS results (|2D|∼200 cm−1). Therefore, the Orbach process (last term in the following multiprocess equation for the magnetic relaxation) can be ruled out. For this reason, the 1/τ vs. T data were fitted to a combination of Raman and QTM (third and second terms in eqn (2), respectively), because the direct process (first term in the equation) should not be active at zero field.
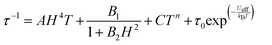 | (2) |
The best fit parameters are gathered in Table S8 (ESI†). It should be noted that the Raman process dominates above approximately 10 K, whereas below this temperature QTM is predominant. Contrarily to that observed for 1a and 2a, compounds 1 and 2 clearly show slow magnetic relaxation at zero field, which could be due to the following issues: (i) their smaller distortion from TPR-6 geometry, (ii) their shortest intermolecular Co⋯Co distances are significantly longer than those observed for 1a and 2a, and (iii) the magnetic anisotropy axes involving neighboring molecules with the shortest Co⋯Co distances are mutually parallel. All these factors, contribute to reduce the fast QTM, thus favoring the observation of slow magnetic relaxation at zero field.5j Ac measurements were also performed under an optimal field of 0.15 T (determined from the field dependence of τ at 13 K; see Fig. S7 and S14, ESI†) with the aim of quenching QTM. The extracted 1/τ vs. T data were fitted to a Raman process (the contribution of the direct process at 0.15 T, if any, should be negligible, Fig. S7 and S14, ESI†), affording the best fit parameters reported in Table S8 (ESI†). As it can be observed in this table, the values of the C and n parameters extracted for the optimal field decrease and increase, respectively, with respect to the corresponding values extracted at zero field, which ultimately leads to a slowdown of the magnetic relaxation (Fig. 4). Since the spin relaxation can involve a vibrational excited state of the electronic ground state, the analysis of the τ−1vs. T data at 0.15 T was also performed using the Raman mechanism through vibrational modes9 instead of the Tn law (see ESI†). The best fit led to vibrational modes with energy of 55(1) and 66(1) cm−1 for 1 and 2, respectively, which match with low energy vibrations in metal complexes.9 Nevertheless, the quality of the fit is similar to that of the power law. Regardless of the Raman mechanism, through vibrational modes or power law, it should be highlighted that the Raman relaxation times slightly increase on going from 1 to 2 and, moreover, they are significantly larger than those observed for 1a and 2a. Magnetization curves in full cycle pulsed magnetic field at 0.4 K with a maximum applied field of 15 T and under adiabatic conditions are given in Fig. 4 (right) and Fig. S20 (ESI†) for 2 and 1, respectively. Both compounds show hysteresis loops with small values of coercive field and remnant magnetization of about 70 G and 1.30 μB at zero field, respectively (see Fig. S20 (ESI†) and inset of Fig. 4), that increase with the increasing magnetic sweep rate, and a sharp adiabatic reversal of magnetization around zero field due to unquenched QTM. In addition, as expected from SMM behavior, the hysteresis increases when the sweeping rate becomes higher. All these facts confirm the SMM nature of these compounds. The width of the hysteresis (see dM/dB vs. B plots in Fig. S21, ESI†) for 1 and 2 are larger than for the 1a and 2a counterparts, which is mainly due to larger axial easy-axis anisotropy and slower magnetic relaxation of the former complexes.
The ongoing results allow concluding that the smaller the distortion of the coordination sphere from the ideal TPR-6 geometry in similar trigonal prismatic CoII complexes, the stronger the axial anisotropy, the slower the magnetic relaxation and the wider the magnetic hysteresis, that is to say, an improvement of the SIM properties occurs. This was also observed in previous works on lanthanide complexes.10
Financial support from the Junta de Andalucía (FQM-195), the project I + D + i (P20_00692) and the University of Granada is greatly acknowledged. Part of this work was performed at the NHMFL, which is funded by the National Science Foundation (Cooperative Agreement DMR 1644779) and the State of Florida. H. N. and I. F. D. O. acknowledge GIMRT and ICC-IMR. M. M. Q. M. thanks Junta de Andalucía for a postdoctoral fellowship (DOC_01282) and MCIN for a Juan de la Cierva formación contract (grant FJC2018-035709-I supported by MCIN/AEI/10.13039/501100011033).
Conflicts of interest
There are no conflicts to declare.Notes and references
- Some recent reviews: (a) G. A. Craig and M. Murrie, Chem. Soc. Rev., 2015, 44, 2135 RSC; (b) Y.-S. Ming, S. D. Jiang, B.-W. Wang and S. Gao, Acc. Chem. Res., 2016, 49, 2381 CrossRef PubMed; (c) M. Fen and M.-L. Tong, Chem. – Eur. J., 2018, 24, 7574 CrossRef PubMed; (d) A. Day, P. Kalita and V. V. Chandrasekhar, ACS Omega, 2018, 2108(20), 942 Search PubMed; (e) A. Sarkar, S. Dey and G. Rajaraman, Chem. – Eur. J., 2020, 26, 14036 CrossRef CAS PubMed; (f) A. Zabala-Lekuona, M. Seco and E. Colacio, Coord. Chem. Rev., 2021, 441, 213984 CrossRef CAS.
- (a) S. Gómez-Coca, D. Aravena, R. Morales and E. Ruiz, Coord. Chem. Rev., 2015, 289–290, 379 CrossRef; (b) S. G. McAdams, A.-M. Ariciu, A. K. Kostopoulos, J. P.S.Walsh and F. Tuna, Coord. Chem. Rev., 2017, 346, 216 CrossRef CAS; (c) M.-L. Tong, Chem. Soc. Rev., 2018, 47, 2431 RSC.
- (a) C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Nature, 2017, 548, 439 CrossRef CAS PubMed; (b) F. S. Guo, B. M. Day, Y. C. Chen, M. L. Tong, A. Mansikkamäki and R. A. Layfield, Angew. Chem., Int. Ed., 2017, 56, 11445 CrossRef CAS PubMed; (c) F. S. Guo, B. M. Day, Y. C. Chen, M. L. Tong, A. Mansikkamäki and R. A. Layfield, Science, 2018, 362, 1400 CrossRef CAS PubMed.
- P. C. Bunting, M. Atanasov, E. Damgaard-MØller, M. Perfetti, I. Crassee, M. Orlita, J. Overgaard, J. van Slageren, F. Neese and J. R. Long, Science, 2018, 362, 7319 CrossRef PubMed.
- (a) S. Gómez-Coca, E. Cremades, N. Aliaga-Alcalde and E. Ruiz, J. Am. Chem. Soc., 2013, 135, 7010 CrossRef PubMed; (b) Y. Y. Zhu, Y. Q. Zhang, T. T. Yin, C. Gao, B. W. Wang and S. Gao, Inorg. Chem., 2015, 54, 5475 CrossRef CAS PubMed; (c) Y. Peng, T. Bodenstein, K. Fink, V. Mereacre, C. E. Anson and A. K. Powell, Phys. Chem. Chem. Phys., 2016, 18, 30135 RSC; (d) B. Yao, Y. F. Deng, T. Li, J. Xiong, B. W. Wang, Z. Zheng and Y. Y. Zhang, Inorg. Chem., 2018, 57, 14047 CrossRef CAS PubMed; (e) A. A. Pavlov, D. Y. Aleshin, S. A. Savkina, A. S. Belov, N. N. Efimov, J. Nehrkorn, M. Ozerov, Y. Z. Voloshin, Y. V. Nelyubina and V. V. Novikov, ChemPhysChem, 2019, 20, 1001 CrossRef CAS PubMed; (f) C. Villa-Pérez, I. Oyarzabal, G. A. Echeverría, G. C. Valencia-Uribe, J. M. Seco and D. B. Soria, Eur. J. Inorg. Chem, 2016, 4835 CrossRef; (g) C. M. Klug, T. J. Ozumerzifon, I. Bhowmick, B. N. Livesay, A. K. Rappé and M. P. Shores, Dalton Trans., 2019, 48, 9117 RSC; (h) A. S. Belov, Y. Z. Voloshin, A. A. Pavlov, Y. V. Nelyubina, S. A. Belova, Y. V. Zubavichus, V. V. Avdeeva, N. N. Efimov, E. A. Malinina, K. Y. Zhizhin and N. T. Kuznetsov, Inorg. Chem., 2020, 59, 5845 CrossRef CAS PubMed; (i) M. R. Saber, M. K. Singh and K. R. Dunbar, Chem. Commun., 2020, 56, 8492 RSC; (j) A. Landart-Gereka, M. M. Quesada-Moreno, I. F. Díaz-Ortega, H. Nojiri, M. Ozerov, J. Krzystek, M. A. Palacios and E. Colacio, Inorg. Chem. Front., 2022, 9, 2810 RSC.
- F. Neese, Software update: The ORCA program system, version 5.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606 Search PubMed.
- L. Ungur, M. Thewissen, J.-P. Costes, W. Wernsdorfer and L. F. Chibotaru, Inorg. Chem., 2013, 52, 6328 CrossRef CAS PubMed.
- N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, J. Comput. Chem., 2013, 34, 1164 CrossRef CAS PubMed.
- (a) A. Lunghi and S. Sanvito, J. Chem. Phys., 2020, 153, 174113 CrossRef CAS PubMed; (b) F. S. Santana, M. Perfetti, M. Briganti, F. Sacco, G. Poneti, E. Ravera, J. F. Soares and R. Sessoli, Chem. Sci., 2022, 13, 5860 RSC; (c) M. Briganti, F. Santanni, L. Tesi, F. Totti, R. Sessoli and A. Lunghi, J. Am. Chem. Soc., 2021, 143, 13633 CrossRef CAS PubMed.
- (a) J. J. Baldoví, S. Cardona-Serra, J. M. Clemente-Juan, E. Coronado, A. Gaita-Ariño and A. Palii, Inorg. Chem., 2012, 51, 12565 CrossRef PubMed; (b) M. A. Sørensen, U. B. Hansen, M. Perfetti, K. S. Pedersen, E. Bartolomé, G. G. Simeoni, H. Mutka, S. Rols, M. Jeong, I. Zivkovic, M. Retuerto, A. Arauzo, J. Bartolomé, S. Piligkos, H. Weihe, L. H. Doerrer, J. van Slageren, H. M. Rønnow, K. Lefmann and J. Bendix, Nat. Commun., 2018, 9, 1292 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. CCDC 2216062 and 2216063. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2cc06012d |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2023 |