 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Optical absorption and dichroism of single melanin nanoparticles†
David
Regan
 a,
Alexandra
Mavridi-Printezi
a,
Alexandra
Mavridi-Printezi
 b,
Lukas
Payne
b,
Lukas
Payne
 ac,
Marco
Montalti
ac,
Marco
Montalti
 b,
Paola
Borri
b,
Paola
Borri
 a and
Wolfgang
Langbein
a and
Wolfgang
Langbein
 *c
*c
aSchool of Biosciences, Cardiff University, Museum Avenue, Cardiff CF10 3AX, UK
bDepartment of Chemistry “Giacomo Ciamician”, University of Bologna, Via Selmi 2, 40126 Bologna, Italy. E-mail: langbeinww@cardiff.ac.uk
cSchool of Physics and Astronomy, Cardiff University, The Parade, Cardiff CF24 3AA, UK
First published on 9th June 2023
Abstract
Melanin nanoparticles (NPs) have important biological functions including photoprotection and colouration, and artificial melanin-like NPs are relevant for catalysis, drug delivery, diagnosis and therapy. Despite their importance, the optical properties of single melanin NPs have not been measured. We combine quantitative differential interference contrast (qDIC) and extinction microscopy to characterise the optical properties of single NPs, both naturally sourced from cuttlefish ink, as well as synthetic NPs using polydopamine (PDA) and L-3,4-dihydroxyphenylalanine (L-DOPA). Combining qDIC with extinction, we determine the absorption index of individual NPs. We find that on average the natural melanin NPs have a higher absorption index than the artificial melanin NPs. From the analysis of the polarisation-dependent NP extinction, the NP aspect ratio is determined, with mean values at 405 nm wavelength in agreement with transmission electron microscopy. At longer wavelengths, we observe an additional optical anisotropy which is attributed to dichroism by structural ordering of the melanin. Our quantitative analysis yields a dichroism of 2–10% of the absorption index, increasing with wavelength from 455 nm to 660 nm for L-DOPA and PDA. Such an in-depth quantification of the optical properties of single melanin NPs is important for the design and future application of these ubiquitous bionanomaterials.
1 Introduction
The advent of nanoscience has revolutionised many fields, ranging from biotechnology, nanomedicine and therapeutics, to cosmetics and food. Since nature creates numerous biomaterials with extraordinary properties, the development of efficient and biocompatible nanotechnology platforms from naturally existing precursors is highly advantageous, as they can mimic in many cases the natural systems while being biosafe.1Melanins are a large family of ubiquitous functional macromolecules derived from the oxidation and polymerisation of phenolic compounds via quinones, and have important biological functions including photoprotection and colouration.2 Closely resembling the natural pigment, artificial melanin-like nanoparticles (NPs), such as those formed from L-3,4-dihydroxyphenylalanine (L-DOPA) or polydopamine (PDA), have been utilised in a wide variety of fields from catalysis to drug delivery, diagnosis and therapy.3 However, even if both artificial and naturally extracted melanin NPs are utilised, the complete structure of the pigment is unknown, and any differences between the synthetic and natural materials are still obscure.4
Synthetic melanin-like PDA NPs can be synthetized by the oxidative self-polymerization of dopamine under alkaline and aerobic conditions in ethanol/water mixture. Size-control of the resulting PDA NPs can be achieved by tuning the ratio of base to dopamine,5,6 and the absorption of PDA can be regulated by the addition of new functionalities.7 For L-DOPA, stronger oxidants such as potassium permanganate are essential for the formation of NPs.8 Cuttlefish of the genus sepia are one of the most exploited sources of natural melanin pigments and sepia NPs of various sizes in the range of 100–260 nm have been reported in the literature, a wider size distribution compared to artificial melanin, indicating that the acquisition of melanin from different sepia sources results in inherent variations.6,9,10
Despite its importance, surprisingly little information is available on the optical properties of melanin NPs on the single NP level. Notably, such information is bound to provide insight into the intrinsic properties of these materials, overcoming obstacles related to inhomogeneities across the NP ensemble, and revealing possible differences between the bulk material and individual NPs. In addition to their optical properties, knowledge of the size of NPs is important not only from a toxicity point of view, but also for their endocytosis. Currently, there are no reports on correlations between size and optical or chemical properties across the NP ensemble, which could play a significant role in the function of melanin NPs. Notably, such correlations can be measured using widefield optical extinction11 and phase12,13 microscopy, which allow measurement of the size and optical properties of individual NPs with high throughput, thus providing a statistically relevant dataset to identify correlations in the ensemble.
One important property of melanin NPs is chirality. A study monitoring the chirality of L-DOPA during NP synthesis indicated a reduction in the circular dichroism (CD) of L-DOPA during oxidation, resulting in the formation of achiral melanin. However, according to the same study, chiral oligomer aggregates can be formed from the decomposition of non-chiral products of a chiral precursor, a phenomenon that may also occur in melanin.14 In the case of water-dispersed PDA, no appreciable CD is observed.15 Importantly, in both cases measurements on single NPs have not yet been reported.
Another key optical property of melanin NPs is their complex refractive index ñ = n + iκ. Investigations on PDA and L-DOPA melanin films showed that the refractive index n increases below 600 nm upon UV exposure of the films.16 However the absorption index κ can differ depending on the fabrication of the film, and can also be different for film and NPs. Studies of the complex refractive index of natural melanin using barbules of feathers where multi-layered melanin is present found that κ ranges from 0.127 at 400 nm to 0.029 at 800 nm,17 while for PDA NPs, κ has been found to decrease monotonically from 0.33 at 400 nm to 0.19 at 800 nm.18 The somewhat lower κ reported for natural melanin could be due to the presence of non-melanin cellular materials in the samples studied.19
To address the need for accurate characterisation of individual NPs such as melanin with high-throughput to obtain statistically relevant single NP information, we have recently developed the optical nanosizer method.11 This technique can measure the extinction cross-section σext (the sum of absorption and scattering cross-sections) of NPs deposited on a glass surface using conventional widefield microscopy. Since σext is dependent on NP radius and complex refractive index, and given that many NPs may be contained within a single field of view, the optical nanosizer enables information on the size and optical properties of large numbers of individual NPs to be extracted from single bright-field images. Furthermore, by using linearly polarised light in the illumination and measuring σext as a function of the polarisation angle, information on NP shape can also be obtained, while spectral information is gained by sequentially imaging the NPs at multiple illumination wavelengths. We have also recently shown that accurate size information about single NPs can be obtained from quantitative differential interference contrast (qDIC) images,13 providing quantitative phase maps from pairs of DIC images taken at opposite phase offsets.
In this work, we combine both of these techniques to characterise the optical properties of natural melanin NPs sourced from cuttlefish ink, as well as PDA and L-DOPA synthetic melanin NPs. For reference, a list of abbreviations used in this work is given in Table 1.
| NP | Nanoparticle |
| qDIC | Quantitative differential interference contrast |
| PDA | Polydopamine |
| L-DOPA | L-3,4-Dihydroxyphenylalanine |
| CD | Circular dichroism |
| UV | Ultraviolet |
| LED | Light emitting diode |
| CMOS | Complementary metal–oxide semiconductor |
| DLS | Dynamic light scattering |
| PMMA | Polymethyl methacrylate |
| TEM | Transmission electron microscopy |
| PDI | Polydispersity index |
| PSF | Point spread function |
2 Materials and methods
2.1 Sample preparation
To synthesise PDA NPs, we exploited a widely used, mild, and easily scalable protocol based on the oxidation of dopamine hydrochloride in alkaline and aerobic conditions.20 For the synthesis of L-DOPA NPs, a stronger oxidant is instead needed, and potassium permanganate (KMnO4) was used.21 In order to compare the artificial melanin NPs with naturally extracted ones, sepia melanin NPs were retrieved by centrifugation from sepia ink paste received from the ink sac of cuttlefish (Sepia officinalis).22 More details on the synthesis and extraction of the three types of melanin NPs are given in the ESI sec. S1.†For imaging, glass coverslips (24 × 24 mm2 #1.5, Menzel Gläser) were cleaned by wiping with acetone-soaked cleanroom paper to remove residual dirt and debris. For the L-DOPA NPs, the coverslips were further cleaned using a Piranha etching procedure in which the glass was left in a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of sulphuric acid and 30% hydrogen peroxide for one hour at 95 °C. This step was skipped for the PDA and sepia samples as the resulting polar glass surface led to a weak attachment of the NPs. To deposit the NPs on the coverslip surface, a 100 μl volume of aqueous NP dispersion was pipetted onto the coverslip. Each dispersion was left on the coverslip surface for two hours at room temperature to allow the NPs to settle. During this time, the sample was kept in a sealed humidified environment to prevent evaporation of the solvent and sample contamination. The concentrations of the NP dispersions were chosen to provide an average distance between NPs on the coverslip of around 10 μm, and 0.27 mg ml−1 for L-DOPA, 0.27 μg ml−1 for PDA, and 3 μg ml−1 for sepia were used. Afterwards, the coverslip was gently washed under distilled water for 10 seconds to remove excess NP dispersion, and then dried under nitrogen flow. The coverslip was then attached to a microscope slide using a SecureSeal imaging spacer (Grace Bio-Labs, USA) for imaging. The NPs were imaged in air as it was found that the NPs tended to detach from the surface when surrounded by a medium such as immersion oil index matched to glass, which was used in our previous experiments11 to reduce background from glass surface roughness.
1 mixture of sulphuric acid and 30% hydrogen peroxide for one hour at 95 °C. This step was skipped for the PDA and sepia samples as the resulting polar glass surface led to a weak attachment of the NPs. To deposit the NPs on the coverslip surface, a 100 μl volume of aqueous NP dispersion was pipetted onto the coverslip. Each dispersion was left on the coverslip surface for two hours at room temperature to allow the NPs to settle. During this time, the sample was kept in a sealed humidified environment to prevent evaporation of the solvent and sample contamination. The concentrations of the NP dispersions were chosen to provide an average distance between NPs on the coverslip of around 10 μm, and 0.27 mg ml−1 for L-DOPA, 0.27 μg ml−1 for PDA, and 3 μg ml−1 for sepia were used. Afterwards, the coverslip was gently washed under distilled water for 10 seconds to remove excess NP dispersion, and then dried under nitrogen flow. The coverslip was then attached to a microscope slide using a SecureSeal imaging spacer (Grace Bio-Labs, USA) for imaging. The NPs were imaged in air as it was found that the NPs tended to detach from the surface when surrounded by a medium such as immersion oil index matched to glass, which was used in our previous experiments11 to reduce background from glass surface roughness.
2.2 Imaging
Samples were imaged on a Nikon Ti-U inverted microscope, using a 100× 1.45NA oil-immersion objective (Nikon MRD01905) and a 1.0× tube lens. The illumination was focussed by a 1.34NA oil-immersion condenser (Nikon MEL41410), though the numerical aperture (NA) range reaching the NPs was limited to 1.0 due to the air gap. For the extinction measurements, each field of view was imaged at four illumination wavelengths (405, 455, 530 and 660 nm), generated using a 4-wavelength light emitting diode (LED) source (LED4D067, Thorlabs, US), and with a motorised linear polariser in the collimated illumination beam path before the condenser23 to control the light polarisation direction at the sample. The sample position was controlled using a NanoLP200 (Mad City Labs, USA) nanopositioning stage. Differential interference contrast (DIC) images were taken using the 660 nm LED, an objective DIC slider (Nikon MBH76190) and condenser module (Nikon MEH52500). A quarter-waveplate added below the linear polariser forms a de Sénarmont compensator allowing switching between opposite phase offsets ψ = 2θ = ±60° by changing the polariser angle θ. All images were acquired using a scientific-CMOS camera (PCO Edge 5.5, PCO, Germany) of full well capacity Nfw = 30 ke, 16-bit digitisation, about 400 Hz frame rate for a region of interest of 1280 × 540 pixels, and averaged over 256 frames.2.3 Dynamic light scattering
Dynamic light scattering (DLS) measurements were performed with a Malvern Panalytical Zetasizer Nano ZS (Malvern, UK), using PMMA semi-micro cuvettes (BRAND, Germany). For these measurements, a concentration of 4.5 μg ml−1 was used for the L-DOPA and PDA NPs, while a concentration of approximately 5 μg ml−1 was used for the sepia NPs.2.4 UV-Vis absorption spectroscopy
UV-Vis absorption spectroscopy experiments were carried out in air-equilibrated solutions at 25 °C. Absorption spectra were recorded with a PerkinElmer Lambda 650 spectrophotometer using UV disposable cuvettes (BRAND). Measurements were carried out at a concentration of 9.0 μg ml−1 for L-DOPA and PDA NPs, and 10.0 μg ml−1 for the sepia NPs.2.5 Circular dichroism spectroscopy
CD experiments were recorded with a JASCO spectropolarimeter model J-810150S in the range of 200–500 nm at 25 ± 0.2 °C using UV transparent disposable cuvettes (BRAND) of 1 cm path length. The measurements were carried out at a concentration of 27 μg ml−1 for L-DOPA and PDA NPs, and 30 μg ml−1 for the sepia NPs.2.6 Transmission electron microscopy
Transmission electron microscopy (TEM) images were obtained using a Philips CM 100 electron microscope at an accelerating voltage of 80 kV. For the acquisition, the samples were deposited on Formvar on 400 mesh Cu grids (Ted Pella Inc. USA).3 Results and discussion
3.1 Sample characterisation – UV-Vis, DLS, TEM
The UV-Vis absorbance spectra of the aqueous NP dispersions shown in Fig. 1d indicate that despite the different origins and precursors, all three NPs exhibit a broad band UV-Vis absorption spectrum increasing towards shorter wavelengths, characteristic of melanin.21,24,25 Diameters of the NPs were determined from TEM micrographs using the ‘Analyse Particles’ tool in ImageJ,26 manually excluding any overlapping NPs to ensure only single NPs were measured. The TEM images (Fig. 1a–c) showed that all three types of NPs exhibited spheroidal shape and a relatively narrow size distribution; DLS measurements gave a polydispersity index (PDI) of 0.02 to 0.04. The PDA NPs exhibited an average diameter of (107 ± 2) nm (error given is the standard error of the mean) with a standard deviation of 19 nm from TEM, and a hydrodynamic diameter of 138 nm by fitting to the DLS distribution (Fig. 1e). The sepia NPs showed a wider size distribution with an average diameter of (130 ± 3) nm and a standard deviation of 33 nm from TEM, and a z-average hydrodynamic diameter of 193 nm measured by DLS (Fig. 1b and e). The L-DOPA NPs exhibited a narrower size distribution with an average diameter of (99.5 ± 1.4) nm and a standard deviation of 14 nm from TEM, and a z-average hydrodynamic diameter of 149 nm found by DLS. Notably, the z-average measured by DLS is an intensity based harmonic mean, and thus gives larger weight to larger NPs. The zeta-potential of the melanin NPs is strongly negative, around −40 mV, providing colloidal stability.27We note that the PDA and L-DOPA NPs appear to have a rougher surface morphology that the sepia NPs, which is attributed to the fabrication process. Importantly, as the surface morphology length scale is well below the light wavelengths employed, and the material refractive index is of the order of one, this is not relevant for NP light absorption and scattering, and the ellipsoidal shape models used later are adequate.
The circular dichroism measured over a path length of 1 cm was negligible for the NP dispersions (NP concentration 27 μg ml−1 for L-DOPA and PDA, 30 μg ml−1 for sepia), as shown in Fig. 1f. This is consistent with reports that the oxidation of melanin precursors (both L-DOPA and dopamine) leads to the formation of achiral melanin, even if the precursor is chiral as in the case of L-DOPA.14,15
3.2 Extinction measurements
Despite having a size below the optical resolution, single NPs are visible in bright-field images due to their absorption and scattering of light. We use a method to quantitatively measure the optical extinction cross section σext which has been described in ref. 11. Briefly, two offset-subtracted bright-field images are acquired; I1, with NPs in focus at position, P1 = (x1, y1), and I2, with the sample laterally shifted to position, P2 = (x2, y2) = (x1 + δx, y1 + δy), with the magnitude of the shift, . Generally, I1 and I2 are averaged over a number, Ni, of individual acquisitions, reducing shot noise in the final image. The normalised transmission is calculated as
. Generally, I1 and I2 are averaged over a number, Ni, of individual acquisitions, reducing shot noise in the final image. The normalised transmission is calculated as | (1) |
 | (2) |
An example Δ+ image showing PDA NPs is given in Fig. 2a, with Fig. 2b showing the same region imaged in qDIC for comparison. It can be seen that the point spread function (PSF) of the NPs in Δ+ is not circularly symmetric; this is a result of the linear polarisation of the illumination, and Fig. 2c shows the changing direction of elongation of the PSF of a single NP as the polarisation is rotated. Characteristic bright-dark doublets separated by the shift can be seen in Fig. 2a and c. To ensure that the PSF of a given NP does not overlap with its shifted position, the shift is chosen to be more than double the radius at which the extinction saturates for the longest light wavelength λ used, given by Ri = 3λ/2NA; we used a shift of s = 1.6 μm.
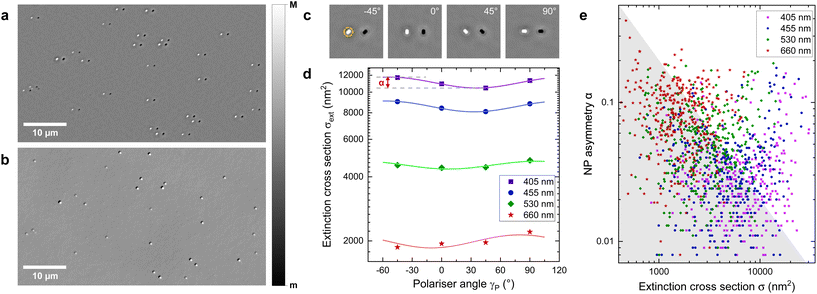 | ||
| Fig. 2 (a) An extinction image of PDA NPs imaged at an illumination wavelength of 405 nm, with a linear polarisation of −45° (greyscale as given from m = −0.05, M = 0.05). (b) The retrieved differential phase δ (see eqn (7)) generated from the DIC images taken of the same region (m = −0.03, M = 0.03). (c) A region (4.8 × 4.8 μm2) showing a single PDA NP imaged at 405 nm at four different polariser angles as given, greyscale as in (a). The yellow circle indicates the region Ai used for integration. (d) Extinction cross-section σext of the NP in (c) measured at wavelengths as indicated versus polariser angle (squares), with fits (lines) by eqn (5). (e) Asymmetry given by α versus mean extinction cross-section σ (see eqn (5)), for PDA NP. In the grey area, α is dominated by measurement noise. | ||
To measure the cross-section of a NP at P1 in Δ+, we integrate Δ+ over an area, Ai, of radius, Ri, centred at P1, and Δ− over the corresponding area at P2, such that the extinction cross-section is given by
 | (3) |
The shot-noise limited noise in the measurement of σext is given by28
 | (4) |
 of 8.2 nm2 at 455 nm, which is much lower than the background noise found in the measurement, which is 150 nm2 at 455 nm. The measured background noise is dominated by surface roughness and debris in the samples (visible in the background of both the extinction and differential phase images in Fig. 2), which are more prominent here than in our previous work due to the refractive index mismatch between air and glass, as well as the lower cleaning efficiency of the acetone-only surface treatment.
of 8.2 nm2 at 455 nm, which is much lower than the background noise found in the measurement, which is 150 nm2 at 455 nm. The measured background noise is dominated by surface roughness and debris in the samples (visible in the background of both the extinction and differential phase images in Fig. 2), which are more prominent here than in our previous work due to the refractive index mismatch between air and glass, as well as the lower cleaning efficiency of the acetone-only surface treatment.
The analysis of the extinction images is handled largely automatically in ImageJ by the Extinction Suite Plug-In developed in-house (https://langsrv.astro.cf.ac.uk/Crosssection). NPs are identified as local maxima in the extinction image at 405 nm. Maxima below a threshold value are excluded to eliminate surface features and small NPs which cannot be reliably analysed, having extinction cross-sections an order of magnitude smaller than typical melanin NPs (200–500 nm2 at 405 nm). Their signal is often below the noise level in higher wavelength extinction and corresponding qDIC images.
For each NP, the extinction σext is measured using eqn (3) for each wavelength and polarisation. The region Ai used for integration is illustrated for the example NP shown in Fig. 2c by a yellow circle. Extinction images taken at different wavelengths and polarisations are registered to compensate for sample drift during imaging. The measured σext as a function of the excitation polariser angle γP is fitted by the function
σ(γP) = σ[1 + α![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos{2(γP − γ)}, cos{2(γP − γ)}, | (5) |
The correlation between αΛ and σΛ for the different wavelengths is shown in Fig. 2e. The grey region is dominated by measurement noise, and is calculated as11 , using
, using  (measured at Λ = 660, the highest value amongst all Λ). The factor
(measured at Λ = 660, the highest value amongst all Λ). The factor  takes into account the averaging over two measurements per parameter of the angular dependence. Generally, it can be seen that most values of αΛ are below 0.2, with an average around 0.1.
takes into account the averaging over two measurements per parameter of the angular dependence. Generally, it can be seen that most values of αΛ are below 0.2, with an average around 0.1.
3.3 Quantitative DIC measurements
qDIC was used to provide information on the size of each particle, correlative with its extinction. As detailed in ref. 13, qDIC produces quantitative phase maps of the sample from two DIC images, I+ and I−, of the same region taken at phase offsets ±ψ. These images are used to calculate a contrast image | (6) |
 | (7) |
 | (8) |
| λ (nm) | n | κ of L-DOPA | κ of PDA | κ of Sepia |
|---|---|---|---|---|
| 405 | 1.793 | 0.400 ± 0.008 | 0.371 ± 0.006 | 0.365 ± 0.006 |
| 455 | 1.763 | 0.364 ± 0.007 | 0.329 ± 0.005 | 0.377 ± 0.006 |
| 530 | 1.732 | 0.241 ± 0.006 | 0.212 ± 0.003 | 0.285 ± 0.005 |
| 660 | 1.702 | 0.185 ± 0.005 | 0.155 ± 0.003 | 0.226 ± 0.005 |
For the L-DOPA NPs, the mean radius obtained using qDIC is 57.8 ± 0.7 nm (using N = 215 NPs measured), somewhat larger than the one obtained from TEM measurements of 49.7 ± 0.7 nm (N = 106). Likewise, for the PDA NPs, we find a mean radius of 59.4 ± 0.7 nm (N = 347) from qDIC compared to 53.4 ± 1.0 nm (N = 104) from TEM. For the sepia NPs, the mean radius is 73.6 ± 0.9 nm (N = 154) from qDIC and 65.0 ± 1.3 nm (N = 150) from TEM.
The larger mean radii retrieved from qDIC compared to TEM can be related to systematic errors of the qDIC results considering the large index difference between air (n = 1) and melanin, for which eqn (8) is only approximately valid.13 Furthermore, the refractive index of the NPs could be different from the value measured for bulk melanin by Stavenga et al.17 which we use for the radius calculations.
3.4 Asymmetry versus particle size
Having measured the size of a NP (eqn (8)) and its extinction anisotropy α (eqn (5)), we now investigate whether the measured anisotropy is due to non-spherical shape, or internal dichroism of the melanin by structural ordering. Let us first determine the effect of the non-spherical shape. Assuming an in-plane ellipsoid shape, α can be calculated from the two cross-sections, σa measured for a polarisation along the major semi-axis a, and σb measured for a polarisation along the minor semi-axis b, as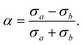 | (9) |
The scattering cross-section of 100 nm diameter melanin NPs in air is about 103 nm2 at 405 nm,11,17 and in the geometry used, 80% of the scattering is collected by the objective,23 so that scattering does not contribute significantly to the measured extinction. It is therefore reasonable to neglect the influence of scattering on the polarisation dependence of the extinction cross-section. The absorption cross-section is proportional to the imaginary part of the in-plane polarisability of the NP (see ref. 11eqn (9)), so that α can be expressed in terms of the polarisability along the two axes, αa and αb, as
 | (10) |
The polarisability of an ellipsoidal particle can be calculated in the Rayleigh regime of small particles using Rayleigh–Gans theory.29 Assuming that the first two of the three semi-axes a, b, c of the ellipsoid are orientated in-plane, the in-plane polarisabilities are given by
 | (11) |
 | (12) |
 . Despite the NPs being attached to glass, for an in-plane polarisation the surfaces of highest polarisation are the ones orthogonal to the field, which are exposed to air. We therefore chose to use air as a homogeneous surrounding medium (εm = 1) to keep the analytical treatment. Using eqn (11) and (12) in eqn (10), the aspect ratio b/a can be determined from α, as detailed in the ESI sec. S3.† We note that if assuming oblate (a = c > b) instead of prolate particles, the resulting aspect ratio is very similar, as shown in the ESI sec. S3.†
. Despite the NPs being attached to glass, for an in-plane polarisation the surfaces of highest polarisation are the ones orthogonal to the field, which are exposed to air. We therefore chose to use air as a homogeneous surrounding medium (εm = 1) to keep the analytical treatment. Using eqn (11) and (12) in eqn (10), the aspect ratio b/a can be determined from α, as detailed in the ESI sec. S3.† We note that if assuming oblate (a = c > b) instead of prolate particles, the resulting aspect ratio is very similar, as shown in the ESI sec. S3.†
At the two shorter measured wavelengths of 405 nm and 455 nm, the mean and standard error of the mean of the aspect ratio from extinction for the PDA NPs is found to be 0.944 ± 0.002 and 0.933 ± 0.003 respectively. To determine whether α indeed originates from the particle shape, these ensemble average aspect ratios are compared to the one measured using the TEM images of the PDA NPs, which was found to be 0.946 ± 0.007. This is consistent with the above aspect ratios from extinction, confirming the particle shape interpretation. Likewise, the aspect ratio values for the sepia NPs are also consistent between extinction and TEM measurements. The aspect ratio from TEM was 0.925 ± 0.005, in good agreement with those calculated using the extinction (0.930 ± 0.003 and 0.921 ± 0.004). This indicates that for PDA and sepia NPs, the particle shape can explain the observed optical asymmetry at these wavelengths.
In the case of the L-DOPA NPs, slightly different aspect ratios were observed in extinction and TEM measurements. At 405 nm and 455 nm, the aspect ratio from extinction for the L-DOPA NPs was 0.922 ± 0.003 and 0.911 ± 0.004 respectively, compared to the value of 0.891 ± 0.012 from TEM. This discrepancy is relatively small, and may be the result of systematic errors in the optical analysis. These NPs also show a significantly decreasing aspect ratio with increasing radius, both in TEM and extinction. This observation is attributed to the incorporation of low valence states of Mn ions, reduced from KMnO4, into the NPs, resulting in the formation of coordination species that affect the packing and lead to larger particles with distorted shape. It has been reported that the amount of oxidant affects the shape of the NPs and higher amounts hinder efficient generation of particle-shaped melanin.30,31
The calculated aspect ratios across all wavelengths are shown in Fig. 3versus the NP radius for each NP type. Interestingly, it can be seen that the spread of the aspect ratio values increases with increasing wavelength; this is not a result of the noise in the data, since the spread does not depend on the radius, and the noise is generally only relevant for radii below around 40 nm (see grey areas). The increase is thus evidence for dichroism in the long wavelength tail of the absorption. At these wavelengths such dichroism would also be most expected, as the lowest excitations of larger chains are probed.
Assuming that the melanin of the NPs does have structural ordering leading to material dichroism, the measured extinction at a given wavelength Λ as a function of the polariser angle γp can be expressed as a sum of dichroic and geometric contributions,
 | (13) |
(αcΛ)2 = (αc405)2 + (αdΛ)2 + 2αc405αdΛ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos{2(γc405 − γdΛ)}, cos{2(γc405 − γdΛ)}, | (14) |
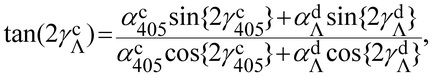 | (15) |
The orientation γdΛ of the dichroism is related to the direction of structural ordering, which should be independent of wavelength. We can therefore evaluate the variation of this orientation as function of wavelength to verify if the data support the dichroism hypothesis. To ensure that the retrieved orientation γdΛ is not dominated by noise, we analysed only NPs with αcΛ > 0.1 for at least one wavelength and σΛ above the noise level for α at all wavelengths ( ). These are 16% of the ensemble for the L-DOPA NPs, 12% for the PDA NPs, and 9% of the sepia NPs, and are indicated in Fig. 3.
). These are 16% of the ensemble for the L-DOPA NPs, 12% for the PDA NPs, and 9% of the sepia NPs, and are indicated in Fig. 3.
In order to quantify the consistency of γd, we first combine αd and γd at each wavelength into a single complex parameter, zd = αdexp(iγd), allowing for a visual representation in the complex plane. To isolate the dichroism effect, we use its wavelength dependence, by evaluating the difference between the complex parameters at 530 nm and 660 nm to the one at 455 nm: ΔΛ = zdΛ− zd455. Since both differences are expected to have the same angle given by the direction of structural ordering, we evaluate their angle difference γΔ = arg(Δ*530Δ660), where * denotes the complex conjugate. Because the structural direction has a unique angular range of π, we consider γΔ modulo π over the range −π/2…π/2. Histograms of γΔ for each NP type are given in Fig. 4a–c. It can be seen that for all three NP types, there is a clustering of values around zero, consistent with the hypothesis that the orientation of the observed dichroism is related to a given direction of structural ordering. This clustering of values is verified by a 1D Ripley's K test,33 which confirms that the observed γΔ distributions are not random, indicating that dichroism is present in all three NP types. Such clustering is still present if the thresholds are adjusted, indicating that it is not an artefact of the above noise selection used (see ESI sec. S4†).
To provide a direct representation of the amplitude and orientation of the dichroism versus wavelength, we show in Fig. 4d–fzdexp(−iγd660) for each particle included in the histograms. In this plot, the distance of the points from the origin indicates the magnitude of αd, while their polar angle is γdΛ− γd660. The elongated distribution centred on the positive real axis shows the consistent orientation of the dichroism. The statistical distribution parameters of αd for the different wavelengths are shown in Fig. 4g and h. An increase with increasing wavelength is found for L-DOPA and PDA NPs, while the sepia NPs show no strong wavelength dependence, tighter distributions at the higher wavelengths, and values similar to the wavelength average of L-DOPA and PDA at 455 nm and 530 nm. Overall, the dichroism observed is in the range of 2–10% of the absorption cross-section and thus approximately also of the absorption index, since for κ ≪ 1 both quantities are proportional to each other (see ESI sec. S3†).
3.5 Absorption index versus particle size
The extinction and qDIC radius data can be combined to obtain measurements of the absorption index κ of individual melanin NPs. The particle's radius in the dipole limit is related to its absorption cross-section at a given wavelength by | (16) |
While for smaller particles the contribution of the scattering to the measured extinction is negligible compared to the absorption, for some of the larger particles we measure, the scattering leads to a small but notable correction. To account for this, we calculated the scattering cross-section versus radius11 using the refractive index values from Stavenga et al.17 In our excitation-collection geometry, 80% of the scattered light is collected by the objective,23 so that only 20% contributes to the measured extinction cross-section. We thus subtract this estimated scattering contribution from the measured extinction σΛ to determine the absorption cross-section. Recalling that εp = (n + iκ)2, and using the refractive index n of melanin from Stavenga et al.,17 we can use eqn (16) determine the absorption index κ from the absorption cross-section σabs and qDIC particle radius r. The resulting values are shown in Fig. 5, with mean values given in Table 2. To represent the relevance of the compensated scattering contribution, we show by orange dashed lines the value of κ which would result from it.
We find that for the sepia NPs, κ is higher than that of either of the synthetic types of melanin, except at the lowest wavelengths. This is interesting, considering that literature values for the absorption index of natural melanin tend to be lower than those of synthetic melanin. This points to the presence of non-melanin components which have a lower absorption, such as lipids or other proteins, within the natural melanin structures measured in the literature.19 By measuring the single particles directly, we avoid such contamination. Measuring individual particles also allows us to see that the distribution of absorption indices is fairly broad. We also note that while the distribution is narrowing with increasing size for PDA NPs, it is rather size-independent for L-DOPA and sepia NPs.
The values we measure for the PDA NPs are consistent (within 10–20%) with those reported for films of PDA NPs at comparable wavelengths by Xiao et al.18 The differences may be partially related to systematic errors in the qDIC originating from the high index contrast, or the dipole limit, as well as neglecting the influence of the substrate. These issues could be reduced by measuring the particles in a medium with lower refractive index contrasts to melanin.
4 Conclusions
We demonstrated that combining optical extinction micro-spectroscopy with quantitative differential interference contrast (qDIC) microscopy allows to measure the shape and size of both natural and artificial single melanin nanoparticles, as well as characterise their optical properties. Analysing the particle extinction as a function of the excitation polarisation direction, we determine the particle aspect ratios, and find values typically in the range from 0.83 to 0.98, with mean values at 405 nm wavelength in general agreement with those measured using TEM. At longer wavelengths, the apparent aspect ratio increases, which is evidence for structural ordering of the melanin, giving rise to dichroism. An analysis of the dichroism yields values of 2–10% absorption difference, which is increasing with wavelength across 455, 530, and 660 nm for L-DOPA and PDA, while being rather constant for the sepia particles. Using qDIC, we determined the size of individual particles. Combining these measurements with extinction, we extract the absorption index of individual melanin nanoparticles. We find that on average the natural melanin source has a higher absorption index than the artificial melanin, different from previous findings. We attribute this to the lack of non-melanin contaminants in the present single particle data, compared to the bulk natural melanin sources used in literature.The reported optical methods and the novel findings regarding the inhomogeneity and dichroism of melanin nanoparticles pave the way to a better understanding of their function, as well as provide an analysis tool to characterise nanoparticles of technical or natural relevance.
Author contributions
W.L. conceived the work. D.R. performed the sample preparation, optical microscopy, and related data analysis D.R., L.P., P.B. and W.L. developed the numerical model and methods. A.M.P. and M.M. contributed to the synthesis and characterisation of NPs. All authors contributed to interpreting the data and writing the manuscript.| CRediT author roles | DR | AM | LP | MM | PB | WL |
|---|---|---|---|---|---|---|
| L: lead, E: equal, S: supporting | ||||||
| Conceptualization | S | S | L | |||
| Methodology | S | S | S | S | L | |
| Software | E | E | S | |||
| Validation | L | E | S | S | ||
| Formal Analysis | L | E | ||||
| Investigation | L | L | ||||
| Resources | E | E | E | |||
| Data curation | L | L | ||||
| Writing – orig. draft | E | E | E | |||
| Writing – review&ed. | E | E | S | S | S | E |
| Visualization | E | E | S | |||
| Supervision | E | E | E | |||
| Project admin. | E | S | E | |||
| Funding acq. | L | L | S | |||
Data availability
Information about the data created during this research, including how to access it, is available from Cardiff University data archive at https://doi.org/10.17035/d.2023.0264667943.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
We thank Iestyn Pope for support in the development of the hardware for the optical measurements. We thank Giulio Cerullo, Vasilis Petropoulos, and Margherita Maiuri, Politechnico di Milano, Italy, for discussions. We acknowledge funding from the Engineering and Physical Sciences Research Council under grant numbers EP/M028313/1 and EP/R51150X/1.References
- A. Huguet-Casquero, E. Gainza and J. L. Pedraz, Biotechnol. Adv., 2021, 46, 107657 CrossRef CAS PubMed
.
- L. Huang, M. Liu, H. Huang, Y. Wen, X. Zhang and Y. Wei, Biomacromolecules, 2018, 19, 1858–1868 CrossRef CAS PubMed
.
- A. Mavridi-Printezi, M. Guernelli, A. Menichetti and M. Montalti, Nanomaterials, 2020, 10, 2276 CrossRef CAS PubMed
.
- D. R. Dreyer, D. J. Miller, B. D. Freeman, D. R. Paul and C. W. Bielawski, Langmuir, 2012, 28, 6428–6435 CrossRef CAS PubMed
.
- J. Liebscher, Eur. J. Org. Chem., 2019, 4976–4994 CrossRef CAS
.
- K.-Y. Ju, Y. Lee, S. Lee, S. B. Park and J.-K. Lee, Biomacromolecules, 2011, 12, 625–632 CrossRef CAS PubMed
.
- Y. Zou, X. Chen, P. Yang, G. Liang, Y. Yang, Z. Gu and Y. Li, Sci. Adv., 2020, 6, eabb4696 CrossRef CAS PubMed
.
- J. Pyo, K.-Y. Ju and J.-K. Lee, J. Photochem. Photobiol., B, 2016, 160, 330–335 CrossRef CAS PubMed
.
- I. de la Calle, D. Soto-Gómez, P. Pérez-Rodríguez and J. E. López-Periago, Food Anal. Methods, 2019, 12, 1140–1151 CrossRef
.
- K. Ghattavi, A. Homaei, E. Kamrani and S.-K. Kim, Dyes Pigm., 2022, 201, 110214 CrossRef CAS
.
- L. M. Payne, W. Albrecht, W. Langbein and P. Borri, Nanoscale, 2020, 12, 16215–16228 RSC
.
- Y. Park, C. Depeursinge and G. Popescu, Nat. Photonics, 2018, 12, 578–589 CrossRef CAS
.
- S. Hamilton, D. Regan, L. Payne, W. Langbein and P. Borri, Analyst, 2022, 147, 1567–1580 RSC
.
- M. Gaeta, R. Randazzo, V. Villari, N. Micali, A. Pezzella, R. Purrello, M. d'Ischia and A. D'Urso, Front. Chem., 2020, 8, 616961 CrossRef CAS PubMed
.
- D. Mallinson, A. B. Mullen and D. A. Lamprou, J. Mater. Sci., 2018, 53, 3198–3209 CrossRef CAS PubMed
.
- W. Li, A. Patil, X. Zhou, Z. Wang, M. Xiao, M. D. Shawkey, N. C. Gianneschi and A. Dhinojwala, Appl. Phys. Lett., 2020, 117, 203701 CrossRef CAS
.
- D. G. Stavenga, H. L. Leertouwer, D. C. Osorio and B. D. Wilts, Light: Sci. Appl., 2015, 4, e243–e243 CrossRef
.
- M. Xiao, Y. Li, M. C. Allen, D. D. Deheyn, X. Yue, J. Zhao, N. C. Gianneschi, M. D. Shawkey and A. Dhinojwala, ACS Nano, 2015, 9, 5454–5460 CrossRef CAS PubMed
.
- M. Xiao, M. D. Shawkey and A. Dhinojwala, Adv. Opt. Mater., 2020, 8, 2000932 CrossRef CAS
.
- Y. Liu, K. Ai and L. Lu, Chem. Rev., 2014, 114, 5057–5115 CrossRef CAS PubMed
.
- K.-Y. Ju, M. C. Fischer and W. S. Warren, ACS Nano, 2018, 12, 12050–12061 CrossRef CAS PubMed
.
- L.-F. Wang and J.-W. Rhim, LWT – Food Sci. Technol., 2019, 99, 17–23 CrossRef CAS
.
- A. Zilli, W. Langbein and P. Borri, ACS Photonics, 2019, 6, 2149–2160 CrossRef CAS PubMed
.
- Y. Huang, Y. Li, Z. Hu, X. Yue, M. T. Proetto, Y. Jones and N. C. Gianneschi, ACS Cent. Sci., 2017, 3, 564–569 CrossRef CAS PubMed
.
- Y. Wang, X. Wang, T. Li, P. Ma, S. Zhang, M. Du, W. Dong, Y. Xie and M. Chen, ACS Appl. Mater. Interfaces, 2018, 10, 13100–13106 CrossRef CAS PubMed
.
- C. A. Schneider, W. S. Rasband and K. W. Eliceiri, Nat. Methods, 2012, 9, 671–675 CrossRef CAS PubMed
.
- M. Caldas, A. C. Santos, F. Veiga, R. Rebelo, R. L. Reis and V. M. Correlo, Acta Biomater., 2020, 105, 26–43 CrossRef CAS PubMed
.
- L. M. Payne, W. Langbein and P. Borri, Phys. Rev. Appl., 2018, 9, 034006 CrossRef CAS
.
-
C. F. Bohren and D. R. Huffman, Absorption and scattering of light by small particles, John Wiley & Sons, New York, 1983 Search PubMed
.
- D. J. Kim, K.-Y. Ju and J.-K. Lee, Bull. Korean Chem. Soc., 2012, 33, 3788–3792 CrossRef CAS
.
- H. Liu, C. Chu, Y. Liu, X. Pang, Y. Wu, Z. Zhou, P. Zhang, W. Zhang, G. Liu and X. Chen, Adv. Sci., 2018, 5, 1800032 CrossRef PubMed
.
- F. R. Kohl, C. Grieco and B. Kohler, Chem. Sci., 2020, 11, 1248–1259 RSC
.
-
M. L. Yunta, T. Lagache, J. Santi-Rocca, P. Bastin and J.-C. Olivo-Marin, 2014 IEEE 11th International Symposium on Biomedical Imaging (ISBI), 2014, pp. 541–544 Search PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Fig. S1–S5. See DOI: https://doi.org/10.1039/d3an00654a |
| This journal is © The Royal Society of Chemistry 2023 |




