Gold nanoshells with magnetic cores and a urea-based receptor for SERS sensing of fluoride anions: experimental and computational study

Abstract

The study demonstrates that a combination of plasmonic nanostructures and artificial receptors can be applied for sensing small molecular species. Gold nanoshells containing magnetic cores are used as the SERS-active substrates, which opens the way for the development of multimodal contrast agents with applicability extended to sensing or for the separation of analytes by magnetic solid-phase extraction. Disubstituted ureas forming hydrogen-bonded complexes with certain anions can be employed as molecular sensors. In this case study, gold nanoshells with silica-coated Mn–Zn ferrite cores were prepared by a multistep procedure. The nanoshells were co-functionalized with an N-(4-mercaptophenyl)-N′-(4-nitrophenyl)urea sensor synthesized directly on the gold surface, and with 4-nitrothiophenol, which is adopted as an internal standard. SERS measurements were carried out with acetonitrile solutions of tetrabutylammonium fluoride (Bu₄NF) over a concentration range of 10⁻¹⁰–10⁻¹ mol L⁻¹. The spectral response of the sensor is dependent on the fluoride concentration in the range of 10⁻⁵–10⁻¹ mol L⁻¹. To investigate further the SERS mechanism, a model sensor, N-(4-bromophenyl)-N′-(4-nitrophenyl)urea, was synthesized and used in Raman spectroscopy with solutions of Bu₄NF, up to a molar ratio of 1 : 20. The spectra and the interactions between the sensors and fluoride anions were also studied by extensive DFT computations.

---

1. Introduction

Surface-enhanced Raman spectroscopy (SERS) employs so-called plasmonic substrates, most frequently Au, Ag or Cu metals in the form of rough surfaces or nanostructures. A dramatic enhancement of the Raman scattering of adsorbed molecules may occur, with an enhancement factor of up to 10¹⁰–10¹².¹ Thus, the detection of single molecules should be possible.^1–4 Two main enhancement mechanisms are considered: electromagnetic and chemical effects.^5,6 The dominant former one is based on the excitation of localized surface plasmons, i.e. collective oscillations of conduction electrons. If a resonance of plasmon oscillations with the incident light is achieved, an enhancement of the electric field occurs near the surface, boosting the Raman scattering of molecules in the proximity. The chemical effect assumes a chemical interaction of molecules with the metal surface, e.g., accompanied by charge transfer phenomena that enhance the Raman scattering.

Gold nanostructures are established and very popular SERS substrates.⁶ An interesting variety are gold nanoshells grown on a dielectric core.^7–10 By controlling their geometry, the surface plasmon resonance (SPR) frequency can be tuned from the visible to the infrared region, including the near-infrared (NIR) window convenient for biological tissues. In the present study, we investigate nanoshells with magnetic nanoparticles embedded in their core. This extends their functionality by visualization in magnetic imaging techniques or magnetically assisted separation. In medical applications, they can serve as multimodal contrast agents,^11,12 theranostic tools^12–14 or components of complex biosensors.¹⁵ The magnetic core ensures a contrast effect in magnetic resonance imaging (MRI) or a signal in magnetic particle imaging (MPI), whereas the golden part of the nanoshell can be employed for photoacoustic or SERS imaging. This is promising for novel contrast agents with extended applicability for the sensing of local physiological properties or the detection of certain analytes.¹¹

Previous studies combining principles of molecular recognition with SERS substrates focused mostly on receptors based on biomolecules, like antibodies, and synthetic aptamers, i.e., short single-stranded nucleic acids capable of binding diverse analytes.^16,17 The transduction of the binding event to the SERS signal was almost exclusively achieved either by controlling the distance between a reporter moiety and the SERS substrate (e.g., the binding of an analyte induced a conformational change of the receptor) or by the aggregation of plasmonic nanostructures induced by the analyte. Some studies described the application of low-molecular-weight sensors other than aptamers and relied mostly on simple aggregation-based transduction, e.g., gold nanoparticles modified with 2,4,6-trimercapto-1,3,5-triazine were used for the detection of Hg²⁺ and Cd²⁺ ions.¹⁸ However, the development of systems with canonical molecular sensors of small molecular species, and especially anions, seems to be impeded by experimental difficulties, such as a weak response of the analyte in the SERS spectrum of the receptor, complicated analysis of SERS data, and cumbersome synthetic procedures. The present study attempts to demonstrate the feasibility of such SERS sensing by utilizing urea-based receptors of small anions coupled with gold nanoshells. The fluoride anion is not chosen arbitrarily as a model analyte; its increased concentration in water or food poses a risk to public health and the environment, and novel analytical methods may improve its monitoring and the detection of toxic levels.

The power of urea- and thiourea-based receptors was recognized in the early ‘90s when strong coordination of various oxoanions by N,N′-disubstituted ureas and thioureas was observed in chloroform^19,20 and dimethylsulfoxide (DMSO)²¹ solutions. The urea/thiourea moiety forms hydrogen bonds with certain anions, typically oxoanions like H₂PO₄⁻ or carboxylates, but also with halide anions (see the complexation of fluoride anion in Scheme 1).²² Many studies have focused on increasing the binding constant (cf.Scheme 1, eqn (1)), on increasing selectivity for certain anions, and on improving the sensitivity by coupling urea/thiourea with efficient chromophores and fluorophores, which are active in UV-vis spectrophotometry/colorimetric analysis or spectrofluorimetry (see the excellent reviews by Kundu et al.,²² Li et al.²³ or Bregović et al.²⁴). An important observation was made by Boiocchi et al. in 2004, who studied interactions of N,N′-bis(4-nitrophenyl)urea with a series of various anions (including strongly interacting carboxylates, H₂PO₄⁻, F⁻ and others) in acetonitrile and DMSO and showed that the interaction of the sensor with the fluoride anion was different.²⁵ The fluoride formed not only the usual 1 : 1 complex with the receptor, but also the [HF₂]⁻ anion accompanied by the deprotonation of the receptor according to eqn (2). Although the strongly electron-withdrawing groups in the para-position increase the polarization of both N–H bonds, thus shifting the equilibria 1 and 2 to the right side, these groups are not a necessary condition for deprotonation. The deprotonation is caused primarily by the strong Lewis base character of fluoride anions and the high stability of [HF₂]⁻ species.^25,26

Scheme 1 The interaction of a typical urea/thiourea-based sensor (LH₂), which has strong electron-withdrawing groups (R¹ and R²) in the para-position of phenyl substituents, with fluoride anions in aprotic solvents according to ref. 25.

In the present study, a urea-based sensor is attached to the gold nanoshells via the Au–S bond. N-(4-Mercaptophenyl)-N′-(4-nitrophenyl)urea (MPNPU) is synthesized directly on the gold surface, taking advantage of the facile reaction between p-aminothiophenol and gold in the first step and of the facile nucleophilic addition of an amine to p-nitrophenyl isocyanate in the second step (Scheme 2), which is reminiscent of the famous synthesis of the unsubstituted urea by Friedrich Wöhler in 1828. By the on-surface synthesis, the isolation of the pure MPNPU compound is avoided. This is convenient taking into account that free MPNPU would be prone to oxidation in air, accompanied by the formation of the corresponding disulphide. Importantly, a small amount of 4-nitrothiophenol (NTP) is added during the first step to achieve co-functionalization with a SERS-active molecule that will not interact with fluoride anions. Its SERS signal is used for the normalization of the SERS intensity during the analysis.

Scheme 2 Synthesis of the urea-based sensors in the present study. The MPNPU compound is synthesized directly on the gold surface, Au(s), of the nanoshells. The BrPNPU compound is a model sensor prepared for Raman spectroscopy measurements.

Moreover, free N-(4-bromophenyl)-N′-(4-nitrophenyl)urea (BrPNPU) is synthesized (Scheme 2) as a model urea-based sensor, which is not air-sensitive and enables well-defined measurements in solutions containing fluoride anions. The Raman study of such solutions complements previous analyses based on UV-vis spectrophotometric, fluorimetric and ¹H NMR investigations of the host–guest interaction between urea/thiourea-based sensors and small anions (see also the recent reviews^27,28 on the binding of fluoride with synthetic receptors). Finally, as shown below, the Raman and SERS spectra and the interactions between the MPNPU/BrPNPU sensors and fluoride anions are rationalized by DFT calculations.

Regarding the synthesis of gold nanoshells, a multistep procedure is applied, combining the layer-by-layer self-assembly technique²⁹ and the seed-and-growth method.⁸ Using the self-assembly technique, a dense seeding of silica-coated cores with a fine gold colloid is achieved, and the growth of the gold seeds in the next phase leads to the formation of continuous nanoshells. Hydrothermally prepared Mn–Zn ferrite nanoparticles with a composition close to Mn_0.6Zn_0.4Fe₂O₄ and a mean size of ∼10 nm are employed as the magnetic cores, due to their magnetic properties and peculiarities and the ease of preparation of their silica-coated products. Such magnetic nanoparticles possess a reasonably high magnetization of M(3T) = 55–57 A m² kg⁻¹ at room temperature while being in the superparamagnetic regime.^30,31 Moreover, well-defined silica-coated ∼30 nm clusters of these crystallites can be easily obtained, exhibiting transverse relaxivity as high as 450 s⁻¹ mmol(Me₃O₄)⁻¹ L, which makes them an excellent negative contrast agent for T₂-weighted MRI at the same time.³² Last but not least, a detailed study of cytotoxic effects demonstrated negligible toxicity of silica-coated Mn–Zn ferrite particles and their excellent properties in the comparative assessment of cytotoxicity.³³

2. Materials and methods

2.1 Synthesis and functionalization

The synthesis is summarized in Scheme 3; full details are provided in the ESI (see section 1).†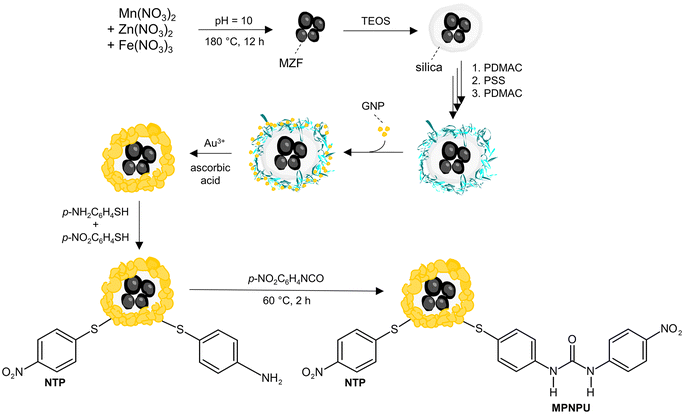

Scheme 3 Scheme of the synthesis of gold nanoshells with magnetic cores and their co-functionalization with the urea-based sensor (MPNPU) and the internal standard (NTP).

2.1.1 Synthesis of gold nanoshells with silica-coated Mn–Zn ferrite cores. The synthesis of Mn–Zn ferrite nanoparticles of the approximate composition Mn_0.6Zn_0.4Fe₂O₄ followed the procedure by Kaman et al.³² and is described in detail in sect. 1.2 of the ESI.† In brief, the nanoparticles were prepared by alkaline precipitation of Fe(III), Mn(II) and Zn(II) nitrates in an Fe : Mn : Zn metal ratio of 1.80 : 0.6 : 0.4 and subsequent hydrothermal treatment at 180 °C for 12 h. The resulting Mn–Zn ferrite particles (further denoted as MZF) were encapsulated into silica by a method proposed by Graf et al.³⁴ that involves the stabilization of particles in water by PVP followed by the growth of silica on their surface by hydrolysis and polycondensation of tetraethoxysilane (TEOS). Specifically, PVP K90 was applied for colloidal stabilization, 5.2 μL of TEOS per 1 mg of MZF particles was employed, and the procedure was completed by mass fractionation through centrifugation at 260 RCF for 15 min, whereby the fine fraction of silica-coated particles (MZF@sil) was isolated (see sect. 1.3 of the ESI†).

For the synthesis of gold nanoshells (MZF@sil@Au), a multistep procedure was adopted with some modifications from the report by Koktan et al.³⁵ and consisted of the following steps: (i) preparation of ultrafine gold nanoseeds (GNPs) by Duff's method;³⁶ (ii) consecutive adsorption of poly(diallyldimethylammonium chloride) (PDADMAC), poly(sodium 4-styrenesulfonate) (PSS), and again PDADMAC on the MZF@sil surface; (iii) adsorption of the gold seeds on the so-obtained polyelectrolyte multilayer (the resulting product is denoted as MZF@sil@GNP), and (iv) their growth and coalescence by the reduction of an Au(III) precursor obtained from HAuCl₄ in an alkaline solution. More details regarding each step are provided in sect. 1.4 of the ESI.†

Moreover, to probe the growth of nanoshells and the effects of nanoshell thickness, a series of supplemental products with varying amounts of gold per mass of ferrite cores was prepared by applying the same procedure and by collecting individual samples during the growth stage. The respective samples with gradually increasing content of gold are denoted as MZF@sil@Au-x, where x = I, II, III, and IV, and full details regarding the preparation are provided in sect. 1.5 of the ESI.†

2.1.2 Functionalization of gold nanoshells. The gold nanoshells were co-functionalized in a molar ratio of 1 : 10 with 4-nitrothiophenol and N-(4-mercaptophenyl)-N′-(4-nitrophenyl)urea (MPNPU), which acted as the internal standard and the fluoride sensor, respectively. The latter compound was synthesized directly on the gold surface by reacting 4-aminothiophenol, chemisorbed to the gold surface in the first step, with 4-nitrophenyl isocyanate in the second step.

At first, gold nanoshells were separated from the stock aqueous suspension by exhaustive centrifugation (7000 RCF for 30 min) and washed twice with acetonitrile. The residue was redispersed in an acetonitrile solution of NTP (1 mmol L⁻¹) and 4-aminothiophenol (10 mmol L⁻¹), and the suspension was agitated in an ultrasound bath overnight while the temperature was maintained at ∼25 °C. The modified nanoshells were separated by centrifugation and washed twice with acetonitrile. Then the nanoshells were redispersed in an acetonitrile solution of 10 mmol L⁻¹ 4-nitrophenyl isocyanate, and the mixture was agitated by ultrasound for 2 h at 60 °C and then for an additional 2 h at ∼25 °C. Thereafter, the nanoshells were separated by centrifugation, washed twice with acetonitrile, and redispersed in acetonitrile (the stock solution of functionalized MZF@sil@Au nanoshells).

By using the same procedure, additional experiments were carried out to achieve gold nanoshells functionalized with either NTP or MPNPU to facilitate the interpretation of the SERS spectra of nanoshells functionalized with both compounds. In both cases, the thiol compound was used at a concentration of 10 mmol L⁻¹. The supplemental products MZF@sil@Au-x (x = I, II, III, IV) were functionalized just with NTP at a concentration of 10 mmol L⁻¹ to analyse the effect of varying gold content/nanoshell thickness on SERS spectra. The final volume of the acetonitrile suspensions of functionalized MZF@sil@Au-x was carefully adjusted to the same concentration of MZF cores.

2.1.3 Synthesis of N-(4-bromophenyl)-N′-(4-nitrophenyl)urea (BrPNPU). Dichloromethane (150 mL) was added to a 250 mL flask containing 4-bromoaniline (0.51 g, 3.0 mmol) and 4-nitrophenyl isocyanate (0.49 g, 3.0 mmol), and a magnetic stirrer was inserted. The mixture was heated under a reflux condenser to 60 °C for 24 h while stirring. The yellow precipitate was filtered off, washed several times with dichloromethane, and dried in vacuo. The yield was 84%.

¹H NMR (500 MHz, DMSO-d₆): δ 9.42 (s, 1H, H_a′), 9.01 (s, 1H, H_a), 8.19–8.12 (m, 2H, H_c′), 7.69–7.61 (m, 2H, H_b′), 7.48–7.38 (m, 4H, H_b + H_c) (see also Fig. S1 of the ESI†). Calculated/experimental (%) for C₁₃H₁₀BrN₃O₃: C 46.45/46.50, H 3.00/3.19, N 12.50/12.36.

2.2 Characterization of the nanoparticles and nanoshells

The phase composition, crystal structure, and mean size of the crystallites of MZF particles were analyzed by powder X-ray diffraction (XRD) with Cu K_α radiation. The XRD pattern was collected at room temperature using a Bruker D8 Advance diffractometer and analyzed by the Rietveld method in the FullProf program. To resolve the size, strain and instrumental contributions to line broadening, the instrumental function was measured on a strain-free LaB₆ standard and the Thompson–Cox–Hastings pseudo-Voigt function was employed in the profile analysis.

The ratio of metal atoms in bare MZF particles was determined by X-ray fluorescence analysis (XRF) using a Thermo Scientific ARL Perform'X wavelength-dispersive X-ray fluorescence spectrometer.

The size and morphology of the particles, from the bare MZF nanoparticles via different intermediates to the final MZF@sil@Au nanoshells, were studied using an FEI Tecnai G² 20 transmission electron microscope (TEM) with a LaB₆ cathode and an acceleration voltage of 200 kV. To prepare the sample for microscopy, a droplet of aqueous suspension was transferred on a formvar/carbon Cu grid and dried in air. To evaluate the size distribution of gold nanoshells and silica-coated particles, the area of the observed cross-section, S, was determined for 100 nanoparticles using ImageJ 1.52a software. The particle size was then estimated based on the spherical approximation as .

Dynamic light scattering (DLS) of the aqueous suspensions of MZF@sil and MZF@sil@GNP particles and of MZF@sil@Au nanoshells was performed at 25 °C using a Malvern Zetasizer Nano-ZS instrument to analyze the colloidal stability and hydrodynamic size of respective samples. The hydrodynamic size and the distribution width were described by the Z-average value, d_Z, and the polydispersity index, pdi, respectively. The same instrumentation was also employed to measure the zeta potential of MZF@sil@Au nanoshells functionalized with MPNPU and NTP based on electrophoretic light scattering (ELS). The functionalized nanoshells were separated from the stock acetonitrile suspension by centrifugation, washed with water and redispersed in deionized water. The resulting aqueous suspension was carefully adjusted to pH = 7.0 using a highly diluted NaOH solution. ELS measurement was carried out at 298 K.

The surface plasmon resonance of gold nanostructures, including GNP seeds and MZF@sil@Au nanoshells, was investigated by UV-vis absorption spectroscopy, and the study was supplemented by the measurement of MZF@sil particles. The spectra of dilute suspensions were measured in quartz cuvettes at room temperature using an Agilent Cary 300 UV-vis spectrophotometer.

The magnetic properties of bare MZF nanoparticles were probed by SQUID magnetometry in DC fields using an MPMS XL system from Quantum Design. The powder sample (∼8 mg) was packed into a gelatine capsule (∼40 mg) together with a small amount of Teflon tape (∼20 mg) and subsequently mounted in a plastic straw. The characterization included hysteresis loops at 5 K and 300 K, measurement of the temperature dependence of remanence, and temperature-variable measurements of susceptibility. Susceptibility measurements were carried out in zero-field-cooled (ZFC) and field-cooled (FC) regimes in the temperature range of 5–390 K with a probe field of 2 mT.

In the present study, the concentrations of functionalized gold nanoshells and silica-coated particles are specified by the weight content of Mn–Zn ferrite particles, which was accurately and with a minimum risk of interferences determined by magnetometric analysis. An aliquot of the suspension was transferred onto a small piece of Teflon tape spread on a clock glass and dried on a steam bath. The dry sample was mounted in a gelatine capsule similarly to the sample of bare MZF particles, and the magnetization curve was measured at 5 K. The ferrite content was calculated as the magnetic moment of the sample divided by the magnetization of bare MZF cores. The analysis was based on values measured in a magnetic field of 0.3 T and corrected for the diamagnetic contribution of the Teflon tape and the gelatine capsule.

2.3 Identification of molecular compounds

The ¹H NMR spectrum of the model urea-based sensor BrPNPU was recorded using a JEOL JNM-ECZR 500 MHz spectrometer and was referenced to the residual ¹H signal of the deuterated solvent. To confirm the purity of the compound, CHN analysis was performed in the Central laboratories of the University of Chemistry and Technology, Prague, using a Vario EL III analyser.

In order to confirm the presence of MPNPU molecules on the surface of functionalized nanoshells, a model functionalization of GNP particles, as an easily accessible gold colloid with a large surface-to-volume ratio, was carried out under the same conditions. The resulting sample was subjected to leaching with 0.05 M KCN solution in air for 3 days, whereby gold was dissolved. The insoluble residue was extracted with acetonitrile, and the extract was dried in vacuo. Mass spectrometry (MS) with the atmospheric-pressure chemical ionization technique (APCI), namely a Thermo Scientific LTQ Orbitrap Velos mass spectrometer, was used for its analysis.

2.4 Raman spectroscopy

The SERS study was carried out with the functionalized nanoshells in acetonitrile, which provided the best spectral window and a good dispersibility of nanoshells among various aprotic solvents. Tetrabutylammonium fluoride (Bu₄NF) was used as a soluble fluoride with a non-interacting counterion. A series of acetonitrile suspensions was prepared with a constant concentration of MZF@sil@Au nanoshells of 8.3 mg(MZF) L⁻¹ and a concentration of Bu₄NF varying in the range of 10⁻¹⁰–10⁻¹ mol L⁻¹. Actually, hexaplicates of each concentration of Bu₄NF were prepared in the range of 5 × 10⁻⁷–10⁻¹ mol L⁻¹, whereas triplicates were used for the lower concentrations. All suspensions were equilibrated overnight (∼14 h) to avoid any time-dependent effects in the SERS study and were measured in a single run under the same conditions.

Conventional Raman spectroscopy was employed to study the spectral changes that accompany the interaction of the model sensor BrPNPU with fluoride ions in the range of molar ratios from 1 : 0.1 to 1 : 20. DMSO was used as the solvent because of the low solubility of BrPNPU in acetonitrile. A series of samples with a constant concentration of BrPNPU of 0.05 mol L⁻¹ and varying concentrations of Bu₄NF was prepared and measured in a single run in the same day.

Both the Raman spectroscopy and SERS measurements were performed using a dispersive Thermo Scientific DXR Smart Raman spectrometer with a laser excitation wavelength of 780 nm and a spectral resolution of ∼5 cm⁻¹ in the range of 50–3300 cm⁻¹. Raman/SERS spectra were recorded in the 180° geometry, with a laser power of 86 mW/90 mW, and averaged from 10 scans with acquisition times of 5 s/10 s, respectively. All samples were measured in glass cuvettes.

The spectra were subjected to pre-processing procedures using OMNIC 9.2.86 software for further analysis. Raman spectra had a relatively simple background and thus the automatic baseline correction was applied. However, SERS spectra with a complex background in the 2200–1200 cm⁻¹ region required a different approach. They were transformed into their second derivatives by the Savitzky–Golay algorithm with a second-degree polynomial and a window of 11 points. This procedure allows for removing both additive and multiplicative background effects from the spectra,³⁷ while maintaining relevant spectral features and completely eliminating any user-related bias.

2.5 DFT calculations

Raman spectra were calculated using the Gaussian 16 suite of programs.³⁸ The geometry was optimized successively by the Hartree–Fock method with the 6-31G basis set and at the DFT level with the B3LYP hybrid functional combined with the 6-311++G(d,p) Pople basis set and tight/very tight convergence criteria. In the case of MPNPU attached to the gold layer through an Au–S bond, the gold shell was approximated by 3, 5, or 7 Au atoms – odd numbers were used to keep the system closed shell and the fragment electroneutral at the same time. For gold the MWB60 effective core potential was applied.³⁹ A superfine integration grid was employed in all DFT calculations. The DMSO and acetonitrile solvents were included via the polarizable continuum model (PCM), which utilizes the integral equation (IEFPCM), and continuous surface charge formalism, as implemented in Gaussian 16. No geometry restrictions, were applied.

Frequency calculations were performed at the same level of the theory as the structure optimization, and all frequencies were positive. Raman intensities were calculated by employing the harmonic approximation and an excitation wavelength of 780 nm. Smooth spectra were calculated from the line intensities using a temperature of 296 K for the Boltzmann correction and Lorentzian shapes with a full width at half maximum of 10 cm⁻¹. Raw calculated frequencies were used without scaling.

3. Results and discussion

3.1 Basic characterization of the nanoparticles and nanoshells

The powder XRD pattern of bare MZF particles (see Fig. S2 of the ESI†) confirmed the single-phase character of the sample and its spinel structure of the Fd3̄m space group. An analysis of the pattern by the Rietveld method provided the lattice parameter a = 8.4519(2) Å and the mean size of crystallites d_XRD = 10 nm, both of which are almost identical to the values determined for the Mn–Zn ferrite nanoparticles of the same composition in the original study,³² according to which the present sample was prepared. By assuming no deviation in the oxygen stoichiometry of the spinel phase, the chemical composition of the MZF particles was refined to Mn_0.63Zn_0.41Fe_1.96O₄ based on the XRF analysis.

The magnetic properties of hydrothermally prepared Mn_1−xZn_xFe₂O₄ nanoparticles, including the present composition, were discussed in detail in the previous report,³¹ and the magnetic data collected on the present sample of MZF nanoparticles are provided in the ESI (Fig. S3†). Briefly, their specific magnetization in a field of 3 T was M = 106 A m² kg⁻¹ at 5 K and 54.5 A m² kg⁻¹ at 300 K. At room temperature and at the timescale of DC magnetometry, the particles were mostly in the superparamagnetic regime, which was evidenced by the ZFC/FC curves (more specifically, by the distribution of blocking temperatures) and confirmed by an anhysteretic magnetization loop at 300 K.

The morphology and size of the MZF, MZF@sil, MZF@GNP, and MZF@sil@Au particles are illustrated in Fig. 1 by representative transmission electron micrographs. The magnetic cores of the silica-coated intermediate predominantly consist of small clusters with a mean size of ∼50 nm rather than of individually coated crystallites (see Fig. 1b). This has consequences for magnetic properties and applicability, e.g., as contrast agents for MRI or magnetic carriers for magnetically assisted separation. In a magnetic field (above a certain intensity threshold), the clusters show a larger magnetic moment than individual crystallites, whereby a higher transverse relaxivity of an MRI contrast agent could be achieved.⁴⁰ At the same time, the Néel relaxation time is not dramatically increased (the superparamagnetic behaviour is not impeded) by the increase in the energy barrier for magnetization reversal that will occur if ∼50 nm sized magnetic particles are used instead of the clusters.

Fig. 1 TEM images: (a) MZF, (b) MZF@sil, and (c) MZF@sil@GNP nanoparticles and (d) the final MZF@sil@Au nanoshells.

The image analysis of TEM micrographs and a fitting of the data by a lognormal distribution provided a mean diameter of 92(1) nm and a standard deviation of 12(1) nm for MZF@sil particles, and a mean diameter of 112(1) nm and a standard deviation of 13(1) nm for individual MZF@sil@Au nanoshells, disregarding their aggregation (see the histograms in Fig. 2a). The MZF@sil nanoparticles are characterized by a homogeneous silica shell with a smooth surface. The shell is about 21 nm thick and relatively uniform. Regarding the MZF@sil@GNP intermediate, small gold nanoparticles of a mean size of ∼3.6 nm are attached to the silica surface in a fairly high density, see Fig. 1c. During the growth phase, when a soluble Au(III) precursor was reduced with ascorbic acid, these gold nanoparticles grew and their coalescence led to the formation of continuous nanoshells. The resulting nanoshells (see Fig. 1d) are thus somewhat rough and porous compared to the smooth and homogeneous silica shells. The roughness of the gold nanoshell is beneficial as it provides a higher density of hot spots and a larger surface area for functionalization by the Au–S bonds. The formation of gold nanoshells via the gradual growth of gold seeds is documented by the TEM images of the supplemental MZF@sil@Au-x (x = I, II, III, IV) samples in Fig. S4 of the ESI.† The MZF@sil@Au-I sample is formed by silica-coated ferrite particles decorated with enlarged gold seeds rather than by gold nanoshells. The next sample, MZF@sil@Au-II, is a transition to highly porous and highly coarse nanoshells in MZF@sil@Au-III, whereas the last sample MZF@sil@Au-IV is comparable with the main product MZF@sil@Au.

Fig. 2 Size distribution of the particles: (a) histograms based on the image analysis of TEM data, fitted with lognormal distribution and (b) intensity-weighted distribution of hydrodynamic sizes obtained from DLS.

According to the DLS measurements of dilute aqueous suspensions, the hydrodynamic sizes of MZF@sil, MZF@sil@GNP and MZF@sil@Au were d_Z = 144 nm (pdi = 0.08), 522 nm (pdi = 0.17) and 221 nm (pdi = 0.20), respectively. An intensity-weighted distribution of hydrodynamic sizes is depicted for each sample in Fig. 2b. The results suggest that the preparation of the gold-seeded intermediate was accompanied by agglomeration, partially suppressed during the growth of gold nanoshells under ultrasound agitation. The zeta potential measurement of an aqueous suspension of nanoshells functionalized with MPNPU and NTP showed a negative value of ζ = −40 mV at pH = 7.0, indicating a strong coulombic repulsion, which hinders agglomeration and increases the colloidal stability in water and similar polar solvents.

The multistep synthesis of gold nanoshells was monitored by UV-vis spectroscopy; the spectra of the intermediates and the final product are shown in Fig. 3. Since GNP nanoparticles are very small (∼3.6 nm), the SPR absorption is significantly damped and manifests as a broad shoulder at ∼520 nm. The surface damping mechanism was ascribed to the inelastic scattering of electrons and small sizes of the particles.^41,42 The same feature is observed in the spectrum of MZF@sil@GNP nanoparticles. In contrast, the SPR band of gold nanoshells is red-shifted and very broad, forming a plateau that starts at ∼750 nm and continues to the NIR region. The position of the SPR band of gold nanoshells should be given by the inner diameter and the nanoshell thickness, e.g., ∼40 nm gold nanoshells deposited on a ∼30 nm silica core exhibit a SPR band at λ = 650 nm.⁴³ Nevertheless, such a correlation may not apply to the present case because of the broad plateau. The width of the band of gold nanoshells originates not only in the radiation damping of the collective electron excitation,⁴¹ but also in the size distribution of nanoshells and the size distribution of gold crystallites forming these nanoshells, and could be further increased by their aggregation. Note that the nanoshells were not subjected to any size/mass fractionation, to maintain even aggregated gold nanoshells in the sample that would provide additional hot spots for SERS.

Fig. 3 UV-vis absorption spectra of dilute aqueous suspensions of gold nanostructures, including the final gold nanoshells, and the UV-vis absorption spectrum of the suspension of initial MZF@sil nanoparticles.

The successful synthesis of MNPU and the presence of its molecules on the surface of model gold particles was evidenced by APCI-MS analysis. The spectrum revealed the molecular ion [M − H]⁻ as the most intense peak at m/z = 288.04449 (mass error of 1.22 ppm, Fig. S5†).

3.2 Raman spectroscopy and DFT calculations

The interaction of the urea-based sensors with fluoride anions was studied in aprotic solvents to avoid the competition of other hydrogen-bonding molecules. Acetonitrile was preferred as the suspensions of gold nanoshells were reasonably stable in this solvent. Also, most of the acetonitrile Raman-active vibrations do not overlap with the bands of the MPNPU sensor. Only in model experiments with the BrPNPU sensor was DMSO used, in which the compound is more soluble.

3.2.1 Raman spectrum of BrPNPU. The experimental spectrum of the 0.1 M BrPNPU solution in DMSO and the spectra calculated for BrPNPU in the gas phase and in DMSO described by the PCM are shown in Fig. 4 within 1810–720 cm⁻¹. The full range is provided in Fig. S6,† and the assignment of the Raman bands of BrPNPU is summarized in Table 1. We can see that the PCM, compared to the vacuum computation, corresponds better to the experiment for most of the theoretical frequencies, such as for C=O stretching (vac. 1772/PCM 1730/exp. 1717 cm⁻¹) or C=C stretching (1640/1627/1506 cm⁻¹). Only the shape of the strongest bands at around 1332 cm⁻¹ in the experimental spectrum, coming mostly from the aromatic ring vibrations, is somewhat better reproduced by the vacuum model.

Fig. 4 Raman spectra of BrPNPU: (a) experimental spectrum in DMSO supplemented by the spectrum of the solvent, both normalized to unity at the maximum of the DMSO band at 669 cm⁻¹ and (b) calculated spectra in the gas phase and in DMSO.

Table 1 Selected Raman bands of BrPNPU and MPNPU and their assignment (description based on gas-phase spectra). For BrPNPU, the following parameters are given: experimental Raman shifts in DMSO, ν_exp, Raman shifts calculated in the gas phase, ν_calc. (gas), and in DMSO described by the PCM approximation, ν_calc. (DMSO), together with respective Raman scattering activities, I_νcalc. (gas) and I_νcalc. (DMSO). The modes calculated for BrPNPU are compared to analogical modes calculated for the MPNPU molecule bonded to an Au₇ cluster (see sect. 3.2.3), again in the gas phase and in acetonitrile modelled with the PCM. Ring 1 denotes the phenyl ring bearing the nitro group, whereas the one carrying Br/S is denoted as ring 2

(A) BrPNPU					(B) MPNPU				Assignment
ν exp (DMSO) [cm^−1]	ν calc. (gas) [cm^−1]	I ν calc. (gas) [Å^4 amu^−1]	ν calc. (DMSO) [cm^−1]	I ν calc. (DMSO) [Å^4 amu^−1]	ν calc. (gas) [cm^−1]	I ν calc. (gas) [Å^4 amu^−1]	ν calc. (MeCN) [cm^−1]	I ν calc. (MeCN) [Å^4 amu^−1]
856	869	45	867	194	870	85	867	334	NO2 sciss. + N–C stretch and ring out-of-phase breath.
897	908	99	908	256	909	147	908	396	NCN sciss. + ring in-phase breath.
1008	1020, 1025	75, 64	1014, 1020	260, 129	1024, 1025	384, 69	1023, 1019	693, 204	Ring 2, 1 trigonal deform.
1075	1088	126	1083	288	1098	2225	1096	4235	Br(S)–C stretch. and ring 2 semicircle stretch.
1111	1123	671	1118	3343	1123	957	1118	4577	Ring 1 C–NO2 stretch.
1120sh	1139, 1142	16, 34	1140, 1142	11, 61	1140, 1145	518, 202	1140, 1143	190, 242	Ring C–H out-of-phase sciss.
1178	1206	282	1204	984	1209	859	1205	2995	Ring C–H in-phase sciss.
1268	1284	752	1288	3726	1283	1377	1286	6771	OCN2 sym. stretch. + ring 1 distort. + ring 2 Kekulé vibr.
			1318	6481			1317	5365	NO2 sym. stretch. + ring 1 C–H rock
1306	1327	292	1333	2400	1327	513	1333	4675	Ring 1 C–H rock
1311	1334	234	1325	2441	1337	598	1321	11 153	Ring 2 C–H rock
1332	1356	2599			1356	4163			Ring 1 Kekulé vibr. + ring 1 C–N sym. stretch.
			1338	4675			1338	8479	Ring 2 Kekulé vibr. + ring 2 C–N stretch.
1333	1367	732	1369	148	1367	1051	1369	469	Ring 1 Kekulé vibr. + ring 1 C–N antisym. stretch.
1511w(?)	1548	14	1554	1187	1545	584	1546	1695	C-N2 asym. stretch. + N-O2 asym. stretch.
1596	1632, 1640	1113, 2138			1634, 1640	7294, 3793			Ring 2, 1 C–C stretch.
			1624, 1638	1182, 1643			1620, 1638	1080, 1754	Ring 2, 1 C–C stretch.
			1627	3856			1629	19 389	Ring C–C stretch.
1717	1772	517	1730	1369	1772	996	1730	2820	C=O stretch.
	3608	22	3598	229	3607	7	3607	165	N–H stretch. – antisym.
	3623	541	3610	1119	3622	1049	3610	2144	N–H stretch. – sym.

---

As an alternative model, an additional spectrum was calculated for a complex of BrPNPU and DMSO (1 : 1), with the DMSO molecule attached to the urea moiety via the O⋯H–N bonds (see Fig. S7 in the ESI†), while the PCM with DMSO was also used. This, however, did not bring significant change. The explicit inclusion of the DMSO molecule resulted in a blue shift of several Raman bands compared to the BrPNPU spectrum calculated with DMSO included solely via the PCM. The band at 1730 cm⁻¹ shifted to 1743 cm⁻¹ (C=O stretching), from 1638 to 1648 cm⁻¹ (ring C–C stretching accompanied by N–C–N asym. stretching with H rocking), from 1338 to 1341 cm⁻¹ (ring Kekulé vibrations connected with C–N–C stretching), and from 1288 to 1300 cm⁻¹ (OCN₂ sym. stretching with H scissoring). In contrast, the N–H symmetrical and antisymmetrical stretching modes at 3610 and 3598 cm⁻¹ were red-shifted to 3373 and 3339 cm⁻¹, respectively, due to the elongation of the N–H bonds.

3.2.2 Interaction of BrPNPU with Bu₄NF. The effect of fluoride anions on the Raman spectra of the model sensor was investigated with a series of solutions where the molar ratio of BrPNPU and Bu₄NF varied from 1 : 0.1 to 1 : 20, see Fig. 5. In the figure, the Raman spectra of pure DMSO and Bu₄NF in DMSO are plotted as well. Clearly, dramatic changes occur in the mixture, and the resultant curves are not explicable as sums of individual components. We attribute the observed changes to an interaction of BrPNPU with the fluoride anions.

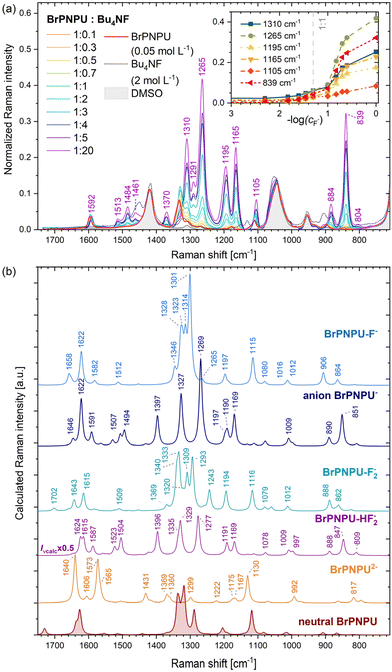Fig. 5 (a) Raman spectra of BrPNPU (0.05 mol L⁻¹) in the presence of Bu₄NF (0.005–1 mol L⁻¹) in DMSO, supplemented by the spectra of pure DMSO and Bu₄NF (2 mol L⁻¹) in DMSO. The spectra were normalized to the DMSO band at 669 cm⁻¹. The inset shows the dependence of the normalized intensities of selected Raman bands on the concentration of Bu₄NF. (b) Calculated spectra of some species (see Fig. 6) that might be, in principle, formed upon the interaction of BrPNPU with fluoride anions.

According to the mechanism described in the Introduction section, the fluoride anion forms a complex with BrPNPU, and further addition of fluoride anions leads to deprotonation of one of the urea –NH groups and the formation of the [HF₂]⁻ anion (Scheme 1). To support this interpretation, Raman spectra of various complexes and BrPNPU anionic forms were calculated (Fig. 5b) including (i) the neutral BrPNPU bonded to the fluoride anion (BrPNPU-F⁻), (ii) the BrPNPU⁻ monoanion, (iii) the neutral BrPNPU with two hydrogen-bonded fluoride anions (BrPNPU-F₂²⁻), (iv) BrPNPU with the hydrogen-bonded [HF₂]⁻ anion (BrPNPU-HF₂⁻), and (v) the doubly deprotonated molecule BrPNPU²⁻ (Fig. 6). The presence of a hydrogen-bonded complex of the fluoride anion and two BrPNPU molecules cannot be excluded at very low concentrations of Bu₄NF,⁴⁴ but it was not considered in the present study.

Fig. 6 Optimized geometries of various species possibly formed during the interaction of BrPNPU with fluoride anions. The DMSO solvent was approximated by the PCM; calculated bond lengths in Å are indicated for BrPNPU and BrPNPU⁻ (C atoms – grey, H – white, N – blue, O – red, Br – wine, and F – turquoise; non-planar species (bottom) are shown in two different orientations).

The complexation leads to geometry changes in the sensor molecule, enhanced by the electron conjugation (Fig. 6, see also ref. 25). In the BrPNPU-F⁻ complex, the calculated H_a⋯F and H_a′⋯F distances are 1.685 Å and 1.622 Å, respectively. A shorter distance and thus a stronger N–H⋯F hydrogen bond are formed by the amino group substituted with p-nitrophenyl, which induces higher polarization of the N–H bond than the p-mercaptophenyl group. In most structures, BrPNPU has a planar geometry; however, in BrPNPU²⁻ and BrPNPU-F₂²⁻, the angles between the planes defined by the two phenyl rings are 87.14° and 54.21°, respectively.

The comparison of the experimental and calculated spectra (Fig. 5) suggests the formation of the BrPNPU⁻ anion upon the addition of Bu₄NF. This species is manifested in the spectra already at low concentrations of Bu₄NF (∼0.7 eq.); Raman bands attributed to BrPNPU⁻ appear in the 1530–1440 cm⁻¹ region (ν_calc. ≈ 1550–1460 cm⁻¹) and at 1370 cm⁻¹ (ν_calc. ≈ 1397 cm⁻¹), and the finding is consistent with the two equilibria introduced in Scheme 1. The presence of the sensor with hydrogen-bonded fluoride anions can be deduced from the band at 1291 cm⁻¹ (ν_calc. ≈ 1301 cm⁻¹, ring 2 Kekulé vibr. + ring 1 C–N stretching accompanied by H scissoring at the urea subunit) and from the red shift and an increased intensity of the band corresponding to C–NO₂ stretching at 1105 cm⁻¹ (ν_calc. ≈ 1115 cm⁻¹, in the neutral molecule at ν_exp ≈ 1111 cm⁻¹). The signal of neutral BrPNPU vanishes at about 5 eq. of Bu₄NF, due to the formation of the anion. The calculated spectrum of BrPNPU⁻ complexed with [HF₂]⁻ is very similar to that of BrPNPU⁻; the experimental shape corresponds slightly better to BrPNPU⁻. This suggests that [HF₂]⁻ is dissociated from the deprotonated urea.

Compared to BrPNPU, the calculated symmetrical and antisymmetrical N–H stretching vibrations in the BrPNPU-F⁻ complex (3095 and 2925 cm⁻¹) were much smaller (by 515 and 673 cm⁻¹), due to the elongation of N–H bonds involved in the hydrogen bonding (from 1.010 Å to 1.047 and 1.039 Å for N–H_a′ and N–H_a, respectively). The calculated shift roughly follows the observed empirical relationship between the frequency of the stretching vibration of the hydrogen donating group and the hydrogen bond length,⁴⁵ predicting a shift of ∼644 cm⁻¹ for the average H⋯F⁻ bond length. Nevertheless, these bands were not assigned in the experimental spectra due to their overlap with the DMSO bands within 3050–2790 cm⁻¹.

3.2.3 SERS study on functionalized nanoshells and the interaction of MPNPU with fluoride anions. SERS spectra of gold nanoshells functionalized with both MPNPU and NTP as well as with individual compounds were measured (Fig. S8–S11†). The raw spectra contained a variable background (Fig. 7a and, e.g., Fig. S11†), and their second derivatives (Fig. 7b and, e.g., Fig. S11†) appeared more convenient for an analysis of the dependence on fluoride concentration, c_F−. To account for a non-reproducible magnitude of SERS in a suspension of gold nanostructures, the second derivatives were normalized to unity at a local minimum that corresponded to the Raman band of the NTP internal standard at 854 cm⁻¹.

Fig. 7 A series of (a) SERS spectra and (b) their normalized second derivatives for MZF@sil@Au nanoshells functionalized with both MPNPU and NTP and measured in acetonitrile with varying concentration of Bu₄NF (the concentration of nanoshells is 8.3 mg (MZF) L⁻¹). Raman shifts given in (a) refer to the spectrum with the lowest concentration of Bu₄NF, and the arrows highlight the Raman bands that arise due to the deprotonation of MPNPU molecules. Normalization of the 2^nd derivatives was carried out by dividing them by the absolute value of the 2^nd derivative at 854 cm⁻¹, where a Raman band of NTP appears.

For selected Raman bands of the MPNPU sensor, the dependence of the normalized intensities at a fixed Raman shift on the analytical concentration of Bu₄NF in a logarithmic scale is depicted in Fig. 8. Clear changes in the experimental spectra can be observed in the presence of fluoride anions at concentrations of c_F− ≥ 5 × 10⁻⁵ mol L⁻¹. In the concentration range of 5 × 10⁻⁵ mol L⁻¹ ≤ c_F− ≤ 10⁻² mol L⁻¹, the linear regression of the normalized second derivative of intensity at 1341 cm⁻¹ in dependence on −log(c_F−) provides a slope of −22.5 and is characterized by a coefficient of determination R² = 0.99.

Fig. 8 The dependence of intensities in the second derivatives at selected Raman shifts on the concentration of Bu₄NF, normalized to the internal standard, i.e., divided by the absolute value of the second derivative at 854 cm⁻¹. The points are arithmetic means based on six (c_F− ≥ 5 × 10⁻⁷ mmol L⁻¹) or three (c_F− < 5 × 10⁻⁷ mmol L⁻¹) independent experiments, the error bars show the standard error of the mean, and the highlighted zones indicate a 95% confidence interval. The connecting lines between individual points are only meant to guide the eye.

The acetonitrile solvent contributes to the measured spectra by intense lines at 2943 cm⁻¹ (CH₃ sym. stretch.), 2253 cm⁻¹ (C≡N stretch.), 920 cm⁻¹ (C–C stretch.) and 380 cm⁻¹ (C–C≡N bend.).⁴⁶ The internal standard NTP has a large Raman cross-section in general, and possesses an intense band at 1343 cm⁻¹ (NO₂ sym. stretch.) and less intense ones at 1572 cm⁻¹ (C–C ring stretch.), 1110 cm⁻¹ (C–H bend.), 1082 cm⁻¹ (C–H bend.) and 854 cm⁻¹ (C–H wag.),⁴⁷ see also Fig. S8 and S9 in the ESI.†

SERS measurements on the supplemental series of MZF@sil@Au-x samples functionalized with NTP showed that an increasing relative content of gold per mass of ferrite cores leads to a higher SERS intensity (see Fig. S12†), which reflects the growing area of the gold surface and the increasing density of hot spots. SERS spectra with well-developed NTP bands, including peaks of lower intensity, were recorded for all MZF@sil@Au-x samples except for MZF@sil@Au-I, containing predominantly isolated gold nanoparticles on the silica surface. The principal features of the SERS spectrum (the presence of bands and the overall shape) of NTP are not significantly affected by the relative content of gold once more or less continuous nanoshells are achieved.

In the DFT calculations of the spectra of various species containing the MPNPU moiety, the gold surface was modelled by clusters of Au₃, Au₅, and Au₇. As the number of gold atoms increased, the cluster tended to form a platelet. Similarly to the observation of Zhao et al.,⁴⁸ only one Au–S bond was formed in the optimized geometry of MPNPU-Au₃, whereas lower energy was achieved if the S atom was bridging two Au atoms in the case of the Au₅ and Au₇ clusters (see Fig. 9). In contrast to the completely planar BrPNPU, the planes defined by the two phenyl rings of MPNPU formed an angle of 4° in the optimized geometry.

Fig. 9 Optimized geometries in acetonitrile of the MPNPU molecule bonded to gold clusters of varying size: (a) Au₃, (b) Au₅, and (c) Au₇. The angles between the plane of the urea moiety and the plane through S and Au atoms (coplanar arrangement) are 78°, 81° and 85°, respectively (S – orange and Au – yellow).

The calculated Raman shapes, either in the gas phase or in acetonitrile approximated by the PCM, did not differ much from the calculated spectra of free BrPNPU (see Table 1 and Fig. S13†), but some intensity enhancement due to the gold atoms is apparent. Two bands were significantly enhanced in the MPNPU spectrum compared to BrPNPU, namely the band at 1629 cm⁻¹ (in acetonitrile) corresponding predominantly to the ring C–C stretching, and the Au–S bond stretching at 1096 cm⁻¹ (in acetonitrile, 1098 cm⁻¹ in the gas phase, with lower intensity). The calculated intensity of the bands decreased rapidly upon increasing the size of the gold cluster from 3 to 5 atoms and then only mildly to the Au₇ cluster, although the intensity remained higher than in the case of BrPNPU (see Fig. S14†). The calculated shifts discussed below refer to results based on the Au₅ cluster, if not stated otherwise.

The Raman spectra of the two most probable species that may result from the interaction of MPNPU with fluoride anions, namely the supramolecular complex of MPNPU-F⁻ and the deprotonated urea MPNPU⁻, were recorded with different sizes of the gold cluster using the PCM approximation of acetonitrile. In Fig. 10, the calculated spectra are compared to the experimental spectra of the MZF@sil@Au nanoshells functionalized with MPNPU, and to those from the series of suspensions with varying concentrations of Bu₄NF at the two limits. In general, the calculated Raman intensity decreased slightly with the increasing size of the gold cluster, except for the constant intensity of the band at 850 cm⁻¹ related to the vibration of the nitro group (NO₂ sciss. + N–C stretch, ring 1 breath.), see Fig. S15 of the ESI.†

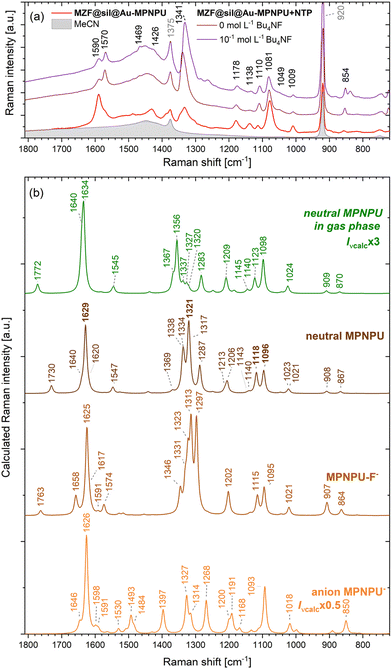Fig. 10 Comparison of selected experimental SERS and calculated Raman spectra. (a) Experimental SERS spectra measured for gold nanoshells functionalized with both MPNPU and NTP in acetonitrile suspension with two different concentrations of Bu₄NF and the spectrum measured for nanoshells functionalized only with MPNPU. (b) Calculated Raman spectra of the MPNPU compound in the gas phase and in acetonitrile modelled by the PCM, followed by the calculated Raman spectra of the supramolecular complex of MPNPU-F⁻ and the deprotonated urea MPNPU⁻ in acetonitrile. In the spectra, the gold surface was approximated with a cluster of five Au atoms (i.e., a difference of up to 2 cm⁻¹ can occur for the neutral MPNPU at some bands compared to Table 1).

For the SERS sensing of fluoride ions, the fingerprint peaks selected for Fig. 8 are the most important ones. The largest effect of fluoride ions on the intensity is observed for the most intense peak at 1341 cm⁻¹, which contains contributions of both the MPNPU and the NTP bands. The contribution of MPNPU occurs at a slightly lower Raman shift (∼1332 cm⁻¹, see Fig. S9 of the ESI†) and is largely (but not exclusively) formed by the vibration mode with a calculated Raman shift of ν_calc. = 1321 cm⁻¹ in acetonitrile (C–NO₂ stretching with in-phase hydrogen rocking at the rings and urea moiety). However, the range of 1350–1250 cm⁻¹ also contains the C–NO₂ stretching and vibrations of both rings and urea with pronounced hydrogen rocking. These modes are significantly affected by the complexation of a fluoride anion through hydrogen bonds and they probably contribute to the discussed peak as well. The decreasing intensity at a fixed Raman shift of 1341 cm⁻¹ is caused by the gradual red shift of the original peak, which points to the formation of the sensor–F⁻ complex. The overall experimental red shift amounts to ∼6 cm⁻¹ upon increasing the fluoride concentration to 10⁻¹ mol L⁻¹. This can be explained by increasing intensity of a contributing mode/modes at lower Raman shifts. At the same time, shifting of other modes that originally did not contribute to the discussed peak at 1341 cm⁻¹ should be considered as well, e.g., the MPNPU mode calculated at ν_calc. = 1287 cm⁻¹ (at ∼1303 cm⁻¹ in the measured spectrum; C-NO₂ stretching with ring 1 quinoidal and ring 2 Kekulé vibrations) is blue-shifted by 10 cm⁻¹ in the calculated spectrum of the MPNPU-F⁻ complex (see Fig. 10b).

The second most pronounced change in the Raman intensity occurs at 1081 cm⁻¹. This peak also consists of the bands of both MPNPU and NTP, but clearly with a dominant contribution of MPNPU. It originates in the C–S stretching accompanied by the deformation of ring 2 (ν_calc. = 1096 and 1095 cm⁻¹ in the neutral MPNPU molecule and in the MPNPU-F⁻ complex). The other bands at 1590, 1178 and 1110 cm⁻¹ with lower intensities change less, but the intensity of their second derivatives also slightly varies between the concentrations of Bu₄NF below 5 × 10⁻⁵ mol L⁻¹ and 10⁻¹ mol L⁻¹. The peak at 1590 cm⁻¹ contains a large contribution of the MPNPU band (ν_calc. = 1629 and 1625 cm⁻¹ in MPNPU and MPNPU-F⁻), which combines the urea C=O stretching and ring 2 deformations. The band at 1178 cm⁻¹ (ν_calc. = 1191 and 1187 cm⁻¹ in MPNPU and MPNPU-F⁻) is dominated by the asymmetric stretching of the N–C bonds in the urea subunit, whereas the one at 1114 cm⁻¹ (ν_calc. = 1118 and 1115 cm⁻¹ in MPNPU and MPNPU-F⁻) contributing to the band observed at 1110 cm⁻¹ is determined by the C–NO₂ stretching. The variation in the intensity of these bands may originate in the modification of the local orientation of the MPNPU-F⁻ complex with respect to the gold surface. The discussed calculated vibration modes are depicted in Fig. 11. The NH stretching vibrations of MPNPU-F⁻ were not identified in the second derivatives due to their low intensity/possible overlap with the acetonitrile bands in the range of 3050–2830 cm⁻¹ shifts.

Fig. 11 Selected vibrations of MPNPU discussed in the text; ν_g and ν_ac denote the calculated Raman shifts in the gas phase and in acetonitrile (depicted) approximated by the PCM.

Only at the highest concentration of Bu₄NF do the first signs of urea deprotonation emerge, namely the bands at 1265 cm⁻¹ (ν_calc. = 1268 cm⁻¹, C–NO₂ stretching with ring vibrations and N–H bending of the urea moiety) and 835 cm⁻¹ (ν_calc. = 850 cm⁻¹, in-plane scissoring of NO₂ with in-phase breathing of ring 1 and weaker out-of-phase breathing of ring 2). In general, the spectral responses of the free BrPNPU and the attached MPNPU sensors to the presence of fluoride anions are consistent. Smaller changes observed for MPNPU can be in part ascribed to the lower polarity of acetonitrile compared to DMSO. The lower polarity of the solvent leads to higher stability of the sensor–F⁻ complex in acetonitrile, thus leading to deprotonation of the receptor at a higher fluoride concentration.²⁶

4. Conclusion

This study demonstrated the feasibility of sensing of fluoride ions in aprotic solvents by means of SERS measurements with gold nanoshells functionalized with a urea-based molecular sensor, namely N-(4-mercaptophenyl)-N′-(4-nitrophenyl)urea. Model experiments in solution, employing an analogical sensor without gold nanoshells, indicated the consecutive formation of two urea-based species: the supramolecular complex of the sensor with the fluoride anion and the monodeprotonated sensor, which is due to the formation of [HF₂]⁻ species. The SERS spectra of the sensor attached to the gold surface manifested less distinct changes than the model molecule in solution, but the data suggested the formation of an analogical supramolecular complex and eventually signs of the deprotonation at a higher fluoride concentration. In principle, certain peaks in the SERS spectrum responding to the fluoride concentration could be used, after a careful calibration and analysis of the statistics, for quantitative analysis of fluorides in aprotic solvents. Importantly, such an analysis requires: (i) an internal standard attached to the gold surface that does not interact with the analyte and (ii) evaluation of the second derivatives of the spectra to resolve the complex background.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

The authors would like to thank Bohumil Dolenský for NMR measurements and Josef Chudoba for the MS analysis. This work was supported by the Czech Science Foundation, project no. 19-02584S. P. B. and J. K would like to acknowledge also the project no. 22-04669S. The experimental infrastructure of the Institute of Physics was funded within the Operational Program Research, Development and Education financed by the European Structural and Investment Funds and by the Czech Ministry of Education, Youth and Sports (MŠMT), project no. CZ.02.1.01/0.0/0.0/16_019/0000760 (SOLID21). The magnetic data were collected in MGML (mgml.eu), which is funded by MŠMT under the project no. LM2018096 (Czech Research Infrastructures).

References

1. E. C. Le Ru, E. Blackie, M. Meyer and P. G. Etchegoin, J. Phys. Chem., 2007, 111, 13794–13803.
2. K. Kneipp, Y. Wang, H. Kneipp, L. T. Perelman, I. Itzkan, R. Dasari and M. S. Feld, Phys. Rev. Lett., 1997, 78, 1667.
3. Y. X. Qiu, C. F. Kuang, X. Liu and L. H. Tang, Sensors, 2022, 22, 4889.
4. G. Q. Wallace and D. Graham, Nat. Rev. Chem., 2022, 6, 842.
5. X. Wang, S. C. Huang, S. Hu, S. Yan and B. Ren, Nat. Rev. Phys., 2020, 2, 253.
6. Y. Ying, Z. Y. Tang and Y. L. Liu, Nanoscale, 2023, 15, 10860.
7. H. S. Zhou, I. Honma, H. Komiyama and J. W. Haus, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 12052.
8. S. J. Oldenburg, R. D. Averitt, S. L. Westcott and N. J. Halas, Chem. Phys. Lett., 1998, 288, 243.
9. Y.-C. Wang, É. Rhéaume, F. Lesage and A. Kakkar, Molecules, 2018, 23, 2851.
10. T. H. Park, D. W. Jeong, J. H. Lee and D. J. Jang, Nanotechnology, 2022, 33, 155605.
11. D. T. Bui, R. Havelek, K. Královec, L. Kubíčková, J. Kuličková, P. Matouš, V. Herynek, J. Kupčík, D. Muthná, P. Řezanka and O. Kaman, Nanomaterials, 2022, 12, 428.
12. P. C. Xu, R. Wang, W. Q. Yang, Y. Y. Liu, D. S. He, Z. X. Ye, D. Q. Chen, Y. Ding, J. S. Tu and Y. Shen, J. Nanobiotechnol., 2021, 19, 77.
13. P. Manivasagan, V. T. Nguyen, S. W. Jun, G. Hoang, S. Mondal, H. Kim, V. H. M. Doan, J. Kim, C. S. Kim and J. Oh, J. Controlled Release, 2019, 311, 26.
14. Q. Dong, H. Yang, C. F. Wan, D. D. Zheng, Z. G. Zhou, S. W. Xie, L. Xu, J. Du and F. H. Li, Nanoscale Res. Lett., 2019, 14, 235.
15. T. Bertok, L. Lorencova, S. Hroncekova, V. Gajdosova, E. Jane, M. Hires, P. Kasak, O. Kaman, R. Sokol, V. Bella, A. A. Eckstein, J. Mosnacek, A. Vikartovska and J. Tkac, Biosens. Bioelectron., 2019, 131, 24.
16. M. Muhammad and Q. Huang, Talanta, 2021, 227, 122188.
17. V. Nocerino, B. Miranda, C. Tramontano, G. Chianese, P. Dardano, I. Rea and L. De Stefano, Chemosensors, 2022, 10, 150.
18. V. M. Zamarion, R. A. Timm, K. Araki and H. E. Toma, Inorg. Chem., 2008, 47, 2934.
19. P. J. Smith, M. V. Reddington and C. S. Wilcox, Tetrahedron Lett., 1992, 33, 6085.
20. P. J. Smith, M. V. Reddington and C. S. Wilcox, Abstr. Pap. Am. Chem. Soc., 1992, 204, 398.
21. E. Fan, S. A. Vanarman, S. Kincaid and A. D. Hamilton, J. Am. Chem. Soc., 1993, 115, 369.
22. S. Kundu, T. K. Egboluche and M. A. Hossain, Acc. Chem. Res., 2023, 56, 1320.
23. A. F. Li, J. H. Wang, F. Wang and Y. B. Jiang, Chem. Soc. Rev., 2010, 39, 3729.
24. V. B. Bregović, N. Basarić and K. Mlinarić-Majerski, Coord. Chem. Rev., 2015, 295, 80.
25. M. Boiocchi, L. Del Boca, D. E. Gomez, L. Fabbrizzi, M. Licchelli and E. Monzani, J. Am. Chem. Soc., 2004, 126, 16507.
26. V. Amendola, D. Esteban-Gomez, L. Fabbrizzi and M. Licchelli, Acc. Chem. Res., 2006, 39, 343.
27. U. Manna, G. Das and M. A. Hossain, Coord. Chem. Rev., 2022, 454, 214357.
28. D. Udhayakumari, Spectrochim. Acta, Part A, 2020, 228, 117817.
29. G. Decher, Science, 1997, 277, 1232.
30. O. Kaman, J. Kuličková, M. Maryško, P. Veverka, V. Herynek, R. Havelek, K. Královec, D. Kubániová, J. Kohout, P. Dvořák and Z. Jirák, IEEE Trans. Magn., 2017, 53, 5300908.
31. O. Kaman, D. Kubániová, K. Knížek, L. Kubíčková, M. Klementová, J. Kohout and Z. Jirák, J. Alloys Compd., 2021, 888, 161471.
32. O. Kaman, J. Kuličková, V. Herynek, J. Koktan, M. Maryško, T. Dědourková, K. Knížek and Z. Jirák, J. Magn. Magn. Mater., 2017, 427, 251.
33. O. Kaman, T. Dědourková, J. Koktan, J. Kuličková, M. Maryško, P. Veverka, R. Havelek, K. Královec, K. Turnovcová, P. Jendelová, A. Schröfel and L. Svoboda, J. Nanopart. Res., 2016, 18, 100.
34. C. Graf, D. L. J. Vossen, A. Imhof and A. van Blaaderen, Langmuir, 2003, 19, 6693.
35. J. Koktan, K. Královec, R. Havelek, J. Kuličková, P. Řezanka and O. Kaman, Colloids Surf., A, 2017, 520, 922.
36. D. G. Duff, A. Baiker and P. P. Edwards, Langmuir, 1993, 9, 2301.
37. Å. Rinnan, F. van den Berg and S. B. Engelsen, TrAC, Trends Anal. Chem., 2009, 28, 1201.
38. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, et al., Gaussian 16 Rev. A.03, 2016.
39. M. Dolg, U. Wedig, H. Stoll and H. Preuss, J. Chem. Phys., 1987, 86, 866.
40. T. Dědourková, O. Kaman, P. Veverka, J. Koktan, M. Veverka, J. Kuličková, Z. Jirák and V. Herynek, IEEE Trans. Magn., 2015, 51, 5300804.
41. S. Berciaud, L. Cognet, P. Tamarat and B. Lounis, Nano Lett., 2005, 5, 515.
42. S. Link and M. A. El-Sayed, Int. Rev. Phys. Chem., 2000, 19, 409.
43. L. R. Hirsch, A. M. Gobin, A. R. Lowery, F. Tam, R. A. Drezek, N. J. Halas and J. L. West, Ann. Biomed. Eng., 2006, 34, 15.
44. L. Pfeifer, K. M. Engle, G. W. Pidgeon, H. A. Sparkes, A. L. Thompson, J. M. Brown and V. Gouverneur, J. Am. Chem. Soc., 2016, 138, 13314.
45. M. Rozenberg, A. Loewenschuss and Y. Marcus, Phys. Chem. Chem. Phys., 2000, 2, 2699.
46. T. Shimanouchi, Tables of molecular vibrational frequencies, consolidated vol. I, National Bureau of Standards, 1972.
47. B. O. Skadtchenko and R. Aroca, Spectrochim. Acta, Part A, 2001, 57, 1009.
48. Y. Zhao, F. Zhou, H. Zhou and H. Su, Phys. Chem. Chem. Phys., 2013, 15, 1690.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3an00625e

---